Measurement Method for Fluid Pressure Fluctuation in Fluid-Conveying Pipe Using PVDF Piezoelectric Film Sensor
Abstract
:1. Introduction
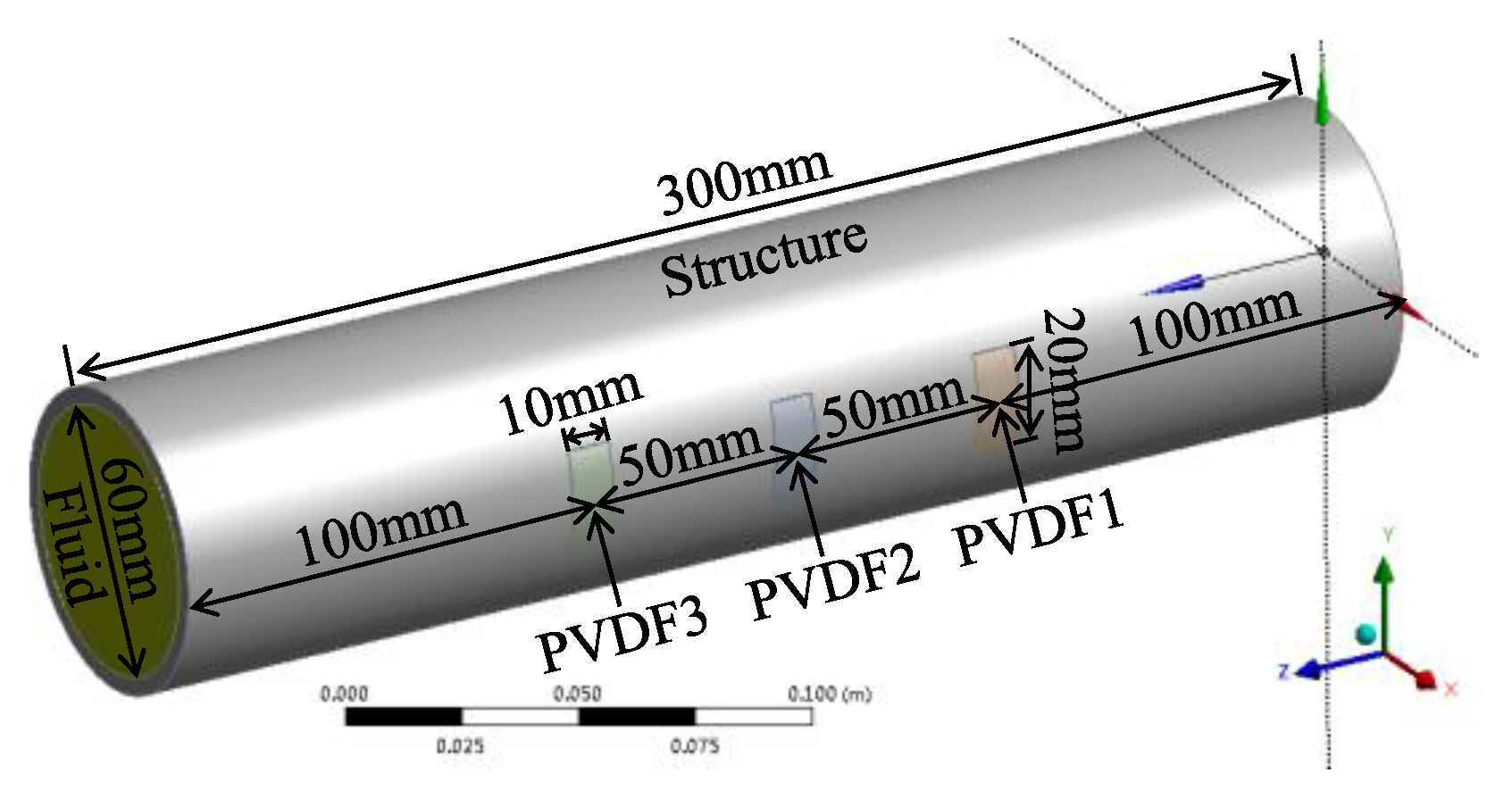
2. Modeling a Fluid-Conveying Pipe with PVDF Piezoelectric Film Sensor
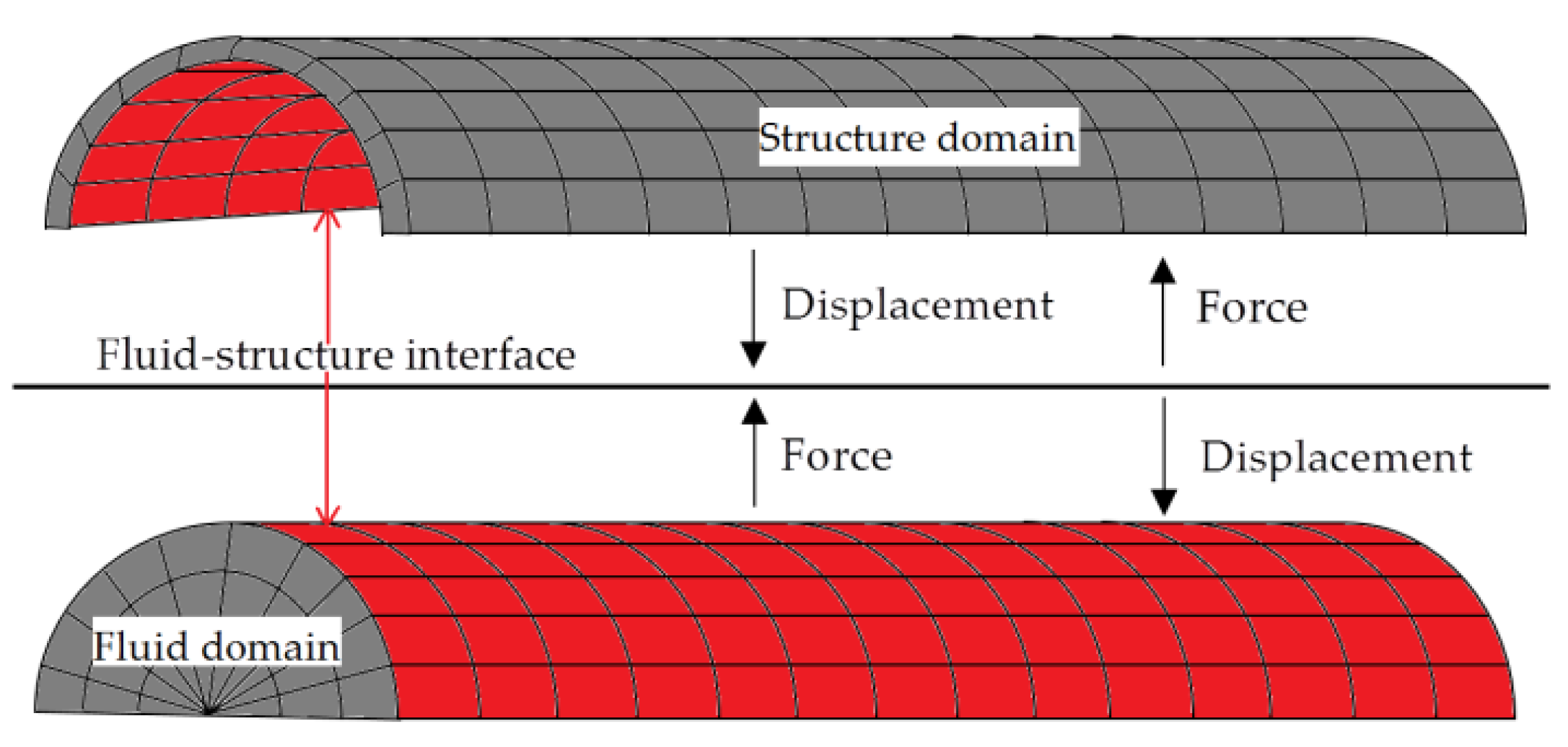
2.1. Fluid–Structure Interaction
2.2. Electromechanical Coupling
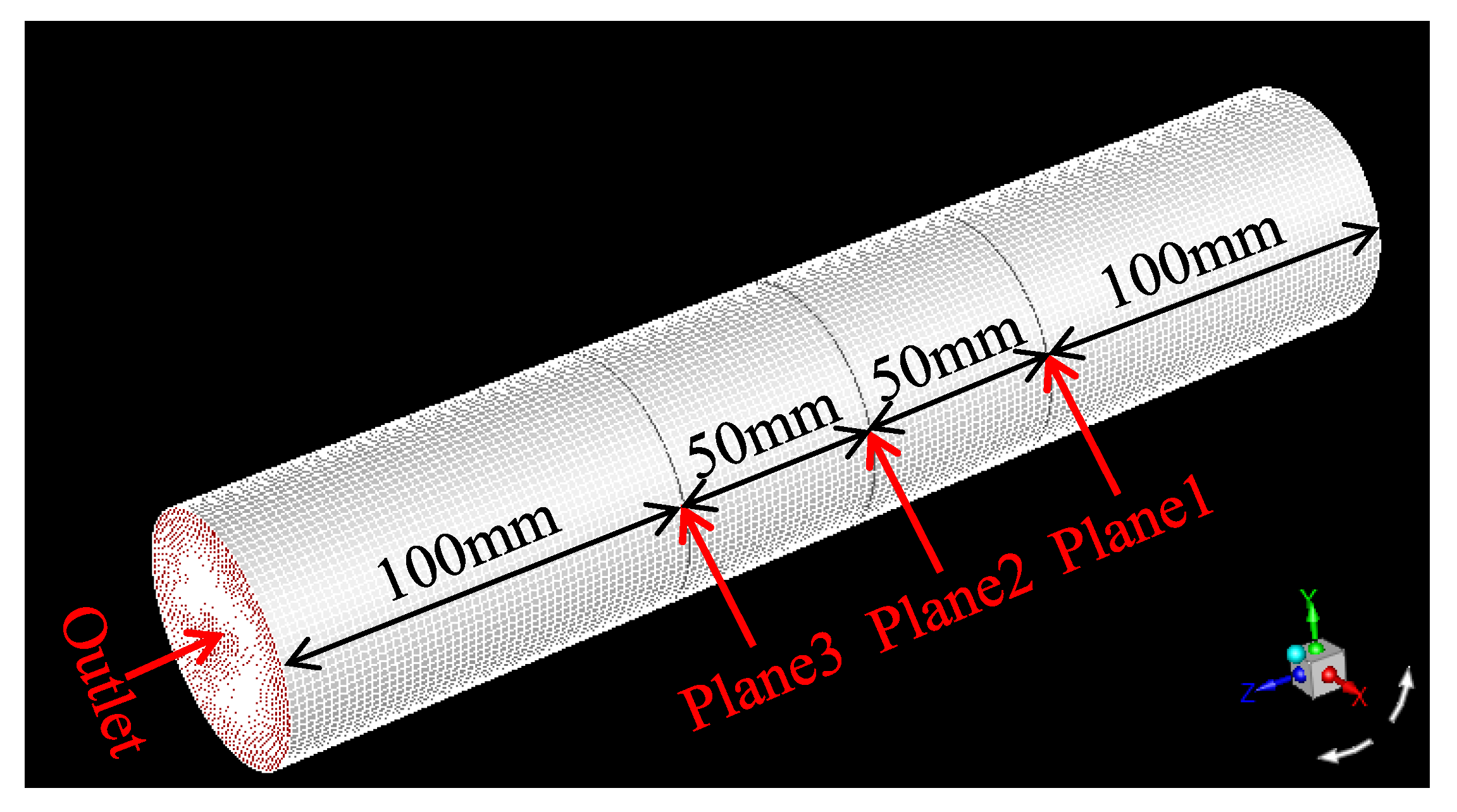
3. Parameter Setting
4. Results and Analysis
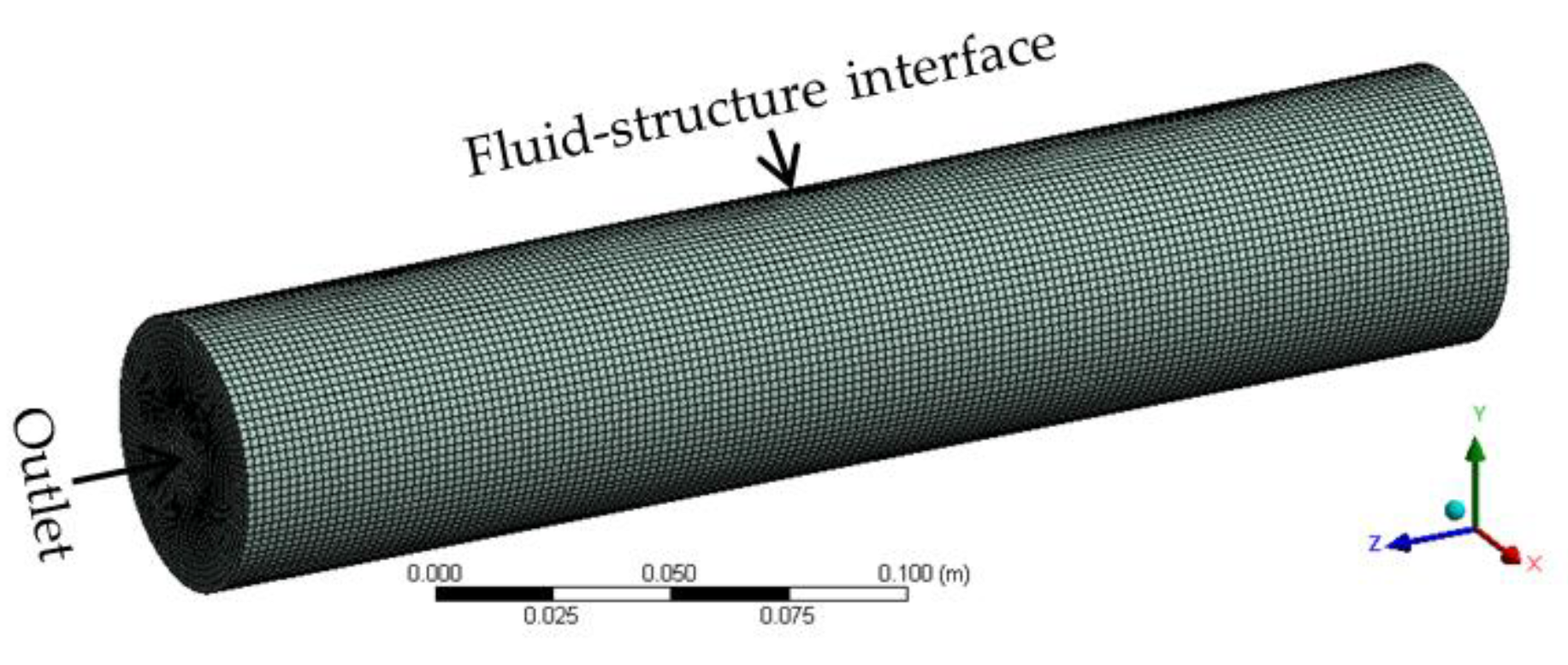
4.1. Fluid–Structure Interaction Analysis
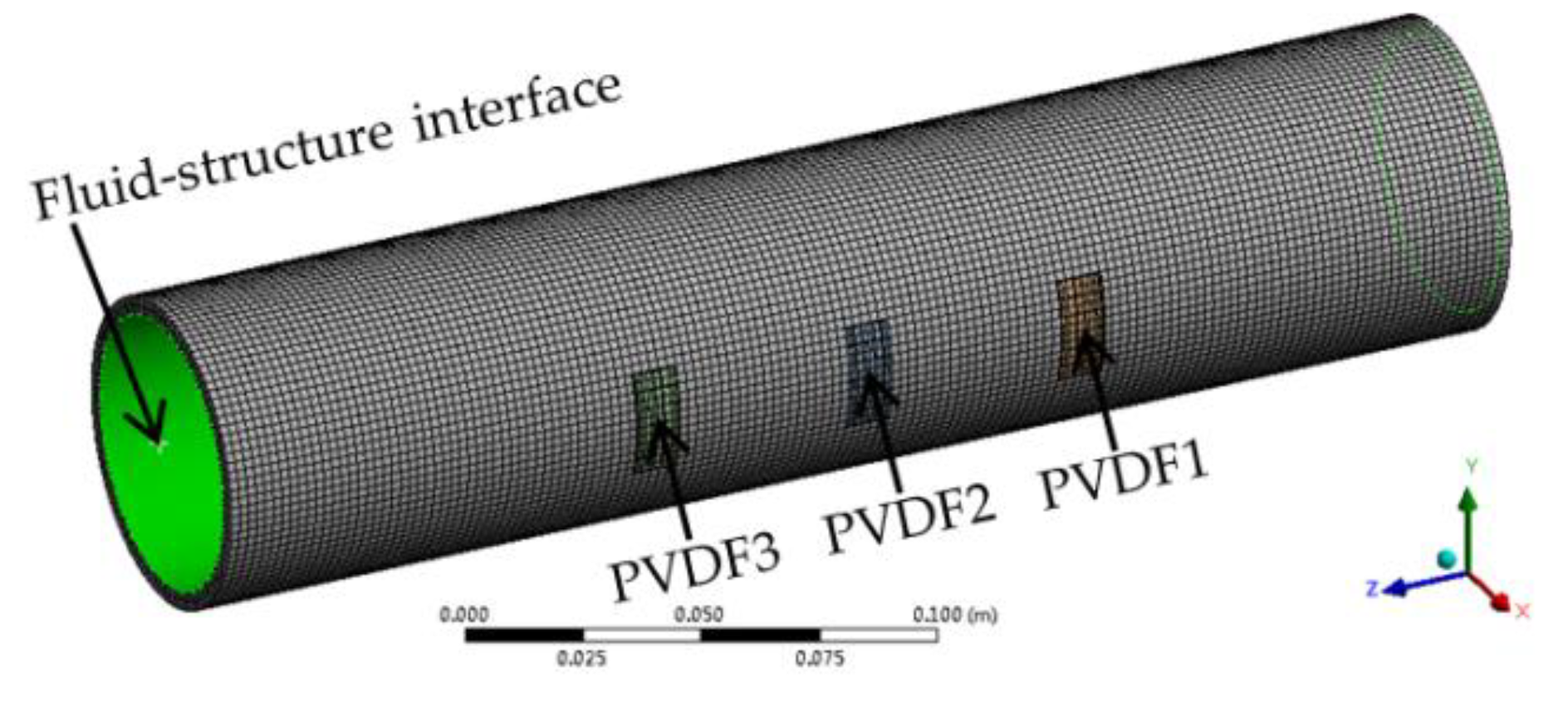
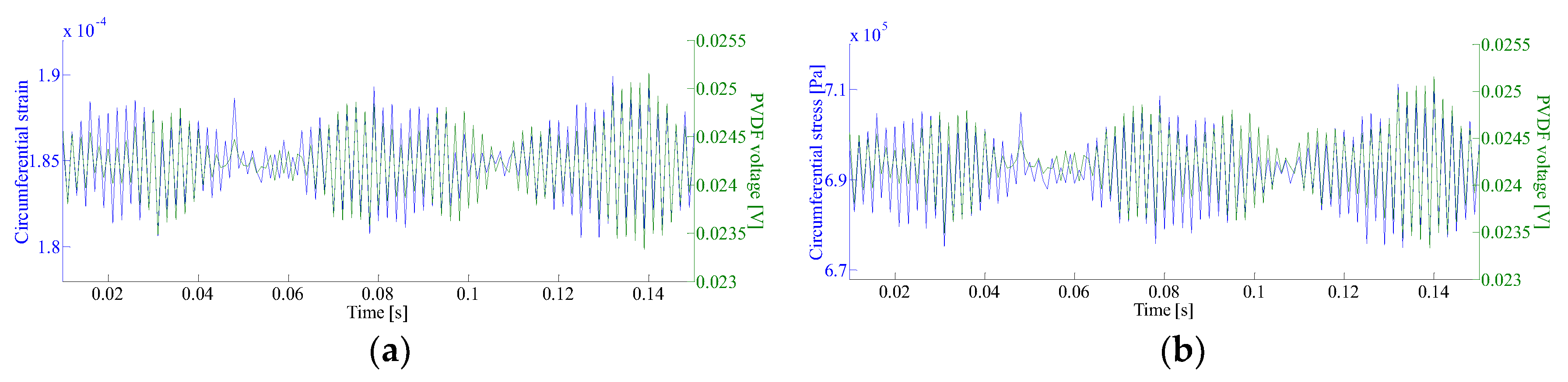
4.2. Electromechanical Coupling Analysis
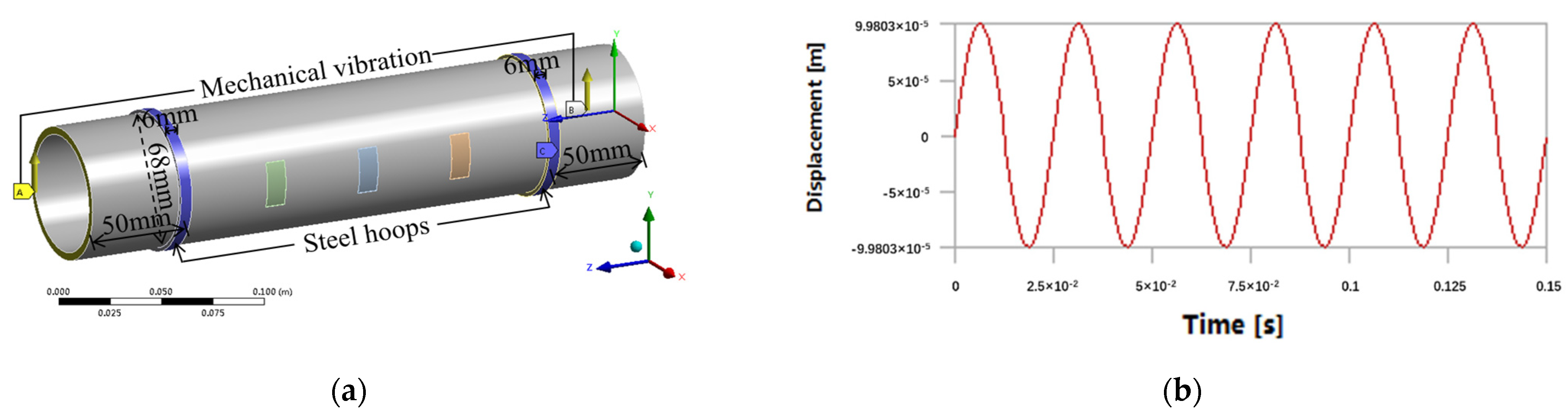
5. Influences of Flow Velocity Pulsation and Mechanical Vibration
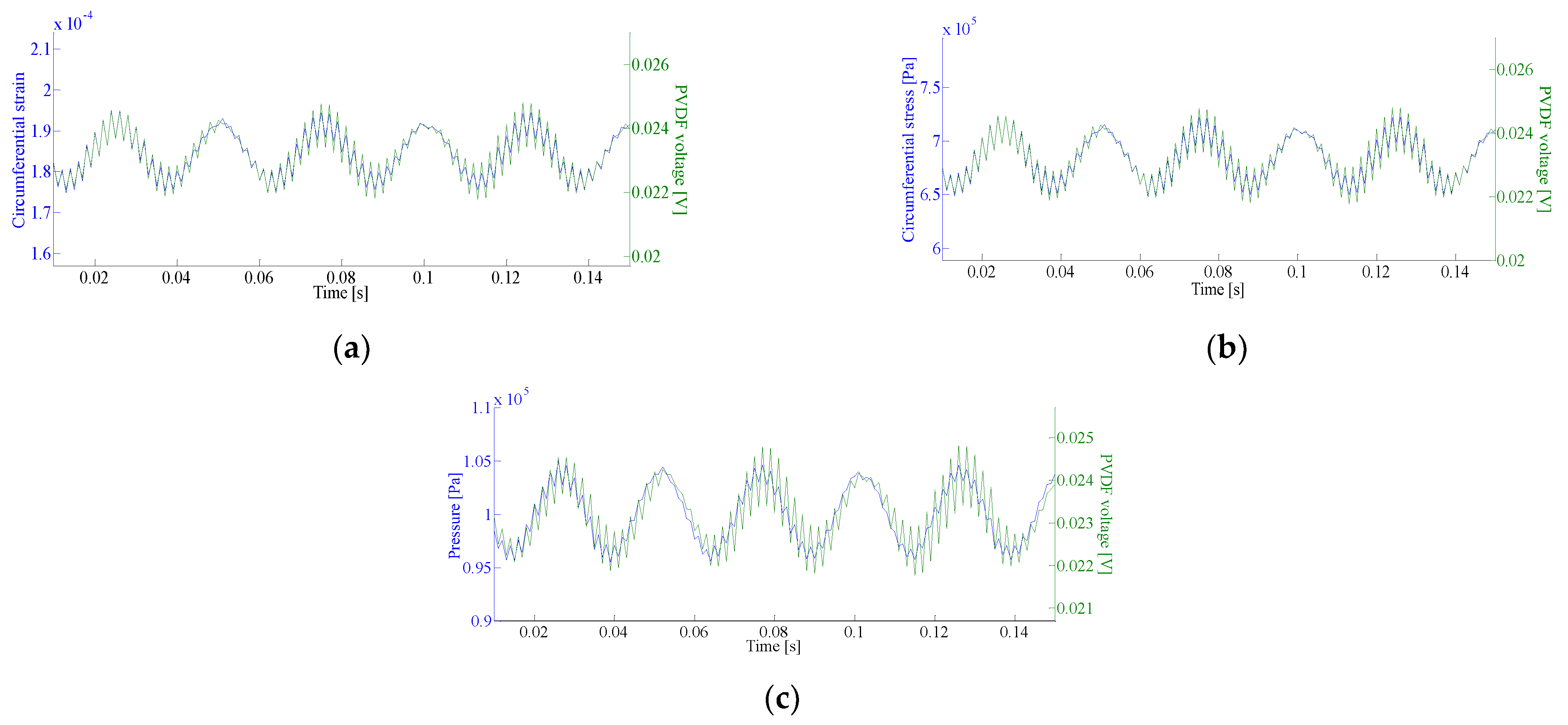
5.1. Flow Velocity Pulsation
5.2. Mechanical Vibration
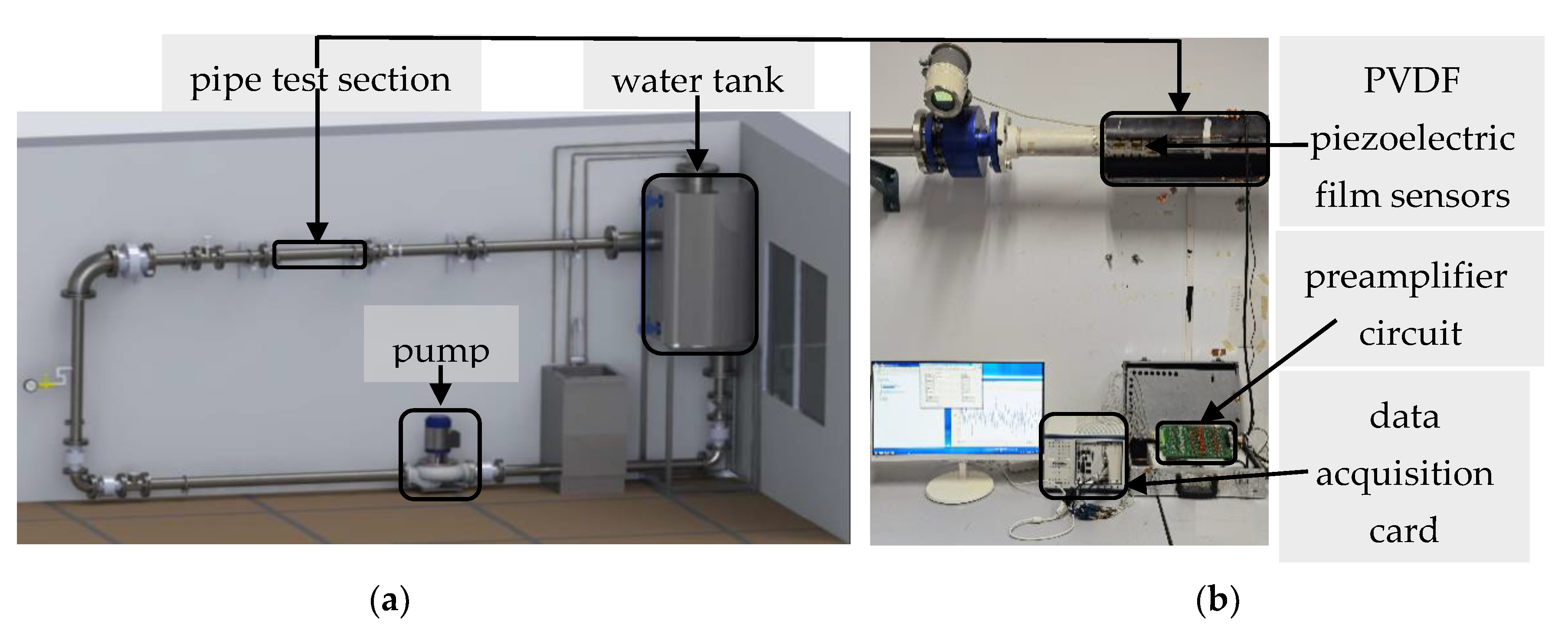
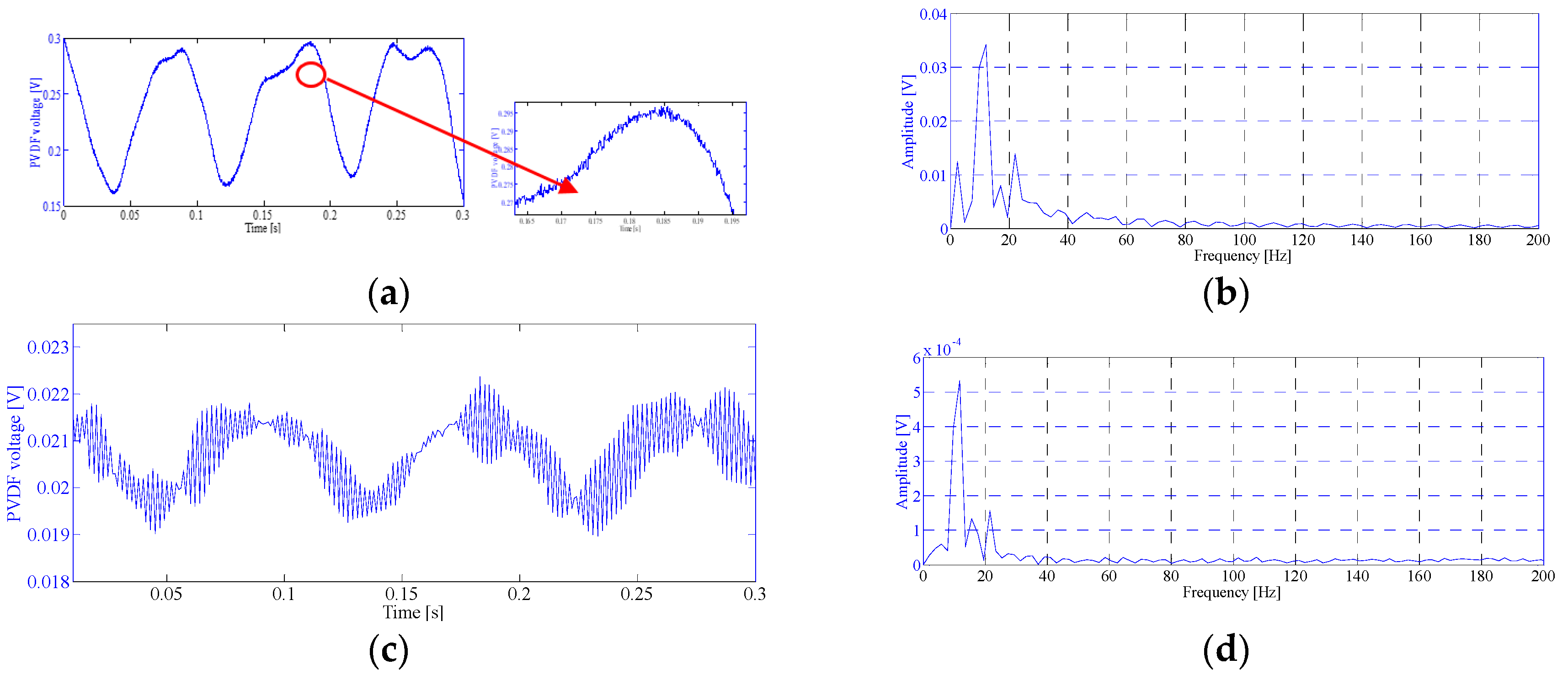
6. Experimental Testing
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, T. Dynamic Analysis and Vibration Control Analysis of Liquid-Conveying Pipe System Based on ANSYS Workbench; Hebei University of Science & Technology: Shijiazhuang, China, 2011. [Google Scholar]
- Drewczynski, M.; Solution, G.E.; Rzadkowski, R. A stress analysis of a compressor blade in partially blocked inlet condition. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2015, 230, 934–952. [Google Scholar] [CrossRef]
- Gong, C.D.; Lee, H.S.; Kim, I.K. Aerodynamic and Structural Design of A High Efficiency Small Scale Composite V ertical Axis Wind Turbine Blade. J. Korean Soc. Aeronaut. Space Sci. 2011, 39, 758–765. [Google Scholar]
- Kang, H.S.; Kim, Y.J. Optimal design of impeller for centrifugal compressor under the influence of one-way fluid-structure interaction. J. Mech. Sci. Technol. 2016, 30, 3953–3959. [Google Scholar] [CrossRef]
- Ying, Q.; Zhuge, W.; Zhang, Y.; Zhang, L. Design Optimization of A Small Scale High Expansion Ratio Organic Vapour Turbo Expander for Automotive Application. Energy Procedia 2017, 129, 1133–1140. [Google Scholar] [CrossRef]
- Gu, Y.; Pei, J.; Yuan, S.; Xing, L.; Stephen, C.; Zhang, F.; Wang, X. Effects of blade thickness on hydraulic performance and structural dynamic characteristics of high-power coolant pump at overload condition. Proc. Inst. Mech. Eng. Part A J. Power Energy 2018, 232, 992–1003. [Google Scholar] [CrossRef]
- Chen, X. Study on the Dynamic Characteristics of Hydraulic Flexible Pipe Fluid-Structure Coupling Vibration; Hunan University of Science and Technology: Xiangtan, China, 2015. [Google Scholar]
- Dai, Z. Vibration Analysis of L Type Hydraulic Bellows Based on Fluid Solid Coupling; Hunan University of Science and Technology: Xiangtan, China, 2017. [Google Scholar]
- Liu, B.; Chen, Z.; Bao, J.; Cui, Z. Numerical simulation for effects of pipeline internal flow on vibration of flexible marine pipe. J. Vib. Shock 2020, 39, 117–185. [Google Scholar]
- Yang, C.; Yi, M. Numerical solution of fluid-structure interaction in liquid-filled pipes by method of characteristics. J. Chin. J. Mech. Eng. 2007, 20, 48–53. [Google Scholar] [CrossRef]
- Nan, B.; Lchiki, M.; Ueno, N.; Fukuda, O.; Akiyama, M. A flexible piezoelectric film sensor for fault diagnosis of pipe systems. In Proceedings of the 33rd IEEE Annual Conference on Industrial Electronics Society, Taipei, Taiwan, 5–8 November 2007; pp. 2181–2186. [Google Scholar]
- Liang, R.; Wang, Q.M. Pulse pressure sensor based on flexible PZT thick-film composite device. In Proceedings of the 2014 IEEE International Ultrasonics Symposium, Chicago, IL, USA, 3–6 September 2014; pp. 1559–1562. [Google Scholar]
- Muggleton, J.M.; Brennan, M.J.; Pinnington, R.J.; Gao, Y. A novel sensor for measuring the acoustic pressure in buried plastic water pipes. J. Sound Vib. 2006, 295, 1085–1098. [Google Scholar] [CrossRef]
- Okosun, F.; Cahill, P.; Hazra, B.; Pakrashi, V. Vibration-based leak detection and monitoring of water pipes using output-only piezoelectric sensors. Eur. Phys. J. Spec. Top. 2019, 228, 1659–1675. [Google Scholar] [CrossRef]
- Okosun, F.; Celikin, M.; Pakrashi, V. A Numerical Model for Experimental Designs of Vibration-Based Leak Detection and Monitoring of Water Pipes Using Piezoelectric Patches. Sensors 2020, 20, 6708. [Google Scholar] [CrossRef] [PubMed]
- Ni, Z. Vibration Mechanics; Xi’an Jiaotong University Press: Xi’an, China, 1986; pp. 342–388. [Google Scholar]
- Peng, G.; Wang, Z.; Yan, Z.; Liu, R. Strength analysis of a large centrifugal dredge pump case. Eng. Fail. Anal. 2009, 16, 321–328. [Google Scholar]
- Saeed, R.; Galybin, A. Simplified model of the turbine runner blade. Eng. Fail. Anal. 2009, 16, 2473–2484. [Google Scholar] [CrossRef]
- Cook, R.D. Concepts and Applications of Finite Element Analysis; John Wiley & Sons: New York, NY, USA, 2002. [Google Scholar]
- Dong, X.; Peng, Z.; Zhang, W.; Hua, H.; Meng, G. Research on spillover effects for vibration control of piezoelectric smart structures by ANSYS. J. Math. Probl. Eng. 2014, 2014, 1–8. [Google Scholar] [CrossRef]
- Nicoud, F.; Frédéric, D. Subgrid-Scale Stress Modelling Based on the Square of the Velocity Gradient Tensor. J. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]



| Circumferential Strain and Fluid Pressure | Circumferential Stress and Fluid Pressure | |
|---|---|---|
| Point1 and Plane1 | 0.9256 | 0.9225 |
| Point2 and Plane2 | 0.9318 | 0.9311 |
| Point3 and Plane3 | 0.9223 | 0.9261 |
| Circumferential Strain and PVDF Voltage | Circumferential Stress and PVDF Voltage | |
|---|---|---|
| Point1 and PVDF1 | 0.9437 | 0.9570 |
| Point2 and PVDF2 | 0.9924 | 0.9912 |
| Point3 and PVDF3 | 0.9583 | 0.9483 |
| Pulsation Frequency (Hz) | Ponit1 and PVDF1 | Point2 and PVDF2 | Ponit3 and PVDF3 | |||
|---|---|---|---|---|---|---|
| Circumferential Strain and PVDF Voltage | Circumferential Stress and PVDF Voltage | Circumferential Strain and PVDF Voltage | Circumferential Stress and PVDF Voltage | Circumferential Strain and PVDF Voltage | Circumferential Stress and PVDF Voltage | |
| 0 | 0.9437 | 0.9570 | 0.9924 | 0.9912 | 0.9583 | 0.9483 |
| 5 | 0.9277 | 0.9438 | 0.9989 | 0.9973 | 0.9187 | 0.9309 |
| 10 | 0.9453 | 0.9668 | 0.9981 | 0.9977 | 0.9368 | 0.9542 |
| 20 | 0.9609 | 0.9695 | 0.9974 | 0.9980 | 0.9608 | 0.9717 |
| 40 | 0.9728 | 0.9786 | 0.9986 | 0.9989 | 0.9668 | 0.9767 |
| Pulsation Frequency (Hz) | Plane1 and PVDF1 | Plane2 and PVDF2 | Plane3 and PVDF3 |
|---|---|---|---|
| Pressure and Voltage | Pressure and Voltage | Pressure and Voltage | |
| 0 | 0.8651 | 0.9754 | 0.8598 |
| 5 | 0.8323 | 0.9631 | 0.8397 |
| 10 | 0.8686 | 0.9712 | 0.8536 |
| 20 | 0.8971 | 0.9598 | 0.8911 |
| 40 | 0.9164 | 0.9457 | 0.9098 |
| Pulsation Amplitude (m/s) | Point1 and PVDF1 | Point2 and PVDF2 | Point3 and PVDF3 | |||
|---|---|---|---|---|---|---|
| Circumferential Strain and PVDF Voltage | Circumferential Stress and PVDF Voltage | Circumferential Strain and PVDF Voltage | Circumferential Stress and PVDF Voltage | Circumferential Strain and PVDF Voltage | Circumferential Stress and PVDF Voltage | |
| 0 | 0.9437 | 0.9570 | 0.9924 | 0.9912 | 0.9583 | 0.9483 |
| 0.025 | 0.9498 | 0.9605 | 0.9952 | 0.9973 | 0.9589 | 0.9687 |
| 0.05 | 0.9676 | 0.9748 | 0.9973 | 0.9979 | 0.9636 | 0.9737 |
| 0.1 | 0.9728 | 0.9786 | 0.9986 | 0.9989 | 0.9668 | 0.9767 |
| Pulsation Amplitude (m/s) | Plane1 and PVDF1 | Plane2 and PVDF2 | Plane3 and PVDF3 |
|---|---|---|---|
| Pressure and Voltage | Pressure and Voltage | Pressure and Voltage | |
| 0 | 0.8651 | 0.9754 | 0.8598 |
| 0.025 | 0.8756 | 0.9704 | 0.8689 |
| 0.05 | 0.8085 | 0.9562 | 0.8897 |
| 0.1 | 0.9164 | 0.9457 | 0.9098 |
| Vibration Frequency (Hz) | Ponit1 and PVDF1 | Point2 and PVDF2 | Ponit3 and PVDF3 | |||
|---|---|---|---|---|---|---|
| Circumferential Strain and PVDF Voltage | Circumferential Stress and PVDF Voltage | Circumferential Strain and PVDF Voltage | Circumferential Stress and PVDF Voltage | Circumferential Strain and PVDF Voltage | Circumferential Stress and PVDF Voltage | |
| 0 | 0.9544 | 0.9632 | 0.9641 | 0.9735 | 0.9533 | 0.9660 |
| 5 | 0.9611 | 0.9692 | 0.9535 | 0.9656 | 0.9293 | 0.9468 |
| 10 | 0.9752 | 0.9802 | 0.9564 | 0.9677 | 0.9387 | 0.9539 |
| 20 | 0.9775 | 0.9783 | 0.9716 | 0.9756 | 0.9389 | 0.9473 |
| 40 | 0.9727 | 0.9781 | 0.9812 | 0.9834 | 0.9436 | 0.9592 |
| Vibration Frequency (Hz) | Plane1 and PVDF1 | Plane2 and PVDF2 | Plane3 and PVDF3 |
|---|---|---|---|
| Pressure and Voltage | Pressure and Voltage | Pressure and Voltage | |
| 0 | 0.9207 | 0.9179 | 0.9075 |
| 5 | 0.9211 | 0.9145 | 0.8973 |
| 10 | 0.9234 | 0.9187 | 0.9046 |
| 20 | 0.9198 | 0.9221 | 0.8996 |
| 40 | 0.9317 | 0.9373 | 0.9012 |
| Vibration Amplitude (mm) | Point1 and PVDF1 | Point2 and PVDF2 | Point3 and PVDF3 | |||
|---|---|---|---|---|---|---|
| Circumferential Strain and PVDF Voltage | Circumferential Stress and PVDF Voltage | Circumferential Strain and PVDF Voltage | Circumferential Stress and PVDF Voltage | Circumferential Strain and PVDF Voltage | Circumferential Stress and PVDF Voltage | |
| 0 | 0.9544 | 0.9632 | 0.9641 | 0.9735 | 0.9533 | 0.9660 |
| 0.1 | 0.9727 | 0.9781 | 0.9812 | 0.9834 | 0.9436 | 0.9592 |
| 0.2 | 0.9873 | 0.9898 | 0.9772 | 0.9828 | 0.9576 | 0.9689 |
| 0.3 | 0.9907 | 0.9925 | 0.9767 | 0.9856 | 0.9589 | 0.9696 |
| 0.4 | 0.9866 | 0.9893 | 0.9768 | 0.9824 | 0.9534 | 0.9654 |
| Vibration Amplitude (mm) | Plane1 and PVDF1 | Plane2 and PVDF2 | Plane3 and PVDF3 |
|---|---|---|---|
| Pressure and Voltage | Pressure and Voltage | Pressure and Voltage | |
| 0 | 0.9207 | 0.9179 | 0.9075 |
| 0.1 | 0.9317 | 0.9373 | 0.9012 |
| 0.2 | 0.9282 | 0.9314 | 0.9063 |
| 0.3 | 0.9369 | 0.9195 | 0.8982 |
| 0.4 | 0.9305 | 0.9294 | 0.8874 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Wu, X.; Kong, Y.; Peng, X. Measurement Method for Fluid Pressure Fluctuation in Fluid-Conveying Pipe Using PVDF Piezoelectric Film Sensor. Appl. Sci. 2021, 11, 1299. https://doi.org/10.3390/app11031299
Liu S, Wu X, Kong Y, Peng X. Measurement Method for Fluid Pressure Fluctuation in Fluid-Conveying Pipe Using PVDF Piezoelectric Film Sensor. Applied Sciences. 2021; 11(3):1299. https://doi.org/10.3390/app11031299
Chicago/Turabian StyleLiu, Song, Xianmei Wu, Yuanyuan Kong, and Xiuqian Peng. 2021. "Measurement Method for Fluid Pressure Fluctuation in Fluid-Conveying Pipe Using PVDF Piezoelectric Film Sensor" Applied Sciences 11, no. 3: 1299. https://doi.org/10.3390/app11031299





