Parametric Analysis of Tensegrity Plate-Like Structures: Part 2—Quantitative Analysis
Abstract
:Featured Application
Abstract
1. Introduction
- determination of the minimum and maximum initial prestress levels,
- assessment of the influence of the initial prestress on the structural displacements,
- assessment of the influence of the initial prestress on the effort of the structure, and
- assessment of the influence of the initial prestress on the rigidity of the structure.
2. Mathematical Description
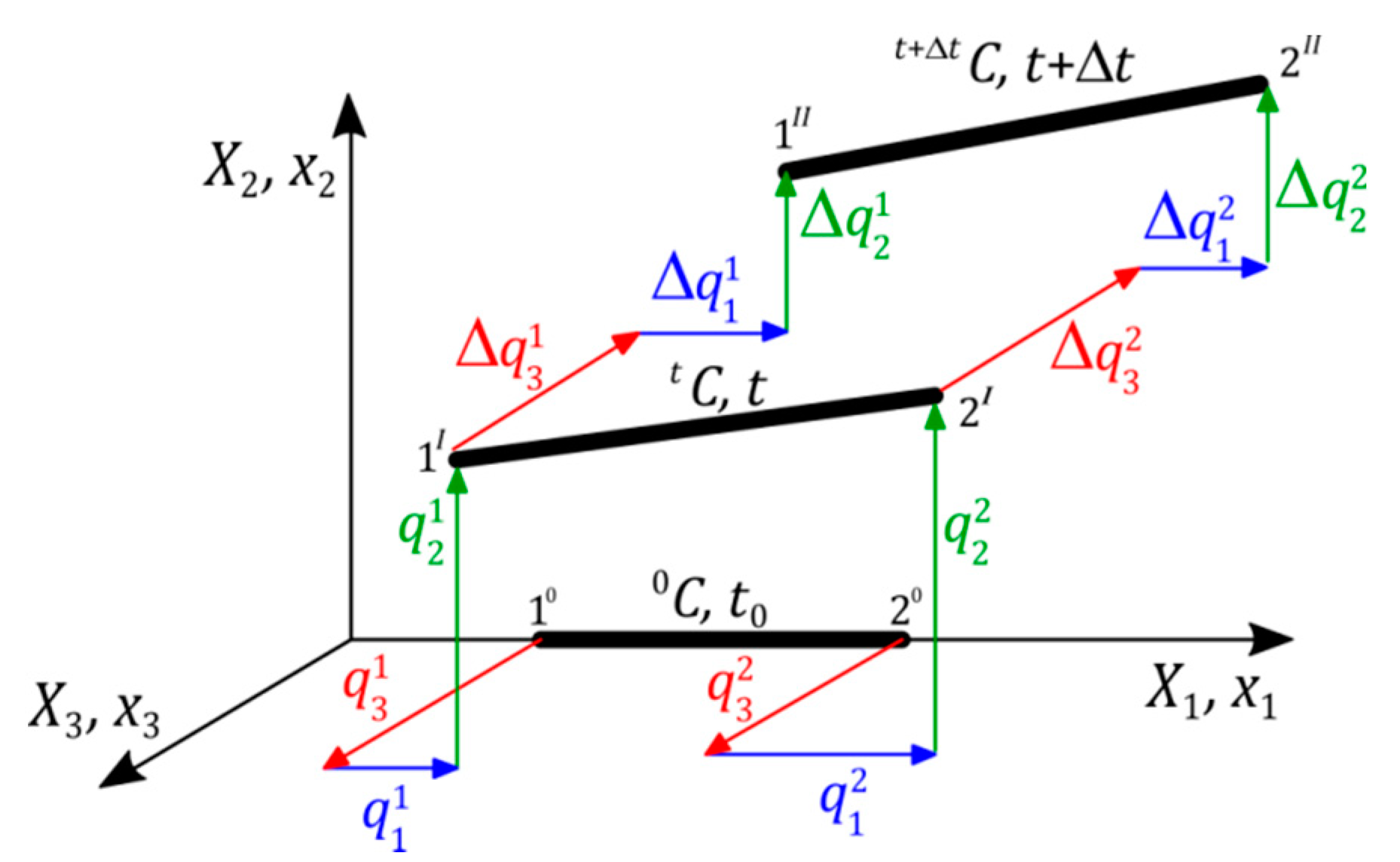
2.1. Geometrical Non-Linear Model of Tensegrity Element
2.2. Model of Tensegrity Structure
3. Influence of the Initial Prestress Level on Static Properties of Tensegrity Structures (Quantitative Analysis)
4. Examples
- for cables (S460N): diameter , moment of inertia , cross-sectional area , load-bearing capacity (calculated with taking into account partial factor for structural resistance): ; the maximum value of the tensile force depends on the self-stress state,
- for struts (made of hot-finished circular hollow section, steel S355J2): diameter: , thickness: , moment of inertia: , cross-sectional area: , load-bearing capacity: ; the maximum value of the compressed force is equal to (—the initial prestress force).
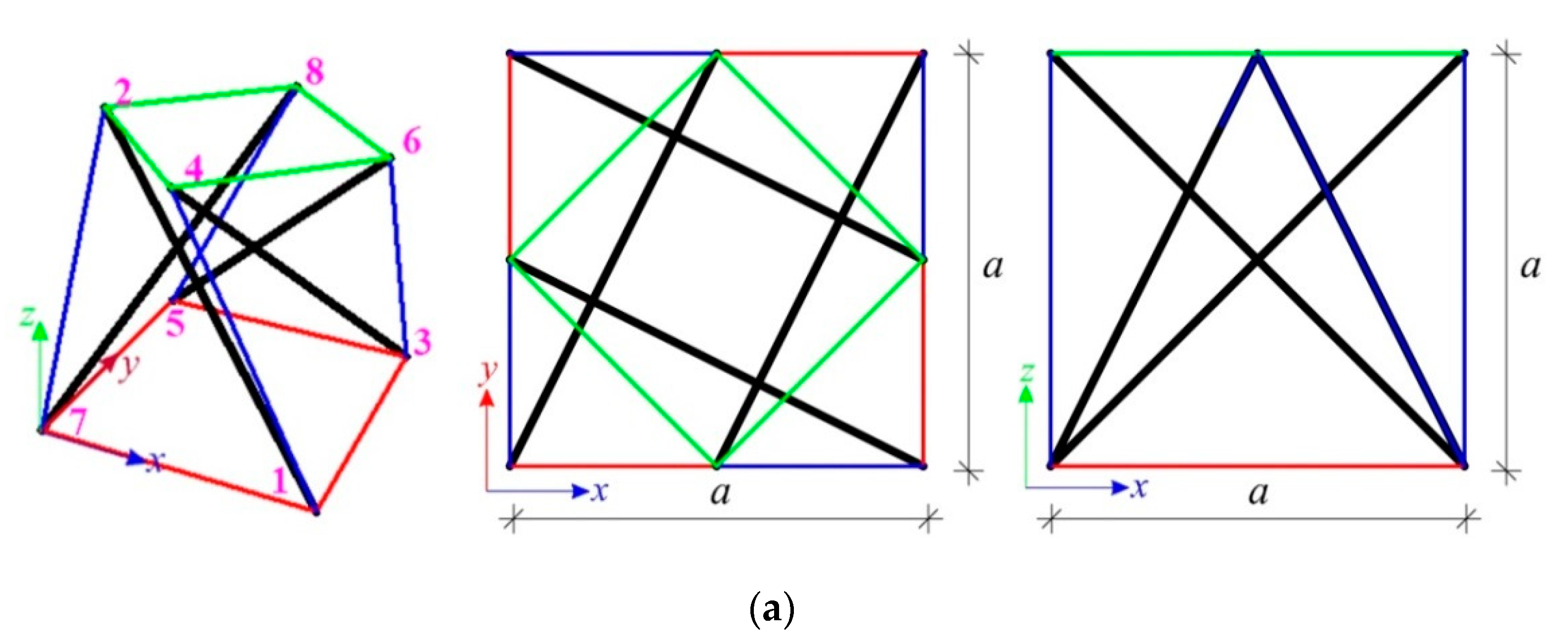
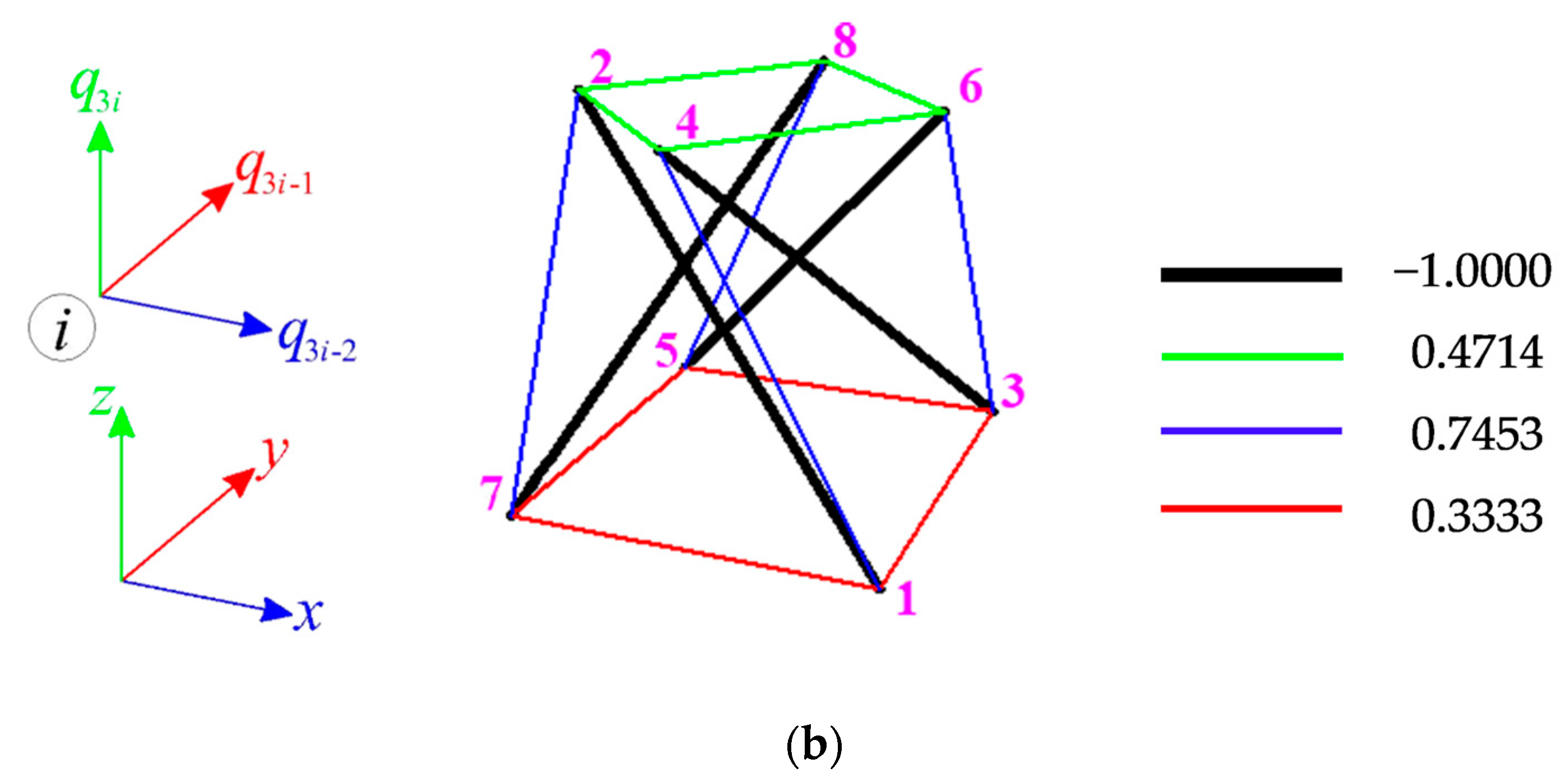
4.1. Single Modified Quartex Module
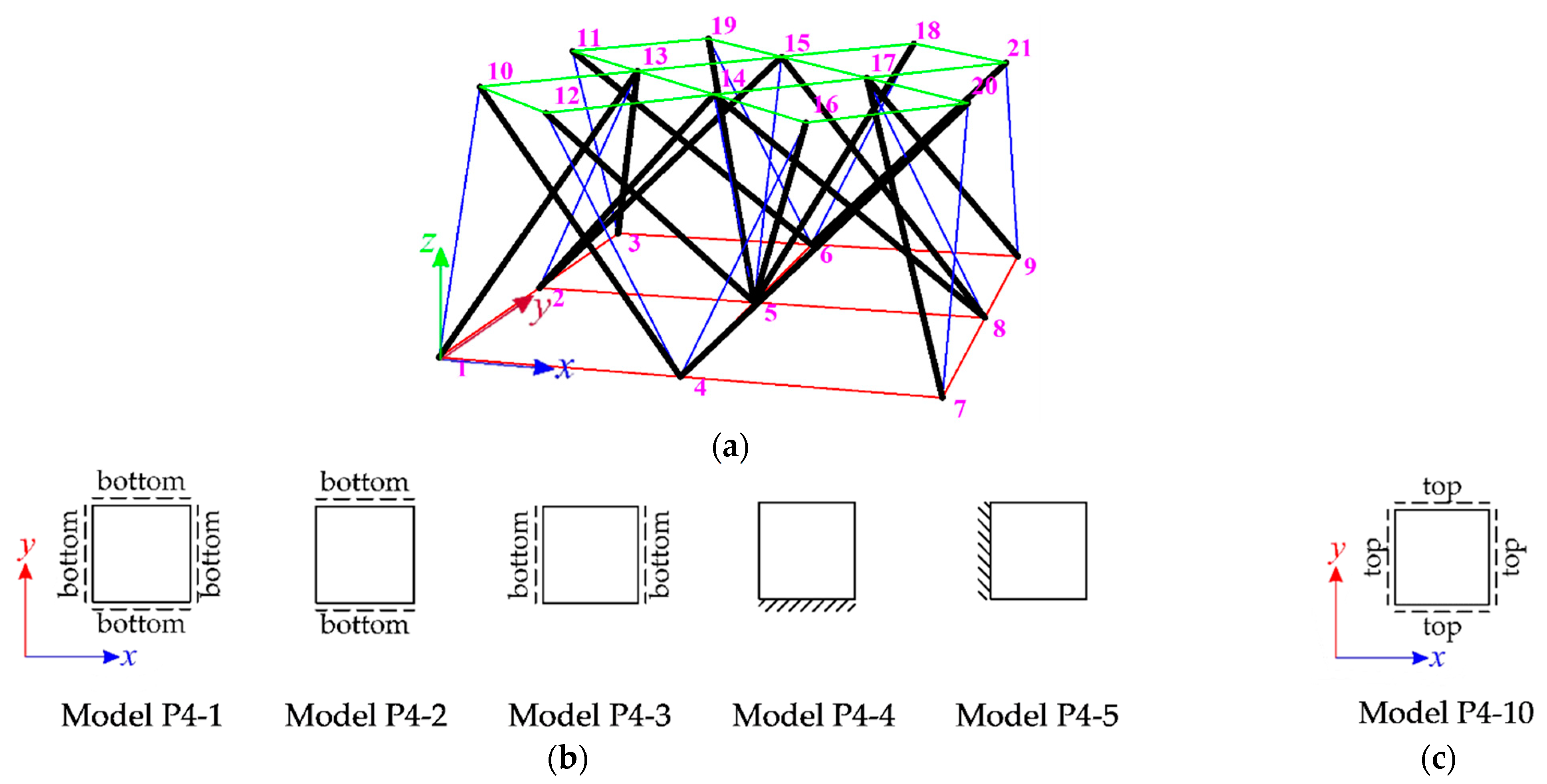
4.2. Four-Module Tensegrity Plate-Like Structures
4.3. Sixteen-Module Tensegrity Plate-Like Structures and Plate Strips
4.4. Sixty-Four-Module Tensegrity Plate-Like Structures
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, L.-Y.; Zhu, S.-X.; Chen, X.-F.; Xu, G.-K. Analytical Form-Finding for Highly Symmetric and Super-Stable Configurations of Rhombic Truncated Regular Polyhedral Tensegrities. J. Appl. Mech. 2019, 86. [Google Scholar] [CrossRef]
- Schek, H.-J. The force density method for form finding and computation of general networks. Comput. Methods Appl. Mech. Eng. 1974, 3, 115–134. [Google Scholar] [CrossRef]
- Xu, X.; Wang, Y.; Luo, Y. Finding member connectivities and nodal positions of tensegrity structures based on force density method and mixed integer non-linear programming. Eng. Struct. 2018, 166, 240–250. [Google Scholar] [CrossRef]
- Barnes, M.R. Form Finding and Analysis of Tension Structures by Dynamic Relaxation. Int. J. Space Struct. 1999, 14, 89–104. [Google Scholar] [CrossRef]
- Domer, B.; Fest, E.; Lalit, V.; Smith, I.F.C. Combining Dynamic Relaxation Method with Artificial Neural Networks to Enhance Simulation of Tensegrity Structures. J. Struct. Eng. 2003, 129, 672–681. [Google Scholar] [CrossRef] [Green Version]
- Estrada, G.G.; Bungartz, H.-J.; Mohrdieck, C. Numerical form-finding of tensegrity structures. Int. J. Solids Struct. 2006, 43, 6855–6868. [Google Scholar] [CrossRef] [Green Version]
- Pagitz, M.; Mirats Tur, J.M. Finite element based form-finding algorithm for tensegrity structures. Int. J. Solids Struct. 2009, 46, 3235–3240. [Google Scholar] [CrossRef]
- Tran, H.C.; Lee, J. Advanced form-finding of tensegrity structures. Comput. Struct. 2010, 88, 237–246. [Google Scholar] [CrossRef]
- Koohestani, K.; Guest, S.D. A new approach to the analytical and numerical form-finding of tensegrity structures. Int. J. Solids Struct. 2013, 50, 2995–3007. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.; Lee, J.; Kang, J. A Genetic Algorithm Based Form-finding of Tensegrity Structures with Multiple Self-stress States. J. Asian Archit. Build. Eng. 2017, 16, 155–162. [Google Scholar] [CrossRef] [Green Version]
- Djouadi, S.; Motro, R.; Pons, J.C.; Crosnier, B. Active Control of Tensegrity Systems. J. Aerosp. Eng. 1998, 11, 37–44. [Google Scholar] [CrossRef]
- Fest, E.; Shea, K.; Smith Ian, F.C. Active Tensegrity Structure. J. Struct. Eng. 2004, 130, 1454–1465. [Google Scholar] [CrossRef] [Green Version]
- Domer, B.; Smith, I.F.C. An Active Structure that Learns. J. Comput. Civ. Eng. 2005, 19, 16–24. [Google Scholar] [CrossRef] [Green Version]
- Adam, B.; Smith, I.F.C. Active tensegrity: A control framework for an adaptive civil-engineering structure. Comput. Struct. 2008, 86, 2215–2223. [Google Scholar] [CrossRef] [Green Version]
- Raja, M.G.; Narayanan, S. Active control of tensegrity structures under random excitation. Smart Mater. Struct. 2007, 16, 809–817. [Google Scholar] [CrossRef]
- Sabouni-Zawadzka, A. Active Control of Smart Tensegrity Structures. Arch. Civ. Mech. Eng. 2014, 60, 517–534. [Google Scholar] [CrossRef]
- Amouri, S.; Averseng, J.; Dubé, J.-F. Active control design of modular tensegrity structures. In Proceedings of the International Association for Shell and Spatial Structures (IASS) Symposium 2013, Wroclaw, Poland, 23–27 September 2013. [Google Scholar]
- Oliveto, N.D.; Sivaselvan, M.V. Dynamic analysis of tensegrity structures using a complementarity framework. Comput. Struct. 2011, 89, 2471–2483. [Google Scholar] [CrossRef]
- Fraternali, F.; Senatore, L.; Daraio, C. Solitary waves on tensegrity lattices. J. Mech. Phys. Solids 2012, 60, 1137–1144. [Google Scholar] [CrossRef]
- Faroughi, S.; Lee, J. Analysis of tensegrity structures subject to dynamic loading using a Newmark approach. J. Build. Eng. 2015, 2, 1–8. [Google Scholar] [CrossRef]
- Ashwear, N.; Tamadapu, G.; Eriksson, A. Optimization of modular tensegrity structures for high stiffness and frequency separation requirements. Int. J. Solids Struct. 2016, 80, 297–309. [Google Scholar] [CrossRef]
- Kan, Z.; Peng, H.; Chen, B.; Zhong, W. Non-linear dynamic and deployment analysis of clustered tensegrity structures using a positional formulation FEM. Compos. Struct. 2018, 187, 241–258. [Google Scholar] [CrossRef]
- Tibert, G.; Pellegrino, S. Deployable Tensegrity Reflectors for Small Satellites. J. Spacecr. Rockets. 2002, 39, 701–709. [Google Scholar] [CrossRef] [Green Version]
- Veuve, N.; Safaei, S.; Smith, I. Deployment of a Tensegrity Footbridge. J. Struct. Eng. 2015, 141, 04015021. [Google Scholar] [CrossRef] [Green Version]
- Gilewski, W.; Kłosowska, J.; Obara, P. Applications of Tensegrity Structures in Civil Engineering. Procedia Eng. 2015, 111, 242–248. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Li, K.; He, Q.; Cai, S. A Light-Powered Ultralight Tensegrity Robot with High Deformability and Load Capacity. Adv. Mater. 2019, 31, 1806849. [Google Scholar] [CrossRef]
- Park, S.; Park, E.; Yim, M.; Kim, J.; Seo, T.W. Optimization-Based Nonimpact Rolling Locomotion of a Variable Geometry Truss. IEEE Robot. Autom. Lett. 2019, 4, 747–752. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, D.; Dobah, Y.; Scarpa, F.; Fraternali, F.; Skelton, R.E. Tensegrity cell mechanical metamaterial with metal rubber. Appl. Phys. Lett. 2018, 113, 031906. [Google Scholar] [CrossRef] [Green Version]
- Fabbrocino, F.; Carpentieri, G. Three-dimensional modeling of the wave dynamics of tensegrity lattices. Compos. Struct. 2017, 173, 9–16. [Google Scholar] [CrossRef]
- Fraddosio, A.; Marzano, S.; Pavone, G.; Piccioni, M.D. Morphology and self-stress design of V-Expander tensegrity cells. Compos. Part B Eng. 2017, 115, 102–116. [Google Scholar] [CrossRef]
- Sabouni-Zawadzka, A.; Gilewski, W. Soft and Stiff Simplex Tensegrity Lattices as Extreme Smart Metamaterials. Materials 2019, 12, 187. [Google Scholar] [CrossRef] [Green Version]
- Gilewski, W.; Sabouni-Zawadzka, A. On possible applications of smart structures controlled by self-stress. Arch. Civ. Mech. Eng. 2014, 15, 469–478. [Google Scholar] [CrossRef]
- Hanaor, A.; Liao, M.-K. Double-Layer Tensegrity Grids: Static Load Response. Part I: Analytical Study. J. Struct. Eng. 1991, 117, 1660–1674. [Google Scholar] [CrossRef]
- Hanaor, A. Double-Layer Tensegrity Grids: Static Load Response. Part II: Experimental Study. J. Struct. Eng. 1991, 117, 1675–1684. [Google Scholar] [CrossRef]
- Murakami, H. Static and dynamic analyses of tensegrity structures. Part 1. Non-linear equations of motion. Int. J. Solids Struct. 2001, 38, 3599–3613. [Google Scholar] [CrossRef]
- Murakami, H. Static and dynamic analyses of tensegrity structures. Part II. Quasi-static analysis. Int. J. Solids Struct. 2001, 38, 3615–3629. [Google Scholar] [CrossRef]
- Fu, F. Non-linear static analysis and design of Tensegrity domes. Steel Compos. Struct. 2006, 6, 417–433. [Google Scholar] [CrossRef] [Green Version]
- Angellier, N.; Dubé, J.F.; Quirant, J.; Crosnier, B. Behavior of a Double-Layer Tensegrity Grid under Static Loading: Identification of Self-Stress Level. J. Struct. Eng. 2013, 139, 1075–1081. [Google Scholar] [CrossRef] [Green Version]
- Gilewski, W.; Obara, P.; Kłosowska, J. Self-stress control of real civil engineering tensegrity structures. AIP Conf. Proc. 2018, 1922, 150004. [Google Scholar]
- Gilewski, W.; Kłosowska, J.; Obara, P. Parametric analysis of some tensegrity structures. MATEC Web Conf. 2019, 262, 10003. [Google Scholar] [CrossRef]
- Gilewski, W.; Kłosowska, J.; Obara, P. The influence of self-stress on the behavior of tensegrity-like real structure. MATEC Web Conf. 2017, 117, 00079. [Google Scholar] [CrossRef] [Green Version]
- Obara, P. Analysis of orthotropic tensegrity plate strips using a continuum two-dimensional model. MATEC Web Conf. 2019, 262, 10010. [Google Scholar] [CrossRef]
- Obara, P. Application of linear six-parameter shell theory to the analysis of orthotropic tensegrity plate-like structures. J. Theor. App. Mech. 2019, 57, 167–178. [Google Scholar] [CrossRef]
- Obara, P. Dynamic and Dynamic Stability of Tensegrity Structures; Wydawnictwo Politechniki Świętokrzyskiej: Kielce, Poland, 2019. (In Polish) [Google Scholar]
- Obara, P.; Tomasik, J. Parametric Analysis of Tensegrity Plate-Like Structures: Part 1—Qualitative Analysis. Appl. Sci. 2020, 10, 7042. [Google Scholar] [CrossRef]
- Argyris, J.; Scharpf, D.W. Large Deflection Analysis of Prestressed Networks. J. Struct. Div. 1972, 98, 633–654. [Google Scholar]
- Motro, R. Forms and Forces in Tensegrity Systems. In Proceedings of the Third International Conference on Space Structures, Amsterdam, The Netherlands, 11–14 September 1984; Nooshin, H., Ed.; Elsevier: London, UK, 1984; pp. 180–185. [Google Scholar]
- Kebiche, K.; Kazi-Aoual, M.N.; Motro, R. Geometrical non-linear analysis of tensegrity systems. Eng. Struct. 1999, 21, 864–876. [Google Scholar] [CrossRef]
- Tran, H.C.; Lee, J. Geometric and material non-linear analysis of tensegrity structures. Acta Mech. Sin. 2011, 27, 938–949. [Google Scholar] [CrossRef]
- Faroughi, S.; Lee, J. Geometrical Non-linear Analysis of Tensegrity Based on a Co-Rotational Method. Adv. Struct. Eng. 2014, 17, 41–51. [Google Scholar] [CrossRef]
- Szmelter, J. Computer Methods in Mechanics; Państwowe Wydawnictwo Naukowe: Warsaw, Poland, 1980. [Google Scholar]
- Crisfield, M.A. Non-Linear Finite Element Analysis of Solids and Structures, Essentials; Wiley: Hoboken, NJ, USA, 1991; ISBN 978-0-471-92956-7. [Google Scholar]
- Bathe, K.-J. Finite Element Procedures in Engineering Analysis; Prentice-Hall: New York, NY, USA, 1982. [Google Scholar]
- Borst, R.; Crisfield, M.; Remmers, J.; Verhoosel, C. Non-Linear Finite Element Analysis of Solids and Structures: Second Edition; Wiley: Chichester, UK, 2012. [Google Scholar]
- Rakowski, G.; Kacprzyk, Z. Finite Element Method in Structural Mechanics; Oficyna Wydawnicza Politechniki Warszawskiej: Warsaw, Poland, 2016. [Google Scholar]

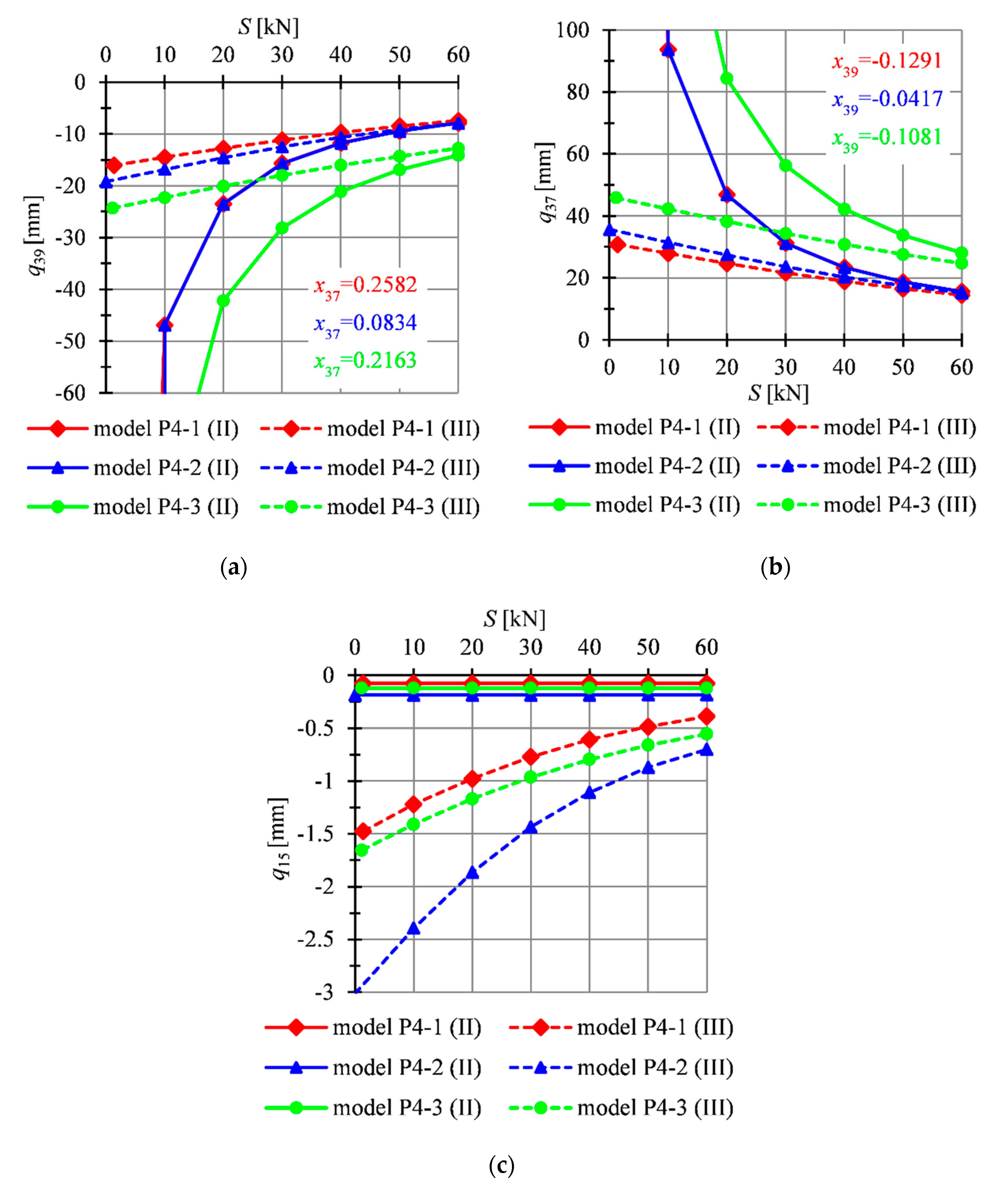
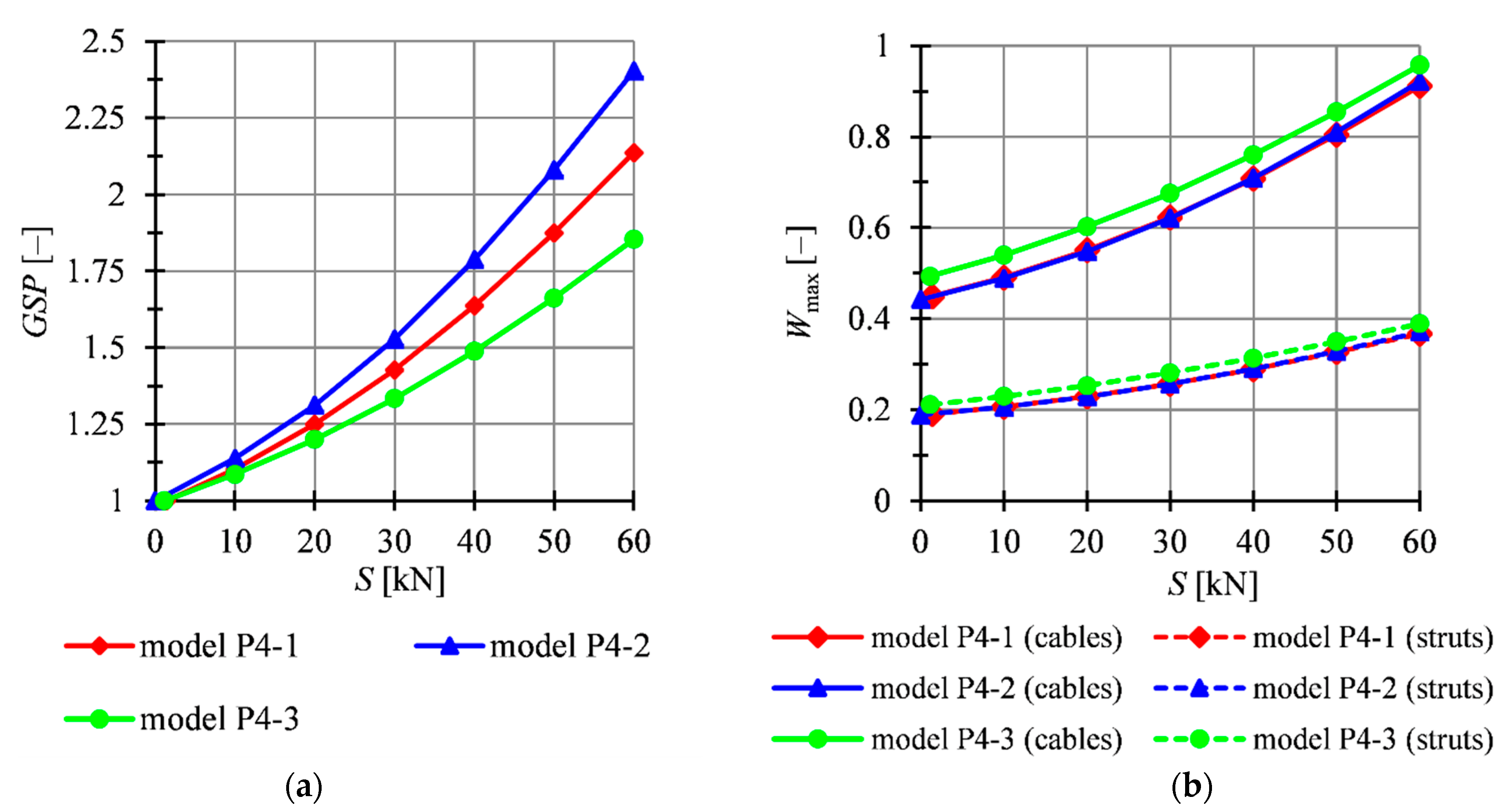
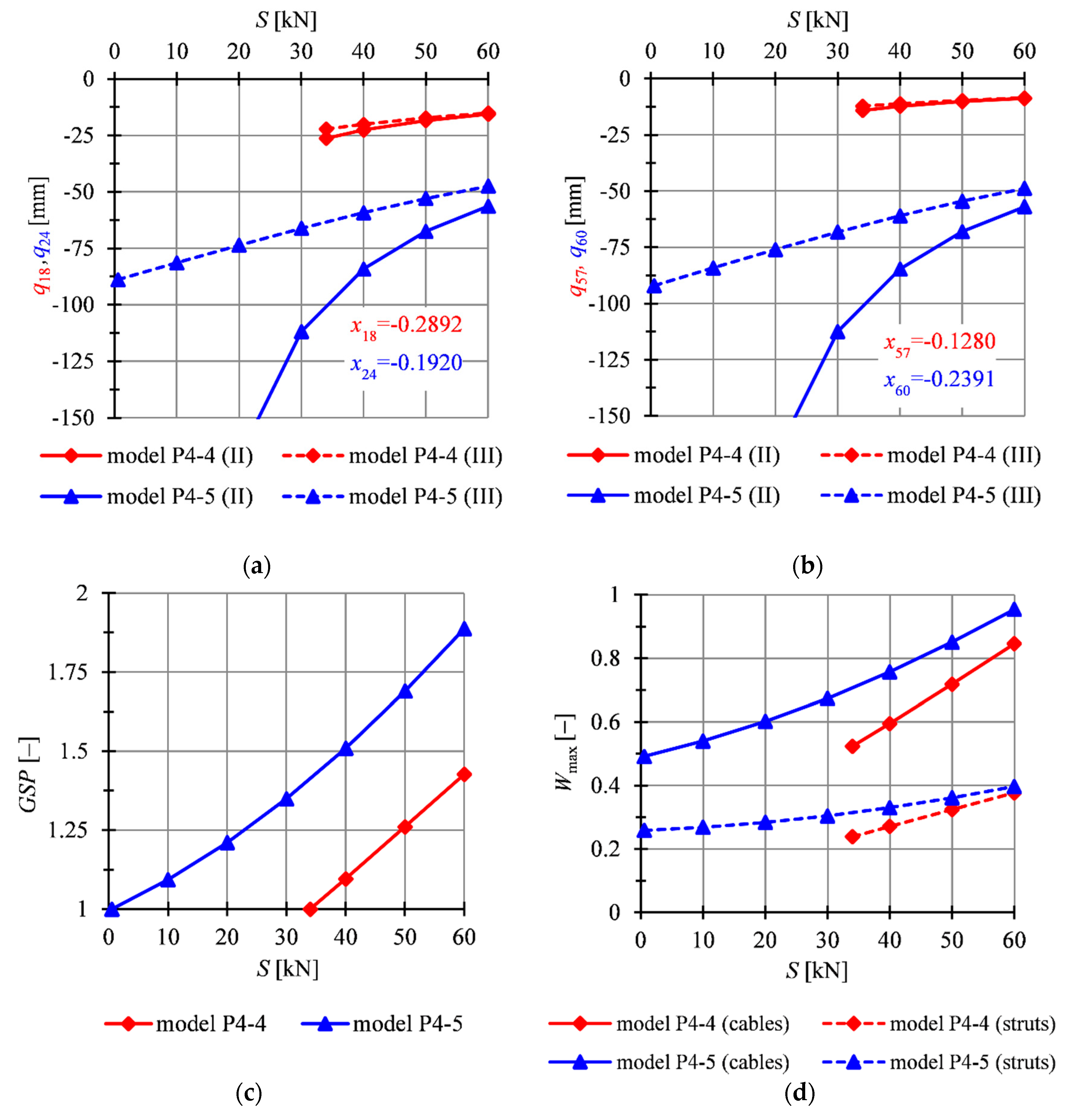
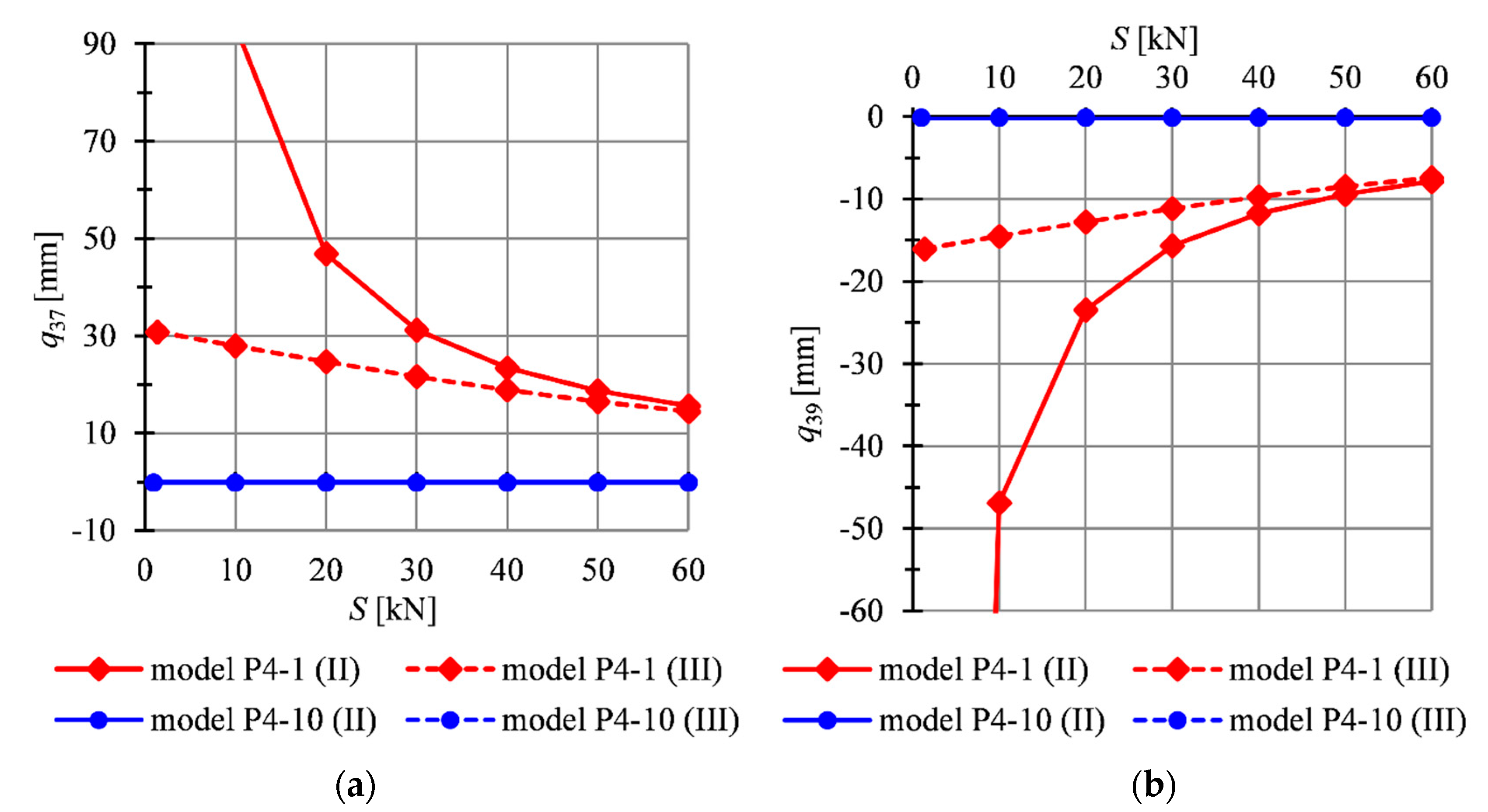

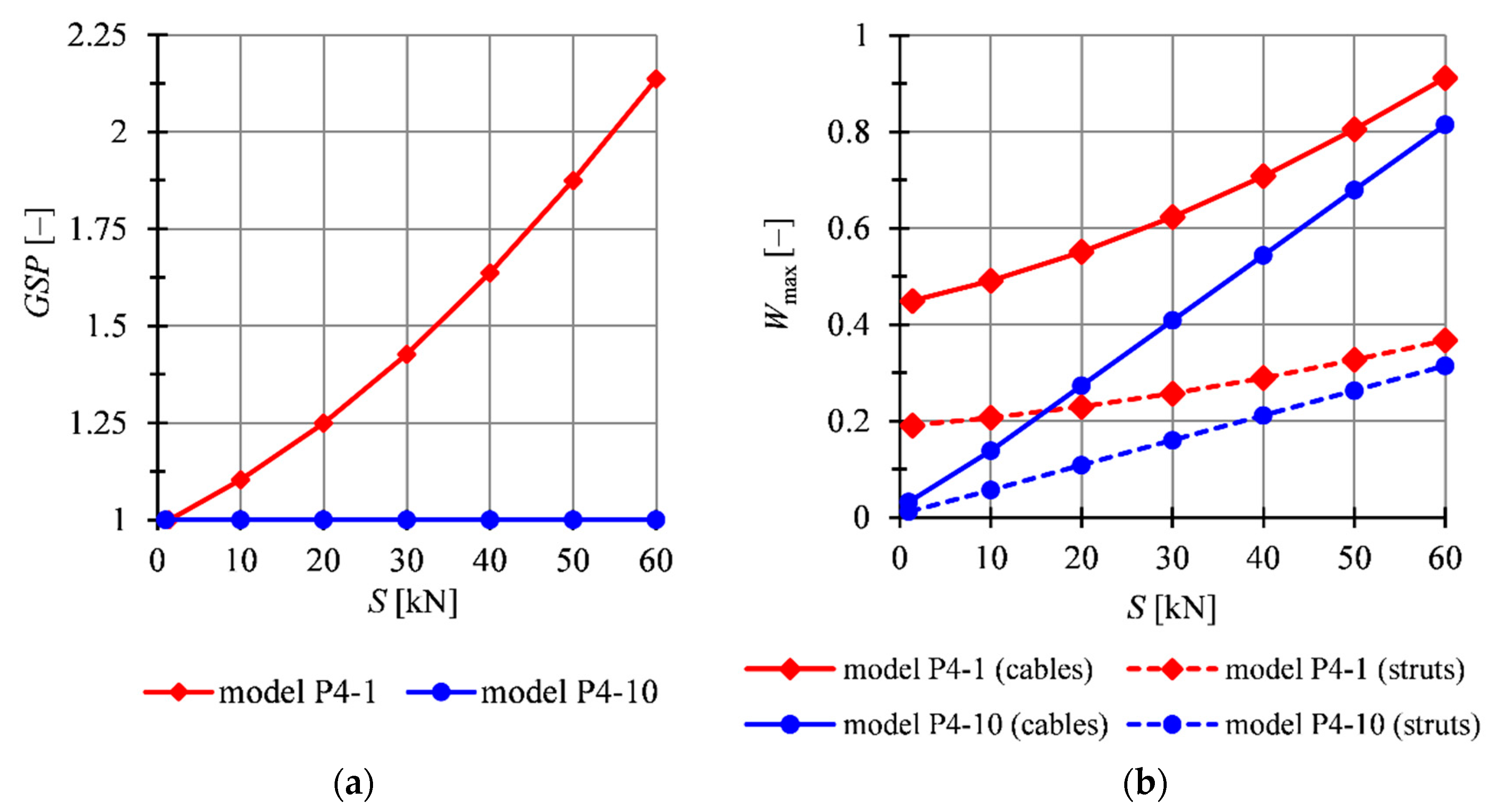
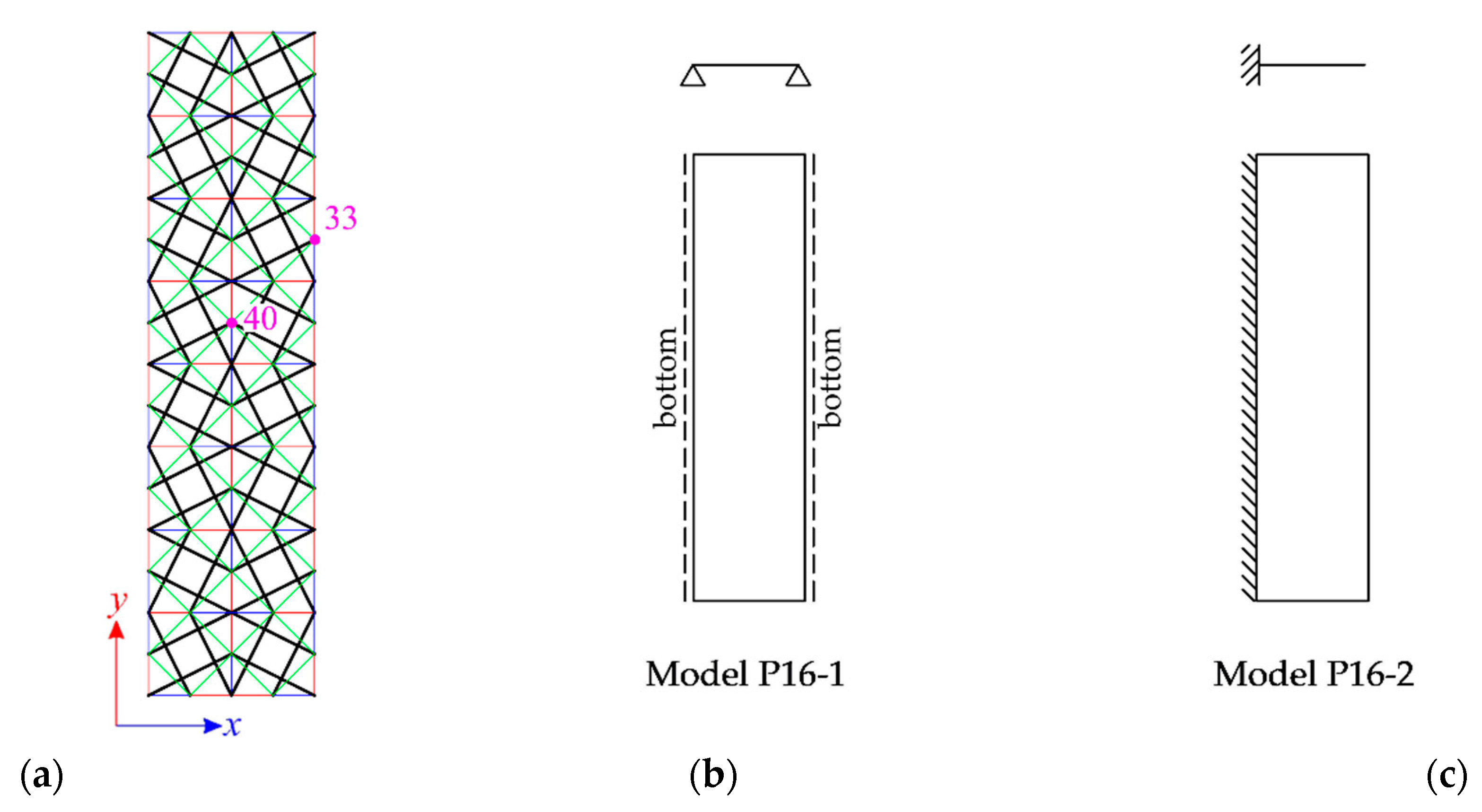


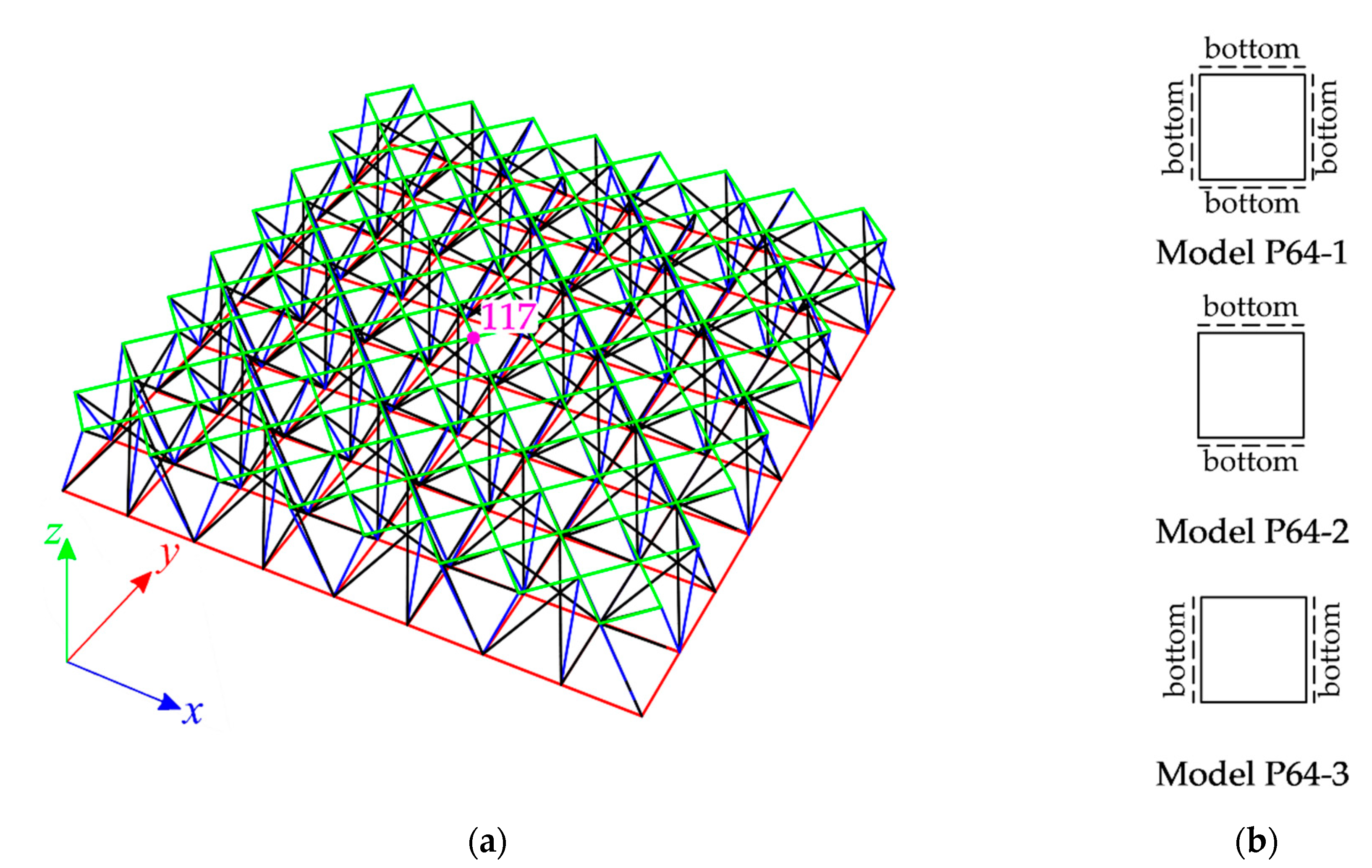
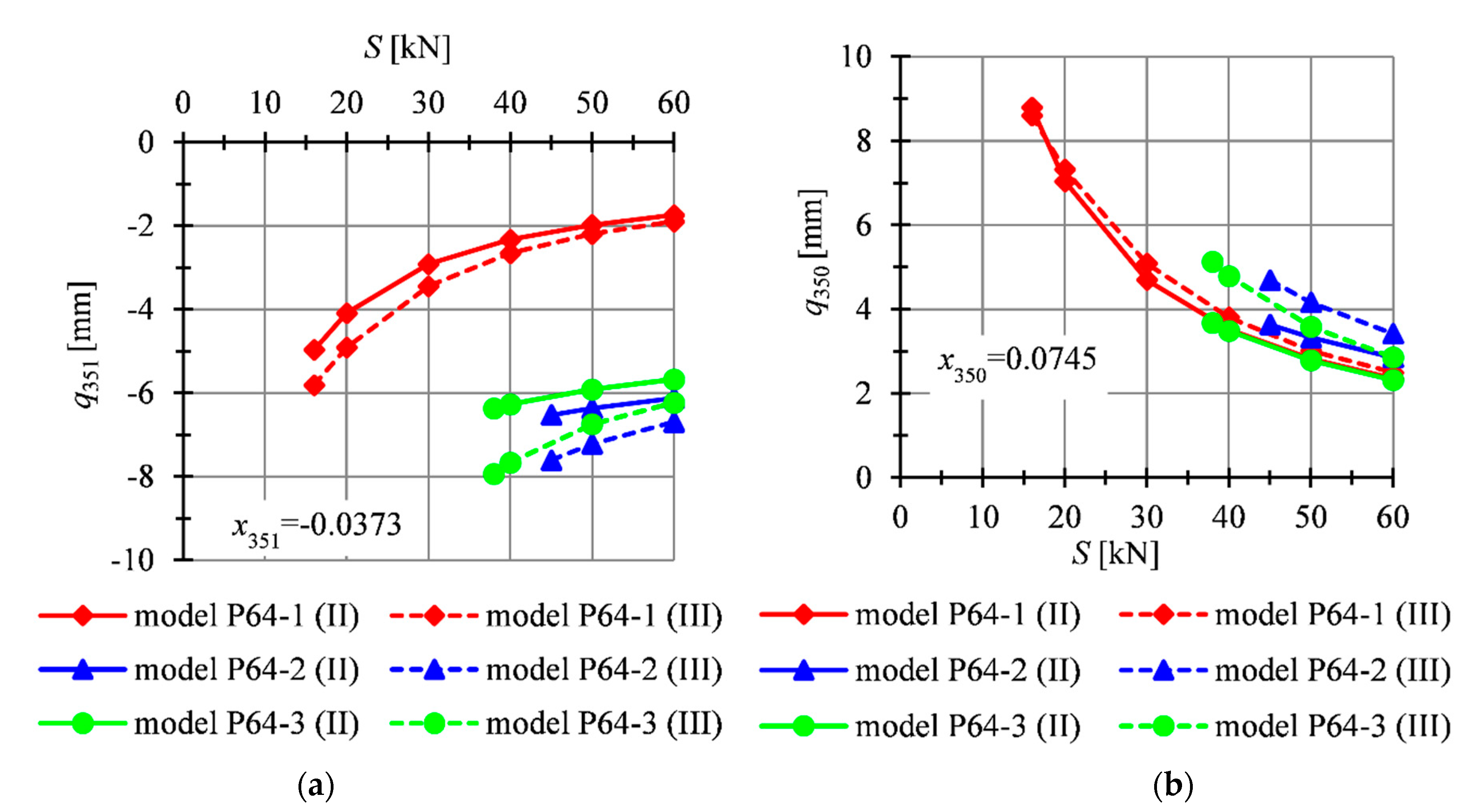

| S [kN] | Type of Element | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.01 | cables | 26.5 | 0.241 | 1.0 | 35.7 | 0.324 | 1.0 | 44.1 | 0.400 | 1.0 |
| struts | −35.6 | 0.184 | −47.8 | 0.246 | 59.1 | 0.305 | ||||
| 110 | cables | 87.3 | 0.792 | 3.7 | 91.1 | 0.826 | 2.9 | 95.3 | 0.865 | 2.5 |
| struts | −117.2 | 0.604 | −122.2 | 0.630 | −128.0 | 0.660 | ||||
| S [kN] | Type of Element | Model P4-1 () | Model P4-2 | Model P4-3 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Smin | cables | 49.54 | 0.450 | 1.0 | 48.8 | 0.443 | 1.0 | 54.4 | 0.493 | 1.0 |
| struts | −37.0 | 0.191 | −36.6 | 0.189 | −41.0 | 0.211 | ||||
| 60 | cables | 100.5 | 0.912 | 2.1 | 101.5 | 0.921 | 2.4 | 105.6 | 0.958 | 1.9 |
| struts | −71.2 | 0.367 | −71.93 | 0.371 | −75.4 | 0.389 | ||||
| S [kN] | Type of Element | Model P4-4 | Model P4-5 | ||||
|---|---|---|---|---|---|---|---|
| Smin | cables | 57.7 | 0.524 | 1.0 | 54.1 | 0.491 | 1.0 |
| struts | −46.3 | 0.239 | −50.1 | 0.258 | |||
| 60 | cables | 93.2 | 0.846 | 1.4 | 105.2 | 0.954 | 1.9 |
| struts | −73.1 | 0.376 | −77.0 | 0.397 | |||
| Simply Supported | Cantilever | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Second Order Theory | Third Order Theory | Second Order Theory | |||||||
| S | Plate Strip PS-1x | Plate Model P16-1 | Relative Error | Plate Strip PS-1x | Plate Model P16-1 | Relative Error | Plate Strip PS-2x | Plate Model P16-2 | Relative Error |
| [mm] | [mm] | [%] | [mm] | [mm] | [%] | [mm] | [mm] | [%] | |
| 3 | −156.339 | −156.342 | 0.00 | −17.056 | −17.605 | −3.11 | − | − | − |
| 10 | −46.965 | −46.967 | −0.01 | −15.672 | −16.131 | −2.85 | − | − | − |
| 21 | −23.527 | −23.530 | −0.01 | −13.751 | −14.091 | −2.41 | −0.737 | −0.793 | −7.08 |
| 30 | −15.715 | −15.717 | −0.02 | −11.954 | −12.193 | −1.95 | −0.736 | −0.793 | −7.08 |
| 40 | −11.808 | −11.811 | −0.02 | −10.345 | −10.505 | −1.52 | −0.736 | −0.792 | −7.07 |
| 50 | −9.465 | −9.467 | −0.03 | −8.962 | −9.066 | −1.15 | −0.736 | −0.792 | −7.07 |
| 60 | −7.902 | −7.905 | −0.03 | −7.810 | −7.878 | −0.86 | −0.735 | −0.791 | −7.08 |
| S [kN] | Type of Element | Model PS-1x () | Model PS-1y () | ||||
|---|---|---|---|---|---|---|---|
| Smin | cables | 54.1 | 0.491 | 1.0 | 52.7 | 0.478 | 1.0 |
| struts | −40.2 | 0.207 | −39.2 | 0.202 | |||
| 60 | cables | 103.3 | 0.937 | 2.2 | 102.6 | 0.931 | 2.2 |
| struts | −73.0 | 0.377 | −72.5 | 0.374 | |||
| S [kN] | Type of Element | Model P64-1 () | Model P64-2 () | Model P64-3 () | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Smin | cables | 28.9 | 0.262 | 1.0 | 72.5 | 0.658 | 1.0 | 64.8 | 0.588 | 1.0 |
| struts | −23.7 | 0.123 | −63.0 | 0.324 | −58.4 | 0.301 | ||||
| 60 | cables | 91.1 | 0.827 | 3.3 | 94.4 | 0.857 | 1.2 | 97.0 | 0.880 | 1.3 |
| struts | −64.6 | 0.333 | −77.9 | 0.402 | 79.9 | 0.412 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Obara, P.; Tomasik, J. Parametric Analysis of Tensegrity Plate-Like Structures: Part 2—Quantitative Analysis. Appl. Sci. 2021, 11, 602. https://doi.org/10.3390/app11020602
Obara P, Tomasik J. Parametric Analysis of Tensegrity Plate-Like Structures: Part 2—Quantitative Analysis. Applied Sciences. 2021; 11(2):602. https://doi.org/10.3390/app11020602
Chicago/Turabian StyleObara, Paulina, and Justyna Tomasik. 2021. "Parametric Analysis of Tensegrity Plate-Like Structures: Part 2—Quantitative Analysis" Applied Sciences 11, no. 2: 602. https://doi.org/10.3390/app11020602





