Numerical Simulation of Intrachamber Processes in the Power Plant
Abstract
:1. Introduction
2. Materials and Methods
2.1. Problem Statement and Mathematical Model
2.2. Numerical Schemes and Algorithms
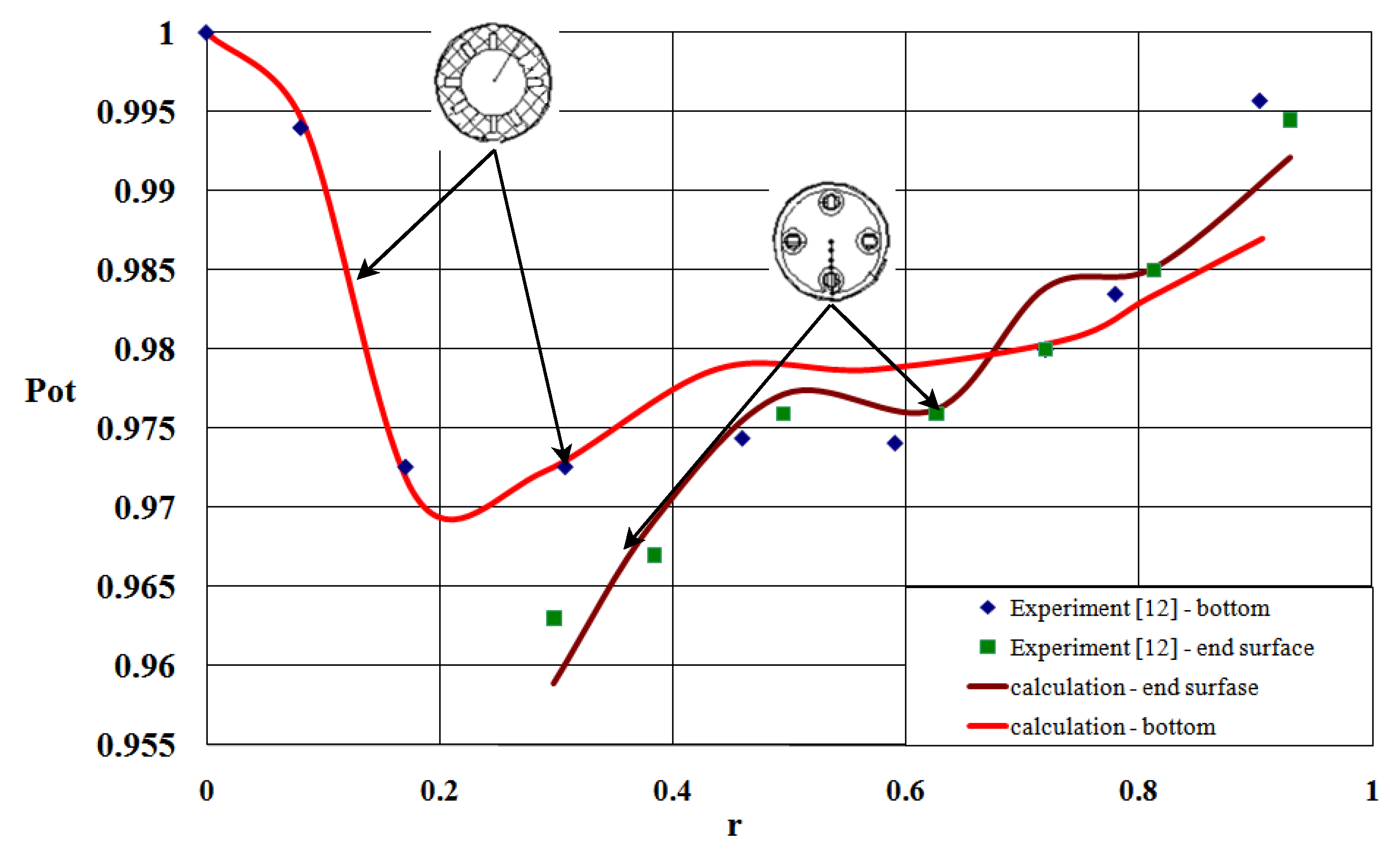
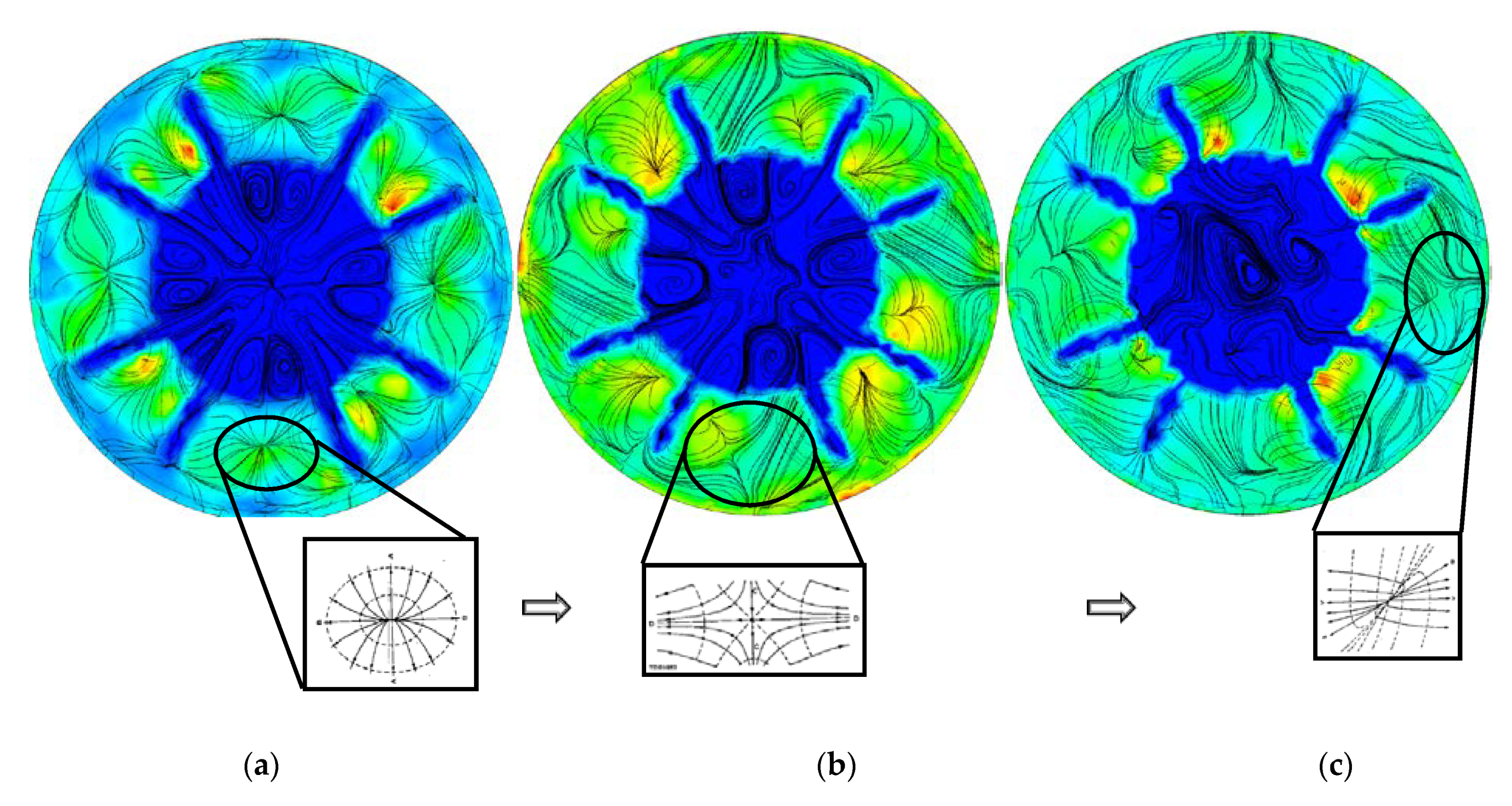
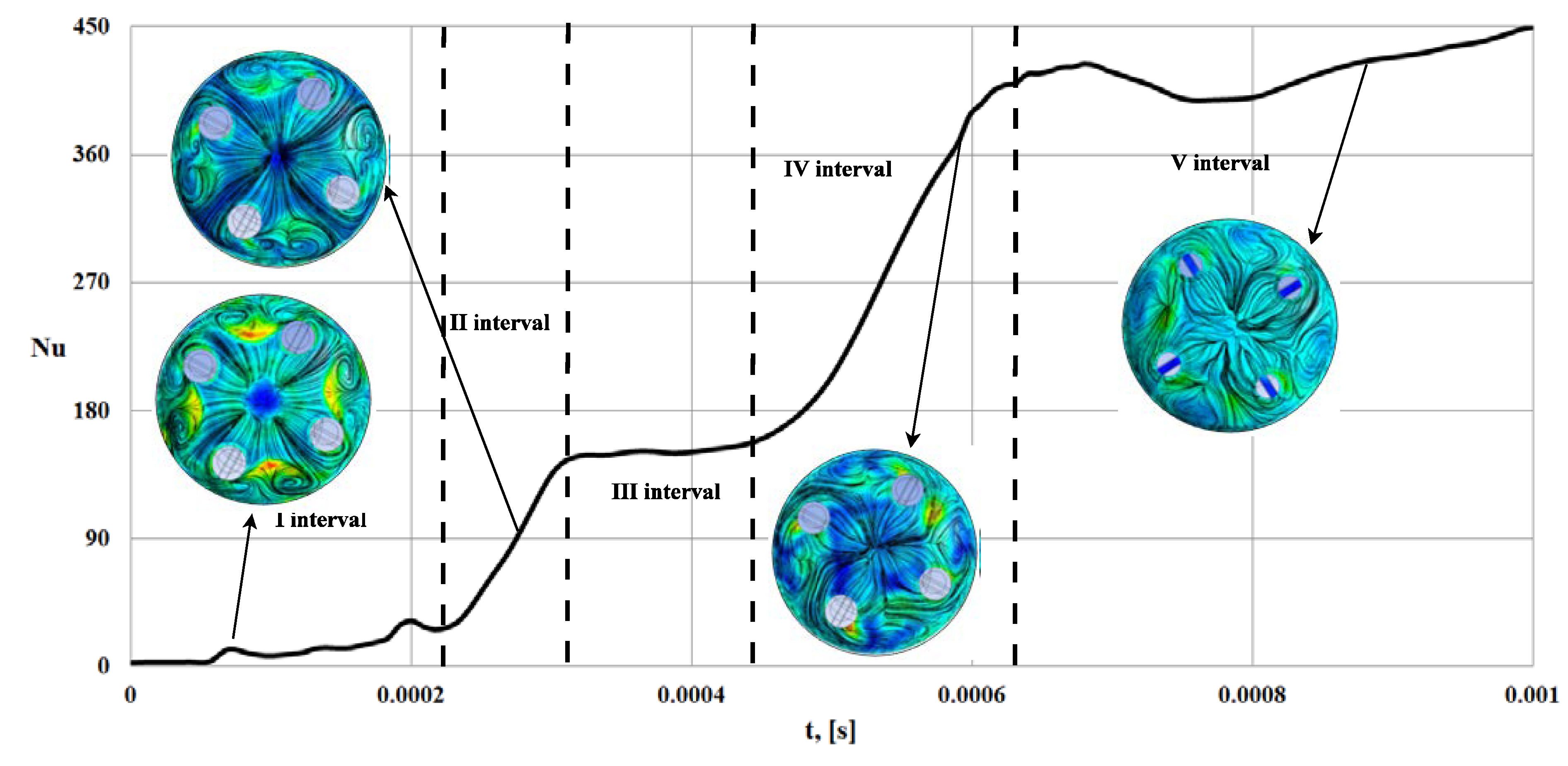
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Aliev, A. Mathematical Modeling in Power Engineering; ISTU: Izhevsk, Russia, 2001; pp. 25–156. [Google Scholar]
- Volkov, K.; Emelyanov, V. Mass Sypply Gas Flows in Channels and Paths of Power Plants; Fizmatlit: Moscow, Russia, 2011; pp. 5–460. [Google Scholar]
- Molchanov, A.M.; Bykov, L.V.; Platonov, I.M.; Yanyshev, D.S. Influence of geometric parameters and chemical kinetics model on combustion in a supersonic flow. J. Fluid Mech. Res. 2017, 44, 553–563. [Google Scholar] [CrossRef]
- Udaev, B. Heat Transfer; Higher School: Moscow, Russia, 1972; pp. 55–327. [Google Scholar]
- Fakhrutdinov, I.; Kotelnikov, A. Design and Engineering of Solid Propellant Rocket Motors; Mashinostroenie: Moscow, Russia, 1987; pp. 12–108. [Google Scholar]
- Andersen, D.; Tannehill, J.; Pletcher, R. Computational Hydromechanics and Heat Transfer; Mir: Moscow, Russia, 1990; pp. 203–717. [Google Scholar]
- Olson, R.V.; Eckert, E.R.G. Experimental studies of turbulent flow in a porous circular tube with uniform fluid injection through the tube wall. J. Appl. Mech. 1966, 33, 82–88. [Google Scholar] [CrossRef]
- Zieblend, H. Problems of heat transfer in rocket engines. J. Quest. Rocket Technol. 1971, 195, 4. [Google Scholar]
- Alemasov, V.; Dregalin, A.; Tishin, A. Theory of Rocket Engines: Textbook for Students of Mechanical Engineering Specialties of Higher Education Institutions; Mashinostroenie: Moscow, Russia, 1980; pp. 23–500. [Google Scholar]
- Vinnik, A.; Dureev, V. Estimation of convective heat transfer coefficient. Syst. Inf. Process. 2001, 2, 161–162. [Google Scholar]
- Zaykovsky, V.N.; Melamed, B.M. Experimental investigation of heat exchange in the subsonic flow path of rotating nozzles. In Proceedings of the III International School-Seminar “Unsteady Combustion and Internal Ballistics”, Saint-Petersburg, Russia, 26–30 June 2000; pp. 112–114. [Google Scholar]
- Savelyev, S.; Emelyanov, V.; Bendersky, B. Experimental Methods of Research of Gas Dynamics of SPRM; Nedra: Saint-Petersburg, Russia, 2007; pp. 31–200. [Google Scholar]
- Terekhov, V.; Kalinina, S. Heat transfeer suppression at the interaction of the impact jet with a hemispherical cavity. Tech. Phys. Lett. 2011, 37, 984–987. [Google Scholar] [CrossRef]
- Egorov, M. Numerical research of intra-chamber processes dynamics during startup of a special propellant engine. Russ. Aeronaut. 2017, 60, 591–599. [Google Scholar] [CrossRef]
- Volkov, K.; Denisikhin, S.; Emelyanov, V. Modeling problems of internal ballistics of power plants by means of modern computing packages. Chem. Phys. Mesoscopy 2006, 8, 327–335. [Google Scholar]
- Lipanov, A.; Dadikina, S.; Shumikhin, A.; Koroleva, M.; Karpov, A. Numerical modeling of intra-chamber unsteady turbulent flows. Part 1. Bull. South Ural State Univ. Ser. Math. Modeling Program. 2019, 12, 32–43. [Google Scholar] [CrossRef]
- Volkov, K.; Emel’yanov, V.; Denisikhin, S. Formation of vortex structures in the pre-nozzle space of an engine with a vectorable thrust nozzle. J. Eng. Phys. Thermophys. 2016, 89, 660–670. [Google Scholar] [CrossRef]
- Volkov, K.; Denisikhin, S.; Emel’yanov, V. Gas dynamics of a recessed nozzle in its displacement in the radial direction J. Eng. Phys. Thermophys. 2017, 90, 932–940. [Google Scholar] [CrossRef]
- Benderskiy, B.; Tenenev, V. Experimental and numerical investigation of flows in complex-shaped axisymmetric channels with mass injection. Fluid Dyn. 2001, 36, 336–340. [Google Scholar] [CrossRef]
- Benderskiy, B.; Chernova, A. Formation of vortex structures in channels with mass injection and their interaction with surfaces in solid-fuel rocket engines. Thermophys. Aeromech. 2015, 22, 185–190. [Google Scholar] [CrossRef]
- Tenenev, V.; Rusyak, I. Numerical Solution of Hydrodynamics and Heat Exchange Problems in Complex Shape Areas; ISTU Publ.: Izhevsk, Russia, 1995; pp. 10–32. [Google Scholar]
- Benderskiy, B.; Chernova, A. Features of heat transfer in a pre-nozzle volume of a solid-propellant rocket motor with charges of complex shapes. Thermophys. Aeromech. 2018, 25, 265–272. [Google Scholar] [CrossRef]
- Benderskyi, B.; Chernova, A. Influence of recessing nozzle extent on a process of heat exchange in the combustion chamber of a solid fuel rocket engine. J. Phys. Conf. Ser. 2020, 1677, 012035. [Google Scholar] [CrossRef]
- Dunaev, V.; Evlanov, A. Gas flow in a solid propellant rocket motor with a diaphragm. Proc. Tula State Univ. Tech. Sci. 2014, 12, 58–63. [Google Scholar]
- Volkov, K.; Emelyanov, V. Modeling of Large Eddies in Calculations of Turbulent Flows; Fizmatlit: Moscow, Russia, 2008; pp. 231–323. [Google Scholar]
- Isaev, S.; Popov, I.; Gritckevich, M.; Leontiev, A. Abnormal enhancement of separated turbulent air flow and heat transfer in inclined single-row oval-trench dimples at the narrow channel wall. Acta Astronaut. 2019, 163, 202–207. [Google Scholar] [CrossRef]
- Cernecky, J.; Valentova, K.; Pivarčiova, E.; Bozek, P. Ionization impact on the air cleaning efficiency in the interior. Meas. Sci. Rev. 2015, 15, 156–166. [Google Scholar] [CrossRef] [Green Version]
- Platonov, I.; Bykov, L. Investigation of the influence of the grid model quality on determining the location of laminar-turbulent transition on a gliding wing. Proc. Mai 2016, 89, 12. Available online: http://trudymai.ru/published.php?ID=72677 (accessed on 10 February 2021).
- Menter, F.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Murcinkova, Z.; Krenicky, T. Applications utilizing the damping of composite microstructures for mechanisms of production machines and manipulator devices. In Proceedings of the 13th Int. Multidisciplinary Sci. Geoconf. (SGEM 2013), Sofia, Bulgaria, 16–22 June 2013; Albena: Sofia, Bulgaria, 2013; pp. 23–30, ISBN 978-954-91818-9-0. [Google Scholar]
- OpenFoam. Free CFD Software. Available online: http://openfoam.org/ (accessed on 22 March 2019).
- Lambert, T. Automated Boundary Layer Mesh Generation for Simulation of Convective Cooling. Bachelor’s Thesis, RWTH Aachen University, Aachen, Germany, 2018. [Google Scholar]
- Yau, L.C. Conjugate Heat Transfer with the Multiphysics Coupling Library preCICE. Master’s Thesis, Techniche Universitet Munchen, Munchen, Germany, 2016. [Google Scholar]
- Murcinkova, Z.; Krenicky, T. Implementation of virtual instrumentation for multiparametric technical system monitoring. In Proceedings of the 13th Int. Multidisciplinary Sci. Geoconf. (SGEM 2013), Sofia, Bulgaria, 16–22 June 2013; Albena: Sofia, Bulgaria, 2013; pp. 139–144, ISBN 978-954-91818-9-0. [Google Scholar]
- Lakota, S.; Görög, A. Flatness Measurement by Multi-Point Methods and by Scanning Methods. Ad Alta J. Interdiscip. Res. 2011, 1, 124–127. [Google Scholar]
- Trebuňa, F.; Šimčák, F.; Bocko, J.; Trebuňa, P. Identification of causes of radial fan failure. Eng. Fail. Anal. 2009, 16, 2054–2065. [Google Scholar] [CrossRef]
- Kawalec, A.; Magdziak, M. An Influence of the Number of Measurement Points on the Accuracy of Measurements of Free-Form Surfaces on CNC Machine Tool. Adv. Manuf. Sci. Technol. 2011, 35, 17–27. [Google Scholar]
- Mikó, B. Assessment of Flatness Error by Regression Analysis. Meas. J. Int. Meas. Confed. 2021, 171, 108720. [Google Scholar] [CrossRef]
- Nowakowski, L.; Skrzyniarz, M.; Blasiak, S.; Bartoszuk, M. Influence of the Cutting Strategy on the Temperature and Surface Flatness of the Workpiece in Face Milling. Materials 2020, 13, 4542. [Google Scholar] [CrossRef] [PubMed]
- Trebuňa, F.; Šimčák, F.; Bocko, J.; Trebuňa, P. Failure analysis of mechanical elements in steelworks equipment by methods of experimental mechanics. Eng. Fail. Anal. 2010, 17, 787–801. [Google Scholar] [CrossRef]
- Trebuňa, F.; Šimčák, F.; Bocko, J.; Trebuňa, P.; Pástor, M.; Šarga, P. Analysis of crack initiation in the press frame and innovation of the frame to ensure its further operation. Eng. Fail. Anal. 2011, 18, 244–255. [Google Scholar] [CrossRef]
- Toh, C.K. A Study of the Effects of Cutter Path Strategies and Orientations in Milling. J. Mater. Process. Technol. 2004, 152, 346–356. [Google Scholar] [CrossRef]
- Repko, A.; Sága, M.; Sentyakov, B.; Sviatskii, V. Development and Testing of a Block Hydrocyclone. Processes 2020, 8, 1577. [Google Scholar] [CrossRef]
- Blatnicky, M.; Sága, M.; Dižo, J.; Bruna, M. Application of Light Metal Alloy EN AW 6063 to Vehicle Frame Construction with an Innovated Steering Mechanism. Materials 2020, 13, 817. [Google Scholar] [CrossRef] [Green Version]
- Tlach, V.; Císar, M.; Kuric, I.; Zajačko, I. Determination of the Industrial Robot Positioning Performance. In Modern Technologies in Manufacturing. MATEC Web Conf. 2017, 137, 01004. [Google Scholar] [CrossRef] [Green Version]
- Holubčík, M.; Klačková, I.; Ďurčanský, P. Pyrolysis Conversion of Polymer Wastes to Noble Fuels in Conditions of the Slovak Republic. Energies 2020, 13, 4849. [Google Scholar] [CrossRef]
- Kuric, I.; Císar, M.; Tlach, V.; Zajačko, I.; Gál, T.; Więcek, D. Technical Diagnostics at the Department of Automation and Production Systems. In Intelligent Systems in Production Engineering and Maintenance; Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2019; pp. 474–484. [Google Scholar]
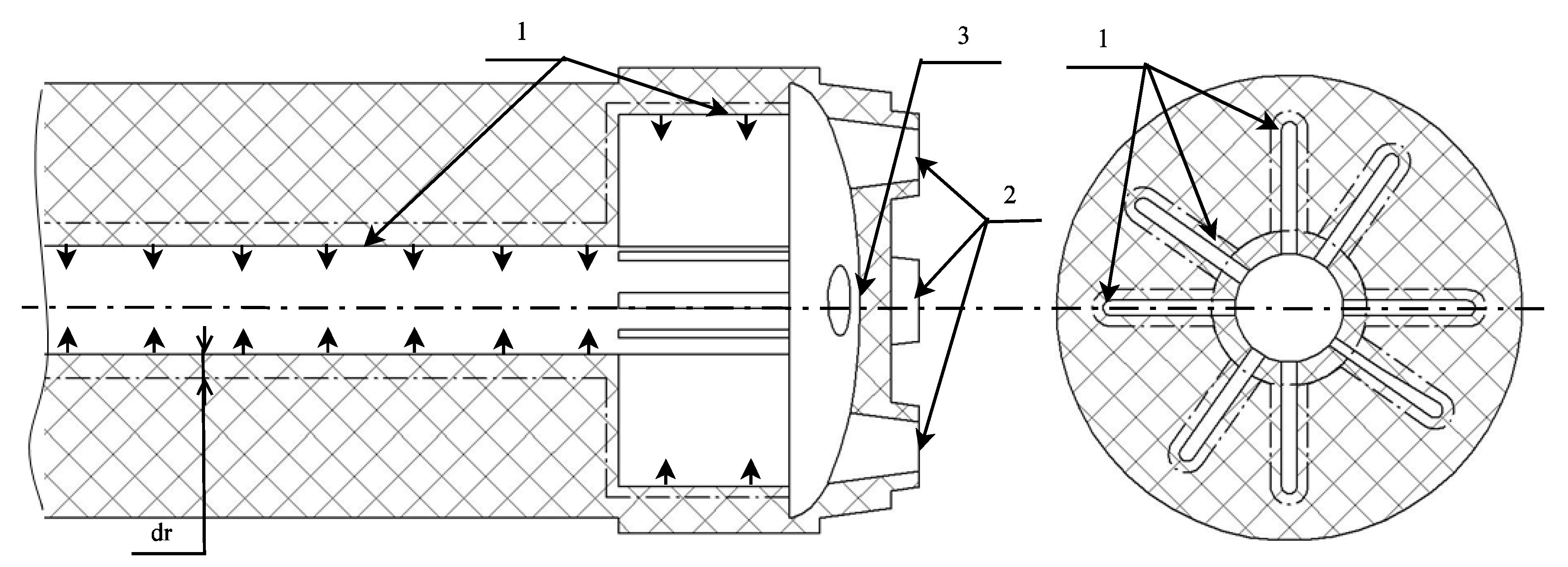

| Boundary | Condition |
|---|---|
| Mass supply surface Inlet | T = 2500K, G = 15 m/s, |
| Nozzle outlet | |
| Nozzle bottom and end surface (walls) | U = V = W = 0, Twall (x, y, z, t)|wall = Tgas(x, y, z, t)|gas, |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benderskiy, B.; Frankovský, P.; Chernova, A. Numerical Simulation of Intrachamber Processes in the Power Plant. Appl. Sci. 2021, 11, 4990. https://doi.org/10.3390/app11114990
Benderskiy B, Frankovský P, Chernova A. Numerical Simulation of Intrachamber Processes in the Power Plant. Applied Sciences. 2021; 11(11):4990. https://doi.org/10.3390/app11114990
Chicago/Turabian StyleBenderskiy, Boris, Peter Frankovský, and Alena Chernova. 2021. "Numerical Simulation of Intrachamber Processes in the Power Plant" Applied Sciences 11, no. 11: 4990. https://doi.org/10.3390/app11114990
APA StyleBenderskiy, B., Frankovský, P., & Chernova, A. (2021). Numerical Simulation of Intrachamber Processes in the Power Plant. Applied Sciences, 11(11), 4990. https://doi.org/10.3390/app11114990






