Driving Safety Improved with Control of Magnetorheological Dampers in Vehicle Suspension
Abstract
:1. Introduction
1.1. Vehicle Suspension
1.2. Modelling of the Vehicle
1.3. Control of Semi-Active Suspension
1.4. Highlights
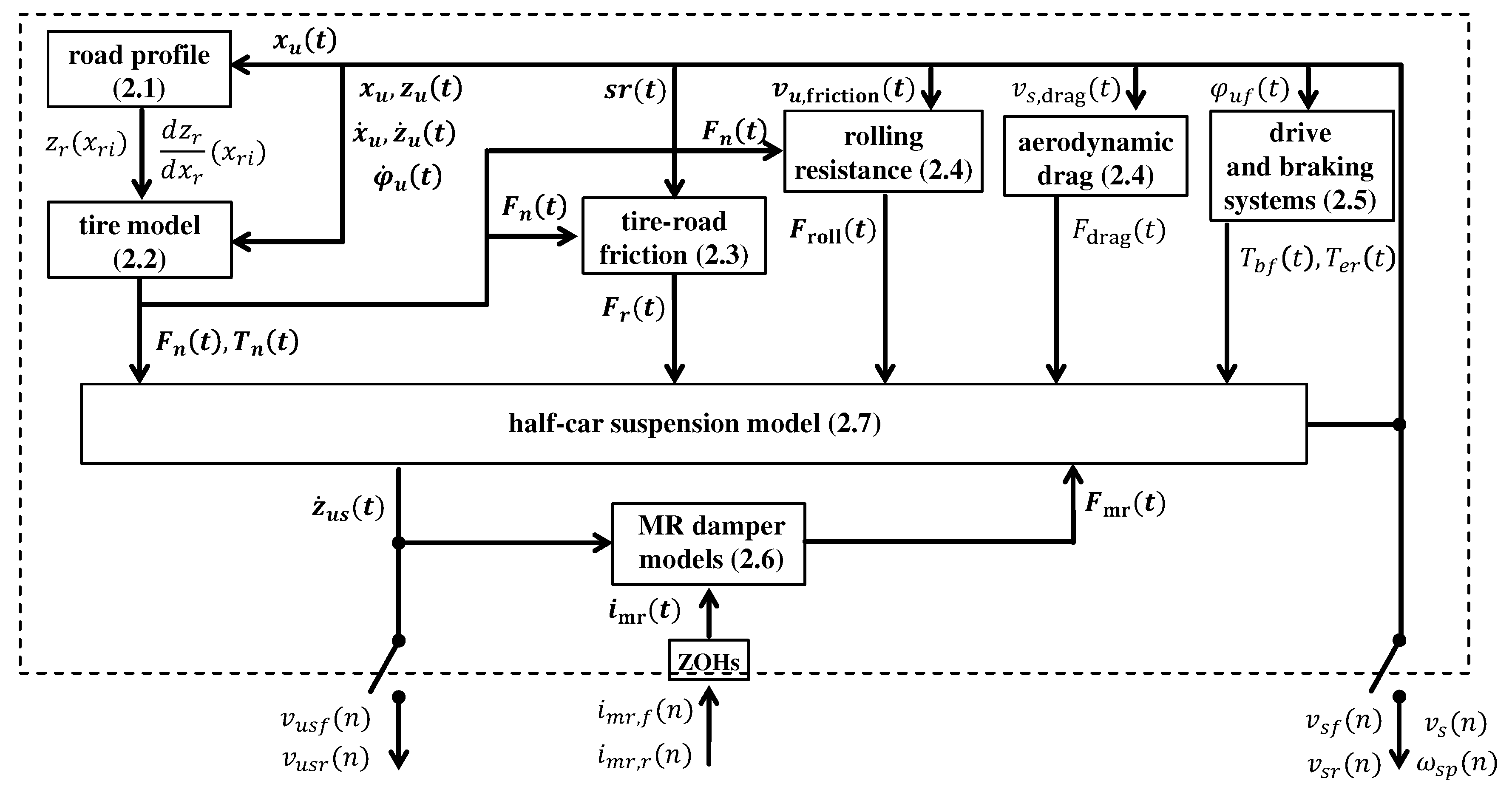
2. Vehicle Model and Its Coupling with Road and Environment
2.1. Road Profile
2.2. Wheel and Tire Model
2.3. Burckhardt Model of Tire to Road Friction
2.4. Wheel Rolling Resistance and Aerodynamic Drag of the Vehicle
2.5. Vehicle Drive and Braking Systems
2.6. MR Damper Model
2.7. Longitudinal and Vertical Dynamics of Half-Car Vehicle Model
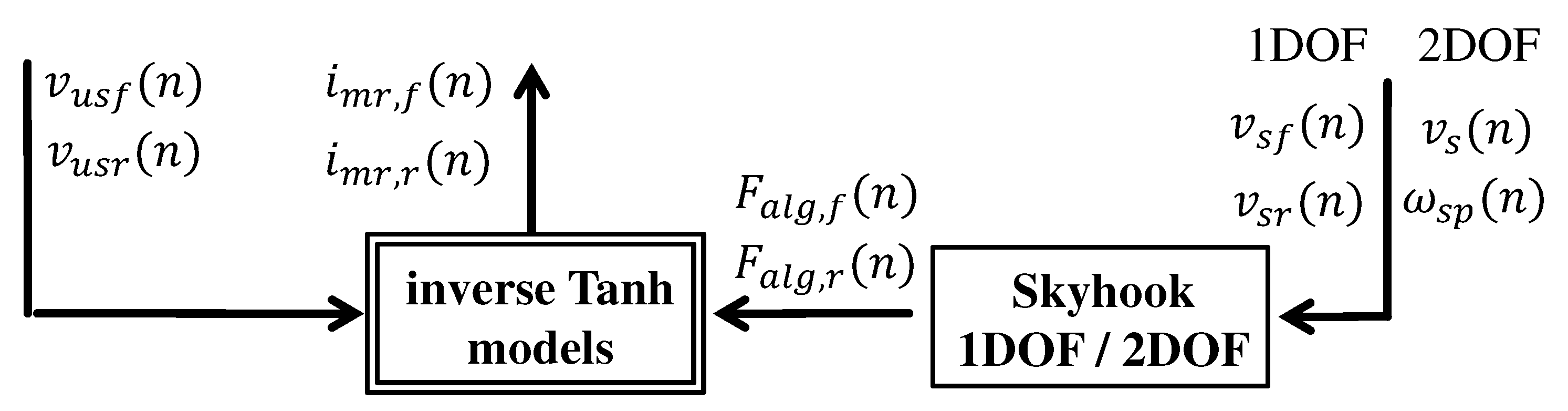
3. Control Algorithms
3.1. Skyhook Control of the Suspension Quarter (Skyhook-1DOF)
3.2. Skyhook Control of Heave and Pitch Vibration Modes (Skyhook-2DOF)
4. Simulation Results
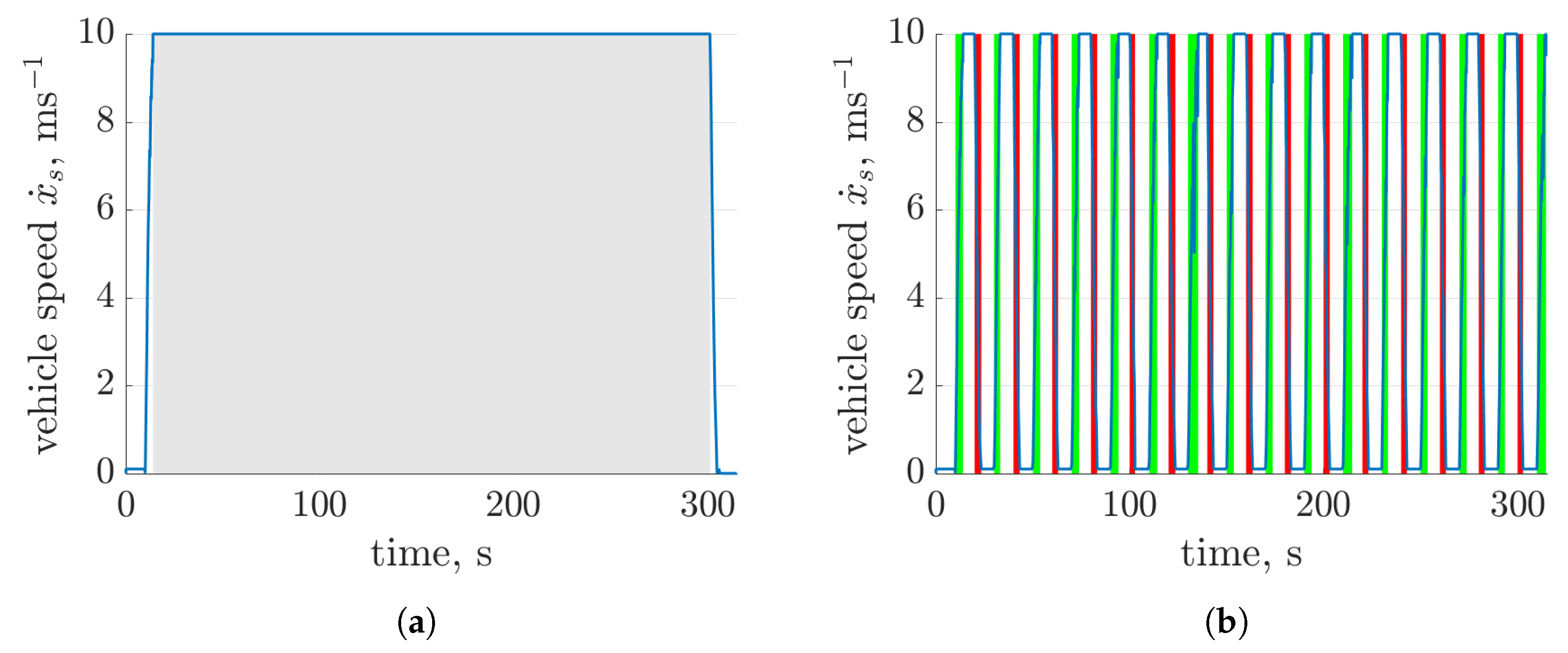
4.1. Simulation Environment
4.2. Test Procedure
4.3. Emulation of Passive Suspension
4.4. Skyhook Control of the Suspension Quarter (Skyhook-1DOF)
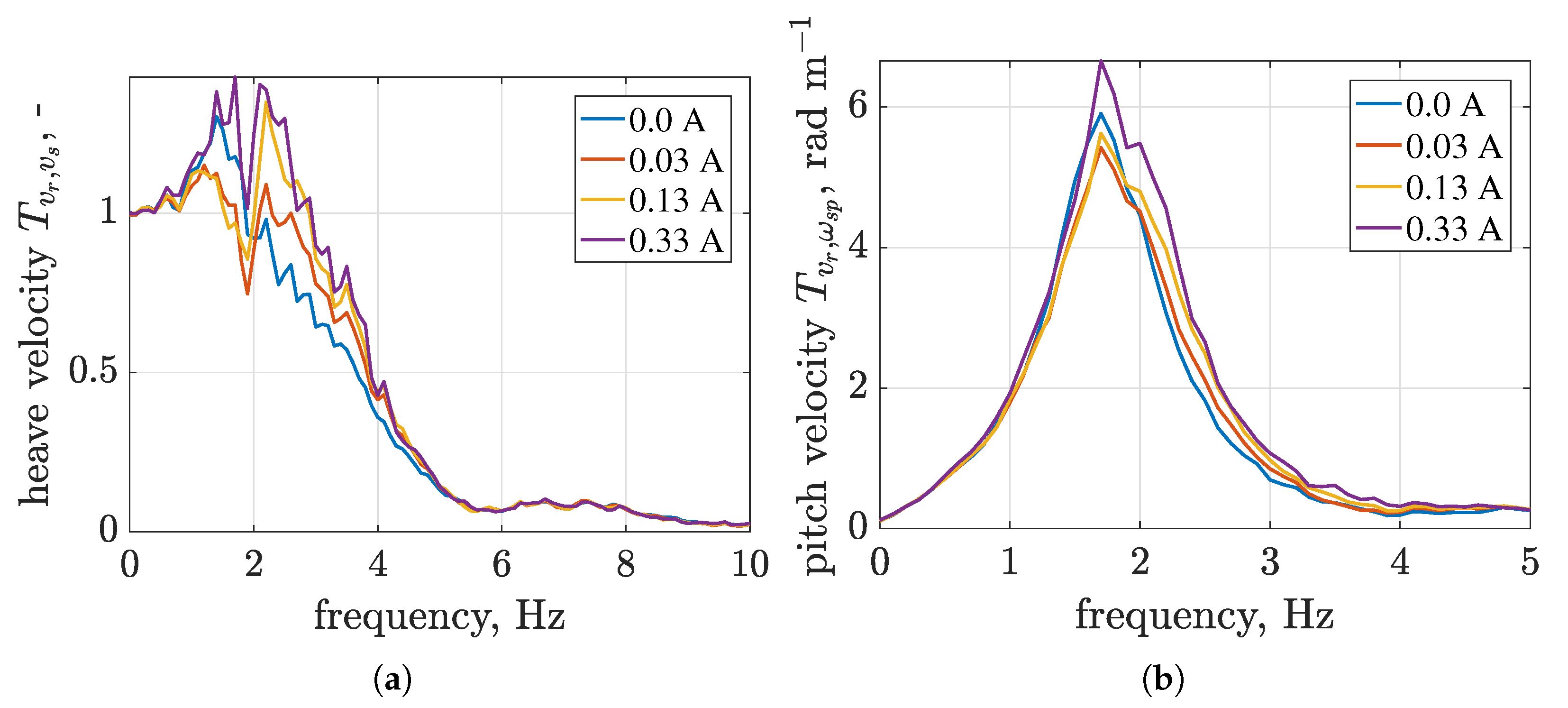
4.5. Skyhook Control of Vehicle Body Vibration Modes (Skyhook-2DOF)
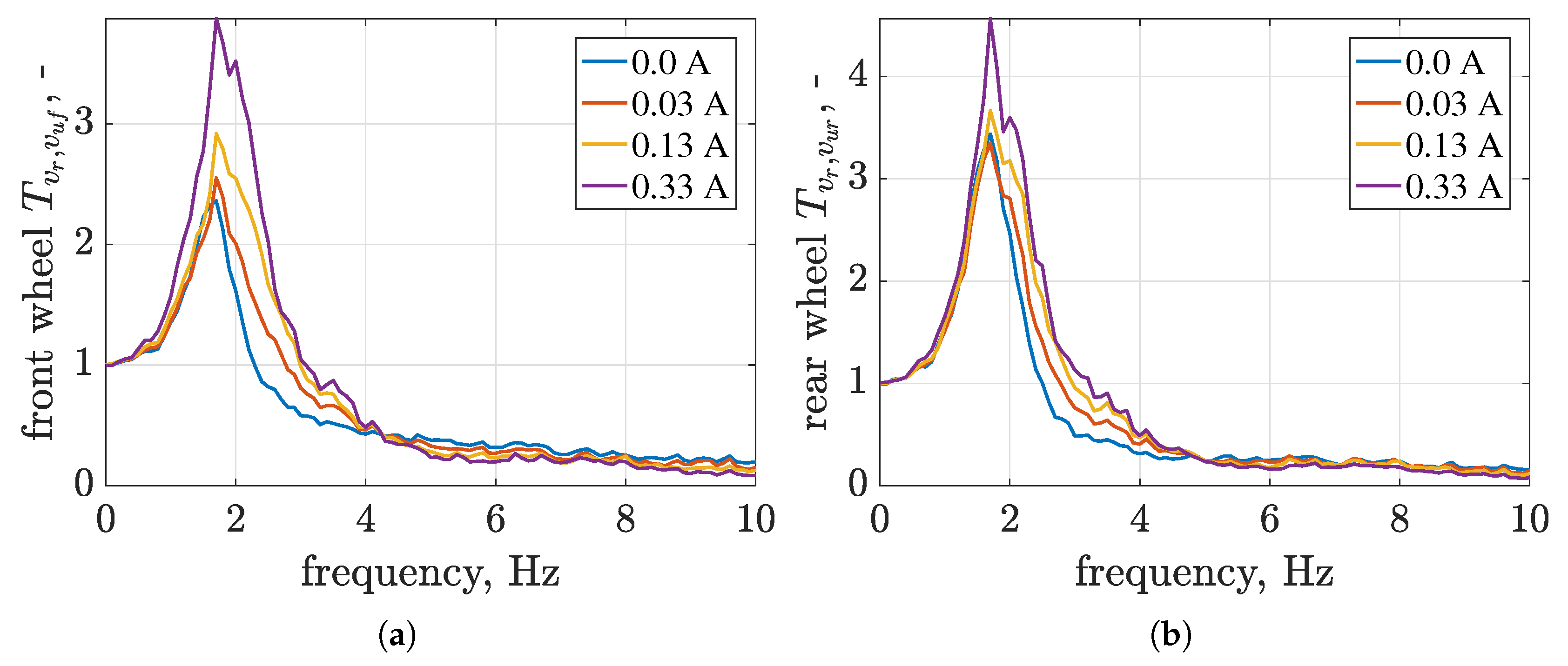
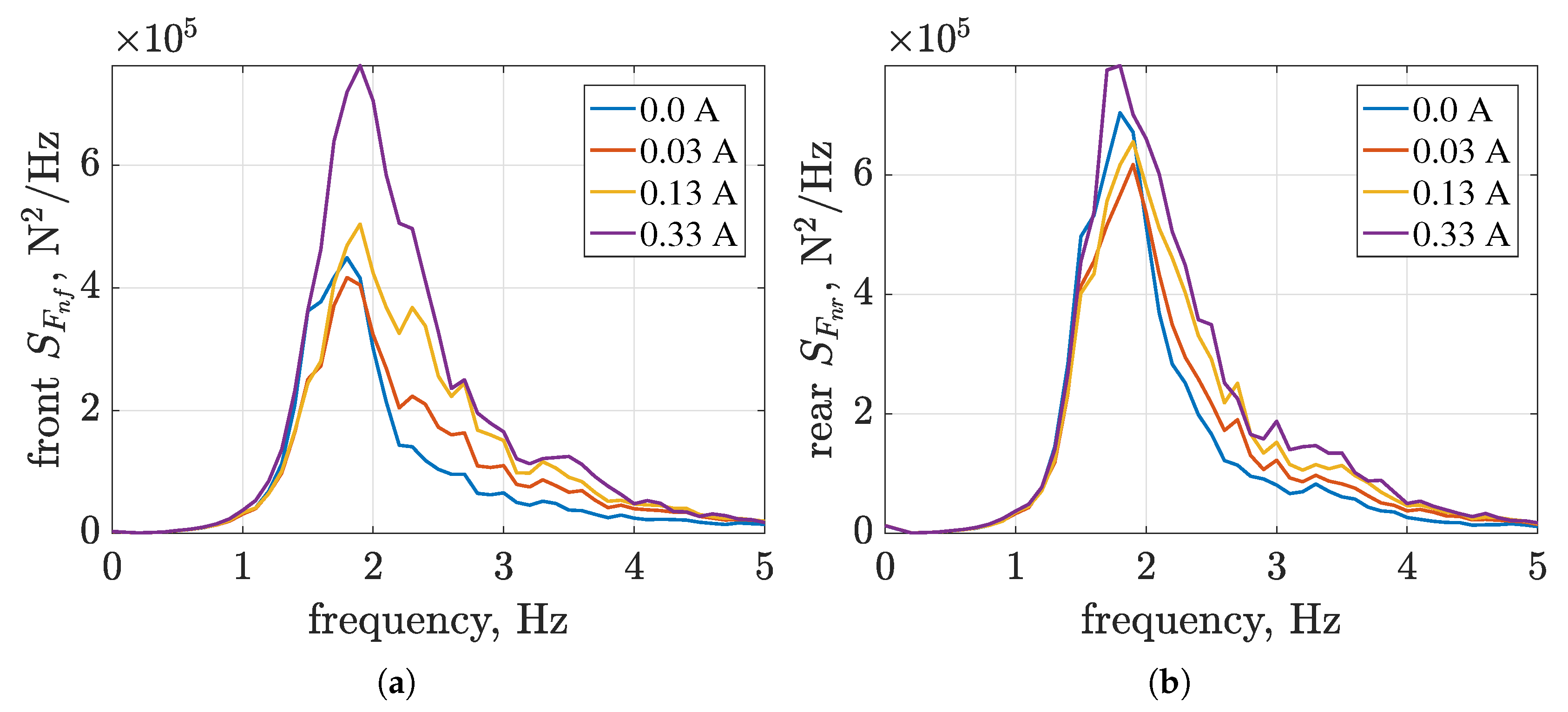
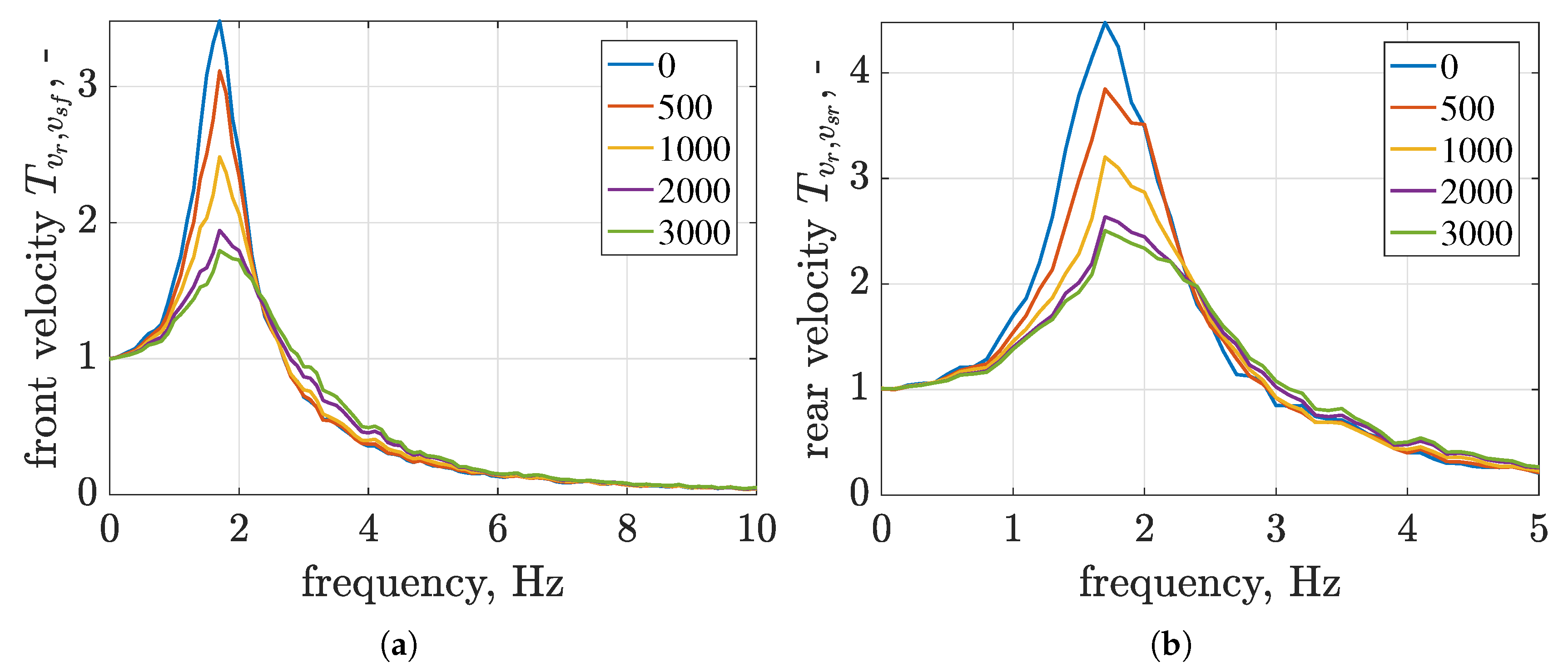
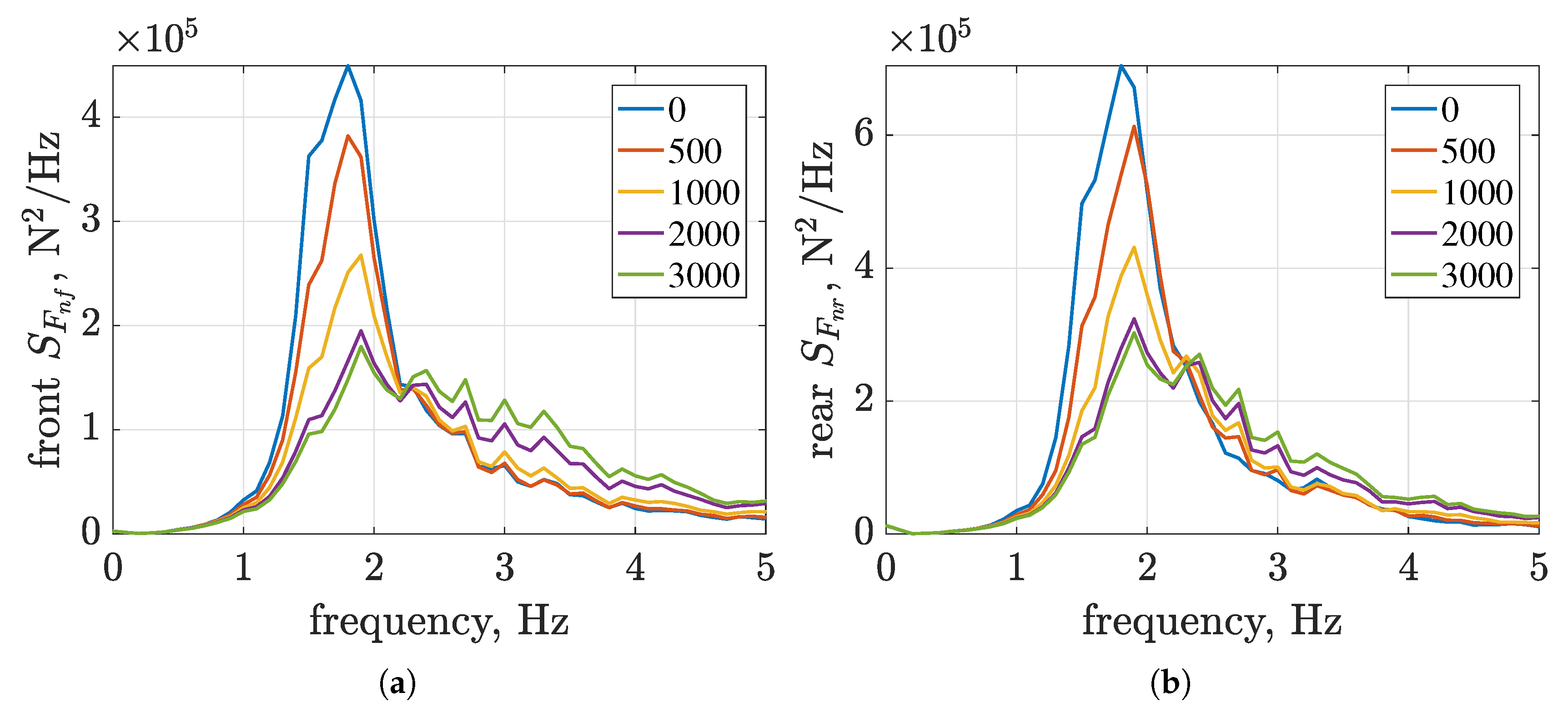
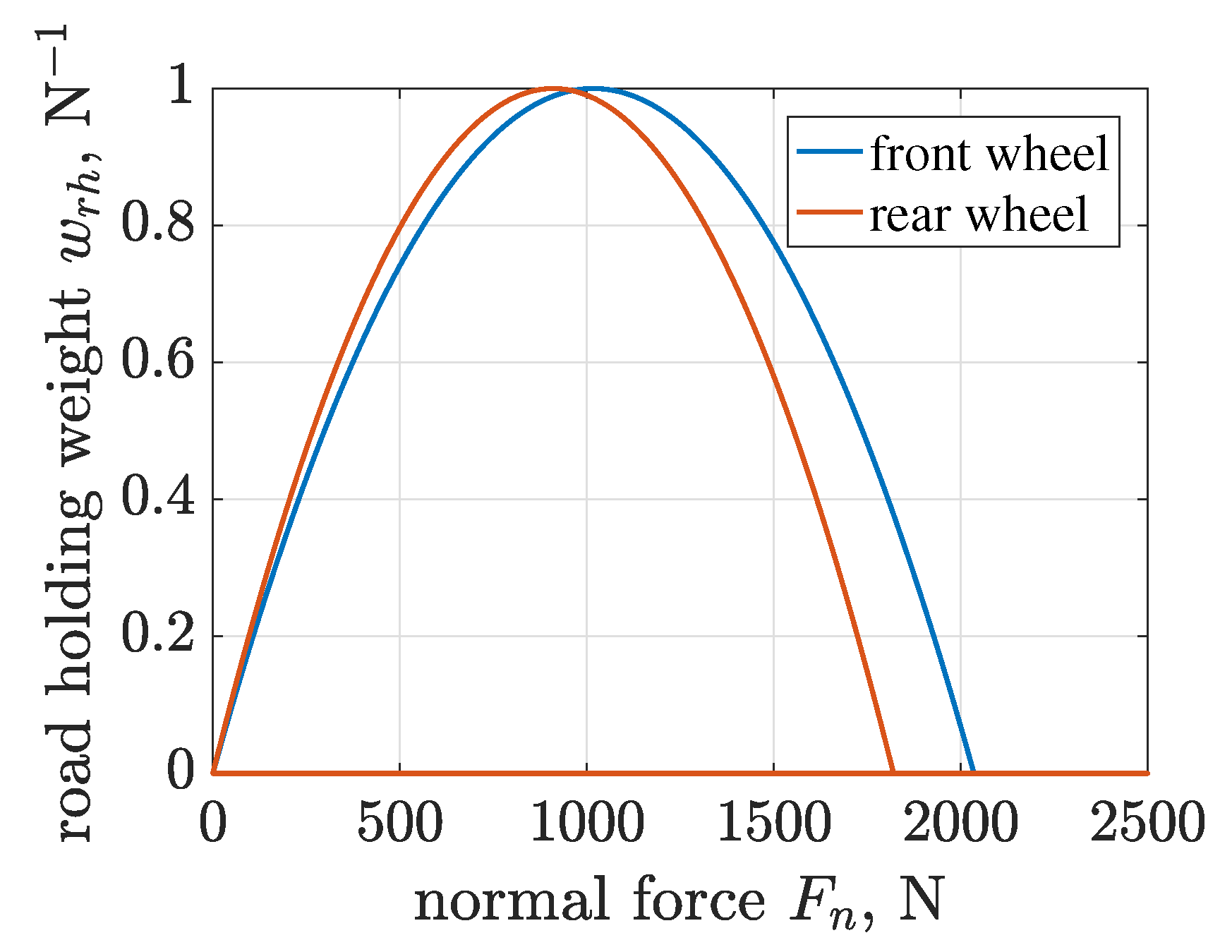
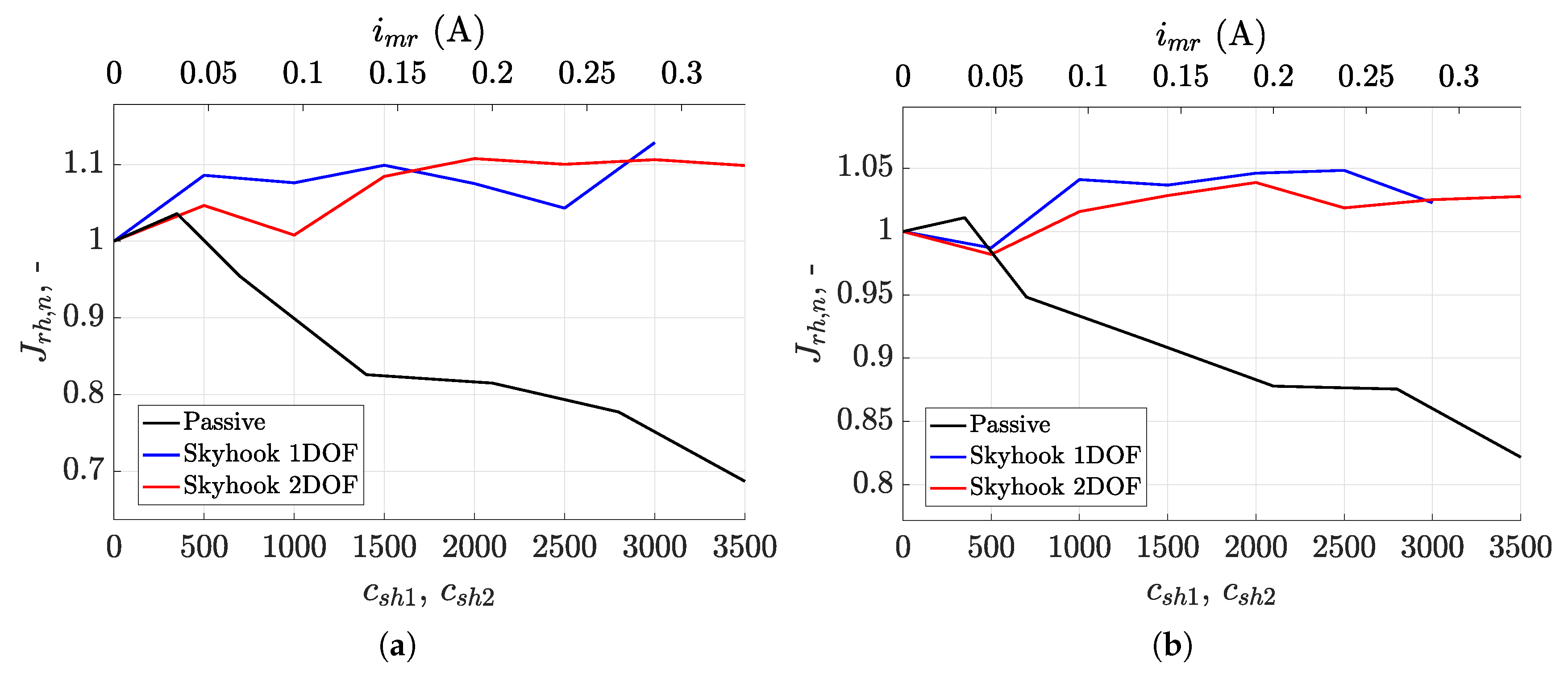
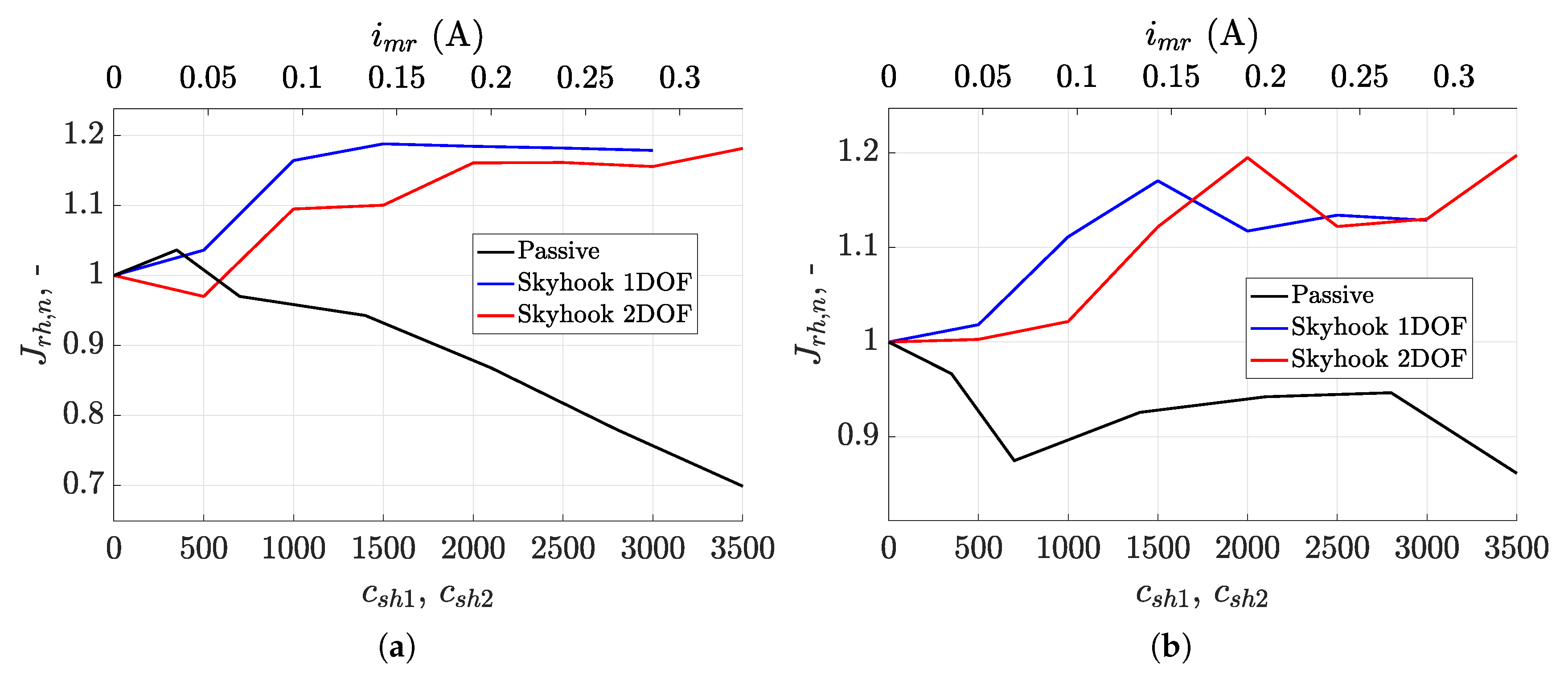
4.6. Road Holding
4.7. Vehicle Handling
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Osueke, E.C.O.; Uguru-Okorie, D.C. The role of tire in car crash, its causes, and prevention. Int. J. Emerg. Technol. Adv. Eng. 2012, 2, 54–57. [Google Scholar]
- Jazar, N.J. Chapter 3: Tire dynamics. In Vehicle Dynamics: Theory and Applications, 1st ed.; Springer: New York, NY, USA, 2008; pp. 95–164. [Google Scholar]
- El-Kholy, S.A.; Galal, S.A. A study on the effects of non-uniform tyre inflation pressure distribution on rigid pavement. Int. J. Pavement Eng. 2012, 13, 244–258. [Google Scholar] [CrossRef]
- Uys, P.E.; Els, P.S.; Thoresson, M.J. Criteria for handling measurement. J. Terramech. 2006, 43, 43–67. [Google Scholar] [CrossRef]
- Els, P.S.; Theron, N.J.; Uys, P.E.; Thoresson, M.J. The ride comfort vs. handling compromise for off-road vehicles. J. Terramech. 2007, 44, 303–317. [Google Scholar] [CrossRef] [Green Version]
- Dahlberg, E. A method determining the dynamic rollover threshold of commercial vehicles. SAE Trans. 2000, 109, 789–801. [Google Scholar]
- Choi, S.B.; Lee, H.K.; Chang, E.G. Field results of a semi-active ER suspension system associated with skyhook controller. Mechatronics 2001, 11, 345–353. [Google Scholar] [CrossRef]
- Krauze, P.; Kasprzyk, J.; Rzepecki, J. Experimental attenuation and evaluation of whole body vibration for an off-road vehicle with magnetorheological dampers. J. Low Freq. Noise Vib. Act. Control 2019, 38, 852–870. [Google Scholar] [CrossRef] [Green Version]
- Sibielak, M.; Konieczny, J.; Kowal, J.; Rączka, W.; Marszalik, D. Optimal control of slow-active vehicle suspension—Results of experimental data. J. Low Freq. Noise Vib. Act. Control 2013, 32, 99–116. [Google Scholar] [CrossRef]
- Konieczny, J.; Rączka, W.; Sibielak, M.; Kowal, J. Energy consumption of an active vehicle suspension with an optimal controller in the presence of sinusoidal excitations. Shock Vib. 2020, 2020, 6414352. [Google Scholar] [CrossRef]
- Koo, J.-H.; Goncalves, F.D.; Ahmadian, M. A comprehensive analysis of the response time of MR dampers. Smart Mater. Struct. 2006, 15, 351–358. [Google Scholar] [CrossRef]
- Bai, X.-X.; Zhong, W.-M.; Zou, Q.; Zhu, A.-D.; Sun, J. Principle, design and validation of a power-generated magnetorheological energy absorber with velocity self-sensing capability. Smart Mater. Struct. 2018, 27, 1–18. [Google Scholar] [CrossRef]
- Sapiński, B. Real-time control for a magnetorheological shock absorber in a driver seat. J. Theor. Appl. Mech. 2005, 43, 631–653. [Google Scholar]
- Spencer, B.F.; Dyke, S.J.; Sain, M.K.; Carlson, J.D. Phenomenological model of a magnetorheological damper. J. Eng. Mech. 1997, 123, 1–23. [Google Scholar] [CrossRef]
- Kasprzyk, J.; Wyrwał, J.; Krauze, P. Automotive MR damper modeling for semi-active vibration control. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Besancon, France, 8–11 July 2014; pp. 500–505. [Google Scholar]
- Wiora, J.; Wiora, A. Measurement uncertainty evaluation of results provided by transducers working in control loops. In Proceedings of the 23rd International Conference on Methods and Models in Automation and Robotics MMAR, Miedzyzdroje, Poland, 27–30 August 2018; pp. 763–767. [Google Scholar]
- Karnopp, D.; Crosby, M.J.; Harwood, R.A. Vibration control using semi-active force generators. J. Eng. Ind. 1974, 96, 619–626. [Google Scholar] [CrossRef]
- Prabakar, R.S.; Sujatha, C.; Narayanan, S. Optimal semi-active preview control response of a half car vehicle model with magnetorheological damper. J. Sound Vib. 2009, 326, 400–420. [Google Scholar] [CrossRef]
- Lagraa, N.; Boukhetala, D.; Bloch, G.; Boudjema, F. Nonlinear control design of active suspension based on full car model. Arch. Control. Sci. 2007, 17, 439–457. [Google Scholar]
- Pacejka, H.B. Chapter 4: Semi-empirical tyre models. In Tire and Vehicle Dynamics, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2006; pp. 156–215. [Google Scholar]
- Blundell, M.; Harty, D. Chapter 5: Tyre characteristics and modelling. In The Multibody Systems Approach to Vehicle Dynamics, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2015; pp. 335–450. [Google Scholar]
- Lugner, P.; Pacejka, H.; Ploechl, M. Recent advances in tyre models and testing procedures. Veh. Syst. Dyn. 2005, 43, 413–436. [Google Scholar] [CrossRef]
- Boere, S.; Arteaga, I.L.; Kuijpers, A.; Nijmeijer, H. Tyre/road interaction model for the prediction of road texture influence on rolling resistance. Int. J. Veh. Des. 2014, 65, 202–221. [Google Scholar] [CrossRef]
- Wei, C.; Olatunbosun, O.A.; Behroozi, M. Simulation of tyre rolling resistance generated on uneven road. Int. J. Veh. Des. 2016, 70, 113–136. [Google Scholar] [CrossRef]
- Kim, S.; Nikravesh, P.E.; Gim, G. A two-dimensional tire model on uneven roads for vehicle dynamic simulation. Veh. Syst. Dyn. 2008, 46, 913–930. [Google Scholar] [CrossRef]
- Rajamani, R. Chapter 4: Longitudinal vehicle dynamics. In Vehicle Dynamics and Control, 1st ed.; Springer: New York, NY, USA, 2006; pp. 95–122. [Google Scholar]
- Rajamani, R. Chapter 13: Lateral and longitudinal tire forces. In Vehicle Dynamics and Control, 1st ed.; Springer: New York, NY, USA, 2006; pp. 433–461. [Google Scholar]
- Farroni, F.; Russo, M.; Russo, R.; Timpone, F. Tyre-road interaction: Experimental investigations about the friction coefficient dependence on contact pressure, road roughness, slide velocity and temperature. In Proceedings of the ASME 2012 11th Biennial Conference on Engineering Systems Design and Analysis, Nantes, France, 2–4 July 2012; pp. 1–10. [Google Scholar]
- Svendenius, J.; Wittenmark, B. Brush tire model with increased flexibility. In Proceedings of the European Control Conference, Cambridge, UK, 1–4 September 2003; pp. 1–6. [Google Scholar]
- Li, L.; Wang, F.-Y.; Zhou, Q. Integrated longitudinal and laterl tire/road friction modeling and monitoring for vehicle motion control. IEEE Trans. Intell. Trasp. Syst. 2006, 7, 1–19. [Google Scholar] [CrossRef]
- Salehi, M.; Noordermeer, J.W.; Reuvekamp, L.A.; Dierkes, W.K.; Blume, A. Measuring rubber friction using a Laboratory Abrasion Tester (LAT100) to predict car tire dry ABS braking. Tribol. Int. 2019, 131, 191–199. [Google Scholar] [CrossRef]
- Burckhardt, M. Fahrwerktechnik: Radschlupf-Regelsysteme; Vogel Fachbuch: Wuerzburg, Germany, 1993. [Google Scholar]
- Kiencke, U.; Nielsen, L. Vehicle modelling. In Automotive Control Systems: For Engine, Driveline and Vehicle, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 301–350. [Google Scholar]
- Reimpell, J.; Sponagel, P. Fahrwerktechnik: Reifen und Raeder; Vogel Fachbuch: Wuerzburg, Germany, 1995. [Google Scholar]
- Rahman, M.; Ong, Z.C.; Julai, S.; Ferdaus, M.M.; Ahamed, R. A review of advances in magnetorheological dampers: Their design optimization and applications. J. Zhejiang Univ. Sci. A 2017, 18, 991–1010. [Google Scholar] [CrossRef]
- Moczko, P.; Pietrusiak, D.; Więckowski, J. Investigation of the failure of the bucket wheel excavator bridge conveyor. Eng. Fail. Anal. 2019, 106, 1–12. [Google Scholar] [CrossRef]
- Savaresi, S.M.; Poussot-Vassal, C.; Spelta, C.; Sename, O.; Dugard, L. Chapter 6: Classical control for semi-active suspension system. In Semi-Active Suspension Control Design for Vehicles, 1st ed.; Butterworth-Heinemann: Oxford, UK, 2010; pp. 107–120. [Google Scholar]
- Rafajłowicz, W.; Więckowski, J.; Moczko, P.; Rafajłowicz, E. Iterative learning from suppressing vibrations in construction machinery using magnetorheological dampers. Autom. Constr. 2020, 119, 1–10. [Google Scholar] [CrossRef]
- Kurczyk, S.; Pawełczyk, M. Fuzzy control for semi-active suspension. J. Low Freq. Noise Vib. Act. Control 2013, 32, 217–226. [Google Scholar] [CrossRef] [Green Version]
- Lu, S.-B.; Li, Y.-N.; Choi, S.-B.; Zheng, L.; Seong, M.-S. Integrated control of MR vehicle suspension system associated with braking and steering control. Veh. Syst. Dyn. 2011, 49, 361–380. [Google Scholar] [CrossRef]
- ISO 8608:2016. Mechanical Vibration—Road Surface Profiles–Reporting of Measured Data; International Organization for Standarization: Geneva, Switzerland, 2016. [Google Scholar]
- Grzebieta, R.; Rechnitzer, G.; Simmons, K. Static Stability Test Results; Transport and Road Safety (TARS), University of New South Wales: Sydney, Australia, 2015; Available online: http://www.tars.unsw.edu.au/research/Current/Quad-Bike_Safety/Reports/Quad_Project_Final_Report1_Static_Stabilty_Test_Results_Jan-2015.pdf (accessed on 16 November 2020).
- Arczyński, S. Chapter 3: Opory ruchu samochodu. In Mechanika Ruchu Samochodu; Wydawnictwo Naukowo Techniczne: Warszawa, Poland, 1993. [Google Scholar]
- Ubysz, A. Problems of rotational mass in passenger vehicles. Transp. Probl. 2010, 5, 33–40. [Google Scholar]
- Kim, B.S.; Chi, C.H.; Lee, T.K. A study on radial directional natural frequency and damping ratio in a vehicle tire. Appl. Acoust. 2007, 68, 538–556. [Google Scholar] [CrossRef]
- Antunes, J.P.M. Torque Vectoring for a Formula Student Prototype. Master’s Thesis, Technical University of Lisbon, Lisbon, Portugal, 2017. [Google Scholar]
- Gillespie, T.D. Chapter 4: Road loads. In Fundamentals of Vehicle Dynamics, 1st ed.; Society of Automotive Engineers: Warrendale, PA, USA, 1992; pp. 79–123. [Google Scholar]
- Chevrefils, A.R. Modelling and Design of an Electric All-Terrain Vehicle. Master’s Thesis, University of Manitoba, Winnipeg, MB, Canada, 2008. [Google Scholar]
- Sunil, K.; Kiran, J.K.; Reddy, G.V. Braking system for an all terrain vehicle. Int. J. Mech. Eng. Technol. 2017, 8, 360–367. [Google Scholar]
- Negi, V.S.; Deshmukh, N.; Deshpande, A. Design of braking system of BAJA vehicle. Int. J. Adv. Eng. Res. Dev. 2017, 4, 1059–1064. [Google Scholar]
- Diwakar, L.B.; Diwakar, S.L.; Deshpande, V.V. Design and selection of the braking system for all terrain vehicle. Int. J. Eng. Res. Technol. 2020, 9, 730–733. [Google Scholar]
- Krauze, P. Control of Semiactive Vehicel Suspension System Using Magnetorheological Dampers. Ph.D. Thesis, Silesian University of Technology, Gliwice, Poland, 2015. [Google Scholar]
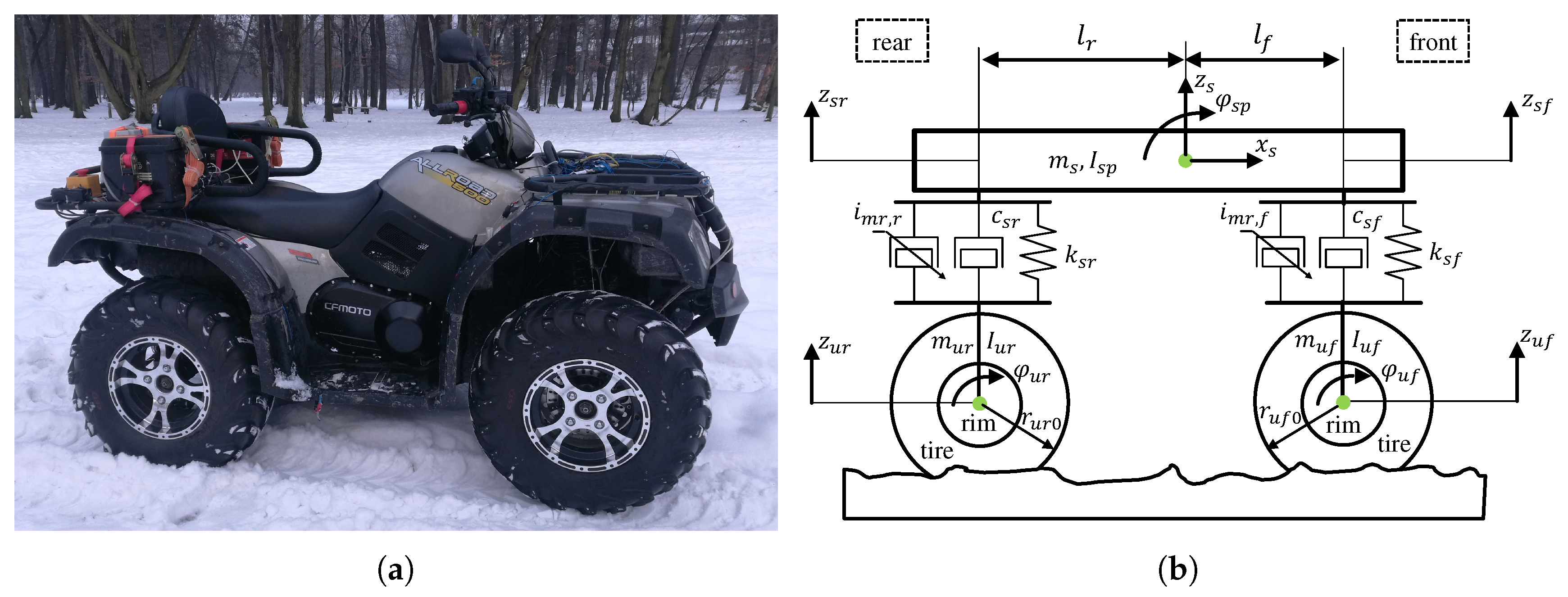
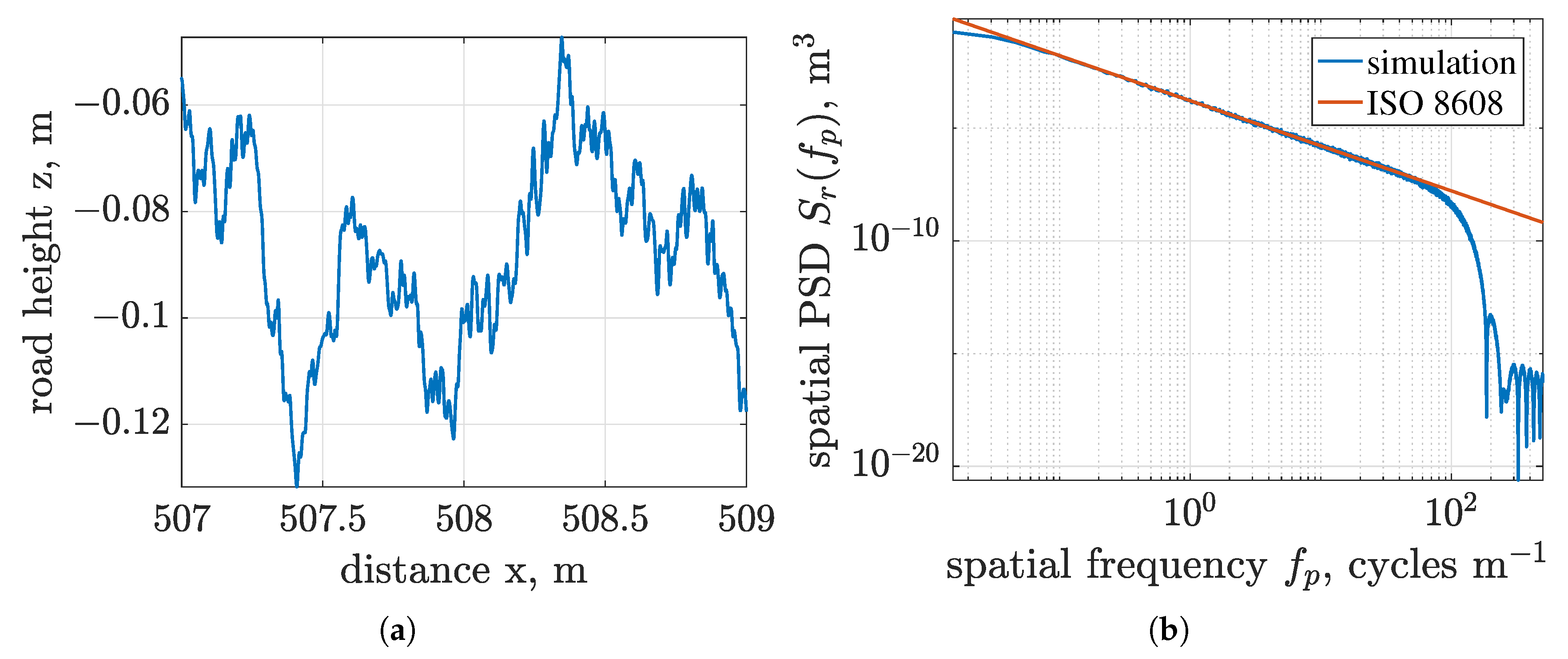

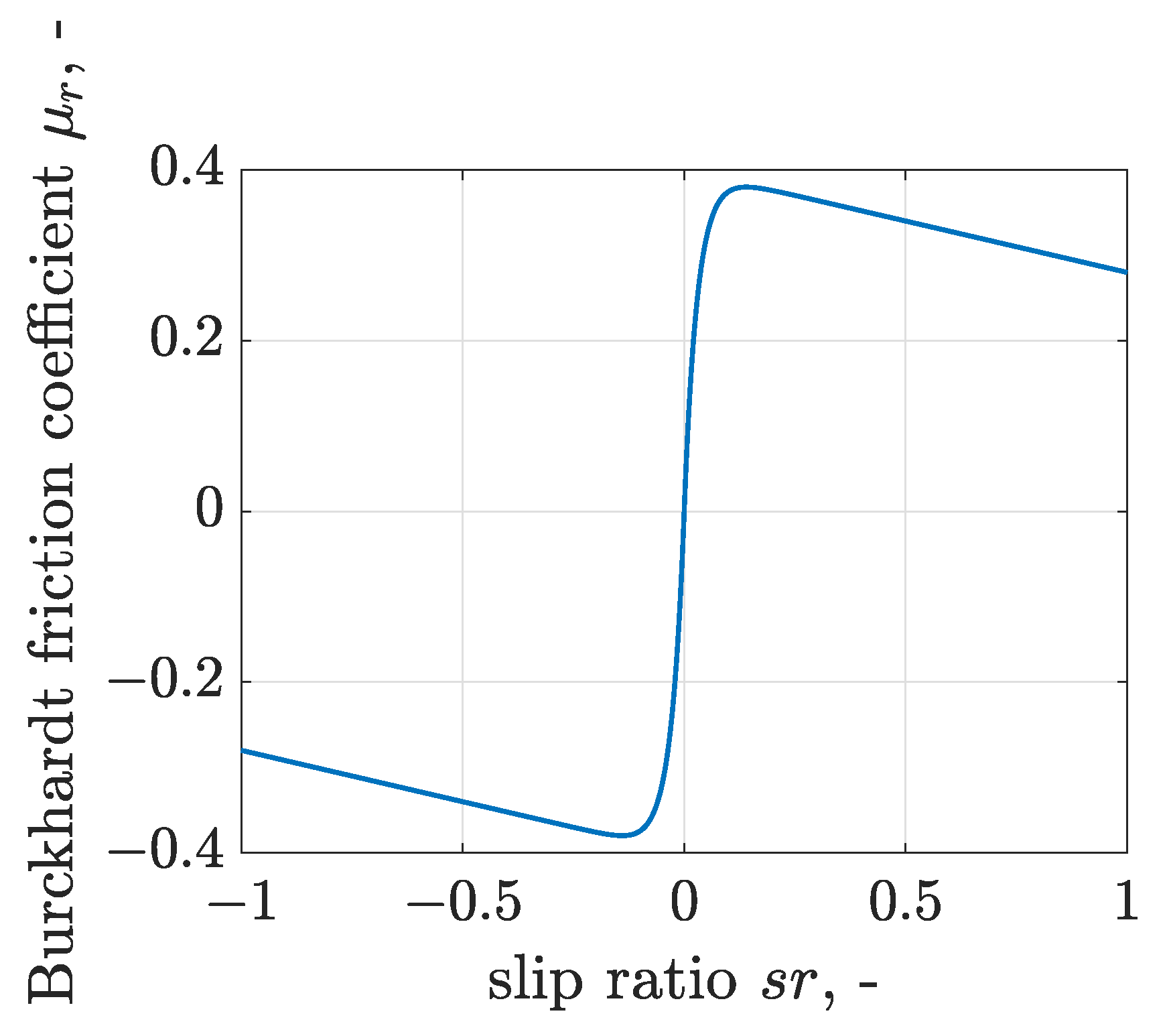
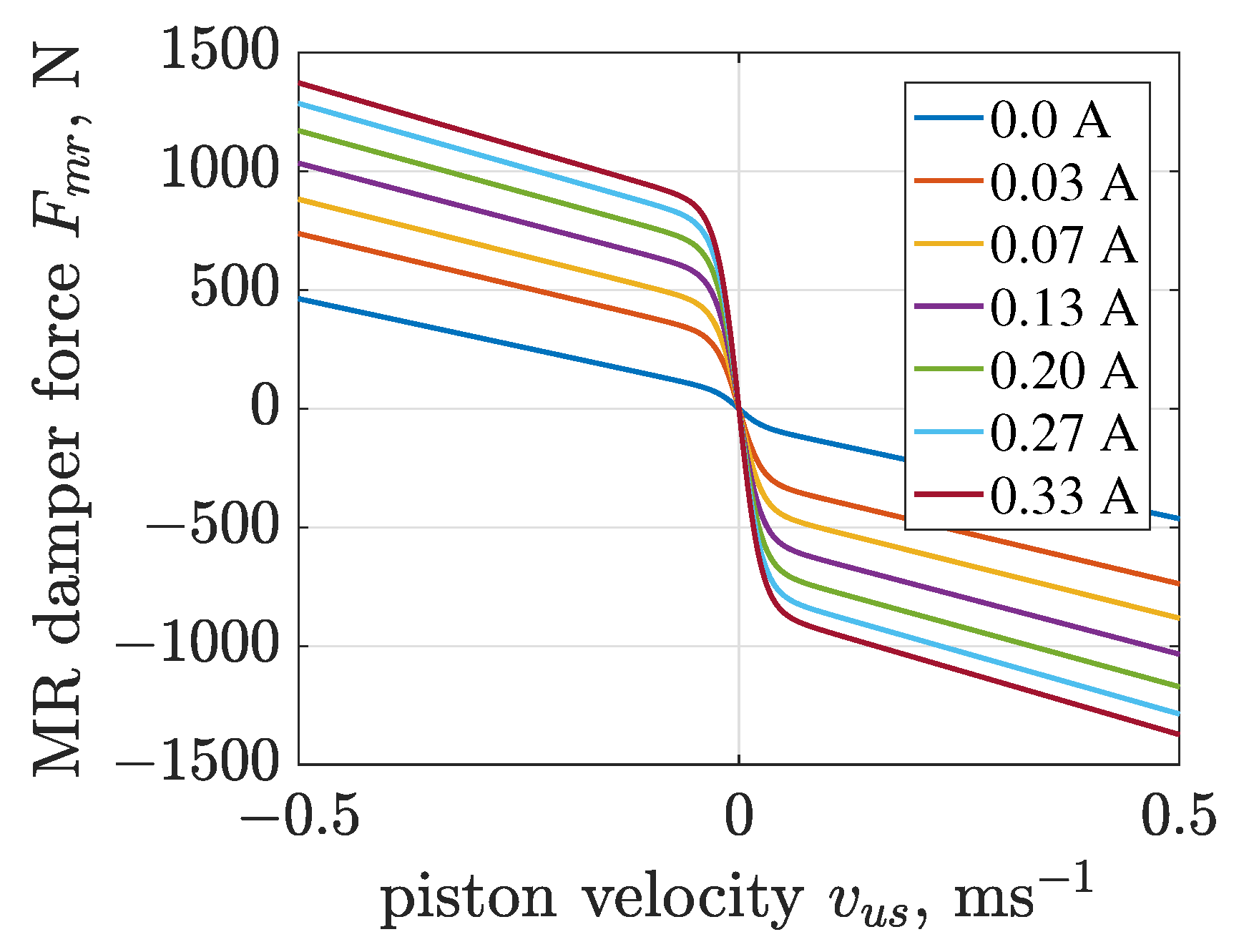




| Road profile and simulation parameters | |||||||||||
| = 1000 Hz | = 1000 points m | rc (road class) = F | = 6.6 m | ||||||||
| 4 DoFs half-car suspension model | |||||||||||
| = 171.5 kg | = 74.3 kgm | ||||||||||
| = 0.609 m | = 0.681 m | = 0.554 m | |||||||||
| = 22.208 kNm | = 34.857 kNm | = 300 Nsm | = 300 Nsm | ||||||||
| based model of the MR damper | |||||||||||
| (0.0; 1.33) A | = 62.42 N | = 1340 N | |||||||||
| = 39.96 sm | = 802.8 Nsm | = 488.5 Nsm | |||||||||
| Wheel and tire models | |||||||||||
| = 10 kg | = 15 kg | = 0.6 kgm | = 0.9 kgm | ||||||||
| = 0.317 m | = 0.317 m | = 0.244 m | = 0.244 m | ||||||||
| = 5234.1 Nm | = 5113.6 Nm | = 447.3 Nsm | = 560.4 Nsm | ||||||||
| Burckhardt model of tire to road friction for wet concrete surface | |||||||||||
| = 0.4004 | = 33.7080 | = 0.1204 | |||||||||
| Rolling resistance for concrete surface and aerodynamic drag | |||||||||||
| = 0.008 | |||||||||||
| = 1.223 kgm | = 0.72 | = 1.75 m | |||||||||
| Parameters of front braking and rear drive systems for half-car model | |||||||||||
| = 160 Nm | = 225 Nm | ||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krauze, P.; Kasprzyk, J. Driving Safety Improved with Control of Magnetorheological Dampers in Vehicle Suspension. Appl. Sci. 2020, 10, 8892. https://doi.org/10.3390/app10248892
Krauze P, Kasprzyk J. Driving Safety Improved with Control of Magnetorheological Dampers in Vehicle Suspension. Applied Sciences. 2020; 10(24):8892. https://doi.org/10.3390/app10248892
Chicago/Turabian StyleKrauze, Piotr, and Jerzy Kasprzyk. 2020. "Driving Safety Improved with Control of Magnetorheological Dampers in Vehicle Suspension" Applied Sciences 10, no. 24: 8892. https://doi.org/10.3390/app10248892





