Experimental and Numerical Study on a Grouting Diffusion Model of a Single Rough Fracture in Rock Mass

Abstract

Grouting reinforcement is an important method used to solve problems encountered during tunnel construction, such as collapse and water gushing. The grouting diffusion process is greatly influenced by the structural characteristics of the fractures in a rock mass. First, an analytical grouting diffusion model of a single rough fracture under constant-pressure control is established based on the constitutive equation of a Bingham fluid. Second, the “quasi-elliptical” grouting diffusion pattern under the influence of roughness is revealed through a grouting diffusion experiment, which is conducted with an independently developed visualized testing apparatus. Furthermore, the analytical formula of roughness-corrected grouting diffusion characterized by the saw tooth density is established. Finally, an elaborate numerical simulation of the diffusion process of cement slurry (Bingham flow type) in a single rough fracture is carried out by introducing the Bingham–Papanastasiou rheological model. The temporal and spatial distribution characteristics of the velocity field and pressure field during the grouting diffusion process are analyzed as well. Moreover, the method and range of the roughness correction factor in the analytical grouting diffusion model are proposed based on the fracture roughness unit.

1. Introduction

Collapse and gushing water disasters often occur due to the concealment and unpredictability of the geological conditions during the tunnel construction process. Grouting, an effective control technique, can improve the strength of the surrounding rock and form a water blockage section to effectively improve and solve the abovementioned problems. This technique is quick, short in its time limit, simple in construction, and easy to control. Simultaneously, some considerable progress also has been made in the theoretical research of grouting diffusion.

The grouting diffusion process and the final effect are the result of the joint action of the fracture’s structural characteristics, grouting technology, and other factors. The study of the grouting diffusion process of a single rough fracture is the basis for investigating the grouting diffusion law in multi-dimensional space and practical engineering. Many scholars have carried out research on the law and factors influencing grouting diffusion in fractures, which is often modeled based on a Newtonian fluid and non-Newtonian fluid, such as a power-law fluid and Bingham fluid [1,2,3,4]. In terms of theoretical research, the theory of grouting diffusion in fractures is mainly divided into two categories: the permeation diffusion theory and filling diffusion theory. The grouting diffusion process in fractures is characterized as a nonlinear Darcy permeation process. The Forchheimer permeation equation for grouting in fractures was developed by establishing the permeability coefficient equation for a slurry of a Bingham fluid in fractures [5]. A grouting diffusion model of a single parallel plate fracture can be obtained based on the solution of the continuity equation and Navier-Stokes (N-S) equation for the grout flow process. A grouting diffusion model based on Newtonian fluids is derived to reveal the relationship between the grouting pressure, flow rate, and diffusion radius during the grouting diffusion process [6]. A maximum radius exists during the grouting diffusion process of a Bingham-flow-based slurry when given a certain grouting pressure [7]. Based on a constant flow rate, a Bingham-flow-based model of grouting diffusion is derived, which reveals the spatiotemporal distribution of pressure during the grouting diffusion process [8]. In addition, modified grouting diffusion analytical models considering the temporal variability of the slurry viscosity or under the influence of temperature are obtained [9,10]. In terms of experimental studies, the grouting diffusion process in a circular tube is also studied [11]. The diffusion process of a Bingham-fluid-type cement slurry in the fractures of artificial slabs is being observed and studied [12,13,14]. In addition, the grouting diffusion process influenced by the temperature and dynamic water environment has also been studied, revealing the variation of physical quantities, such as the velocity and viscosity, in the diffusion process of a slurry under different influencing factors [10,15]. In respect to numerical simulation studies, the simulation of the grouting diffusion process is studied by a finite element method (FEM), finite volume method (FVM), and particle flow code (PFC). The FEM calculation software COMSOL Multiphysics (COMSOL Inc., Stockholm, Sweden) is used to establish a numerical simulation model to study the diffusion of different types of slurries under hydrostatic and dynamic water environments in plate fractures. The circular and U-shaped grouting diffusion patterns are revealed. Additionally, the pressure and velocity fields are discussed [16,17]. Based on the FVM, the triangular collapse process of the concrete is simulated by using the Herschel–Bulkley rheological model, revealing the rheological behaviors of the Bingham fluid [18]. Three different approaches of gap grouting modeling are investigated with the FLAC3D software, paying special attention to the influence of the grout material hardening process [19]. Based on PFC3D, the splitting and diffusion process of the slurry in the fractures are simulated, and the interaction between the slurry and soil particles is revealed [20].

Throughout the existing theoretical, experimental and numerical simulation studies on the problems of grouting diffusion in fractures, there are few studies considering the roughness of the structural surface of fractures. There is a substantial difference between the actual jointed rock fractures and the hypothetical parallel plate fractures. Therefore, the grouting diffusion model in the actual jointed rock fractures needs to be revised. In this paper, the roughness correction factor is introduced to establish a grouting diffusion analytical model in a single rough fracture based on the constant-pressure-controlled condition. Then, through the independently developed grouting diffusion visualized testing apparatus, the “quasi-elliptical” grouting diffusion pattern under the influence of roughness is revealed, and the roughness-corrected grouting diffusion analytical formula characterized by the saw tooth density is further established. Finally, based on the FEM calculation software, the Bingham–Papanastasiou rheological model is introduced to carry out an elaborate numerical simulation of the grouting diffusion process in a single rough fracture. The temporal and spatial distribution characteristics of the velocity and pressure fields during the diffusion process of the injection test are analyzed. Based on the fracture roughness unit, the method and range of the roughness correction coefficient in the analytical grouting diffusion model are proposed.

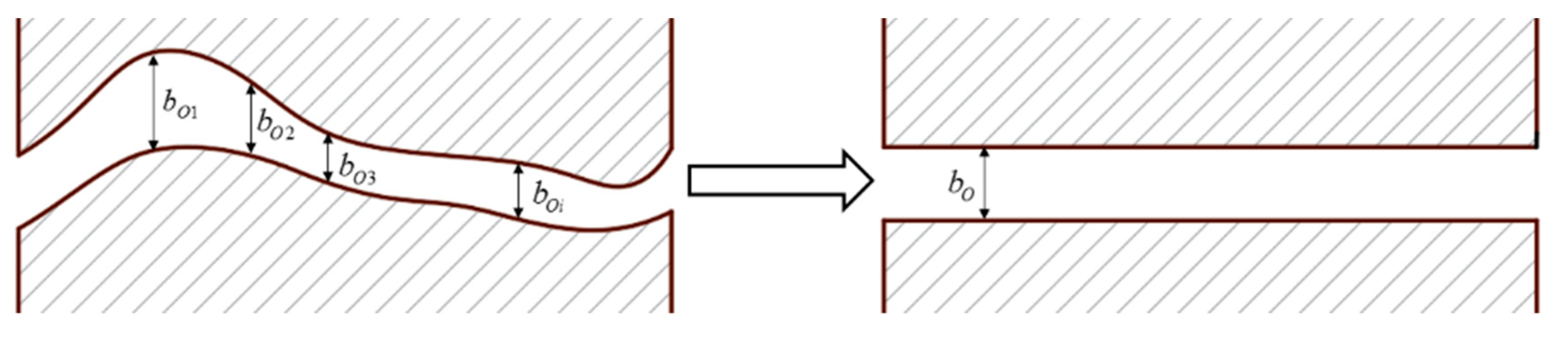
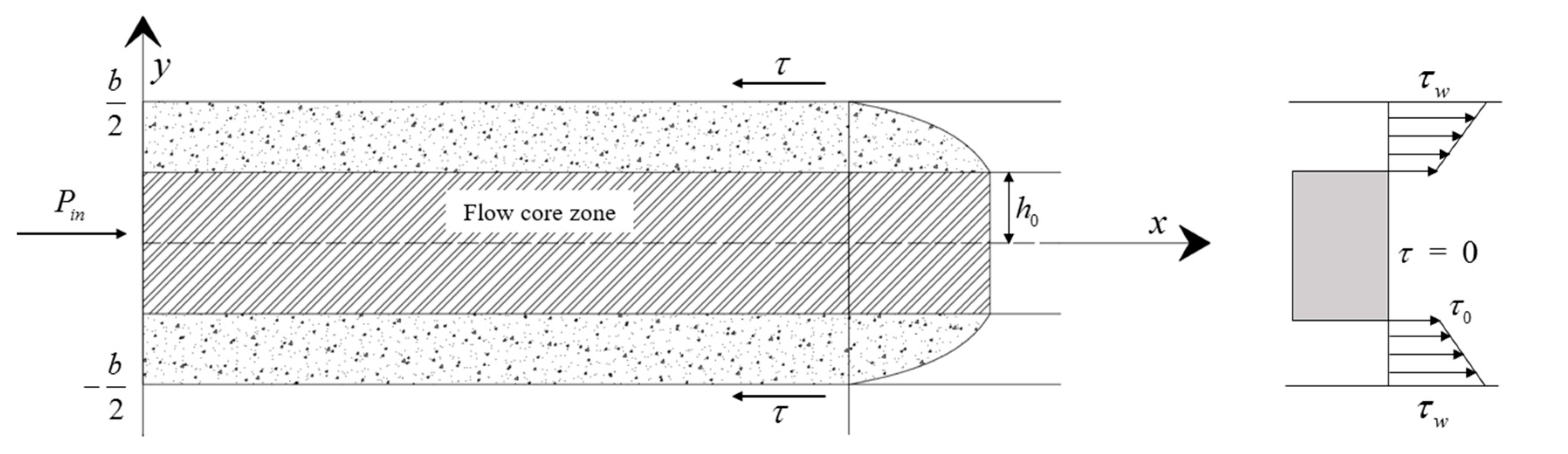
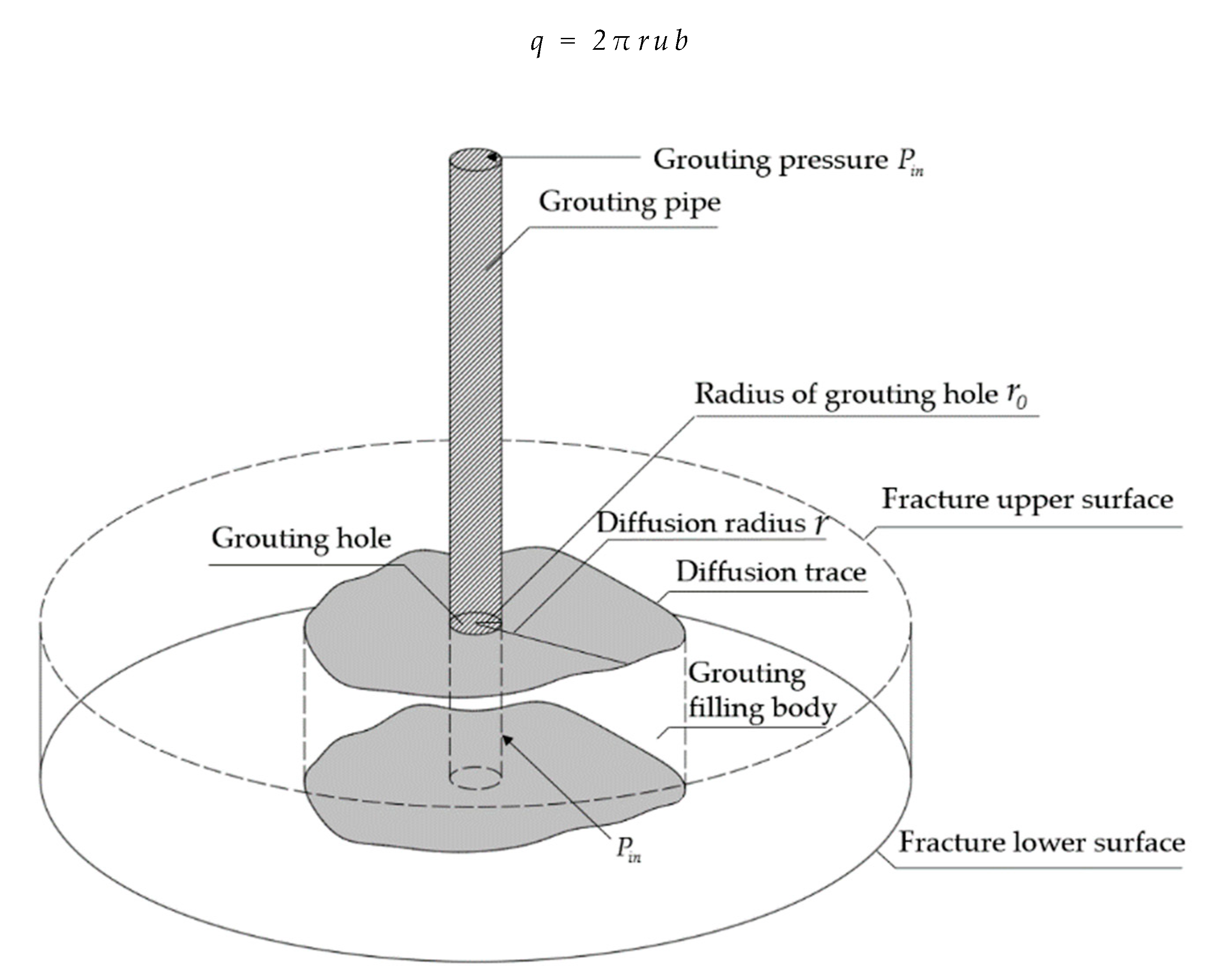
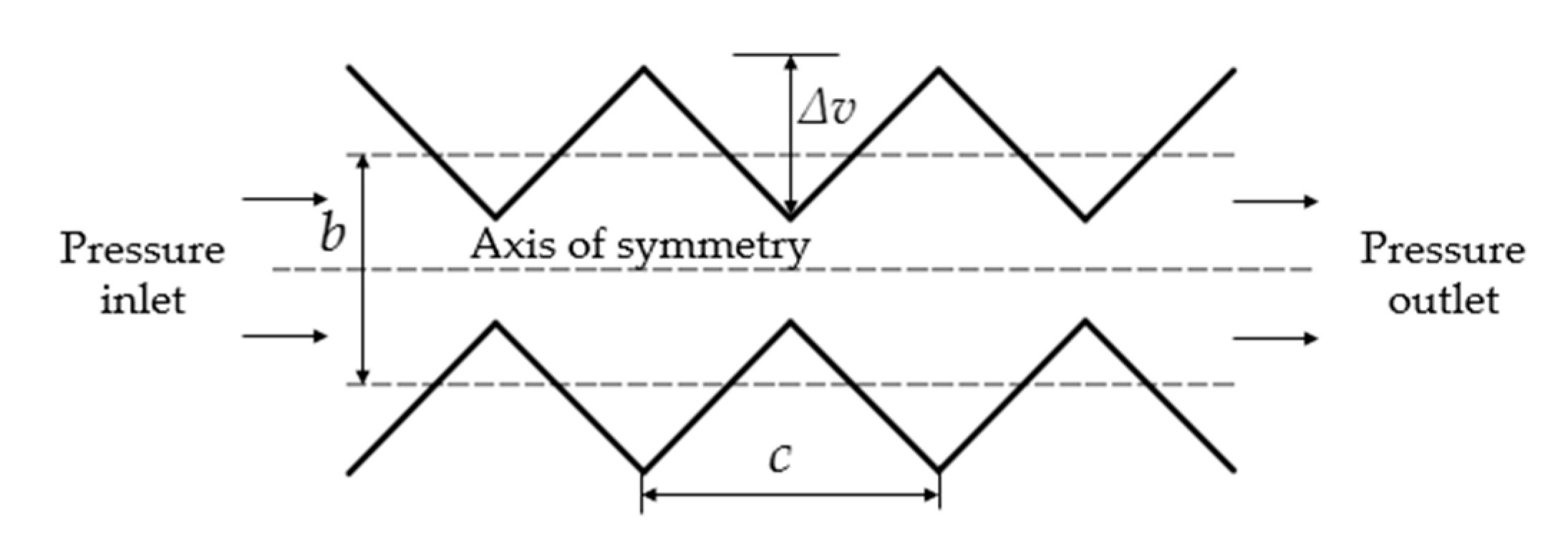
2. Analytical Model

The characteristics of the fracture distribution in rock mass directly affect the flow process of grouting diffusion and the reinforcement effect. The actual joints in rock mass are generally rough fractures rather than smooth plate fractures, as shown in Figure 1. In order to obtain a more effective formula to reflect the actual diffusion effect, it is necessary to correct the fracture openness by more precise methods. At present, there are many ways based on different theoretical formulas to get the value of equivalent fracture openness. There is variability in the fracture openness at each location. The original average openness $b_O$ can be obtained by mathematical statistics.

$$b_O= \frac{1}{N}{\displaystyle \sum }_{i=1}^N{b}_{Oi}$$

(1)

In Equation (1), $b_{Oi}$ is the fracture openness of the ith measurement point, and $N$ is the number of measurements. The grouting diffusion process in the rough fracture is difficult to be solved directly based on the structural characteristics of the irregular fracture surface. Therefore, by introducing roughness correction coefficients $\xi$, the rough fracture original average openness is corrected to the equivalent fracture openness $b$, as shown in Figure 1. Set $b=\xi b_O$. Then, based on the established plate fracture model characterized by the equivalent fracture openness b, the grouting diffusion model can be deduced.

In the field of grouting engineering during tunnel construction, the cementitious slurry, one of the most widely used slurry material, is often judged to be a Bingham fluid. The diffusion diagram of a Bingham’s fluid during laminar movement in parallel fractures is shown in Figure 2. Assume that the roughness-corrected equivalent fracture openness is $b$. There is a flow core zone and initial shear stress in the movement process of the Bingham flow type slurry. The flow core’s height is $h_0$, the initial shear stress is ${\tau }_0$, the shear stress at the junction position between the slurry and above and below the fracture surface is ${\tau }_w$, the constant grouting pressure is $P_{in}$, and the diffusion radius is $r$. According to the Bingham flow behavior, the peak surface of grouting diffusion is a quasi-trapezoidal shape. The diffusion velocity of the flow core zone is large, and ${\tau }_w\ge {\tau }_0$.

$${\tau }_w=\frac{dp}{dr}\frac{b}{2},{\tau }_0=\frac{dp}{dr}{h}_0$$

(2)

$$u=-\frac{dp}{dr}\times \frac{b^2}{12\mu }\left[1-3\frac{h_0}{b}+4{\left(\frac{h_0}{b}\right)}^3\right]$$

(3)

Equation (3) determines the average grouting diffusion velocity $u$, where $\mu$ is the viscosity.

When grouting during practical tunnel construction, the slurry spreads and fills around and through the grouting anchor, in which the grouting hole acts as the center. The diffusion diagram is shown in Figure 3. The grouting flow $q$ in the fracture at any moment can be expressed as Equation (4).

$$q=2\pi rub$$

(4)

$$r=\frac{2\mu q}{\pi b^2{\tau }_0}\times \frac{3B^2}{2B^3-3B^2+1},\mathrm{including}B=-\frac{b}{2{\tau }_0}\times \frac{dp}{dr}$$

(5)

Equation (5) shows the relationship between the grouting flow, diffusion radius, and pressure at any time under constant-pressure-controlled conditions, which can be obtained from Equations (2), (3) and (4), respectively. These three properties are all variables.

To solve the abovementioned problem, the grouting pressure gradient among the three variables needs to be eliminated by introducing a boundary condition. For the above problem, J. Claesson obtained the solution by mathematical methods [21]. In this paper, Equation (6) is obtained based on the Gustafson Model [22] for the grouting diffusion distance and time in a rough fracture under controlled constant pressure by introducing the roughness correction factor.

$$\frac{dx}{dt}=\frac{{\tau }_{0}b}{12\mu }\times \frac{3x\times f^{\prime }\left(A{x}_D,A\right)}{(x+r_0)}$$

(6)

$$A=\frac{x_m}{r_0}=\frac{\xi b_O{P}_{in}}{2r_0{\tau }_0},x_D=\frac{x}{x_m}=\frac{2{\tau }_{0}x}{\xi b_O{P}_{in}},x_m=\frac{\xi \zeta b_O{P}_{in}}{2{\tau }_0}$$

(7)

In the abovementioned equations, $t$ is the time of grouting diffusion (s is the unit), $x$ is the grout diffusion distance (m is the unit), $r_0$ is the radius of the grouting hole (m is the unit), and $r=x+r_0$. $f^{\prime }(A{x}_D,A)$ is an expression about $q^{\prime }$, and $q^{\prime }$ is the expression after the elimination measure of $q$.

$$q^{\prime }=f^{\prime }(A{x}_D,A)\iff A=q^{\prime }\left[\tilde{\phi }\left(q^{\prime }\right)-\tilde{\phi }\left(\frac{q^{\prime }}{1+A{x}_D}\right)\right]$$

(8)

$\tilde{\phi }\left(q^{\prime }\right)$ and $\tilde{\phi }\left(\frac{q^{\prime }}{1+A{x}_D}\right)$ can be solved by Equations (9)–(11). It is difficult to obtain the analytical solution directly from Equation (6), which needs to be solved by MATLAB (MathWorks. Inc., Natick, USA).

$$\tilde{\phi }\left(m\right)=\phi \left[\tilde{B}\left(m\right)\right]$$

(9)

$$\tilde{B}\left(m\right)=B=\frac{1}{2\sqrt{1+m}\times sin\left\{\frac{1}{3}\times arcsin\left[{\left(1+m\right)}^{-1.5}\right]\right\}}$$

(10)

$$\phi \left(B\right)=\frac{4}{3}\times ln\left(B-1\right)+\frac{1}{6}\times ln\left(2B+1\right)-\frac{1}{B-1}-\frac{3B^3}{\left(2B+1\right){\left(B-1\right)}^2}$$

(11)

$b$ = 0.005 m, ${\tau }_0$ = 20 Pa, $\mu$ = 0.05 Pa·s, $r_0$ = 0.005 m, and $P_{in}$ = 10 kPa are applied as examples to solve Equation (6). Keeping the abovementioned parameters unchanged, the change in the diffusion distance with time is shown in Figure 4, when the roughness correction factors are 0.4, 0.6, 0.8, and 1. The results of Figure 4 are calculated by mathematical calculation software MATLAB directly according to Equations (6)–(11). It can be found that the equivalent fracture openness, the grouting diffusion velocity, and the maximum diffusion distance also increase as the roughness correction factor increases.

3. Experimental Study

3.1. Experimental Design

This section presents the details of the model test, including the goals, the integrated apparatus, and the methodology and materials used. The parameters measured during the test include the grouting pressure change, the grouting diffusion trace, and the grouting diffusion area distribution.

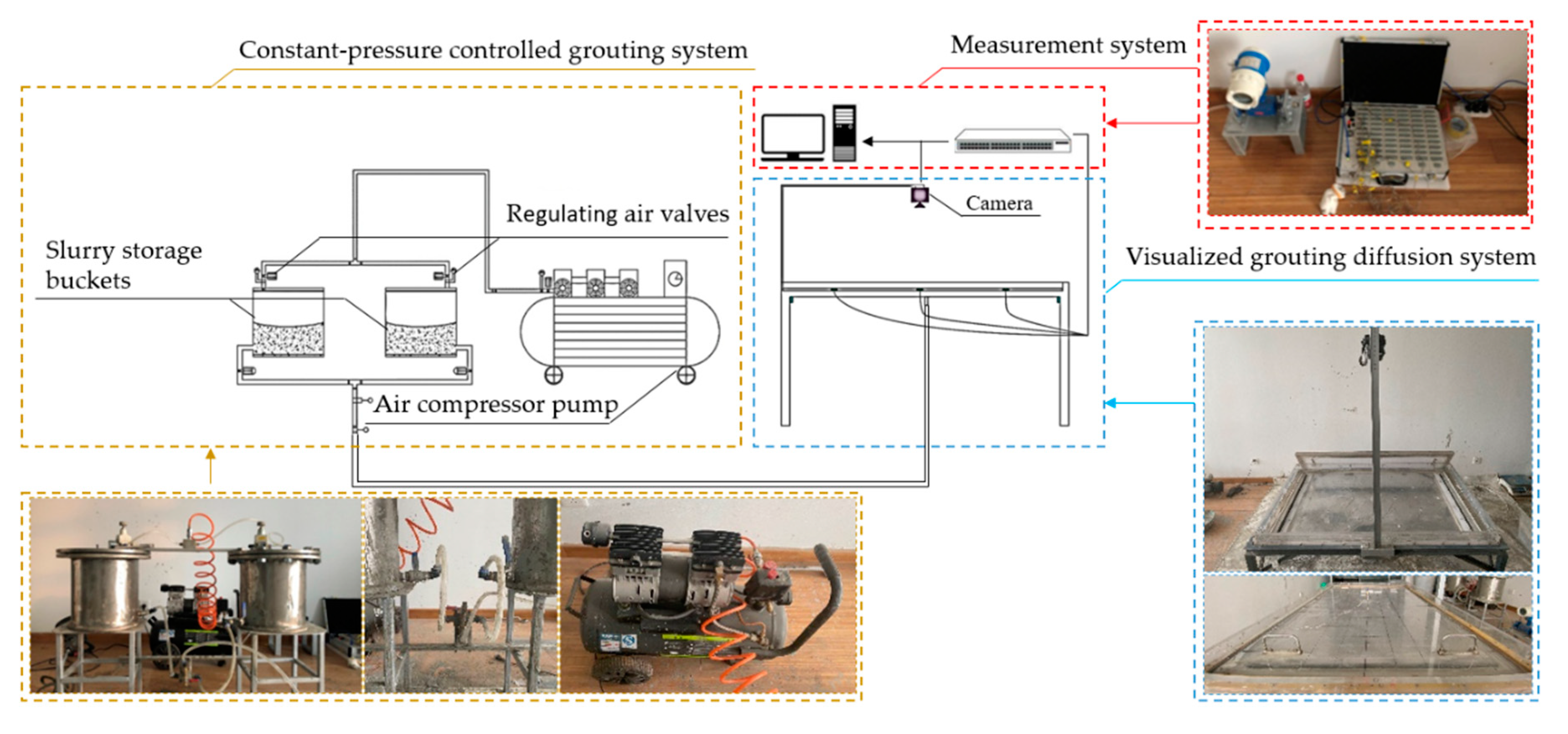
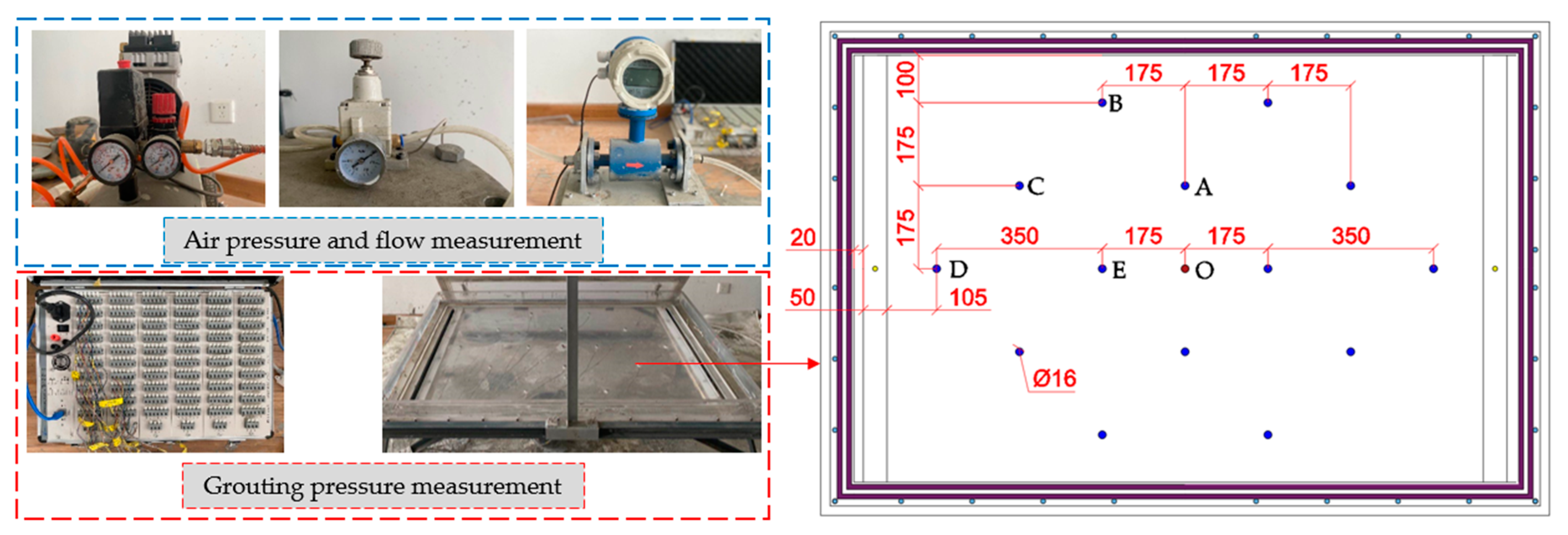
3.1.1. Experimental Configuration

The integrated testing apparatus consists of three parts: a constant-pressure-controlled grouting system, visualized grouting diffusion system, and measurement system. Their relationship and the overall experimental layout are illustrated in Figure 5.

Constant-Pressure-Controlled Grouting System

The constant-pressure-controlled grouting system mainly includes an air compressor pump, slurry storage buckets, grouting pipes, control valves, and sealing rings, as shown in Figure 5. The slurry storage bucket is cylindrical. It is made of aluminum alloy, which has a certain resistance to corrosion. The storage bucket has a 300 mm height, an inner diameter of 300 mm, and a wall thickness of 5 mm, and it has a strong pressure-bearing capacity. This system can meet the test requirements of single-slurry and double-slurry grouting. An air inlet hole is opened at the top of the slurry storage bucket to connect the regulating air valve. One end of the regulating air valve is connected to the storage bucket, while the other end is connected to the air delivery pipe of the air compressor pump. The regulating valve can realize the double function of pressure adjustment and a monitoring display to ensure that the grouting pressure is maintained at a constant value during the testing process.

Visualized Grouting Diffusion System

In the visualized grouting diffusion system, the grouting diffusion platform is the main body, which is made of a transparent polymethyl methacrylate. Its dimension from the vertical view is 1550 mm × 1050 mm (length × width). The original size of the fracture openness is 5 mm, which can be finely adjusted by adding different thickness gaskets. The grouting platform is mainly composed of an upper fracture surface, a lower fracture surface, a sealing connection device, and a water inlet and outlet device, which constitutes the visualization system of grouting diffusion with an additional filming system. A grating is drawn on the outside of the upper fracture surface, which is convenient for observing and recording the grouting diffusion trace. The whole system is shown in Figure 6.

Measurement System

The main objects of the measurement system are the grouting pressure and the diffusion trace and area. The measurement system and the distribution of pressure sensors are shown in Figure 7.

3.1.2. Materials

The grouting material used in the test is ordinary Portland cement slurry, which is commonly used in the practical project and can be obtained easily through simple mixing. The cement conforms to the requirements of Chinese national standard GB175-99. Its main contents are shown in

Table 1. Portland cement composition.

Components	CaO	SiO2	Fe2O3	MgO	Al2O3	SO3	Loss
Ratio (%)	62	22.6	3.2	3.3	4.7	2.9	1.3

.

The cement slurry used in the test has a water:cement ratio of 0.5 and does not contain any admixture. The rheological properties are measured by a Brookfield viscometer, and the rheological curve is shown in Figure 8. The rheological equation can be expressed as Equation (12).

$$\tau =18.204+0.1913\gamma$$

(12)

It is shown that the viscosity of the cement slurry with a water:cement ratio of 0.5 is 0.1913 Pa·s, and the initial yield stress is 18.204 Pa. The grouting diffusion process only takes a short time, in which the main influence factor is the mechanical characteristics of cement slurry. The change in the chemical properties is mainly reflected in the transformation process of grout from liquid to solid, which is the process of forming a stable reinforcement zone after the grout diffusion. This process has a high significance for the grout to improve the strength of surrounding rocks but has a relatively small influence in the diffusion process.

3.1.3. Design of Test Conditions

To effectively and quantitatively analyze the influence of roughness on grouting diffusion, a triangular saw-tooth model was used to simulate the fracture roughness in this test. The cross profile of saw-tooth strips is an isosceles right-angled triangle with a height of 2 mm and a width of 4 mm. The saw-tooth strips are equally spaced on the lower surface of the fracture. The density of the saw-tooth distribution varies in different test conditions. To clearly observe the grouting diffusion process, the upper surface was kept smooth. The saw teeth were glued to the lower surface with a distribution density of one per 100 mm, one per 50 mm, and one per 25 mm. The different test conditions were defined as R1, R2, and R3, which are shown in Figure 9. During the experiment, the grouting pressure was maintained at 0.05 MPa, and the original fracture openness was 5 mm.

3.2. Experimental Results and Analysis

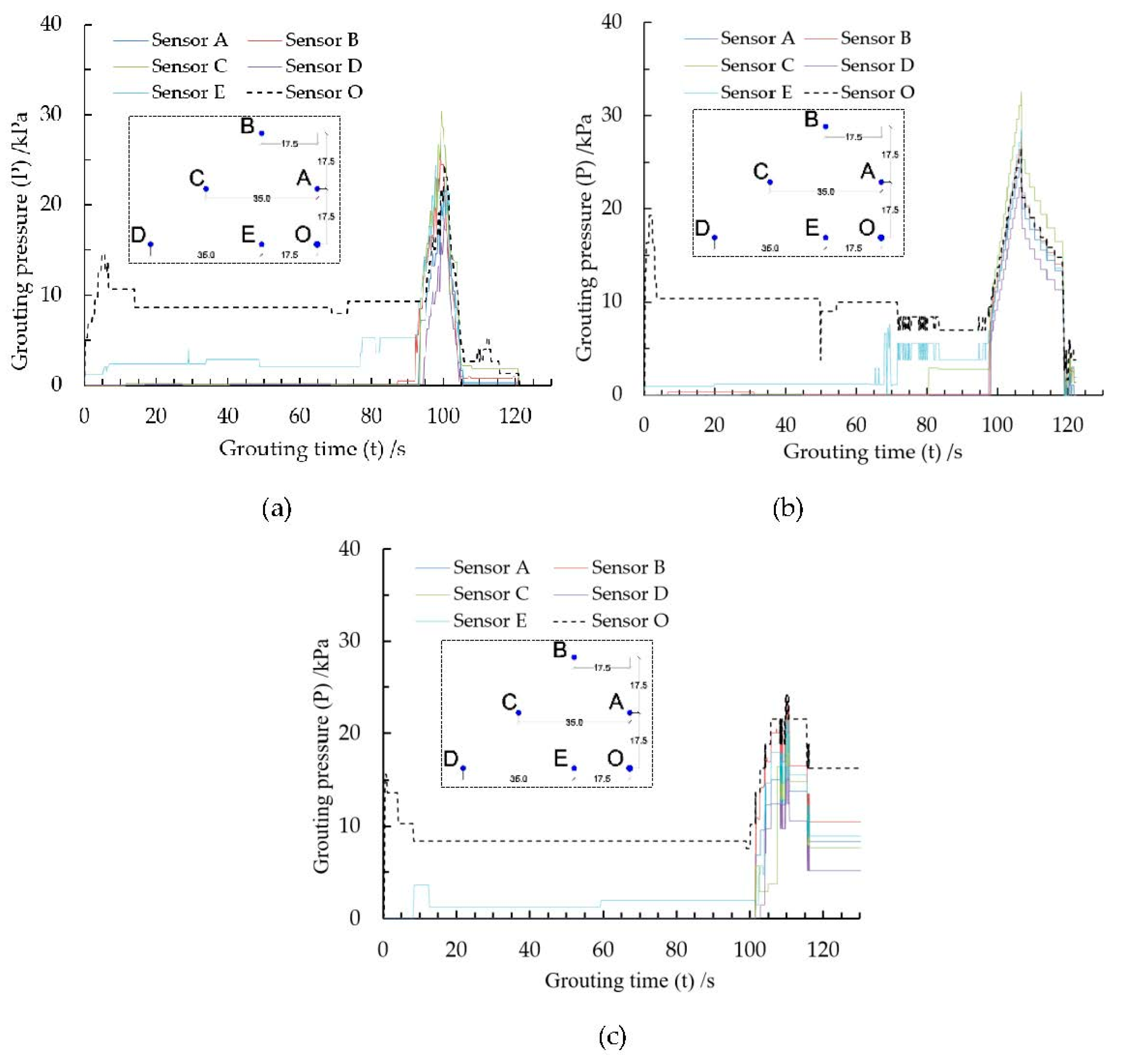
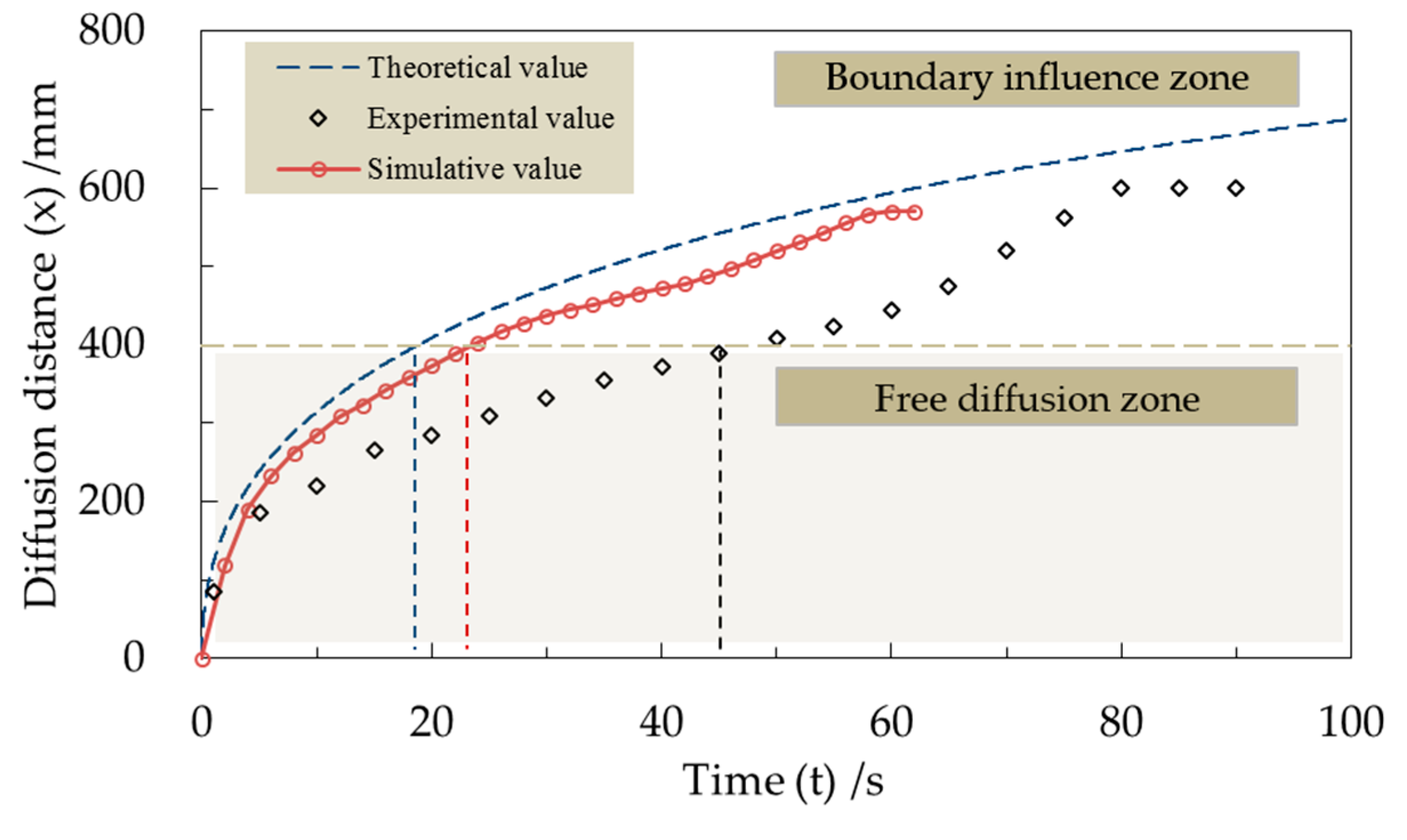
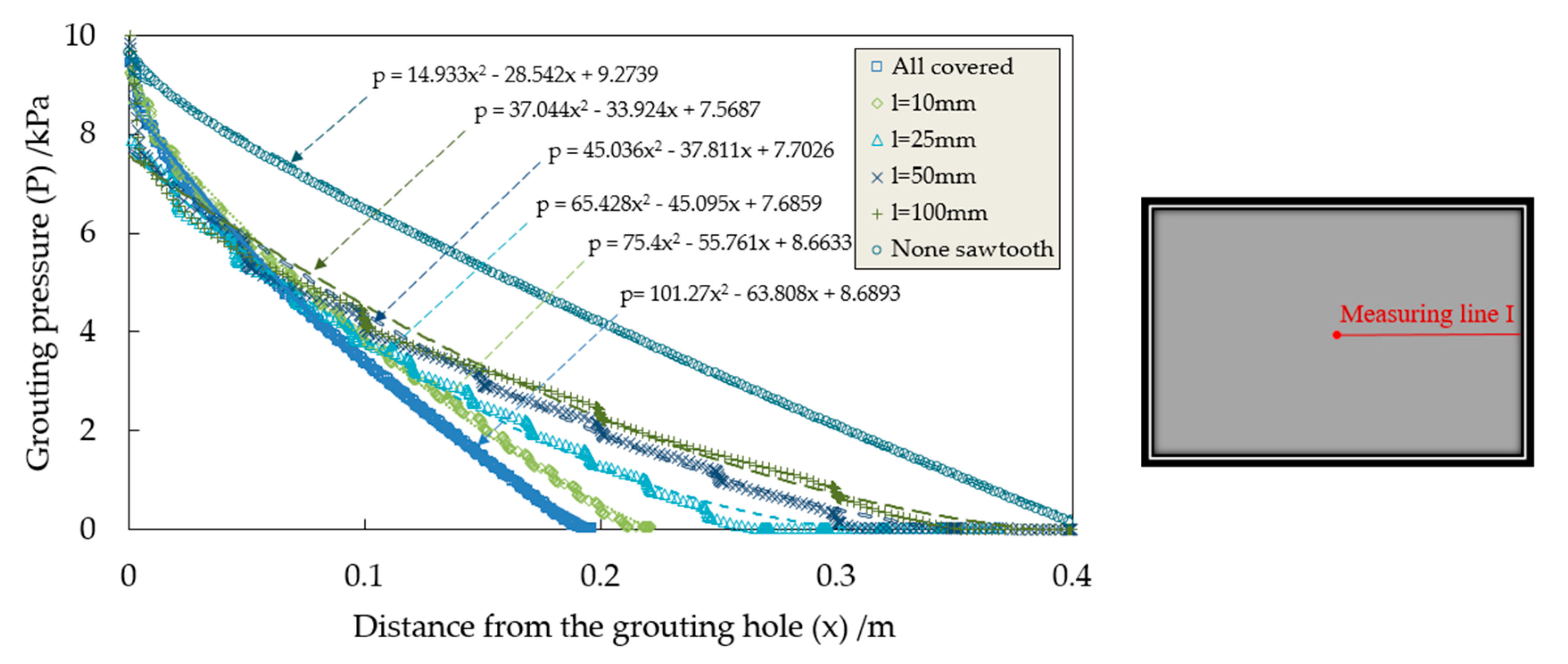
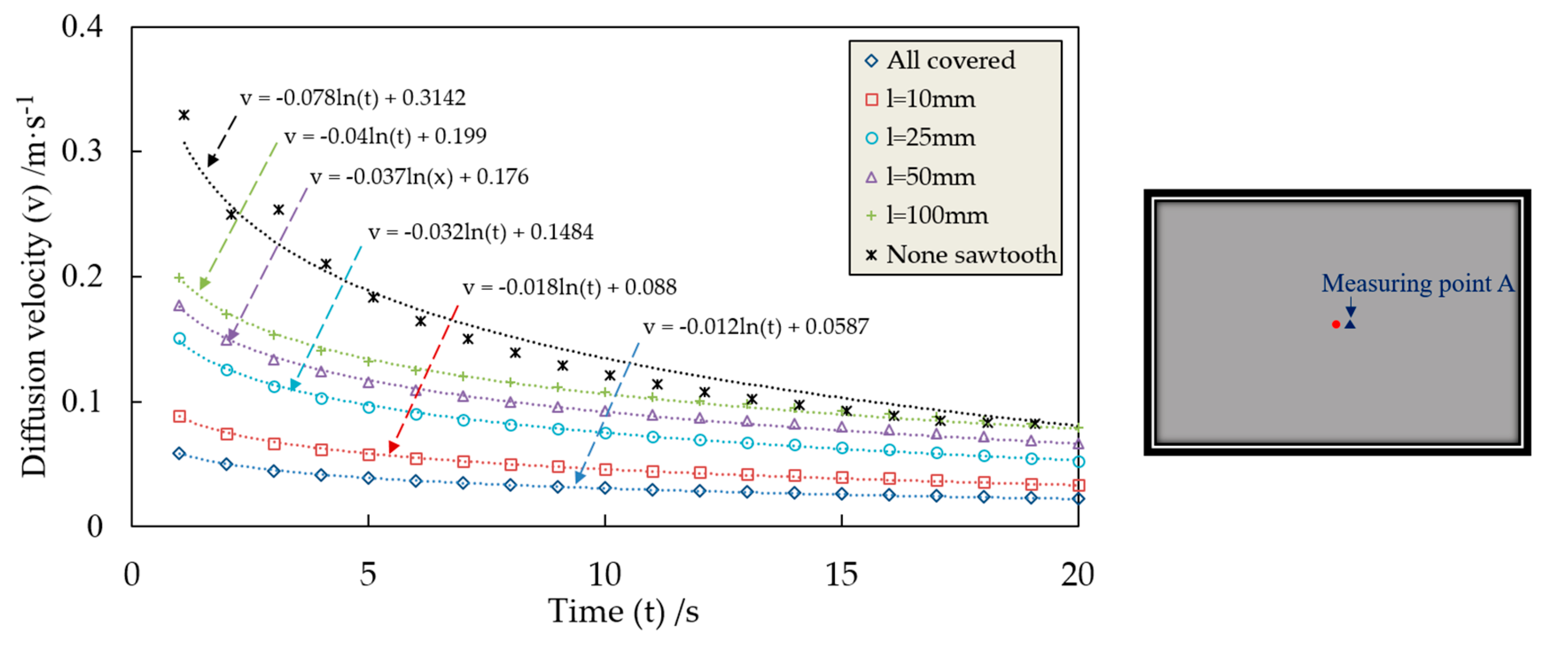
3.2.1. Grouting Pressure

Due to the symmetry of the grouting pressure sensors’ distribution, one-fourth of the sensors are selected for the analysis. In the grouting diffusion process, the curves of the changing grouting pressure with time are shown in Figure 10.

The pressure curves show that grouting does not exert much pressure on the fracture surface during the spreading process. The pressure value is only monitored at point O from the grouting inlet. When the slurry fills the whole fracture, the grouting pressure rises sharply due to the filling effect of the slurry. After grouting is stopped, the slurry pressure slowly decays to the starting state. Therefore, while filling the slurry in the plate fracture, the grouting pressure at the free diffusion stage is mainly horizontal pressure, and the vertical force is small and negligible.

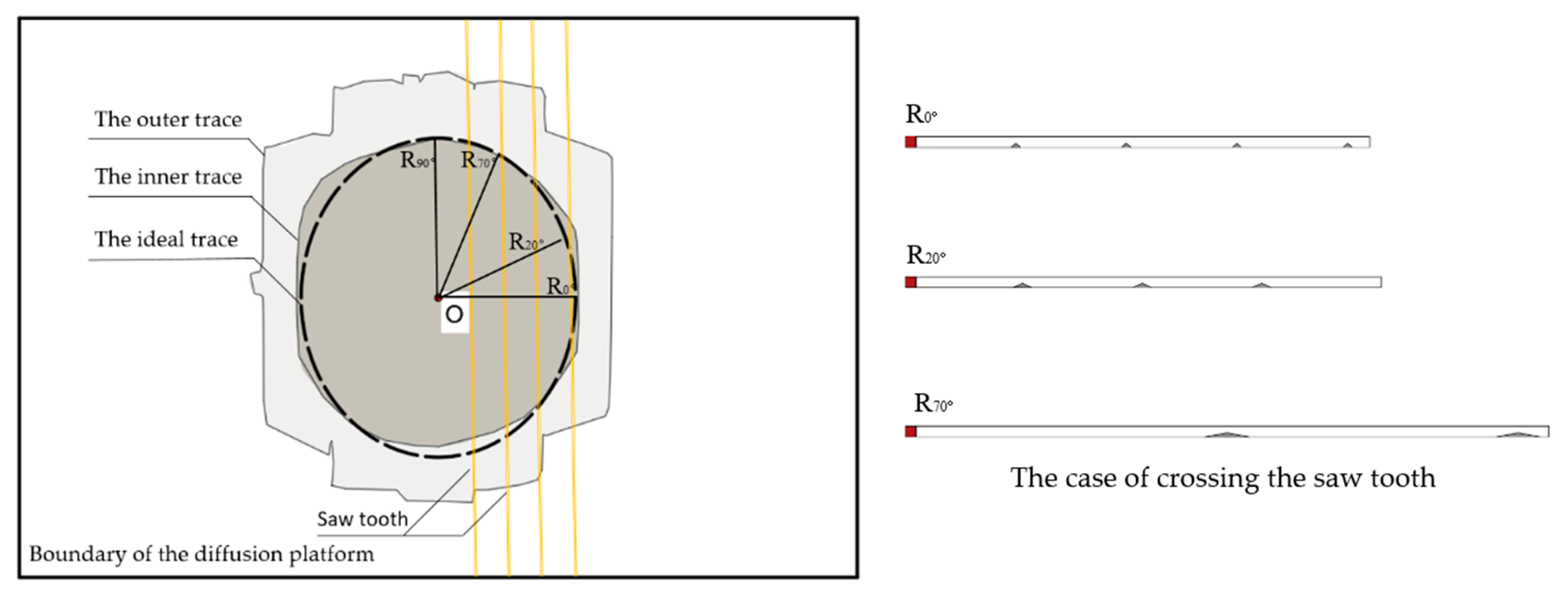
3.2.2. Grouting Diffusion Traces and Areas

During the test, the diffusion process of the cement slurry in the rough fracture is recorded by a video camera. The actual grouting diffusion process is shown in Figure 11a by taking the R1 condition as an example. The diffusion process of the cement slurry in the smooth fracture is also recorded, which is shown in Figure 11b. It can be found that the diffusion mode under smooth conditions is circular, while that under a saw-tooth surface on the bottom plate are serrated.

The peak profile of the grouting diffusion can be observed to be in the shape of a slope drop. It can be found that there are two forms of grouting diffusion paths. One is the outer trace, and the other is the inner trace. In this paper, the area between the outer trace and the inner trace is called the semi-reinforced zone, while the area within the inner trace is called the fully reinforced zone; these zones are defined according to the significance of grouting reinforcement for fracture. The shape enclosed by the outer trace is irregularly toothed, while the shape enclosed by the inner trace is quasi-ellipsoidal. The average normal distance between the outer trace and the inner trace remains essentially unchanged after reaching the steady state.

To facilitate the observation of the slurry diffusion changes in the rough fracture, the cloud maps are drawn, as shown in Figure 12. The time interval of each diffusion trace is 5 s. By observing the changes in the morphology of grouting diffusion, it is found that, with the increase in roughness (that is, the increase in the saw tooth density), the slurry diffusion rate shows a decreasing trend. The time required for the slurry to diffuse throughout the whole fracture is 89 s, 92 s, and 102 s. It can be found that the grouting diffusion velocity in the x direction is significantly lower than that in the y direction. Taking Rx/Ry as the grouting diffusion reduction coefficient, the reduction coefficient values are 0.819, 0.776, and 0.74 when the test conditions are R1, R2, and R3, respectively, before the grout reaches the y-directional diffusion boundary.

To quantitatively describe the grouting diffusion rate with respect to roughness, the curves showing the change in the grouting diffusion area with time under four test conditions (including one condition with no saw teeth) are statistically calculated according to the diffusion traces, as shown in Figure 13. It can be found that, under any of these conditions, slurry diffusion is a process that first increases and then stabilizes. The denser the saw teeth, the more slowly the slurry diffusion area changes and the smaller the area of the semi-reinforced zone.

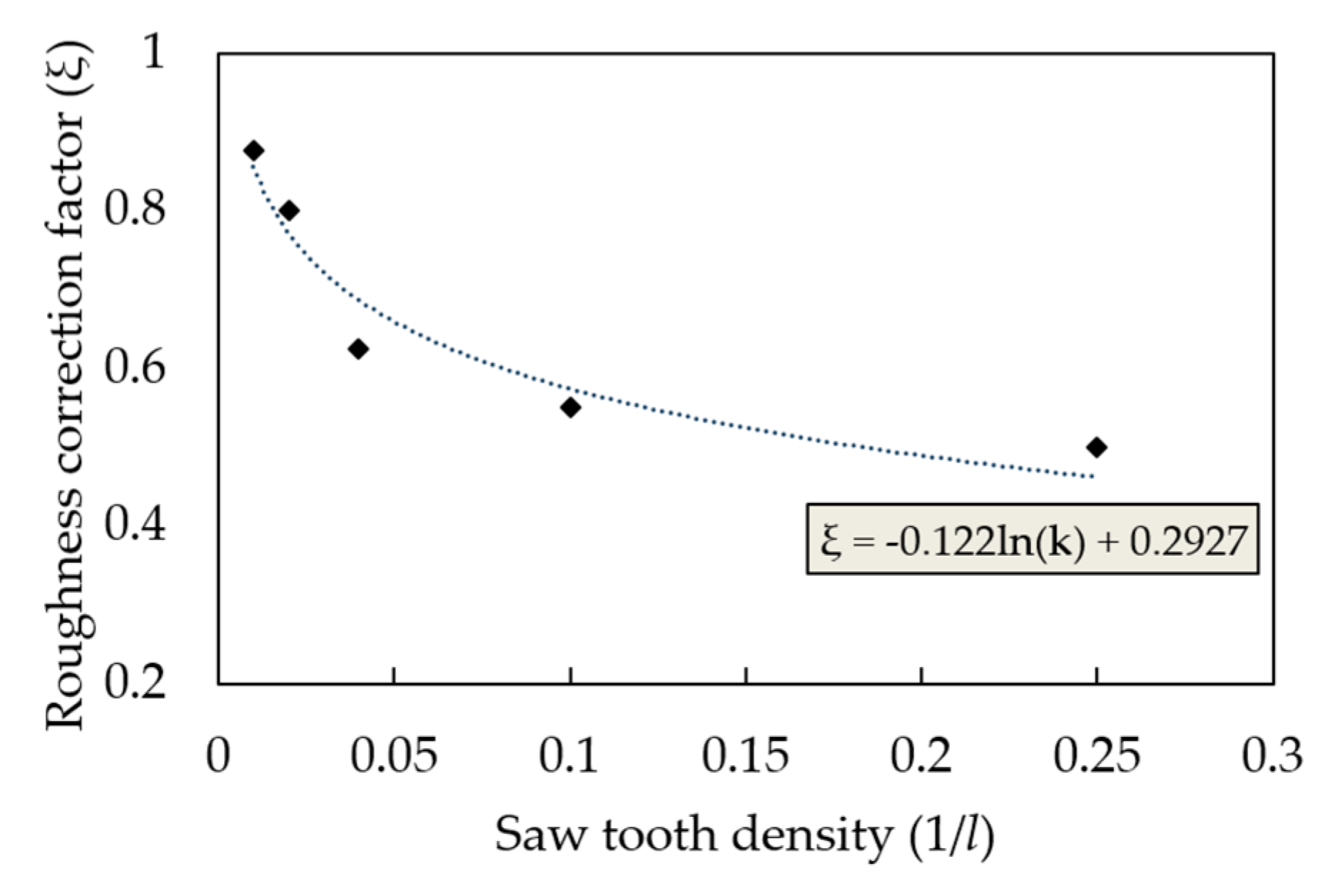
3.3. Grouting Diffusion Pattern

In this test, the saw teeth are uniformly distributed in the vertical direction. Therefore, there is an anisotropy of the roughness in each direction, with the grouting hole acting as the center. After the slurry spreads out, the density of the saw teeth and the climbing angle encountered in each direction are different. As a result, the slurry anisotropically propagates through the rough fracture, and its diffusion distance is related to the roughness in that direction. When calculating the diffusion distance for this experiment, an anisotropic roughness correction factor ${\xi }_{\theta }$ needs to be introduced into the analytical grouting diffusion model.

$$\frac{dx}{dt}=\frac{{\tau }_{0}b}{12\mu }\times \frac{3f\left(\frac{x}{r_0},\frac{{\xi }_{\theta }b{P}_{in}}{2r_0{\tau }_0}\right)}{1+\frac{x}{r_0}}$$

(13)

In the formula, ${\xi }_{\theta }$ is the correction factor of roughness in different directions. It assumes that the diffusion in each direction is independent of each other during the grouting diffusion process. Taking the saw-tooth density of one per 50 mm as an example, as shown in Figure 14, it can be found that, when the slurry spreads along the 0°, 20°, 70°, and 90° directions to a certain distance, the numbers of saw teeth encountered during the diffusion process in each direction are 4, 3, 2, and 0, respectively. Additionally, the climbing angle is different. Figure 15 shows the curve of the grouting diffusion distance in each direction changing with time. It can be seen that the grouting diffusion velocity and distance increment in each direction from 0° to 90° increase with increasing angles.

As the relationship between the grouting diffusion distance and time is known, the test correction factor of 0.63 can be introduced to find that the goodness of fit between the test data and the theoretical solution is high. Then, the equivalent openness of the fracture is obtained by the theoretical model in reverse. In Figure 16, the equivalent openness for the grouting diffusion process becomes smaller with the increase in the saw tooth density. Taking diffusion along the x+ direction as an example, the equivalent openness under conditions R1, R2, and R3 is 3.72, 3.61, and 3.51, respectively.

Under the same condition of the saw-tooth density, the equivalent openness exhibits a non-linear increase with the increasing angles. The roughness correction factor ${\xi }_{\theta }$ for different directions can be obtained from the equivalent and actual openness. In this study, it is found that the trend of experimental results and theoretical results are almost the same. The roughness correction factor is divided from 0 to 1 with an accuracy of 0.001. Then, the test data is selected and brought into a mathematical calculation procedure. The theoretical curve approximates the test result when the value of correction factor is chosen, so as to obtain the corresponding roughness correction factor. The saw-tooth density $\kappa$ is defined as shown in Equation (14).

$$\kappa =\frac{cos\theta }{l}$$

(14)

In Equation (14), $l$ denotes the separation distance of the saw teeth, and $\theta$ denotes the diffusion angle.

Roughness correction factor under different saw tooth combination conditions are shown is Figure 17. It can be assumed that there is a linear relationship between the roughness correction factor ${\xi }_{\theta }$ and the saw-tooth density in all directions, which can be expressed in the following equation.

$${\xi }_{\theta }=a\kappa +1$$

(15)

In Equation (15), $a$ is the slope of the fitting curve, which can respond to the sensitivity of a change in direction to a particular roughness. When $\kappa =0$, ${\xi }_{\theta }=1$, which means there is no roughness effect. As the saw-tooth density increases, $\left|a\right|$ becomes smaller, and each direction becomes increasingly more insensitive to the roughness.

4. Numerical Study

Grouting diffusion in a fracture is a complex process. It is difficult to analyze completely only through theoretical analysis; it is also time-consuming and laborious to analyze grouting diffusion through many groups of tests. Therefore, a numerical simulation can effectively reduce the workload and the testing error, find the test pattern, and summarize the analysis quickly.

In this section, a multi-condition numerical simulation of the grouting diffusion test under a single rough fracture is carried out by applying the Bingham–Papanastasiou fluid constitutive model through the CFD module of the FEM software COMSOL Multiphysics. The two-phase flow module is used to study the grouting diffusion pattern in different fractures based on solving the N-S equation. The spatial-temporal patterns of pressure and velocity are analyzed. Moreover, the numerical simulation results are compared with the model test results and the analytical model results.

4.1. Grouting Diffusion Simulation under Anisotropic Rough Fractures

4.1.1. Modeling

Under standard conditions, the numerical simulation calculates the model as a plate fracture with dimensions of 800 × 1200 × 5 mm, which is shown in Figure 18. The diameter of the grouting hole is 10 mm, which is arranged in the middle of the model. The mesh is divided by the sweep method, which is encrypted near the grouting hole and saw tooth.

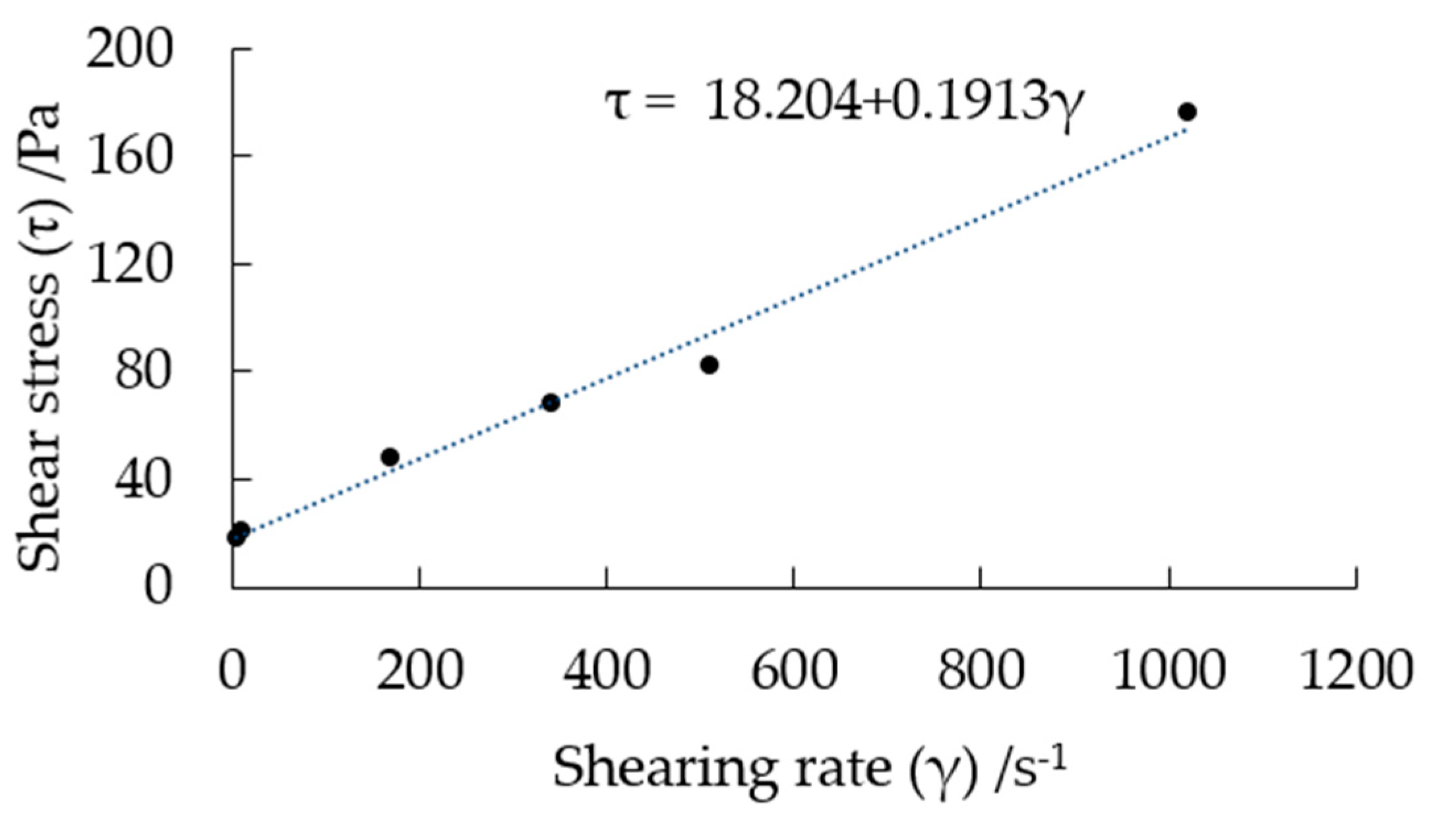
4.1.2. Constitutive Model of the Slurry

The Bingham–Papanastasiou rheology model is used to characterize the rheological properties of the cement slurry. The aforementioned rheology model is based on the following equations.

$$\mu ={\eta }_p+\frac{{\tau }_0}{\dot{\gamma }}[1-exp(-m{p}_1)\dot{\gamma }]$$

(16)

In the formula, $\dot{\gamma }$ denotes the shearing rate, $m{p}_1$ denotes the model parameters, and ${\eta }_p$ denotes the plastic viscosity. When $m{p}_1$ takes the maximum value, the abovementioned equation is equivalent to Bingham’s equation ($\tau ={\tau }_0+{\eta }_p\dot{\gamma }$).

4.1.3. Simulation Conditions

In the numerical simulation process, the original fracture openness is 5 mm, and the slurry W:C ratio is set at 0.5. The initial pressure boundary P_in = 0.01 MPa is given at the position of the injection port. Additionally, the upper and lower boundaries are fixed without a slippage boundary, and the outlet boundary pressure is set at 0 MPa on both sides. The air density is 1.293 kg/m³, and its viscosity is 17.9 × 10⁻⁶ Pa·s. The slurry density is 1810 kg/m³. Its viscosity is 0.1913 Pa·s, and the initial yield stress is 18.204 Pa. The saw-tooth density’s range is from 0 to a full spread of saw teeth, as shown in

Table 2. Simulation condition setting.

Program	Saw Tooth Density
roughness	None	1/100	1/50	1/25	1/10	All covered

.

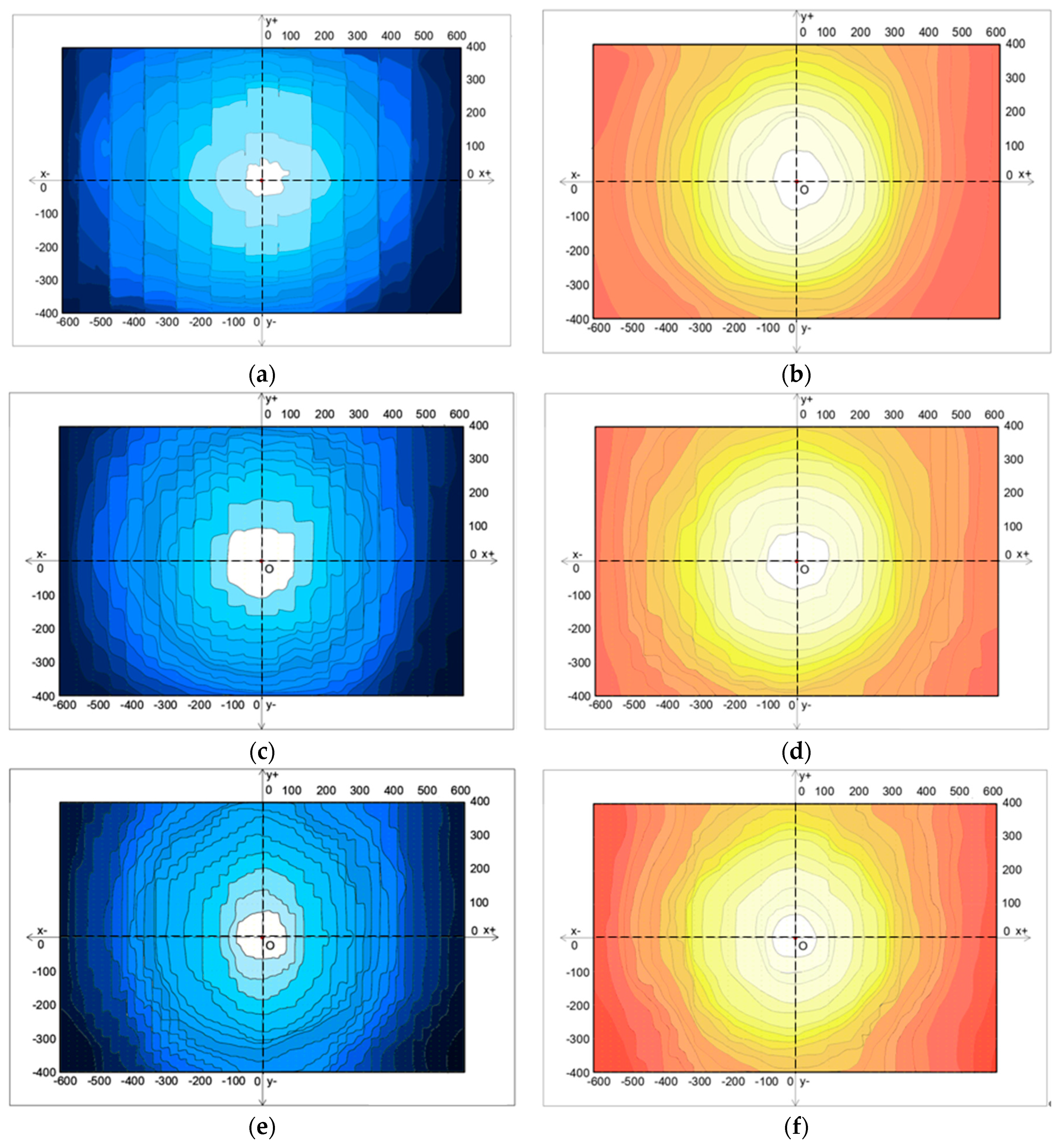
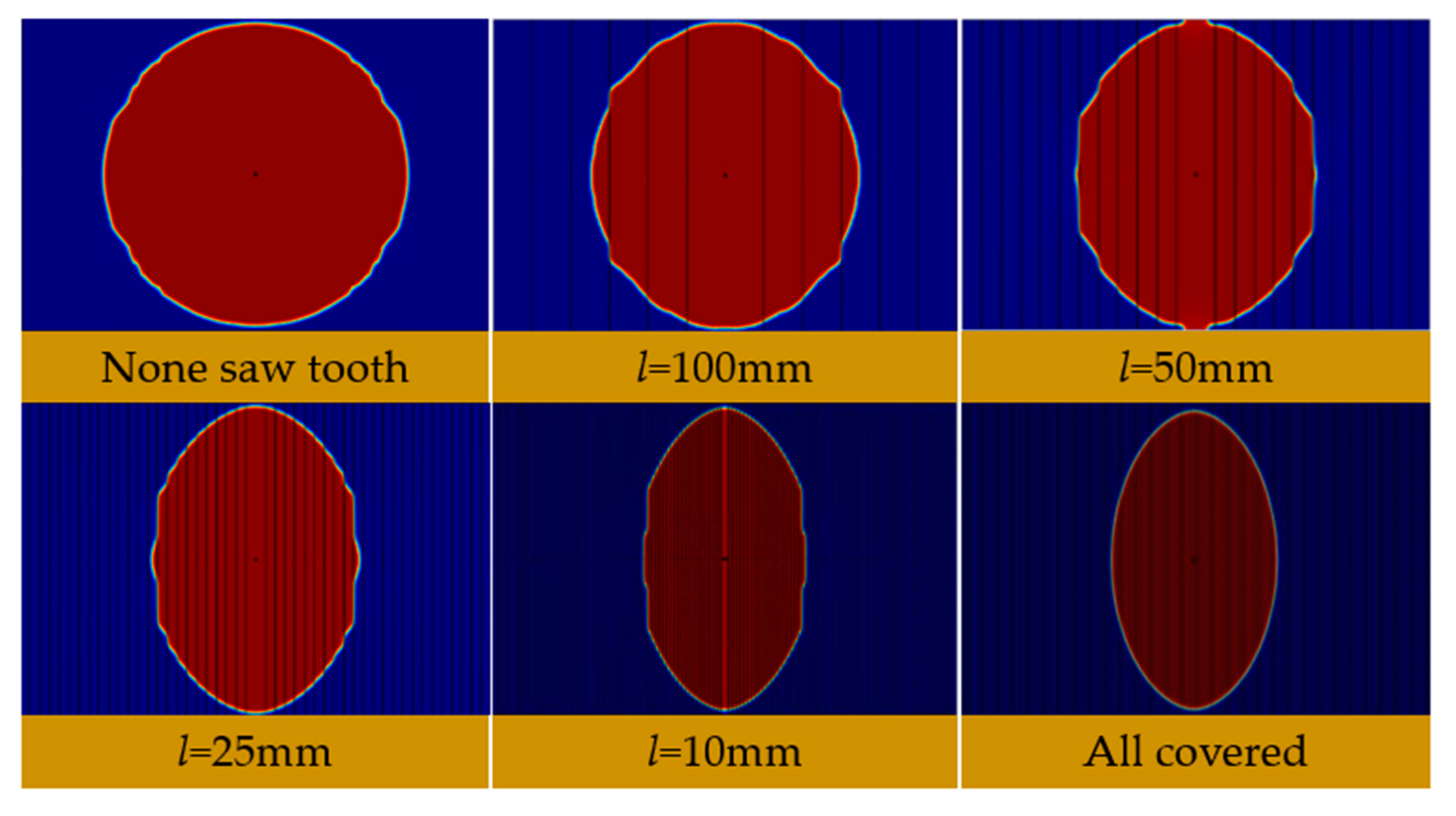
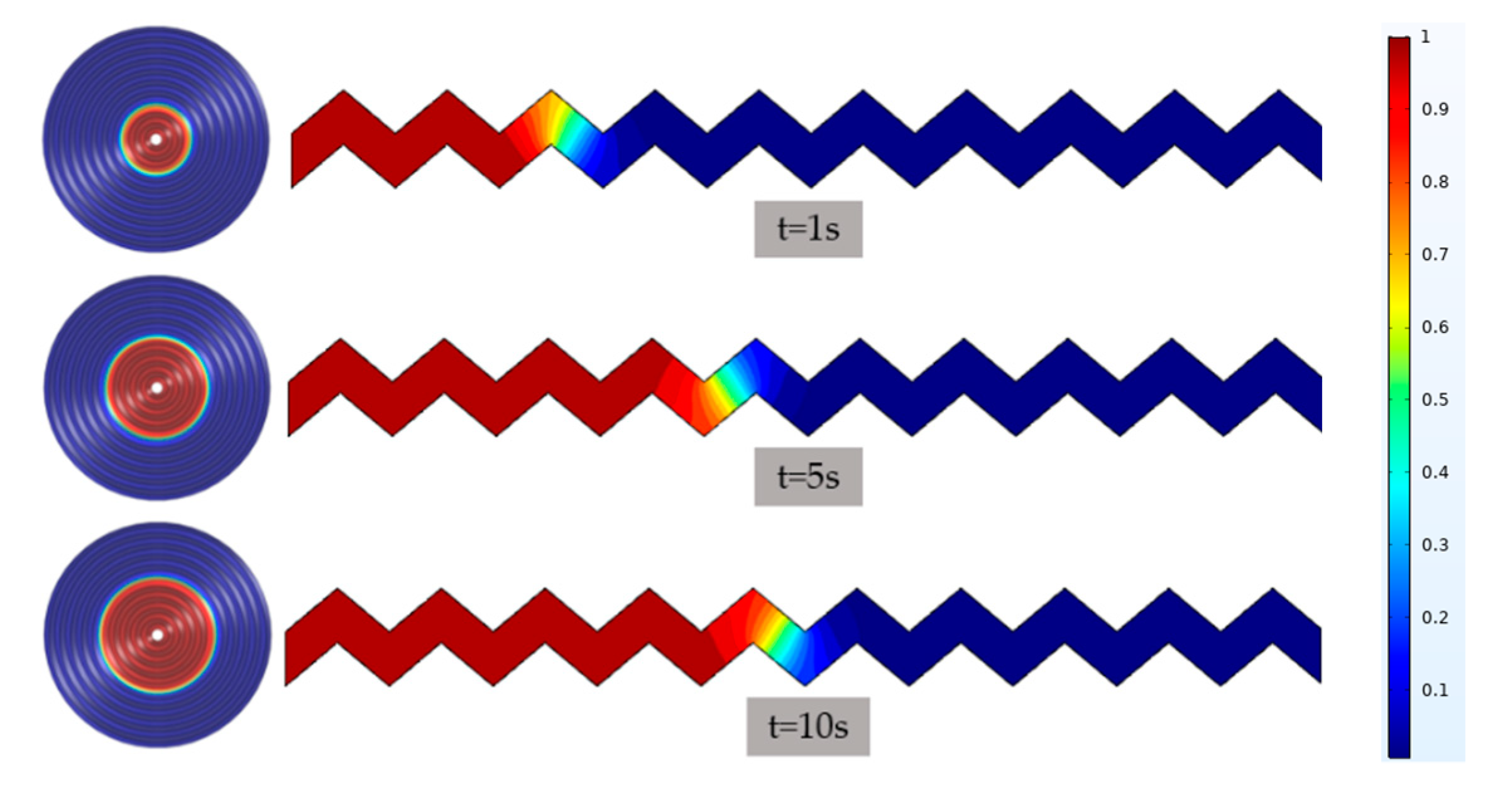
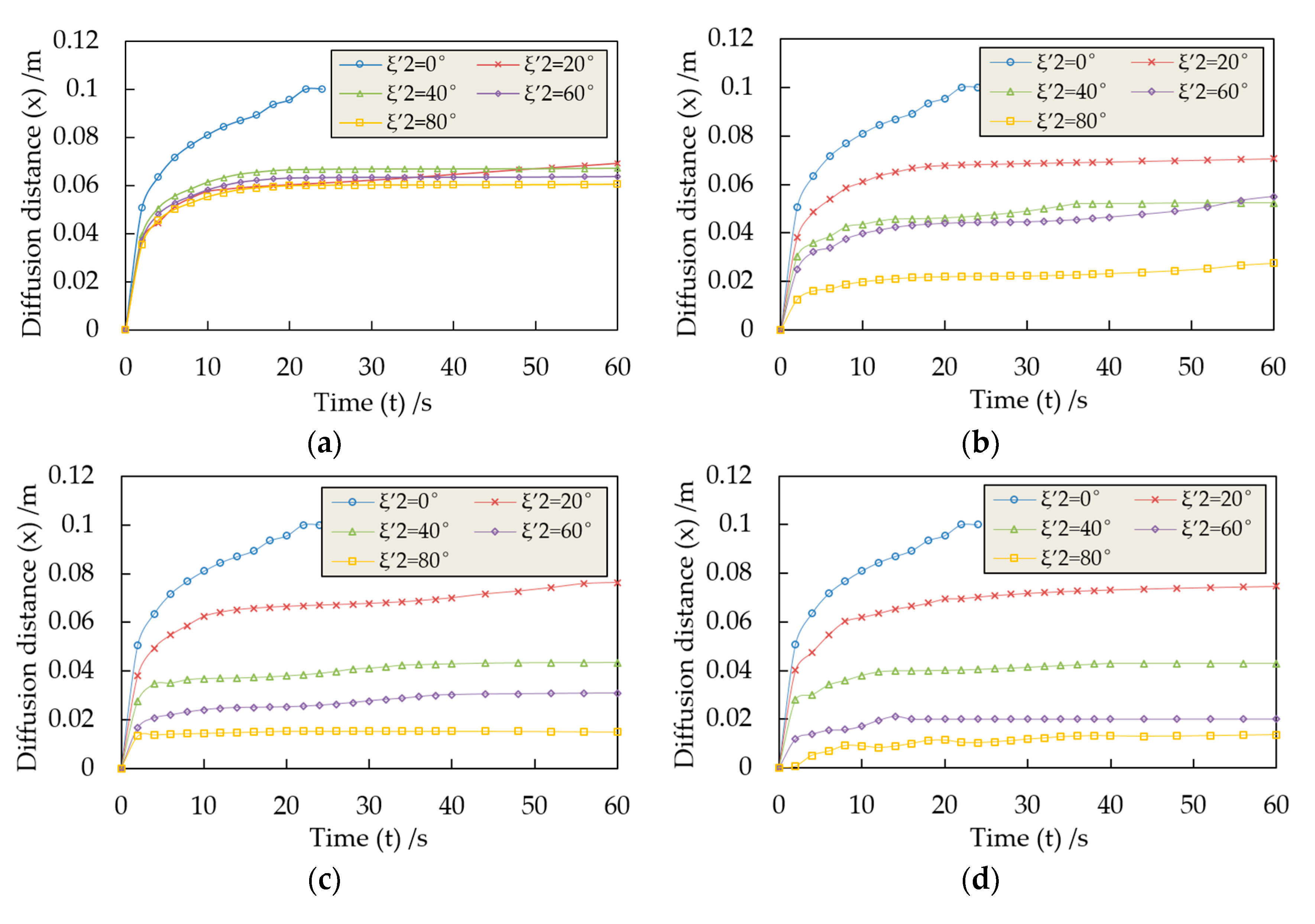
4.1.4. Simulation Results

By comparing the simulation results of grouting diffusion under the no-saw teeth condition with the theoretical and experimental values, it is found that the changes in the grouting diffusion distance with time are basically consistent, as shown in Figure 19. Since the theoretical solution does not consider the boundary influence, the theoretical diffusion results agree well with the simulation results in the free diffusion zone (r < 400 mm). The test results are slightly smaller than the theoretical and simulated results because the fracture surface is not completely smooth in the test, and there are some errors caused by other effects.

In this set of numerical simulations, the free grouting diffusion states in different conditions of saw tooth combinations, which use the uniform criterion that the slurry just touches the y-direction boundary, are shown in Figure 20.

It can be found that, under the saw-tooth conditions, the final grouting diffusion pattern in the free diffusion zone is quasi-oval. With the increase in the saw tooth density, the ratios of the short edge’s length to the long edge’s length gradually decrease and are 1.0, 0.88, 0.78, 0.69, 0.57, and 0.56, indicating that the grouting diffusion speed is negatively correlated to the fracture roughness. The time for the slurry to diffuse to the y-direction boundary under different conditions of saw tooth combinations is 23 s, 22 s, 19 s, 24 s, and 31 s, indicating that the anisotropic roughness has a certain influence on slurry diffusion. As the saw-tooth density increases in the x direction, the grouting diffusion velocity in the y-direction exhibits some discreteness. When the saw-tooth density is not too high, the diffusion velocity in the y direction increases slightly with the increase in the saw tooth density of the x direction. The change is not magnificent. When the saw teeth are too dense, the influence between each direction intensifies, the overall equivalent fracture openness decreases greatly, and the y-directional diffusion velocity decreases with the increase in the x-directional saw-tooth density. The increase in the grouting diffusion distance along the x+ direction with time under different simulative conditions of saw tooth combinations is shown in Figure 21.

It can be found that, as the saw-tooth density increases, the roughness increases, and the equivalent fracture openness decreases. In addition, the diffusion velocity slows down. The influence of the saw-tooth density on grouting diffusion shows a certain decay after the density is greater than “one per 25 mm.” The pressure distribution along measuring line I in the grouting diffusion process at t = 20 s under each simulative condition is shown in Figure 22. The velocity decay at measuring point A is shown in Figure 23.

The comparative analysis shows that the pressure attenuation in the x-direction is a step-type under different conditions of saw tooth combinations. Additionally, the attenuation gradient increases with the increase in the saw-tooth density. The attenuation speed also exhibits a significant difference with the different angles. In the y-direction (90°), the pressure attenuation state is almost the same as that in the smooth fracture condition. The grouting diffusion velocity of measuring point A decreases with the increase in the saw-tooth density under different conditions, which also shows some non-linearity.

By the numerical simulation of multiple simulation conditions, the roughness correction factor for different conditions is given based on the calculation of the analytical grouting diffusion model, as shown in Figure 24. It can be found that the roughness correction factor decreases with the increase in the saw tooth density. The fitting relationship between the roughness correction factor and saw-tooth density is given based on the least-squares method.

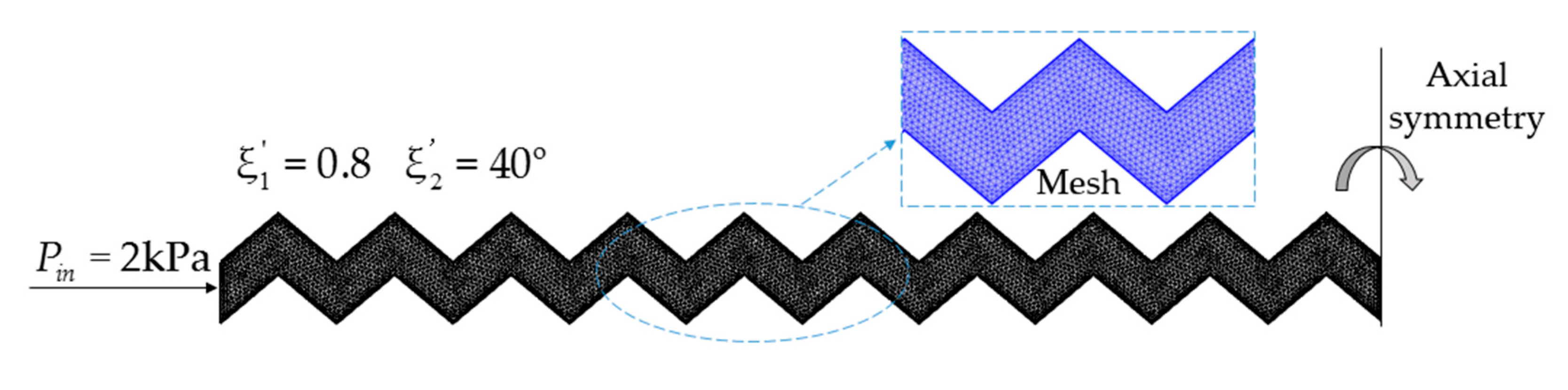
4.2. Grouting Diffusion Simulation under Isotropic Rough Fractures

4.2.1. Modeling

The roughness is very complex and irregular in actual joint fractures. Therefore, there is a certain difference between the theoretical rock mass fracture and the actual rock mass fracture. In order to study the mesoscopic flow laws of fluid under different roughness, many researchers have described roughness units in simplified geometrical structures based on the basic structure of a rough fracture [23,24,25,26]. The more widely used roughness units include sinusoidal, triangular and rectangular units. The generalized fracture roughness unit which is shown in Figure 25, whether triangular units or sinusoidal units, consists of three geometric parameters: the undulation height $\Delta v$, unit spacing $c$, and average fracture openness $b$. The average fracture openness is independent of the roughness and properties of the fracture surface. The roughness parameter for a single fracture surface can be expressed in terms of two dimensionless shape parameters.

$${\xi }_1^{\prime }=\frac{\Delta v}{b},{\xi }_2^{\prime }=arctan\left(\frac{2\Delta v}{c}\right)$$

(17)

In Equation (15), ${\xi }_1^{\prime }$ denotes the relative height of the crack roughness unit, and ${\xi }_2^{\prime }$ denotes the angle of inclination of the crack roughness unit.

By observing Equation (15), it can be found that ${\xi }_1^{\prime }$ and ${\xi }_2^{\prime }$ are two dimensionless parameters independent of average openness $b$ and independent of the absolute size of fracture roughness element. Under the condition that the average openness is determined, the roughness element can be completely described by these two parameters. The two dimensionless shape parameters have good consistency at different scales, so the fracture roughness element constructed by this method can well describe the cross-scale effect of fracture roughness.

A fixed pressure of 2 kPa is applied at the inlet of the fracture characterized by serrated roughness units, and the outlet is a free boundary. The flow is driven by the pressure difference. The upper and lower walls of the fracture are slip-free boundaries. The numerical model is shown in Figure 26. Two-phase flow is used for the simulation, and the slurry and air parameters are the same as the values in Section 4.1. The grouting diffusion characteristics of different fractures characterized by roughness units can be obtained.

The geometric parameters of the roughness unit are taken as follows. The average fracture openness is 5 mm. The relative heights are 0, 0.2, 0.4, 0.6, and 0.8. The relative inclination angles are 0°, 20°, 40°, 60°, and 80°. There is a total of 17 simulative conditions in this set of simulations.

4.2.2. Simulation Results

Taking the condition of ${\xi }_1^{\prime }$ = 0.8 and ${\xi }_1^{\prime }$ = 40° as an example, the diffusion process is shown in Figure 27. It can be found that, in each isotropic rough fracture, the grouting diffusion pattern also shows a standard round shape. The velocity of grouting diffusion also increases rapidly at first and then keeps steady. The grouting diffusion distance increases with time under different fractures formed by the roughness units of different geometric parameters, as shown in Figure 28. When ${\xi }_1^{\prime }$ is 0, the model is a parallel plate model. It can be found that as the relative height and angle of the roughness unit increase, the diffusion velocity becomes slower, and the greatest diffusion distance becomes smaller.

The roughness correction factors for each condition, which are back-solved by the analytical model, are shown in

Table 3. The roughness correction factor under different roughness elements.

Roughness Correction Factor (ξ)	20°	40°	60°	80°
0	1
0.2	0.884	0.884	0.876	0.872
0.4	0.862	0.514	0.506	0.242
0.6	0.868	0.510	0.302	0.240
0.8	0.864	0.470	0.242	0.196

. It can be found that the equivalent fracture openness and roughness correction factors decrease nonlinearly with the increase in the relative height and relative inclination angle of the roughness unit. When the relative height is greater than 0.4 and the relative inclination angle is greater than 40°, the correction factor is lower than 0.5, and the correction effect is more obvious.

5. Conclusions

1. Based on the Bingham fluid constitutive equation, this paper establishes the grouting diffusion analytical model in a single rough fracture under constant-pressure control. As the roughness increases, the grouting diffusion velocity and the maximum diffusion distance decreased. The diffusion will tend to stagnate.

2. By carrying out the grouting diffusion test in single rough fractures, the “quasi-elliptical” grouting diffusion mode under the influence of roughness is revealed. Furthermore, the roughness-corrected grouting diffusion analytical formula characterized by the saw-tooth density is established.

The slurry diffusion rate shows a decreasing trend with the increase in roughness. The equivalent openness for the grouting diffusion process becomes smaller with the increase in the saw tooth density. Under the same conditions of the saw-tooth density, the equivalent openness exhibits a non-linear increase with the increasing angles.

3. Based on the FEM calculation software COMSOL Multiphysics, the Bingham–Papanastasiou rheological model is introduced to establish an elaborative numerical simulation model for the Bingham fluid diffusion process in a single rough fracture. Through numerical simulation analysis, the temporal and spatial distribution characteristics of the velocity field and pressure field in the grouting diffusion process are obtained. The pressure attenuation in the x-direction is a step-type under different conditions of saw tooth combinations. Additionally, the attenuation gradient increases with the increase in the saw tooth density. The grouting diffusion velocity decreases with the increase in the saw tooth density under different conditions.

4. Based on the isotropic roughness unit, the roughness correction factor of this analytical model of grouting diffusion is expressed quantitatively with respect to the relative height and relative inclination angle. When the relative height is greater than 0.4 and the relative inclination angle is greater than 40°, the correction factor is lower than 0.5, and the correction effect is more obvious.