Proposal of UWB-PPM with Additional Time Shift for Positioning Technique in Nondestructive Environments

Abstract

The ultra-wide band (UWB) technology has many advantages in positioning and measuring systems; however, powers of UWB signals rapidly reduce while traveling in propagation environments, hence detecting UWB signals are difficult. Various modulation techniques are applied for UWB signals to increase the ability for detecting the reflected signal from transmission mediums, such as pulse amplitude modulation (PAM), pulse position modulation (PPM), and so on. In this paper, we propose an ultra-wide band pulse position modulation technique with optimized additional time shift (UWB-PPM-ATS) to enhance the accuracy in locating buried object in nondestructive environments. Moreover, the Levenberg–Marquardt Fletcher algorithm (LMFA) is applied to determine the medium parameters and buried object location simultaneously. The influences of proposed modulation technique on determining system’s parameters, such as a propagation time, distance, and properties of the medium are analyzed. Calculation results indicate that the proposed UWB-PPM-ATS gives higher accuracy than the conventional one such as UWB-OOK and UWB-PPM in both homogeneous and heterogeneous environments. Furthermore, the LMFA with the proposed UWB-PPM-ATS outperforms the LMFA with the traditional modulation method, especially for unknown propagation environment.

1. Introduction

With ultra-wide bandwidth, the ultra-wide band (UWB) signal is considered as an ideal locating technique in a short-range with high spatial resolution. As defined by the Federal Communications Commission (FCC), UWB technology has a center frequency higher than 2.5 GHz, or if less than 2.5 GHz, there must be a minimum bandwidth ratio of 0.2 [1], or the minimum bandwidth must reach 500 MHz [2]. To avoid affecting other narrow band systems, the rules of FCC allow the effective isotropic radiated power (EIRP) level of UWB devices to be lower than −41.3 dBm/MHz in the frequencies range of 3.1 to 10.6 GHz [3], so the UWB devices can work for more extended periods than narrow band systems with the same battery power, and due to the use of very narrow pulses, UWB signals are better able to penetrate in the nondestructive environments. General modulation techniques are used for UWB signals such as pulse amplitude modulations (PAMs), On-Off Keying (OOK), and pulse position modulation (PPM) [4]. One can use time-hopping (TH) in UWB systems to create TH-PPM, TH-BPSK signal types [5], or design a generator circuit which generates the 4-th and 5-th order derivative of Gaussian pulses in TH-QPSK system applied to multipath channels [6]. Each modulation technique has a different application range. The choice of the right modulation configuration not only increases the efficiency of system implementation but also maximizes the benefits of ultra-wide bandwidth and reduces the complexity of device hardware. In [7], a simple peak detection based on noncoherent UWB receiver is proposed for low data rate wireless sensor networks (WSN) and Internet of things (IoT) applications. It has improved receiver performance with TH-PPM UWB signal. In [8], to reduce the complexity of the TH-UWB receiver, a channel shortening equalizer design method is proposed based on an eigen filter using a new objective function, whereby the proposed system has dramatically reduced the power of channel impulse response, spectral distortion, multiaccess interference, and noise power. Therefore, different UWB signal modulation types have affected the quality and application of the UWB system.

In those modulation techniques, the PPM technique is one of the widely used configurations in UWB systems. Studies on UWB-PPM in wireless communication networks mainly focus on solutions to reduce the conflicts in multiuser access systems; for example, [9] proposed an M-ary PPM modulation configuration for the UWB (M-PPM) system and indicated that the proposed system significantly improved performance compared to systems using direct spreading sequences in the environments with a low signal to noise (SNR) ratio. In [10], Vinod Venkatesan et al. proposed the application of a direct spreading sequence with the optimized UWB-PPM technique for multiaccess systems. The proposed method reduced the impact of multiaccess interference (MAI) and significantly reduced the floor error compared to the orthogonal signal configuration at a large SNR ratio. Besides, there are several studies on improving the quality of the receiver for UWB-PPM signals [11], determining the optimal integration time for the energy detector of the UWB-PPM system [12], and developing a measurement matrix combined with randomly Fourier transform converters for UWB-PPM signals [13]. The combination of PPM symbols and time of arrival (TOA) estimation algorithm using the Sub-Nyquist IR-UWB signal in the IR-UWB device is discussed in [14]. Turbo codes for PPM-IR UWB signals to improve the power spectral density (PSD) power signal density [15] and randomizing the pulses to improve the UWB system [16] were proposed. The noncoherent modulation techniques based on the use of the receiver adaptive thresholds applied to enhanced PPM in the IR-UWB and the direct chaotic communication UWB (DCC-UWB) systems were proposed to improve the bit error rate (BER) performance of the system in a multipath transmission environment [17].

For testing purposes, material penetrating systems using UWB technology to examine nondestructive environments are discussed in [18]; the result indicated that this system can detect imperfect structures of metal. Besides that, the estimation of the layer’s thickness based on the processing of the GPR’s data with the optimized techniques (such as neural networks) is discussed in [19,20]. When using UWB technology in the testing, positioning, or another application in communication to improve the resolution of the systems, one of the main problems is choosing the appropriate modulation technique combined with the receiver’s signal processing methods. The selection of a modulation scheme based on determination distance was discussed in [21]. From those results, we can recognize that the correct detection of UWB pulse signals is one of the essential factors which affect the accuracy of the distance estimation technique. In [22], an UWB indoor positioning system is presented to exploit two-way flight time to calculate range measurements to determine the transceiver location based on Pozyz inner algorithm with a range accuracy of 320 ± 30 mm. In [23], to locate underground personnel in coal mines, an UWB wireless sensor network and time difference of arrival (TDOA) algorithm was proposed, and this system can achieve high-precision positioning in real-time. Furthermore, in the nondestructive environment, direct sequence ultra-wide band (DS-UWB) transmission system with an adaptive pseudo random sequence length is proposed in [24] to reduce processing time and increase positioning accuracy. As mentioned above, the PPM modulation is widely applied to the UWB system, especially for detecting the location of objects; however, the accuracy of estimated results is still low. In this paper, we focus on proposing a new modulation scheme based on PPM modulation to improve the resolution of the estimated distance. The main contributions of this research are listed as follows.

• Firstly, the UWB-PPM signal which is used in determining the distance under the homogeneous and heterogeneous propagation conditions is mathematically analyzed.
• Secondly, based on the analysis of received signal, the delay time and then the propagation distances are estimated.
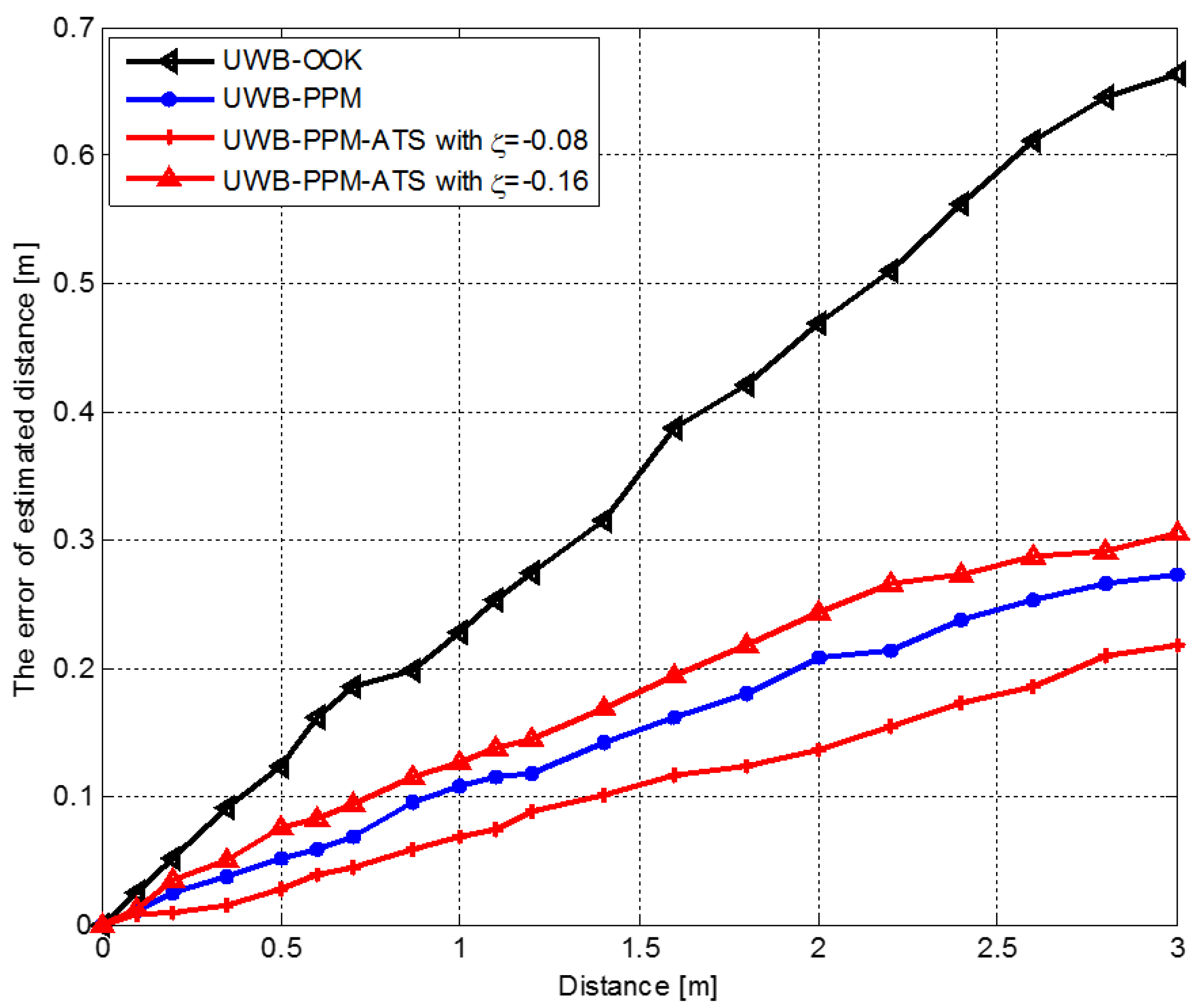
• Thirdly, to increase the accuracy of the estimated distance, an enhanced UWB-PPM modulation technique, called ultra-wide band pulse position modulation with additional time shift (UWB-PPM-ATS) is proposed and compared with other techniques such as conventional UWB-PPM, UWB- OOK with the properties of transmission environment is known.
• Finally, the Levenberg–Marquardt nonlinear estimation algorithm is applied to estimate the system parameter and the target when the propagation environment is unknown.

The remainder of this paper is organized as follows. Section 2 describes the system model for estimating distances in nondestructive environments. The proposed system model and the parameters are presented in Section 3. The simulation results are provided in Section 4, and finally, conclusions and further work are discussed in Section 5.

2. System Model

A distance measurement and positioning system using UWB technology is illustrated in Figure 1, where $d_i$ and ${\epsilon }_i$ are the thickness and the relative permittivity of the $i^{th}$ layer in the nondestructive environment, respectively. $s\left(t\right)$ denotes the transmitted pulse signals, and $r\left(t\right)$ is the received signal.

For the environment with three layers and one buried object, the $r\left(t\right)$ is represented by

$$\begin{array}{cc}\hfill r\left(t\right)=& \sum r_i\left(t\right)+r_{ob}\left(t\right)+n\left(t\right),\hfill \\ \hfill r_1\left(t\right)=& A_{1}s(t-{\tau }_1),\hfill \\ \hfill r_2\left(t\right)=& A_1{A}_{2}s(t-{\tau }_1-{\tau }_2),\hfill \\ \hfill r_3\left(t\right)=& A_1{A}_2{A}_{3}s(t-{\tau }_1-{\tau }_2-{\tau }_3),\hfill \\ \hfill r_{ob}\left(t\right)=& A_{ob}s(t-{\tau }_{ob}),\hfill \end{array}$$

(1)

where $A_i$ denotes the amplitude factor which represents the reflection and transmission properties of the propagation environment, and its value depends on the properties of the ith layers, ${\tau }_i$ is the traveling time of UWB pulse in the ith layer. $A_{ob}$ and ${\tau }_{ob}$ are respectively the amplitude and traveling time of the signal which is reflected from the buried object. $n\left(t\right)$ represents the additive white Gaussian noise.

At the receiver side, the procedure for determining the position of buried object is indicated in Figure 2. Accordingly, the position of buried object is determined by the distance from it to the transceiver. The LMFA method is applied to calculate the relative permittivity of environment and these distances.

In the UWB system, $s\left(t\right)$ is generated based on Gaussian [25] or Hermite [26] functions and their derivatives. Compared to Gaussian pulses, the Hermite pulse is useful for parallel data transmission with high data rates, but it is hard to achieve in the real world [27]. Therefore, the Gaussian pulses UWB signals are applied in this work. A typical Gaussian pulse usually takes the form [25]:

$$\begin{array}{c}\hfill g\left(t\right)=A_p{e}^{-2\pi {\left(\frac{t}{{\mu }_p}\right)}^2},\end{array}$$

(2)

where $A_p$ denotes the amplitude of pulse, ${\mu }_p$ is a factor which influences the amplitude and the width of Gaussian pulse, also called time normalization factor, the width of a pulse becomes narrower when the ${\mu }_p$ is reduced. The $n^{th}$ derivative of Gaussian pulse, named $n^{th}$-order monocycle, is

$$\begin{array}{c}\hfill g_n\left(t\right)=A_{np}\frac{d^n}{d{t}^n}{e}^{-2\pi {\left(\frac{t}{{\mu }_p}\right)}^2},\end{array}$$

(3)

where $A_{np}$ is the amplitude of the $n^{th}$-order monocycle. The shapes of different types of Gaussian monocycles are indicated in Figure 3.

The selected Gaussian pulse shape must meet FCC requirements about power and frequency range used. According to Figure 4, it is observed that for the power spectral density (PSD), only the first-order Gaussian monocycle does not comply with the FCC requirements about the effective isotropic radiated power (EIRP) level. In this paper, we restrict our performance analysis of UWB system to the fourth-order Gaussian monocycle in (4). However, our method can be applied for any Gaussian pulse shape.

$$g_4\left(t\right)=A_p\left[-12\pi +96{\pi }^2{\left(\frac{t}{{\mu }_p}\right)}^2-64{\pi }^3{\left(\frac{t}{{\mu }_p}\right)}^4\right]e^{-2\pi .{\left(\frac{t}{{\mu }_p}\right)}^2}.$$

(4)

It is observed that with impulse radio UWB (IR-UWB) signal, the correlation and therefore the propagation time can be calculated. However, the IR-UWB signal is not strong enough to be processed at the receiver in the case of multiple layers medium (the value of cross-correlation is lower than the noise lever). Hence, an orthogonal pseudo sequence $a\left(n\right)$ is applied to the UWB signal in pulse position modulation (PPM) to ensure the cross-correlation is obtained when receiving many reflected signals from many surfaces and buried objects. The conventional UWB-PPM signal with the fourth-order Gaussian monocycle is given as:

$$s\left(t\right)=\sum _{n=1}^N{g}_4(t-n{T}_r-a_n{T}_{\mathrm{PPM}}),$$

(5)

where $T_r$ is pulse repetition period and $T_{\mathrm{PPM}}$ is the time shift associated with binary PPM, $a_n\in \{0,1\}$, and N is the length of UWB pulses. In this modulation technique, when $a_n$ is 0, there is no additional time shift that modulates the pulse $g_4\left(t\right)$ and a time shift $T_{\mathrm{PPM}}$ is added to $g_4\left(t\right)$ when $a_n$ is 1. In our system model, $a_n$ does not carry information, it only indicates whether the corresponding pulse is shifted or not.

The propagation distance d in the UWB-PPM system used for positioning the buried object in nondestructive medium is computed by:

$$d=\frac{c\tau }{2\sqrt{\epsilon }},$$

(6)

where c is the velocity of light, and $\tau$, $\epsilon$ are the traveling time of UWB pulses and the relative permittivity of the nondestructive medium, respectively.

The traveling time $\tau$ is calculated by the correlation between the received signal from the $i^{th}$ layer, $r_i\left(t\right)$, and the template waveform $\omega \left(t\right)$:

$$\begin{array}{c}\hfill {\displaystyle R_i\left(\tau \right)=\underset{-\infty }{\overset{\infty }{\int }}{r}_i\left(t\right)\omega \left(t\right)dt.}\end{array}$$

(7)

With the conventional UWB-PPM systems, the template waveform at the receiver is $(g_4\left(t\right)-g_4(t-T_{\mathrm{PPM}}))$ and the correlation of this system is denoted by $R_{0i}$ and has the form:

$$\begin{array}{cc}\hfill R_{0i}\left(\tau \right)=& {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{r}_i\left(t\right)[g_4\left(t\right)-g_4(t-T_{\mathrm{PPM}})]dt.}\hfill \end{array}$$

(8)

Define the autocorrelation function of the fourth-order Gaussian monocycle in (4) as $R_{G4}\left(\tau \right)$, we have

$$\begin{array}{cc}\hfill R_{G4}\left(\tau \right)=& {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{g}_4\left(t\right)g_4(t-\tau )dt,}\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill R_{0i}\left(\tau \right)=& R_{G4}\left(\tau \right)-R_{G4}(\tau -T_{\mathrm{PPM}}).\hfill \end{array}$$

(10)

The traveling time of UWB signal is the value that makes the correlation function hit its maximum; it corresponds to twice the transmission time from the transceiver to the reflective surface of the $i^{th}$ layer as shown in Figure 5 and given as

$$\begin{array}{c}\hfill \tau =ar{g}_{\tau }\left(max\left(R_i\right)\right),\end{array}$$

(11)

where $max\left(R_i\right)$ is the local extreme value corresponding to the reflected signals from the surface of the layers or object.

According to (6), $\tau$ is a function of $\epsilon$ and the distance d, due to both d and $\epsilon$ are unknown; they should be estimated by large enough values of $\tau$ using LMFA. To increase the accuracy in the $\tau$ determination procedure, and in estimation of d, $\epsilon$, the proposed UWB-PPM-ATS technique is applied.

3. Proposal of Positioning Approach in Nondestructive Environments

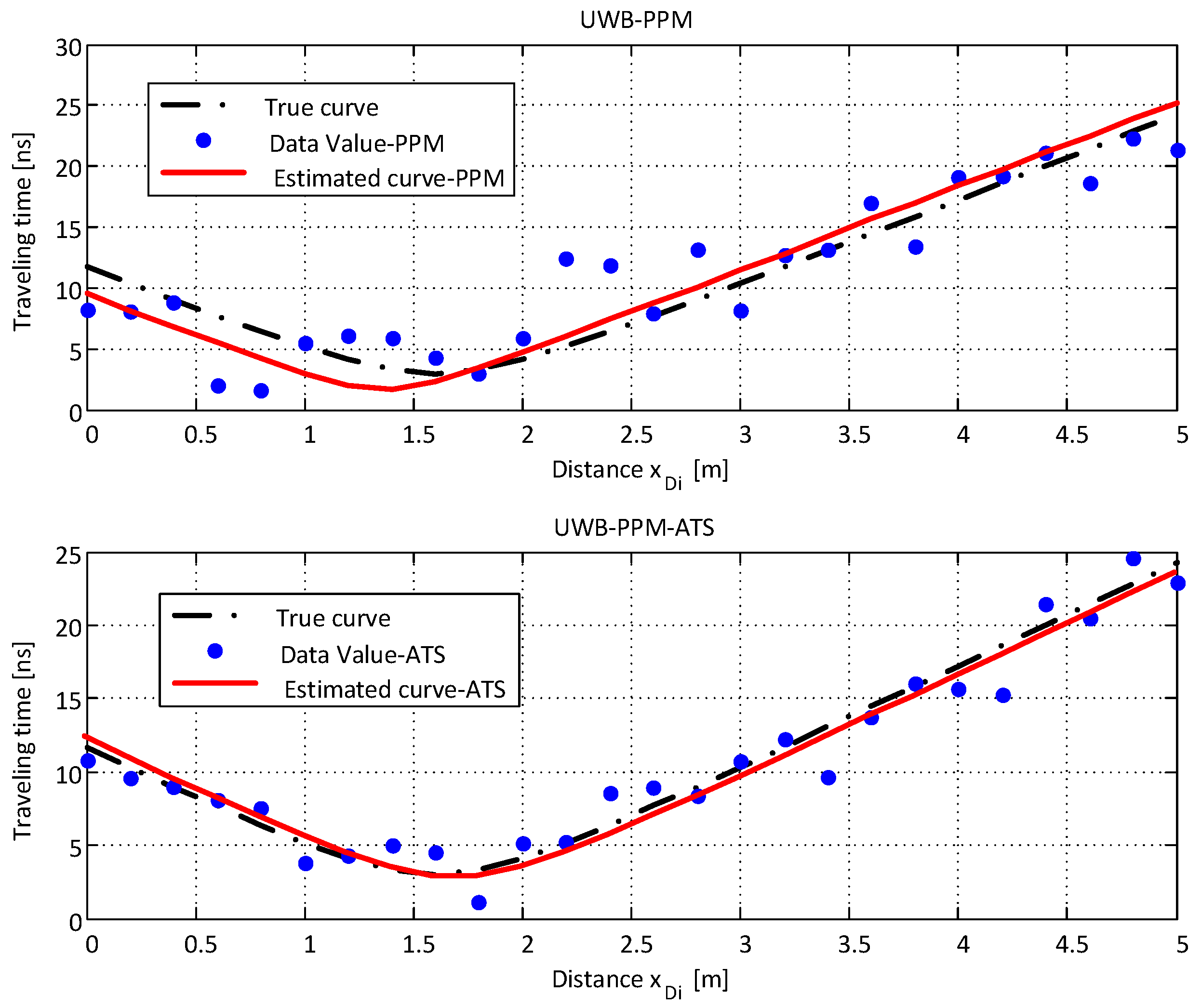
3.1. Proposal of UWB-PPM-ATS

From (1), (5), and (6), it can be seen that the time shift $T_{\mathrm{PPM}}$ directly affects the quality of UWB-PPM systems in positioning applications. The performance of the system can be improved by selecting the appropriate value of the time shift. To increase the accuracy in the estimated distance and the position of buried objects by using the UWB-PPM system, the time shift in this system should be selected so that the ability to detect the received UWB pulse is the best. To accomplish this task, in UWB-PPM systems with the time shift $T_{\mathrm{PPM}}$ is invariant, we recommend adjusting this time shift with a certain time constant to achieve its optimal value. The optimal value of $T_{\mathrm{PPM}}$ defined in this paper is the value at which the UWB-PPM system gives the smallest error in distance estimation. So we propose an UWB pulse position modulation with an additional time shift (UWB-PPM-ATS). In the proposed technique, the pulse position will be changed with a time constant denoted by $\zeta$. The signal of UWB-PPM-ATS is given as:

$$s\left(t\right)=\sum _{n=1}^N{g}_4(t-n{T}_r-a_n·(T_{PPM}+\zeta )).$$

(12)

The "+" sign in (12) means that algebraic additions, so $\zeta$, can take either positive or negative values. The effect of $\zeta$ on the quality of the system will be evaluated later.

An example of the conventional UWB, UWB-PPM, and UWB-PPM-ATS signal shapes are illustrated in Figure 6. In Figure 6, there is an example of a seven pulses sequence carrying seven bits 1010101. The pulse width is 0.28 ns, and it adopts the fourth derivative of the Gaussian function described by the blue line; the conventional PPM modulated pulses sequence is denoted by the red line. Whereby, when the bit value is 0, the transmitter will send out a pulse $g_{40}\left(t\right)$ as the original pulse (without any change from the unmodulated pulse) when the value bit is 1, the transmitter will send out a pulse $g_{41}\left(t\right)$ which is the original pulse with a time shift of $T_{\mathrm{PPM}}$. With the proposed UWB-PPM-ATS (black line), instead of the normal $T_{\mathrm{PPM}}$ time shift, the new shift level is set to ($T_{\mathrm{PPM}}$ + $\zeta$).

The procedure for estimating distances in UWB-PPM-ATS system is the same as in the conventional system (UWB-PPM) and in (7); the template waveform is $(g_4\left(t\right)-g_4(t-T_{\mathrm{PPM}}-\zeta ))$. The correlation of the proposed system denoted by $R_{1i}$ and determined as:

$$\begin{array}{cc}\hfill R_{1i}\left(\tau \right)=& {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{r}_i\left(t\right)[g_4\left(t\right)-g_4(t-T_{\mathrm{PPM}}-\zeta )]dt.}\hfill \end{array}$$

(13)

So, we have:

$$\begin{array}{cc}\hfill R_{1i}\left(\tau \right)=& R_{G4}\left(\tau \right)-R_{G4}(\tau -T_{\mathrm{PPM}}-\zeta )]dt.\hfill \end{array}$$

(14)

The shapes of $R_{G4}\left(\tau \right)$,$R_{0i}\left(\tau \right)$ and $R_{1i}\left(\tau \right)$ are shown in Figure 7.

Figure 7 indicates the autocorrelation function of the fourth-order Gaussian monocycle $R_{G4}$ and correlation functions of UWB-PPM $R_{0i}$ and UWB-PPM-ATS $R_{1i}$ systems (with additional time $\zeta =-0.08$ ns and $\zeta =0.08$ ns); those functions are compared at the value of $\tau =0$. In the figure below inside Figure 7, the blue line with "+" sign denotes the value of $R_{0i}\left(\tau \right)$, the red line denotes the value of $R_{1i}\left(\tau \right)$ with $\zeta$ gets a negative value of −0.08 ns, and the dashed black line denotes the value of $R_{1i}\left(\tau \right)$ with $\zeta$ gets a positive value of 0.08 ns. We can observe that the choice of a negative value of $\zeta$ makes $R_{1i}\left(\tau \right)$ get the maximum value at $\tau =0$ and this value is greater than $R_{1i}\left(0\right)$- with a positive value of $\zeta$ and also $R_{0i}\left(0\right)$ (both of these functions are not maximized at $\tau =0$). Thus $\zeta$ will be selected that makes the value of $R_{G4}(\tau -T_{\mathrm{PPM}}-\zeta )$ reaches to the minimum point of the $R_{G4}$ function which is denoted by $R{\tau }_{opt}$ as shown in Figure 7. It is clear that, in the UWB-PPM-ATS scheme, the negative values of $\zeta$ give the better correlation function than positive values. The variation of the correlation function with the different of $\zeta$ values is illustrated in Figure 8. In Figure 8, the different values of $\zeta$ lead to the different shapes of the correlation function; the optimal value of $\zeta$ in this case is ${\zeta }_{opt}=-0.08$ ns which makes $R_{1i}\left(0\right)$ have the maximum value. When the magnitude of the $\zeta$ increases close to the pulse width ($\zeta =-0.16$ ns, −0.25 ns in Figure 8), the corresponding correlation functions will not reach the global maximum near the value of $\tau =0$ and its local maximum points have the values close to the global maximum. This leads to the higher error in determining the global maximum point of these functions. Therefore, depending on the specific parameter configuration of each UWB-PPM system, the value of $\zeta$ will be chosen such that $R_{1i}\left(0\right)$ in the (14) has the largest value.

The procedure for estimating distances is based on the traveling time mentioned above and can be applied to a well-known propagation environment; however, it is unavailable for an unknown propagation environment. Consequently, we propose to apply LMFA [28] into the calculation of distances, relative permittivities, and determination of buried object location (depth and horizontal direction) in the case of the unknown propagation environment. The proposed method comes from the fact that the traveling time depends on the relative permittivities, buried object location, and transceiver position. So in order to find the value of these parameters, we change the position of the receiver horizontally and calculate the traveling time corresponding to each position of the transceiver. Based on the transceiver location and computed traveling time, the remaining parameters will be estimated.

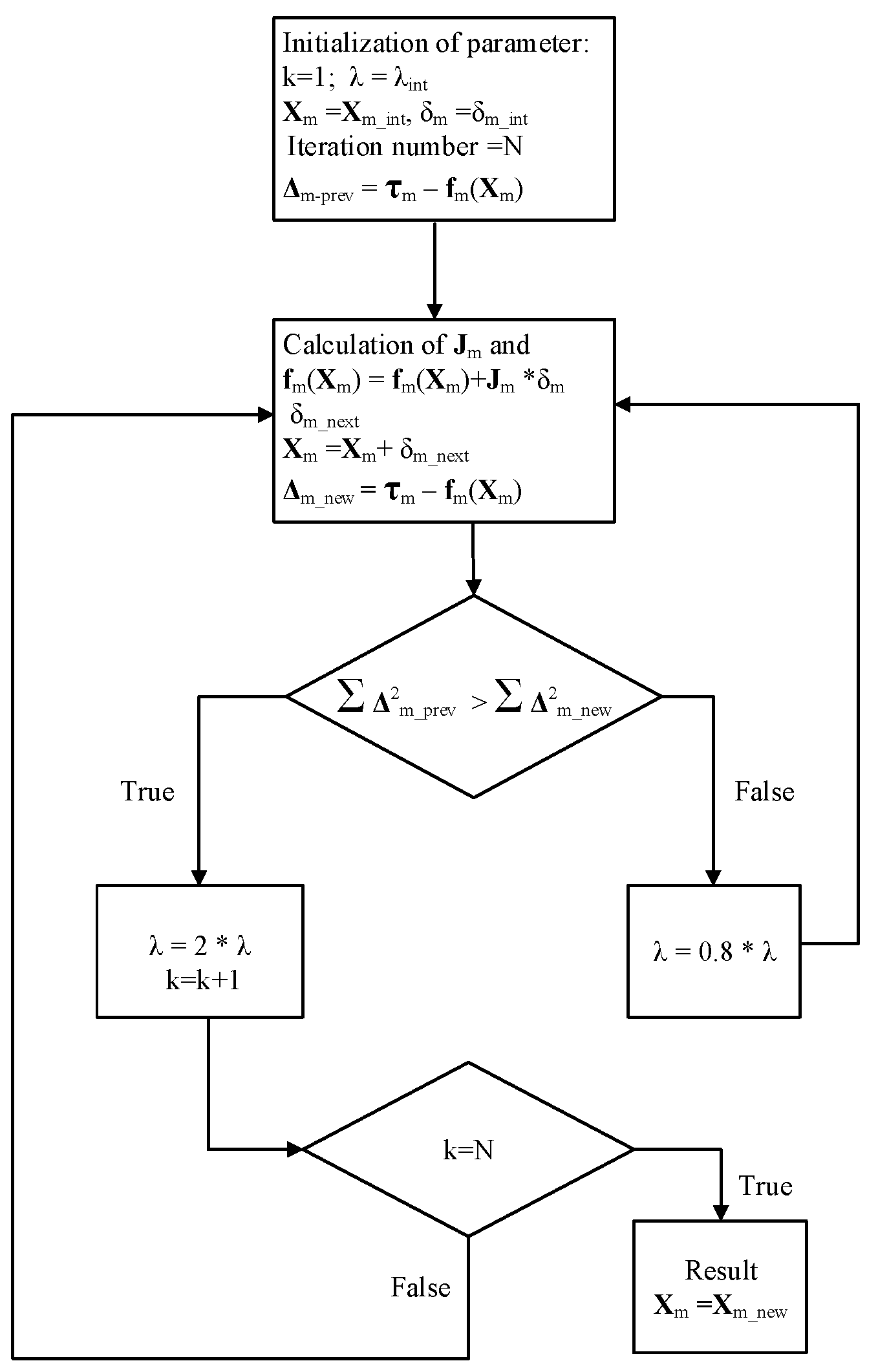
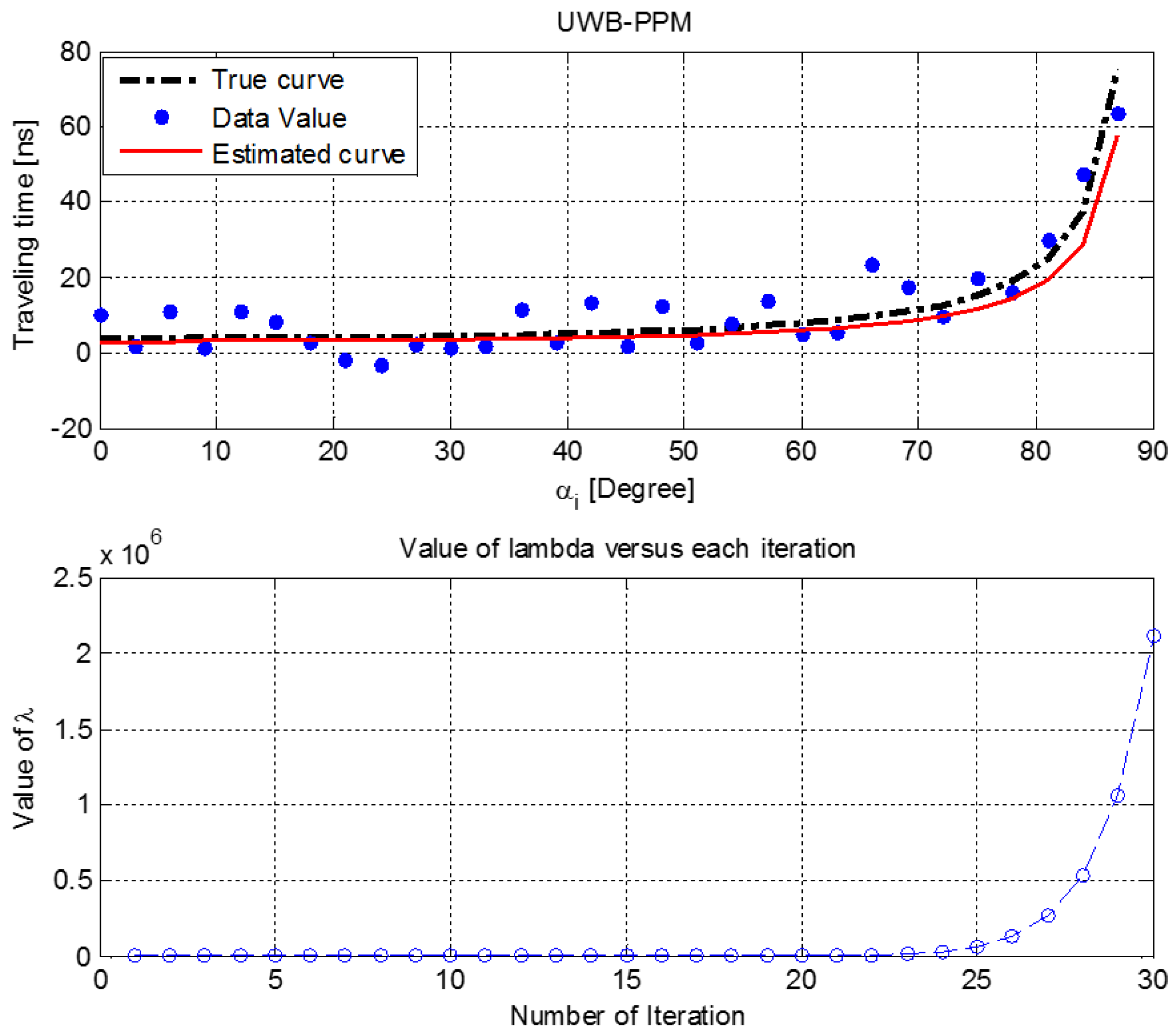
3.2. Estimation Algorithm

Let us consider a specific system model of UWB-PPM systems illustrated in Figure 9, in which the environment is assumed to have a nondestructive structure that has two layers with relative permittivities of ${\epsilon }_1$ and ${\epsilon }_2$.

To determine the environmental parameters and also the location of the target “T”, the transceiver generates UWB pulses with rotation angles of the transceiver antenna are ${\alpha }_i$ and get the reflected pulses. The traveling time ${\tau }_{1i}$ corresponding to the $i^{th}$ time of emission is calculated according to (11), the geometric relationship between ${\tau }_{1i}$, $d_1$, and ${\epsilon }_1$ is indicated in (15).

$$\begin{array}{c}\hfill {\tau }_{1i}=\frac{2d_1\sqrt{{\epsilon }_1}}{c.cos{\alpha }_i},\end{array}$$

(15)

where ${\alpha }_i$ is the rotation angle of antenna and:

$$\begin{array}{c}\hfill {\alpha }_i=i.\Delta \alpha ;\end{array}$$

(16)

where $\Delta \alpha$ is the minimum rotation angle of the transceiver antenna. Thus the values of ${\epsilon }_1$ and $d_1$ in (15) are estimated based on known pairs (${\alpha }_i$, ${\tau }_{1i}$). Then, to locate buried objects, the device is moved horizontally, and the transmitter emits pulses in the perpendicular direction after every movement step of $\Delta x$. Denote ${\tau }_{2i}$ is the traveling time of the transmitted signals, reflected from the buried object and returned to the transceiver at position of $x_{Di}$, it is computed by:

$$\begin{array}{c}\hfill {\tau }_{2i}={\tau }_{10}+\frac{\sqrt{{\epsilon }_2(d_2^2+{(x_T-x_{Di})}^2)}}{c},\end{array}$$

(17)

where $x_T$ is the horizontal coordinates of the buried object and ${\tau }_{10}$ is the traveling time of reflected signal at the interface between two layers of the environment in d direction. ${\tau }_{2i}$ also computed according to (11), the values of ${\epsilon }_2$, $d_2$, and $x_T$ in (17) are estimated based on known pairs (${\tau }_{2i}$, ${\tau }_{10}$, $x_{Di}$), and

$$\begin{array}{c}\hfill x_{Di}=i.\Delta x.\end{array}$$

(18)

The proposed algorithm to estimate the values of those parameters is indicated in Figure 10 and described in detail as below

In Figure 10, the unknown parameter vectors are denoted by:

$$\begin{array}{c}\hfill {\mathbf{X}}_1=({\widehat{\epsilon }}_1,{\widehat{d}}_1);{\mathbf{X}}_2=({\widehat{\epsilon }}_2,{\widehat{d}}_2,{\widehat{x}}_T),\end{array}$$

(19)

and the index m in Figure 10 is used to replace for 1, 2. With the known pairs (${\tau }_{1i}$, ${\alpha }_i$) and (${\tau }_{2i}$, $x_{Di}$), the unknown parameter vectors ${\mathbf{X}}_1$ and ${\mathbf{X}}_2$ are determined such that the sum of the squares of the deviations $S_i\left({\mathbf{X}}_i\right)$ are minimized:

$$\begin{array}{cc}\hfill X_1=& arg\underset{{\mathbf{X}}_1}{min}{S}_1\left({\mathbf{X}}_1\right)=arg\underset{{\mathbf{X}}_1}{min}\sum _{i=1}^M{[{\tau }_{1i}-f_1({\alpha }_i,{\mathbf{X}}_1)]}^2,\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill X_2=& arg\underset{{\mathbf{X}}_2}{min}{S}_2\left({\mathbf{X}}_2\right)=arg\underset{{\mathbf{X}}_2}{min}\sum _{i=1}^M{[{\tau }_{2i}-f_2(x_{Di},{\mathbf{X}}_2)]}^2,\hfill \end{array}$$

(21)

where $f_1({\alpha }_i,{\mathbf{X}}_1)$ and $f_2(x_{Di},{\mathbf{X}}_2)$ are:

$$\begin{array}{cc}\hfill f_1({\alpha }_i,{\mathbf{X}}_1)=& \frac{{\widehat{d}}_1·\sqrt{{\widehat{\epsilon }}_1}}{c.cos{\alpha }_i},\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill f_2(x_{Di},{\mathbf{X}}_2)=& \frac{\sqrt{{\widehat{\epsilon }}_2({\widehat{d}}_2^2+{({\widehat{x}}_T-x_{Di})}^2)}}{c},\hfill \end{array}$$

(23)

where $\widehat{.}$ denotes the estimated values of the parameters; the vectors ${\mathbf{X}}_{\mathbf{1}}$ and ${\mathbf{X}}_{\mathbf{2}}$ were estimated according to the steps as shown in Figure 10 as follows:

+ Assign to ${\mathbf{X}}_1$, ${\mathbf{X}}_2$ any arbitrary initialization values, denoted by ${\mathbf{X}}_{1-int}$, ${\mathbf{X}}_{2-int}$;

+ In each iteration step, the parameter vectors ${\mathbf{X}}_1$, ${\mathbf{X}}_2$ are replaced by new estimates (${\mathbf{X}}_1$ + ${\delta }_1$), (${\mathbf{X}}_2$ + ${\delta }_1$) with ${\delta }_1$, ${\delta }_2$ are updated step vectors and we have:

$$\begin{array}{cc}{\mathbf{S}}_1({\mathbf{X}}_1+{\delta }_1)\approx \hfill & {[{\tau }_1-{\mathbf{f}}_1\left({\mathbf{X}}_1\right)]}^T[{\tau }_1-{\mathbf{f}}_1\left({\mathbf{X}}_1\right)]\hfill \\ \hfill & -2{[{\tau }_1-{\mathbf{f}}_1\left({\mathbf{X}}_1\right)]}^T{\mathbf{J}}_1{\delta }_1+{\delta }_1^T{\mathbf{J}}_1^T{\mathbf{J}}_1{\delta }_1,\hfill \\ {\mathbf{S}}_2({\mathbf{X}}_2+{\delta }_2)\approx \hfill & {[{\mathbf{x}}_D-{\mathbf{f}}_2\left({\mathbf{f}}_2\right)]}^T[{\mathbf{x}}_D-{\mathbf{f}}_2\left({\mathbf{X}}_2\right)]\hfill \\ \hfill & -2{[{\mathbf{x}}_D-{\mathbf{f}}_2\left({\mathbf{X}}_2\right)]}^T{\mathbf{J}}_2{\delta }_2+{\delta }_2^T{\mathbf{J}}_2^T{\mathbf{J}}_2{\delta }_2,\hfill \end{array}$$

with ${\mathbf{J}}_{1,2}$ is the Jacobian matrix, whose $i^{th}$ row equals ${\mathbf{J}}_{1i}$ and ${\mathbf{J}}_{2i}$, respectively:

$$\begin{array}{c}\hfill {\mathbf{J}}_{1i}=\frac{\partial f_1({\alpha }_i,{\mathbf{X}}_1)}{\partial {\mathbf{X}}_1},\end{array}$$

(24)

$$\begin{array}{c}\hfill {\mathbf{J}}_{2i}=\frac{\partial f_2(x_{Di},{\mathbf{X}}_2)}{\partial {\mathbf{X}}_2}.\end{array}$$

(25)

To get the minimum value of the sums ${\mathbf{S}}_1$, ${\mathbf{S}}_2$, the update step vectors ${\delta }_{1,2}$ is calculated such that the derivative of ${\mathbf{S}}_{1,2}({\mathbf{X}}_{1,2}+{\delta }_{1,2})$ with respect to ${\delta }_{1,2}$ has a result of zero, so, ${\delta }_{1,2}$ can be determined satisfying:

$$\begin{array}{c}\hfill [{\mathbf{J}}_1^T{\mathbf{J}}_1+\lambda \mathrm{diag}\left({\mathbf{J}}_1^T{\mathbf{J}}_1\right)]{\delta }_1={\mathbf{J}}_1^T[{\tau }_1-{\mathbf{f}}_1\left({\mathbf{X}}_1\right)],\end{array}$$

(26)

$$\begin{array}{c}\hfill {\mathbf{J}}_2^T{\mathbf{J}}_2+\lambda \mathrm{diag}\left({\mathbf{J}}_2^T{\mathbf{J}}_2\right)]{\delta }_2={\mathbf{J}}_2^T[{\mathbf{x}}_D-{\mathbf{f}}_2\left({\mathbf{X}}_2\right)],\end{array}$$

(27)

where the damping factor $\lambda$ (non-negative) is adjusted at each iteration. If ${\mathbf{S}}_{1,2}$ is reduced rapidly, a smaller value of $\lambda$ can be used, whereas if in an iteration does not reduce the residual, $\lambda$ can be increased. The update step vectors are computed as follows:

$$\begin{array}{c}\hfill {\delta }_1={[{\mathbf{J}}_{\mathbf{1}}^{\mathbf{T}}{\mathbf{J}}_1+\lambda \mathrm{diag}\left({\mathbf{J}}_1^T{\mathbf{J}}_1\right)]}^{-1}{\mathbf{J}}_1^T[{\tau }_1-{\mathbf{f}}_1\left({\mathbf{X}}_1\right)],\end{array}$$

(28)

$$\begin{array}{c}\hfill {\delta }_2={[{\mathbf{J}}_2^T{\mathbf{J}}_2+\lambda \mathrm{diag}\left({\mathbf{J}}_2^T{\mathbf{J}}_2\right)]}^{-1}{\mathbf{J}}_2^T[{\mathbf{x}}_D-{\mathbf{f}}_2\left({\mathbf{X}}_2\right)].\end{array}$$

(29)

After a certain number of iterations, the output of LMFA is the final estimated values of system parameters that meet the constraint condition in (21), as shown in Figure 10.

4. Simulation Results and Discussion

4.1. Simulation Parameters

The accuracy of methods for determining the distance and characteristics of a multilayered reflective environments using UWB pulses is strongly dependent on UWB signal processing techniques. UWB-PPM is one of the candidates for positioning technology in a nondestructive environment with multiple reflective layers; with the proposed UWB-PPM-ATS, our trials indicated that the UWB-PPM pulses shifted with a certain time constant can be used to improve the precision in estimating the distance. All the numerical results in this paper were computed using Matlab.

First, we compare the exact estimation errors of the UWB-OOK, UWB-PPM and UWB-PPM-ATS systems with the results obtained from the simulations and the actual value of the parameters use (6), (8), (11), (13) and (30). Here OOK is one of the UWB pulse amplitude modulation techniques and has two level modulation with the bits are 0 and 1. When sending a bit 0, the transmitter will not send anything. When sending a bit 1, the transmitter will send a pulse [29], and the template waveform $\omega \left(t\right)$ at the receiver of UWB-OOK system is $g_4\left(t\right)$. In addition, the performance of UWB-OOK, UWB-PPM and UWB-PPM-ATS systems were evaluated for an environment with known characteristics (for example, here are three layers as indicated in Figure 1). Finally, the location determination technique in a unknown environment with multiple reflection layers using the LMFA based on the estimated parameters of those UWB systems is presented with the system model as shown in Figure 9. The comparisons between the above systems are evaluated in term of errors between the estimated values from the considered system and the true values. Based on the PSD plot of the Gaussian impulses shown in Figure 4, most of the numerical results presented in this section are based on analysis using the fourth-order Gaussian monocycle. The parameters of the example UWB systems are listed in

Table 1. Simulation parameters.

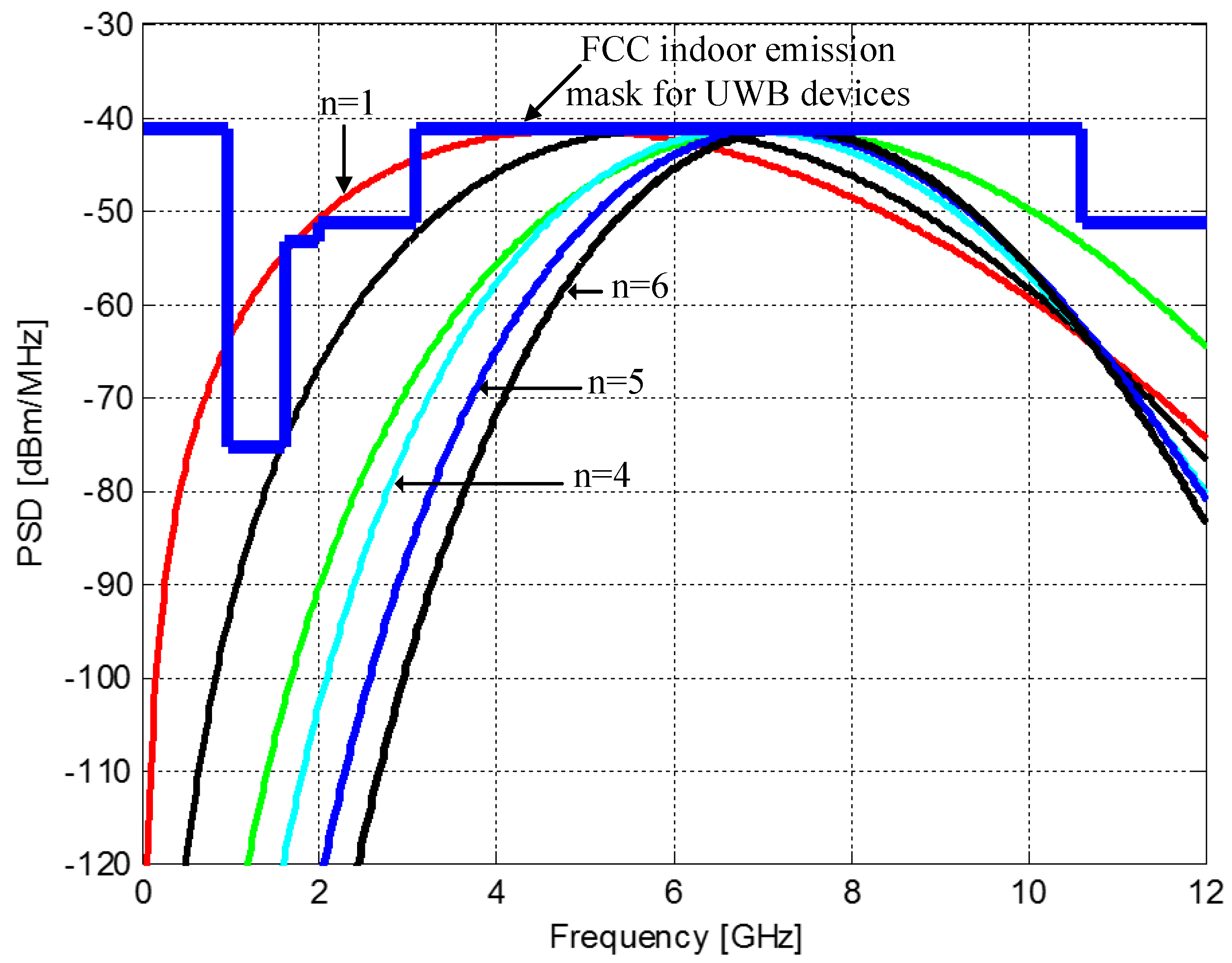
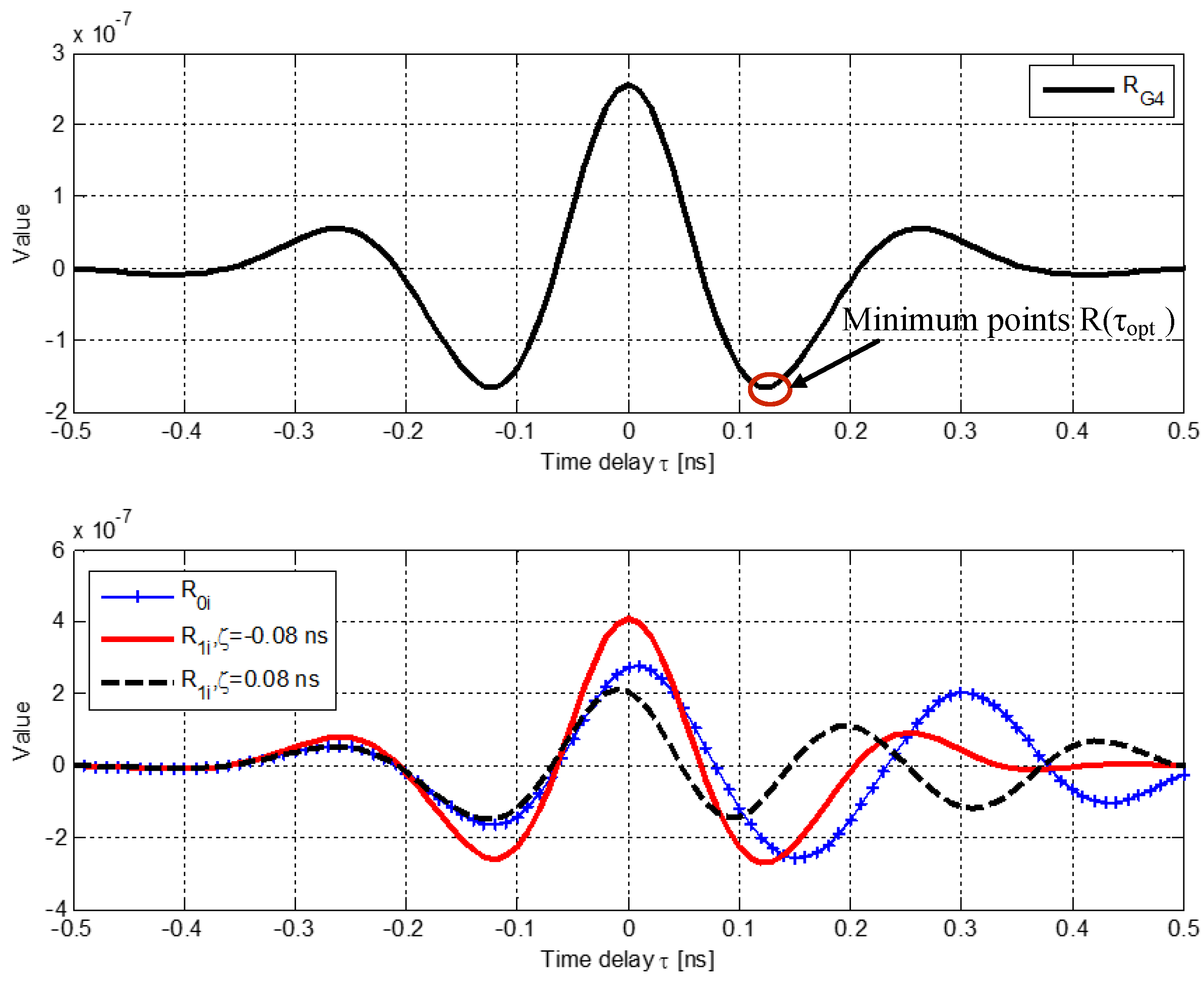
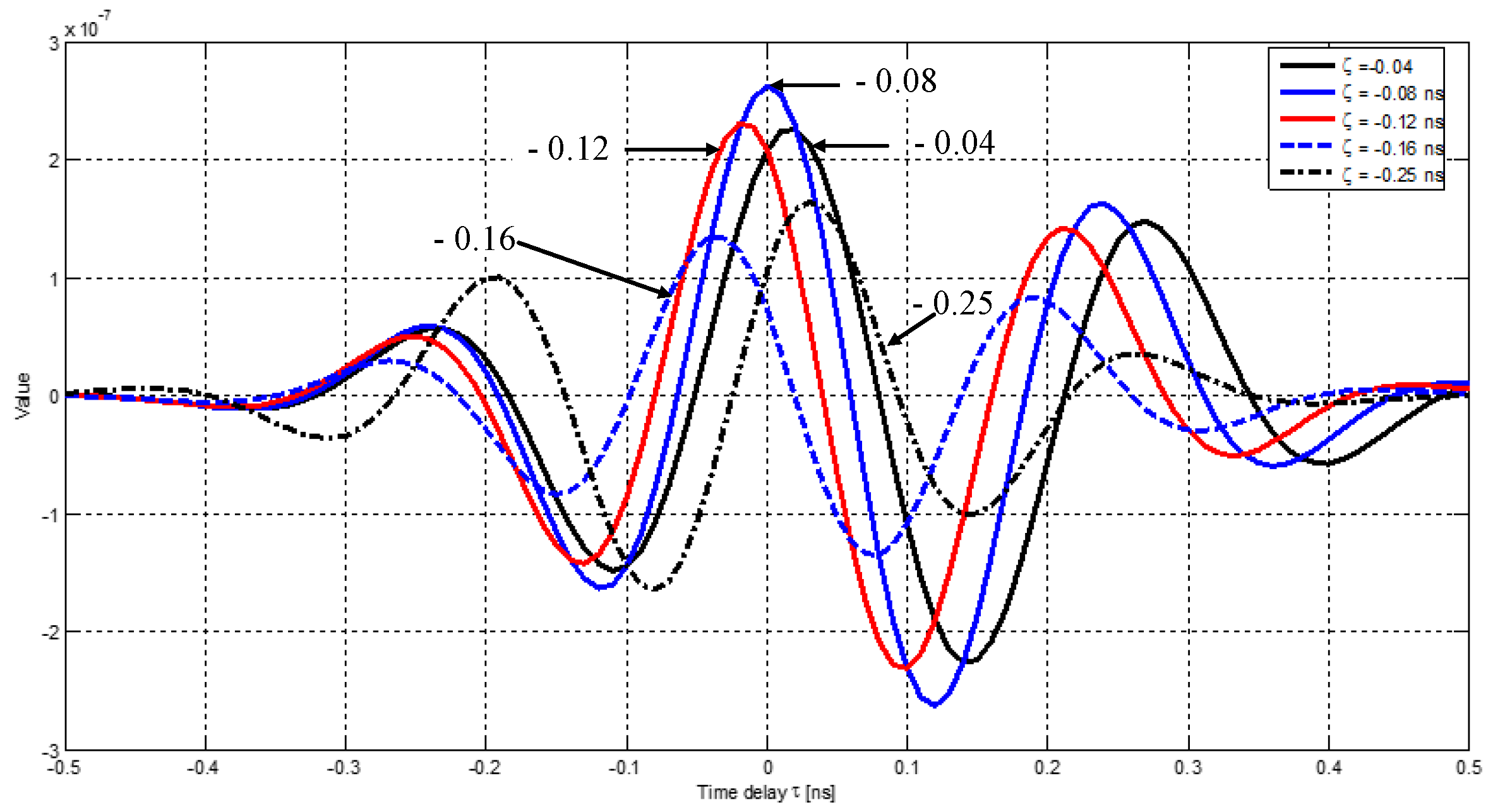
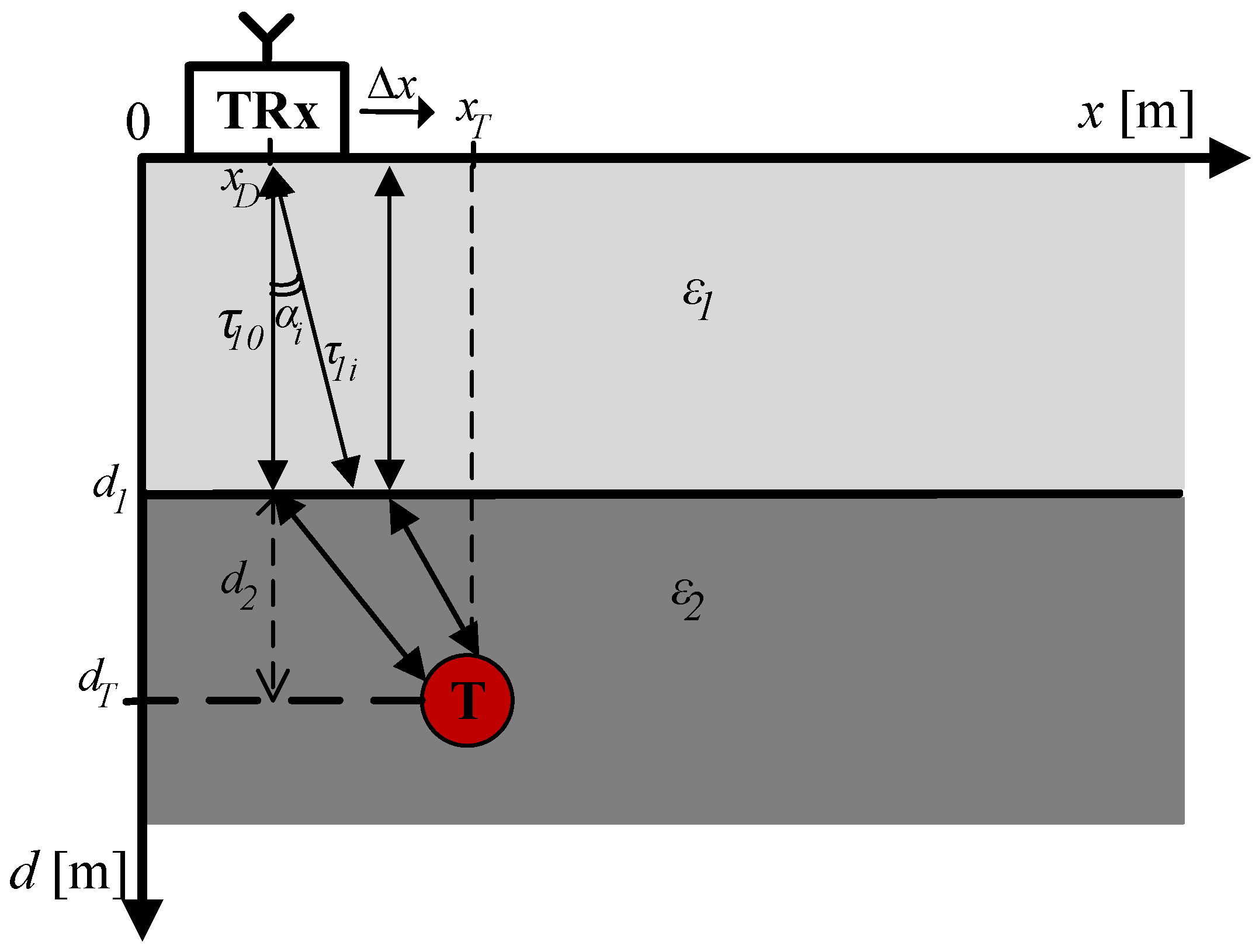
Parameter	Notation	Value
Time normalization factor	${\mu }_p$	0.2877 ns
Transmitted power	$P_{Tx}$	−35.4 dB
The amplitude factors	$A_1,A_2,A_3$	0.33, 0.13, 0.14
Number of pulses	N	100
Noise power	$N_0/2$	−102 dB
Time shift of PPM	$T_{PPM}$	0.2 ns
Additional time shift	$\zeta$	−0.08 ns, −0.16 ns
Relative permittivity
with heterogeneous medium	${\epsilon }_1$, ${\epsilon }_2$, ${\epsilon }_3$	4; 3; 5

and follow [5].

To assess the performance of those UWB systems, the error of estimated distance is defined as follows:

$$\begin{array}{c}\hfill {\delta }_d=\left|\widehat{d_i}-d_{tri}\right|,\end{array}$$

(30)

where $\widehat{d_i}$ denotes the estimated distance and $d_{tri}$ is the true value.

In Figure 1, without generality, we assume that the propagation environment is heterogeneous with three layers: sand (dry), sandy soil (dry) and granite (dry) and the relative permittivities ${\epsilon }_1,{\epsilon }_2,{\epsilon }_3$ are 4, 3, 5, respectively. Those layers are assumed to be dry to reduce the attenuation of environment, so propagation velocity in those layers are 15 cm/ns, 17.32 cm/ns, 13.42 cm/ns and the attenuation is 0.01 dB/m [30]. With a known transmission environment, those distance can be estimated using (6), where ${\tau }_i$ is computed according to (8), (11) and (13). Then the errors of estimated distances are calculated according to (30) and illustrated in Figure 11 for OOK, PPM, ATS systems with $\zeta =-0.08$ ns and $\zeta =-0.16$ ns. In Figure 11, the black line denotes the average error of the OOK system, the blue line denote the error of the PPM system and the red lines denote the error of the ATS system, all with the same system parameters. Observe that the relative error of the UWB-OOK system is about 24%, of UWB-PPM is about 11%, of UWB-PPM-ATS with $\zeta =-0.08$ ns is about 7%, with $\zeta =-0.16$ ns is about 13%; so the UWB-PPM- ATS with $\zeta =-0.08$ ns performs better for all distance values. This can be explained by comparing the correlation functions which are given in (8), (13) and Figure 7 and Figure 8; we observe that $R_{1i}\left(0\right)$ is significantly greater than $R_{0i}\left(0\right)$ for $\zeta =-0.08$ ns and $R_{0i}\left(0\right)$ is not the maximum value of $R_{0i}\left(\tau \right)$, which leads to a smaller than average error in the PPM-ATS with $\zeta =-0.08$ ns when compared to PPM scheme; but with $\zeta =-0.16$ ns, $R_{1i}\left(0\right)$ is less than $R_{0i}\left(0\right)$ thus the PPM outperforms the PPM-ATS. Besides that, the UWB-OOK is one of the amplitude modulation techniques, thus it is affected by the transmission environment and more difficult to separate the received signal from noise interference in comparison with the PPM techniques which have a constant amplitude. The results in Figure 11 indicate that the time shift $\zeta$ directly affects the performance of PPM systems. The value of $\zeta$ is selected so that $(T_{\mathrm{PPM}}+\zeta )$ achieves the optimal value at which $R_{G4}(\tau -T_{\mathrm{PPM}}-\zeta )$ gets the minimum value. From (6) and (13), we also know that $\zeta$ is determined by the pulse shape and the pulse width normalization factor ${\mu }_p$. Due to the influence of the UWB-PPM system to the choice of the time shift, a suitable value of $\zeta$ should be chosen according to the specific pulse shape and pulse width employed in a particular UWB application.

4.2. Determine the Location of Buried Object by LMFA

As mentioned above, the propagation distance can only be determined using the correlation function if the characteristic of the environment is well-known; however, this is impossible with unknown environment. Moreover, the position of buried object cannot be determined by only the propagation distances; it must be determined in both x and d directions ($x_T$, $d_T$ in Figure 9). The parameters of each layer in the system model in Figure 9 are estimated sequentially using LMFA as presented in Section 3.2. The parameters of system model and the initialization vectors of the LMFA algorithm are listed in

Table 2. Initialization parameters of the model.

Parameter	Notation	Value
The thickness of the $1\mathrm{st}$ layer	$d_1$	0.63 m
Depth of ’T’ in the $2\mathrm{nd}$ layer	$d_2$	0.42 m
X-coordinate of ’T’	$x_T$	1.6 m
Relative permittivity	${\epsilon }_1$, ${\epsilon }_2$	3.5, 4.5
Damping factor	$\lambda$	3
Movement step of the device	$\Delta x$	20 cm

in which two layers of environment are assumed to be dry sand and concrete with the corresponding propagation velocity of 16 cm/ns and 14.14 cm/s.

First the parameters ${\epsilon }_1$, $d_1$ are estimated based on the propagation time ${\tau }_{1i}$ and rotation angle ${\alpha }_i$ with both UWB-PPM and UWB-PPM-ATS systems. Then, in a similar way, the parameters $d_2$, ${\epsilon }_2$, and $x_T$ are estimated based on ${\mathsf{ø}}_{\mathbf{2}}$ and ${\mathbf{x}}_{\mathbf{D}}$; therefore, the depth of buried object $d_T=d_1+d_2$ is also determined. The estimated results after 30 iterations and errors of UWB systems are listed in

Table 3. The results of the estimated parameters.

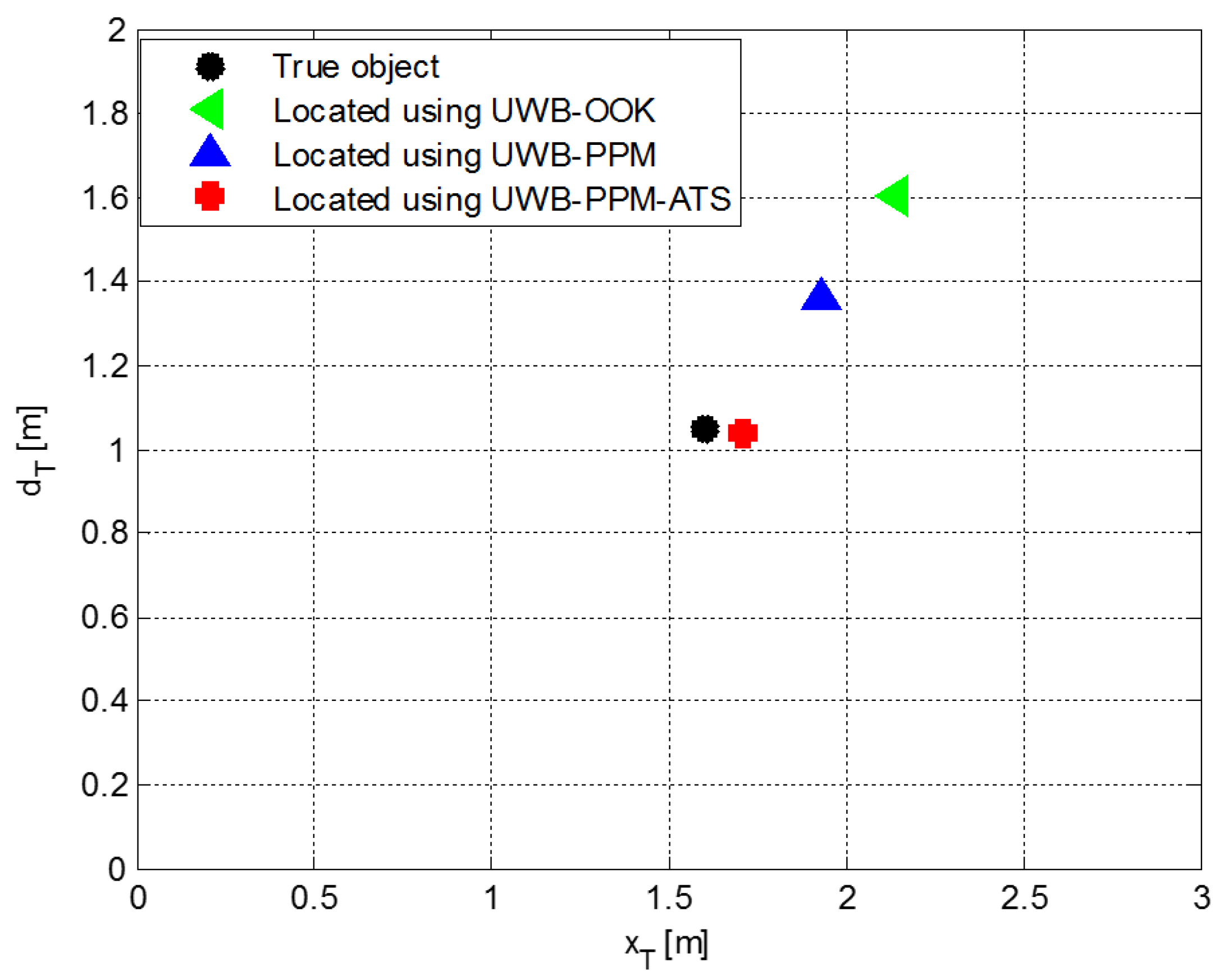
Parameter/Notation	${\mathit{d}}_1$	${\mathit{d}}_2$	${\mathit{x}}_{\mathit{T}}$	${\mathit{\epsilon }}_1$	${\mathit{\epsilon }}_2$
True value [m]	0.63	0.42	1.6	3.5	4.5
By UWB-OOK [m]	0.9418	0.6623	2.1362	4.3216	5.7261
By UWB-PPM [m]	0.7923	0.5742	1.9316	2.7109	3.3590
By UWB-
PPM-ATS [m]	0.6523	0.3899	1.7107	3.2829	4.8167
Error of UWB-OOK	0.3118	0.2423	0.5362	0.8216	1.2261
Error of UWB-PPM	0.1623	0.1542	0.3316	0.7891	1.141
Error of
UWB-PPM-ATS	0.0223	0.0301	0.1107	0.2171	0.3167

and Figure 12, Figure 13 and Figure 14. Figure 12 and Figure 13 show the relationship between ${\tau }_{1i}$ and ${\alpha }_i$ in (15). In those figures, the dashed black line denote the curve of ${\tau }_{1i}$ vs. ${\alpha }_i$ with the true values of $d_1$ and ${\epsilon }_1$; the blue dots are ${\tau }_{1i}$ values measured by simulated UWB systems and the red line denote the curve of ${\tau }_{1i}$ vs. ${\alpha }_i$ with the estimated values $\widehat{d_1}$ and $\widehat{{\epsilon }_1}$. Figure 14 shows the curve of $({\tau }_{2i}-{\tau }_{10})$ depends on $x_{Di}$ according to (17). In those figures, the dashed black line denotes the curve of $({\tau }_{2i}-{\tau }_{10})$ vs. $x_{Di}$ with the true values of $d_2$, ${\epsilon }_2$ and $x_T$; the blue dots are $({\tau }_{2i}-{\tau }_{10})$ values measured by simulated UWB systems and the red line denotes the curve of $({\tau }_{2i}-{\tau }_{10})$ vs. $x_{Di}$ with the estimated values $\widehat{d_2}$, $\widehat{{\epsilon }_2}$ and $\widehat{x_T}$.

Table 3 and Figure 15 show the estimated results by the UWB systems. As seen, the modulation techniques for UWB pulses combine with nonlinear estimation method LMFA can be used to determine the thickness of different layers in the nondestructive environments, their relative permittivities and also the position of buried object. We observe that the UWB-PPM-ATS system outperforms the UWB-PPM system for all parameters of the model. This behavior results directly from the features of the correlation functions of different signals shown in Figure 7 and Figure 8. When using UWB-PPM-ATS technique with the optimal value of $\zeta$, the estimated traveling time values have a smaller error than using UWB-PPM technique, so the results from the LMFA of the PPM-ATS system give the higher accuracy than conventional PPM system.

5. Conclusions

In this paper, the authors have proposed an UWB pulse position modulation with an additional time-shift technique for positioning applications in nondestructive environments of the UWB systems. The proposed method is utilized to determine the distances and the position of a buried object in heterogeneous environments. The proposed technique’s quality is assessed based on the calculation errors compared to the actual values and comparison with the conventional modulation methods. Combining with the Levenberg–Marquardt Fletcher algorithm to determine the buried object location when the propagation environment is unknown, the efficiency of the proposed technique is better than the PPM-UWB system with the same model. Evaluating different UWB systems based on the calculation of errors provides reliable information for choosing modulation schemes with suitable parameters in the design of UWB systems for positioning applications, especially in nondestructive environments.

However, in this work, only one buried object location is determined; multiple buried object estimation algorithm will be researched in our future works. Additionally, the research on parameters of the buried object, such as shape, size, permittivity and so on, is left for the future work.