Axial and Bending Bearing Capacity of Double-Steel-Concrete Composite Shear Walls
Abstract
:1. Introduction
2. Experimental Results Analysis
- The bending failure characteristics of the SC wall are similar. Steel plate at the bottom of the SC wall yields first, followed by the buckling of the steel plate and concrete crushing. All SC wall failures are characterized by concrete crushing at embedded columns. When the studs are closely arranged, the steel plate at the bottom of the wall plate yields before buckling.
- Before the load reaches the peak, the average strain distribution of the surface steel plate at a certain height from the wall base is consistent with the plane assumption.
3. Numerical Analysis
3.1. FE Model
3.2. FE Calculation Results
- Average strain distribution of the cross section
- 2.
- Ultimate compression strain of the concrete
4. Derivation of the Axial and Bending Bearing Capacity
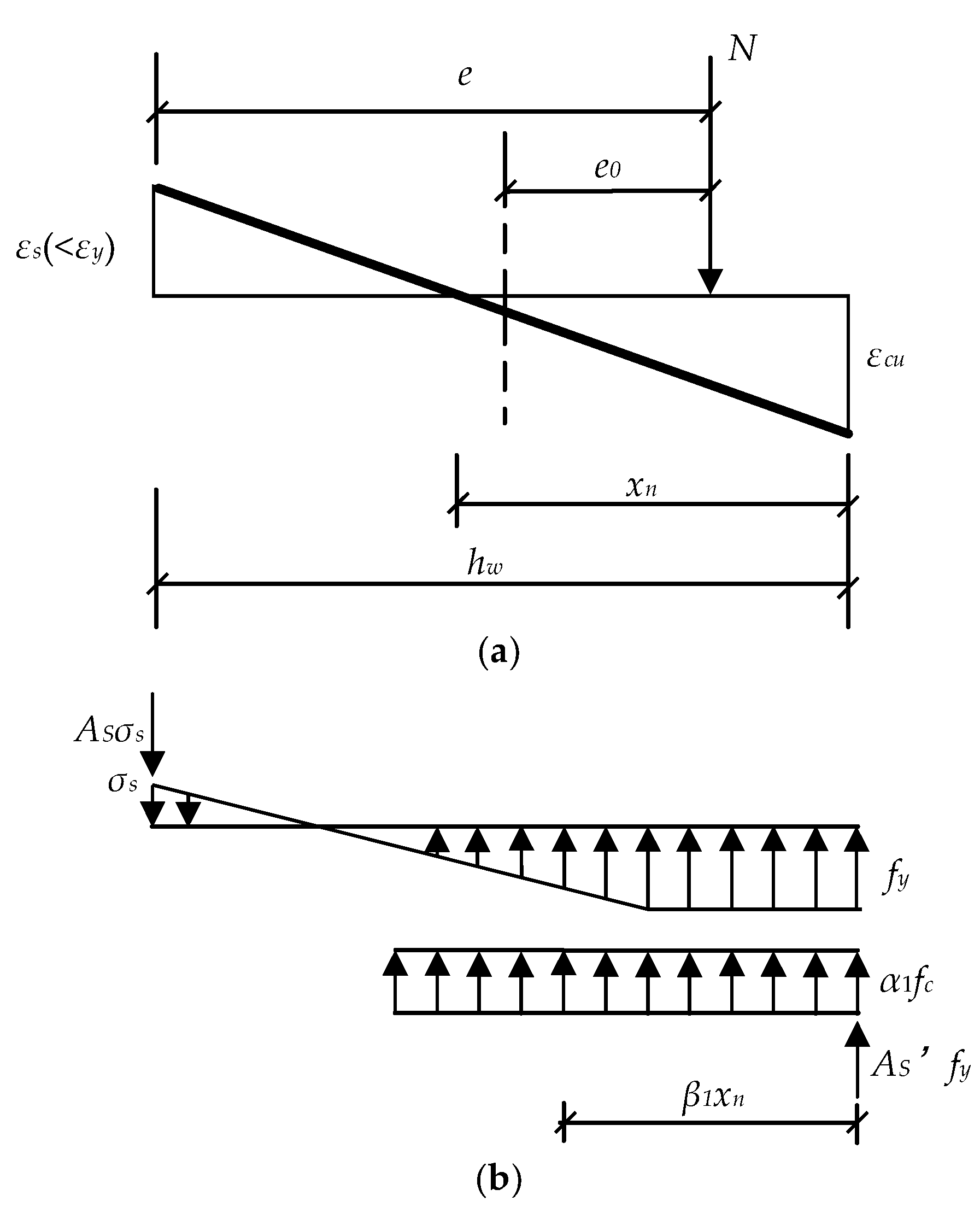
4.1. Basic Assumption
- The failure of SC walls is that the outermost concrete in the compression zone reaches the ultimate compressive strain, and the corresponding bearing capacity is taken as the ultimate bearing capacity;
- The surface steel plate and concrete are well combined without slippage;
- The average strain distribution of the wall cross section is consistent with the plane assumption;
- The tensile effect of the concrete is not taken into account;
- The constitutive of the concrete with the confinement of a rectangular steel tube is introduced to describe the behavior of concrete under a uniaxial load, which was proposed by Han [35]. The ultimate compressive strain of concrete corresponded to a stress value of 0.5fcc in the descending part of the stress-strain curve;
- The ideal elastic-plastic constitutive is introduced to describe the behavior of steel plate, ignoring the strain hardening;
- The concrete compressive stress distribution is replaced by equivalent rectangular stress distribution. The equivalent stress is α1fcc and the equivalent compression zone height is x = β1xn. α1 and β1 are equivalent rectangular stress coefficients, which are related to the concrete grade. The values of α1 and β1 are the same as ordinary concrete. fcc is calculated using Equation (5) [34].where fcc is the compressive strength of confined concrete; fc is the compressive strength of the concrete; and ξ1 is the confinement effect coefficient.
4.2. Section Simplification
4.3. Failure Modes
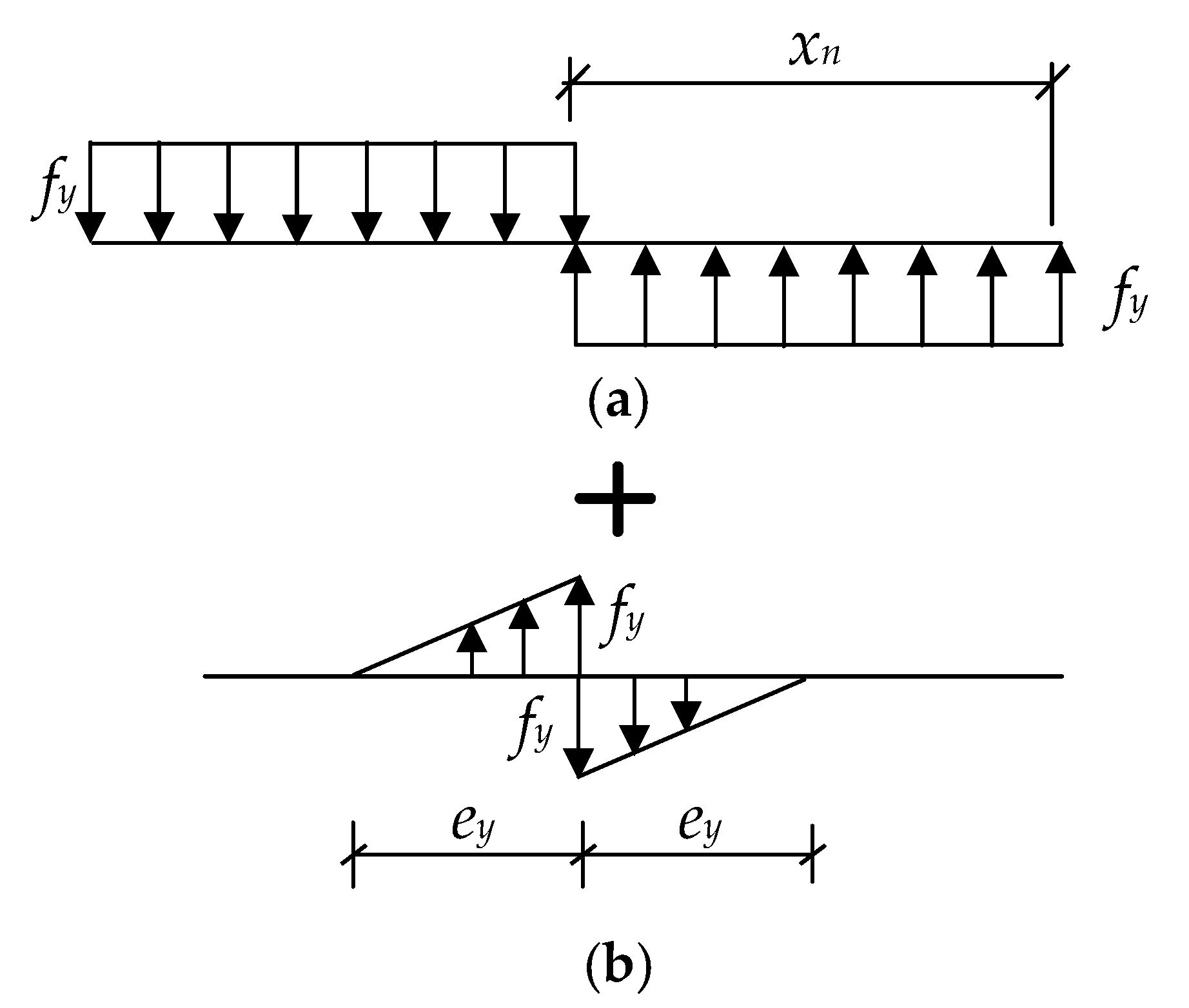
4.4. Large Eccentric Compression Failure (ξ ≤ ξb)
4.5. Small Eccentric Compression Failure (ξ > ξb)
4.6. Verification
5. Conclusions
- The bending failure of SC walls featured the concrete crushing at the column and the average strain distribution of the wall cross section agreed with the plane assumption.
- When studs meet certain construction requirements, the surface steel plates and filled concrete are unified well, and the bond-slip between them is relatively small.
- The ultimate compressive strain of the concrete can be defined as the post-peak strain corresponding to the stress valued 0.5fcc in the declining part of the stress-strain curve; the constitutive of the concrete with the confinement of a rectangular steel tube is applied to descript the behavior of concrete.
- The basic assumption for calculating the axial and bending bearing capacity of SC walls is put forward and the calculation formula applying to both small and large eccentric load is deduced. The calculated results are compared with the experimental results, which present good agreements.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Usami, S.; Akiyama, H.; Suzuki, T.; Sekimoto, H.; Kobayashi, M. Experimental study on concrete filled steel shear wall: Part 2 bensing shear test. In Summaries of Technical Papers of Annual Meeting; Structures. II; Architectural Institute of Japan: Tokyo, Japan, 1991; pp. 1661–1662. [Google Scholar]
- Takeuchi, M.; Narikawa, M.; Matsuo, I.; Hara, K.; Usami, S. Study on a concrete filled structure for nuclear power plants. Nucl. Eng. Des. 1998, 179, 209–223. [Google Scholar] [CrossRef]
- Niwa, N.; Sasaki, N.; Akiyama, H.; Narikawa, M.; Hara, K.; Takeuchi, M.; Usami, S. Study on concrete filled steel structures for nuclear power plants: Part 3 outline of bending shear tests. In Summaries of Technical Papers of Annual Meeting; B-2; Structures II; Structural Dynamics Nuclear Power Plants; Architectural Institute of Japan: Tokyo, Japan, 1995; pp. 987–988. [Google Scholar]
- Ozaki, M.; Akita, S.; Osuga, H.; Nakayama, T.; Adachi, N. Study on steel plate reinforced concrete panels subjected to cyclic in-plane shear. Nucl. Eng. Des. 2004, 228, 225–244. [Google Scholar] [CrossRef]
- Kitano, T.; Akita, S.; Nakazawa, M.; Fujino, Y.; Ohta, H.; Yamaguchi, T.; Nakayama, T. Experimental study on a concrete filled steel structure: Part 4 shear tests (outline of the experimental program nad the results). In Summaries of Technical Papers of Annual Meeting; B-2; Structures II, Structural Dynamics Nuclear Power Plants; Architectural Institute of Japan: Tokyo, Japan, 1997; pp. 1057–1058. [Google Scholar]
- Funakoshi, A.; Akita, S.; Matsumoto, N.; Hara, K.; Hara, K.; Hayashi, N. Experimental study on a concrete filled steel structure: Part 7 bending shear tests(outline of the experimental program nad the results). In Summaries of Technical Papers of Annual Meeting; B-2; Structures II; Structural Dynamics Nuclear Power Plants; Architectural Institute of Japan: Tokyo, Japan, 1997; pp. 1063–1064. [Google Scholar]
- Eom, T.-S.; Park, H.-G.; Lee, C.-H.; Kim, J.-H.; Chang, I.-H. Behavior of double skin composite wall subjected to in-plane cyclic loading. J. Struct. Eng. ASCE 2009, 135, 1239–1249. [Google Scholar] [CrossRef]
- Wu, B.; Liu, C.; Zhao, X.; Liu, Q. Experimental study on seismic behavior of double thin skin hybrid walls filled with demolished concrete lumps. J. Build. Struct. 2011, 32, 116–125. [Google Scholar]
- Nie, J.; Tao, M.; Fan, J.; Bu, F.; Hu, H.; Ma, X.; Li, S.; Liu, F. Research advances of composite shear walls with double steel plates and filled concrete. Build. Struct. 2011, 41, 52–60. [Google Scholar]
- Nie, J.; Bu, F.; Fan, J. Experimental research on seismic behavior of low shear-span ratio composite shear wall with double steel plates and infill concrete. J. Build. Struct. 2011, 32, 74–81. [Google Scholar]
- Ji, X.; Jiang, F.; Qian, J. Seismic behavior of steel tube–double steel plate–concrete composite walls: Experimental tests. J. Constr. Steel Res. 2013, 86, 17–30. [Google Scholar] [CrossRef]
- Tian, C.; Cheng, W. Report of the Experimental Research of Steel Plate and Concrete Composite Shear Wall in Htr; Beihang University: Beijing, China, 2013. [Google Scholar]
- Guo, X.; Qiu, L.; Luo, Y.; Li, J.; Dong, N.; Zhang, J. Seismic performance of concrete-filled double skin composite shear wall with opening. J. Harbin Inst. Technol. 2015, 47, 69–76. [Google Scholar]
- Yang, Y.; Liu, J.; Nie, X.; Fan, J. Experimental research on out-of-plane cyclic behavior of steel-plate composite walls. J. Earthq. Tsunami 2016, 10, 1650001. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Yang, Q.; Liu, J.; Liao, Y. Experimental research on axial compressive behavior of shear wall with double steel plates and filled concrete. J. Sichuan Univ. 2016, 48, 83–90. [Google Scholar]
- Li, X.; Li, X.; Shen, L.; Liu, J. Experimental study of composite shear walls with double steel plates and filled concrete for a nuclear island structure under low cyclic loading. J. Beijing Univ. Technol. 2015, 42, 1498–1508. [Google Scholar]
- Li, X.; Li, X. Study on in-plane flexural behavior of double steel plates and concrete infill composite shear walls for nuclear engineering. Eng. Mech. 2017, 34, 43–53. [Google Scholar]
- Lin, X.; Wu, K.; Skalomenos, K.A.; Lu, L.; Zhao, S. Development of a buckling-restrained shear panel damper with demountable steel-concrete composite restrainers. Soil Dyn. Earthq. Eng. 2019, 118, 221–230. [Google Scholar] [CrossRef]
- Zhao, Q.; Astaneh-Asl, A. Cyclic behavior of traditional and innovative composite shear walls. J. Struct. Eng. ASCE 2004, 130, 271–284. [Google Scholar] [CrossRef] [Green Version]
- Rassouli, B.; Shafaei, S.; Ayazi, A.; Farahbod, F. Experimental and numerical study on steel-concrete composite shear wall using light-weight concrete. J. Constr. Steel Res. 2016, 126, 117–128. [Google Scholar] [CrossRef]
- Varma, A.H.; Malushte, S.R.; Sener, K.C.; Lai, Z. Steel-plate composite (sc) walls for safety related nuclear facilities: Design for in-plane forces and out-of-plane moments. Nucl. Eng. Des. 2014, 269, 240–249. [Google Scholar] [CrossRef]
- Japanese Electric Association. Techinical Guidelines for Aseismic Design of Steel Plate Reinforced Concrete Structures-Buildings and Structures; Japanese Electric Association: Tokyo, Japan, 2005; Volume JEAG4618-2005. [Google Scholar]
- Ma, X.; Nie, J.; Tao, M.; Bu, F. Numerical model and simplified formula of axial force-moment capacity of composite shear wall with double steel plates and infill concrete. J. Build. Struct. 2013, 34, 99–106. [Google Scholar]
- Papanikolaou, V.K.; Kappos, A.J. Confinement-sensitive plasticity constitutive model for concrete in triaxial compression. Int. J. Solids Struct. 2007, 44, 7021–7048. [Google Scholar] [CrossRef] [Green Version]
- Skalomenos, K.A.; Hatzigeorgiou, G.D.; Beskos, D.E. Parameter identification of three hysteretic models for the simulation of the response of cft columns to cyclic loading. Eng. Struct. 2014, 61, 44–60. [Google Scholar] [CrossRef]
- Ding, Z.; Jiang, H.; Zeng, J.; Zhang, H.; Du, G. An innovative application of scs composite wall: Structural design of yancheng tv tower. Build. Struct. 2011, 41, 87–91. [Google Scholar]
- Shafaei, S.; Farahbod, F.; Ayazi, A. Concrete stiffened steel plate shear walls with an unstiffened opening. Structures 2017, 12, 40–53. [Google Scholar] [CrossRef]
- Ollgaard, J.G.; Slutter, R.G.; Fisher, J.W. Shear Strength of Stud Connectors in Lightweight and Normal-Weight Concrete, AISC Eng’g Jr., April 1971 (71-10). 1971, pp. 55–64. Available online: https://preserve.lehigh.edu/cgi/viewcontent.cgi?article=3009&context=engr-civil-environmental-fritz-lab-reports (accessed on 15 July 2020).
- Gattesco, N.; Giuriani, E. Experimental study on stud shear connectors subjected to cyclic loading. J. Constr. Steel Res. 1996, 38, 1–21. [Google Scholar] [CrossRef]
- The European Committee for Standardization (CEN). Design of Composite Steel and Concrete Structures, Part 2: Composite Bridges; CEN: Brussels, Belgium, 1997. [Google Scholar]
- Pallarés, L.; Hajjar, J.F. Headed steel stud anchors in composite structures, part II: Tension and interaction. J. Constr. Steel Res. 2010, 66, 213–228. [Google Scholar] [CrossRef]
- CSSC. Calculation of Beam and Rectangular Plate on Elastic Foundation; National Defense Industry Press: Beijing, China, 1983. [Google Scholar]
- Guo, Q. Report of the Theoretical Research of the Seismic Performance of High-Temperature Gas-Cooled Reactor (HTR-PM) Steel-Concrete Composite Shear Wall; Beihang University: Beijing, China, 2013. [Google Scholar]
- MOHURD. Code for Design of Concrete Structures; China Architecture & Building Press: Beijing, China, 2010; Volume GB50010-2010.
- Han, L. Concrete Filled Steel Tube Structure-Theory and Practice; Science Press: Beijing, China, 2007. [Google Scholar]
- Teng, Z.; Zhu, Z. Concrete Structure and Masonry Structure; China Architecture & Building Press: Beijing, China, 2003. [Google Scholar]
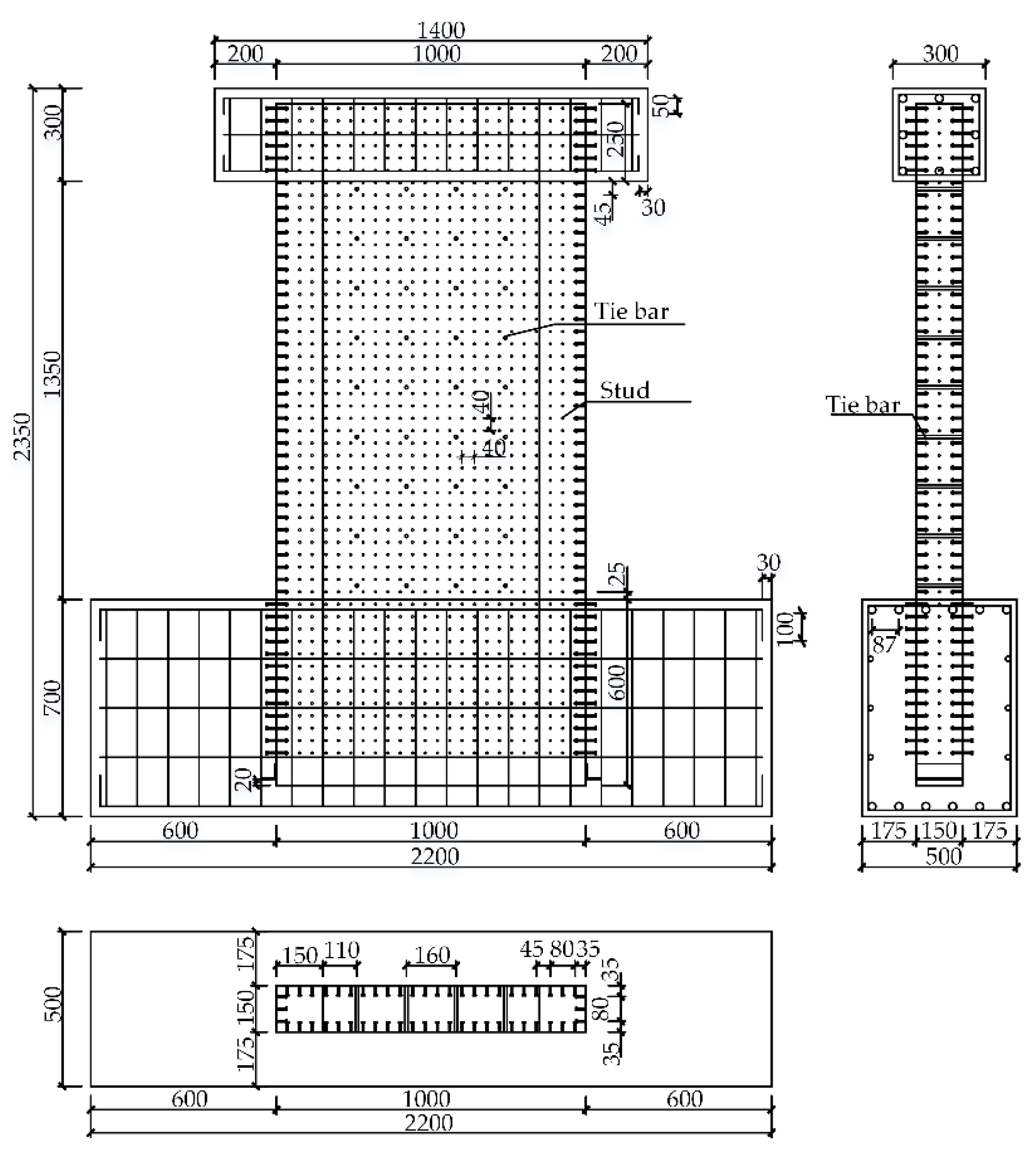
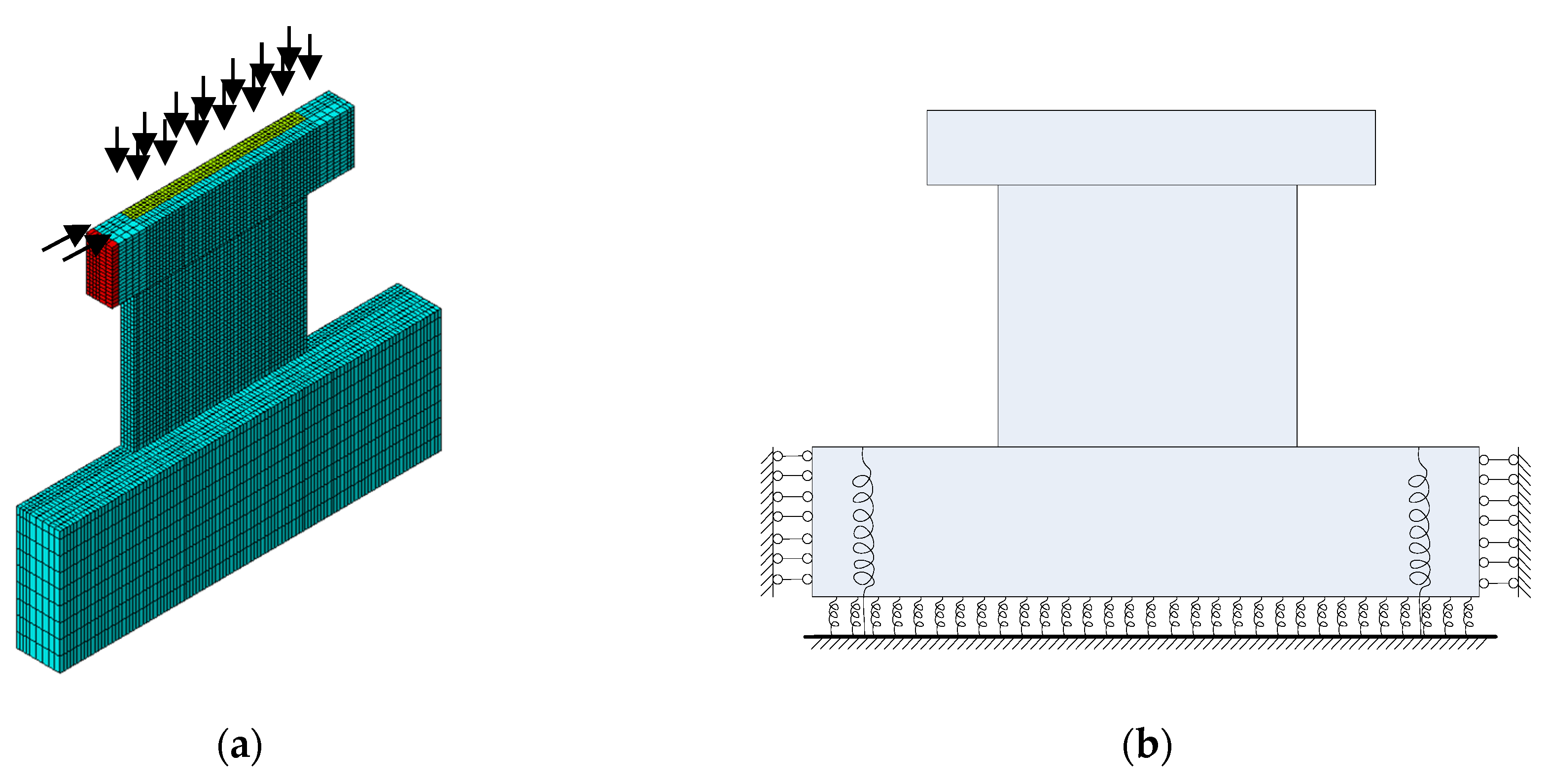



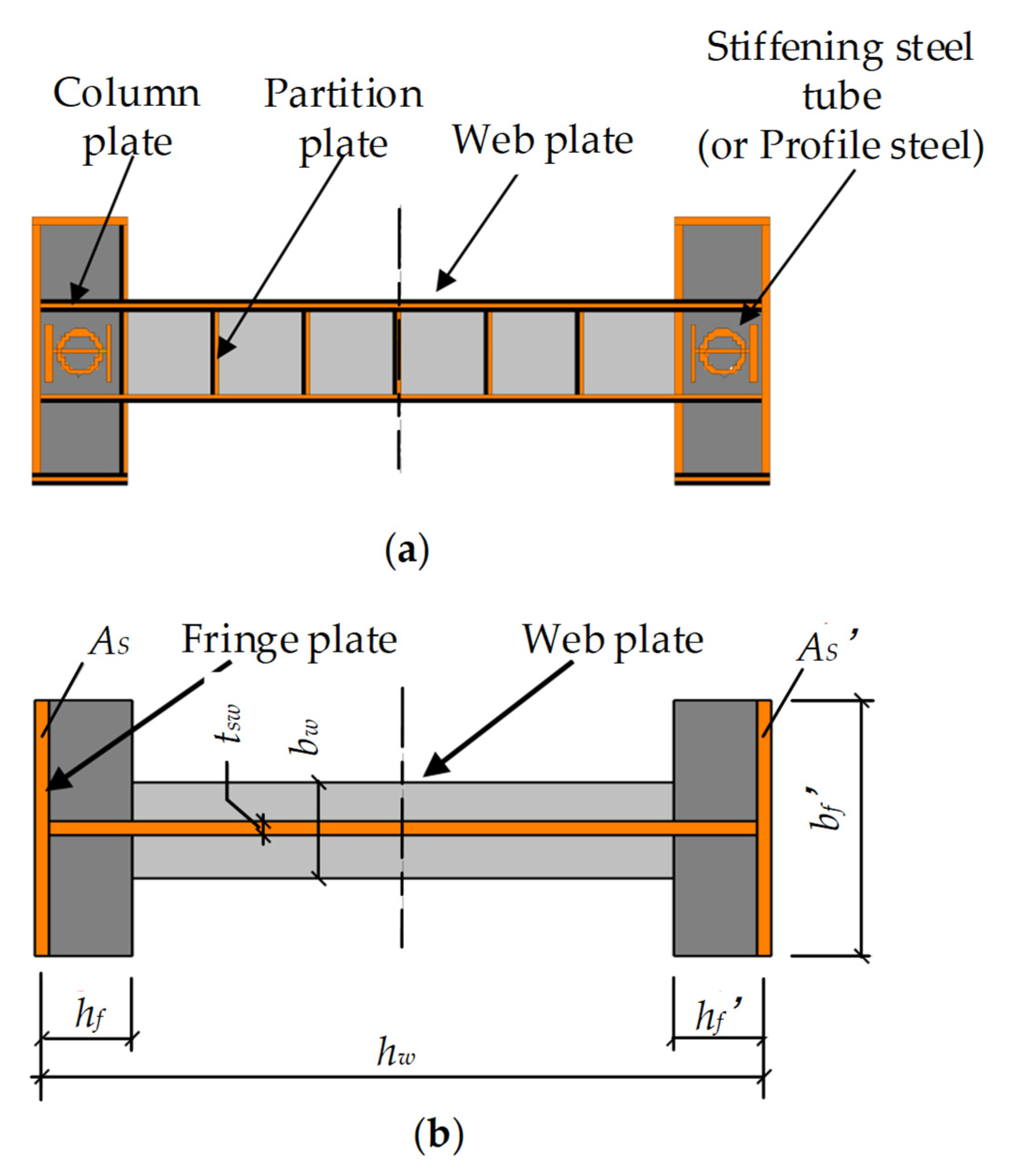
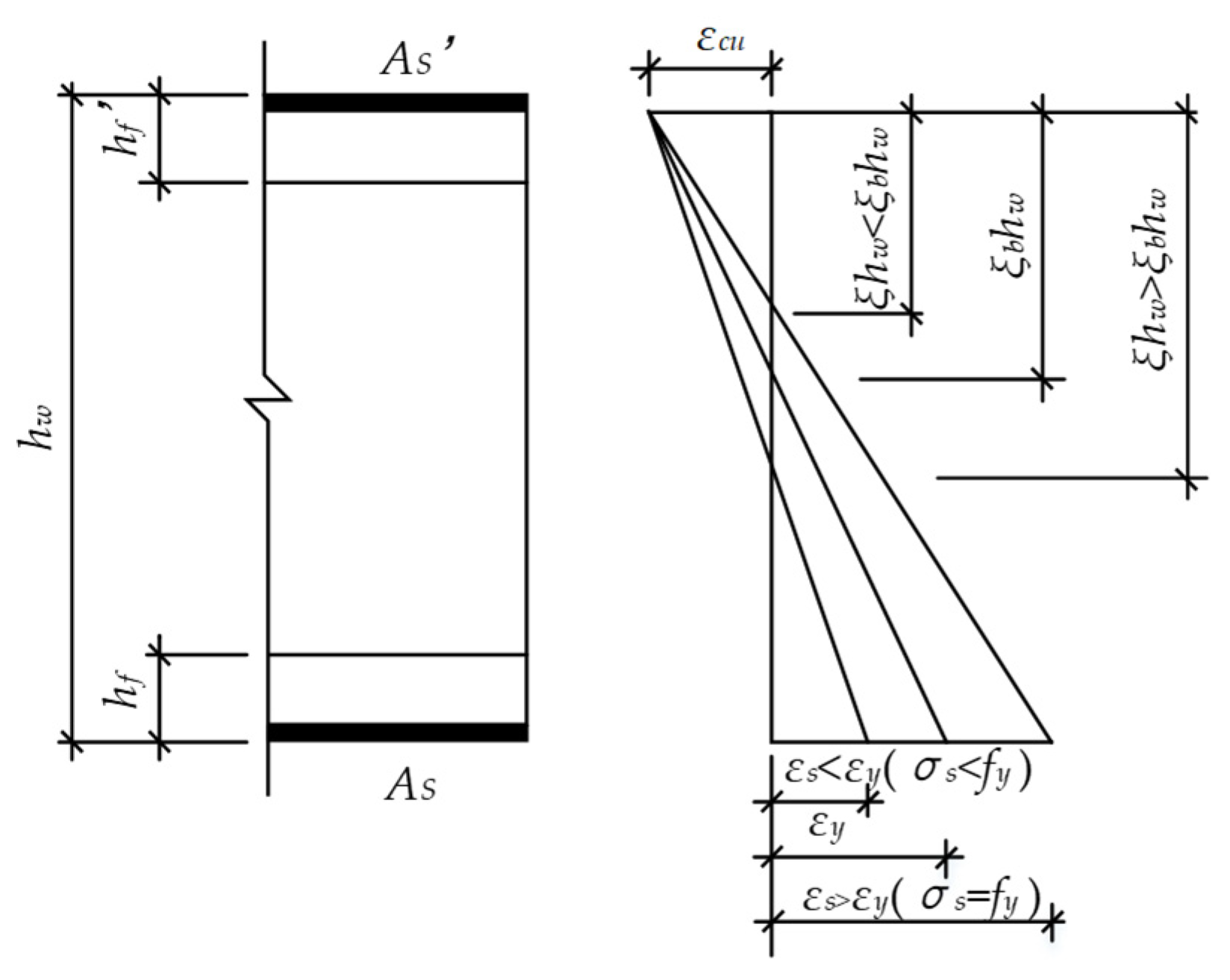



| Reference | Specimen | Pcr1/Pu2 | Buckling Pattern | B/t5 | The Limit of B/t |
|---|---|---|---|---|---|
| [9] | W0 | 0.63 | buckling1 3 | 58.8 | 34 |
| [10] | SCW5 | 0.91 | buckling2 | 40 | 34 |
| [12] | SCW1-1a | 0.95 | buckling2 4 | 13.3 | 33 |
| SCW1-1b | 0.96 | buckling2 | 13.3 | 33 | |
| SCW1-2a | 0.98 | buckling2 | 13.3 | 33 | |
| SCW1-2b | 1.00 | buckling2 | 13.3 | 33 | |
| SCW1-3 | 0.91 | buckling2 | 13.3 | 33 | |
| SCW1-4 | 0.94 | buckling2 | 20 | 34 | |
| SCW1-5 | 0.92 | buckling2 | 10 | 32 | |
| SCW1-6 | 0.90 | buckling2 | 26.7 | 33 |
| Specimen | Specimen Size | Steel Plane Thickness | Design Axial Compression Ratio | Stud Spacing | ||
|---|---|---|---|---|---|---|
| Height | Width | Thickness | ||||
| SCW1-1a | 1000 | 1000 | 150 | 3 | 0.4 | 40 |
| SCW1-1b | 1000 | 1000 | 150 | 3 | 0.4 | 40 |
| SCW1-2a | 1500 | 1000 | 150 | 3 | 0.4 | 40 |
| SCW1-2b | 1500 | 1000 | 150 | 3 | 0.4 | 40 |
| SCW1-3 | 2000 | 1000 | 150 | 3 | 0.4 | 40 |
| SCW1-4 | 1000 | 1000 | 150 | 2 | 0.4 | 40 |
| SCW1-5 | 1000 | 1000 | 150 | 4 | 0.4 | 40 |
| SCW1-6 | 1000 | 1000 | 150 | 3 | 0.4 | 80 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Guo, Q.; Ke, F.; Zhao, W.; Ye, Y. Axial and Bending Bearing Capacity of Double-Steel-Concrete Composite Shear Walls. Appl. Sci. 2020, 10, 4935. https://doi.org/10.3390/app10144935
Zhang P, Guo Q, Ke F, Zhao W, Ye Y. Axial and Bending Bearing Capacity of Double-Steel-Concrete Composite Shear Walls. Applied Sciences. 2020; 10(14):4935. https://doi.org/10.3390/app10144935
Chicago/Turabian StyleZhang, Peiyao, Quanquan Guo, Fei Ke, Weiyi Zhao, and Yinghua Ye. 2020. "Axial and Bending Bearing Capacity of Double-Steel-Concrete Composite Shear Walls" Applied Sciences 10, no. 14: 4935. https://doi.org/10.3390/app10144935





