Experimental Investigation on the Mechanical Properties of Curved Metallic Plate Dampers
Abstract
:1. Introduction
2. Performance Parameters of Curved Plate Damper
2.1. Elastic Stiffness Calculation Formula
2.2. Formula for Calculating Yield Strength
2.3. Formula for Calculating Yield Displacement
3. Mechanical Properties of Curved Plate Damper
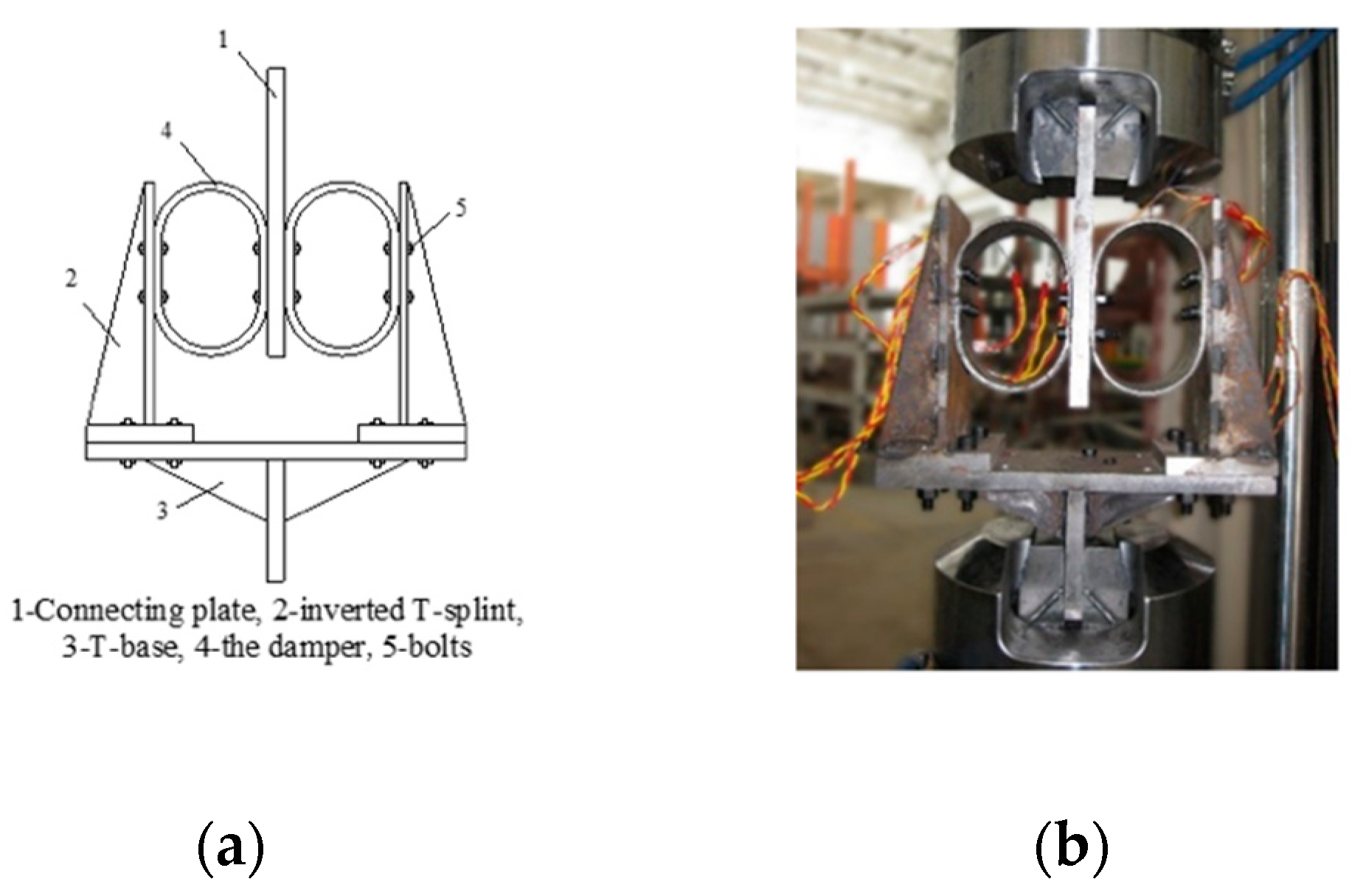
3.1. Loading Device and Test Scheme
3.2. Experiment Result Analysis
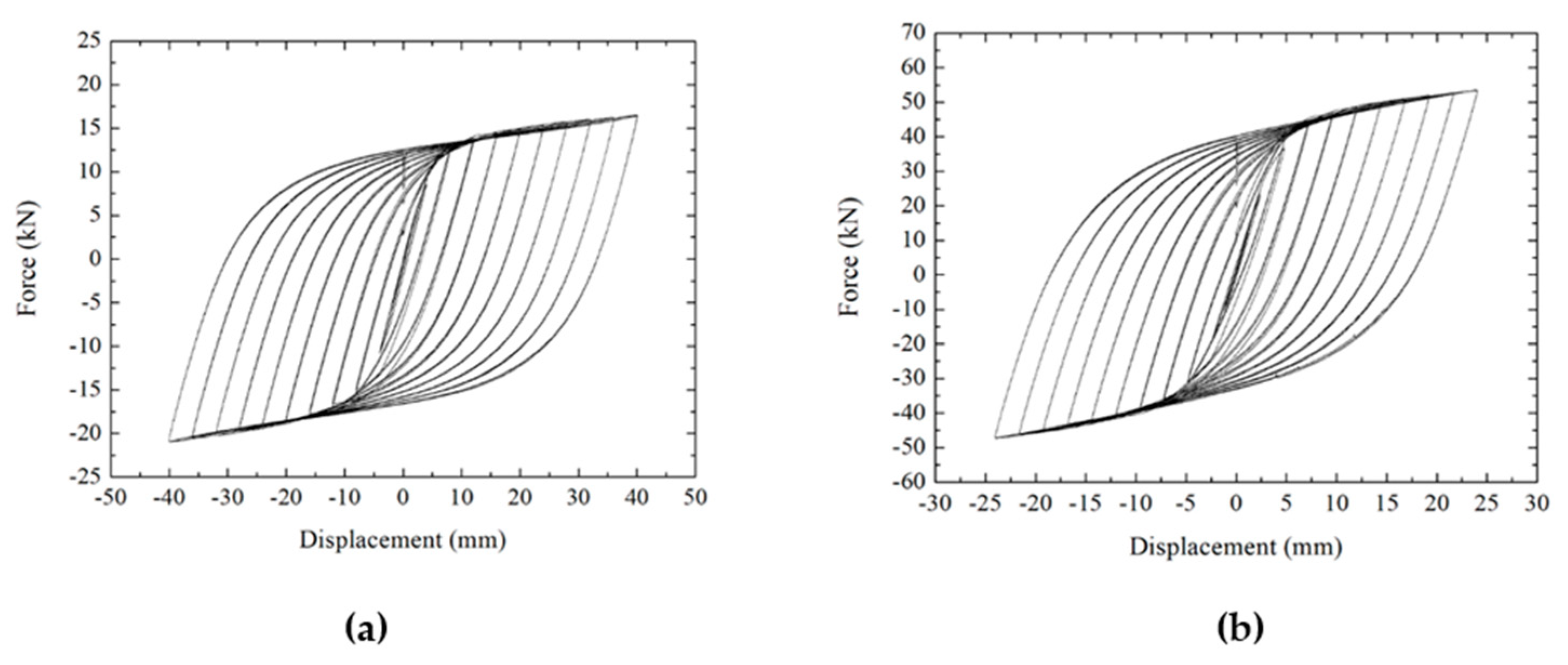
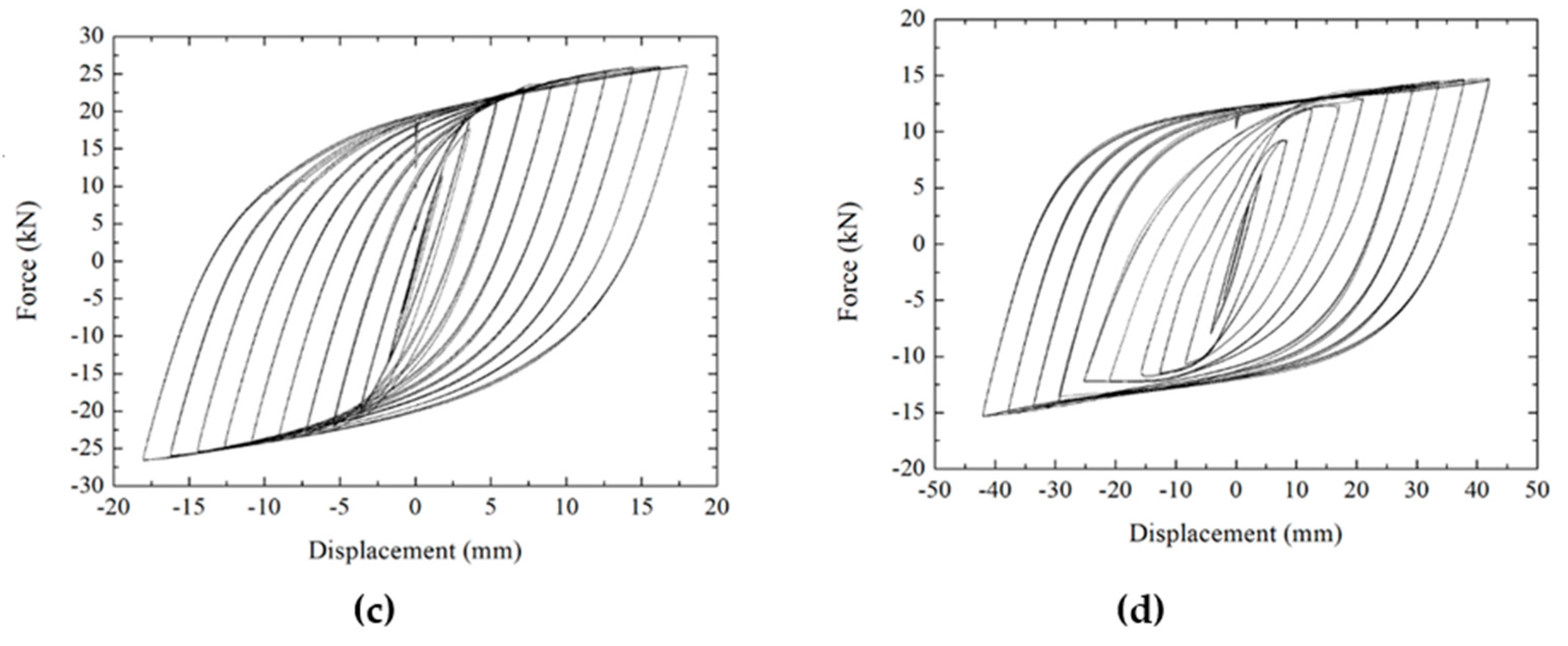
3.2.1. Hysteretic Curve
3.2.2. Ductility Coefficient and Energy Dissipation Coefficient
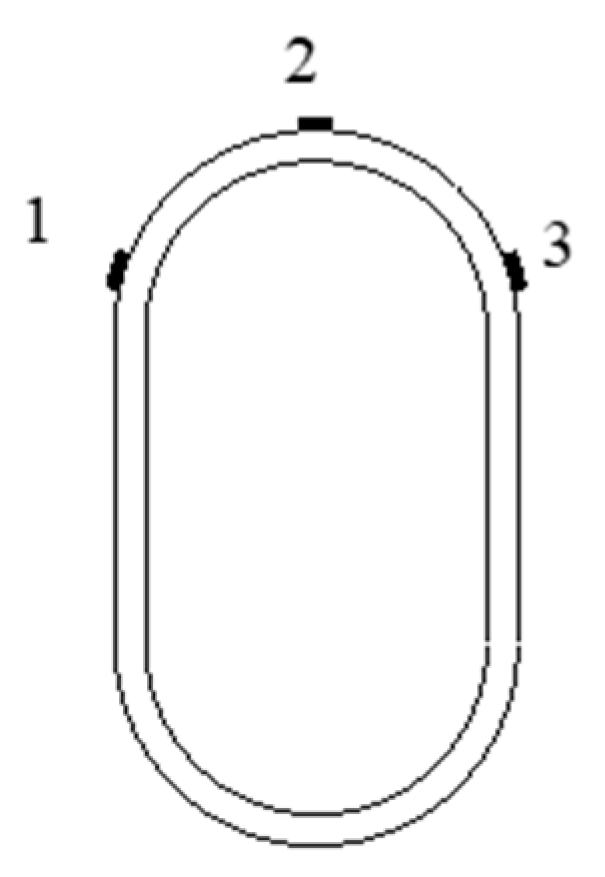
3.2.3. Strain Analysis
3.3. Finite Element Analysis
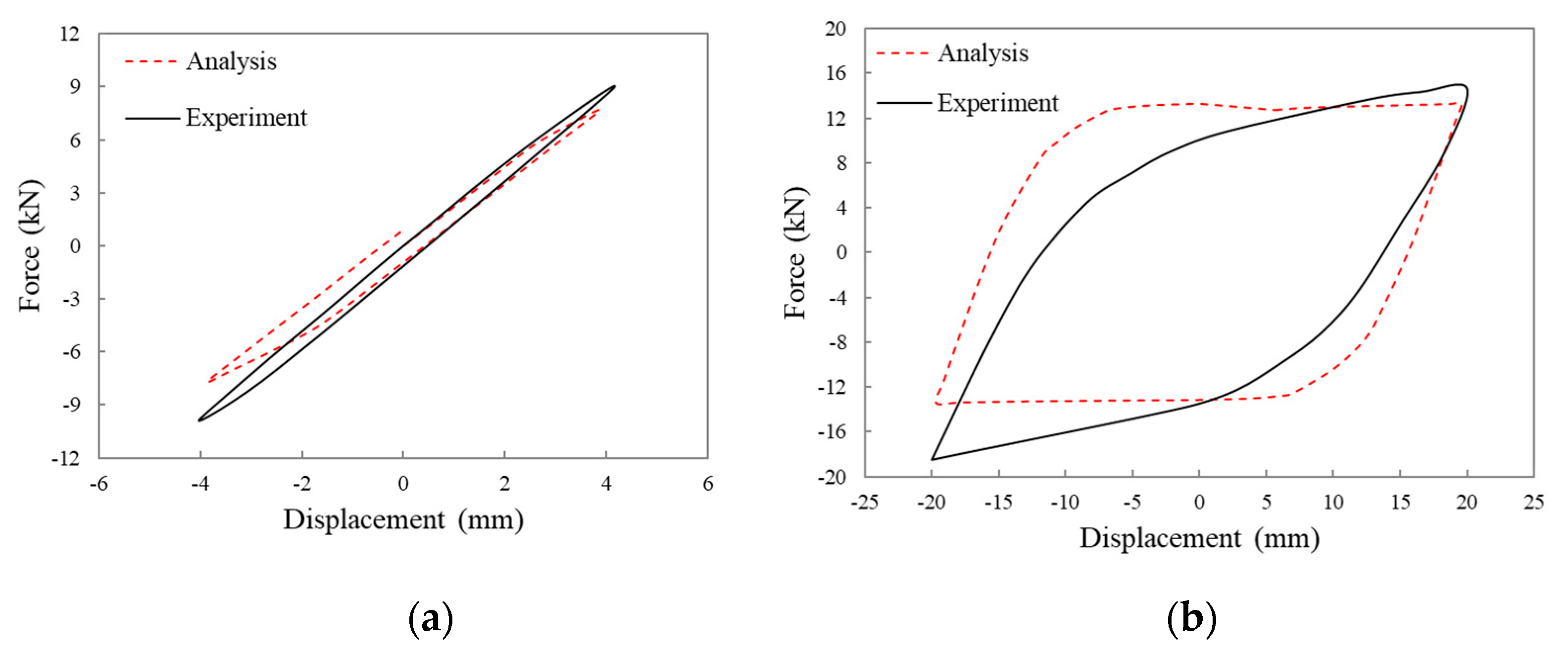
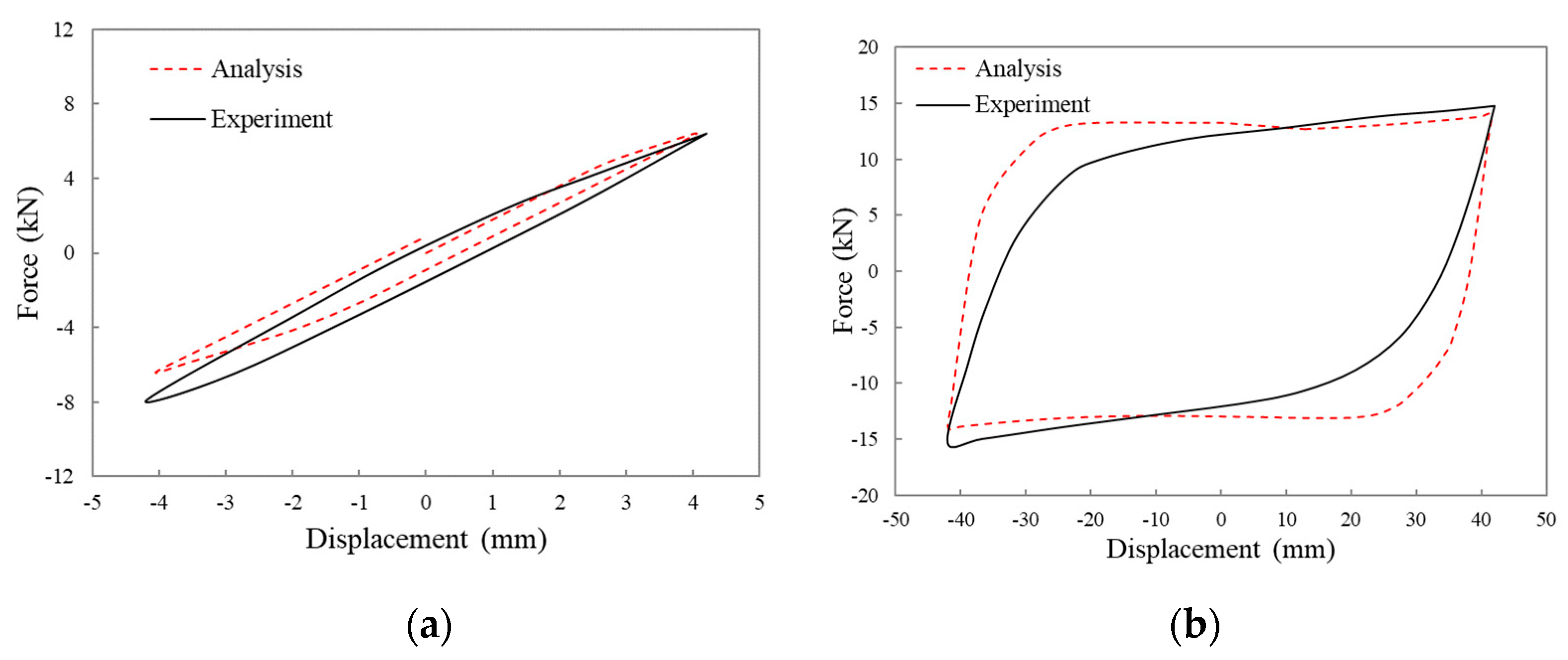
3.3.1. Hysteresis Curve Analysis
- (1)
- In Figure 12, the hysteretic curve coincides well at 4 mm. The positive and negative values are asymmetric in the hysteretic curve at 40 mm. Because the stiffness of CSPD-1 is small, then the horizontal deformation causes an error in the final load value, when the load displacement is large.
- (2)
- In Figure 13, the asymmetry of the hysteretic curve also exists at 2.4 mm. At 24 mm, the maximum load of the test curve and the finite element curve are basically the same, but the envelope area of the finite element curve is slightly larger, and the second stiffness of the damper is smaller.
- (3)
- In Figure 14, the hysteretic curve coincides well at 1.8 mm. The maximum load coincides well at 24 mm, and the envelope area of the finite element curve is slightly larger.
- (4)
- In Figure 15, the hysteretic curve coincides well at 4.2 mm, and the curve of finite element analysis shows an upward trend at 42 mm, which is different from the shape of the test curve. This is because the boundary condition set in the finite element analysis is complete bonding, and a bolt connection is used in the test, which cannot be precisely achieved.
3.3.2. Analysis of Mechanical Property Parameters
4. Conclusions
- (1)
- No visible cracks were found in the dampers during standard loading and fatigue loading, and no obvious damage was observed. The hysteretic curves of standard loading and fatigue loading were very full. In standard loading, each target displacement cycle had three cycles, and the three curves coincided. After 30 cycles of the fatigue cycle, the attenuation of the load index was less than 15%, which indicates that the damper had stable performance. It can be seen from the ductility and energy dissipation coefficient that the four dampers have good deformation and energy dissipation performance.
- (2)
- Through stress analysis, the strain at the top of the semi-circular arc was much smaller than that of the end of the semi-circular arc, which shows that for curved plate dampers, the plastic deformation at the end of the semi-circular arc was large, the stress was also large, and the strain change rate was also large.
- (3)
- The finite element model was established to simulate the loading process of the specimens. Compared with the hysteretic curves obtained in the test, it was found that the two curves were basically the same except for the individual specimens. Because there are many influencing factors in the testing process, the positive and negative hysteretic asymmetry of the test curve will occur when the small displacement is loaded. In case of the large displacement, the hysteretic area of the finite element analysis curve is slightly larger. The mechanical properties of the damper can be obtained through experiments, finite element simulations, and theoretical calculations. It is reasonable to obtain a coefficient beta of 1.78 by numerical and theoretical computations. The maximum error was within the allowable range. At the same time, the correctness of the finite element model and the theoretical formulae was proved.
Author Contributions
Funding
Conflicts of Interest
References
- Housner, G.W.; Bergman, L.A.; Caughey, T.K.; Chassiakos, A.G.; Claus, R.O.; Masri, S.F.; Skelton, R.E.; Soong, T.T.; Spencer, B.F.; Yao, J.T. Structural control: Past, present, and future. ASCE J. Eng. Mech. 1997, 123, 897–971. [Google Scholar] [CrossRef]
- Soong, T.T.; Dargush, G.F. Passive Energy Dissipation Systems in Structural Engineering; Wiley: London, UK, 1997. [Google Scholar]
- Mahmoodi, P.; Keel, C.J. Performance of viscoelastic structural dampers for the Columbia center building. In Building Motion in Wind; ASCE: New York, NY, USA, 1986; pp. 83–106. [Google Scholar]
- De Domenico, D.; Ricciardi, G.; Takewaki, I. Design strategies of viscous dampers for seismic protection of building structures: A review. Soil Dyn. Earthq. Eng. 2019, 118, 144–165. [Google Scholar] [CrossRef]
- Zhang, C.W.; Li, L.Y.; Ou, J.P. Swinging motion control of suspended structures: Principles and applications. Struct. Control Health Monit. 2010, 17, 549–562. [Google Scholar] [CrossRef]
- Fu, W.Q.; Zhang, C.W.; Sun, L.; Askari, M.; Samali, B.; Chung, K.L.; Sharafi, P. Experimental investigation of a base isolation system incorporating mr dampers with the high-order single step control algorithm. Appl. Sci. 2017, 7, 344. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.W.; Ou, J.P.; Zhang, J.Q. Parameter optimization and analysis of a vehicle suspension system controlled by magnetorheological fluid dampers. Struct. Control Health Monit. 2006, 13, 885–896. [Google Scholar] [CrossRef]
- Wei, M.; Sun, L.; Hu, G. Dynamic properties of an axially moving sandwich beam with magnetorheological fluid core. Adv. Mech. Eng. 2017, 9. [Google Scholar] [CrossRef] [Green Version]
- Sun, L.; Huang, W.M. Wet to shrink: An approach to realize negative expansion upon wetting. Adv. Compos. Mater. 2009, 18, 95–103. [Google Scholar] [CrossRef]
- Wei, M.H.; Sun, L.; Zhang, C.; Qi, P.P.; Zhu, J. Shear-thickening performance of suspensions of mixed ceria and silica nanoparticles. J. Mater. Sci. 2019, 54, 346–355. [Google Scholar] [CrossRef]
- Zhang, C.W.; Ou, J.P. Modeling and Dynamical Performance of the Electromagnetic Mass Driver System for Structural Vibration Control. Eng. Struct. 2015, 82, 93–103. [Google Scholar] [CrossRef]
- Zhang, C.W.; Ou, J.P. Control Structure Interaction of Electromagnetic Mass Damper System for Structural Vibration Control. ASCE J. Eng. Mech. 2008, 134, 428–437. [Google Scholar] [CrossRef]
- Zhang, C.W. Control Force Characteristics of Different Control Strategies for the Wind-excited 76-story Benchmark Building Structure. Adv. Struct. Eng. 2014, 17, 543–559. [Google Scholar] [CrossRef]
- Ju, Y.K.; Kim, M.H.; Kim, J.; Kim, S.D. Component tests of buckling-restrained braces with unconstrained length. Eng. Struct. 2009, 31, 507–516. [Google Scholar] [CrossRef]
- Xie, Q. State of the art of buckling-restrained braces in Asia. J. Constr. Steel Res. 2005, 61, 727–748. [Google Scholar] [CrossRef]
- Chen, S.J.; Jhang, C. Experimental study of low-yield-point steel plate shear wall under in-plane load. J. Constr. Steel Res. 2011, 67, 977–985. [Google Scholar] [CrossRef]
- Whittaker, A.S.; Bertero, V.V.; Thompson, C.L.; Alonso, L.J. Seismic testing of steel plate energy dissipation devices. Earthq. Spectra 1991, 7, 563–604. [Google Scholar] [CrossRef]
- Chan, R.W.K.; Albermani, F. Experimental study of steel slit damper for passive energy dissipation. Eng. Struct. 2008, 30, 1058–1166. [Google Scholar] [CrossRef]
- Li, H.N.; Li, G. Experimental study of structure with “dual function” metallic dampers. Eng. Struct. 2007, 29, 1917–1928. [Google Scholar] [CrossRef]
- Whittaker, A.; Bertero, V.; Alonso, J.; Thompson, C. Earthquake Simulator Testing of Steel Plate Added Damping and Stiffness Elements; Report No. UCB/EERC-89/02; Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 1989. [Google Scholar]
- Symans, M.D.; Charney, F.A.; Whittaker, A.S.; Constantinou, M.C.; Kircher, C.A.; Johnson, M.W.; McNamara, R.J. Energy dissipation systems for seismic applications: Current practice and recent developments. J. Struct. Eng. 2008, 134, 3–21. [Google Scholar] [CrossRef] [Green Version]
- Bedon, C.; Amadio, C. Passive control systems for the blast enhancement of glazing curtain walls under explosive loads. Open Civ. Eng. 2017, 11, 396–419. [Google Scholar] [CrossRef] [Green Version]
- Tsai, K.C.; Chen, H.W.; Hong, C.P.; Su, Y.F. Design of steel triangular plate energy absorbers for seismic-resistant construction. Earthq. Spectra 1993, 9, 505–528. [Google Scholar] [CrossRef]
- Gray, M.; Christopoulos, C.; Packer, J.; de Oliveira, C. A new brace option for ductile braced frames. Mod. Steel Constr. 2012, 52, 40–53. [Google Scholar]
- Balendra, T.; Lim, E.L.; Liaw, C.Y. Large scale seismic testing of knee brace frame. J. Struct. Eng. 1997, 123, 11–19. [Google Scholar] [CrossRef]
- Mahmoudi, M.; Montazeri, S.; Abad, M.J.S. Seismic performance of steel X-knee-braced frames equipped with shape memory alloy bars. J. Constr. Steel Res. 2018, 147, 171–186. [Google Scholar] [CrossRef]
- Zhang, C.W.; An, D.; Zhu, L. Axial Compressive Behavior Behavior of Steel-Damping Concrete Composite Wall. Appl. Sci. 2019, 9, 4679. [Google Scholar] [CrossRef] [Green Version]
- Zhu, L.M.; Zhang, C.W.; Guan, X.M.; Uy, B.; Sun, L.; Wang, B.L. The multi-axial strength performance of composite structural B-C-W members subjected to shear forces. Steel Compos. Struct. 2018, 27, 75–87. [Google Scholar]
- Lee, C.H.; Ju, Y.K.; Min, J.K.; Lho, S.H.; Kim, S.D. Non-uniform steel strip dampers subjected to cyclic loadings. Eng. Struct. 2015, 99, 192–204. [Google Scholar] [CrossRef]
- Shih, M.H.; Sung, W.P. A model for hysteretic behavior of rhombic low yield strength steel added damping and stiffness. Comput. Struct. 2005, 83, 895–908. [Google Scholar] [CrossRef]
- Kato, S.; Kim, Y.B.; Nakazawa, S.; Ohya, T. Simulation of the cyclic behavior of J-shaped steel hysteresis devices and study on the efficiency for reducing earthquake responses of space structures. J. Constr. Steel Res. 2005, 61, 1457–1473. [Google Scholar] [CrossRef]
- Kato, S.; Kim, Y.B. A finite element parametric study on the mechanical properties of J-shaped steel hysteresis devices. J. Constr. Steel Res. 2006, 62, 802–811. [Google Scholar] [CrossRef]
- Deng, K.; Pan, P.; Su, Y.; Xue, Y. Shape optimization of U-shaped damper for improving its bi-directional performance under cyclic loading. Eng. Struct. 2015, 93, 27–45. [Google Scholar] [CrossRef]
- Aguirre, M.; Sanchez, A.R. Structural seismic damper. J. Struct. Eng. 1992, 118, 1158–1171. [Google Scholar] [CrossRef]
- Tagawa, H.; Gao, J. Evaluation of vibration control system with U-dampers based on quasi-linear motion mechanism. J. Constr. Steel Res. 2012, 70, 213–225. [Google Scholar] [CrossRef]
- Maleki, S.; Bagheri, S. Pipe damper, part I: Experimental and analytical study. J. Constr. Steel Res. 2010, 66, 1088–1095. [Google Scholar] [CrossRef]
- Maleki, S.; Mahjoubi, S. Dual-pipe damper. J. Constr. Steel Res. 2013, 85, 81–91. [Google Scholar] [CrossRef]
- Aghlara, R.; Tahir, M.M. A passive metallic damper with replaceable steel bar compo-nents for earthquake protection of structures. Eng. Struct. 2018, 159, 185–197. [Google Scholar] [CrossRef]
- Motamedi, M.; Nateghi, F. Study on mechanical characteristics of accordion metallic damper. J. Constr. Steel Res. 2018, 142, 68–77. [Google Scholar] [CrossRef]
- Aghlara, R.; Tahir, M.M.; Adnan, A.B. Experimental study of pipe-fuse damper for passive energy dissipation in structures. J. Constr. Steel Res. 2018, 148, 351–360. [Google Scholar] [CrossRef]
- Zibasokhan, H.; Behnamfar, F.; Azhari, M. Experimental study of a new pure bending yielding dissipater. Bull. Earthq. Eng. 2019, 17, 4389–4410. [Google Scholar] [CrossRef]
- Deng, K.; Pan, P.; Wang, C. Development of crawler steel damper for bridges. J. Constr. Steel Res. 2013, 85, 140–150. [Google Scholar] [CrossRef]
- Lee, C.H.; Lho, S.H.; Kim, D.H.; Oh, J.; Ju, Y.K. Hourglass-shaped strip damper subjected to monotonic and cyclic loadings. Eng. Struct. 2016, 119, 122–134. [Google Scholar] [CrossRef]
- Long, Y.; Bao, S. Structural Mechanics; Higher Education Press: Beijing, China, 1994. [Google Scholar]





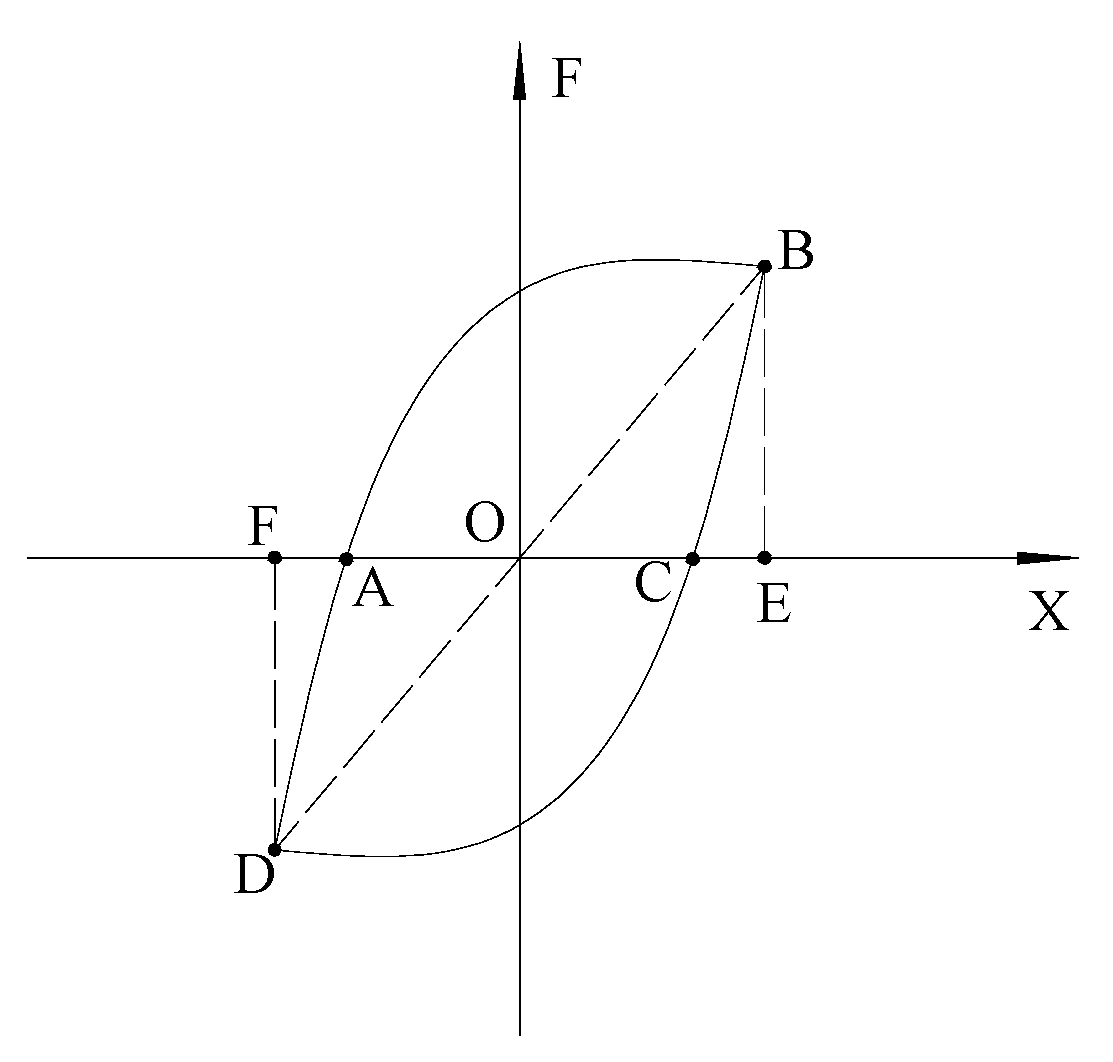




| Specimen | Yield Strength/MPa | Tensile Strength/MPa | Yield Ratio/% | Elongation/% |
|---|---|---|---|---|
| CSPD (curved steel plate dampers)-1 | 249.48 | 375.47 | 66.44 | 35.20 |
| CSPD-2 | 236.64 | 370.03 | 63.95 | 37.71 |
| CSPD-3 | 245.09 | 358.03 | 68.46 | 37.59 |
| CSPD-4 | 253.86 | 372.93 | 68.07 | 33.44 |
| Specimen | b/mm | t/mm | R′/mm | Straight Section/mm |
|---|---|---|---|---|
| CSPD-1 | 105 | 6 | 65 | 70 |
| CSPD-2 | 105 | 10 | 65 | 70 |
| CSPD-3 | 105 | 6 | 43 | 70 |
| CSPD-4 | 85 | 6 | 65 | 70 |
| Specimen | Yield Displacement/mm | Limit Displacement/mm | Ductility Coefficient μ | Energy Dissipation Coefficient E |
|---|---|---|---|---|
| CSPD-1 | 4.37 | 40 | 9.15 | 2.90 |
| CSPD-2 | 2.66 | 24 | 9.02 | 2.83 |
| CSPD-3 | 1.86 | 18 | 9.68 | 2.73 |
| CSPD-4 | 4.52 | 42 | 9.29 | 2.96 |
| Items | CSPD-1 | CSPD-3 | CSPD-4 | CSPD-6 | |
|---|---|---|---|---|---|
| Test result | Yield displacement (mm) | 4.37 | 2.66 | 1.86 | 4.52 |
| Yield bearing capacity (kN) | 8.78 | 25.42 | 12.53 | 6.97 | |
| Elastic stiffness (kN/mm) | 1.92 | 9.56 | 6.74 | 1.54 | |
| Finite element simulation | Yield displacement (mm) | 4.18 | 2.44 | 1.82 | 4.20 |
| Yield bearing capacity (kN) | 9.34 | 27.11 | 14.04 | 7.56 | |
| Elastic stiffness (kN/mm) | 2.13 | 10.11 | 7.71 | 1.80 | |
| Theoretical calculation | Yield displacement (mm) | 2.48β | 1.40β | 1.04β | 2.47β |
| Yield bearing capacity (kN) | 5.00β | 14.37β | 7.76β | 4.05β | |
| Elastic stiffness (kN/mm) | 2.02 | 10.23 | 7.43 | 1.64 | |
| Maximum error | Yield displacement (mm) | 5.50% | 9.02% | 2.20% | 7.62% |
| Yield bearing capacity (kN) | 6.38% | 6.65% | 10.75% | 7.80% | |
| Elastic stiffness (kN/mm) | 9.86% | 7.01% | 12.58% | 14.44% | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, J.; Zhang, C.; Li, A. Experimental Investigation on the Mechanical Properties of Curved Metallic Plate Dampers. Appl. Sci. 2020, 10, 269. https://doi.org/10.3390/app10010269
Zheng J, Zhang C, Li A. Experimental Investigation on the Mechanical Properties of Curved Metallic Plate Dampers. Applied Sciences. 2020; 10(1):269. https://doi.org/10.3390/app10010269
Chicago/Turabian StyleZheng, Jie, Chunwei Zhang, and Aiqun Li. 2020. "Experimental Investigation on the Mechanical Properties of Curved Metallic Plate Dampers" Applied Sciences 10, no. 1: 269. https://doi.org/10.3390/app10010269





