Development of Three-Dimensional Soil-Amplification Analysis Method for Screening for Seismic Damage to Buried Water-Distribution Pipeline Networks
Abstract
:1. Introduction
2. Seismic Soil-Amplification Analysis Method
2.1. Overview
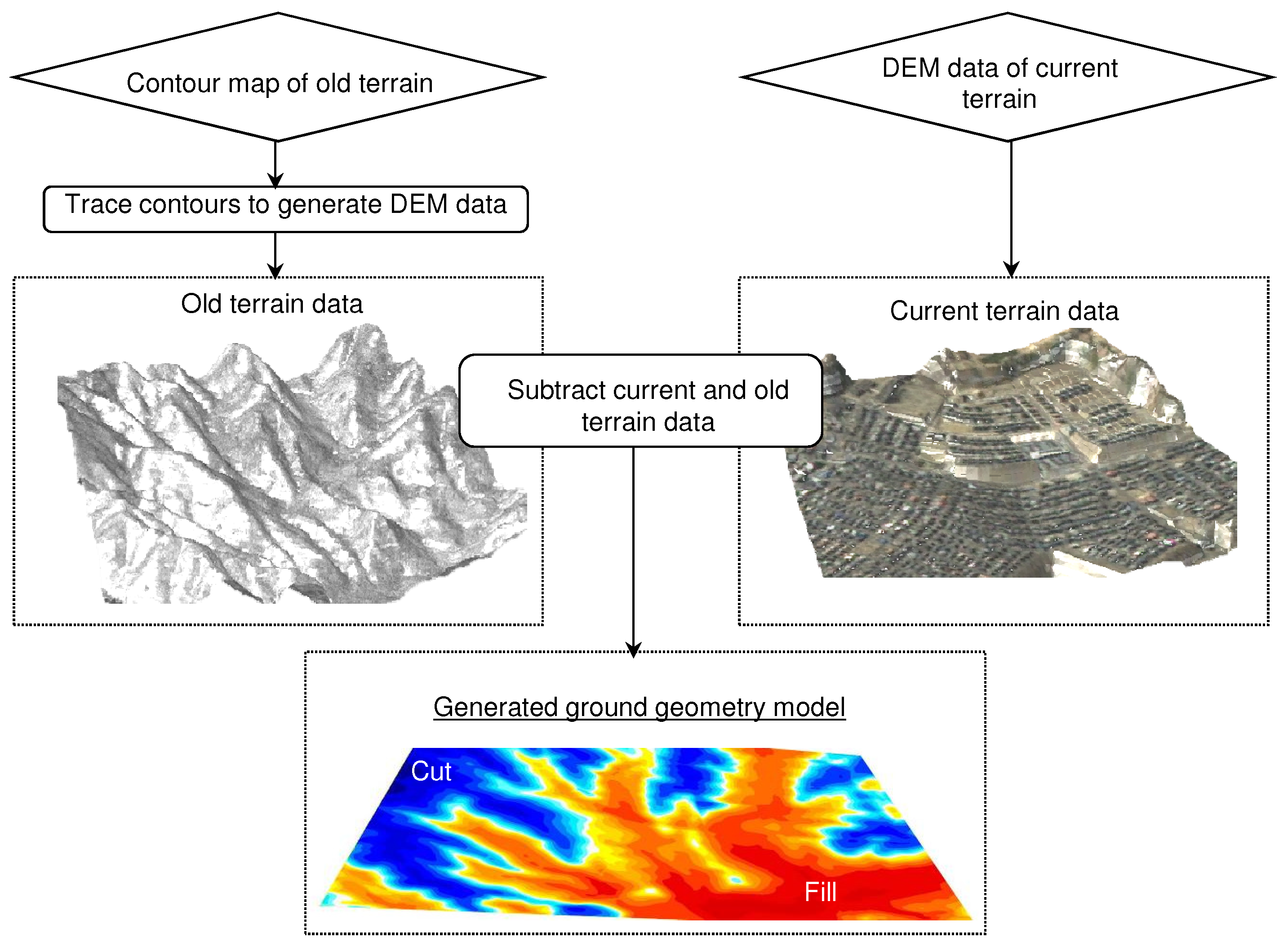
2.2. Method of Generating High-Resolution Ground Models
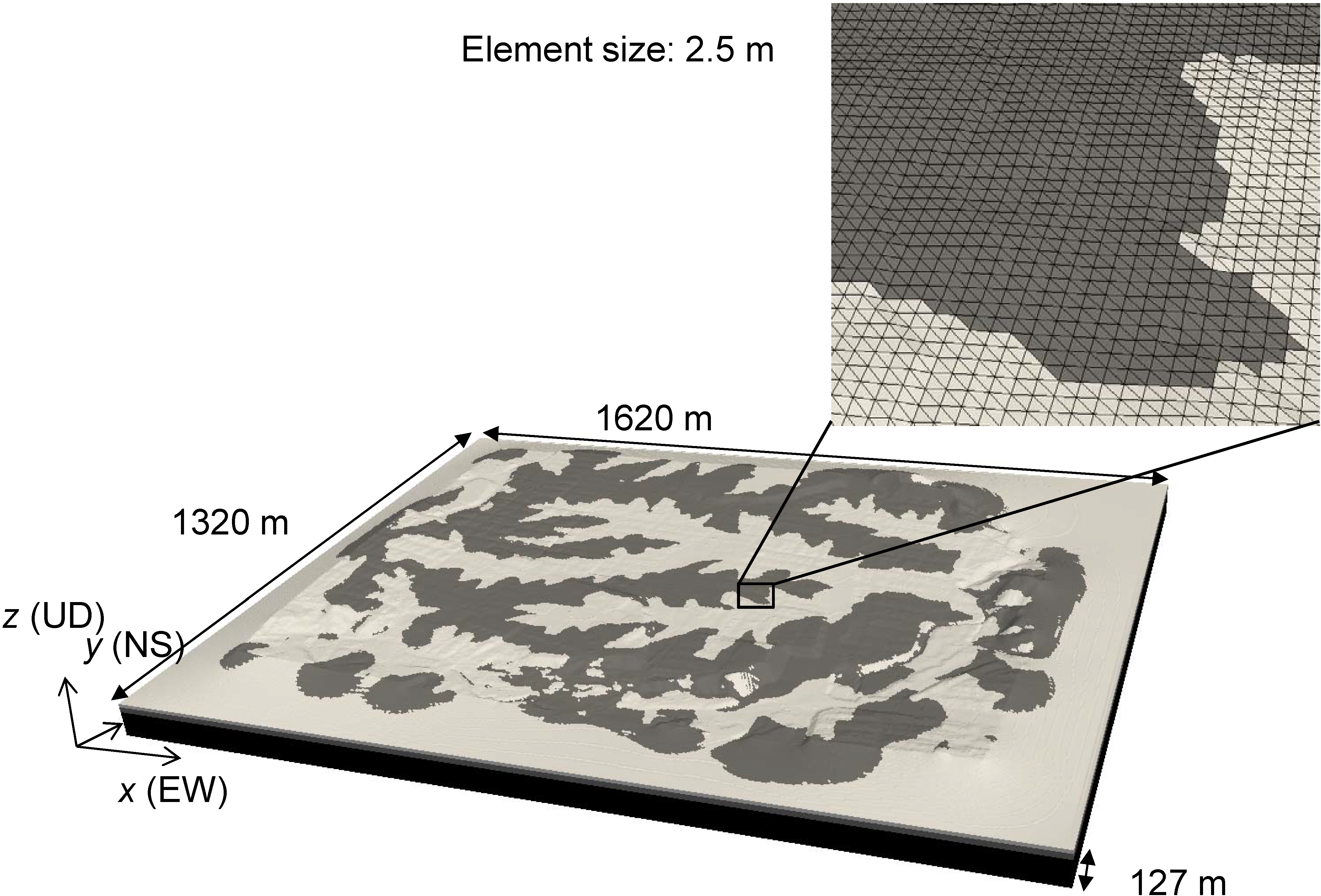
2.3. Large-Scale Soil-Amplification Analysis Method
3. Application of Soil-Amplification Analysis for Screening for Seismic Damage to a Pipeline Network
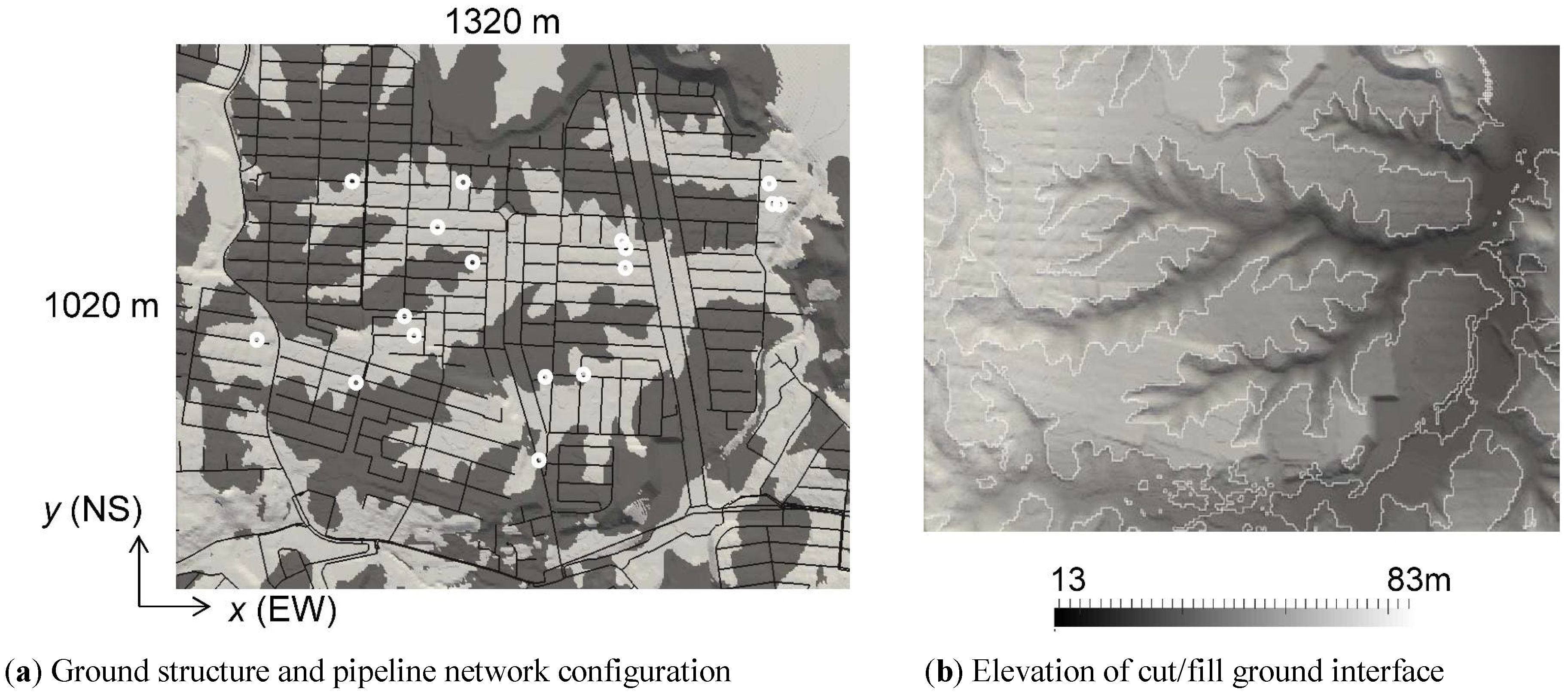
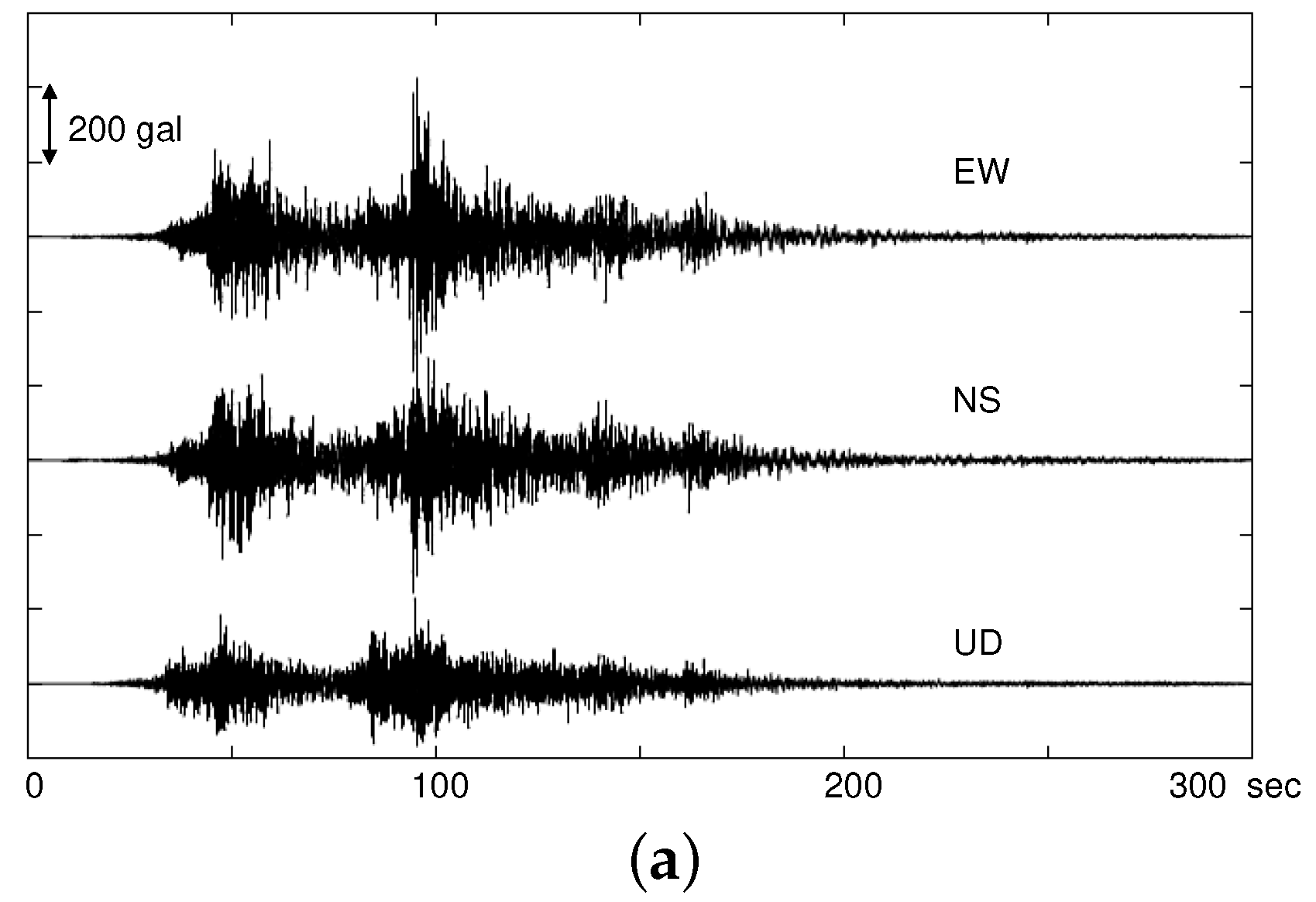
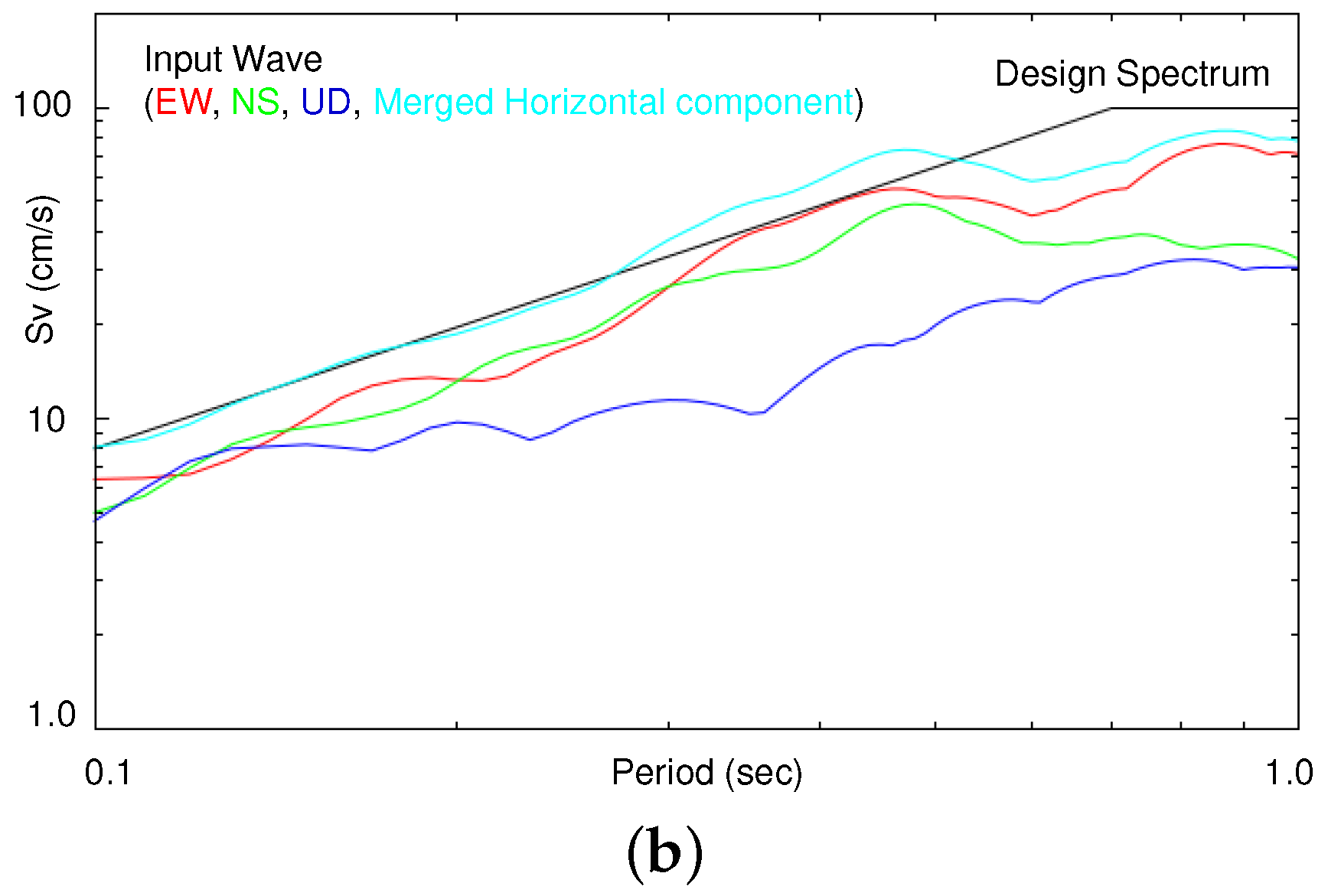
3.1. Problem Settings
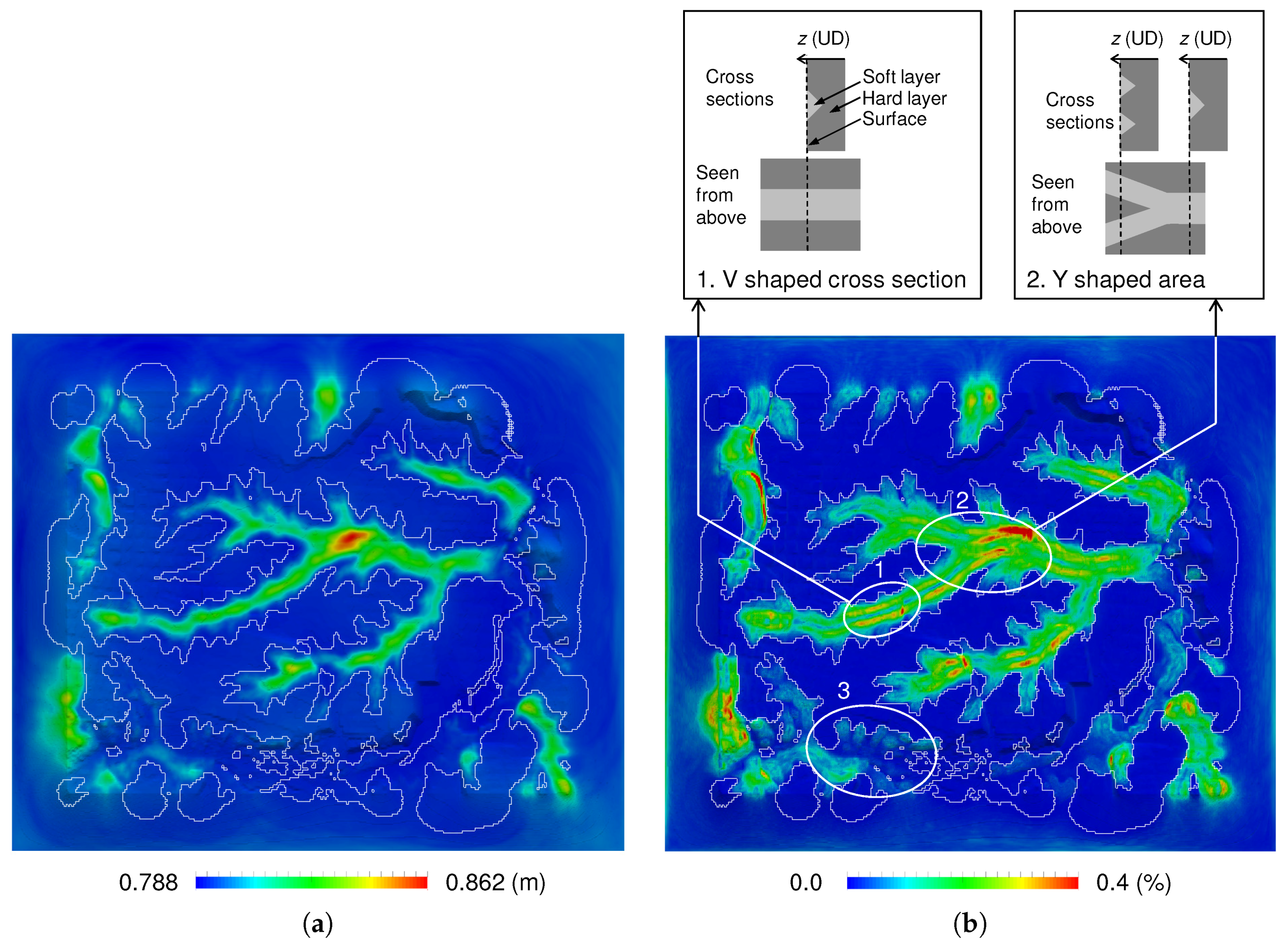
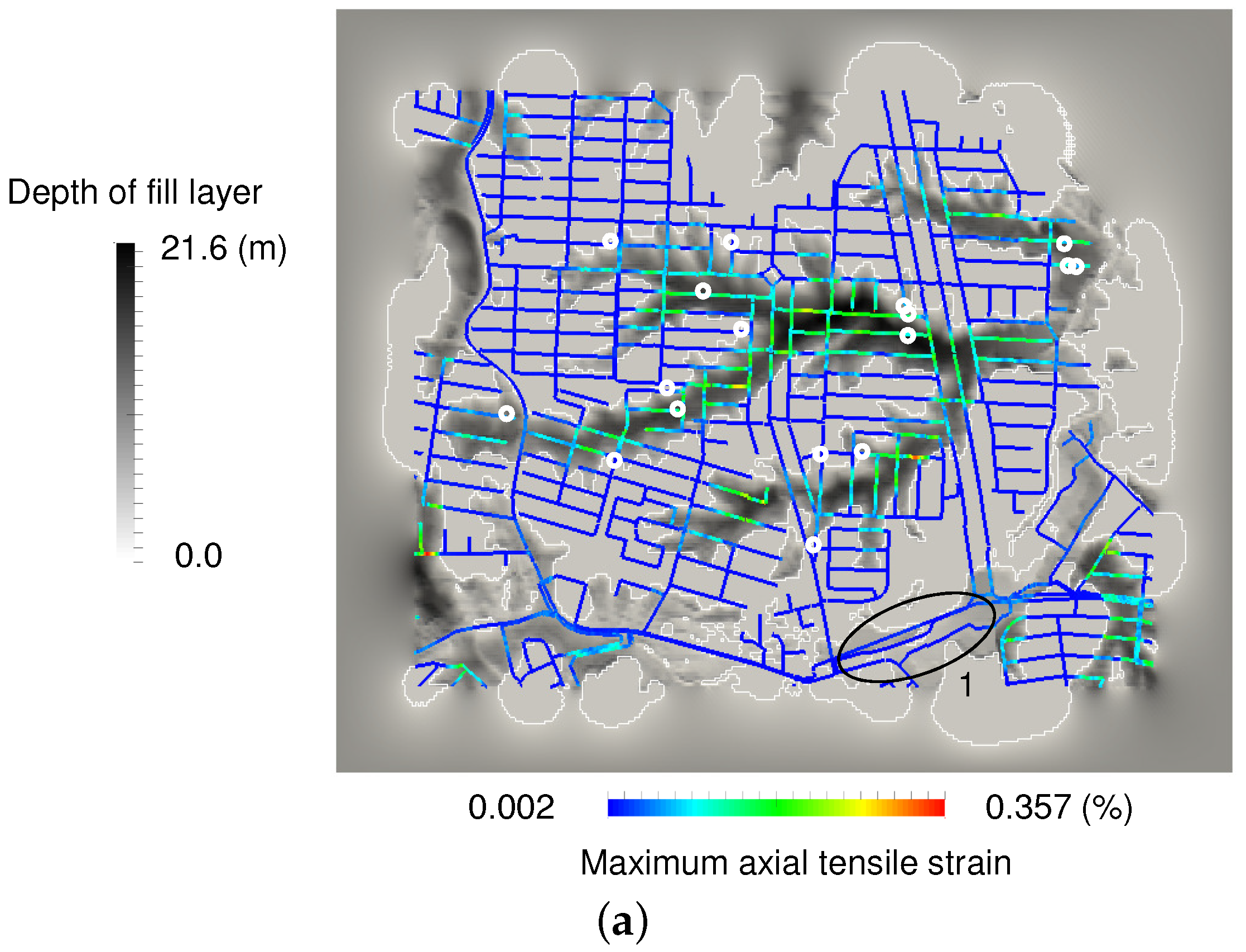
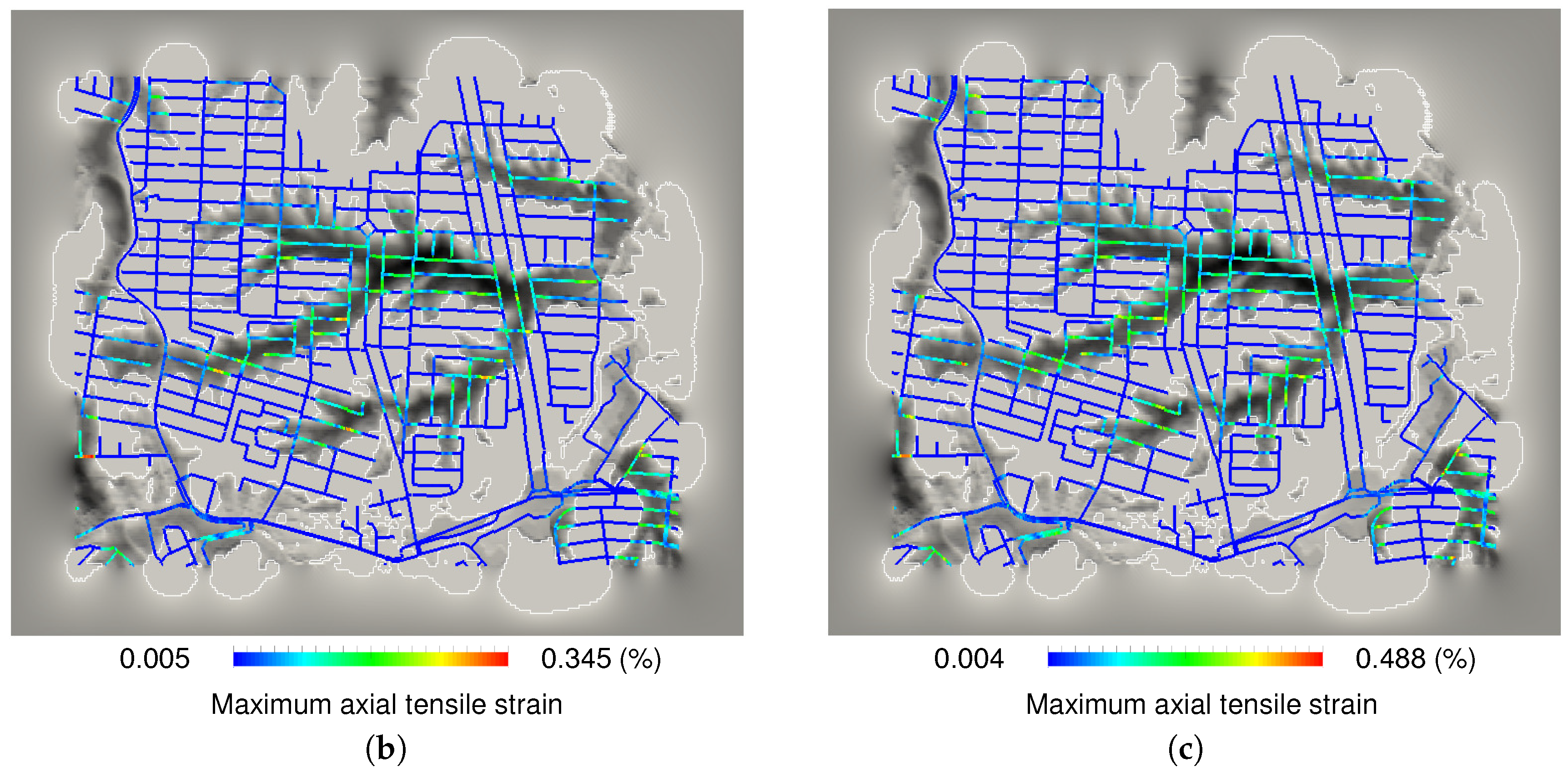
3.2. Comparison of Computed Strain and Design Strain
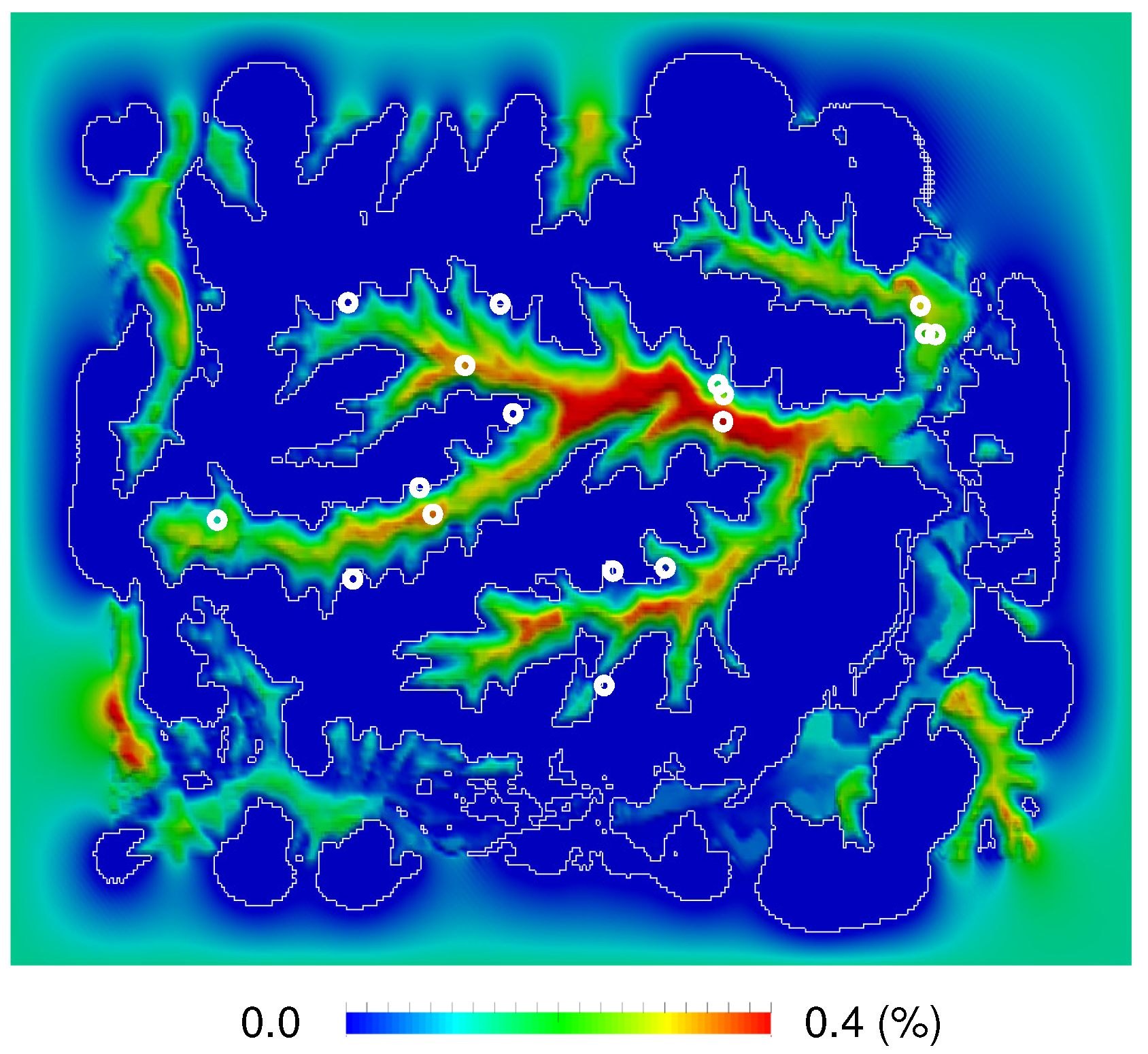
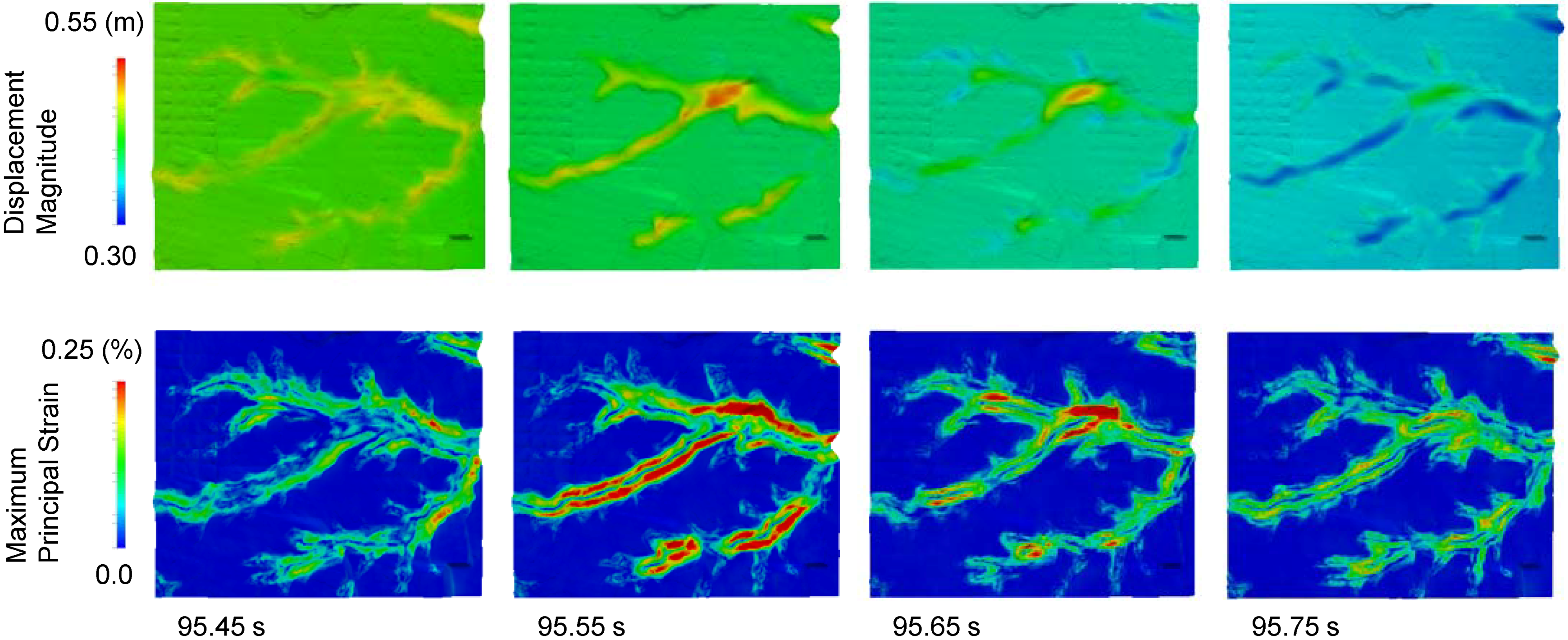
3.3. Screening for Pipeline Damage
4. Closing Remarks
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Laucelli, D.; Giustolisi, O. Vulnerability Assessment of Water Distribution Networks under Seismic Actions. J. Water Resour. Plan. Manag. 2015, 141. [Google Scholar] [CrossRef]
- Yoo, D.G.; Jung, D.; Kang, D.; Kim, J.H.; Lansey, K. Seismic Hazard Assessment Model for Urban Water Supply Networks. J. Water Resour. Plan. Manag. 2016, 142. [Google Scholar] [CrossRef]
- Yoo, D.G.; Jung, D.; Kang, D.; Kim, J.H. Seismic Reliability-Based Multiobjective Design of Water Distribution System: Sensitivity Analysis. J. Water Resour. Plan. Manag. 2017, 143. [Google Scholar] [CrossRef]
- Liang, J.; Sun, S. Site Effects on Seismic Behavior of Pipelines: A Review. J. Press. Vessel Technol. 2000, 122, 469–475. [Google Scholar] [CrossRef]
- Choi, B.; Nishida, A.; Itoi, T.; Takada, T. Engineering Applications Using Probabilistic Aftershock Hazard Analyses: Aftershock Hazard Map and Load Combination of Aftershocks and Tsunamis. Geosciences 2018, 8. [Google Scholar] [CrossRef]
- Somerville, P.; Collins, N.; Abrahamson, N.; Graves, R.; Saikia, C. Ground Motion Attenuation Relations for the Central and Eastern United States, Final Report. 2001. Available online: https://earthquake.usgs.gov/static/lfs/nshm/conterminous/2008/99HQGR0098.pdf (accessed on 7 May 2018).
- Second Report of the Nankai Trough Large Earthquake Model Committee, Cabinet Office, Government of Japan. 28 August 2012. Available online: http://www.bousai.go.jp/jishin/nankai/model/index.html (accessed on 7 May 2018). (In Japanese)
- Disaster Assessment of Tokyo Due to Large Earthquakes Such As the Nankai Trough Earthquake, Tokyo Metropolitan Government. 14 May 2013. Available online: http://www.bousai.metro.tokyo.jp/taisaku/1000902/1000402.html (accessed on 7 May 2018). (In Japanese)
- Pineda-Porras, O.; Najafi, M. Seismic Damage Estimation for Buried Pipelines: Challenges after Three Decades of Progress. J. Pipeline Syst. Eng. Pract. 2010, 1, 19–24. [Google Scholar] [CrossRef]
- Bielak, J.; Graves, R.W.; Olsen, K.B.; Taborda, R.; Ramirez-Guzman, L.; Day, S.M.; Ely, G.P.; Roten, D.; Jordan, T.H.; Maechling, P.J.; et al. The ShakeOut earthquake scenario: Verification of three simulation sets. Geophys. J. Int. 2010, 180, 375–404. [Google Scholar] [CrossRef]
- Graves, R.W.; Jordan, T.; Callaghan, S.; Deelman, E.; Field, E.; Juve, G.; Kesselman, C.; Maechling, P.; Mehta, G.; Milner, K.; et al. CyberShake: A physics-based seismic hazard model for Southern California. Pure Appl. Geophys. 2010, 168, 367–381. [Google Scholar] [CrossRef]
- Jones, L.M.; Bernknopf, R.; Cox, D.; Goltz, J.; Hudnut, K.; Mileti, D.; Perry, S.; Ponti, D.; Porter, K.; Reichle, M.; et al. The Shake Out Scenario; Technical Report USGS-R1150; U.S. Geological Survey and California Geological Survey: Sacramento, CA, USA, 2008.
- Ichimura, T.; Fujita, K.; Hori, M.; Sakanoue, T.; Hamanaka, R. Three-dimensional Nonlinear Seismic Ground Response Analysis of Local Site Effects for Estimating Seismic Behavior of Buried Pipelines. J. Press. Vessel Technol. Am. Soc. Mech. Eng. 2014, 136. [Google Scholar] [CrossRef]
- Ichimura, T.; Fujita, K.; Quinay, P.E.; Hori, M.; Sakanoue, T.; Hamanaka, R.; Ito, F.; Suetomi, I. Comprehensive Seismic Response Analysis for Estimating the Seismic Behavior of Buried Pipelines Enhanced by Three-Dimensional Dynamic Finite Element Analysis of Ground Motion and Soil Amplification. J. Press. Vessel Technol. Am. Soc. Mech. Eng. 2016, 138. [Google Scholar] [CrossRef]
- Advisory Committee for Natural Resources and Energy; Urban Area Thermal Energy Committee; Gas Safety Subcommittee; Working Group for Earthquake Disaster Prevention (2012). Report on Disaster Mitigation for Gas Supply in View of Great East Japan Earthquake 2013; Agency for Natural Resources and Energy: Tokyo, Japan, 2013. (In Japanese)
- Kazama, M.; Noda, T. Damage statistics (Summary of the 2011 off the Pacific Coast of Tohoku Earthquake damage). Soils Found. 2012, 52, 780–792. [Google Scholar] [CrossRef]
- Mori, T.; Tobita, Y.; Okimura, T. The damage to hillside embankments in Sendai city during the 2011 off the Pacific Coast of Tohoku Earthquake. Soils Found. 2012, 52, 910–928. [Google Scholar] [CrossRef]
- Fukken Gijyutsu Consultant Co., Ltd. Map of Development Residential Land 2008; Fukken Gijyutsu Consultant Co., Ltd.: Sendai, Japan, 2008. (In Japanese) [Google Scholar]
- Ichimura, T.; Hori, M.; Bielak, J. A Hybrid Multiresolution Meshing Technique for Finite Element Three-Dimensional Earthquake Ground Motion Modeling in Basins Including Topography. Geophys. J. Int. 2009, 177, 1221–1232. [Google Scholar] [CrossRef]
- Idriss, I.M.; Singh, R.D.; Dobry, R. Nonlinear Behavior of Soft Clays during Cyclic Loading. J. Geotech. Eng. Division 1978, 104, 1427–1447. [Google Scholar]
- Masing, G. Eigenspannungen und Verfestigung beim Messing. In Proceedings of the 2nd International Congress of Applied Mechanics, Zurich, Switzerland, 12–17 September 1926; pp. 332–335. (In German). [Google Scholar]
- Ichimura, T.; Fujita, K.; Tanaka, S.; Hori, M.; Maddegedara, L.; Shizawa, Y.; Kobayashi, H. Physics-based urban earthquake simulation enhanced by 10.7 BlnDOF x 30 K time-step unstructured FE non-linear seismic wave simulation. In Proceedings of the SC14: International Conference for High Performance Computing, Networking, Storage and Analysis, New Orleans, LA, USA, 16–21 November 2014; pp. 15–26. [Google Scholar]
- Ichimura, T.; Fujita, K.; Quinay, P.E.B.; Maddegedara, L.; Hori, M.; Tanaka, S.; Shizawa, Y.; Kobayashi, H.; Minami, K. Implicit Nonlinear Wave Simulation with 1.08T DOF and 0.270T Unstructured Finite Elements to Enhance Comprehensive Earthquake Simulation. In Proceedings of the SC15: International Conference for High Performance Computing, Networking, Storage and Analysis, Austin, TX, USA, 15–20 November 2015; pp. 4:1–4:12. [Google Scholar]
- Housner, G.W. Spectrum intensities of strong-motion earthquakes. In Proceedings of the Symposium on Earthquakes and Blast Effects on Structures, Los Angeles, CA, USA, June 1952. [Google Scholar]
- Fujita, K.; Ichimura, T.; Tanaka, S.; Hori, M.; Maddegedara, L. Numerical Convergence Analysis of Three-dimensional Nonlinear Earthquake Wave Amplification Simulation. In Proceedings of the First International Conference of IASUR, Kashiwa, Japan, 25–26 October 2014. [Google Scholar]
- Working Group of Central Disaster Management Council in Japan for Tokai Earthquake, Cabinet Office, Government of Japan. Available online: http://www.bousai.go.jp/jishin/tokai/senmon/index.html (accessed on 7 May 2018). (In Japanese)
- Kamiyama, M.; Matsukawa, T.; Anazawa, M. Strong-Motion Records Obtained by Small-Titan of Tohoku Institute of Technology during the 2011 Great East Japan Earthquake, 2011. Available online: http://www.tohtech.ac.jp/news/2012/05/311.html (accessed on 7 May 2018). (In Japanese).
- Miyazaki, H.; Kusano, Y.; Shinjou, N.; Shoji, F.; Yokokawa, M.; Watanabe, T. Overview of the K computer system. FUJITSU Sci. Tech. J. 2012, 48, 302–309. [Google Scholar]
- Tsukamoto, K.; Nishio, N.; Satake, M.; Asano, T. Observation of Pipeline Behavior at Geographically Complex Site During Earthquake. In Proceedings of the 8th World Conference on Earthquake Engineering, San Francisco, CA, USA, 21–28 July 1984; Volume 7, pp. 247–254. [Google Scholar]
- Japan Water Works Association. Water Supply Utility Seismic Design Guideline and Analysis; Japan Water Works Association: Tokyo, Japan, 2009. (In Japanese) [Google Scholar]
- American Lifelines Alliance—ALA. Seismic Fragility Formulations for Water Systems. Part 1 Guideline; Technical Report Prepared by a Public-Private Partnership between FEMA and ASCE; American Society of Civil Engineers (ASCE): Reston, VA, USA, 2001; 104p, Available online: https://www.americanlifelinesalliance.com/pdf/Part_1_Guideline.pdf (accessed on 7 May 2018).
- Eidinger, J. Water distribution system. In The Loma Prieta California Earthquake of October 17, 1989 Lifelines; USGS Professional Paper No. 1552-A; Schiff, A.J., Ed.; US Government Printing Office: Washington, DC, USA, 1998; pp. A63–A78. [Google Scholar]
- Isoyama, R.; Ishida, E.; Yune, K.; Shirozu, T. Seismic damage estimation procedure for water supply system pipelines. In Proceedings of the Twelfth World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000. Paper No. 1762. [Google Scholar]
- O’Rourke, T.D.; Stewart, H.E.; Jeon, S.S. Geotechnical aspects of lifeline engineering. Proc. Inst. Civ. Eng. 2001, 149, 13–26. [Google Scholar] [CrossRef]
| m/s | m/s | kg/m | |||
|---|---|---|---|---|---|
| Fill layer | 700 | 100 | 1700 | 0.25 | 0.007 |
| Cut layer | 1450 | 300 | 1900 | 0.20 | 0.08 |
| Bedrock | 1450 | 700 | 2000 | – | – |
| m/s | m/s | kg/m | |||
|---|---|---|---|---|---|
| Fill layer (Case 1) | 700 | 100 | 1700 | 0.25 | 0.0005 |
| Fill layer (Case 2) | 700 | 80 | 1700 | 0.25 | 0.0005 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fujita, K.; Ichimura, T.; Kazama, M.; Ohno, S.; Sato, S. Development of Three-Dimensional Soil-Amplification Analysis Method for Screening for Seismic Damage to Buried Water-Distribution Pipeline Networks. Geosciences 2018, 8, 170. https://doi.org/10.3390/geosciences8050170
Fujita K, Ichimura T, Kazama M, Ohno S, Sato S. Development of Three-Dimensional Soil-Amplification Analysis Method for Screening for Seismic Damage to Buried Water-Distribution Pipeline Networks. Geosciences. 2018; 8(5):170. https://doi.org/10.3390/geosciences8050170
Chicago/Turabian StyleFujita, Kohei, Tsuyoshi Ichimura, Motoki Kazama, Susumu Ohno, and Shingo Sato. 2018. "Development of Three-Dimensional Soil-Amplification Analysis Method for Screening for Seismic Damage to Buried Water-Distribution Pipeline Networks" Geosciences 8, no. 5: 170. https://doi.org/10.3390/geosciences8050170




