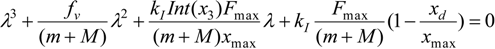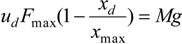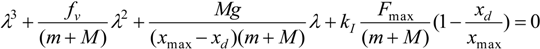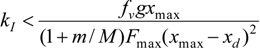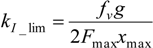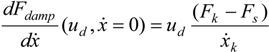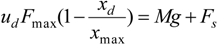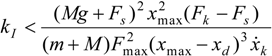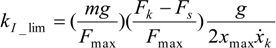We consider three prototypes of McKibben pneumatic artificial muscle, hand-made at the laboratory, with braided sleeves made of three different materials: the first one, inspired by the historical version of the McKibben muscle, the sleeve is braided with cotton (
Figure 2a) and its renewed, also textile version by Bridgestone (
Figure 2b) is made of twisted rayon yarns (
Figure 2c); the second one is made of thin plastic wires (
Figure 2d), as this is sometimes done by McKibben muscle designers; the third one uses a material never before tested, to the best of our knowledge, for McKibben muscle design—thin metal wires (
Figure 2e). These three McKibben muscles illustrate the various material possibilities for braiding McKibben muscles, from a fibrous textile material to a flexible metallic one.
Figure 2.
Various braided sleeves of the pneumatic McKibben artificial muscle, (a) Historical McKibben muscle made of thin cotton yarns; (b) Bridgestone’s “rubbertuator” made of rayon yarns and (c) actual similar McKibben artificial muscle used by the authors; (d) Prototype made of braided thin plastic wires; (e) Prototype made of braided thin metal wires.
3.1. Experimental Friction Analysis of a McKibben Muscle Sleeve made of Rayon Yarns
Experimental studies in friction coefficient for fibers and yarns are generally performed with specific apparatus [
20]. We did not try to use this kind of device because our goal was not to derive the kinetic friction coefficient yarn on yarn, but to estimate the friction inside the braided sleeve during contraction of the artificial muscle. We developed the original experimental setup shown in
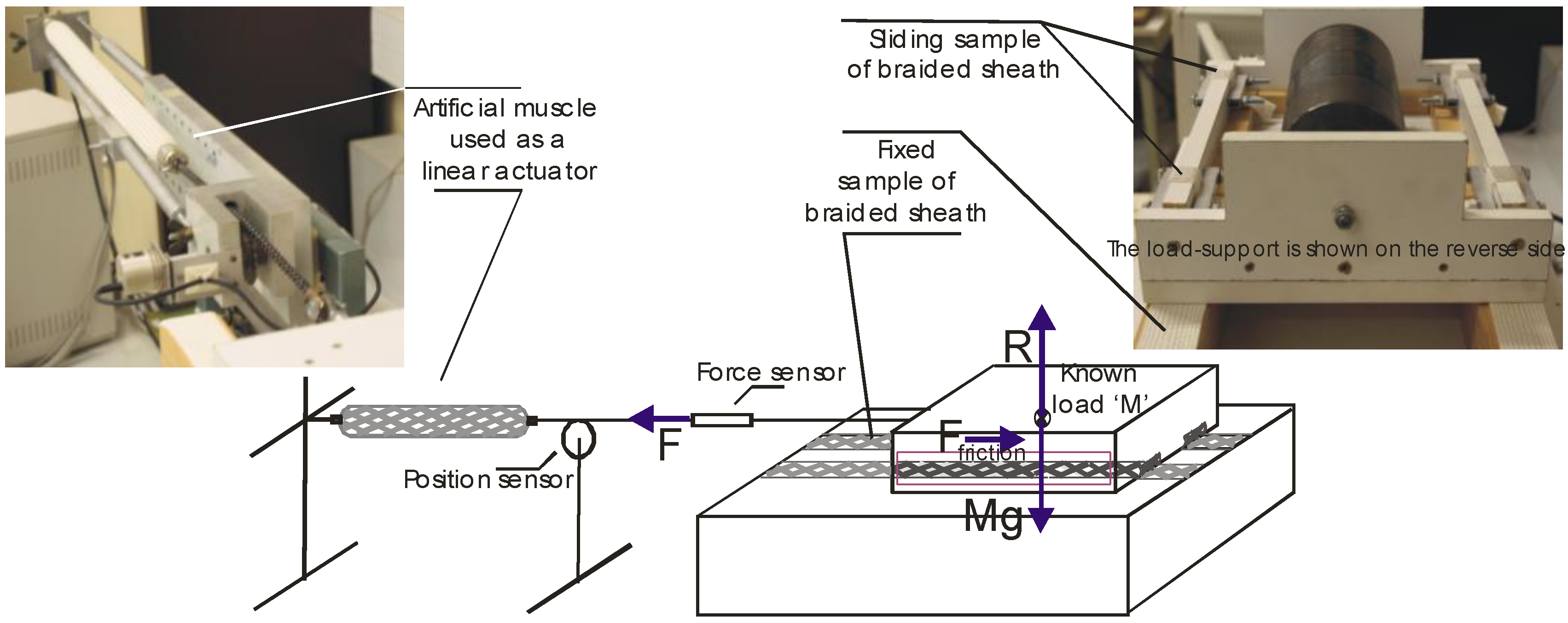
Figure 3: a large sample of flattened braided sheath was attached to a fixed support, while a similar one was attached to a mobile support with a load of about 40 kg; an approximately 1 m long and powerful active McKibben muscle was used to drive this heavy mobile support by means of various step or constant slope input signals; current force and position were recorded during contraction.
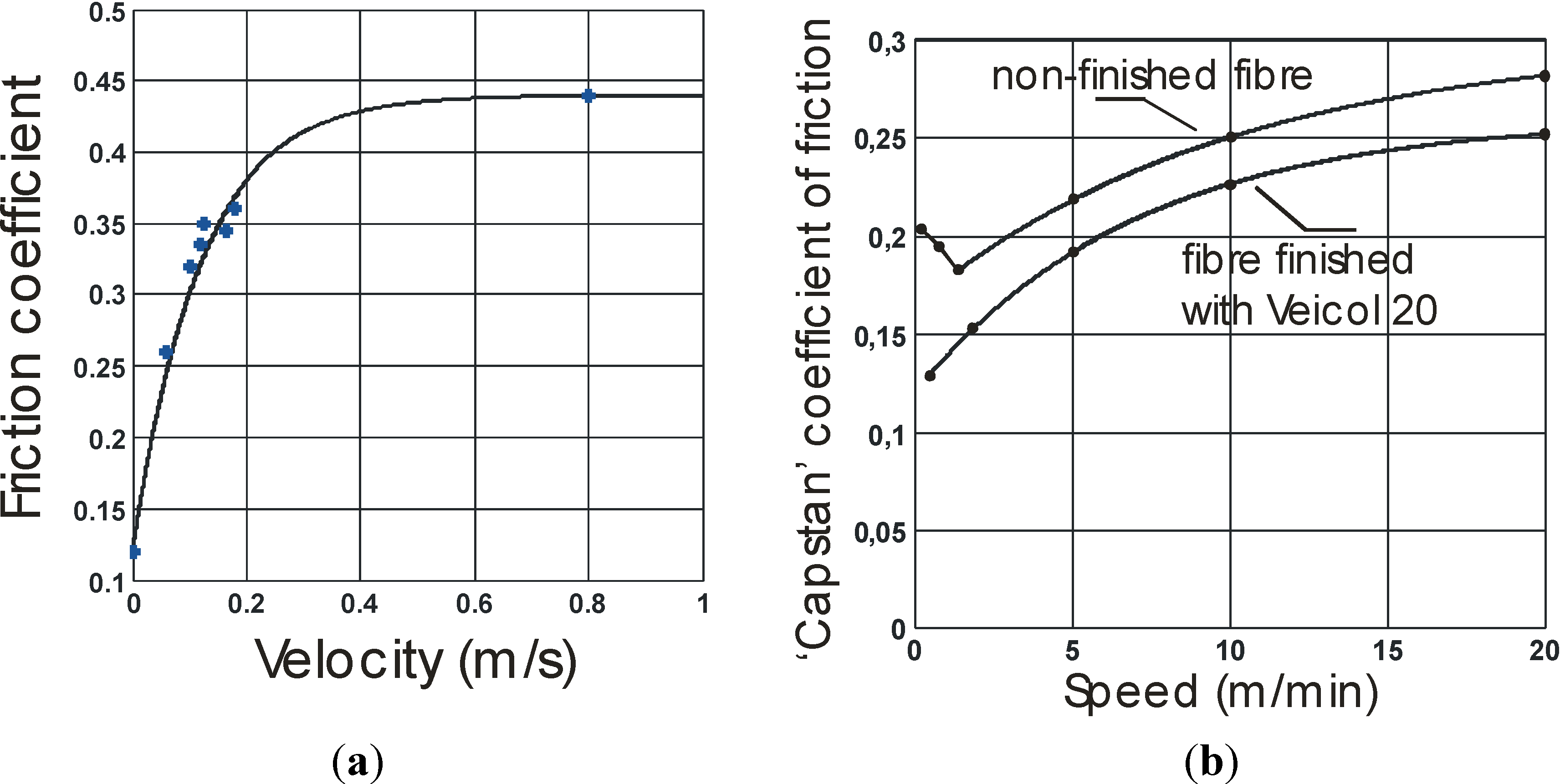
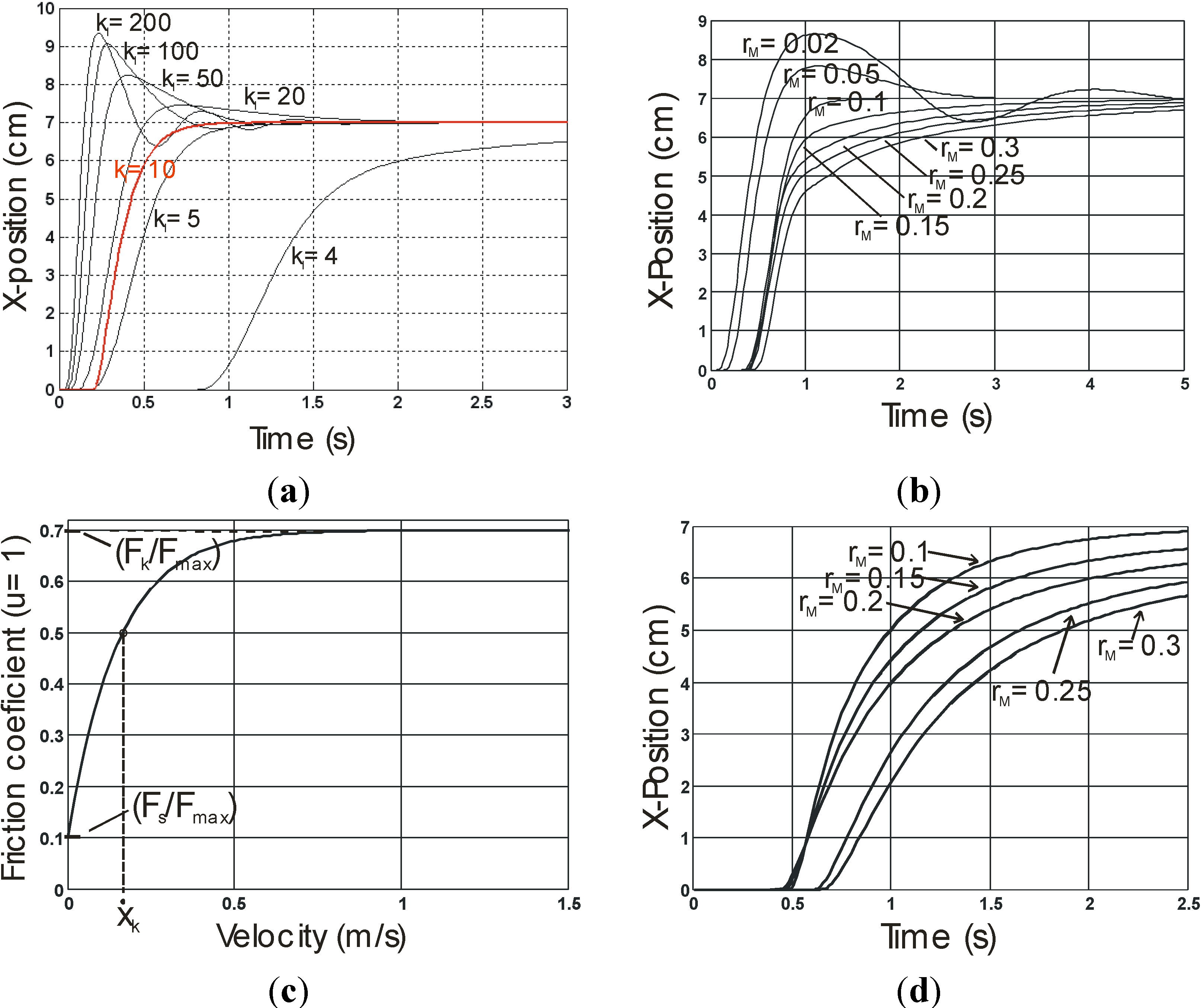
The following principle was considered: if during contraction it is possible to exhibit almost constant velocity portions, the recorded artificial muscle force is a direct estimate of the kinetic friction force corresponding to this velocity, since the inertia force is then negligible. Because the load is accurately known, the kinetic friction coefficient can be estimated for different speed values. We give in
Figure 4a the set of experimental points obtained in this way and its approximation by an exponential law similar to this considered in
Section 2. By comparison with a classical result from textile engineering literature, shown in
Figure 4b, we get very close speed constants—the
ẋk of our theoretical model—a little higher than 0.1 m/s but different ratios of bound-kinetic friction coefficient over static one: while it is equal to about 2 in the case of
Figure 4b for the sample with finishing agent, it is equal to about 3.7 in the case of our experimental curve of
Figure 4a. Such a difference could be explained by the twisted character (see
Figure 2c) of the selected yarns, but also by the fact that friction occurs between yarns put in different directions imposed by the double helix structure of the sheath. Moreover, and although experimental proofs are still missing, this is an interesting fact: although a ratio higher than this is generally given in classic textile engineering data, this ratio is still lower than the one we empirically considered to accurately estimate a full dynamic model of the McKibben muscle contraction: in our 2000 study [
9], a similar ratio of 7 was used to be in accordance with the damped character of a prototype whose sleeve was braided with the same rayon-twisted yarns. This could suggest that the double helix structure—yarns alternatively sliding above and below their neighbors—would amplify the “textile character” of the friction phenomena inside the sleeve by increasing the ratio bound-kinetic friction coefficient over static friction coefficient. Furthermore, as previously analyzed in our paragraph devoted to stability analysis, a large value of this ratio combined with a relatively high speed constant are two stability factors for our single integral action-based closed-loop controller.
Figure 3.
Experimental apparatus used to estimate the kinetic friction of a flattened sample of our rayon braided sleeve sliding over itself.
Figure 3.
Experimental apparatus used to estimate the kinetic friction of a flattened sample of our rayon braided sleeve sliding over itself.
Figure 4.
Experimental estimation of the kinetic friction coefficient of our flattened rayon sheath sliding over itself (
a) and comparison with a typical curve showing the kinetic friction coefficient variation for a rayon staple fiber sliding over a cylindrical array of similar fibers (redrawn from [
19] with data from [
21]).
Figure 4.
Experimental estimation of the kinetic friction coefficient of our flattened rayon sheath sliding over itself (
a) and comparison with a typical curve showing the kinetic friction coefficient variation for a rayon staple fiber sliding over a cylindrical array of similar fibers (redrawn from [
19] with data from [
21]).
3.2. Experimental Closed-Loop Positioning Control of McKibben Artificial Muscle Contraction with a Single Integral Action
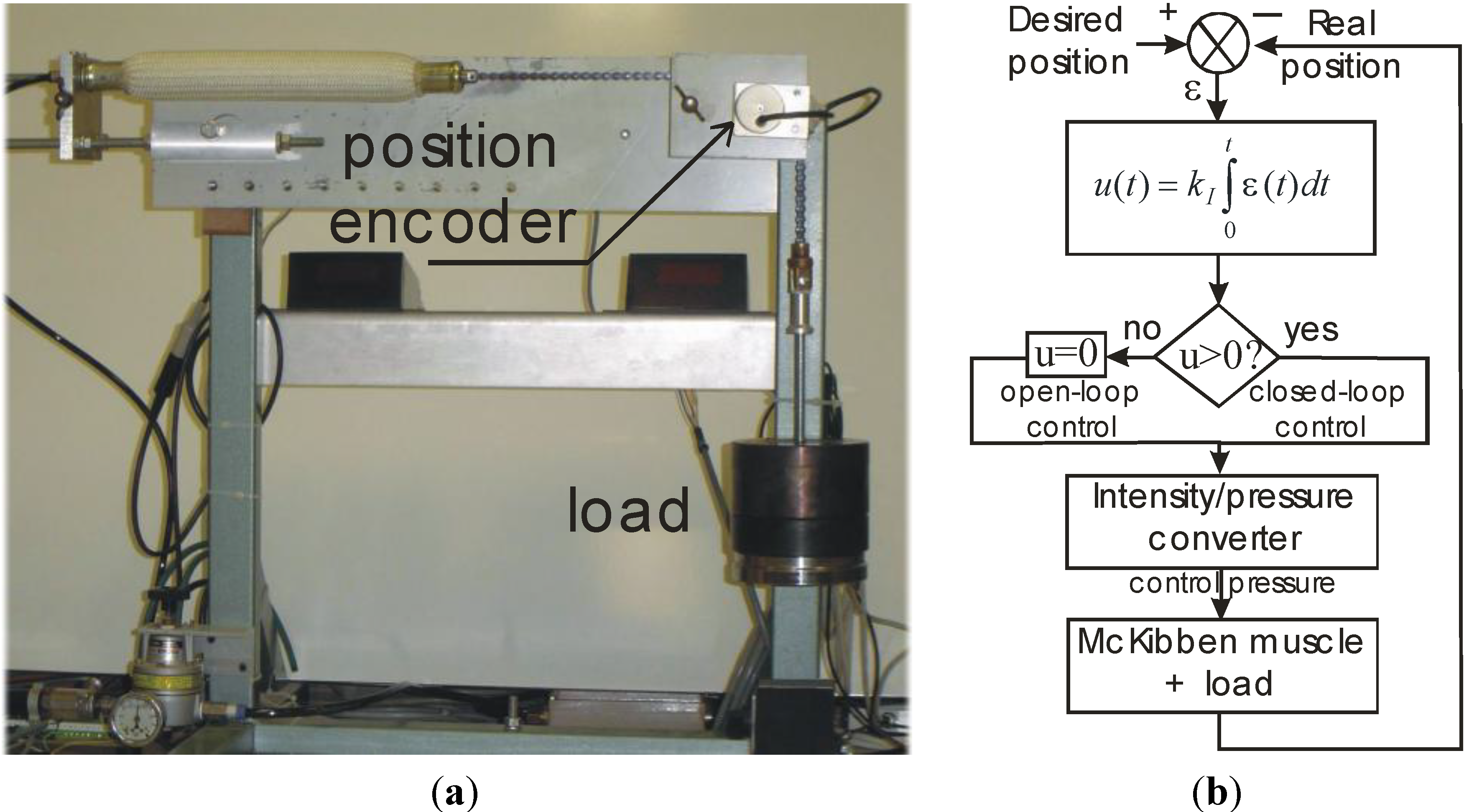
The relevance and efficiency of our proposed controller was experimentally tested on the setup shown in
Figure 5a: the pressure inside the artificial muscle between 0 and 5 bar is generated by means of a Samson Intensity/Pressure converter—details about the role of this system in the McKibben muscle working and its dynamic behavior can be found in our previous study [
9] and references therein—current muscle position is recorded by means of a highly accurate Heinheman optical rotation encoder; various weights can be loaded at the end of a chain driven by the artificial muscle thanks to a pulley on an axis which is fixed to the position encoder. It is important, on the one hand, to note that the real dynamic behavior of the Intensity/Pressure converter is much more complex than the simple linear first-order system considered in the simulation reported in
Section 2. This is due to the fact that the artificial muscle’s internal volume to be filled at a given pressure varies during contraction; nonetheless, we trusted the I controller to make transparent for the user the nonlinear behavior of this actuator chain component. On the other hand, we must keep in mind that, in accordance with the theoretical artificial muscle model considered earlier, a fluidic McKibben muscle is a single-effect actuator with a contraction controlled by a pressure value—in a 0–5 bar range—corresponding to a positive current value of the Intensity/Pressure converter—in a 2–20 mA range—as illustrated in
Figure 5b. As a consequence, a negative control value, as in the case of a negative desired position step, generates a zero control corresponding physically to an open-loop de-swelling of the artificial muscle. The closed-loop control only becomes active again beyond the lower step level, as will be illustrated in further experiments.
Figure 5.
Experimental setup for testing the closed-loop positioning controller of the three considered McKibben pneumatic artificial muscles driving various loads (a) and block scheme emphasizing the single-effect character of the McKibben pneumatic artificial muscle (b)—see text.
Figure 5.
Experimental setup for testing the closed-loop positioning controller of the three considered McKibben pneumatic artificial muscles driving various loads (a) and block scheme emphasizing the single-effect character of the McKibben pneumatic artificial muscle (b)—see text.
This is the reason why, in further reported step responses of experimental curves (see
Figure 6,
Figure 7 and
Figure 8) our closed-loop controller—as will be the case for any other closed-loop controller—is unable to control the failing edge of the step. Only two antagonistic artificial muscles can define a double-effect actuator, but this will be not considered in the frame of this study.
Two kinds of signals were considered for testing static and dynamic accuracy of our McKibben muscle prototypes: step signals and sinus-wave signals. In both cases, the desired position is defined as an
x position of the artificial muscle which must belong to the range [0,
xmax], where 0 corresponds to the initial muscle state
i.e., no contraction while
xmax corresponds to the fully contracted state of the muscle. In the case of a step signal, the desired step position was defined between a lower bound and an upper bound. Because the first prototype made of rayon yarns is relatively long and can generate a relatively high power, we decided to distinguish a “short” step with
x varying from 4 to 7 cm from a “long” step with
x varying from 2 to 9 cm, giving us the possibility to test load robustness with weights varying between 1 and 15 kg. It was important to test these two kinds of steps due to the nonlinear character of the artificial muscle whose dynamic behavior is not
a priori independent on the step ”length.” Moreover, let us remark that with a
Fmax estimated to 105 daN (see
Table 1), the considered range of loads corresponds, with the notation used in section 2, to a range
rM equal to about [0.01, 0.15]. In the case of the two other less powerful plastic and metal wire prototypes, we limited our analysis to a single case of a step from 1 to 5 cm making it possible to test load robustness with weights from 0.2 to 2 kg. We give in
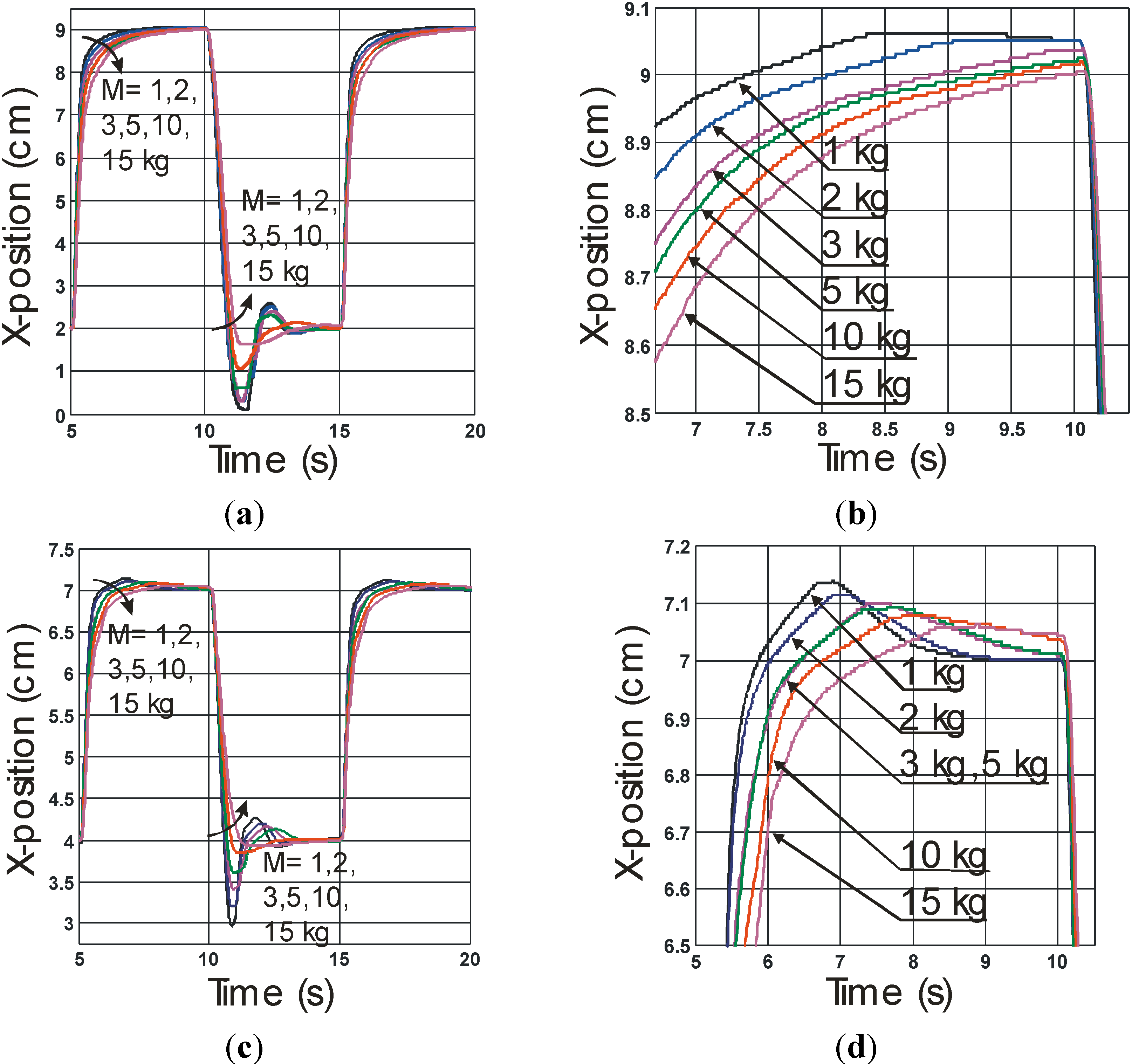
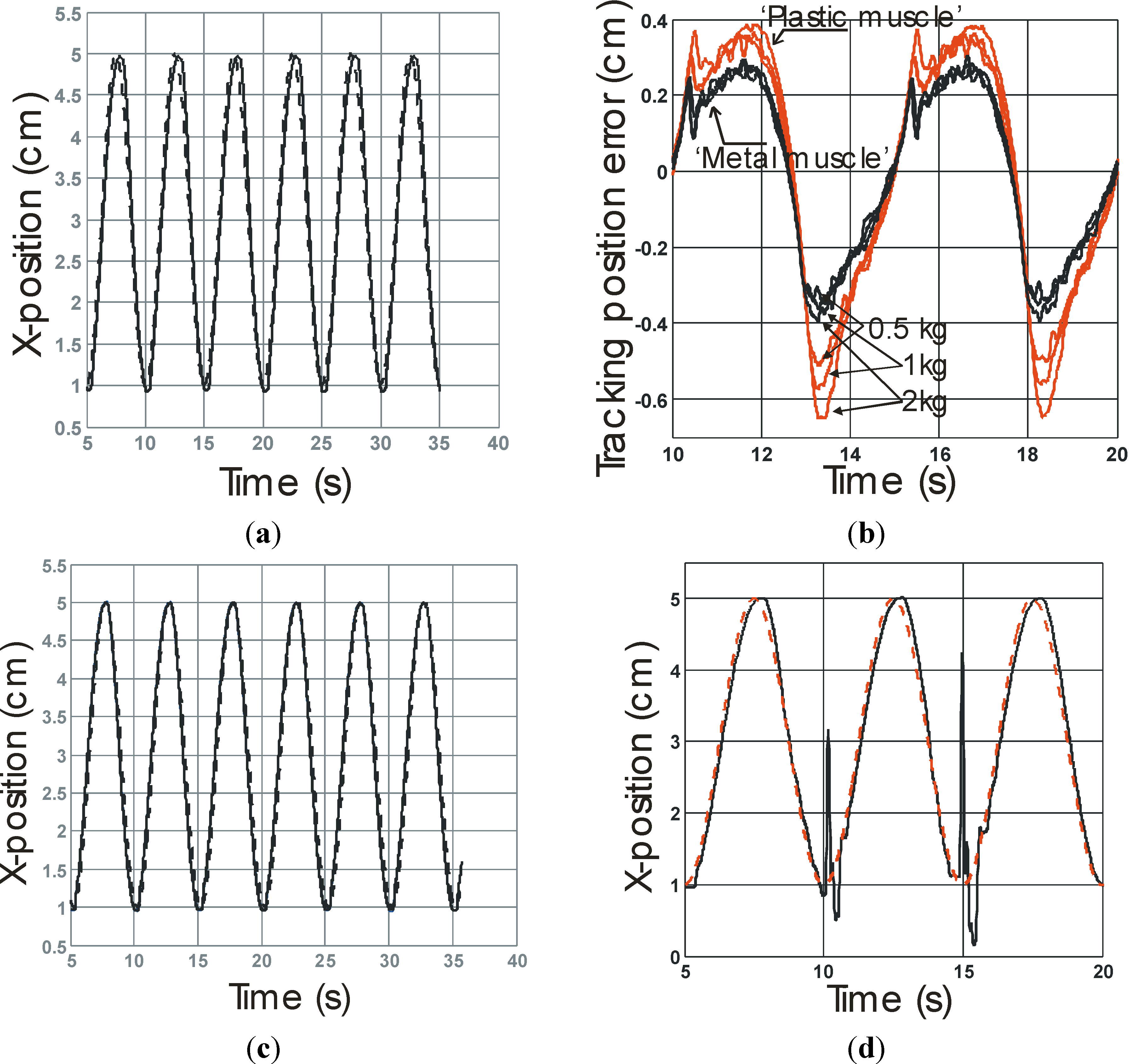
Figure 6 the experimental results obtained with our rayon McKibben muscle performing its “long” and “short” steps with a load range varying from 1 kg to 15 kg. It is worth noting that a standard
kI equal to 0.0075 bar.m
−1·s
−1 was considered in all reported experiments. Moreover, we give in
Figure 6b,d a close-up of the convergence towards the desired position in order to estimate the steady-state error when load is varying. A first point can be remarked: as predicted by our theoretical analysis, for a
kI value tuned at weak load, the system’s stability is kept for any higher load, even when the controller becomes active again after the open-loop descending step phase. Moreover, in accordance with simulations, the artificial muscle contraction appears to be relatively robust to large load variations with a quasi-absence of overshooting and a response-time—estimated, for example, to 95% of the desired steady-state value—increasing from about 1 s for a weak load to about 2 s for a high load. From
Figure 6b,d, a mean absolute accuracy of about 0.5 mm can be estimated, independently of load and step value. If we now consider our two other plastic (
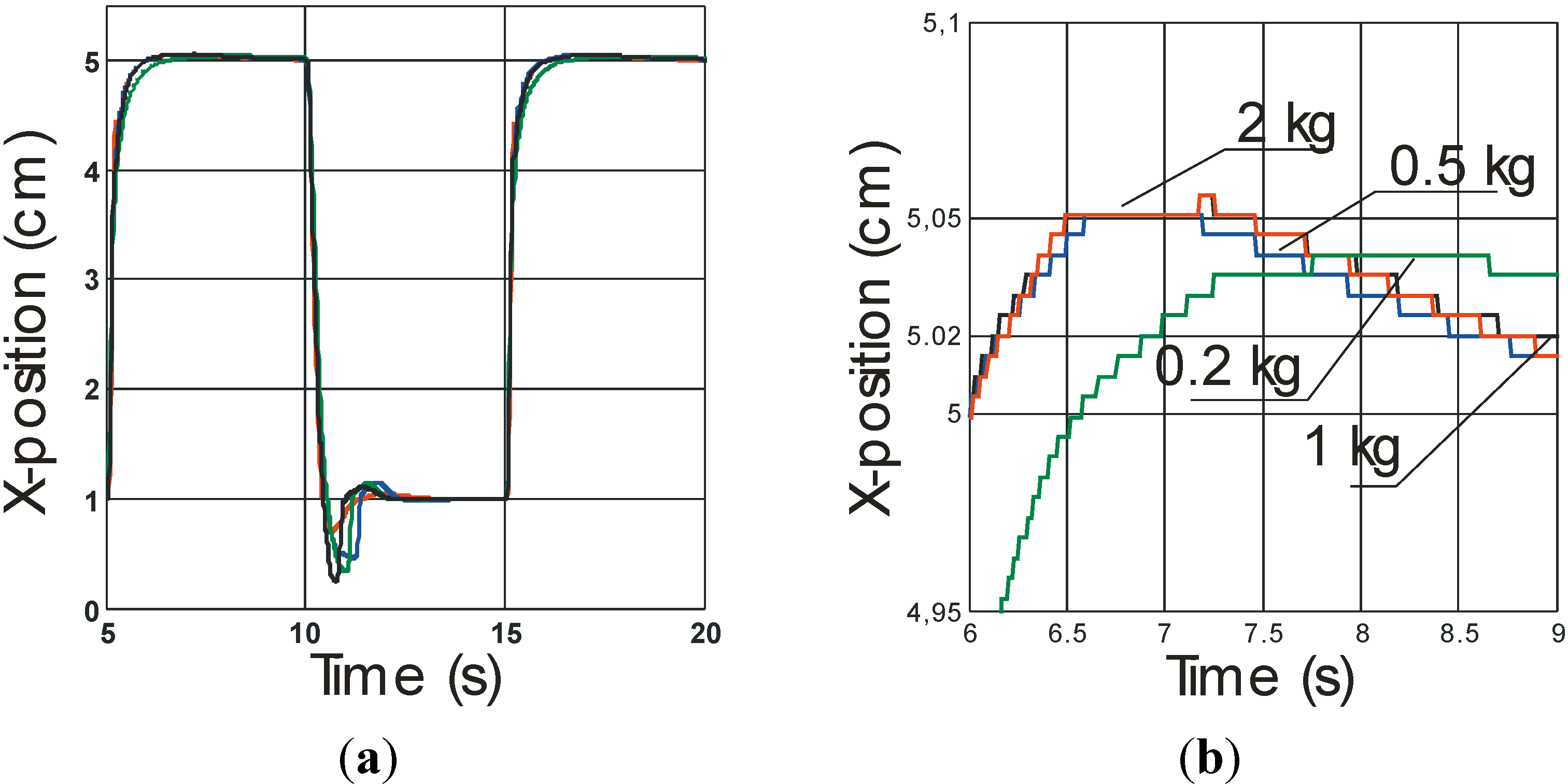
Figure 7) and metal wire (
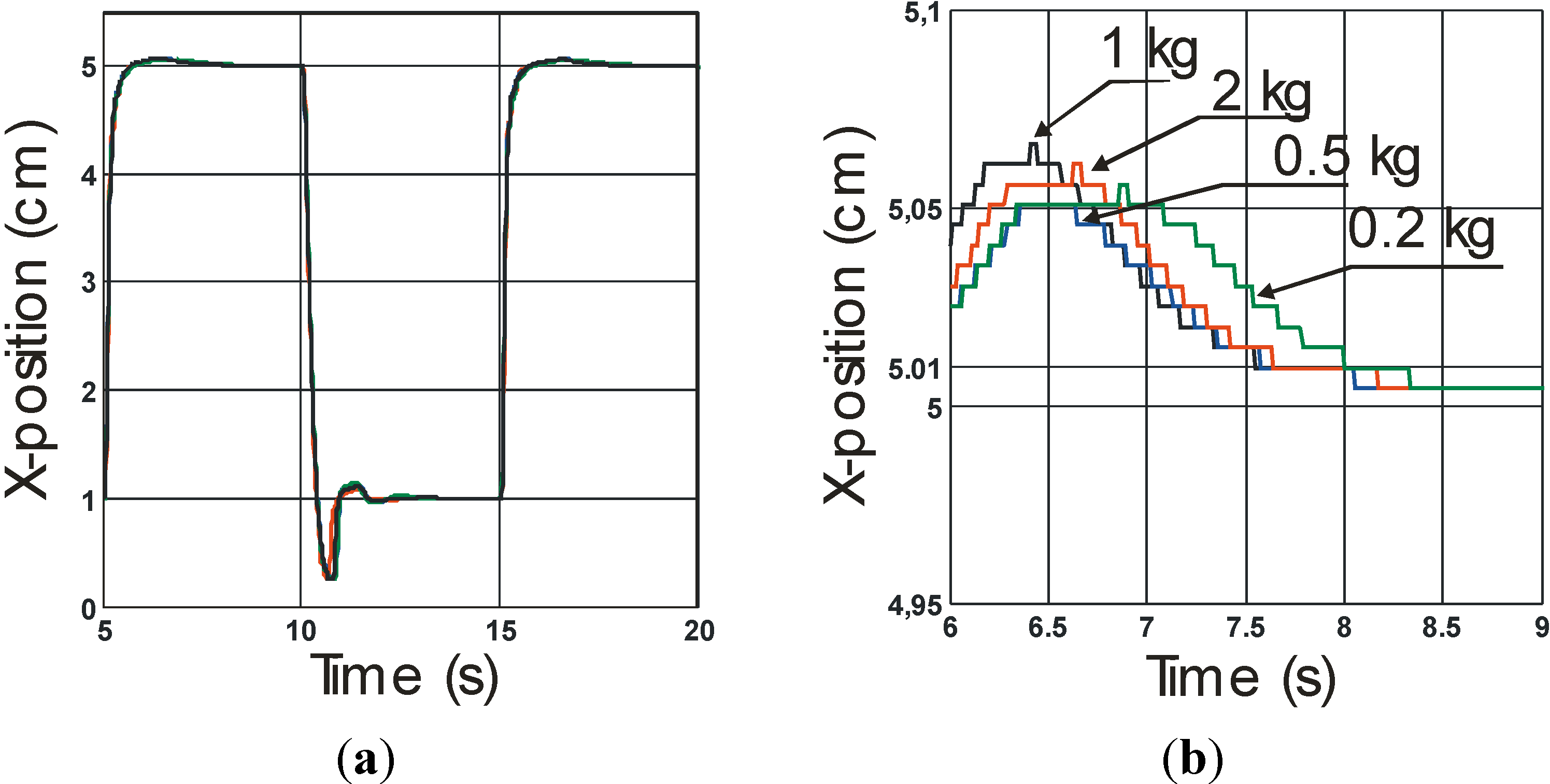
Figure 8) prototypes that we tested in the same experimental conditions of a step between 1 and 5 cm (for both artificial muscles,
kI was tuned to 0.04 bar.m
−1·s
−1), we again highlight the load robustness with a response time of about 1 s, albeit in a tighter load range, due to the weaker artificial muscle power. However, the important point to be emphasized is the impressive accuracy obtained in the case of the artificial metal muscle: an accuracy of 1/10 mm can be read on
Figure 8b.
Figure 6.
Step responses performed by our rayon yarns McKibben muscle driving various loads: “long” (a)—respectively “short” (c)—step with close-up of final convergence (b)—respectively (d).
Figure 6.
Step responses performed by our rayon yarns McKibben muscle driving various loads: “long” (a)—respectively “short” (c)—step with close-up of final convergence (b)—respectively (d).
Figure 7.
Step responses performed by our plastic wire McKibben muscle driving various loads (a) and (b) Close-up of final convergence towards the desired position.
Figure 7.
Step responses performed by our plastic wire McKibben muscle driving various loads (a) and (b) Close-up of final convergence towards the desired position.
Figure 8.
Step responses performed by our metal McKibben muscle driving various loads (a) and (b) Close-up of the convergence towards the final desired position.
Figure 8.
Step responses performed by our metal McKibben muscle driving various loads (a) and (b) Close-up of the convergence towards the final desired position.
If we now consider the case of a sinus-wave tracking, with the value of
kI retuned, we find again the same load robustness, particularly well illustrated in the case of our rayon yarn-braided prototype (
kI was equal to 0.015 bar·m
−1·s
−1 for all loads), as shown in
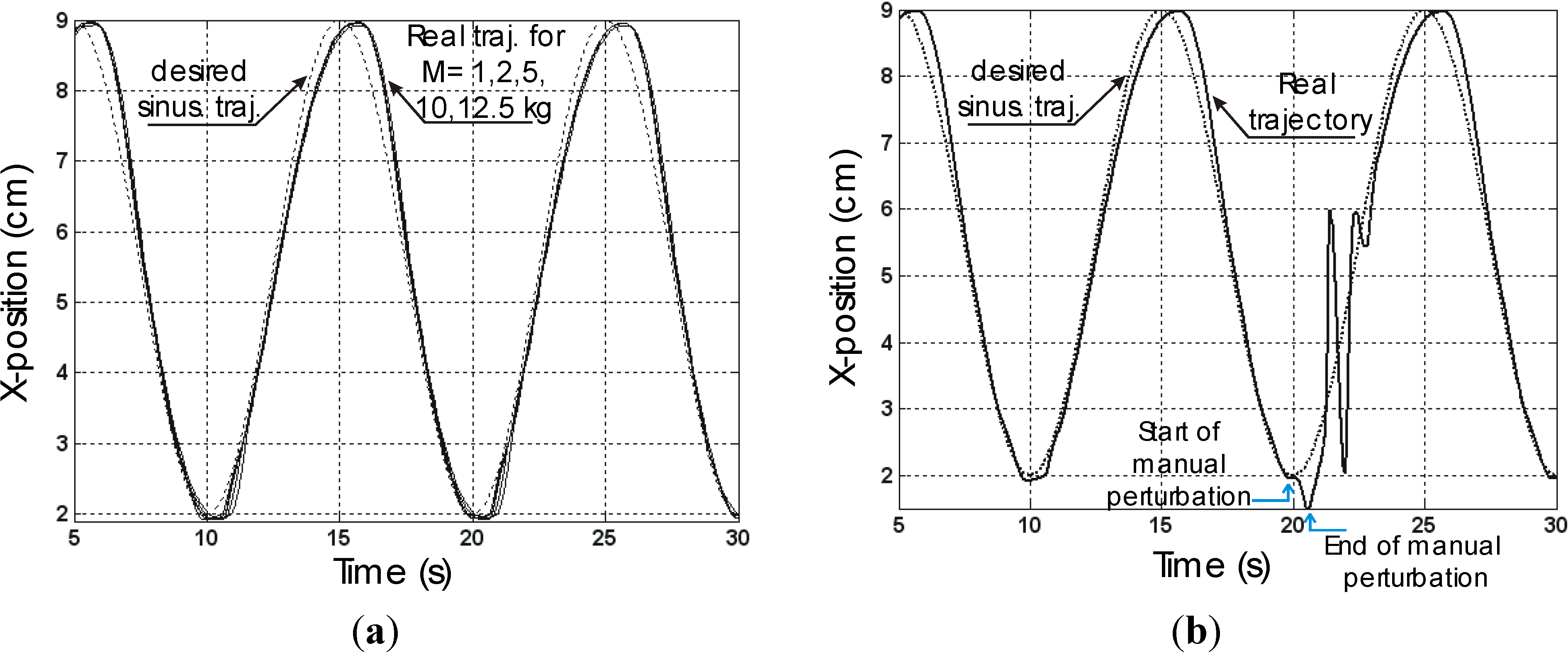
Figure 9a in the case of an imposed frequency equal to 0.1 Hz with embedded loads varying between 1 and 12.5 kg: the tracking position error appears to be independent on a load with a maximum value occurring at the change of direction, estimated to a little less than 1 cm.
Figure 9.
Sinus-wave tracking at a 0.1 Hz operating frequency in the case of the rayon yarn-braided McKibben muscle (a) and (b) Effect of a manual perturbation during closed-loop control movement.
Figure 9.
Sinus-wave tracking at a 0.1 Hz operating frequency in the case of the rayon yarn-braided McKibben muscle (a) and (b) Effect of a manual perturbation during closed-loop control movement.
In the case of plastic and metal wire-braided prototypes, we imposed a higher frequency equal to 0.2 Hz. It is noteworthy that the range of working frequencies of a given McKibben pneumatic artificial muscle depends on the dynamic performances of the pneumatic device feeding it as on the artificial muscle volume to be filled. That is the reason why a lower frequency was used for the first muscle whose initial internal volume is about twice this of the two other prototypes.
Figure 10a,c report the comparison between the desired sinus-wave and the experimental trajectory for a 1 kg load—for both “plastic” and “metal” artificial muscles,
kI was tuned to 0.06 bar.m
−1·s
−1.
Figure 10.
Sinus-wave tracking performed at a 0.2 Hz operating frequency in the case of the plastic and metal wire-braided McKibben muscle, (a) McKibben muscle made of a plastic sheath driving a 1 kg load; (b) McKibben muscle made of a metal sheath driving a 1 kgload; (c) Comparison of tracking position errors for three embedded loads equal to 500 g, 1 kg and 2 kg; (d) Effect of manual perturbations during closed-loop control movement in the case of the metal sheath McKibben muscle.
Figure 10.
Sinus-wave tracking performed at a 0.2 Hz operating frequency in the case of the plastic and metal wire-braided McKibben muscle, (a) McKibben muscle made of a plastic sheath driving a 1 kg load; (b) McKibben muscle made of a metal sheath driving a 1 kgload; (c) Comparison of tracking position errors for three embedded loads equal to 500 g, 1 kg and 2 kg; (d) Effect of manual perturbations during closed-loop control movement in the case of the metal sheath McKibben muscle.
We report in
Figure 10b the tracking position error during two periods, for the two muscles driving successively three loads respectively equal to 500 g, 1 kg and 2 kg. In every case the tracking position error appears to be less to this estimated in the case of the rayon-braided muscle: it belongs to a range of [−0.7 cm, +0.4 cm] in the case of the “plastic muscle” and to a range of [−0.4 cm, +0.3 cm] in the case of the “metal muscle.” On the one hand, this result suggests that the proposed I controller is adapted to a large range of braided McKibben muscles. On the other hand, it also suggests, beyond the limitations of our study, that specific braided materials could generate weak tracking position error, as this appears to be the case in our prototype braided with thin metal wires.
We also tested the ability of the controller to reject a manual perturbation: during the sinus-wave tracking, the operator manually caught the load and released it after some seconds. It can be checked in
Figure 9b and
Figure 10d that the system remains stable—experiment is not reported in the case of the plastic sleeve McKibben muscle but similar results were obtained—and that the real trajectory rapidly converges again on the desired one. It is worth noting that the manual perturbation is never made in a similar way at each time and so its amplitude as its duration are not the same in reported experiments but the idea in doing that is to emphasize the compliant character of the closed-loop control particularly in response to a human interaction. It can be noted that, beyond the various considered experimental conditions, the perturbation seems better damped in the case of the rayon yarn-braided muscle than in the two other cases: this could be explained by the fact that kinetic friction and, as a consequence, damping is more pronounced in the case of this prototype in comparison with the two other considered ones.
The observed similarities in step and sinus-wave responses, as the reported differences in steady state accuracy and oscillations during perturbation rejection suggest that the three considered McKibben artificial muscles follow the same damping model with different parameters. Due to the good accordance between simulated and experimental step responses in all cases, we are led to consider that the assumed nonlinear damping model would be common to the three prototypes. This is, however, a surprising conclusion because if it is expected in the case of the sheath made of rayon yarns, it is more questionable in the non-fibrous case of plastic and metal-wire sheaths. A classic explanation given in textile technology is that the increase of kinetic friction with speed emphasizes the fundamental role of the lubrication agents during sliding. At high speeds and low loads, lubrication is partly hydrodynamic and, as written by Hansen and Tabor in their analysis of hydrodynamic factors in the friction of fibers and yarns [
22]: ‘It is well known that in hydrodynamic lubrication the velocity has exactly the same effect as the viscosity of the lubricant: that is, if the velocity is increased by a factor 2, the frictional behavior is exactly the same as if the velocity had been kept constant and the viscosity has been increased by a factor 2, (assuming that no other changes have been made in the system)”. Our experimental results suggest that such hydrodynamic lubrication effect would be active in the case of a McKibben muscle sheath, whatever the material yarns or thin wires are made of. Such an assumption has to be verified by an accurate analysis of friction inside the artificial muscle braided sheath that has as of yet, to the best of our knowledge, never been undertaken. Beyond this missing understanding of friction phenomena at work during McKibben muscle contraction, a very amazing conclusion can be drawn from our experimental results: a McKibben muscle braided with thin metallic wires would give, in a closed-loop, better static and dynamic performances. Especially our prototype with our closed-loop I controller exhibits a static accuracy of about 1/10 mm, which is unexpected for a “soft actuator” associated with a very good load robustness inside the tested range.
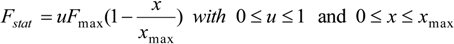
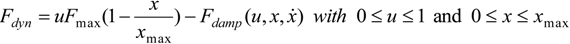
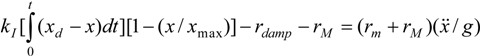
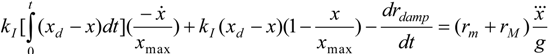
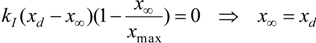
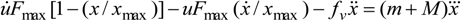
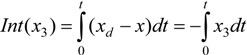
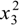 corresponding to a
corresponding to a 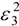 term was neglected:
term was neglected:
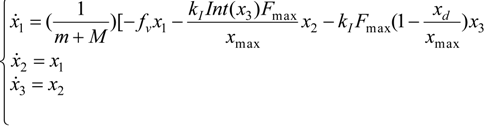
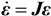 in which ε = [ε1 ε2 ε3]T and the characteristic polynomial corresponding to det(J − λI3) = 0 where I3 is the 3 × 3 unit matrix and λ a complex variable. We get:
in which ε = [ε1 ε2 ε3]T and the characteristic polynomial corresponding to det(J − λI3) = 0 where I3 is the 3 × 3 unit matrix and λ a complex variable. We get: