Review on the Nonlinear Modeling of Hysteresis in Piezoelectric Ceramic Actuators
Abstract
:1. Introduction
2. Microstructure and Poling of Piezoelectric Ceramics
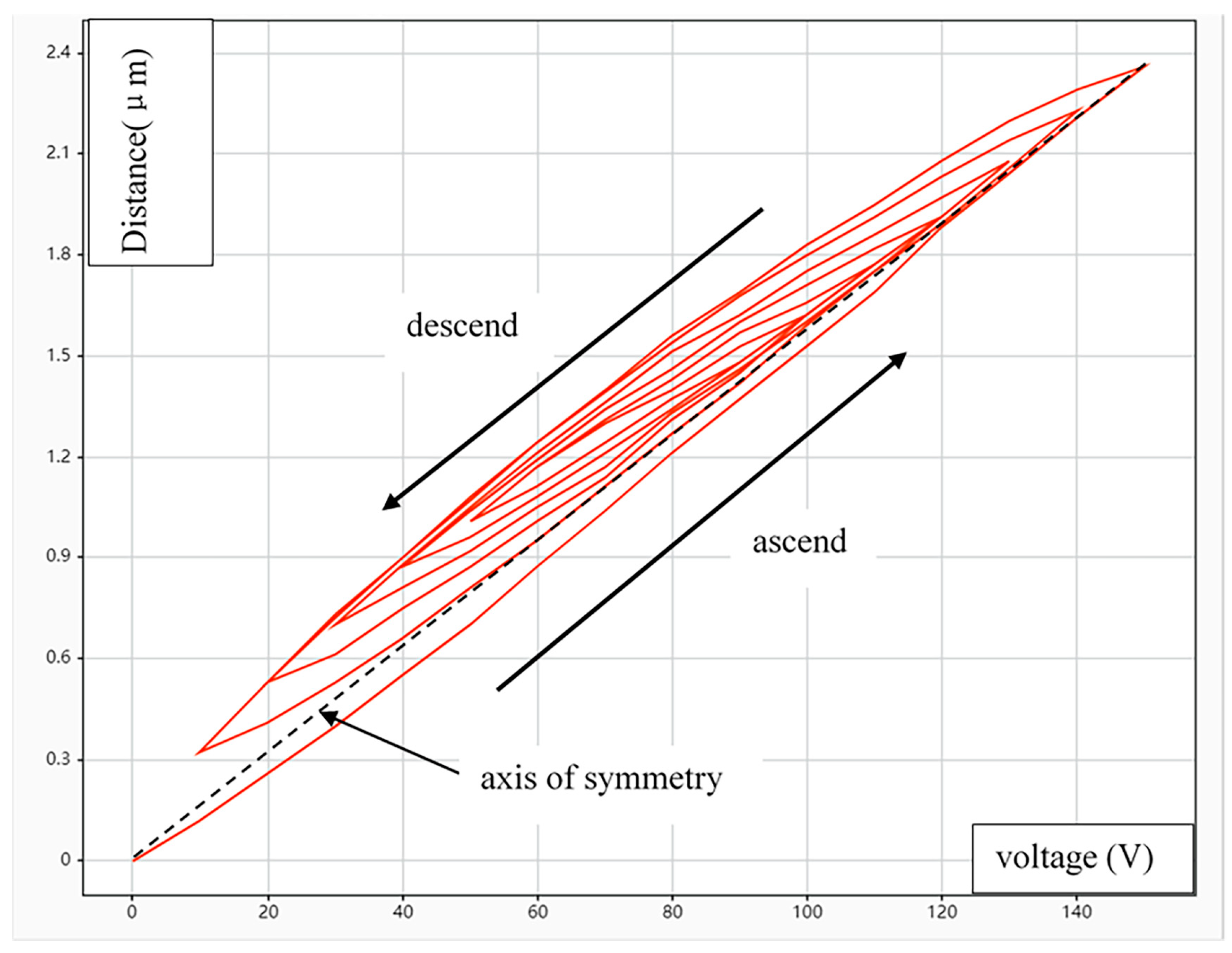
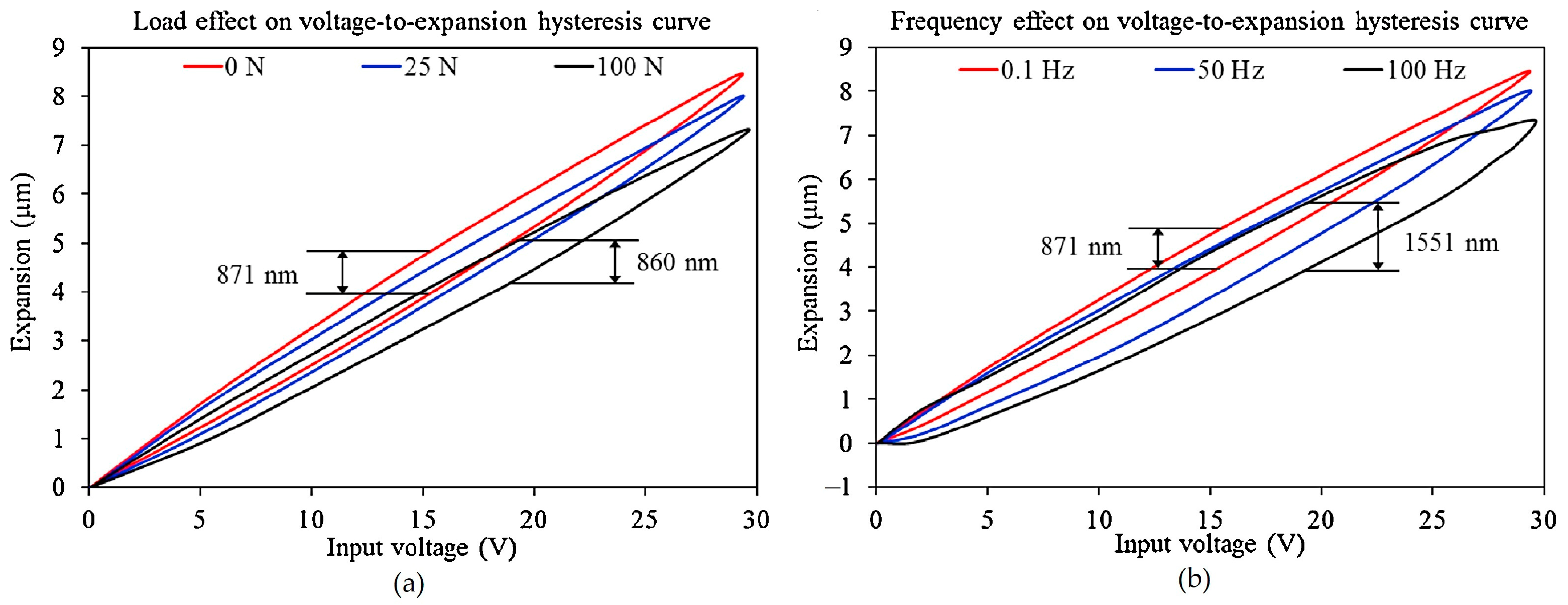
3. Hysteresis Characteristics of Piezoelectric Ceramic Actuators
4. Inverse Model
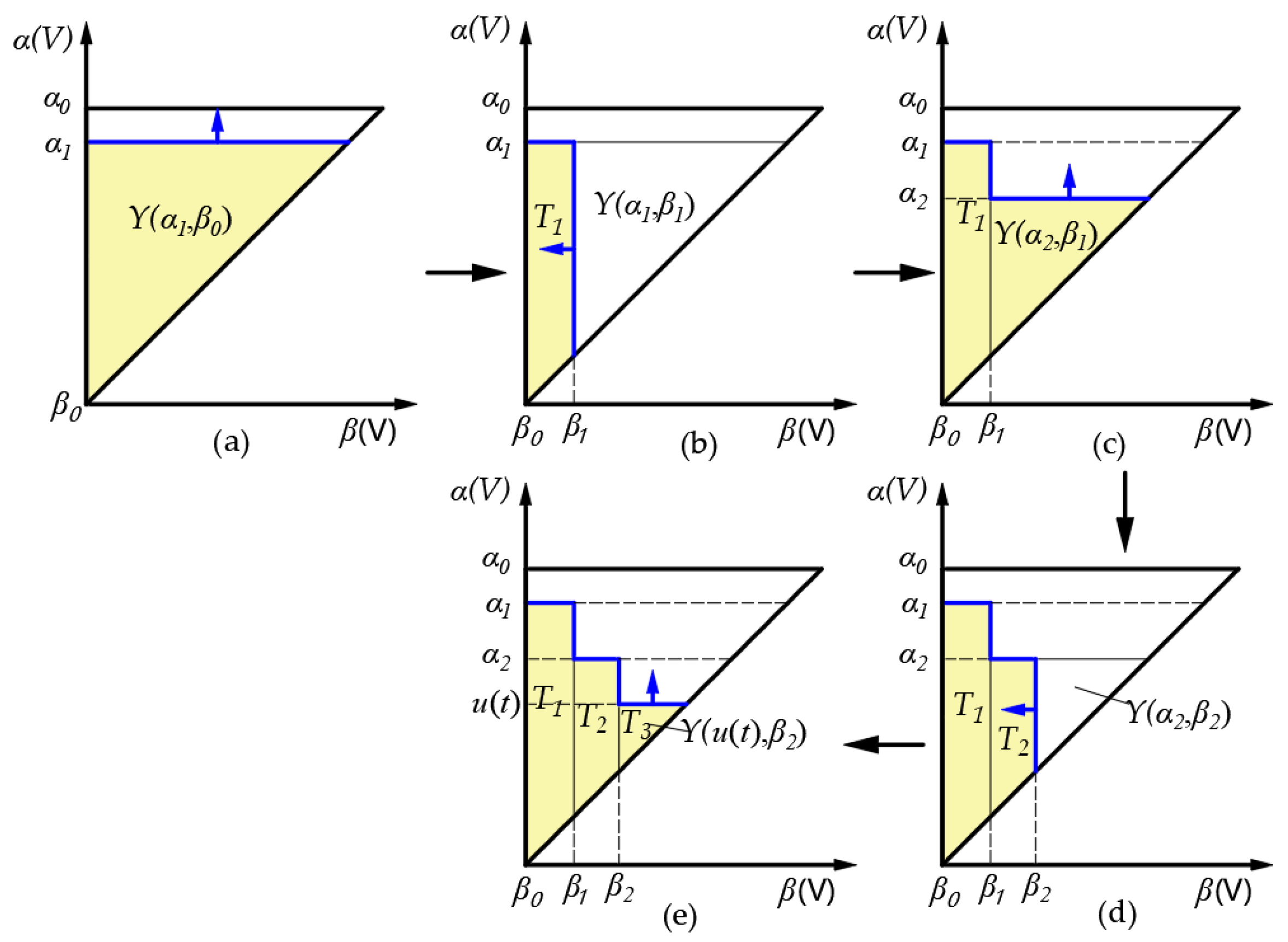
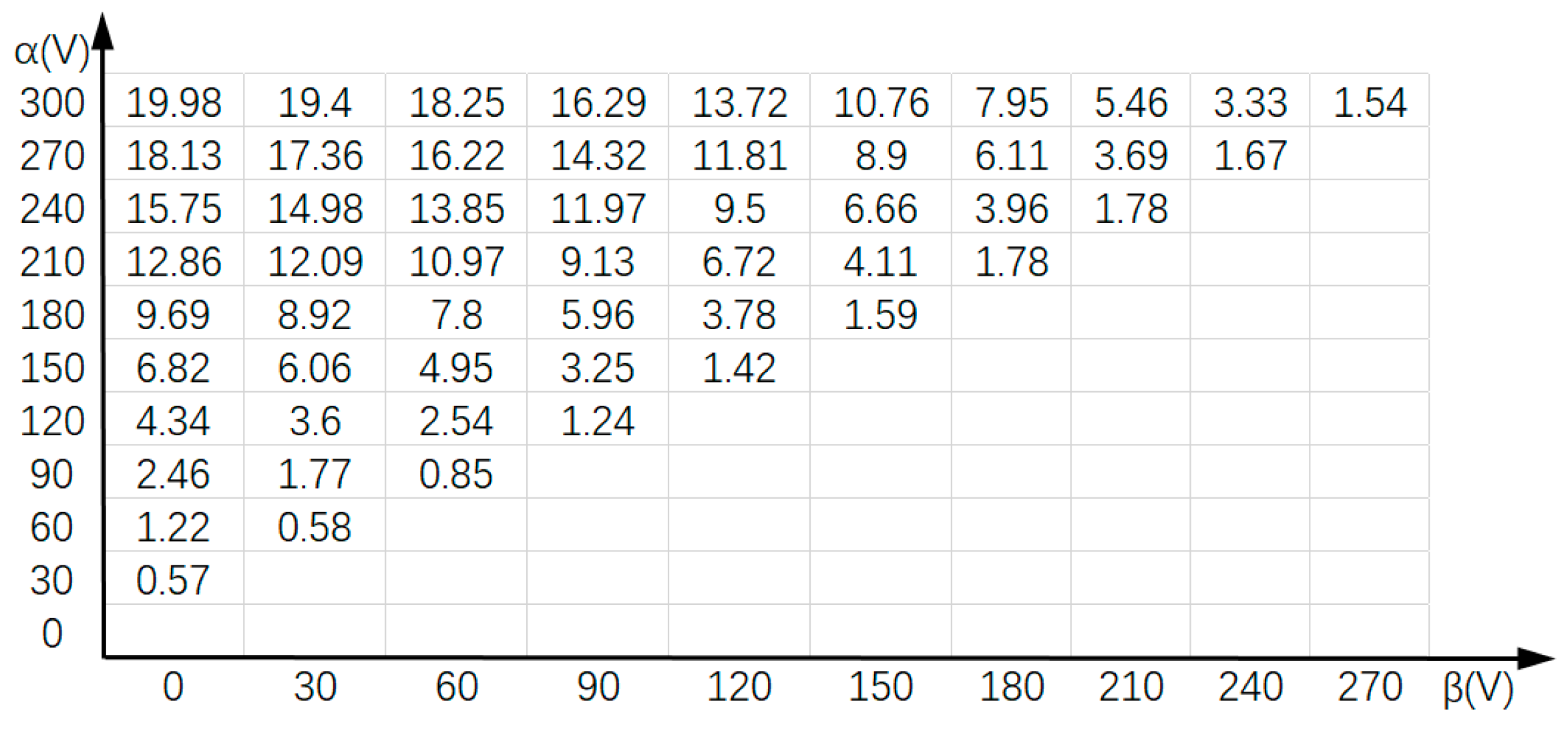
5. Preisach Model
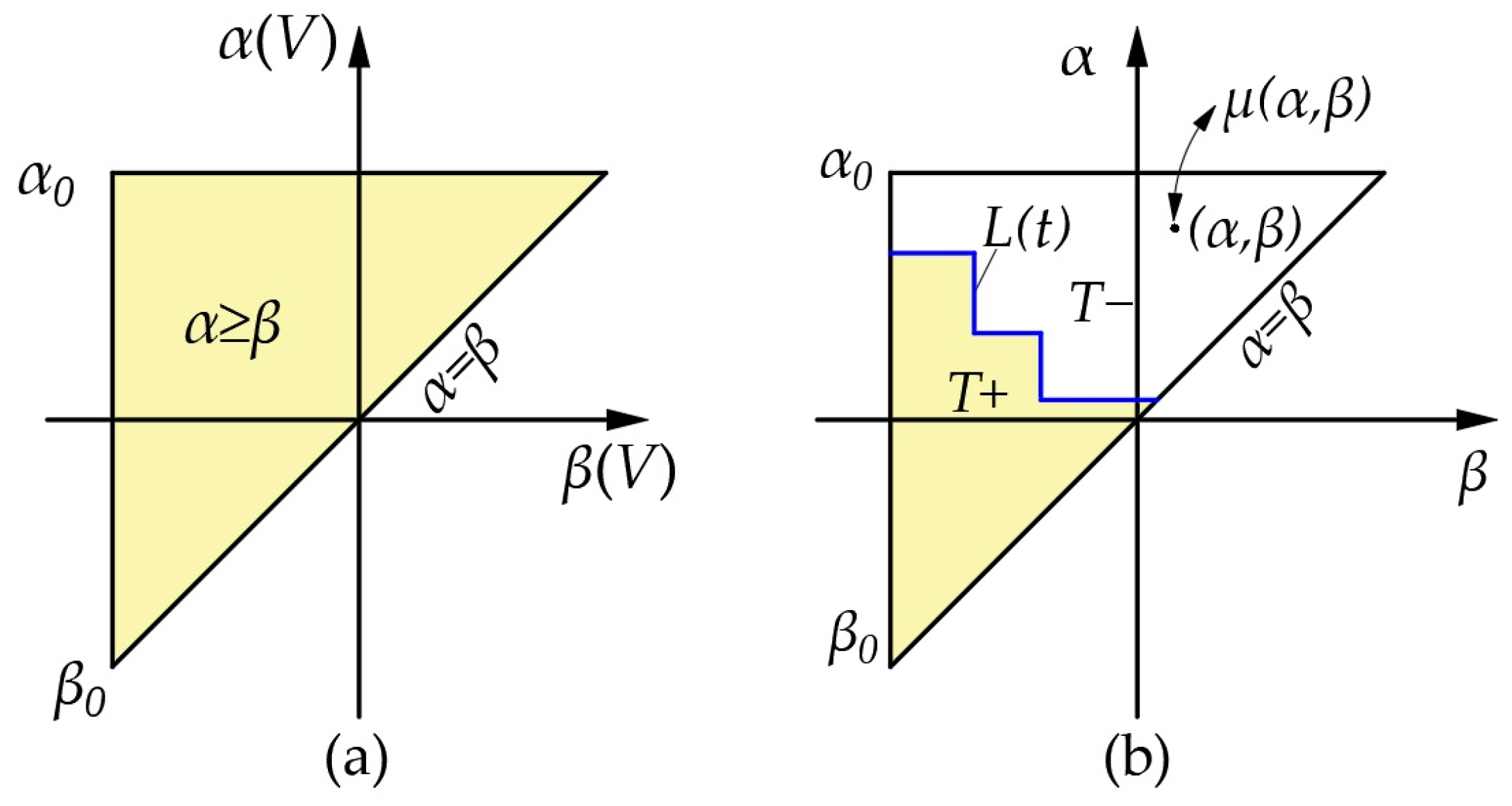
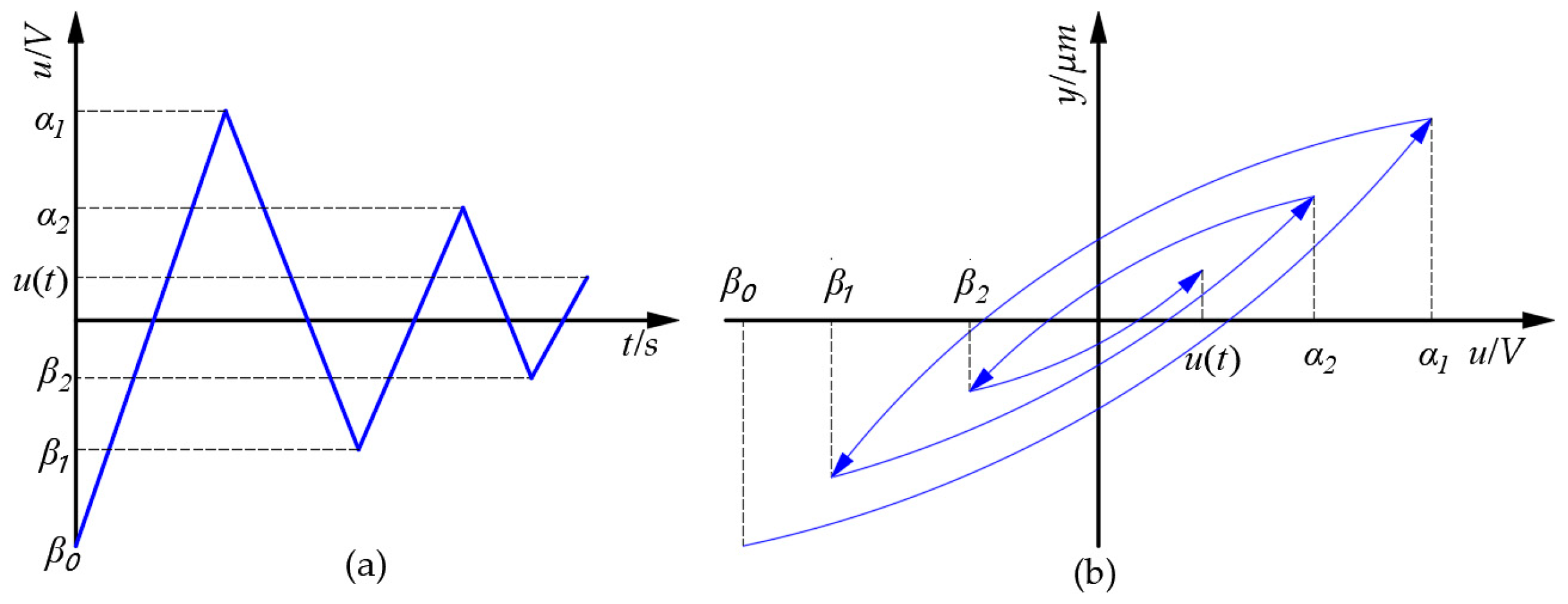
5.1. Model Introduction
5.2. Model Development
6. PI (Prandtl Ishilinskii) Model
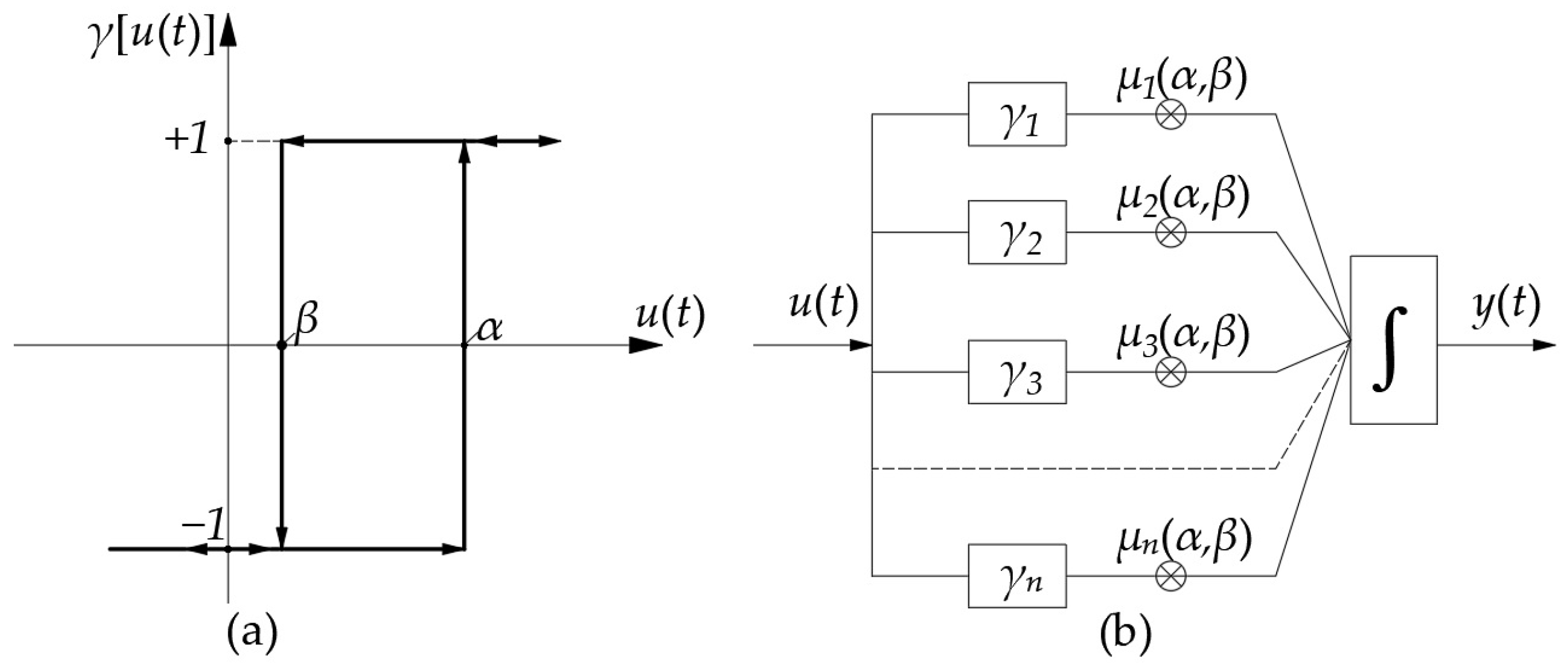
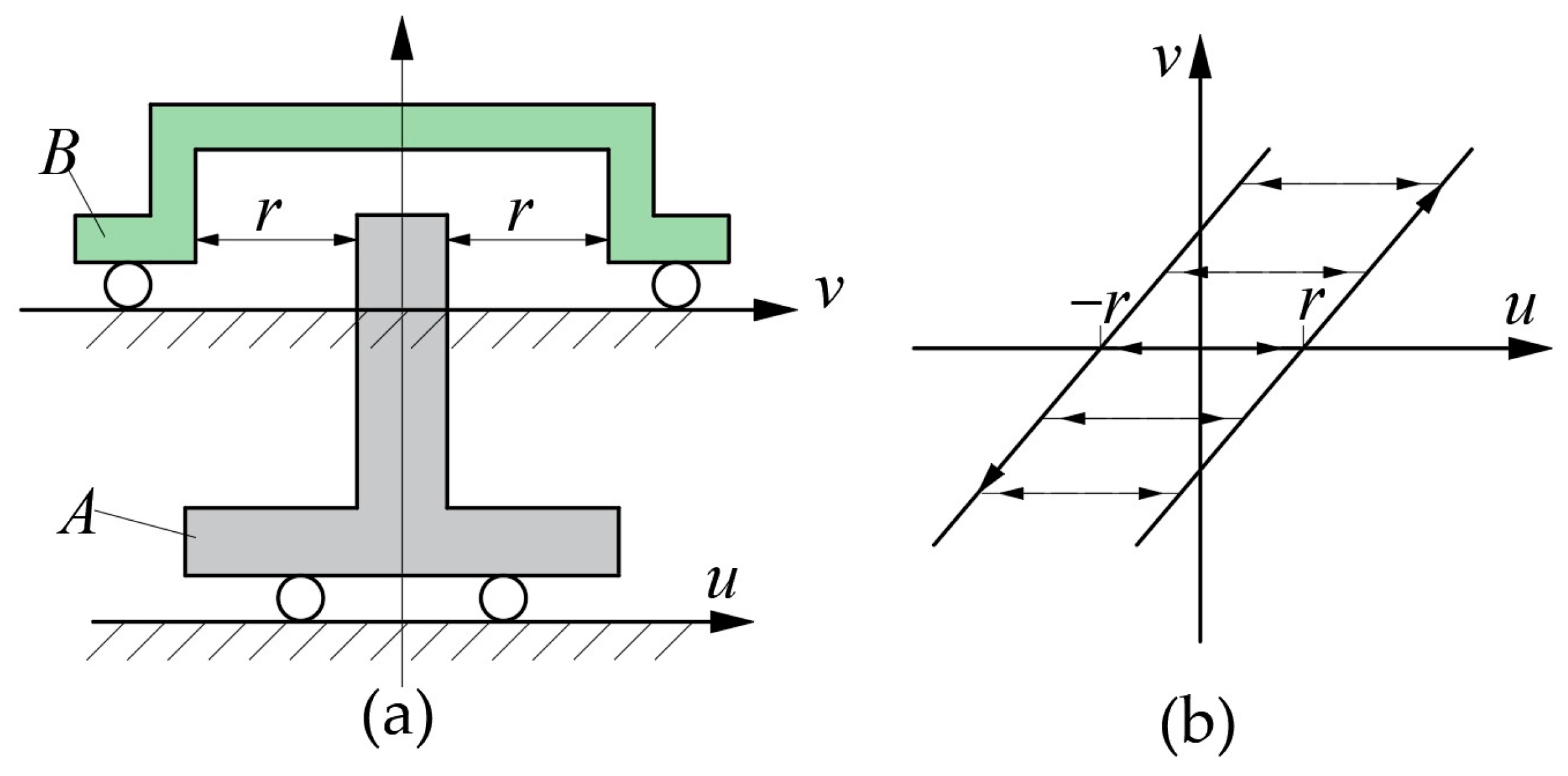
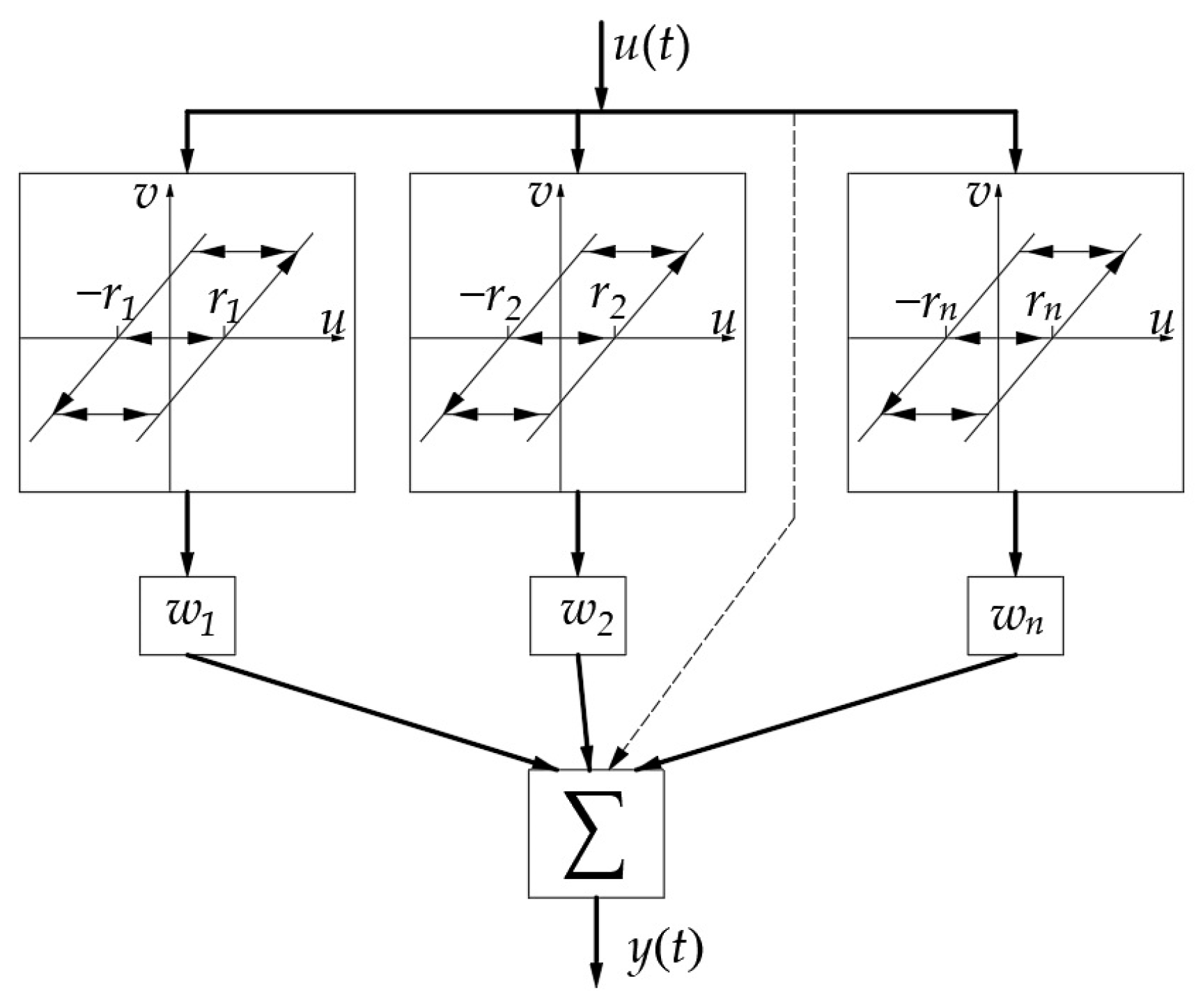
6.1. Classical PI Model Based on the Play Operator
6.1.1. Basic Principles of the Play Operator
6.1.2. Illustrate Play Operator Superposition Process
6.2. A Classical PI Model Based on Stop Operator
6.3. The Complementary Relationship between the Play Operator and the Stop Operator
6.4. Different Expressions of Classical PI Models
6.5. The Development of the PI Model
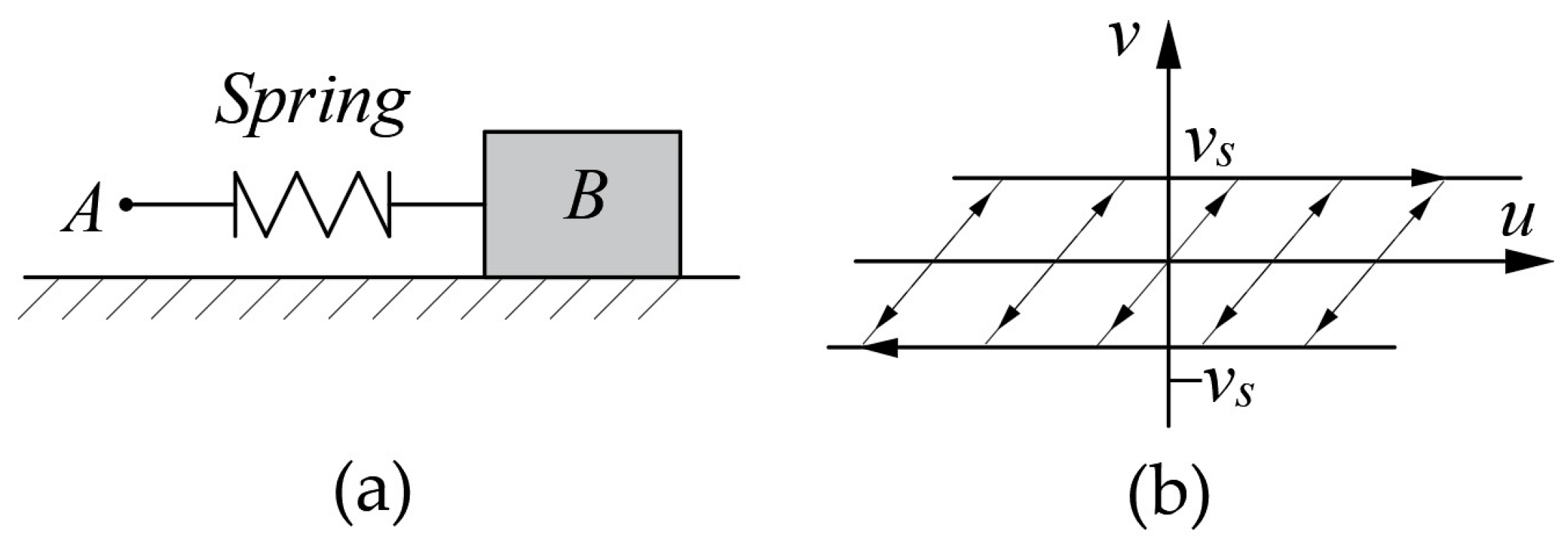
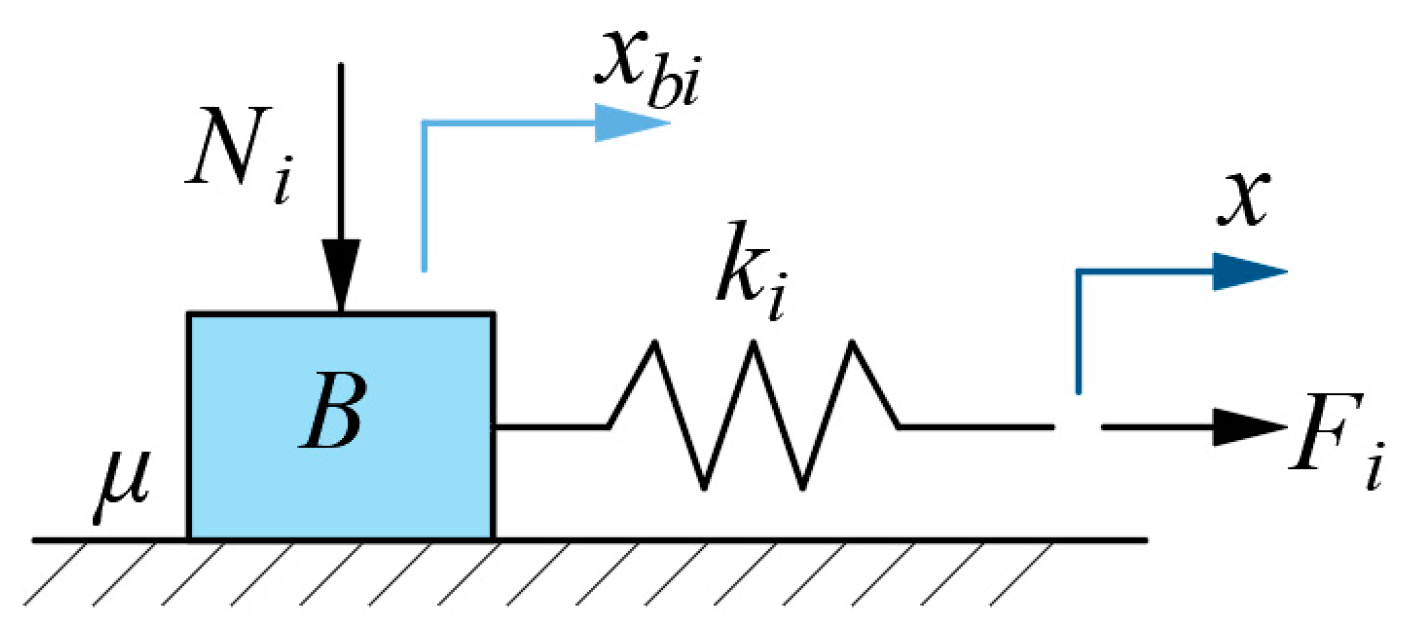
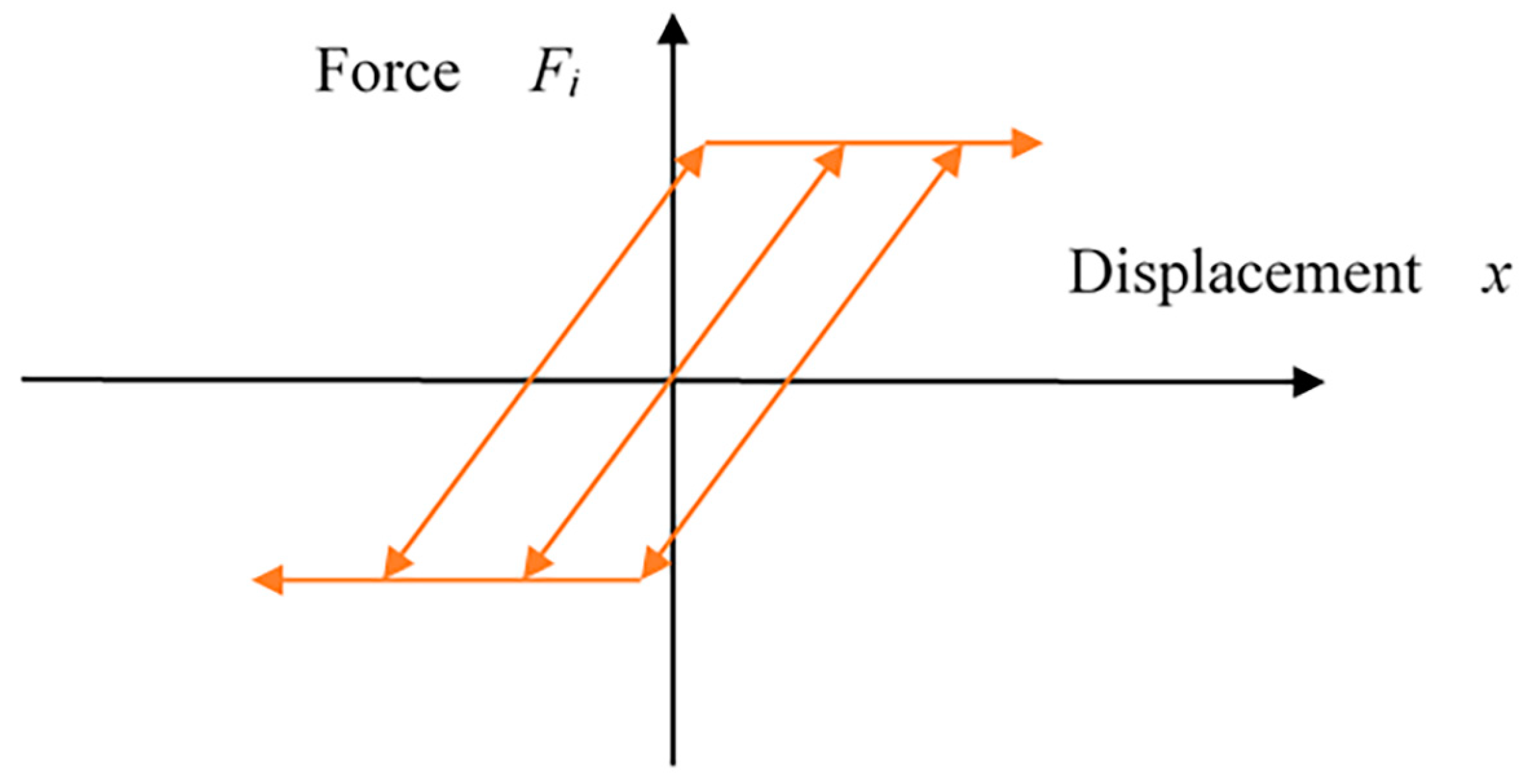
7. Maxwell Model
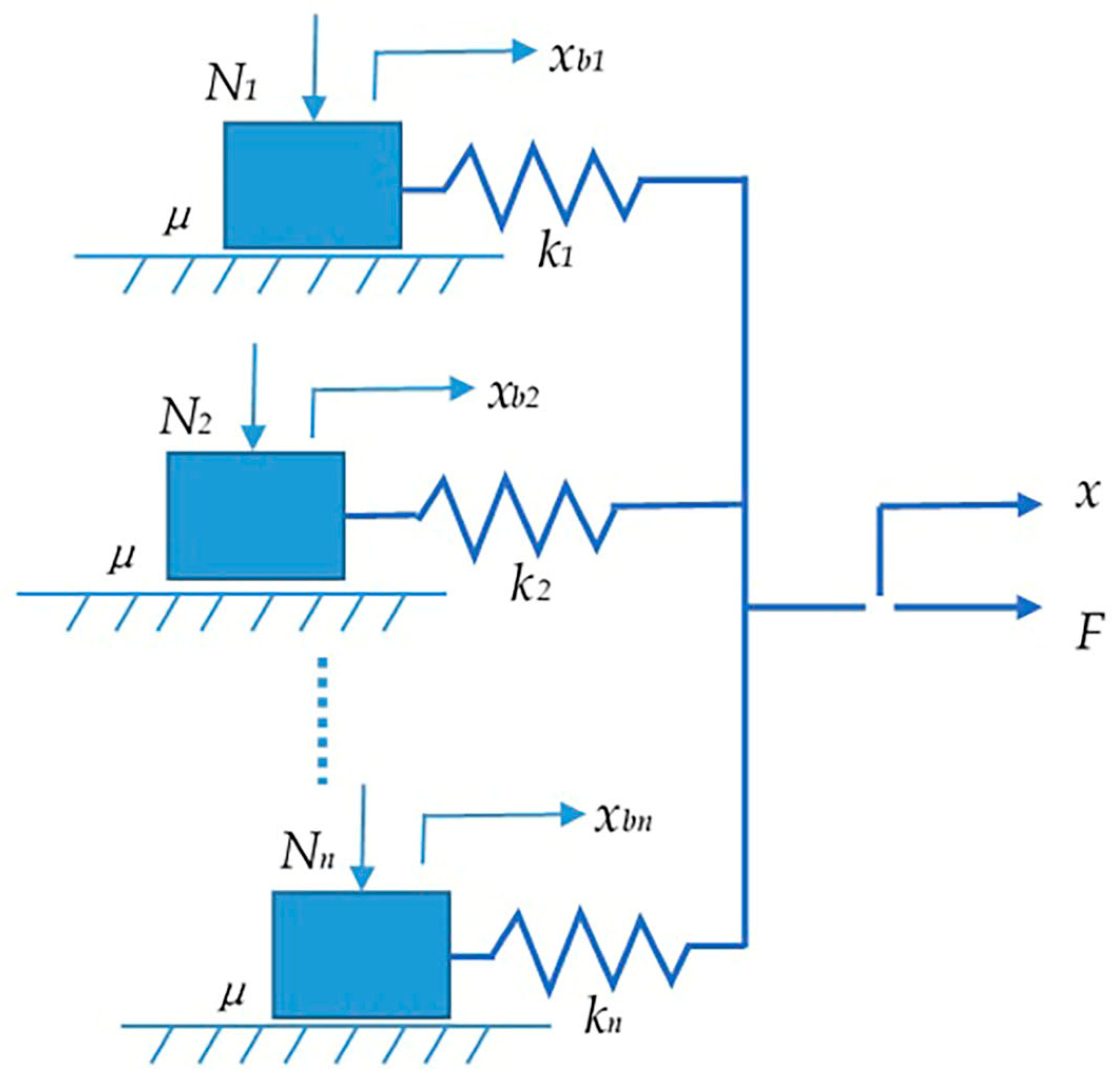
7.1. Generalized Maxwell-Slip Model
7.2. Development of the Generalized Maxwell-Slip Model
7.3. Maxwell Resistor Capacitor Model (MRC Model)
- (1)
- Linear second-order dynamic equation of the mechanical part:where are the mass, damping, and stiffness of the actuator, respectively; represents actuator displacement; is the output force of the actuator; and represents the load from the outside. The dynamic equation here describes the vibration of the system, and the rate-dependent description ability of the entire model mainly comes from this.
- (2)
- The total voltage u and total charge q of the input electrical part arewhere is the voltage at both ends of MRC module in Figure 28 and Figure 27; is the voltage at both ends of the transducer in the electrical part of the model; is the capacitor in parallel with the transducer; and is the charge of the transducer.
- (3)
- Electromechanical conversion relationship:where and represent the electromechanical conversion ratios of actuator voltage to force and displacement to charge, respectively. and can also be uniformly represented by T [65,66,67], but in reality, they have different physical interpretations, and it is best to use different symbols to represent them [68,72].
- (4)
- The nonlinear hysteresis part:is the nonlinear hysteresis part of the actuator, represented by the MRC model described in Equations (38) and (39). In addition to using the MRC model, the nonlinear hysteresis part can also use models such as the Preisach model and the PI model.
7.4. Development of MRC Model
8. Duhem Model
9. Bouc–Wen Model
9.1. Model Introduction
9.2. Model Development
10. Hammerstein Model
11. Model Comparison
12. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Arnau, A.; Soares, D. Fundamentals of Piezoelectricity. In Piezoelectric Transducers and Applications; Vives, A.A., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–38. [Google Scholar]
- Kaltenbacher, M. Piezoelectric Systems. In Numerical Simulation of Mechatronic Sensors and Actuators; Springer: Berlin/Heidelberg, Germany, 2007; pp. 243–266. [Google Scholar]
- Jaffe, B.; Cook, W.R.; Jaffe, H. Chapter 12—Applications of Piezoelectric Ceramics. In Piezoelectric Ceramics; Jaffe, B., Cook, W.R., Jaffe, H., Eds.; Academic Press: Cambridge, MA, USA, 1971; pp. 271–280. [Google Scholar]
- Lai, Z.L.; Liu, X.D.; Geng, J.; Li, L. Sliding mode control of hysteresis of piezoceramic actuator based on inverse Preisach compensation. Opt. Precis. Eng. 2011, 19, 1281–1290. [Google Scholar] [CrossRef]
- Uchino, K. Antiferroelectric Shape Memory Ceramics. Actuators 2016, 5, 11. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, S.; Yan, P.; Li, H. Finite Element Modeling and Test of Piezo Disk with Local Ring Electrodes for Micro Displacement. Micromachines 2022, 13, 951. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y. Hysteresis Modeling and Nonlinear Control of Piezoelectric Actuators. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2013. [Google Scholar]
- Wu-fa, L.; Zhen-bang, G.; Zhen, J. Design of micro piezoelectric ceramic rod angular rate gyro. Opt. Precis. Eng. 2006, 14, 439–442. [Google Scholar]
- Xu, C.; Xie, J.; Zhang, W.; Kong, Q.; Chen, G.; Song, G. Experimental Investigation on the Detection of Multiple Surface Cracks Using Vibrothermography with a Low-Power Piezoceramic Actuator. Sensors 2017, 17, 2705. [Google Scholar] [CrossRef] [PubMed]
- Cao, X.-T.; Li, D.-Q.; Li, H.-W.; Lin, G.-Y.; Yang, W.-F. Precision drive and position control of non-resonance piezoelectric stack linear motor. Opt. Precis. Eng. 2017, 25, 2139–2148. [Google Scholar] [CrossRef]
- Xu, S.A.; Xie, M.; Sun, J.; Chen, L.; Wang, G.R. Long range nano-positioning system based on optoelectronic phase-shift for piezoelectric actuator. Opt. Precis. Eng. 2014, 22, 2773–2778. [Google Scholar] [CrossRef]
- Hu, Y.; Zhang, H.; Ni, K. Mini-piezo-element drive microactuator based on triangular amplification. Opt. Precis. Eng. 2022, 30, 2094–2099. [Google Scholar] [CrossRef]
- Li, J.; Deng, J.; Liu, Y.; Yu, H.; Tian, X.; Li, K. A Linear Piezoelectric Actuator Based on Working Principle of Three-Petal Mouth of a Rabbit. IEEE Trans. Ind. Electron. 2022, 69, 5091–5099. [Google Scholar] [CrossRef]
- Gao, X.; Deng, J.; Zhang, S.; Jing, L.; Liu, Y. A Compact 2-DOF Micro/Nano Manipulator Using Single Miniature Piezoelectric Tube Actuator. IEEE Trans. Ind. Electron. 2022, 69, 3928–3937. [Google Scholar] [CrossRef]
- Deng, J.; Liu, Y.; Zhang, S.; Li, J. Development of a Nanopositioning Platform With Large Travel Range Based on Bionic Quadruped Piezoelectric Actuator. IEEE/ASME Trans. Mechatron. 2021, 26, 2059–2070. [Google Scholar] [CrossRef]
- Fairbairn, M.W.; Moheimani, S.O.R.; Fleming, A.J. Q Control of an Atomic Force Microscope Microcantilever: A Sensorless Approach. J. Microelectromechanical Syst. 2011, 20, 1372–1381. [Google Scholar] [CrossRef]
- Eslami, B.; Solares, S.D. Experimental approach for selecting the excitation frequency for maximum compositional contrast in viscous environments for piezo-driven bimodal atomic force microscopy. J. Appl. Phys. 2016, 119, 084901. [Google Scholar] [CrossRef]
- Li, M.; Yuan, J.; Guan, D.; Chen, W. Application of piezoelectric fiber composite actuator to aircraft wing for aerodynamic performance improvement. Sci. China Technol. Sci. 2011, 54, 395–402. [Google Scholar] [CrossRef]
- Yu, Z.; Wang, Y.; Cao, K.; Chen, H. Hysteresis compensation and composite control for Piezoelectric actuator. Opt. Precis. Eng. 2017, 25, 2113–2120. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Q.; Xu, T. A Novel Piezoelectric Ceramic Actuator with Scissoring Composite Vibration for Medical Applications. Appl. Sci. 2019, 9, 4637. [Google Scholar] [CrossRef]
- Mohith, S.; Karanth, P.N.; Kulkarni, S.M. Experimental investigation on performance of disposable micropump with retrofit piezo stack actuator for biomedical application. Microsyst. Technol. 2019, 25, 4741–4752. [Google Scholar] [CrossRef]
- Hirooka, D.; Yamaguchi, T.; Furushiro, N.; Suzumori, K.; Kanda, T. Highly responsive and stable flow control valve using a PZT transducer. In Proceedings of the 2016 IEEE International Ultrasonics Symposium (IUS), Tours, France, 18–21 September 2016; pp. 1–3. [Google Scholar]
- Li, H.; Liu, J.; Li, K.; Deng, J.; Liu, Y. Development of a High-Pressure Self-Priming Valve-Based Piezoelectric Pump Using Bending Transducers. IEEE Trans. Ind. Electron. 2022, 69, 2759–2768. [Google Scholar] [CrossRef]
- Li, H.; Liu, J.; Feng, Y.; Deng, J.; Liu, Y. A Broadband, High-Power Resonant Piezoelectric Active-Valve Pump Driven By Sandwich Bending Transducers. IEEE Trans. Ind. Electron. 2023, 70, 9336–9345. [Google Scholar] [CrossRef]
- Li, H.; Liu, Y.; Li, K.; Deng, J.; Feng, Y.; Liu, J. A resonant piezoelectric proportional valve for high-flowrate regulation operated by a bending sandwich actuator. Sens. Actuators A Phys. 2021, 331, 112971. [Google Scholar] [CrossRef]
- Yuan, G.; Wang, D.H.; Li, S.D. Single piezoelectric ceramic stack actuator based fast steering mirror with fixed rotation axis and large excursion angle. Sens. Actuators A Phys. 2015, 235, 292–299. [Google Scholar] [CrossRef]
- Dai, M.; Ding, H.; Huang, C.; Zhu, Y.; Wang, M. Design of a Panoramic Scanning Device Based on a Piezoelectric Ceramic Stack Actuator and Friction Transmission. Actuators 2022, 11, 159. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, Q.; Wang, H.; Qiu, J. Hysteresis modeling and tracking control for piezoelectric stack actuators using neural-Preisach model. Int. J. Appl. Electromagn. Mech. 2019, 61, 445–459. [Google Scholar] [CrossRef]
- Yu, Y.; Xiao, Z.; Naganathan, N.G.; Dukkipati, R.V. Dynamic Preisach modelling of hysteresis for the piezoceramic actuator system. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2001, 215, 511–521. [Google Scholar] [CrossRef]
- Yu, Y.H.; Xiao, Z.H.; Naganathan, N.; Dukkipati, R.V. Preisach modeling of hysteresis for piezoceramic actuator system. Proc. Int. J. Ser. C-Mech. Syst. Mach. Elem. Manuf. 2001, 44, 553–560. [Google Scholar] [CrossRef]
- Zhou, X.; Zhao, J.; Song, G.; De Abreu-Garcia, J. Preisach modeling of hysteresis and tracking control of a Thunder actuator system. In Proceedings of the Smart Structures and Materials 2003: Modeling, Signal Processing, and Control, San Diego, CA, USA, 25 September 2003; pp. 112–125. [Google Scholar]
- Li, L.I.; Liu, X.; Wei, W.; Huo, C. Generalized nonlinear Preisach model for hysteresis nonlinearity of piezoceramic actuator and its numerical implementation. Opt. Precis. Eng. 2007, 15, 706–712. [Google Scholar]
- Gao, X.; Ren, X.; Gong, X.a.; Huang, J.; IEEE. The Identification of Preisach Hysteresis Model Based on Piecewise identification method. In Proceedings of the 2013 32nd Chinese Control Conference (CCC), Xi’an, China, 26–28 July 2013; pp. 1680–1685. [Google Scholar]
- Preisach, F. Über die magnetische Nachwirkung. Z. Für Phys. 1935, 94, 277–302. [Google Scholar] [CrossRef]
- Everett, D.H.; Whitton, W.I. A general approach to hysteresis. Trans. Faraday Soc. 1952, 48, 749–757. [Google Scholar] [CrossRef]
- Mayergoyz, I. Mathematical models of hysteresis. IEEE Trans. Magn. 1986, 22, 603–608. [Google Scholar] [CrossRef]
- Mayergoyz, I.D. The Classical Preisach Model of Hysteresis. In Mathematical Models of Hysteresis; Mayergoyz, I.D., Ed.; Springer New York: New York, NY, USA, 1991; pp. 1–63. [Google Scholar]
- Ge, P.; Jouaneh, M. Modeling hysteresis in piezoceramic actuators. Precis. Eng. 1995, 17, 211–221. [Google Scholar] [CrossRef]
- Song, D.; Li, C.J. Modeling of piezo actuator’s nonlinear and frequency dependent dynamics. Mechatronics 1999, 9, 391–410. [Google Scholar] [CrossRef]
- Lv, Y.; Wei, Y. Study on open-loop precision positioning control of a micropositioning platform using a piezoelectric actuator. In Proceedings of the Fifth World Congress on Intelligent Control and Automation (IEEE Cat. No.04EX788), Hangzhou, China, 15–19 June 2004; Volume 1252. pp. 1255–1259. [Google Scholar]
- Zhou, X.; Yang, S.; Qi, G.; Hu, X. Tracking control of piezoceramic actuators by using preisach model. In Proceedings of the ICMIT 2005: Control Systems and Robotics, Chongqing, China, 29 September 2006; p. 604248. [Google Scholar]
- Nguyen, P.-B.; Choi, S.-B.; Song, B.-K. A new approach to hysteresis modelling for a piezoelectric actuator using Preisach model and recursive method with an application to open-loop position tracking control. Sens. Actuators A Phys. 2018, 270, 136–152. [Google Scholar] [CrossRef]
- Dang, X.; Tan, Y. Neural networks dynamic hysteresis model for piezoceramic actuator based on hysteresis operator of first-order differential equation. Phys. B Condens. Matter 2005, 365, 173–184. [Google Scholar] [CrossRef]
- Xiao, S.; Li, Y. Modeling and High Dynamic Compensating the Rate-Dependent Hysteresis of Piezoelectric Actuators via a Novel Modified Inverse Preisach Model. IEEE Trans. Control. Syst. Technol. 2013, 21, 1549–1557. [Google Scholar] [CrossRef]
- Fang, C.; Guo, J.; Xu, X.; Jiang, Z.; Wang, T. Compensating controller for hysteresis nonlinerity of piezoelectric ceramics. Opt. Precis. Eng. 2016, 24, 2217–2223. [Google Scholar] [CrossRef]
- Hassani, V.; Tjahjowidodo, T. A hysteresis model for a stacked-type piezoelectric actuator. Mech. Adv. Mater. Struct. 2017, 24, 73–87. [Google Scholar] [CrossRef]
- Fan, Y.; Tan, U.-X. A Feedforward Controller With Neural-Network Based Rate-Dependent Model For Piezoelectric-Driven Mechanism. In Proceedings of the 2016 Ieee International Conference on Robotics and Biomimetics (ROBIO), Qingdao, China, 3–7 December 2016; pp. 1558–1563. [Google Scholar]
- Al Janaideh, M.; Tan, X.; IEEE. Adaptive Estimation of Threshold Parameters for a Prandtl-Ishlinskii Hysteresis Operator. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019; pp. 3770–3775. [Google Scholar]
- Zuo, S.; Wang, H.; Zhou, D.; Gao, J. Solution of Parameters for PI Inverse Model Based on Geometric Method. Electron. Opt. Control. 2019, 26, 47–50, 60. [Google Scholar]
- Janaideh, M.A.; Xu, R.; Tan, X. Adaptive Estimation of Play Radii for a Prandtl-Ishlinskii Hysteresis Operator. IEEE Trans. Control. Syst. Technol. 2021, 29, 2687–2695. [Google Scholar] [CrossRef]
- Krasnosel’skiǐ, M.A.; Pokrovskiǐ, A.V. Front Matter. In Systems with Hysteresis; Krasnosel’skiǐ, M.A., Pokrovskiǐ, A.V., Eds.; Springer: Berlin/Heidelberg, Germany, 1989; pp. I–XVIII. [Google Scholar]
- Kuhnen, K. Modeling, Identification and Compensation of Complex Hysteretic Nonlinearities: A Modified Prandtl-Ishlinskii Approach. Eur. J. Control. 2003, 9, 407–418. [Google Scholar] [CrossRef]
- Janaideh, M.A.; Rakheja, S.; Su, C.Y. Characterization of Rate Dependent Hysteresis of Piezoceramic Actuators. In Proceedings of the 2007 International Conference on Mechatronics and Automation, Harbin, China, 5–8 August 2007; pp. 550–555. [Google Scholar]
- Chen, X.; Hisayama, T. Adaptive Sliding-Mode Position Control for Piezo-Actuated Stage. IEEE Trans. Ind. Electron. 2008, 55, 3927–3934. [Google Scholar] [CrossRef]
- Janaideh, M.A.; Su, C.Y.; Rakehja, S. Modeling hysteresis of smart actuators. In Proceedings of the 2008 5th International Symposium on Mechatronics and Its Applications, Amman, Jordan, 27–29 May 2008; pp. 1–4. [Google Scholar]
- Jiang, H.; Ji, H.L.; Qiu, J.H.; Chen, Y.S. A Modified Prandtl-Ishlinskii Model for Modeling Asymmetric Hysteresis of Piezoelectric Actuators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2010, 57, 1200–1210. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Farhan, O.; Rakheja, S.; Su, C.-Y.; Janaideh, M. Compensation of play operator-based Prandtl-Ishlinskii hysteresis model using a stop operator with application to piezoelectric actuators. Int. J. Adv. Mechatron. Syst. 2012, 4, 25–31. [Google Scholar] [CrossRef]
- Nie, Z.; Fu, C.; Liu, R.; Guo, D.; Ma, Y. Asymmetric Prandtl–Ishlinskii Hysteresis Model for Giant Magnetostrictive Actuator. J. Adv. Comput. Intell. Intell. Inform. 2016, 20, 223–230. [Google Scholar] [CrossRef]
- Yu, Z.; Wu, Y.; Fang, Z.; Sun, H. Modeling and compensation of hysteresis in piezoelectric actuators. Heliyon 2020, 6, e03999. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Shan, J.; Gabbert, U. A Direct Inverse Model for Hysteresis Compensation. IEEE Trans. Ind. Electron. 2021, 68, 4173–4181. [Google Scholar] [CrossRef]
- Ang, W.T.; Garmon, F.A.; Pradeep, K. Khosla Modeling on Rate-Dependent Hysteresis Nonlinear Characteristics ofPiezoelectric Stack Actuators. Piezoelectrics Acoustooptics 2022, 44, 907–912. [Google Scholar] [CrossRef]
- Ang, W.T.; Khosla, P.K.; Riviere, C.N. Feedforward Controller With Inverse Rate-Dependent Model for Piezoelectric Actuators in Trajectory-Tracking Applications. IEEE/ASME Trans. Mechatron. 2007, 12, 134–142. [Google Scholar] [CrossRef]
- Yang, M.-J.; Li, C.-X.; Gu, G.-Y.; Zhu, L.-M. Modeling and compensating the dynamic hysteresis of piezoelectric actuators via a modified rate-dependent Prandtl–Ishlinskii model. Smart Mater. Struct. 2015, 24, 125006. [Google Scholar] [CrossRef]
- Tao, Y.-D.; Li, H.-X.; Zhu, L.-M. Rate-dependent hysteresis modeling and compensation of piezoelectric actuators using Gaussian process. Sens. Actuators A Phys. 2019, 295, 357–365. [Google Scholar] [CrossRef]
- Goldfarb, M.; Celanovic, N. Modeling piezoelectric stack actuators for control of micromanipulation. IEEE Control. Syst. Mag. 1997, 17, 69–79. [Google Scholar] [CrossRef]
- Goldfarb, M.; Celanovic, N. A lumped parameter electromechanical model for describing the nonlinear behavior of piezoelectric actuators. J. Dyn. Syst. Meas. Control. Trans. Asme 1997, 119, 478–485. [Google Scholar] [CrossRef]
- Yeh, T.-J.; Lu, S.-W.; Wu, T.-Y. Modeling and Identification of Hysteresis in Piezoelectric Actuators. J. Dyn. Syst. Meas. Control 2005, 128, 189–196. [Google Scholar] [CrossRef]
- Liu, Y.; Shan, J.; Gabbert, U.; Qi, N. Hysteresis and creep modeling and compensation for a piezoelectric actuator using a fractional-order Maxwell resistive capacitor approach. Smart Mater. Struct. 2013, 22, 115020. [Google Scholar] [CrossRef]
- Liu, Y.; Shan, J.; Gabbert, U. Feedback/feedforward control of hysteresis-compensated piezoelectric actuators for high-speed scanning applications. Smart Mater. Struct. 2015, 24, 015012. [Google Scholar] [CrossRef]
- Liu, Y.; Du, D.; Qi, N.; Zhao, J. A Distributed Parameter Maxwell-Slip Model for the Hysteresis in Piezoelectric Actuators. IEEE Trans. Ind. Electron. 2019, 66, 7150–7158. [Google Scholar] [CrossRef]
- Joel, S.; Edward, K. Modeling of Piezoceramic Actuators for Control. In Piezoelectric Actuators; Hu, H., Jianping, L., Eds.; IntechOpen: Rijeka, Balkans, 2021; p. Ch. 5. [Google Scholar]
- Georgiou, H.M.S.; Mrad, R.B. Electromechanical Modeling of Piezoceramic Actuators for Dynamic Loading Applications. J. Dyn. Syst. Meas. Control. 2005, 128, 558–567. [Google Scholar] [CrossRef]
- Dong, W.J.; Sun, B.Y. Observer-based piezoelectric self-sensing actuator. In Proceedings of the International Conference on Sensor Technology (ISTC 2001), Proceedings, Wuhan, China, 10–12 October 2001; pp. 472–475. [Google Scholar]
- Choi, G.S.; Lim, Y.A.; Choi, G.H. Tracking position control of piezoelectric actuators for periodic reference inputs. MECHATRONICS 2002, 12, 669–684. [Google Scholar] [CrossRef]
- Dong, W.; Sun, B.; Cui, Y.; Yang, Z. Study on observer based piezoelectric self-sensing actuator. Chin. J. Mech. Eng. 2002, 38, 80–83. [Google Scholar] [CrossRef]
- Miri, N.; Mohammadzaheri, M.; Chen, L. A comparative study of different physics-based approaches to modelling of piezoelectric actuators. In Proceedings of the 2013 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Wollongong, NSW, Australia, 9–12 July 2013; pp. 1211–1216. [Google Scholar]
- Xie, S.; Ni, C.; Duan, H.; Liu, Y.; Qi, N.; IEEE. Hybrid Model Based on the Maxwell-Slip Model and a Support Vector Machine for Hysteresis in Piezoelectric Actuators. In Proceedings of the 2020 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Boston, MA, USA, 6–9 July 2020; pp. 36–41. [Google Scholar]
- Duhem, P. Die dauernden Aenderungen und die Thermodynamik. I. Z. Für Phys. Chem. 1897, 22U, 545–589. [Google Scholar] [CrossRef]
- Coleman, B.D.; Hodgdon, M.L. A Constitutive Relation For Rate-Independent Hysteresis In Ferromagnetically Soft Materials. Int. J. Eng. Sci. 1986, 24, 897–919. [Google Scholar] [CrossRef]
- Oh, J.; Bernstein, D.S. Semilinear Duhem model for rate-independent and rate-dependent hysteresis. IEEE Trans. Autom. Control. 2005, 50, 631–645. [Google Scholar] [CrossRef]
- Du, J.; Feng, Y.; Su, C.Y.; Hu, Y.M. On the robust control of systems preceded by Coleman-Hodgdon hysteresis. In Proceedings of the 2009 IEEE International Conference on Control and Automation, Christchurch, New Zealand, 9–11 December 2009; pp. 685–689. [Google Scholar]
- Ying, F.; Rabbath, C.A.; Chai, T.; Su, C.Y. Robust adaptive control of systems with hysteretic nonlinearities: A Duhem hysteresis modelling approach. In Proceedings of the AFRICON 2009, Nairobi, Kenya, 23–25 September 2009; pp. 1–6. [Google Scholar]
- Chen, H.; Tan, Y.; Zhou, X.; Dong, R.; Zhang, Y. Identification of Dynamic Hysteresis Based on Duhem Model. In Proceedings of the 2011 Fourth International Conference on Intelligent Computation Technology and Automation, Shenzhen, China, 28–29 March 2011; pp. 810–814. [Google Scholar]
- Chen, H.; Tan, Y.; Zhou, X.; Zhang, Y.; Dong, R. Identification and control of dynamic modeling for piezoceramic actuator. Opt. Precis. Eng. 2012, 20, 88–95. [Google Scholar] [CrossRef]
- He, Y. Research on Improved Duhem Hysteresis Modeling and Control of Piezoelectric Actuator. Master’s Thesis, Taiyuan University of Science and Technology, Taiyuan, China, 2021. [Google Scholar]
- He, Y.; Wang, Z.; He, Y.; Liu, H. Improved Duhem Hysteresis Modeling of Piezoelectric Actuators. Piezoelectrics Acoustooptics 2021, 43, 431–434. [Google Scholar]
- Yang, L.; Zhong, R.; Li, D.; Li, Z. A fractional-order Duhem model of rate-dependent hysteresis for piezoelectric actuators. Meas. Control. 2022, 55, 974–982. [Google Scholar] [CrossRef]
- Xu, Q.; Li, Y.; IEEE. Modeling and Control of Rate-Dependent Hysteresis for a Piezo-Driven Micropositioning Stage. In Proceedings of the 2011 IEEE International Conference On Robotics And Automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 1670–1675. [Google Scholar]
- Irakoze, R.Z. Modeling and Identification of Piezoelectric Actuators Using Evolutionary Algorithms. Ph.D. Thesis, Universite de Moncton (Canada), New Brunswick, Canada, 2015. [Google Scholar]
- Tayouri, S.; Izadi, I.; Ghaisari, J.; IEEE. Modeling and Parameter Identification of Piezoelectric Actuator in Micropositioning Systems. In Proceedings of the 2019 27th Iranian Conference On Electrical Engineering (ICEE 2019), Yazd, Iran, 30 April 2019–2 May 2019; pp. 1193–1198. [Google Scholar]
- Low, T.S.; Guo, W. Modeling of a three-layer piezoelectric bimorph beam with hysteresis. J. Microelectromechanical Syst. 1995, 4, 230–237. [Google Scholar] [CrossRef]
- Ismail, M.; Ikhouane, F.; Rodellar, J. The Hysteresis Bouc-Wen Model, a Survey. Arch. Comput. Methods Eng. 2009, 16, 161–188. [Google Scholar] [CrossRef]
- Rakotondrabe, M. Bouc–Wen Modeling and Inverse Multiplicative Structure to Compensate Hysteresis Nonlinearity in Piezoelectric Actuators. IEEE Trans. Autom. Sci. Eng. 2011, 8, 428–431. [Google Scholar] [CrossRef]
- Zhu, W.; Wang, D.-h. Non-symmetrical Bouc–Wen model for piezoelectric ceramic actuators. Sens. Actuators A Phys. 2012, 181, 51–60. [Google Scholar] [CrossRef]
- Zhu, W.; Rui, X.-T. Hysteresis modeling and displacement control of piezoelectric actuators with the frequency-dependent behavior using a generalized Bouc–Wen model. Precis. Eng. 2016, 43, 299–307. [Google Scholar] [CrossRef]
- Kedra, R.; Rucka, M. Modelling of Mechanical Behaviour of High-Frequency Piezoelectric Actuators Using Bouc-Wen Model. Metrol. Meas. Syst. 2017, 24, 413–424. [Google Scholar] [CrossRef]
- Liu, L.; Yun, H.; Li, Q.; Ma, X.; Chen, S.L.; Shen, J. Fractional Order Based Modeling and Identification of Coupled Creep and Hysteresis Effects in Piezoelectric Actuators. IEEE/ASME Trans. Mechatron. 2020, 25, 1036–1044. [Google Scholar] [CrossRef]
- Cai, J.; Dong, W.; Nagamune, R. A survey of Bouc-Wen hysteretic models applied to piezo-actuated mechanical systems: Modeling, identification, and control. J. Intell. Mater. Syst. Struct. 2023, 34, 1045389X231157361. [Google Scholar] [CrossRef]
- Lu, J.; Wang, J.; Bo, Y.; Zhang, X. Hysteresis Modeling and Compensation for a Fast Piezo-Driven Scanner in the UAV Image Stabilization System. Drones 2023, 7, 392. [Google Scholar] [CrossRef]
- Huang, Y.C.; Lin, D.Y. Ultra-fine tracking control on piezoelectric actuated motion stage using piezoelectric hysteretic model. Asian J. Control. 2004, 6, 208–216. [Google Scholar] [CrossRef]
- Gwo-Ruey, Y.; Chun-Sheng, Y.; Rong-Jun, H.; IEEE. Self-tuning fuzzy control of a piezoelectric actuator system. In Proceedings of the 2006 IEEE International Conference on Systems, Man, and Cybernetics, VOLS 1-6, Proceedings, Taipei, Taiwan, 8–11 October 2006; pp. 1108–1113. [Google Scholar]
- Ha, J.-L.; Kung, Y.-S.; Fung, R.-F.; Hsien, S.-C. A comparison of fitness functions for the identification of a piezoelectric hysteretic actuator based on the real-coded genetic algorithm. Sens. Actuators A-Phys. 2006, 132, 643–650. [Google Scholar] [CrossRef]
- Ha, J.L.; Fung, R.F.; Han, C.F.; Chang, J.R. Effects of frictional models on the dynamic response of the impact drive mechanism. J. Vib. Acoust. -Trans. Asme 2006, 128, 88–96. [Google Scholar] [CrossRef]
- Saghafi, M.; Jalili, N.; Meghdari, A. Nonlinear Modeling of piezoelectric layered beams. In Proceedings of the Active And Passive Smart Structuresa Integrated Systems, San Diego, CA, USA, 27 April 2007. [Google Scholar]
- Yuan, H.; Li, D.; Sun, H. Hysteretic Property of Rare Earth Giant Magnetostrictive Actuator. J. Rare Earths 2007, 25, 236–239. [Google Scholar]
- Guo, Y.; Sun, G.; Wang, Y.; Mao, J. Modeling and Control of Rate-Dependent Hysteresis for PEA with MPI Model-Based Hammerstein System. In Proceedings of the 2012 International Conference on Control Engineering and Communication Technology, Shenyang, China, 7–9 December 2012; pp. 523–526. [Google Scholar]
- Qi, C.K.; Gao, F.; Zhao, X.C.; Yue, Y.; Dong, Y. Additive Cascaded Model Identification of Linear and Nonlinear Dynamics of Piezoelectric Actuator. In Proceedings of the 2015 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015; pp. 2112–2117. [Google Scholar]
- Jian, Y.; Huang, D.; Liu, J.; Min, D. High-Precision Tracking of Piezoelectric Actuator Using Iterative Learning Control and Direct Inverse Compensation of Hysteresis. IEEE Trans. Ind. Electron. 2019, 66, 368–377. [Google Scholar] [CrossRef]
- Li, L.; Zhang, S.-X.; Wen, S.-J. Coupling Modeling and Adaptive Control for Piezoelectric-Actuated Positioning Stage. Model. Simul. Eng. 2022, 2022, 2534439. [Google Scholar] [CrossRef]
- Li, W.; Liu, K.; Yang, Z.; Wang, W. Dynamic modeling and disturbance rejection compensation for hysteresis nonlinearity of high voltage piezoelectric stack actuators. Smart Mater. Struct. 2023, 32, 025007. [Google Scholar] [CrossRef]
- Yang, L.; Zhao, Z.; Li, D. Fractional order neural sliding mode control based on the FO-Hammerstein model of piezoelectric actuator. ISA Trans. 2023, 142, 515–526. [Google Scholar] [CrossRef] [PubMed]
- Peng, J.; Chen, X. A Survey of Modeling and Control of Piezoelectric Actuators. Mod. Mech. Eng. 2013, 3, 1–20. [Google Scholar] [CrossRef]
- Kamlah, M. Ferroelectric and ferroelastic piezoceramics—modeling of electromechanical hysteresis phenomena. Contin. Mech. Thermodyn. 2001, 13, 219–268. [Google Scholar] [CrossRef]
- Ewing, J.A.; Jenkin, H.C.F. VII. On the production of transient electric currents in iron and steel conductors by twisting them when magnetised or by magnetising them when twisted. Proc. R. Soc. Lond. 1997, 33, 21–23. [Google Scholar] [CrossRef]
- Zhe, Z. Research on hysteresis characteristics of piezoelectric ceramic stage based on neural network. Master’s Thesis, Kunming University of Science and Technology, Kunming, China, 2021. [Google Scholar]
- Hassani, V.; Tjahjowidodo, T.; Do, T.N. A survey on hysteresis modeling, identification and control. Mech. Syst. Signal Process. 2014, 49, 209–233. [Google Scholar] [CrossRef]
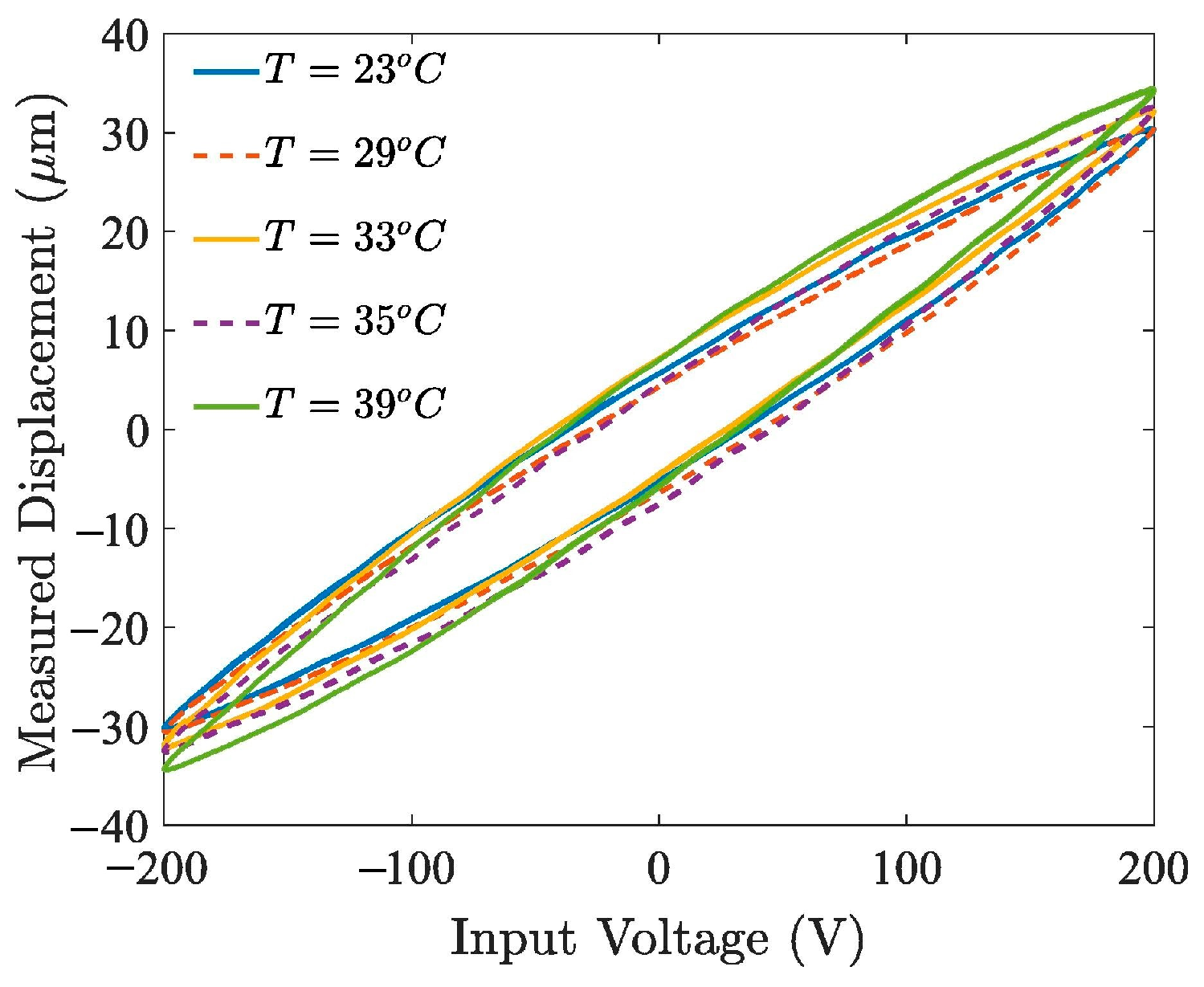
- Al Janaideh, M.; Al Saaideh, M.; Rakotondrabe, M. On hysteresis modeling of a piezoelectric precise positioning system under variable temperature. Mech. Syst. Signal Process. 2020, 145, 106880. [Google Scholar] [CrossRef]
- Liu, Y.; Qi, N.; Li, Z. Modeling and Identification of Temperature-Dependent Hysteresis in Piezoelectric Materials Considering Parameter Sensitivity. IEEE Access 2020, 8, 40901–40908. [Google Scholar] [CrossRef]
- Dong, Y.; Hu, H.; Wang, H. Identification and experimental assessment of two-input Preisach model for coupling hysteresis in piezoelectric stack actuators. Sens. Actuators A Phys. 2014, 220, 92–100. [Google Scholar] [CrossRef]
- Barber, P.; Balasubramanian, S.; Anguchamy, Y.; Gong, S.; Wibowo, A.; Gao, H.; Ploehn, H.J.; Zur Loye, H.-C. Polymer Composite and Nanocomposite Dielectric Materials for Pulse Power Energy Storage. Materials 2009, 2, 1697–1733. [Google Scholar] [CrossRef]
- Arockiarajan, A.; Delibas, B.; Menzel, A.; Seemann, W. Studies on rate-dependent switching effects of piezoelectric materials using a finite element model. Comput. Mater. Sci. 2006, 37, 306–317. [Google Scholar] [CrossRef]
- Kanchan, M.; Santhya, M.; Bhat, R.; Naik, N. Application of Modeling and Control Approaches of Piezoelectric Actuators: A Review. Technologies 2023, 11, 155. [Google Scholar] [CrossRef]
- Damjanovic, D. Chapter 4—Hysteresis in Piezoelectric and Ferroelectric Materials. In The Science of Hysteresis; Bertotti, G., Mayergoyz, I.D., Eds.; Academic Press: Oxford, UK, 2006; pp. 337–465. [Google Scholar]
- Hwang, S.C.; Waser, R. Study of electrical and mechanical contribution to switching in ferroelectric/ferroelastic polycrystals. Acta Mater. 2000, 48, 3271–3282. [Google Scholar] [CrossRef]
- Kaltenbacher, M. The Finite Element (FE) Method. In Numerical Simulation of Mechatronic Sensors and Actuators; Springer: Berlin/Heidelberg, Germany, 2007; pp. 7–49. [Google Scholar]
- Kim, S.-J.; Jiang, Q. A finite element model for rate-dependent behavior of ferroelectric ceramics. Int. J. Solids Struct. 2002, 39, 1015–1030. [Google Scholar] [CrossRef]
- Jung, S.B.; Kim, S.W. Improvement of scanning accuracy of pzt piezoelectric actuators by feedforward model-reference control. Precis. Eng. -J. Am. Soc. Precis. Eng. 1994, 16, 49–55. [Google Scholar] [CrossRef]
- Ge, P.; Jouaneh, M. Tracking control of a piezoceramic actuator. IEEE Trans. Control. Syst. Technol. 1996, 4, 209–216. [Google Scholar] [CrossRef]
- Kwan, C.M.; Xu, R.; Lang, J.; Lin, C.; Stevenson, M.; Lin, Y.; Ren, Z.; Haynes, L. Intelligent control of piezoelectric actuators for precision manufacturing. In Proceedings of the Intelligent Systems in Design And Manufacturing II, Boston, MA, USA, 20 August 1999; pp. 2–11. [Google Scholar]
- Li, P.; Yan, F.; Ge, C.; Li, P.; Sui, Y.; Yang, H. Open-closed loop iterative learning control of piezoelectric actuators. Opt. Precis. Eng. 2014, 22, 414–419. [Google Scholar]
- Yuguo, C.U.I.; Weijie, D.; Baoyuan, S.U.N.; Zhixin, Y. Displacement Compounding Control of Piezoelectric Micro-Motion Worktable. Chin. J. Mech. Eng. 2006, 42, 156–161. [Google Scholar]
- Yun, S.; Ham, Y.-B.; Kim, C.-Y.; Park, J.-H. Hysteresis nonlinearity compensator for piezoelectric actuator. J. Electroceramics 2006, 17, 573–576. [Google Scholar] [CrossRef]
- Nguyen, P.-B.; Choi, S.-B. Compensator design for hysteresis of a stacked PZT actuator using a congruency-based hysteresis model. Smart Mater. Struct. 2012, 21, 015009. [Google Scholar] [CrossRef]
- Mayergoyz, I.D. CHAPTER 1—The Classical Preisach Model of Hysteresis. In Mathematical Models of Hysteresis and Their Applications; Mayergoyz, I.D., Ed.; Elsevier Science: New York, NY, USA, 2003; pp. 1–63. [Google Scholar]
- Gan, J.; Zhang, X. A review of nonlinear hysteresis modeling and control of piezoelectric actuators. AIP Adv. 2019, 9, 040702. [Google Scholar] [CrossRef]
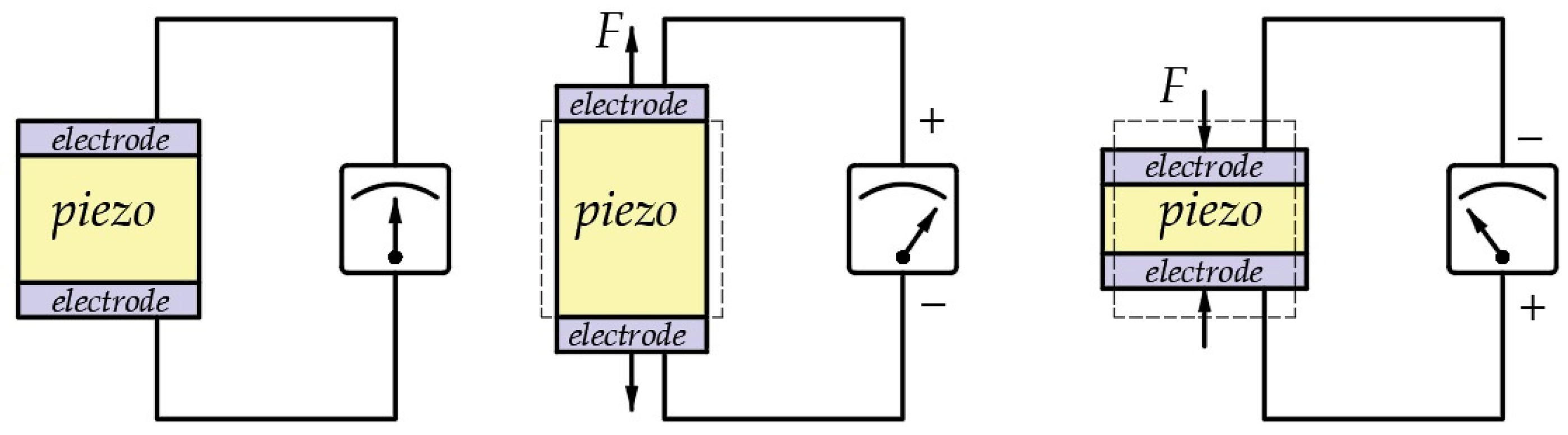
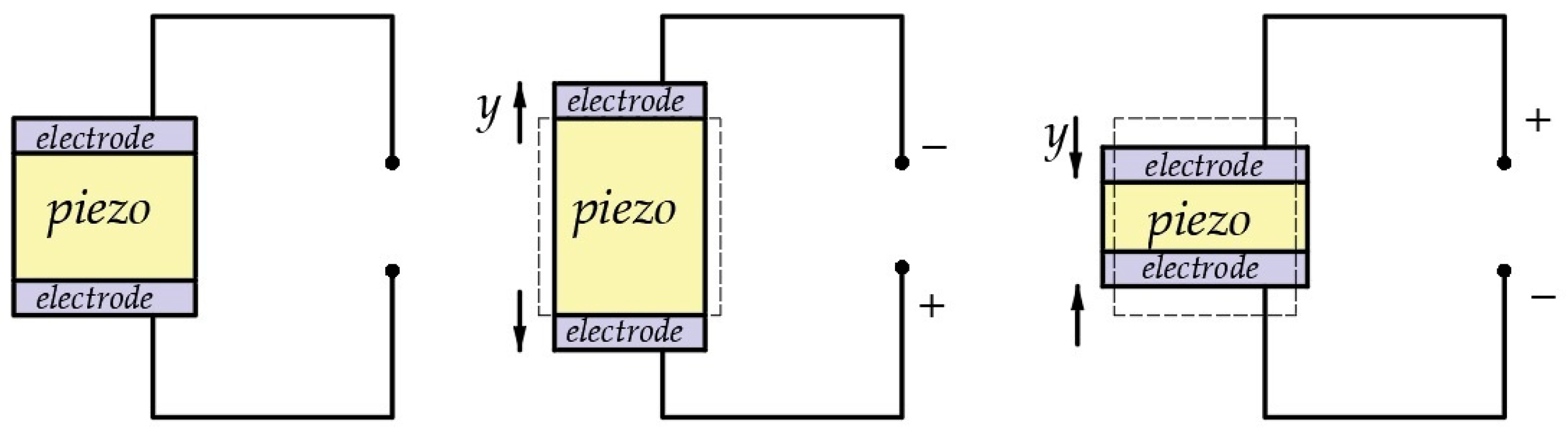















| Models | Operator-Based | Differential-Based | |||
|---|---|---|---|---|---|
| Preisach | PI | Maxwell | Duhem | Bouc–Wen | |
| Frequency range(Hz) | ≤32 [39] | ≤100 [61] | ≤100 [68] | ≤100 [87] | ≤120 k [91,96] |
| Inverse model acquisition method | Direct [60] | Direct [57] Indirect [52] | Direct [70] | Direct [84] | Direct [99] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, Y.; Li, D.; Wang, D. Review on the Nonlinear Modeling of Hysteresis in Piezoelectric Ceramic Actuators. Actuators 2023, 12, 442. https://doi.org/10.3390/act12120442
Dai Y, Li D, Wang D. Review on the Nonlinear Modeling of Hysteresis in Piezoelectric Ceramic Actuators. Actuators. 2023; 12(12):442. https://doi.org/10.3390/act12120442
Chicago/Turabian StyleDai, Yingli, Dequan Li, and Dong Wang. 2023. "Review on the Nonlinear Modeling of Hysteresis in Piezoelectric Ceramic Actuators" Actuators 12, no. 12: 442. https://doi.org/10.3390/act12120442




