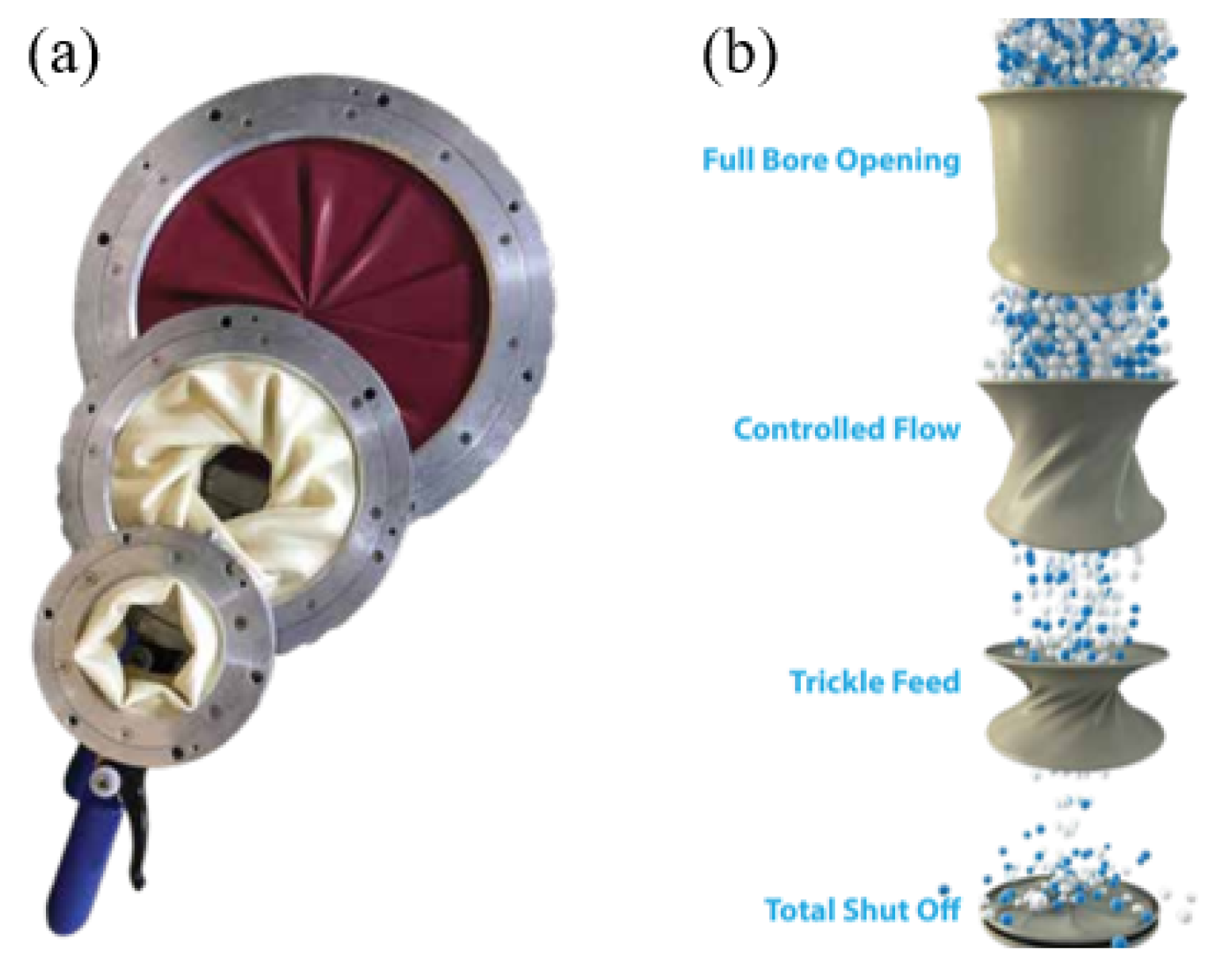
A Novel Radially Closable Tubular Origami Structure (RC-ori) for Valves
Abstract
:1. Introduction
- i
- The radial closability of the Kresling structure is first studied targeting for valve applications.
- ii
- A new crease pattern is created without twisting motion for the valve application.
- iii
- A simplified kinematic modeling method is proposed for the non-rigid foldable cylindrical origami.
2. Radial Closability of the Kresling Pattern
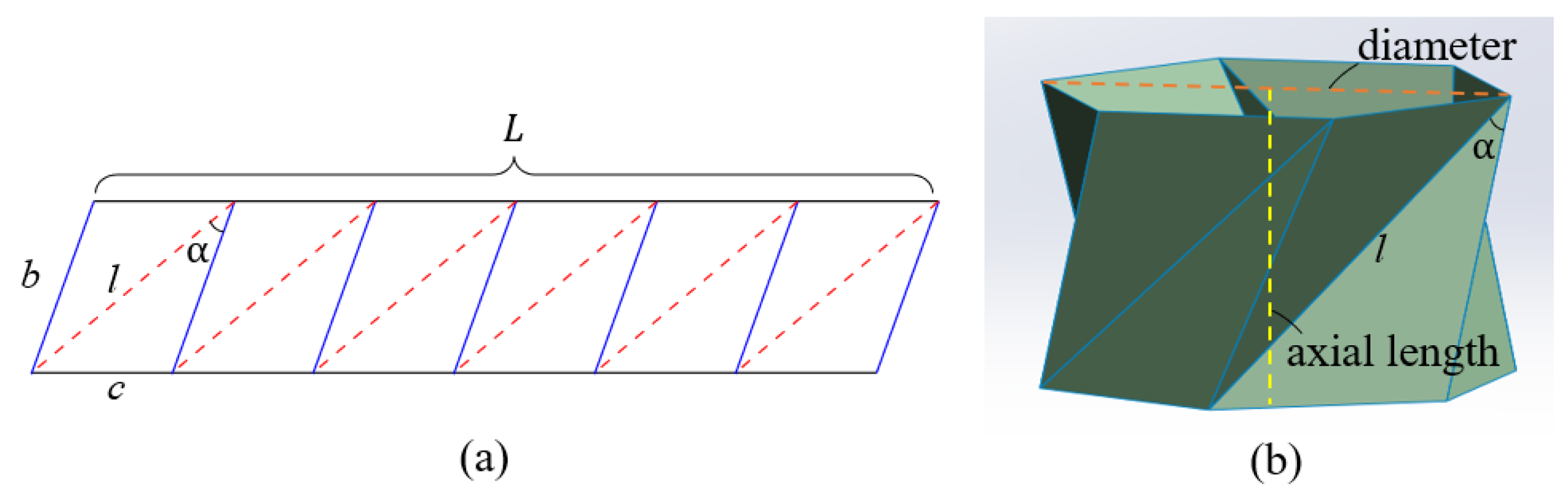
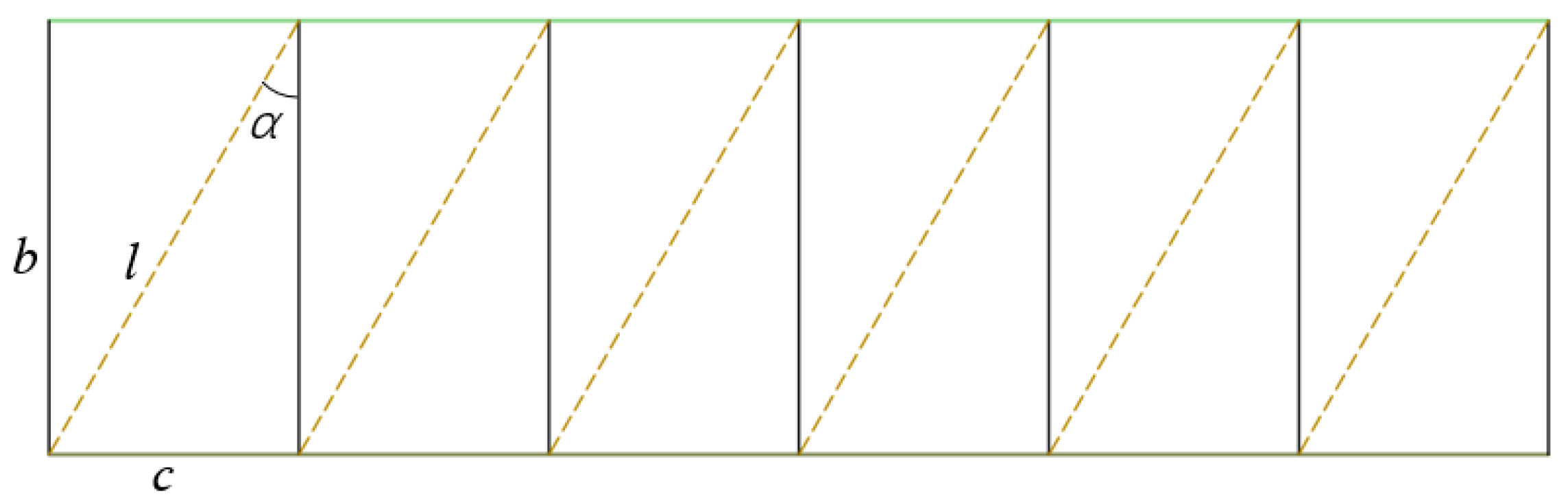
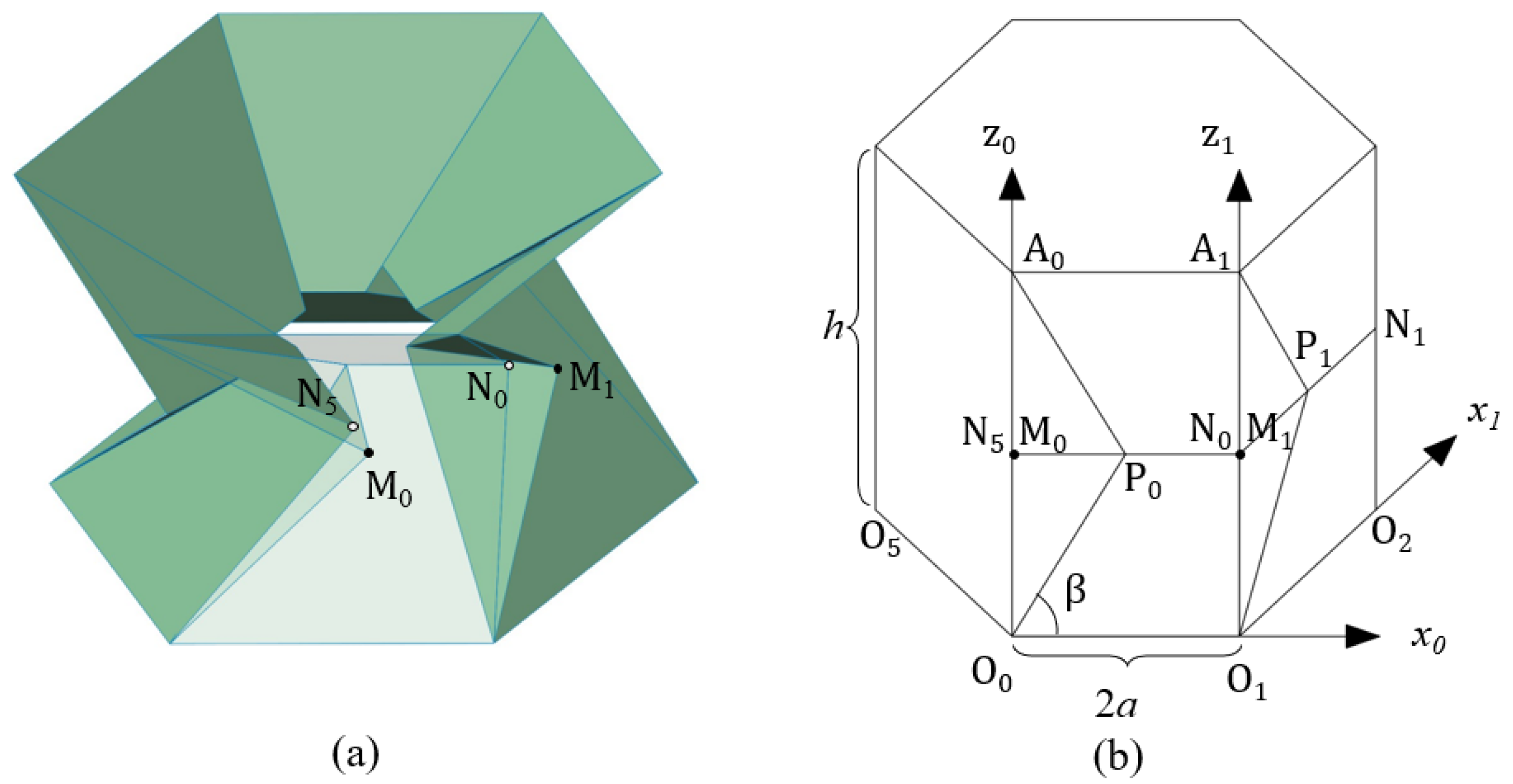
2.1. Geometric Definition of the Kresling Pattern
- (1)
- The parallelograms are inclined and elongated;
- (2)
- The valley-folds are long diagonals;
- (3)
- The structure will create a two-dimensional diaphragm perpendicular to the axis of the cylinder when fully collapsed;
- (4)
- The axial length of the fully deployed diaphragm is less than the diameter of the cylinder (Figure 4b).
- (a)
- ;
- (b)
- ;
- (c)
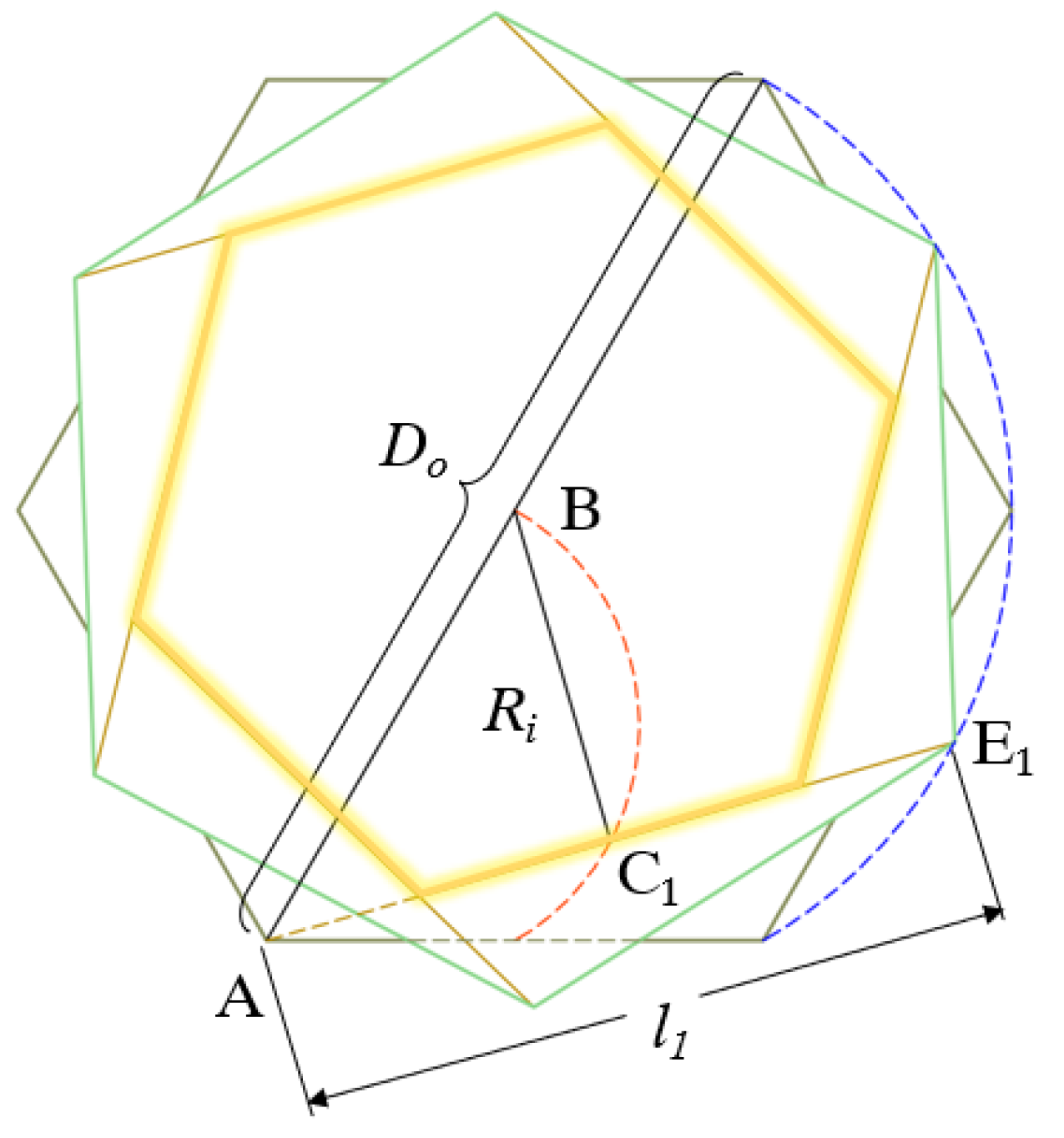
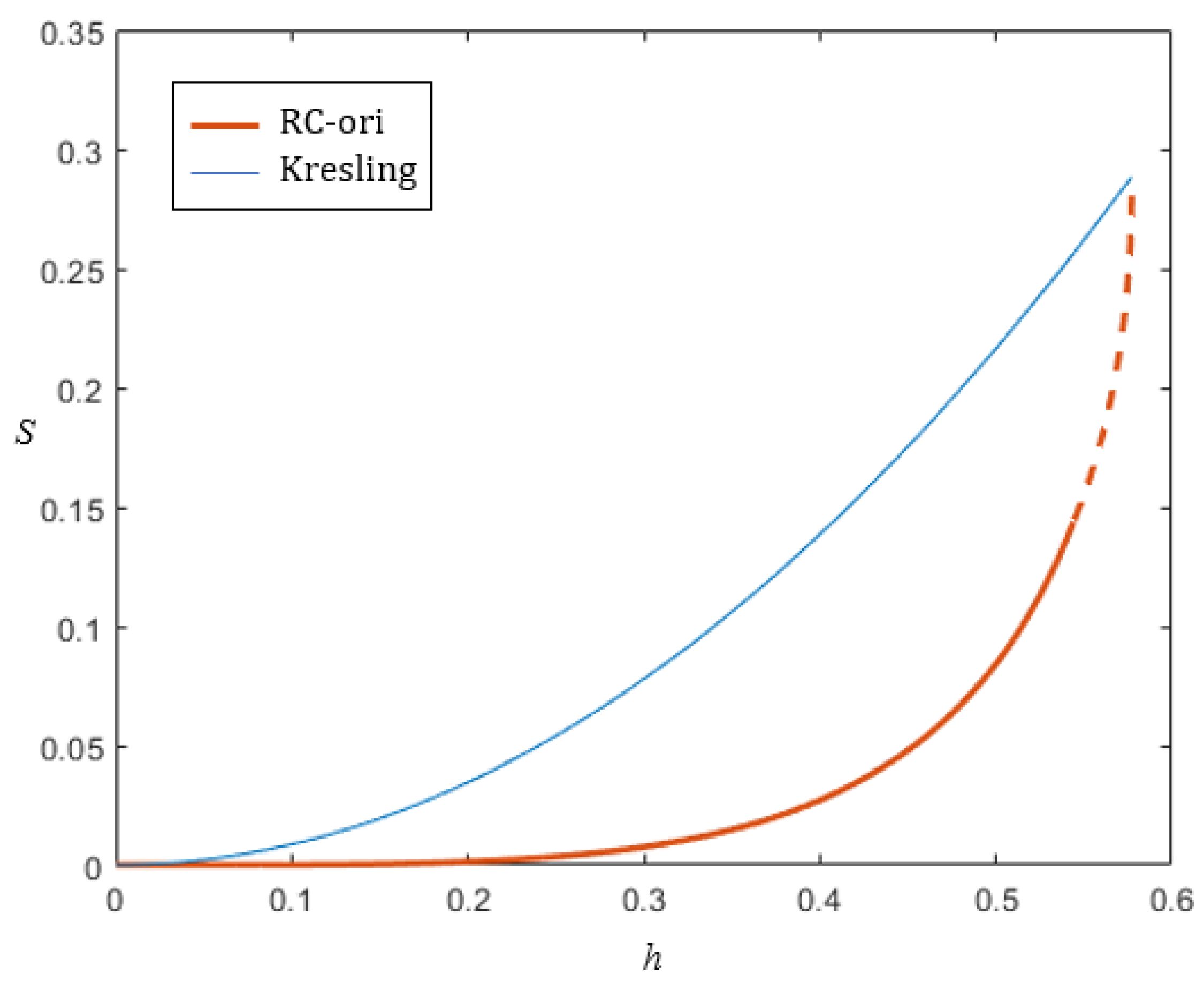
2.2. Radial Closability of the Kresling Pattern
3. New Radially Closable Structure(RC-ori)
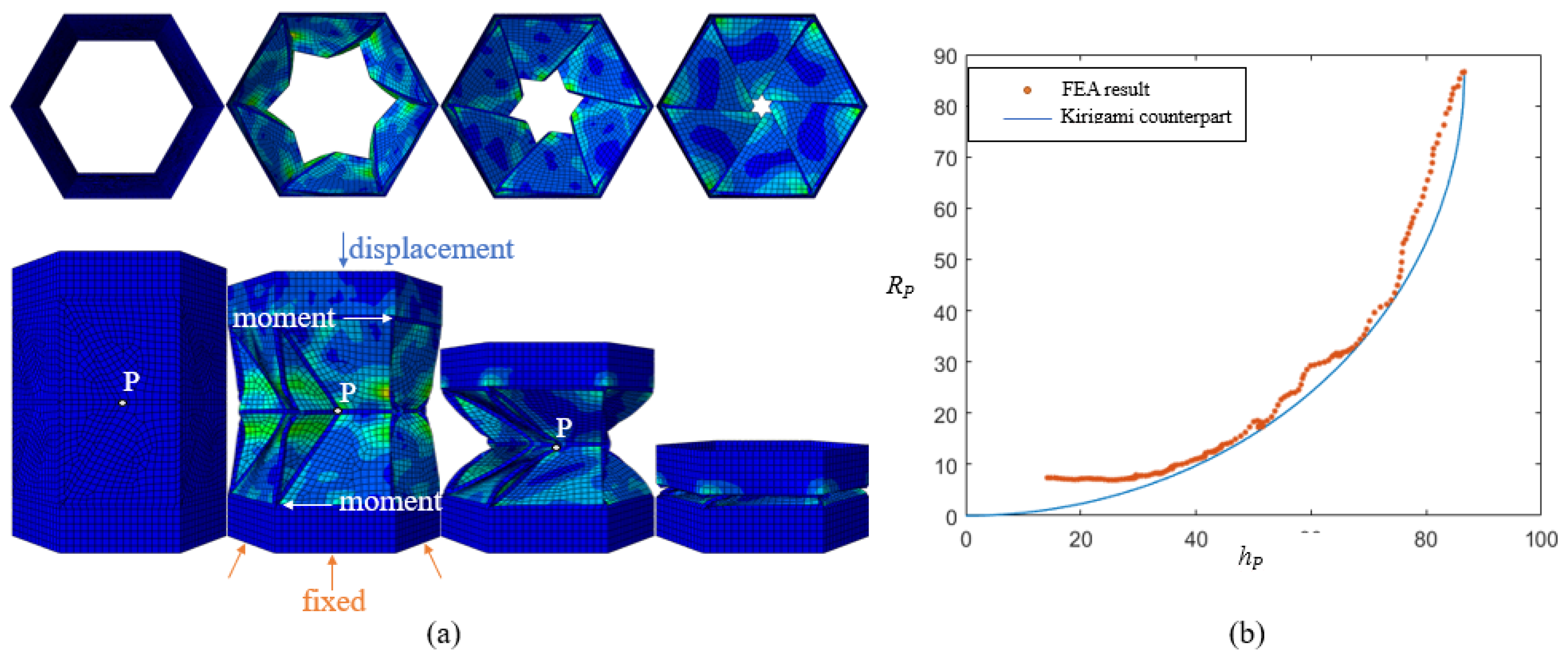
3.1. Non-Rigid Foldability of RC-ori
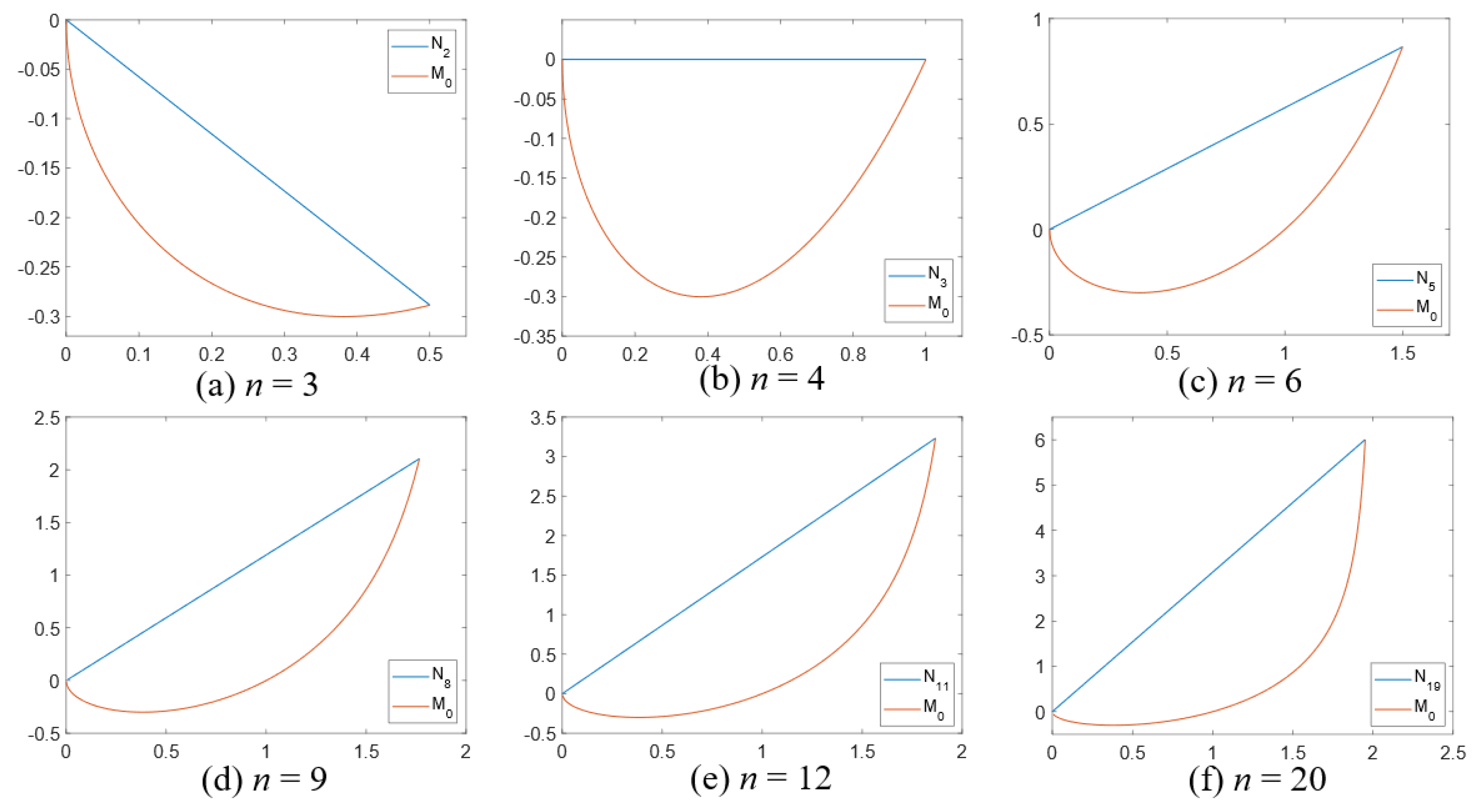
3.2. Kinematic Analysis of RC-ori
4. Conclusions
5. Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Teżyk, M.; Milanowski, B.; Ernst, A.; Lulek, J. Recent progress in continuous and semi-continuous processing of solid oral dosage forms: A review. Drug Dev. Ind. Pharm. 2016, 42, 1195–1214. [Google Scholar] [CrossRef] [PubMed]
- GEA Group. Continuous Processing—Solutions for Oral Solid Dosage Forms. 2020. Available online: https://www.gea.com/en/binaries/Pharmaceutical-Continuous-Processing-for-oral-solid-dosage-forms_tcm11-31710.pdf (accessed on 25 August 2022).
- Glatt GmbH. Modcos—Full Control in Continuous Operation. 2016. Available online: https://www.glatt.com/wp-content/uploads/2021/03/GLATT_BRO_PTPH_168_MODCOS_2016_03_EN.pdf (accessed on 25 August 2022).
- Engisch, W.E.; Muzzio, F.J. Feedrate deviations caused by hopper refill of loss-in-weight feeders. Powder Technol. 2015, 283, 389–400. [Google Scholar] [CrossRef]
- K-Tron International, Inc. Smart Refill Technologyin Loss-in-Weight Feeding. 2009. Available online: https://www.mmsonline.com/cdn/cms/uploadedFiles/Ktron-Smart_Refill.pdf (accessed on 25 August 2022).
- Powderprocess.net. Butterfly Valve for Bulk and Powder Process. Available online: https://www.powderprocess.net/Equipments%20html/Butterfly_valve.html (accessed on 25 August 2022).
- McMillan, G.; Vegas, H. 101 Tips for a Successful Automation Career; ISA: Research Triangle Park, NC, USA, 2013. [Google Scholar]
- Zirbel, S.A.; Lang, R.J.; Thomson, M.W.; Sigel, D.A.; Walkemeyer, P.E.; Trease, B.P.; Magleby, S.P.; Howell, L.L. Accommodating Thickness in Origami-Based Deployable Arrays1. J. Mech. Des. 2013, 135, 111005. [Google Scholar] [CrossRef]
- Schenk, M.; Viquerat, A.D.; Seffen, K.A.; Guest, S.D. Review of Inflatable Booms for Deployable Space Structures: Packing and Rigidization. J. Spacecr. Rocket. 2014, 51, 762–778. [Google Scholar] [CrossRef]
- Butler, J.; Morgan, J.; Pehrson, N.; Tolman, K.; Bateman, T.; Magleby, S.P.; Howell, L.L. Highly Compressible Origami Bellows for Harsh Environments. In Proceedings of the 40th Mechanisms and Robotics Conference, International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Charlotte, NC, USA, 21–24 August 2016;B; Volume 50169, p. V05BT07A001. [Google Scholar] [CrossRef]
- Butler, J.; Magleby, S.; Howell, L.; Mancini, S.; Parness, A. Highly Compressible Origami Bellows for Microgravity Drilling-Debris Containment. In Proceedings of the AIAA SPACE and Astronautics Forum and Exposition, Orlando, FL, USA, 12–14 September 2017; p. 5341. [Google Scholar] [CrossRef]
- Yao, S.; Bao, K.; Liu, X.; Georgakopoulos, S.V. Tunable UHF origami spring antenna with actuation system. In Proceedings of the 2017 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, San Francisco, CA, USA, 9–14 July 2017; pp. 325–326. [Google Scholar]
- Sargent, B.; Butler, J.; Seymour, K.; Bailey, D.; Jensen, B.; Magleby, S.; Howell, L. An Origami-Based Medical Support System to Mitigate Flexible Shaft Buckling. J. Mech. Robot. 2020, 12, 041005. [Google Scholar] [CrossRef]
- Lee, K.; Wang, Y.; Zheng, C. Twister hand: Underactuated robotic gripper inspired by origami twisted tower. IEEE Trans. Robot. 2020, 36, 488–500. [Google Scholar] [CrossRef]
- Qi, J.; Li, C.; Tie, Y.; Zheng, Y.; Duan, Y. Energy absorption characteristics of origami-inspired honeycomb sandwich structures under low-velocity impact loading. Mater. Des. 2021, 207, 109837. [Google Scholar] [CrossRef]
- Li, J.; Chen, Y.; Feng, X.; Feng, J.; Sareh, P. Computational modeling and energy absorption behavior of thin-walled tubes with the Kresling origami pattern. J. Int. Assoc. Shell Spat. Struct. 2021, 62, 71–81. [Google Scholar] [CrossRef]
- Zhai, Z.; Wang, Y.; Jiang, H. Origami-inspired, on-demand deployable and collapsible mechanical metamaterials with tunable stiffness. Proc. Natl. Acad. Sci. USA 2018, 115, 2032–2037. [Google Scholar] [CrossRef]
- Chung, J.; Song, M.; Chung, S.H.; Choi, W.; Lee, S.; Lin, Z.H.; Hong, J.; Lee, S. Triangulated Cylinder Origami-Based Piezoelectric/Triboelectric Hybrid Generator to Harvest Coupled Axial and Rotational Motion. Research 2021, 2021, 7248579. [Google Scholar] [CrossRef]
- Turner, N.; Goodwine, B.; Sen, M. A review of origami applications in mechanical engineering. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 230, 2345–2362. [Google Scholar] [CrossRef]
- Ma, J.; Zang, S.; Feng, H.; Chen, Y.; You, Z. Theoretical characterization of a non-rigid-foldable square-twist origami for property programmability. Int. J. Mech. Sci. 2021, 189, 105981. [Google Scholar] [CrossRef]
- Callens, S.J.; Zadpoor, A.A. From flat sheets to curved geometries: Origami and kirigami approaches. Mater. Today 2018, 21, 241–264. [Google Scholar] [CrossRef]
- Filipov, E.T.; Tachi, T.; Paulino, G.H. Origami tubes assembled into stiff, yet reconfigurable structures and metamaterials. Proc. Natl. Acad. Sci. USA 2015, 112, 12321–12326. [Google Scholar] [CrossRef] [PubMed]
- Miura, K.; Tachi, T. Synthesis of rigid-foldable cylindrical polyhedra. Symmetry Art Sci. 2010, 2010, 204–213. [Google Scholar]
- Kresling, B. Natural twist buckling in shells: From the hawkmoth’s bellows to the deployable Kresling-pattern and cylindrical Miura-ori. In Proceedings of the IASS-IACM 2008 Spanning Nano to Mega, Ithaca, NY, USA, 28–31 May 2008. [Google Scholar]
- Chen, Y.; Feng, H.; Ma, J.; Peng, R.; You, Z. Symmetric waterbomb origami. Proc. R. Soc. Math. Phys. Eng. Sci. 2016, 472, 20150846. [Google Scholar] [CrossRef]
- Morgan, J.; Magleby, S.P.; Howell, L.L. An approach to designing origami-adapted aerospace mechanisms. J. Mech. Des. 2016, 138, 052301. [Google Scholar] [CrossRef]
- Kresling, B. The fifth fold: Complex symmetries in Kresling-origami patterns. Symmetry Cult. Sci. 2020, 31, 403–416. [Google Scholar] [CrossRef]
- Guest, S.D.; Pellegrino, S. The Folding of Triangulated Cylinders, Part II: The Folding Process. J. Appl. Mech. 1994, 61, 778–783. [Google Scholar] [CrossRef]
- Jianguo, C.; Xiaowei, D.; Ya, Z.; Jian, F.; Yongming, T. Bistable Behavior of the Cylindrical Origami Structure With Kresling Pattern. J. Mech. Des. 2015, 137, 061406. [Google Scholar] [CrossRef]
- Kidambi, N.; Wang, K.W. Dynamics of Kresling origami deployment. Phys. Rev. E 2020, 101, 063003. [Google Scholar] [CrossRef] [PubMed]
- Masana, R.; Daqaq, M.F. Equilibria and bifurcations of a foldable paper-based spring inspired by Kresling-pattern origami. Phys. Rev. E 2019, 100, 063001. [Google Scholar] [CrossRef] [PubMed]
- Nayakanti, N.; Tawfick, S.H.; Hart, A.J. Twist-coupled Kirigami cells and mechanisms. Extrem. Mech. Lett. 2018, 21, 17–24. [Google Scholar] [CrossRef]
- Pagano, A.; Yan, T.; Chien, B.; Wissa, A.; Tawfick, S. A crawling robot driven by multi-stable origami. Smart Mater. Struct. 2017, 26, 094007. [Google Scholar] [CrossRef]
- Jianguo, C.; Yangqing, L.; Ruijun, M.; Jian, F.; Ya, Z. Nonrigidly Foldability Analysis of Kresling Cylindrical Origami. J. Mech. Robot. 2017, 9, 041018. [Google Scholar] [CrossRef]
- Li, Z.; Kidambi, N.; Wang, L.; Wang, K.W. Uncovering rotational multifunctionalities of coupled Kresling modular structures. Extrem. Mech. Lett. 2020, 39, 100795. [Google Scholar] [CrossRef]
- Chen, Y.; Fan, L.; Bai, Y.; Feng, J.; Sareh, P. Assigning mountain-valley fold lines of flat-foldable origami patterns based on graph theory and mixed-integer linear programming. Comput. Struct. 2020, 239, 106328. [Google Scholar] [CrossRef]
- Bhovad, P.; Li, S. Using Multi-Stable Origami Mechanism for Peristaltic Gait Generation: A Case Study. In Proceedings of the 42nd Mechanisms and Robotics Conference, Quebec City, QC, Canada, 26–29 August 2018; p. V05BT07A061. [Google Scholar] [CrossRef]
- He, Z.; Guest, S.D. On rigid origami I: Piecewise-planar paper with straight-line creases. Proc. R. Soc. A 2019, 475, 20190215. [Google Scholar] [CrossRef] [Green Version]
- Kresling, B. Folded Tubes as Compared to Kikko (“Tortoise-Shell”) Bamboo. In Origami3; Thomas, H., Ed.; Google Books: Mountain View, CA, USA, 2002; pp. 197–207. [Google Scholar]
- Arora, V.; Kumar, P.; Kumar, R.; Khatait, J.P. Design of Compliant Iris. In Machines, Mechanism and Robotics; Springer: New York, NY, USA, 2022; pp. 911–917. [Google Scholar]
- Ma, J.; Feng, H.; Chen, Y.; Hou, D.; You, Z. Folding of tubular waterbomb. Research 2020, 2020, 1735081. [Google Scholar] [CrossRef]
- Jianguo, C.; Xiaowei, D.; Yuting, Z.; Jian, F.; Ya, Z. Folding Behavior of a Foldable Prismatic Mast With Kresling Origami Pattern. J. Mech. Robot. 2016, 8, 031004. [Google Scholar] [CrossRef]
- Liu, K.; Paulino, G. Nonlinear mechanics of non-rigid origami: An efficient computational approach. Proc. R. Soc. Math. Phys. Eng. Sci. 2017, 473, 20170348. [Google Scholar] [CrossRef] [PubMed]
- Hunt, G.W.; Ario, I. Twist buckling and the foldable cylinder: An exercise in origami. Int. J. Non-Linear Mech. 2005, 40, 833–843. [Google Scholar] [CrossRef]
- Herron, J.D. Augmented Design Capabilities for Origami Tessellations. In All Thesis and Dissertations; Brigham Young University: Provo, UT, USA, 2018; pp. 18–30, 6855. [Google Scholar]
- Liu, X.; Yao, S.; Cook, B.S.; Tentzeris, M.M.; Georgakopoulos, S.V. An Origami Reconfigurable Axial-Mode Bifilar Helical Antenna. IEEE Trans. Antennas Propag. 2015, 63, 5897–5903. [Google Scholar] [CrossRef]
- Yasuda, H.; Tachi, T.; Lee, M.; Yang, J. Origami-based tunable truss structures for non-volatile mechanical memory operation. Nat. Commun. 2017, 8, 962. [Google Scholar] [CrossRef]
- Berre, J.; Geiskopf, F.; Rubbert, L.; Renaud, P. Towards the design of kresling tower origami as a compliant building block. J. Mech. Robot. 2022, 14, 045002. [Google Scholar] [CrossRef]
- Liu, X.; Yao, S.; Georgakopoulos, S.V.; Cook, B.S.; Tentzeris, M.M. Reconfigurable helical antenna based on an origami structure for wireless communication system. In Proceedings of the 2014 IEEE MTT-S International Microwave Symposium (IMS2014), Tampa, FL, USA, 1–6 June 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Zhang, Q.; Cai, J.; Li, M.; Feng, J. Bistable behaviour of a deployable cylinder with Kresling pattern. In Proceedings of the 7th International Meeting on Origami in Science, Mathematics and Education (7OSME), Oxford, UK, 4–7 September 2018; pp. 4–7. [Google Scholar]
- Heath, T.L. A History of Greek Mathematics: From Thales to Euclid; The Clarendon Press: Oxford, UK, 1921; Volume I, p. 131. [Google Scholar]
- Lang, R.J.; Tolman, K.A.; Crampton, E.B.; Magleby, S.P.; Howell, L.L. A Review of Thickness-Accommodation Techniques in Origami-Inspired Engineering. Appl. Mech. Rev. 2018, 70, 010805. [Google Scholar] [CrossRef]
- Chen, Y.; Peng, R.; You, Z. Origami of thick panels. Science 2015, 349, 396–400. [Google Scholar] [CrossRef] [Green Version]
- Bowen, L.; Baxter, W.; Magleby, S.; Howell, L. A position analysis of coupled spherical mechanisms found in action origami. Mech. Mach. Theory 2014, 77, 13–24. [Google Scholar] [CrossRef]
- Dai, J.S.; Rees Jones, J. Mobility in Metamorphic Mechanisms of Foldable/Erectable Kinds. J. Mech. Des. 1999, 121, 375–382. [Google Scholar] [CrossRef]
- Qiu, C.; Zhang, K.; Dai, J.S. Repelling-Screw Based Force Analysis of Origami Mechanisms. J. Mech. Robot. 2016, 8, 031001. [Google Scholar] [CrossRef]
- Chen, Y.; Yan, J.; Feng, J.; Sareh, P. Particle swarm optimization-based metaheuristic design generation of non-trivial flat-foldable origami tessellations with degree-4 vertices. J. Mech. Des. 2021, 143, 011703. [Google Scholar] [CrossRef]
- Bös, F.; Wardetzky, M.; Vouga, E.; Gottesman, O. On the Incompressibility of Cylindrical Origami Patterns. J. Mech. Des. 2016, 139, 021404. [Google Scholar] [CrossRef]
- Cai, J.; Zhang, Y.; Xu, Y.; Zhou, Y.; Feng, J. The Foldability of Cylindrical Foldable Structures Based on Rigid Origami. J. Mech. Des. 2016, 138, 031401. [Google Scholar] [CrossRef]
- Chen, G.; Magleby, S.P.; Howell, L.L. Membrane-Enhanced Lamina Emergent Torsional Joints for Surrogate Folds. J. Mech. Des. 2018, 140, 062303. [Google Scholar] [CrossRef]
- Melancon, D.; Forte, A.E.; Kamp, L.M.; Gorissen, B.; Bertoldi, K. Inflatable Origami: Multimodal Deformation via Multistability. Adv. Funct. Mater. 2022, 2201891. [Google Scholar] [CrossRef]
- Hao, G.; Yu, J.; Li, H. A Brief Review on Nonlinear Modelling Methods and Applications of Compliant Mechanisms. Front. Mech. Eng. 2016, 11, 119–128. [Google Scholar] [CrossRef]
- Hao, G.; Kong, X. A Novel Large-Range XY Compliant Parallel Manipulator With Enhanced Out-of-Plane Stiffness. J. Mech. Des. 2012, 134, 061009. [Google Scholar] [CrossRef]
- Jacobsen, J.O.; Chen, G.; Howell, L.L.; Magleby, S.P. Lamina Emergent Torsional (LET) Joint. Mech. Mach. Theory 2009, 44, 2098–2109. [Google Scholar] [CrossRef]







| Point | x | y | z |
|---|---|---|---|
| 0 | 0 | h | |
| 2a | 0 | h | |
| h/2 | |||
| a | h/2 | ||
| 2a | h/2 | ||
| 2a | 0 | 0 | |
| 0 | 0 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, S.; Zhao, P.; Zhao, Y.; Kavousi, F.; Feng, H.; Hao, G. A Novel Radially Closable Tubular Origami Structure (RC-ori) for Valves. Actuators 2022, 11, 243. https://doi.org/10.3390/act11090243
Ye S, Zhao P, Zhao Y, Kavousi F, Feng H, Hao G. A Novel Radially Closable Tubular Origami Structure (RC-ori) for Valves. Actuators. 2022; 11(9):243. https://doi.org/10.3390/act11090243
Chicago/Turabian StyleYe, Siyuan, Pengyuan Zhao, Yinjun Zhao, Fatemeh Kavousi, Huijuan Feng, and Guangbo Hao. 2022. "A Novel Radially Closable Tubular Origami Structure (RC-ori) for Valves" Actuators 11, no. 9: 243. https://doi.org/10.3390/act11090243






