Inertial Measurement Unit- and Time Series Approach-Based Motion Trajectory Reconstruction of the Safety Rope Fastening Behaviour
Abstract
:1. Introduction
2. Methods
2.1. Quaternions Represent the Action Position of the Safety Harness Screw
2.2. Spatial Motion Trajectory Model of Safety Rope Buckle Fastening Behaviour
2.3. Evaluation of Model Performance
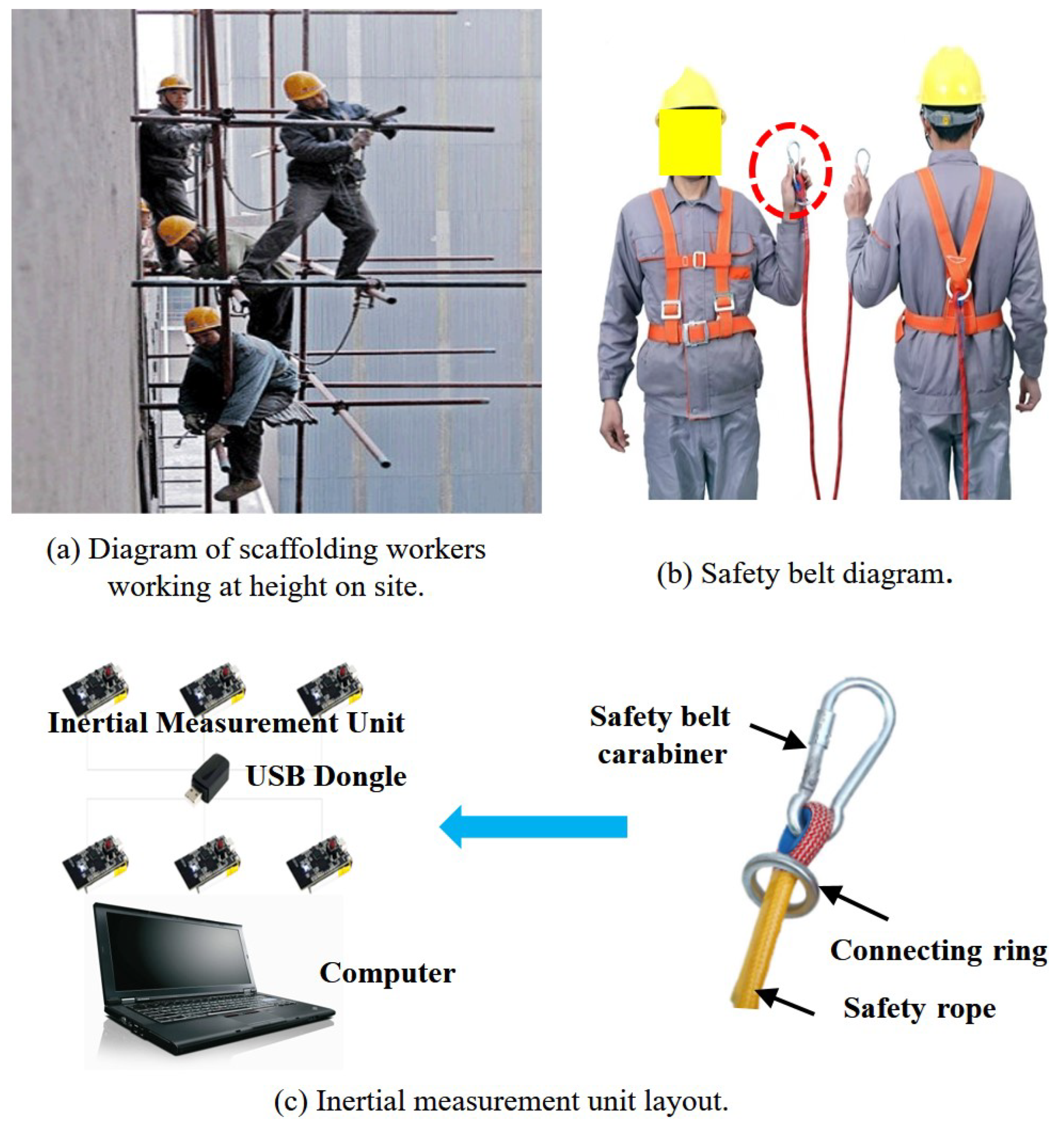
3. Experiment
3.1. Experimental Design
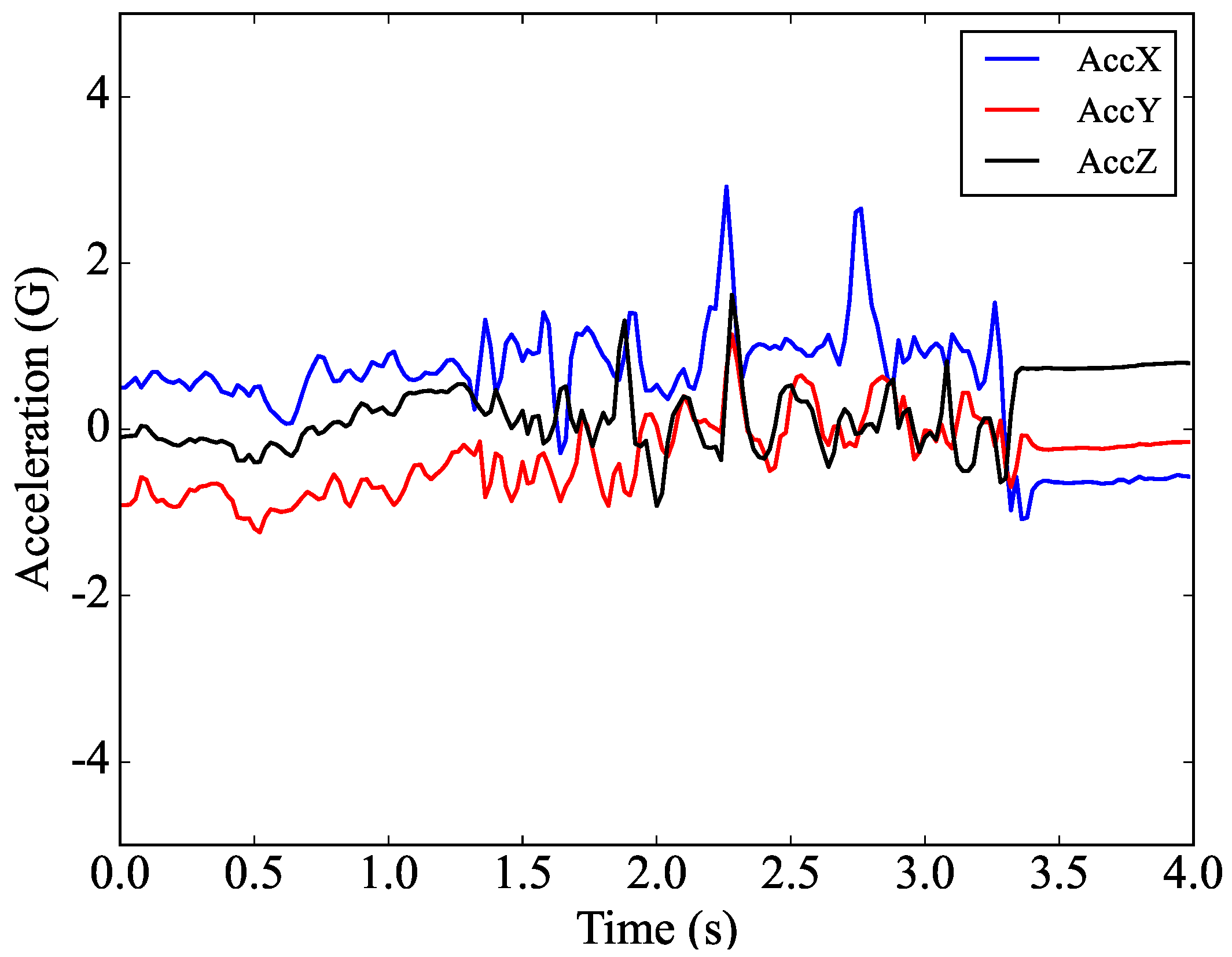
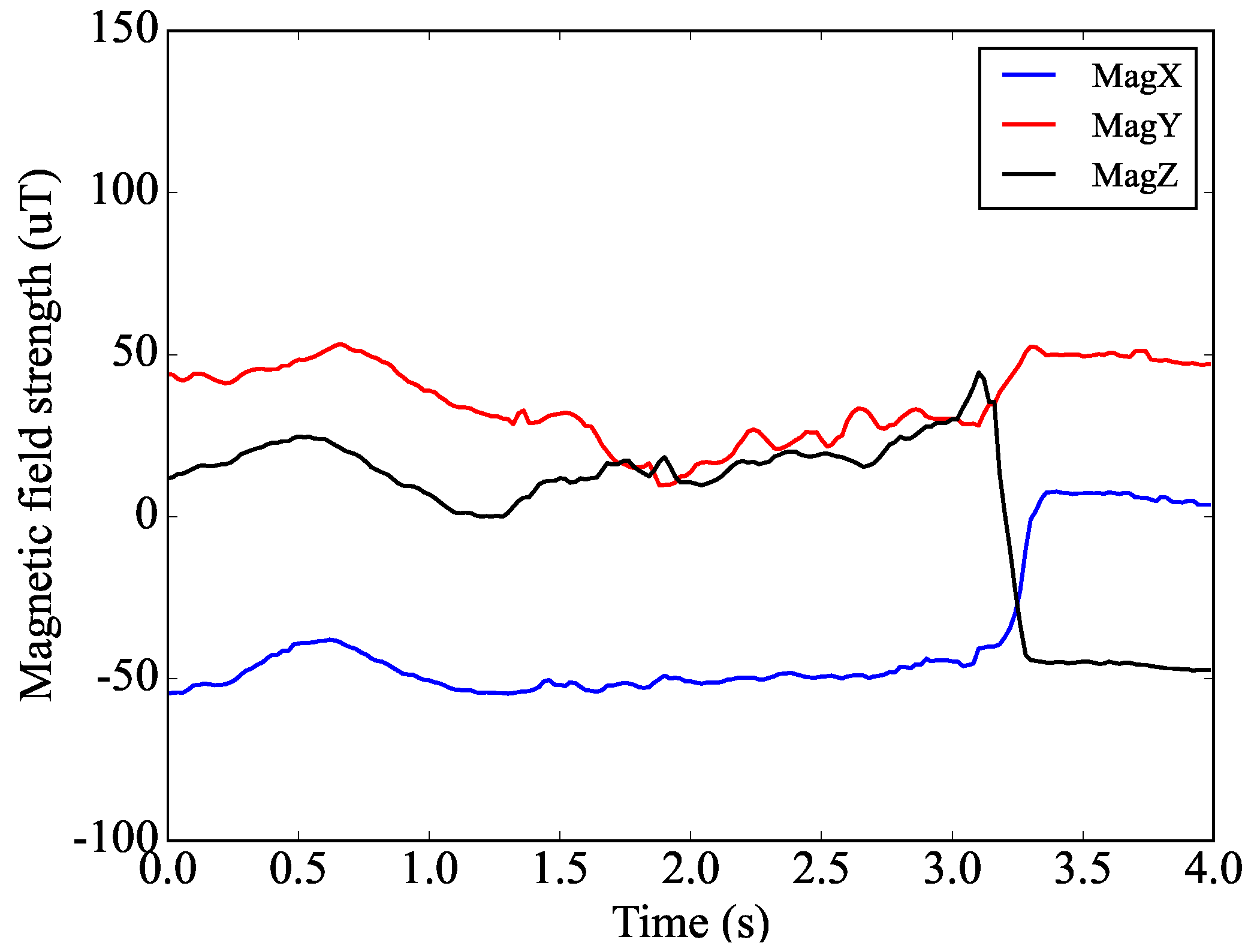
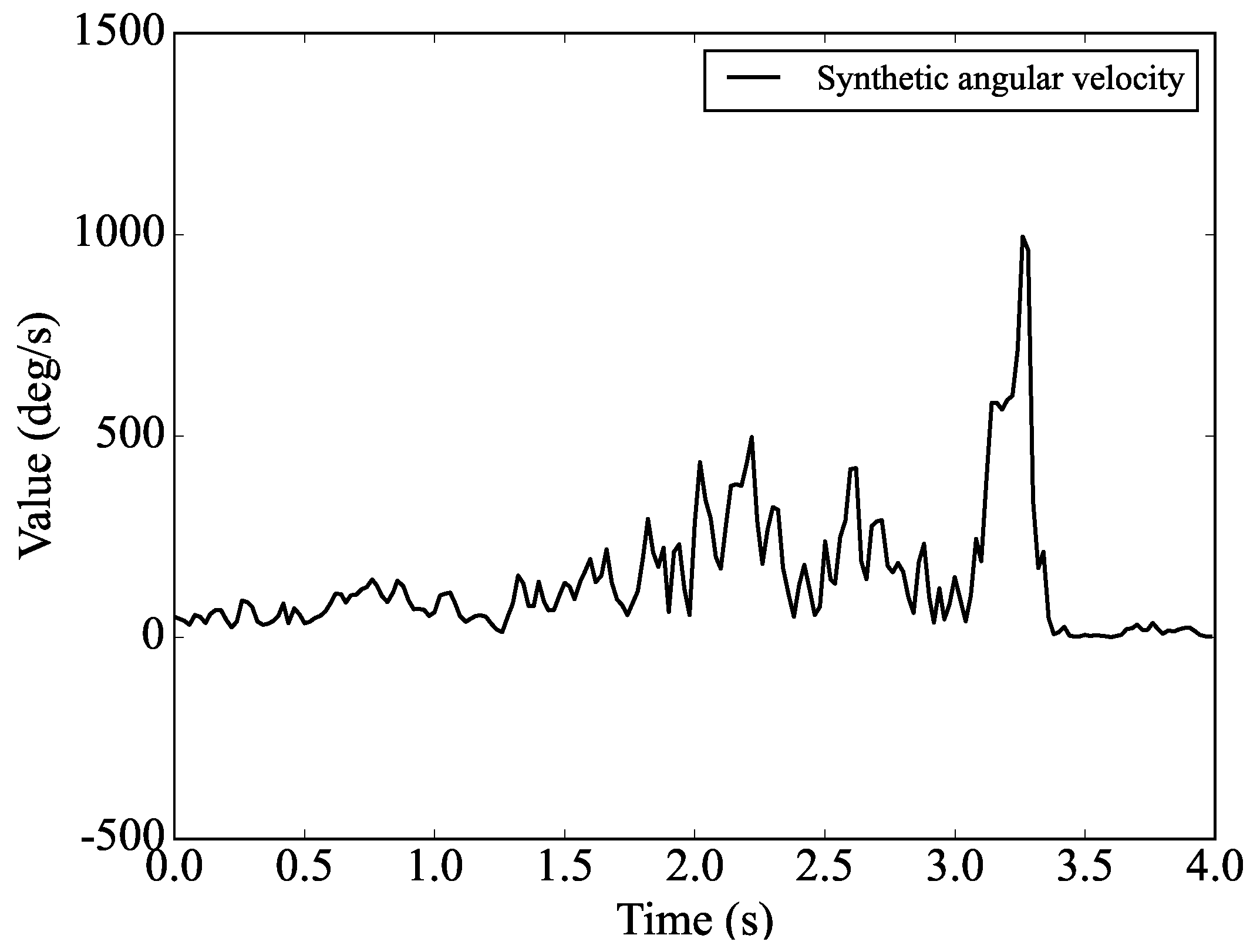
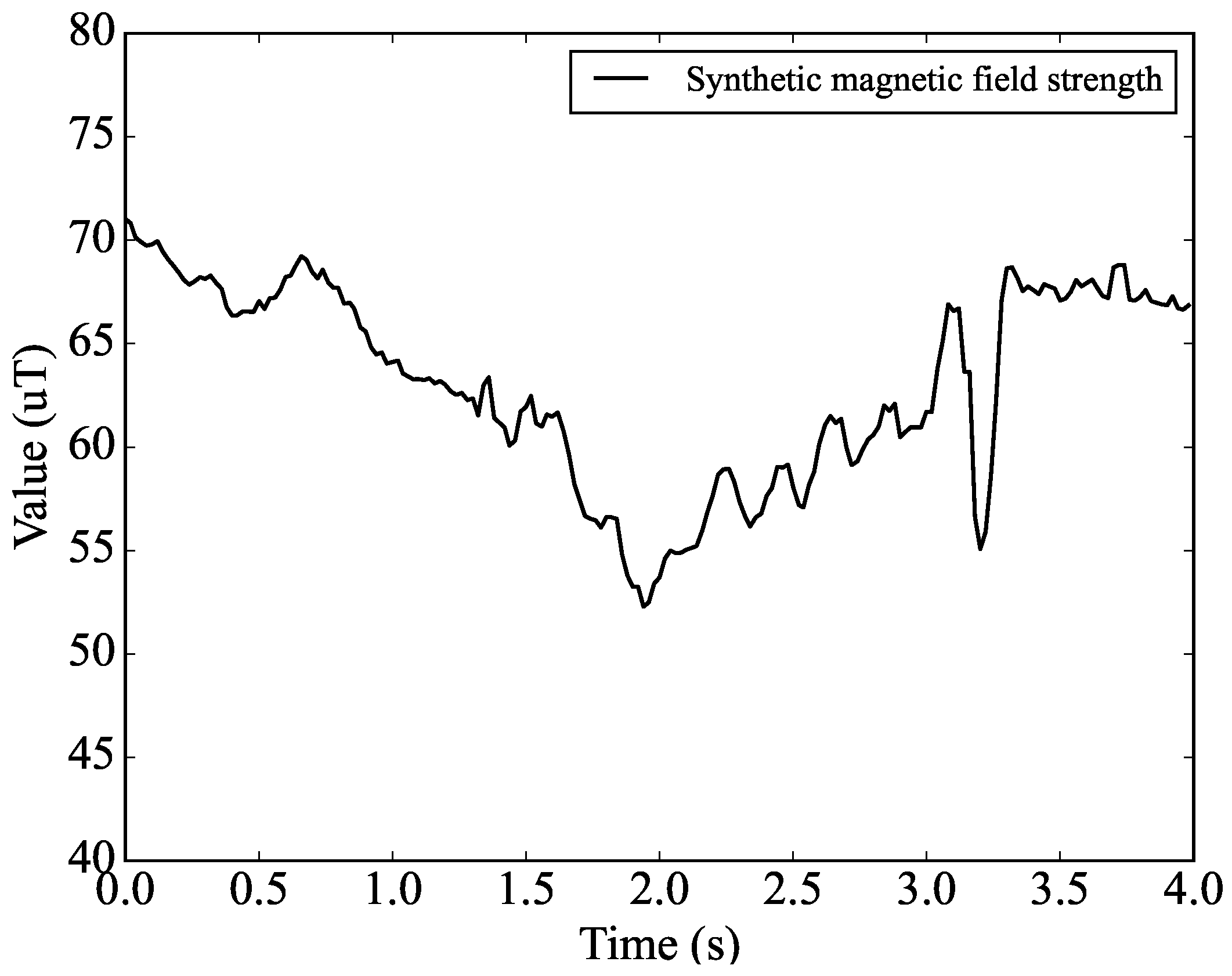
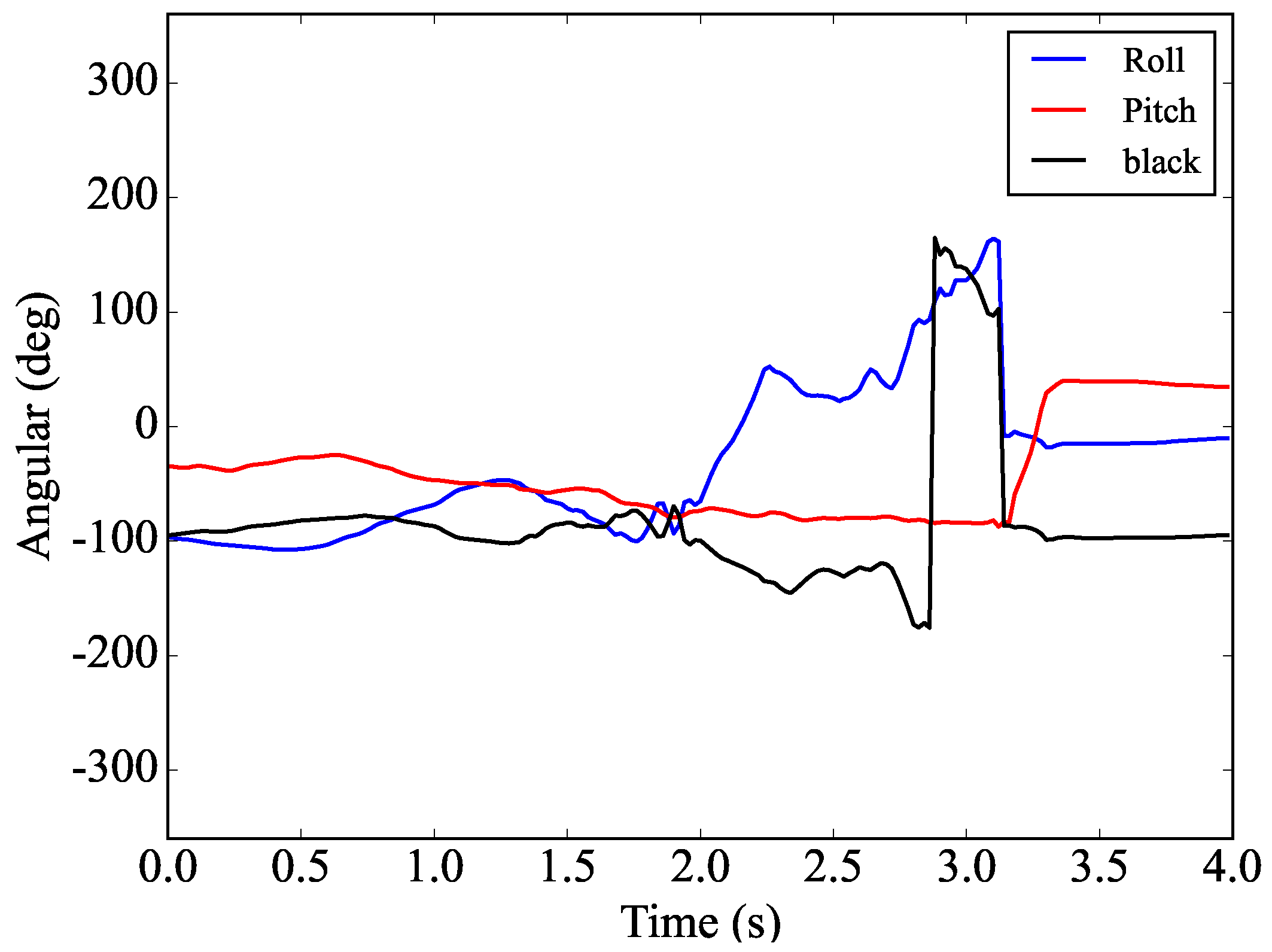
3.2. Data Generation
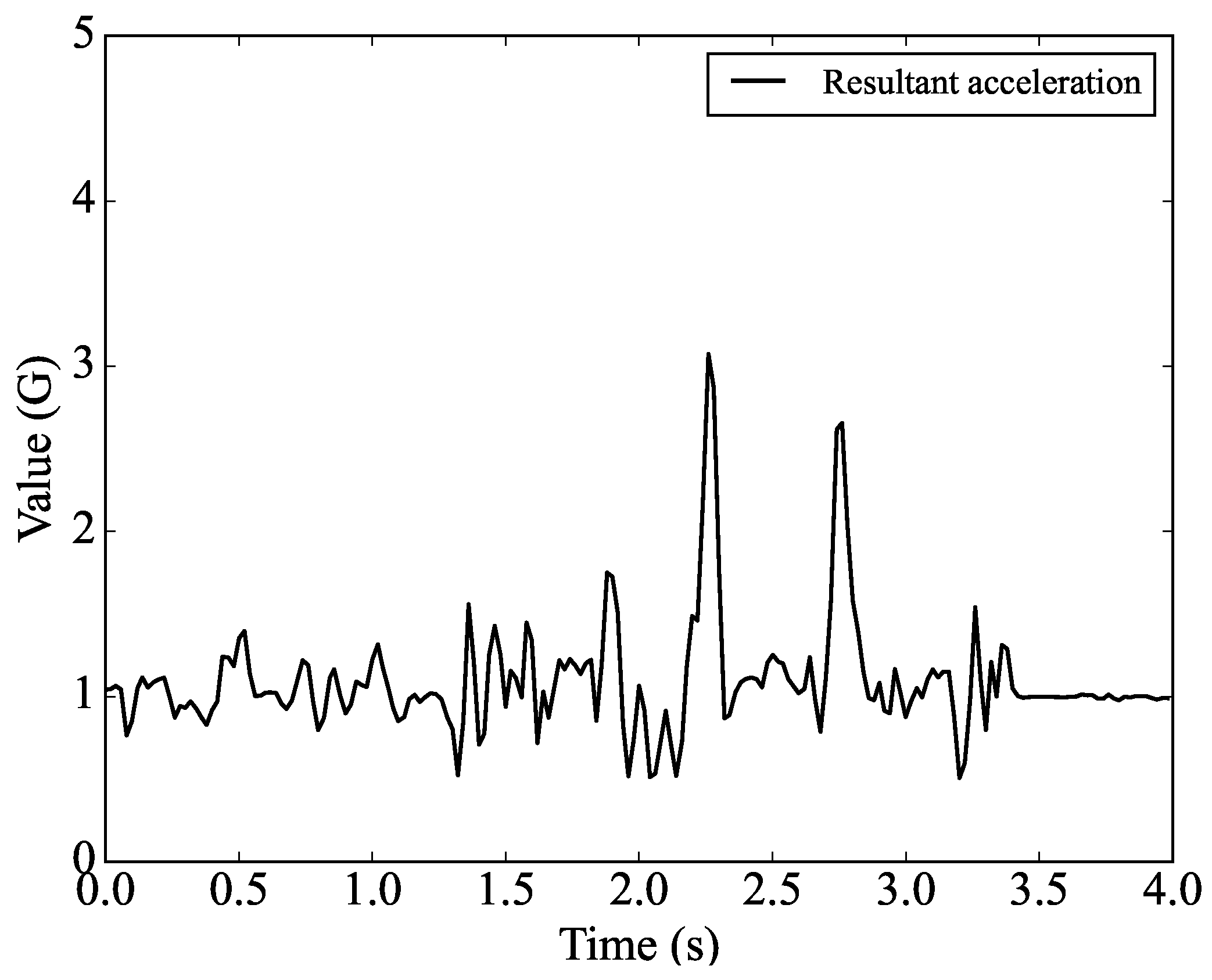
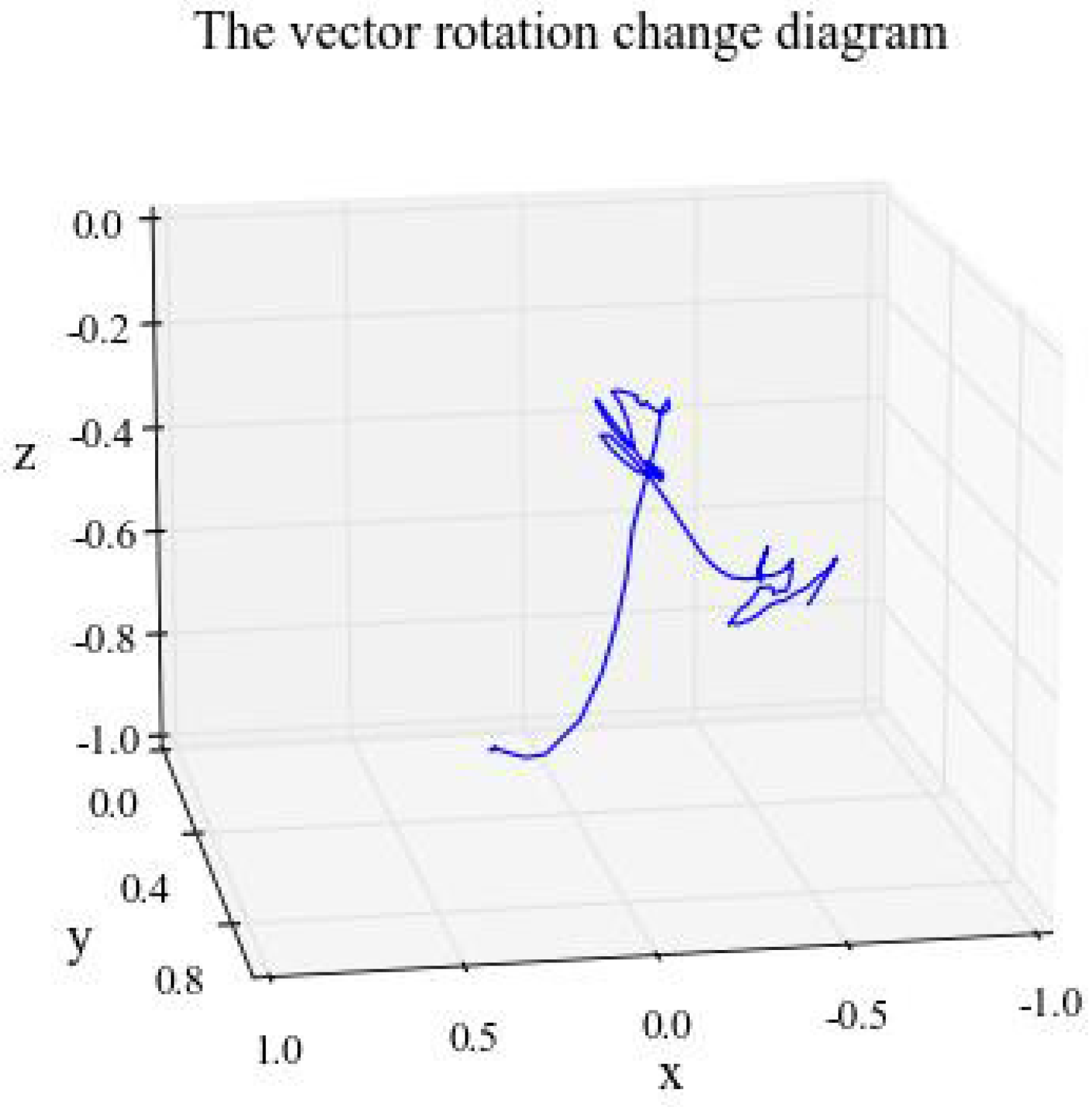
3.3. Data Analysis
4. Results and Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Uddin, S.M.J.; Albert, A.; Alsharef, A.; Pandit, B.; Patil, Y.; Nnaji, C. Hazard Recognition Patterns Demonstrated by Construction Workers. Int. J. Environ. Res. Public Health 2020, 17, 7788. [Google Scholar] [CrossRef] [PubMed]
- Karamoozian, A.; Luo, C.; Wu, D. Risk assessment of occupational safety in construction projects using uncertain information. Hum. Ecol. Risk Assess. Int. J. 2023, 29, 1134–1151. [Google Scholar] [CrossRef]
- Paul, M.L.; Blasko, M. Bureau of Labor Statistics Releases 2021 Construction Industry Fatality Injury Data. Available online: https://www.jacksonlewis.com/insights/bureau-labor-statistics-releases-2021-construction-industry-fatality-injury-data (accessed on 30 March 2023).
- Li, Z. Analysis of the Situation of Construction Safety in China. Available online: http://www.hywit.com/portal/Article/index/id/9986/cid/207.html (accessed on 8 September 2022).
- Goh, Y.M. An Empirical Investigation of the Average Deployment Force of Personal Fall Arrest Energy Absorbers. J. Constr. Eng. Manag. 2014, 141, 04014059. [Google Scholar] [CrossRef]
- Evan, N.; Carol, H.; Bo, X.; Ian, S.; Dongping, F. Falls from Height in the Construction Industry: A Critical Review of the Scientific Literature. Int. J. Environ. Res. Public Health 2016, 13, 638. [Google Scholar] [CrossRef]
- Zhou, T.; Zhu, Q.; Shi, Y.; Du, J. Construction Robot Teleoperation Safeguard Based on Real-Time Human Hand Motion Prediction. J. Constr. Eng. Manag. 2022, 7, 148. [Google Scholar] [CrossRef]
- Terzioglu, T.; Polat, G. Formwork System Selection in Building Construction Projects Using an Integrated Rough AHP-EDAS Approach: A Case Study. Buildings 2022, 12, 1084. [Google Scholar] [CrossRef]
- Heravi, M.Y.; Jang, Y.; Jeong, I.; Sarkar, S. Deep learning-based activity-aware 3D human motion trajectory prediction in construction. Expert Syst. Appl. 2024, 239, 122423. [Google Scholar] [CrossRef]
- Hirakawa, T.; Yamashita, T.; Tamaki, T.; Fujiyoshi, H. Survey on Vision-Based Path Prediction; Springer International Publishing: Cham, Switzerland, 2018; pp. 48–64. [Google Scholar] [CrossRef]
- Du, H.; Manns, M.; Herrmann, E.; Fischer, K. Joint Angle Data Representation for Data Driven Human Motion Synthesis. Procedia CIRP 2016, 41, 746–751. [Google Scholar] [CrossRef]
- Kim, K.; Cho, Y.K. Effective inertial sensor quantity and locations on a body for deep learning-based worker’s motion recognition. Autom. Constr. 2020, 113, 103126. [Google Scholar] [CrossRef]
- Fang, W.; Zhong, B.; Zhao, N.; Love, P.E.; Luo, H.; Xue, J.; Xu, S. A deep learning-based approach for mitigating falls from height with computer vision: Convolutional neural network. Adv. Eng. Inform. 2019, 39, 170–177. [Google Scholar] [CrossRef]
- Han, S.; Lee, S.; Peña-Mora, F. Vision-Based Detection of Unsafe Actions of a Construction Worker: Case Study of Ladder Climbing. J. Comput. Civ. Eng. 2013, 27, 635–644. [Google Scholar] [CrossRef]
- Fang, W.; Ding, L.; Luo, H.; Love, P.E. Falls from heights: A computer vision-based approach for safety harness detection. Autom. Constr. 2018, 91, 53–61. [Google Scholar] [CrossRef]
- Sanhudo, L.; Calvetti, D.; Martins, J.P.; Ramos, N.M.; Mêda, P.; Gonçalves, M.C.; Sousa, H. Activity classification using accelerometers and machine learning for complex construction worker activities. J. Build. Eng. 2021, 35, 102001. [Google Scholar] [CrossRef]
- Akhavian, R.; Behzadan, A.H. Smartphone-based construction workers’ activity recognition and classification. Autom. Constr. 2016, 71, 198–209. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, J.; Chen, L.; Geng, Y.; Wang, X. Single Wearable Accelerometer-Based Human Activity Recognition via Kernel Discriminant Analysis and QPSO-KELM Classifier. IEEE Access 2019, 7, 109216–109227. [Google Scholar] [CrossRef]
- Ahn, C.R.; Lee, S.; Sun, C.; Jebelli, H.; Yang, K.; Choi, B. Wearable Sensing Technology Applications in Construction Safety and Health. J. Constr. Eng. Manag. 2019, 145, 03119007. [Google Scholar] [CrossRef]
- Bangaru, S.S.; Wang, C.; Busam, S.A.; Aghazadeh, F. ANN-based automated scaffold builder activity recognition through wearable EMG and IMU sensors. Autom. Constr. 2021, 126, 103653. [Google Scholar] [CrossRef]
- Barraza Madrigal, J.A.; Contreras Rodríguez, L.A.; Cardiel Pérez, E.; Hernández Rodríguez, P.R.; Sossa, H. Hip and lower limbs 3D motion tracking using a double-stage data fusion algorithm for IMU/MARG-based wearables sensors. Biomed. Signal Process. Control 2023, 86, 104938. [Google Scholar] [CrossRef]
- Joshua, L.; Varghese, K. Accelerometer-Based Activity Recognition in Construction. J. Comput. Civ. Eng. 2011, 25, 370–379. [Google Scholar] [CrossRef]
- Yoon, J.; Lee, B.; Chun, J.; Son, B.; Kim, H. Investigation of the relationship between Ironworker’s gait stability and different types of load carrying using wearable sensors. Adv. Eng. Inform. 2022, 51, 101521. [Google Scholar] [CrossRef]
- Hong, S.; Yoon, J.; Ham, Y.; Lee, B.; Kim, H. Monitoring safety behaviors of scaffolding workers using Gramian angular field convolution neural network based on IMU sensing data. Autom. Constr. 2023, 148, 104748. [Google Scholar] [CrossRef]
- Terze, Z.; Zlatar, D.; Pandža, V. Aircraft attitude reconstruction via novel quaternion-integration procedure. Aerosp. Sci. Technol. 2020, 97, 105617. [Google Scholar] [CrossRef]
- Pellois, R.; Brüls, O. An inertial human upper limb motion tracking method for robot programming by demonstration. Robot. Auton. Syst. 2022, 156, 104201. [Google Scholar] [CrossRef]
- Roy, A.; Nelson, T.; Turaga, P. Functional data analysis approach for mapping change in time series: A case study using bicycle ridership patterns. Transp. Res. Interdiscip. Perspect. 2023, 17, 100752. [Google Scholar] [CrossRef]
- Ligęza, P. Reconstructing the trajectory of the object’s motion on the basis of measuring the components of its velocity. Measurement 2023, 221, 113546. [Google Scholar] [CrossRef]
- Alahi, A.; Goel, K.; Ramanathan, V.; Robicquet, A.; Li, F.; Savarese, S. Social LSTM: Human Trajectory Prediction in Crowded Spaces. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 961–971. [Google Scholar] [CrossRef]
- Karamoozian, A.; Wu, D.; Luo, C. Green Supplier Selection in the Construction Industry Using a Novel Fuzzy Decision-Making Approach. J. Constr. Eng. Manag. 2023, 149, 04023033. [Google Scholar] [CrossRef]



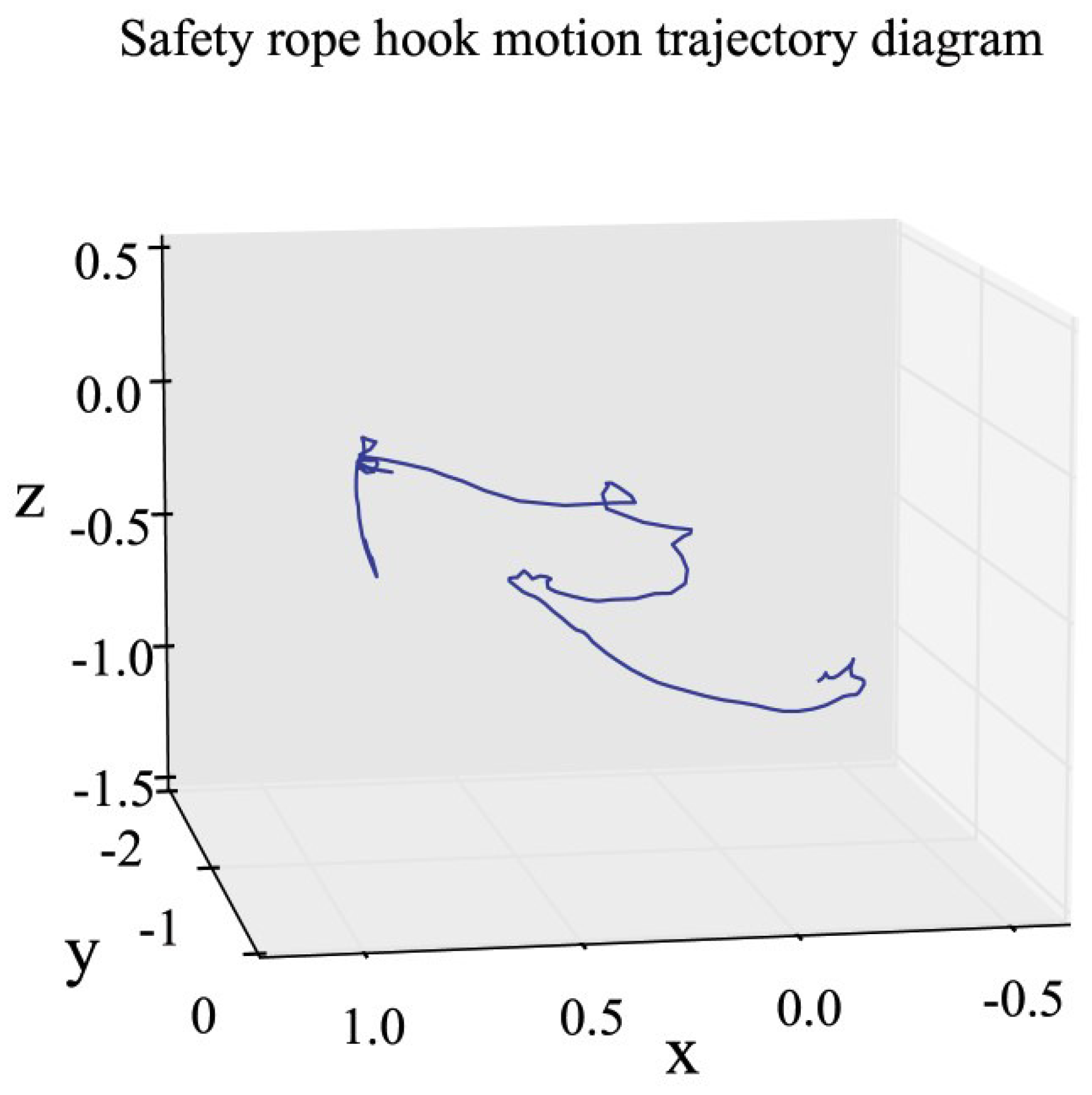
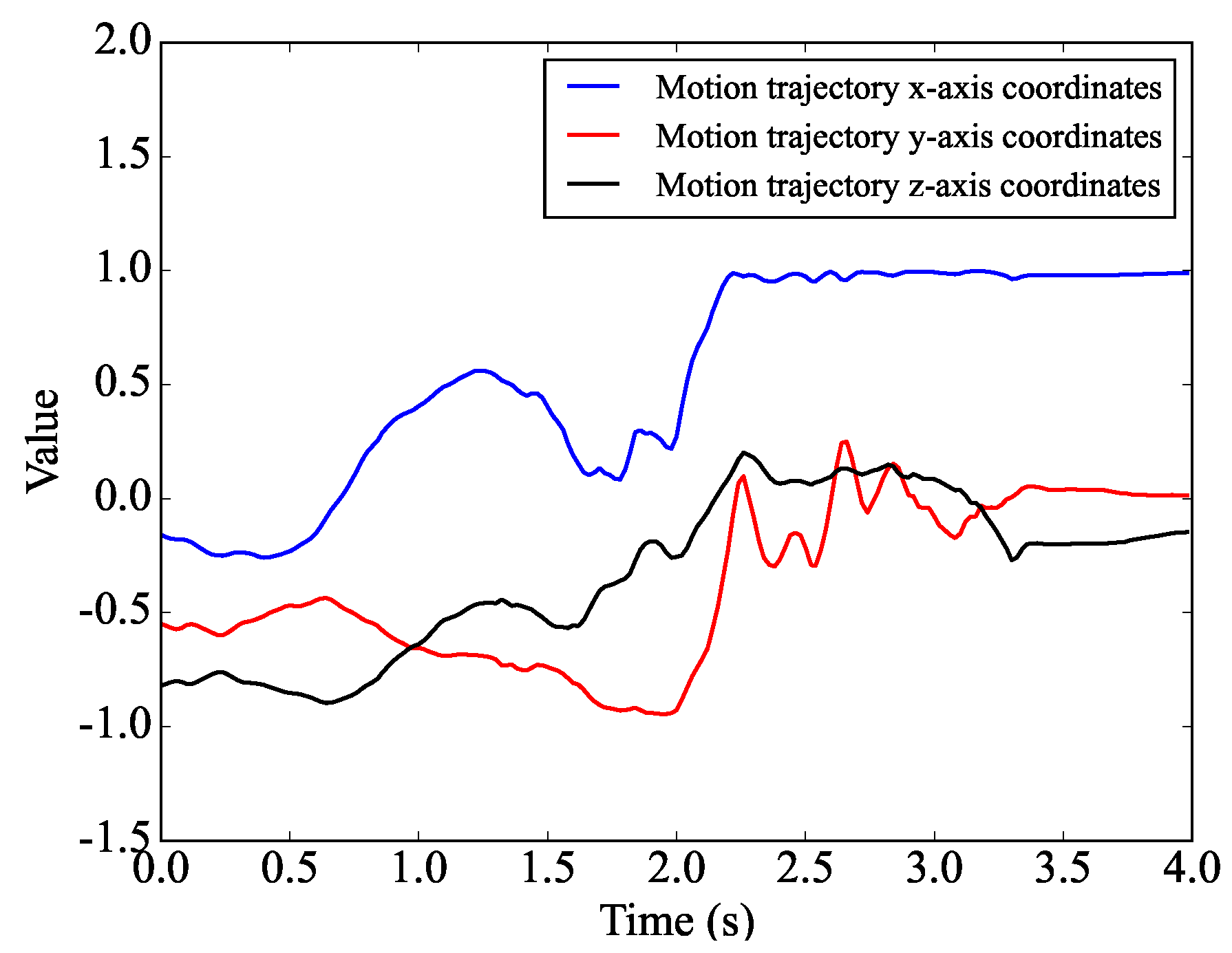
| Time | AccX(0) | AccY(0) | AccZ(0) | GyrX(0) | GyrY(0) | GyrZ(0) | MagX(0) | MagY(0) | MagZ(0) |
|---|---|---|---|---|---|---|---|---|---|
| 0 | −0.14 | −0.412 | 0.37 | −79.6 | 20.5 | −74.1 | 24.5 | 72.3 | −10.2 |
| 0.02 | −0.198 | −0.213 | 0.423 | −76.9 | −5.1 | −56.2 | 23.2 | 73 | −8.6 |
| 0.038 | −0.262 | −0.172 | 0.363 | −98.8 | −21.2 | −39.4 | 22.6 | 73.6 | −7.2 |
| 0.058 | −0.263 | −0.304 | 0.316 | −107.1 | −19.8 | −27.7 | 21.7 | 74 | −6.2 |
| 0.079 | −0.199 | −0.471 | 0.361 | −98.2 | −9.7 | −14.8 | 20.9 | 74 | −4.4 |
| 0.099 | −0.259 | −0.562 | 0.414 | −78.2 | −1.6 | −26 | 19.6 | 73.9 | −2.9 |
| 0.12 | −0.319 | −0.573 | 0.437 | −98.2 | 16.6 | −35.4 | 18.5 | 73.7 | −1.5 |
| 0.138 | −0.314 | −0.523 | 0.478 | −138.1 | 28.6 | −40.2 | 16.9 | 73.5 | 0.3 |
| 0.159 | −0.238 | −0.655 | 0.516 | −85.7 | 51.9 | −6.5 | 15.8 | 73.2 | 2.3 |
| 0.179 | −0.318 | −0.981 | 0.598 | −3.4 | 66.2 | 32.7 | 15.5 | 72.8 | 3.1 |
| 0.2 | −0.393 | −1.127 | 0.53 | −22.3 | 54.2 | 73.2 | 15.1 | 72.2 | 3.4 |
| 0.22 | −0.363 | −1.085 | 0.408 | 10.8 | 55.9 | 67.6 | 15.7 | 71.7 | 3.7 |
| 0.24 | −0.583 | −0.958 | 0.516 | 4.4 | 0.2 | 31 | 16.8 | 71.4 | 3.6 |
| 0.26 | −0.479 | −0.639 | 0.595 | −59.2 | −37.5 | −29.1 | 17 | 71.6 | 3.8 |
| 0.28 | −0.065 | −0.277 | 0.61 | −131.7 | −2 | −6.9 | 16.4 | 71.3 | 5.4 |
| 0.29 | −0.09 | −0.114 | 0.614 | −111.6 | 17.3 | 71.8 | 17.2 | 69.7 | 7.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Z.; Wang, Y. Inertial Measurement Unit- and Time Series Approach-Based Motion Trajectory Reconstruction of the Safety Rope Fastening Behaviour. Buildings 2024, 14, 219. https://doi.org/10.3390/buildings14010219
Han Z, Wang Y. Inertial Measurement Unit- and Time Series Approach-Based Motion Trajectory Reconstruction of the Safety Rope Fastening Behaviour. Buildings. 2024; 14(1):219. https://doi.org/10.3390/buildings14010219
Chicago/Turabian StyleHan, Zixin, and Yaowu Wang. 2024. "Inertial Measurement Unit- and Time Series Approach-Based Motion Trajectory Reconstruction of the Safety Rope Fastening Behaviour" Buildings 14, no. 1: 219. https://doi.org/10.3390/buildings14010219






