Aeolian Vibration Dynamic Analysis of Large-Span, Relaxed Antenna Cable Net Based on Finite Particle Method
Abstract
:1. Introduction
2. Basic Theory of FPM for Analysis of Cable Aeolian Vibration
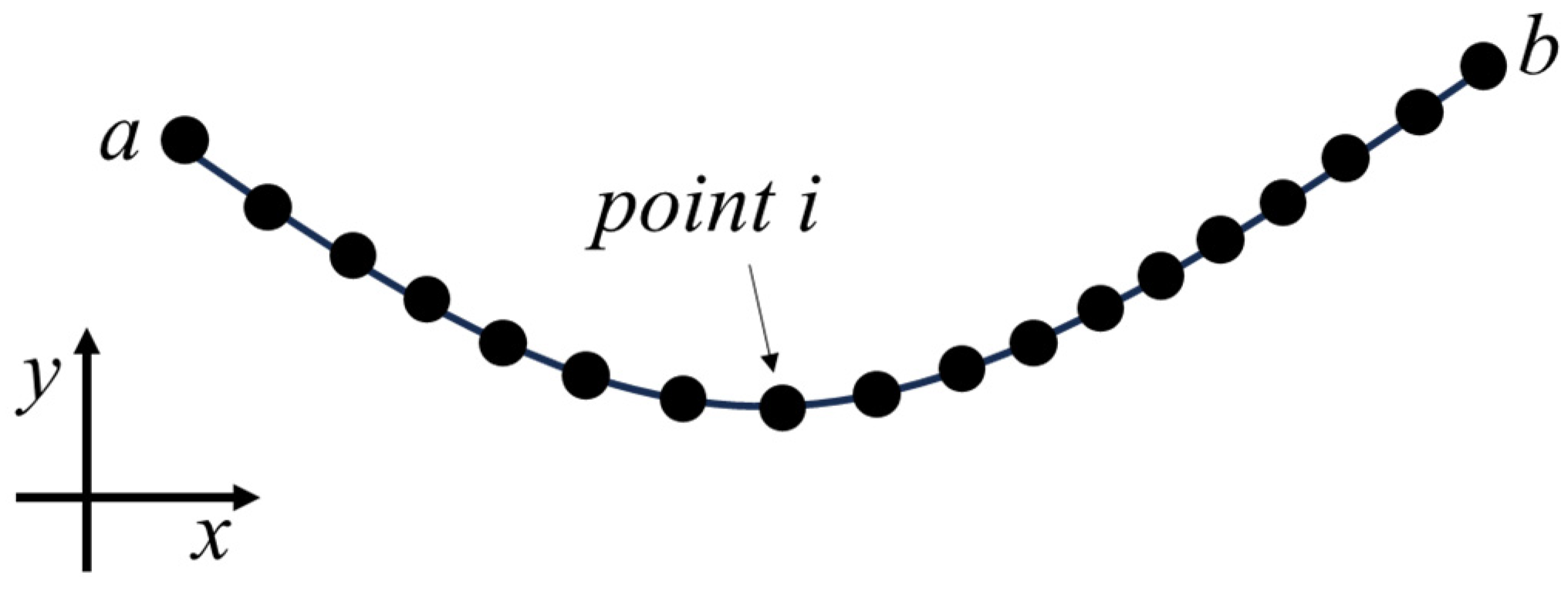
2.1. Point Value Description
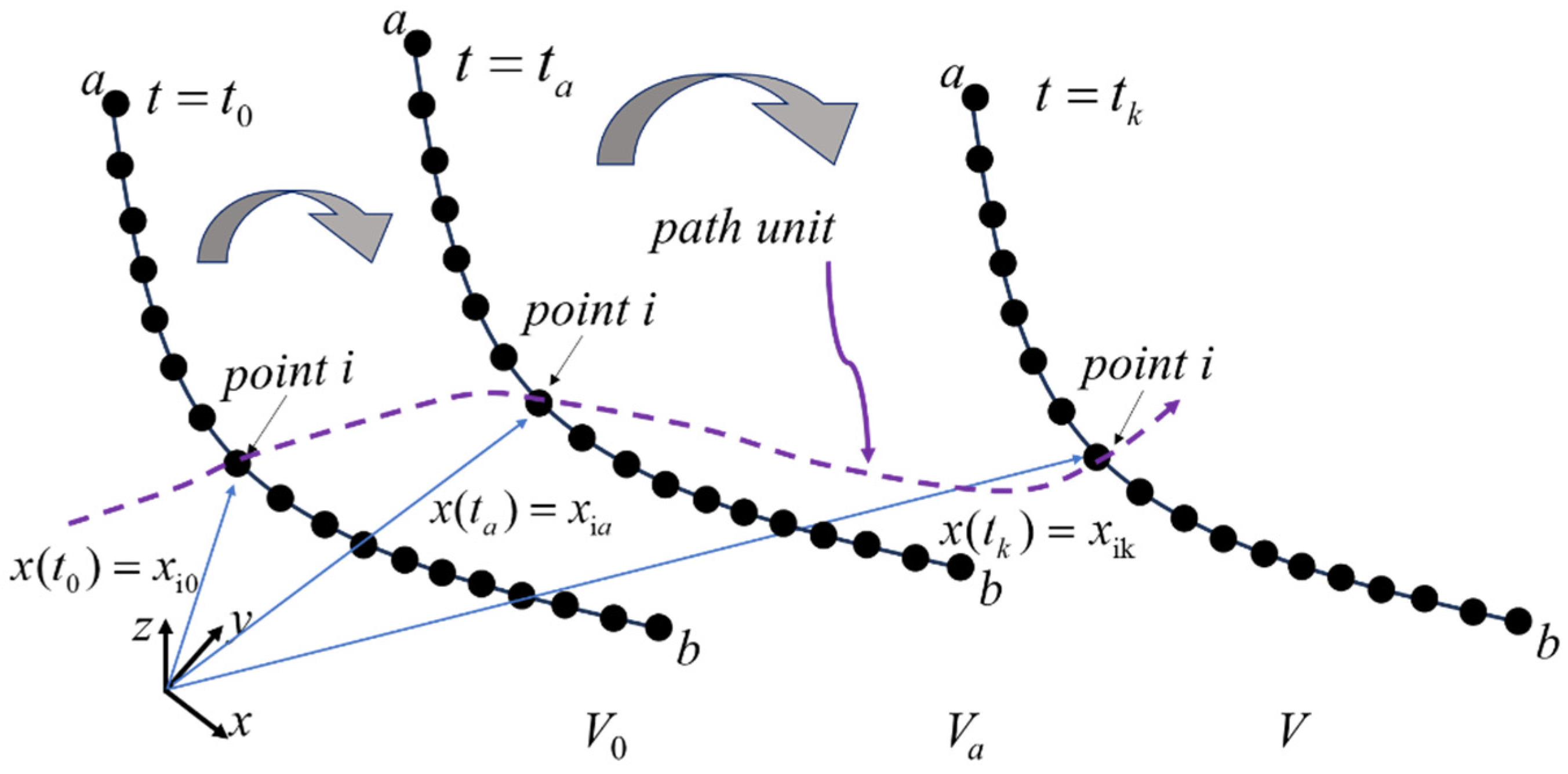
2.2. Path Unit
2.3. Equation of Motion for Particle
2.4. Solutions to Geometric Nonlinear Problems
3. Analysis Model of Antenna Cable Net
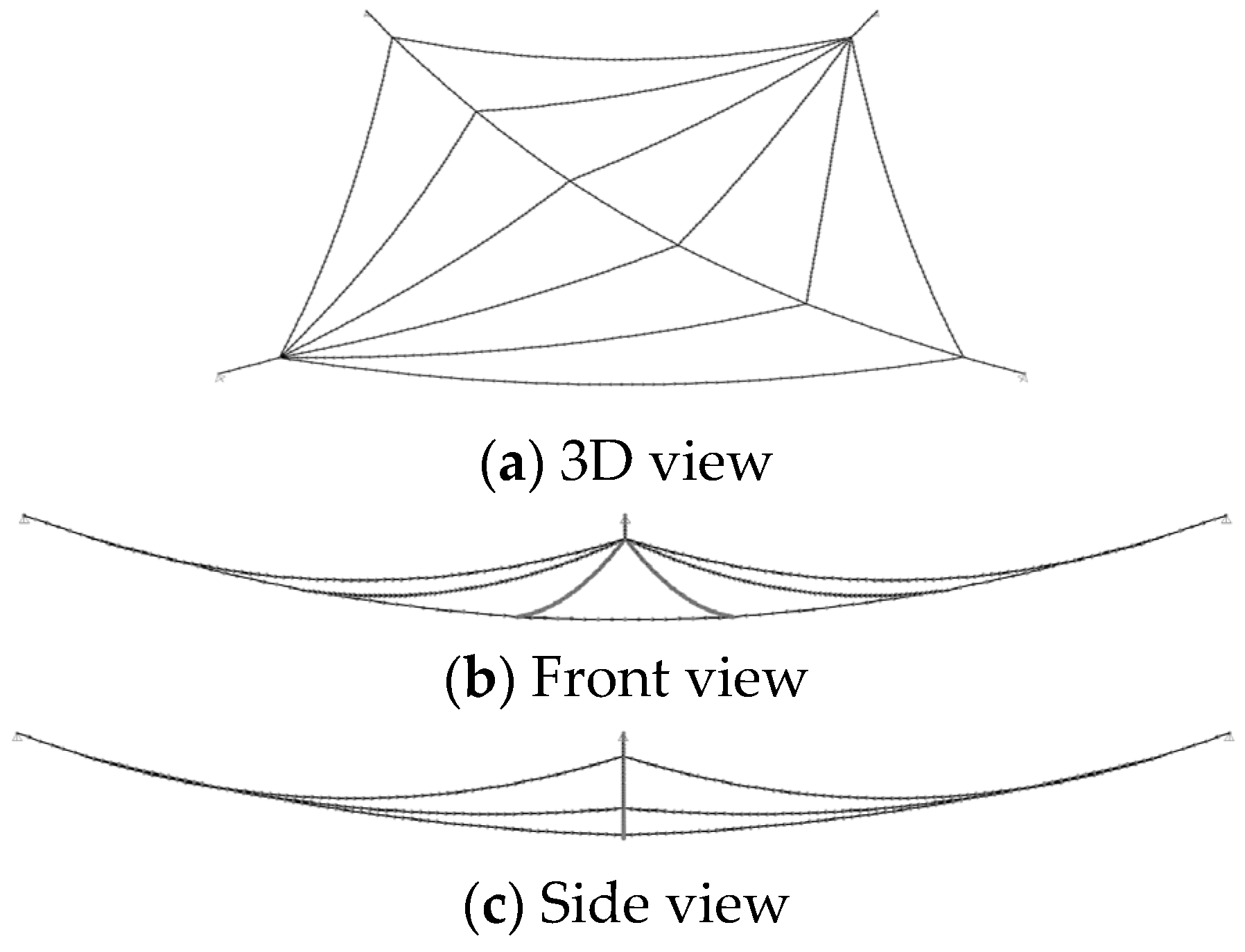
3.1. Antenna Cable Net Structure Information
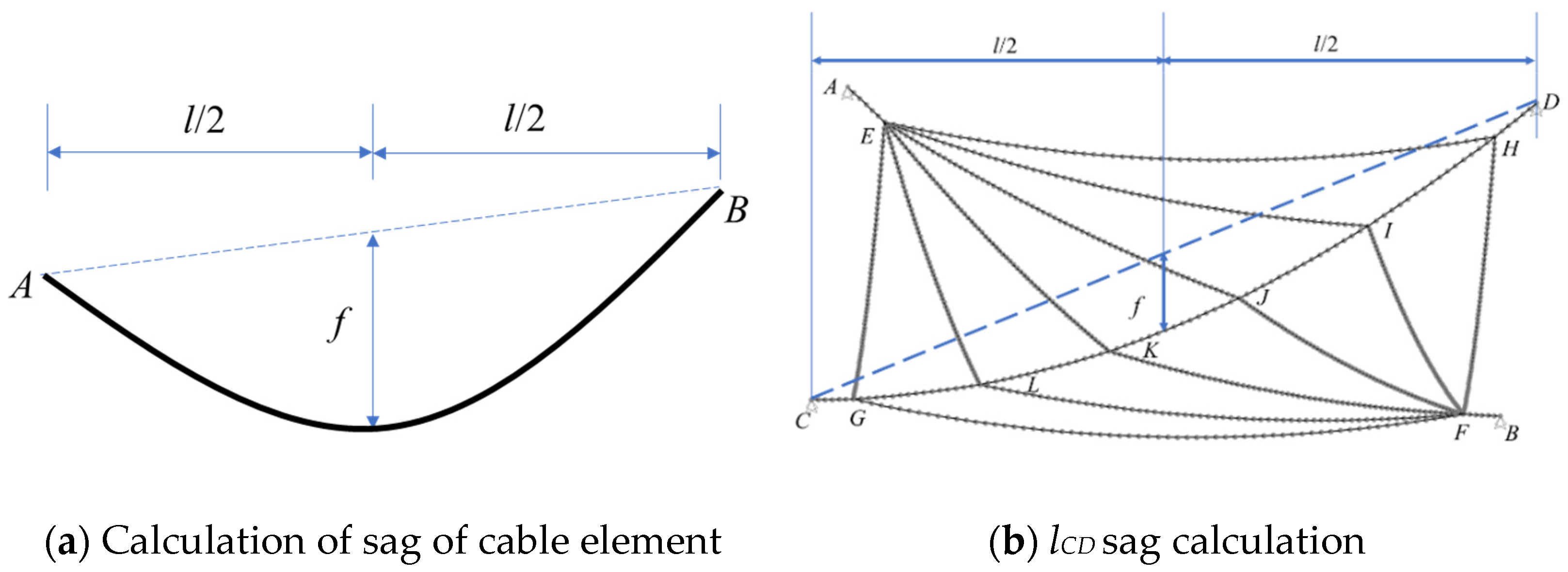
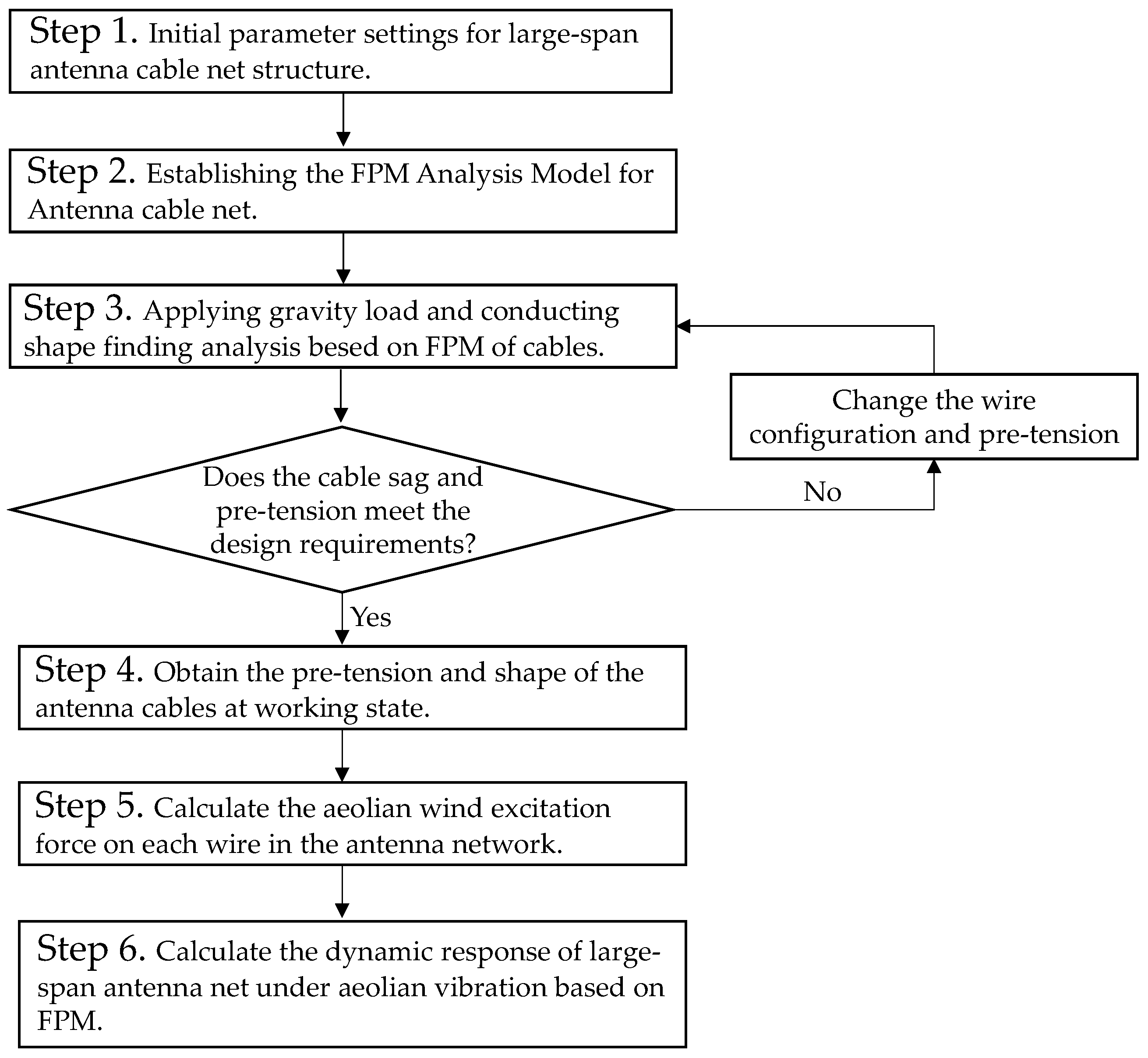
3.2. Initial State Analysis of Antenna Network
4. Analysis of Aeolian Vibration of Antenna Cable Net
4.1. Aeolian Excitation Force
4.2. Cable Self-Damping
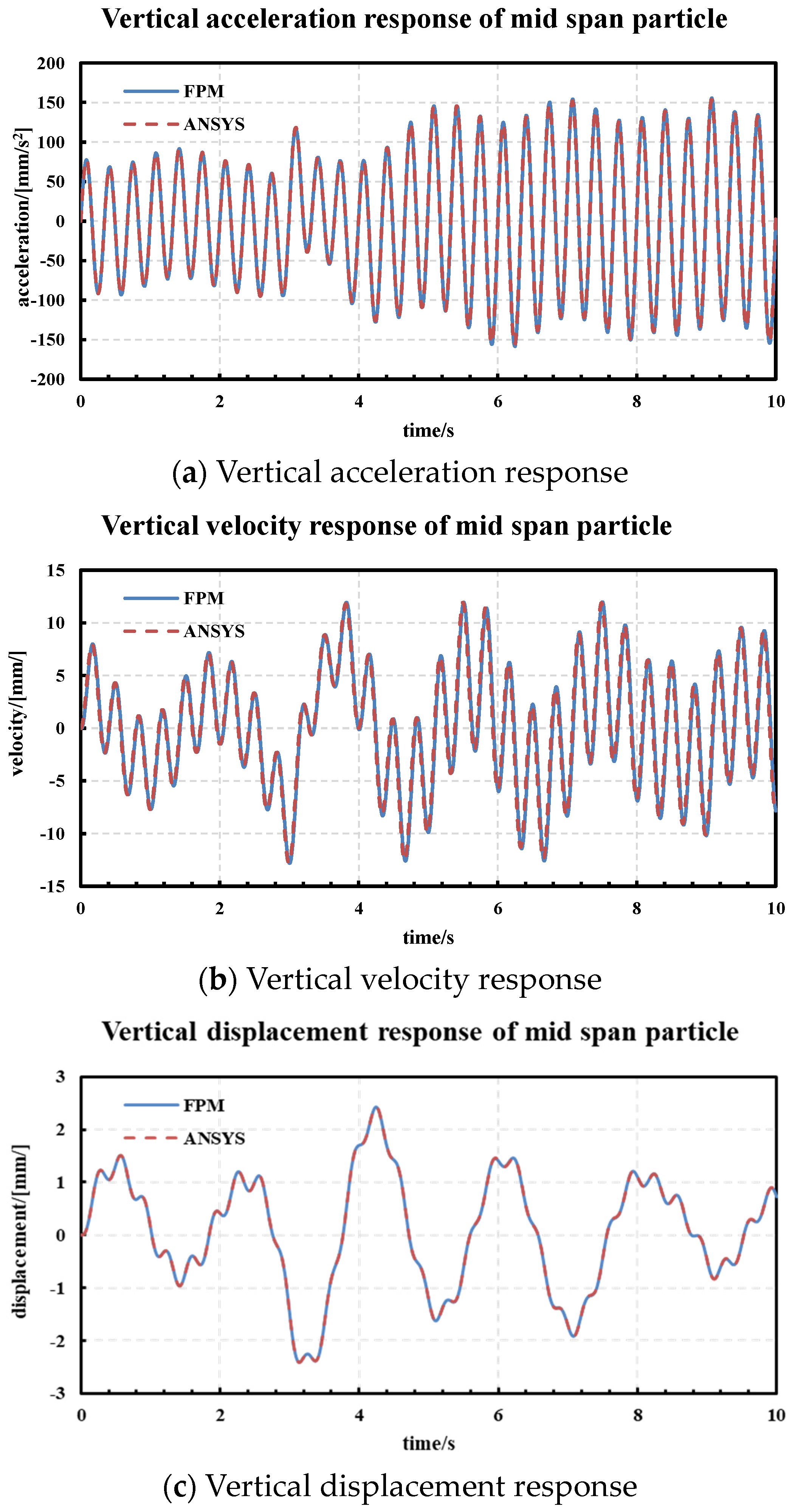
4.3. Vibration Response
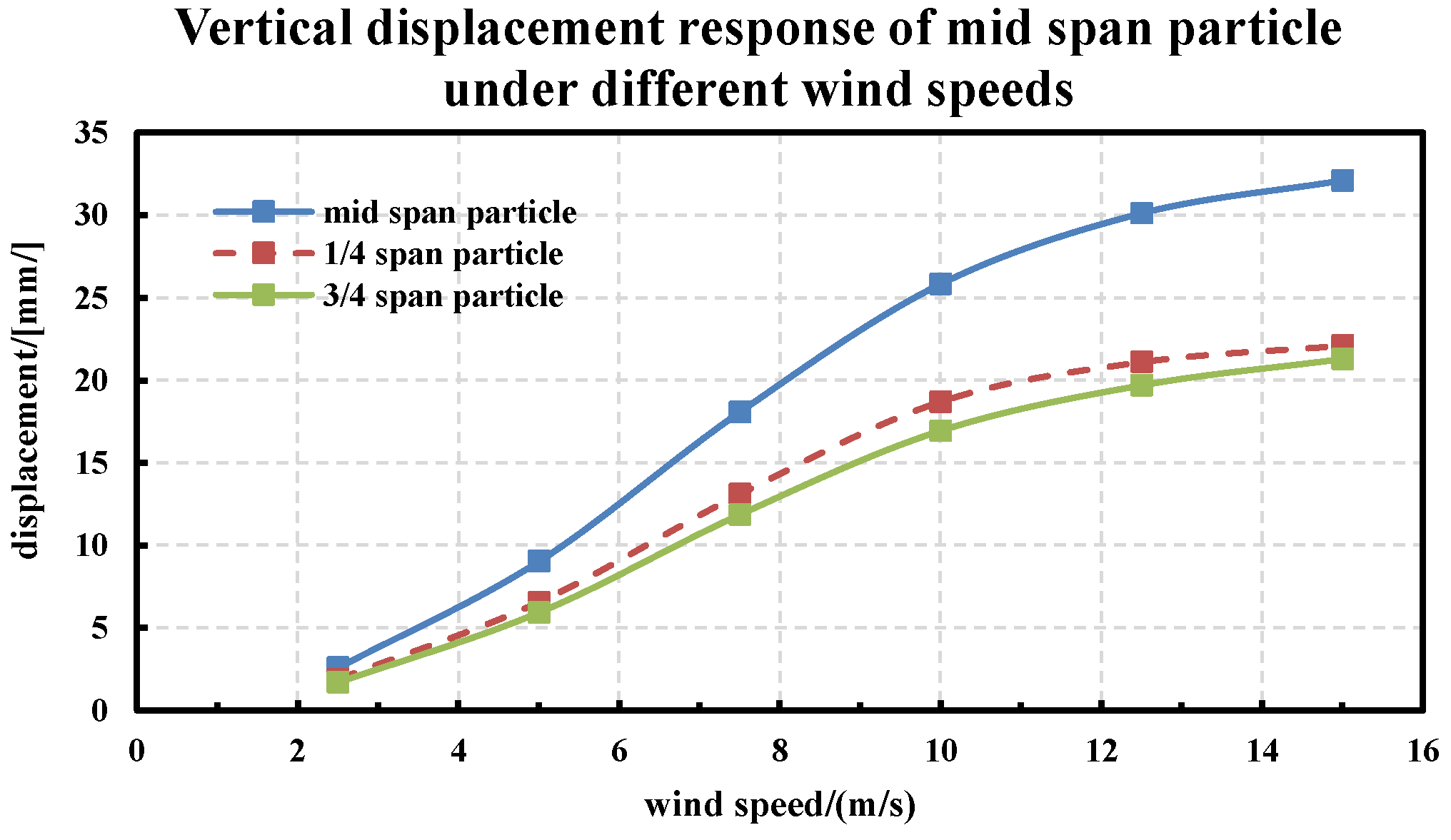
4.4. Parameter Study
4.4.1. Wind Speed
4.4.2. Distribution of Vibration along Cable Span
5. Conclusions
- (1)
- By applying the FPM to the calculation and analysis of the wind-induced vibration of an antenna cable net, the mass and geometric nonlinearity of the cables were considered, and the calculated results were compared with the ANSYS finite element method, indicating the correctness of the finite particle method in the calculation of the wind-induced vibration of a cable net.
- (2)
- Compared with the FEM, using the FPM for the calculation and analysis of the wind-induced vibration of wires does not require the formation of complex nonlinear element stiffness or repeated iterative solutions. Therefore, the computational efficiency and convergence of the FPM are greatly improved.
- (3)
- The scheme proposed in this paper, which introduces the FPM into the analysis of the wind-induced vibration response of wires, is efficient and feasible and has great potential for application in subsequent research fields, such as the wind-induced vibration prevention of large-span antenna cables.
- (4)
- With the increase in the wind speed, the displacement of the cable under a gentle wind vibration gradually increases; with the maximum displacement in the mid-span vibration of the cable and with the increase in wind speed, the vertical vibration displacement of the mid-span particle increases the fastest.
- (5)
- When the wind speed is low, due to the self-damping effect of the cable, the wind-induced vibration of the cable is mainly controlled by the first-order vibration mode. When the wind speed is high, the wind-induced vibration response of the wire is affected by both the low-order and high-order vibration modes.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liang, T.J. Development of VLF communication technology. In Proceedings of the 18th China Aerospace Measurement and Control Technology Annual Conference, Dali, China, 18–20 June 2021; pp. 476–479. [Google Scholar]
- Williamson, R.A.; Stevenson, H.F.; Van der Pas, P.W. Computer design of a tower and cable system. J. Struct. Div. 1966, 92, 341–360. [Google Scholar] [CrossRef]
- Pen, T.; Xie, Q.; Zhang, J.; Xie, W.P. Response of wires to aeolian vibration and anti-vibration treatment. J. Guangdong Electr. Power 2017, 30, 104–108. [Google Scholar]
- Foti, F.; Martinelli, L. A unified analytical model for the self-damping of stranded cables under aeolian vibrations. J. Wind Eng. Ind. Aerod. 2018, 176, 225–238. [Google Scholar] [CrossRef]
- Zhang, J.G.; Liu, J.J.; Li, C.G.; Zhang, Y. Breeze vibration characteristics of large section conductors in UHV transmission lines. J. He Hai Univ. 2017, 45, 53–58. [Google Scholar]
- Vecchiarelli, J.; Currieg, I.G.; Havard, D.G. Computational analysis of aeolian conductor vibration with a stockbridge-type damper. J. Fluid Struct. 2000, 2000, 489–509. [Google Scholar] [CrossRef]
- Barry, O.; Zu, J.W.; Oguamanam, D.C.D. Forced Vibration of Overhead Transmission Line: Analytical and Experimental Investigation. J. Vib. Acoust. 2014, 136, 32–37. [Google Scholar] [CrossRef]
- Kong, D.Y.; Li, L.; Long, X.H.; Liang, Z.P. Analysis of aeolian vibration of UHV transmission conductor by finite element method. J. Vib. Shock. 2007, 26, 64–68. [Google Scholar]
- Ahmadizadeh, M. Three-dimensional geometrically nonlinear analysis of slack cable structures. Comput. Struct. 2013, 128, 160–169. [Google Scholar] [CrossRef]
- Li, X.; Xue, S.; Li, X.; Liu, G.; Liu, R. A numerical method to solve structural dynamic response caused by cable failure. Eng. Comput. 2023, 40, 2049–2067. [Google Scholar] [CrossRef]
- Lynn, K.M.; Isobe, D. Structural collapse analysis of framed structures under impact loads using ASI-Gauss finite element method. Int. J. Impact Eng. 2007, 34, 1500–1516. [Google Scholar] [CrossRef]
- Wu, T.; Lee, J.; Ting, E.C. Motion analysis of structures (MAS) for flexible multibody systems: Planar motion of solids. Multibody Syst. Dyn. 2008, 20, 197–221. [Google Scholar] [CrossRef]
- Bui, T.T.; Limam, A.; Sarhosis, V.; Hjiaj, M. Discrete element modelling of the in-plane and out-of-plane behaviour of dry-joint masonry wall constructions. Eng. Struct. 2017, 36, 277–294. [Google Scholar] [CrossRef]
- Belytschko, T.; Krongauz, Y.; Organ, D.; Fleming, M.; Krysl, P. Meshless methods:An overview and recent developments. Comput. Method Appl. Mach. Eng. 1996, 139, 3–47. [Google Scholar] [CrossRef]
- Luo, Y.Z.; Zheng, Y.F.; Yang, C.; Yu, Y.; Yu, F.; Zhang, P.F. Review of the finite particle method for complex behaviors of structures. J. Eng. Mech. 2014, 31, 1–7+23. [Google Scholar] [CrossRef]
- Yu, Y.; Xu, Y.; Luo, Y.Z. Dynamic nonlinear analysis of structures based on the finite particle method. J. Eng. Mech. 2012, 6, 63–69+84. [Google Scholar]
- Yu, Y.; Luo, Y.Z. Structural collapse analysis based on finite particle method I: Basic approach. J. Build. Struct. 2011, 11, 17–26. [Google Scholar]
- Yu, Y.; Luo, Y.Z. Structural collapse analysis based on finite particle method II: Key problems and numerical examples. J. Build. Struct. 2011, 32, 27–35. [Google Scholar]
- Yu, Y.; Luo, Y. Finite particle method for kinematically indeterminate bar assemblies. J. Zhejiang Univ. A Sci. 2009, 10, 669–676. [Google Scholar] [CrossRef]
- Yu, Y.; Luo, Y.Z. Motion analysis of deployable structures based on the rod hinge element by the finite particle method. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2009, 223, 955–964. [Google Scholar] [CrossRef]
- Luo, Y.; Yang, C. A vector-form hybrid particle-element method for modeling and nonlinear shell analysis of thin membranes exhibiting wrinkling. J. Zhejiang Univ. Sci. A Appl. Phys. Eng. 2014, 15, 331–350. [Google Scholar] [CrossRef]
- Yang, C.; Shen, Y.; Luo, Y. An efficient numerical shape analysis for light weight membrane structures. J. Zhejiang Univ. A Sci. 2014, 15, 255–271. [Google Scholar] [CrossRef]
- Zhang, P.F.; Luo, Y.Z.; Yang, C. Elastic-plastic analysis of 3d solids using the finite particle method. J. Eng. Mech. 2017, 34, 5–12. [Google Scholar]
- Lin, S.; Liang, Z.; Zhao, S.; Dong, M.; Guo, H.; Zheng, H. A comprehensive evaluation of ensemble machine learning in geotechnical stability analysis and explainability. Int. J. Mech. Mater. Des. 2023, 19, 1–22. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, F.H.; Wang, Q.H.; Luo, Y.Z.; Li, Y. Study on damping in finite particle method. J. Eng. Mech. 2019, 36, 34–40. [Google Scholar]
- Xie, W.P.; Xu, N.B.; Li, L.; Wang, Z. Research on form finding of power transmission conductors based on finite particle method. J. Guangdong Electr. Power 2016, 2, 101–106. [Google Scholar]
- Xie, W.P.; Xu, N.B.; Luo, X.Y.; Wang, Z.; Luo, X. Aeolian vibration of power transmission conductors based on finite particle method. J. Guangdong Electr. Power 2016, 29, 127–132. [Google Scholar]
- Diana, G.; Falco, M.; Cigada, A.; Manenti, A. On the Measurement of Over Head Transmission Lines Conductor Self-Damping. IEEE Trans. Power Deliv. 2000, 15, 285–292. [Google Scholar] [CrossRef]
- Campos, D.; Löser, E.; Piovan, M. Self-damping of Optical Ground Wire Cables: A Bayesian Approach. J. Appl. Comput. Mech. 2023, 9, 205–216. [Google Scholar]
- Zanelli, F.; Mauri, M.; Castelli-Dezza, F.; Tarsitano, D.; Manenti, A.; Diana, G. Analysis of Wind-Induced Vibrations on HVTL Conductors Using Wireless Sensors. Sensors 2022, 22, 8165. [Google Scholar] [CrossRef]
- Wang, F.; Wang, F.; Huang, Y.C.; Cheng, C.; Zhao, Q.J.; Bai, X.L. Analysis and experimental study on self-damping characteristics of long-span transmission lines. J. Proc. CSEE 2018, 38, 98–105. [Google Scholar]
- Tang, X.; Hou, W.; Zheng, Q.; Fang, L.; Zhu, R.; Zheng, L. Self-powered wind sensor based on triboelectric nanogenerator for detecting breeze vibration on electric transmission lines. Nano Energy 2022, 99, 107412. [Google Scholar] [CrossRef]




| Number | Section Diameter (mm) | Section Area (mm2) | Elastic Modulus (N/mm2) |
|---|---|---|---|
| 1 | 40 | 1257 | 142,000 |
| 2 | 40 | 1257 | 142,000 |
| 3 | 40 | 1257 | 142,000 |
| 4 | 40 | 1257 | 142,000 |
| 5 | 30 | 707 | 61,700 |
| 6 | 30 | 707 | 61,700 |
| 7 | 30 | 707 | 61,700 |
| 8 | 30 | 707 | 61,700 |
| 9 | 30 | 707 | 61,700 |
| 10 | 30 | 707 | 61,700 |
| 11 | 40 | 1257 | 142,000 |
| 12 | 40 | 1257 | 142,000 |
| 13 | 40 | 1257 | 142,000 |
| 14 | 40 | 1257 | 142,000 |
| 15 | 40 | 1257 | 142,000 |
| 16 | 30 | 707 | 61,700 |
| 17 | 30 | 707 | 61,700 |
| 18 | 30 | 707 | 61,700 |
| 19 | 30 | 707 | 61,700 |
| 20 | 30 | 707 | 61,700 |
| 21 | 30 | 707 | 61,700 |
| Cable Number | Wire Tension/kN | Cable Number | Wire Tension/kN | Cable Number | Wire Tension/kN |
|---|---|---|---|---|---|
| 1 | 173 | 8 | 38 | 15 | 193 |
| 2 | 238 | 9 | 31 | 16 | 27 |
| 3 | 173 | 10 | 27 | 17 | 31 |
| 4 | 237 | 11 | 193 | 18 | 38 |
| 5 | 27 | 12 | 157 | 19 | 38 |
| 6 | 31 | 13 | 141 | 20 | 31 |
| 7 | 38 | 14 | 157 | 21 | 27 |
| Number | Type | Sag | Number | Type | Sag |
|---|---|---|---|---|---|
| 1 | Sling | 0.35% | 12 | Sling | 1.21% |
| 2 | Sling | 0.26% | 13 | Sling | 1.35% |
| 3 | Sling | 0.35% | 14 | Sling | 1.21% |
| 4 | Sling | 0.26% | 15 | Sling | 0.96% |
| 5 | Top capacity line | 5.57% | 16 | Top capacity line | 5.57% |
| 6 | Top capacity line | 3.99% | 17 | Top capacity line | 3.99% |
| 7 | Top capacity line | 2.79% | 18 | Top capacity line | 2.79% |
| 8 | Top capacity line | 2.79% | 19 | Top capacity line | 2.79% |
| 9 | Top capacity line | 3.99% | 20 | Top capacity line | 3.99% |
| 10 | Top capacity line | 5.57% | 21 | Top capacity line | 5.57% |
| 11 | Sling | 0.96% | lCD | Sling | 8.67% |
| Number | Wire Length (m) | Mass per Unit Length of Wire (1 × 10–3 N·s2/m) | Initial Tension (kN) | 1st-Order Frequency (Hz) |
|---|---|---|---|---|
| 1 | 58 | 8.59 | 173 | 4.90 |
| 2 | 58 | 8.59 | 238 | 5.69 |
| 3 | 58 | 8.59 | 173 | 4.90 |
| 4 | 58 | 8.59 | 237 | 5.69 |
| 5 | 643 | 1.90 | 27 | 0.37 |
| 6 | 530 | 1.90 | 31 | 0.48 |
| 7 | 462 | 1.90 | 38 | 0.61 |
| 8 | 462 | 1.90 | 38 | 0.61 |
| 9 | 530 | 1.90 | 31 | 0.48 |
| 10 | 643 | 1.90 | 27 | 0.37 |
| 11 | 179 | 8.59 | 193 | 1.68 |
| 12 | 182 | 8.59 | 157 | 1.49 |
| 13 | 183 | 8.59 | 141 | 1.40 |
| 14 | 182 | 8.59 | 157 | 1.49 |
| 15 | 179 | 8.59 | 193 | 1.68 |
| 16 | 643 | 1.90 | 27 | 0.37 |
| 17 | 530 | 1.90 | 31 | 0.48 |
| 18 | 462 | 1.90 | 38 | 0.61 |
| 19 | 462 | 1.90 | 38 | 0.61 |
| 20 | 530 | 1.90 | 31 | 0.48 |
| 21 | 643 | 1.90 | 27 | 0.37 |
| Comparison Item | FPM | ANSYS | Relative Error |
|---|---|---|---|
| Maximum vertical acceleration response (mm·s−2) | 156.39 | 158.20 | 1.14% |
| Maximum vertical velocity response (mm·s−2) | 12.82 | 12.79 | 0.20% |
| Maximum vertical displacement response (mm·s−2) | 2.42 | 2.43 | 0.42% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, K.; Zhao, F.; Luo, Y.; Fang, B.; Chen, S. Aeolian Vibration Dynamic Analysis of Large-Span, Relaxed Antenna Cable Net Based on Finite Particle Method. Buildings 2024, 14, 105. https://doi.org/10.3390/buildings14010105
Qin K, Zhao F, Luo Y, Fang B, Chen S. Aeolian Vibration Dynamic Analysis of Large-Span, Relaxed Antenna Cable Net Based on Finite Particle Method. Buildings. 2024; 14(1):105. https://doi.org/10.3390/buildings14010105
Chicago/Turabian StyleQin, Kai, Fan Zhao, Yaozhi Luo, Bin Fang, and Shangyuan Chen. 2024. "Aeolian Vibration Dynamic Analysis of Large-Span, Relaxed Antenna Cable Net Based on Finite Particle Method" Buildings 14, no. 1: 105. https://doi.org/10.3390/buildings14010105





