Next Article in Journal
A Seismic Risk Assessment of Concrete-Filled Double-Skin Steel Tube (CFDST) Frames with a Beam-Only-Connection for Reinforced Concrete Shear Walls (BRWs)
Previous Article in Journal
Early Age Performance of OPC-GGBFS-Concretes Containing Belite-CSA Cement Cured at Sub-Zero Temperatures
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Buildings
Volume 13
Issue 9
10.3390/buildings13092376
buildings-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Pressure Optimization in Pneumatic Interfaces Using a Single-Bay Seven-Story Infilled Reinforced Concrete Frame: Experimental and Numerical Investigation

by
Prem Kumar George
1,*,
Thirumurugan Varatharajan
1,
Satyanarayanan Kachabeswara Srinivasan
1,
Ibrahim Y. Hakeem
2 and
Yasin Onuralp Özkılıç
3,4,*
1
Department of Civil Engineering, College of Engineering and Technology, SRM Institute of Science and Technology, SRM Nagar, Kattankulathur 603 203, Tamil Nadu, India
2
Department of Civil Engineering, College of Engineering, Najran University, Najran P.O. Box 1988, Saudi Arabia
3
Department of Civil Engineering, Faculty of Engineering, Necmettin Erbakan University, Konya 42090, Turkey
4
Department of Civil Engineering, Lebanese American University, Byblos 1102-2801, Lebanon
*
Authors to whom correspondence should be addressed.
Buildings 2023, 13(9), 2376; https://doi.org/10.3390/buildings13092376
Submission received: 28 July 2023 / Revised: 28 August 2023 / Accepted: 14 September 2023 / Published: 19 September 2023
(This article belongs to the Section Building Structures)
Browse Figures
Versions Notes

Abstract

:
Reinforced concrete infilled frames have been studied over the years along with the infilled openings. To resist the lateral loads that are applied on the frames, stress is transferred from the reinforced concrete (RC) to infill, which leads to brittle collapse. The conventional interface medium, which was considered by researchers and recent studies, was prepared by changing the interface materials between the RC frame and infill panels to different elastic materials. This study focuses on optimizing the interface pressure using a butyl rubber tube, which reduces the stress distribution to the infill panel from the RC frame. A 50% window opening was adopted in this study, which is the optimized size from previous research. The optimization patterns followed linear and nonlinear patterns, such as the same pressures in all stories and varying pressures in all stories. The third story had a 8 PSI pattern and the other stories had a 2 PSI pattern; all stories with 8 PSI patterns achieved the least displacement when compared to other variations. A monotonic static analysis was performed for both the experimental and analytical study. The boundary conditions were pinned, and coupling interfaces were made for the master and slave surfaces. The pressure conditions were applied in various linear and nonlinear patterns to optimize the pressure. A comparative study was performed on the displacement, stiffness, and drift ratio for the critical position of the interface pressure in both the analytical and experimental studies. The difference was approximately 0.53% in the analytical study and 0.37% in the experimental work. The optimization was performed using both an experimental model and an analytical model, which had an error percentage of 0.61%.

1. Introduction

In the early 20th century, pure masonry infilled walls were used as structural members of load-bearing walls. Then, timber columns and beams were introduced to form framed structures, and masonry infills were used as just partition members [1,2]. Eventually, concrete was invented and still continues to be developed [3,4,5,6,7]. Recent studies have provided new aspects to concrete [8,9,10,11,12]. Therefore, reinforced concrete materials are utilized as structural elements [13,14,15,16,17] and designed according to code provisions, but the masonry infilled walls are not considered a structural element in the analytical frame models and have not been included in the codes. The varying infills present in RC structures significantly alter the lateral load through factors such as energy dissipation, stiffness, mechanical properties, and failure modes. The failures of infill walls in the RC frame model are due to the transfer of load from the RC to the infill wall member. This issue has attracted many researchers to develop infill designs using RC analytical models [18,19].
Infill walls are considered rigid components when compared to the reinforced concrete member. Therefore, the damage created by the lateral loads will be higher in the infill walls than in the reinforced concrete member. These infill walls are somewhat safer when the load is under in-plane action. However, when the load is acting out of the plane, there may be a sudden collapse in the structure [20]. The bare frame structure is displaced more when compared to the infilled RC structures. This response is due to the strut action of the infills present between the RC frames when the lateral load acts on the frame. The infilling materials have been studied, and there have been improvements in the ductility characteristics of the infilled frame, lateral stiffness, and axial strength when lateral or seismic loading occurs in the frame and resisting the drift occurring in the specimen as specified by the code limits [21,22,23,24]. Masonry infills are conventionally built using clay bricks; in recent studies, these structures have also started to be built as hollow blocks, solid blocks, and fly ash bricks [25,26,27,28]. Studies have also been conducted on repairing and retrofitting masonry walls bonded with RC frames of existing buildings that were damaged when exposed to lateral loads [24,29,30]. The masonry infilled structure is stiffer when the in-plane load acts on it compared to the out-of-plane action in the structure [31]. The bare frames are infilled in particular bays of the RC frames to strengthen the reinforced concrete structures. This is to improve the stiffness, stability, and energy that are transferred to the RC frame in the in-plane direction [32]. Various studies have been conducted with models that are scaled down at 1/2 and 1/3 ratios of reinforced concrete frames infilled with masonry walls. Several tests have been performed on various scale-down models [33,34] using shake tables [35].
Recent studies have focused on the strengthening of infills in the reinforced concrete frame to increase the resistance to lateral loads. Several techniques were developed to increase the resistance to load [36], and a review was written by [37] on strengthening the masonry infill structure against lateral loads. Many techniques were developed to strengthen the unreinforced masonry infills that are adjacent to the frame member for increasing loads. The strengthening of masonry walls may increase the cost due to the usage of different materials other than conventional materials. Alternative designs have been developed to enhance the resistance to lateral loads that are transferred from the RC frame element to the unreinforced masonry infill wall. The soft layers shown in Figure 1 were used by researchers to increase the resistance to the lateral load transfer from the bounding frame [38,39,40]. The layers can be placed either parallel to the brick laid or with the interface between the reinforced concrete frames and the unreinforced masonry walls [41,42,43]. This technique could use soft rubber materials, which can give high stiffness toward the three dimensions of the frame. The rubber interface material was tested by a European research project on seismic resistance of infilled frames [44]. In recent years, studies have performed complex simulations of the interaction between reinforced concrete frames and unreinforced masonry walls using finite element modeling [45,46,47].
In reinforced concrete, masonry infills with openings possesses two different positions for windows and doors, which decides the shear resistance of the frame [48,49,50]. Many researchers have optimized the window size and position of the windows and doors so that eccentrically positioned doors and windows achieve less shear resistance than centrically positioned doors and windows. The shear resistance of a reinforced concrete masonry infilled frame with door openings exceeds that of the bare frame. Reinforced concrete infilled walls with doors and window openings, which are positioned at centrical openings, possess a lower deformation capacity when compared to the bare frame and infilled frame without openings [51].
Experimental studies have shown that the introduction of doors and windows, the H/L ratio of the wall, the amount of rebar in the vertical and horizontal directions, and the types of units are some variables that determine the deformation capacity of walls [52,53,54]. There was a negative influence registered for the frames that have openings in the wall panel during the experimental investigations and in past seismic events [55,56,57]. The lateral stiffness of the reinforced concrete infilled frame seems to be less for the wall with openings when compared to the fully infilled panel. The opening present in the walls will experience more lateral displacement, which directly behaves as a less stiff frame [58,59]. There is a large amount of stress that concentrate at the corner of the windows that lead to crack formation at the diagonals, subsequently weakening the wall’s resistance to lateral loads [60]. The suggestion made by experimental studies is that an appropriate confinement should be introduced on all the faces of the openings to minimize the seismic effects on the masonry buildings [61].
To reduce the displacement that leads to the collapse of the structure entirely when an external load acts on frames, an elastic medium is introduced at the interface of the reinforced concrete frame and the masonry infill panel, as shown in Figure 2a [51,62,63,64,65]. Analytically, the specimens are designed and tested for various parameters, in which Abaqus 14.1 software is used by many researchers, and validations are made using the experimental results [66]. Many studies have been carried out to study methods that allow reinforced concrete frames to shift lateral loads to masonry infill panels. Interface materials are utilized to resist the lateral loads between the RC frame and infills. These interface materials can resist lateral loads to some extent as per the elastic property of the material. The lateral loads are transferred by the interface material directly to the infills from the RC after the limit is reached to resist the loads. Improving the lateral load resistance in the frame through the use of a butyl rubber tube filled with air pressure has been introduced in this current study. These pressures are increased with increasing loads applied to the frame. This study mainly focused on applying air pressure to butyl rubber tubes in multi-story building panels; optimization is performed to find the critical floor to resist the lateral load completely. The PSI in the butyl rubber tubes has been optimized in linear and nonlinear patterns in all the story levels to conserve pneumatic energy.

2. Methodology

2.1. Modeling of Seven-Story Frames

One of the most utilized methods for cost-free analysis is finite element modeling [67,68,69,70,71]. A seven-story reinforced concrete infilled wall was modeled in this study using ABAQUS version 6.14 as the finite element modeling tool [72]. A seven-story frame was modeled by decreasing the scale by 1/4th of the building’s dimension, as shown in Figure 2b. A butyl rubber tube mechanism was introduced at the interface of the reinforced concrete frame and the masonry infill. There is a pushing effect from the inside of the RC element and outside of the infill element when the load is applied to the frame. The properties of the concrete, masonry infill, and interface pressures have been prescribed to the elements to compare the experimental and analytical results. The frame and infills were discretized into several meshes for the efficiency of the result. The mesh convergence study was carried out to optimize the mesh size for the RC frame and the masonry infill, which is shown in Figure 3. The deflection was noted at the critical story (3rd floor), and the lateral deflection saturated at 40 mm for the reinforced concrete frame. A further increase in mesh size had no effect, and the flat line indicates the same. The mesh adopted for frames is a hexahedron mesh at 40 mm [66], and for infill, it is 30 mm in size. The boundary conditions and the interactions for the RC frame and interface material and interface material to infill are discussed in detail in Table 1. The concrete grade used for this study was M20, the steel grade was FE500, and their properties were fed into the FEM software Abaqus 14.1 for real-time analysis.
The load was applied at the left top flange of the frame, and pinned support was adopted in this study. The opening was 50% of the area of the infill panel, which is the optimized size for attaining better performance in lateral loads [51].
Initially, a load of 9 kN was applied for the frame to optimize the pressures and the location of the pressure to be applied to conserve the energy. There is a plastic limit zone where the frame initiates the cracks, and it was theoretically calculated and fixed as 9 kN for optimization. Figure 4a indicates the displacement of the frame when the load is applied, and the distribution of the stress is shown clearly in Figure 4b. Plastic hinge formation originated at the 3rd story of the frame, which also matches the theoretical calculations and is evident in Figure 4b. The gray shaded area indicates the maximum stress point which then decreases into the red to blue shades.

2.2. Experimental Setup of Seven Story Frames

A seven-story frame is shown in Figure 5, which is a 2D frame subjected to wind loads. This seven-story frame was cast in a steel formwork that was coated with friction-less elements. Before placing the steel reinforcement inside the formwork, a strain gauge was fixed in the reinforcement at particular locations to observe the internal strain values when the load is applied to the frame. The strain gauge had a 10 mm deflection range and 120 ohms resistance. The strains were fixed at both the windward and leeward sides of the frame up to 3 story levels. The maximum stiffness has been achieved in the bottom 3 stories, so the strain values were measured up to 3 stories. The reinforcements were installed in the formwork, and the concreting was made with 10 mm aggregates due to the scaled-down model size of the frame.
The reinforced concrete frame was cast for 28 days with water curing and then installed in the self-straining steel frame with an ultimate loading capacity of 30 tons for both lateral and axial loading, as shown in Figure 6. The frame was fixed into a foundation with a width 3 times the frame width. Instead, it is a 2-dimensional frame that is exposed to torsion when the load was applied. To eliminate these torsional forces, roller supports were fixed at either side of the frame on two floor levels: 4th and 6th stories. The loading jack with a capacity was fixed at the windward side of the RC frame. In the loading jack, the load cell was fixed in between the frame.
The displacement was measured by using the linear variable displacement transducer (LVDT) in the frame at all the stories with a capacity of 200 mm at the top 3 floors and 100 mm for all the other floors. These displacements and strains were measured by connecting them to the 32-channel data logger, which has the strain indicators and displacement indicators for the respective loads. The load was applied by connecting the jack with the actuator, which has the control meter where the load was applied to the frame in a regular interval of 0.5 kN to 1 kN. The pressure was applied to the interface butyl rubber tube by connecting it with the compressor at the source end and the other end was connected to a pressure regulator. In the pressure regulator, the pressures were controlled by the control panel and then connected to the butyl rubber tube, which was fixed between the frame and infill. The measurements were taken as a report with the use of SYSCON software V 2.1, which was connected to the data logger. The uplift of the frame was restricted by placing a frame structure at the foundation ends of the frame. The load initially applied here was 9 kN, which was taken from a theoretical calculation. The plastic hinge portion was obtained by a theoretical calculation, and its initial cracking was calculated and found to be approximately 9 kN.

3. Results and Discussion

3.1. PSI Optimization—Analytical Study

The pressures were applied to the butyl rubber tubes at varying PSI as trials. The tubes were filled at 2PSI, 4PSI, 6PSI, 8PSI, and 10PSI and controlled by the pneumatic controller setup. For all seven stories, the pressure was filled in a similar manner to optimize the pressure at which the displacement decreased. All the displacements were measured at the 7th story in the frame, and the minimum displacement is clearly pictured in Figure 7. Maintaining 8 PSI at all seven stories showed the least displacement when compared to other PSI dosages, as shown in Figure 4. A further increase in pressure in the tubes showed that the transfer of loads to the infills led to an increase in displacement compared with the 8 PSI dosage. There was a 0.73% difference from 6PSI to 8PSI and a 0.48% difference from 8PSI to 10PSI. The 2PSI specimen attained a higher displacement than the other variations in PSI due to the behavior of the cement–mortar interface effect. The mean value for the linear optimizing pressure was 10.55 mm, and the standard deviation was 0.424, as shown in Figure 8.

3.2. Story Optimization—Analytical Study

The pressure in the linear pattern will consume more energy by maintaining the pressures at all the stories. To overcome this issue, nonlinear patterns were followed in this study by altering the pressures in each story. The patterns followed here are first story 8PSI, other stories 2PSI (1S8P); second story 8PSI, and others 2PSI (2S8P); similarly, the patterns are 3S8P, 4S8P, 5S8P, 6S8P, and 7S8P. The 1S8P pattern showed less displacement when compared to the other variations, which is evident in Figure 9.
However, several tall buildings have soft story effects in the 1st story or ground story. Then, the next level of the minimum displacement profile was obtained with 3S8P, so the pressure at the third story alone was 8 PSI, and the other stories were 2 PSI for this study. There was a gradual increase in displacement in frames when the pressure was moved to the top story, which behaved as a conventional frame. The mean value for the linear optimized pressure was 10.55 and 0.424 for the standard deviation, as shown in Figure 10.

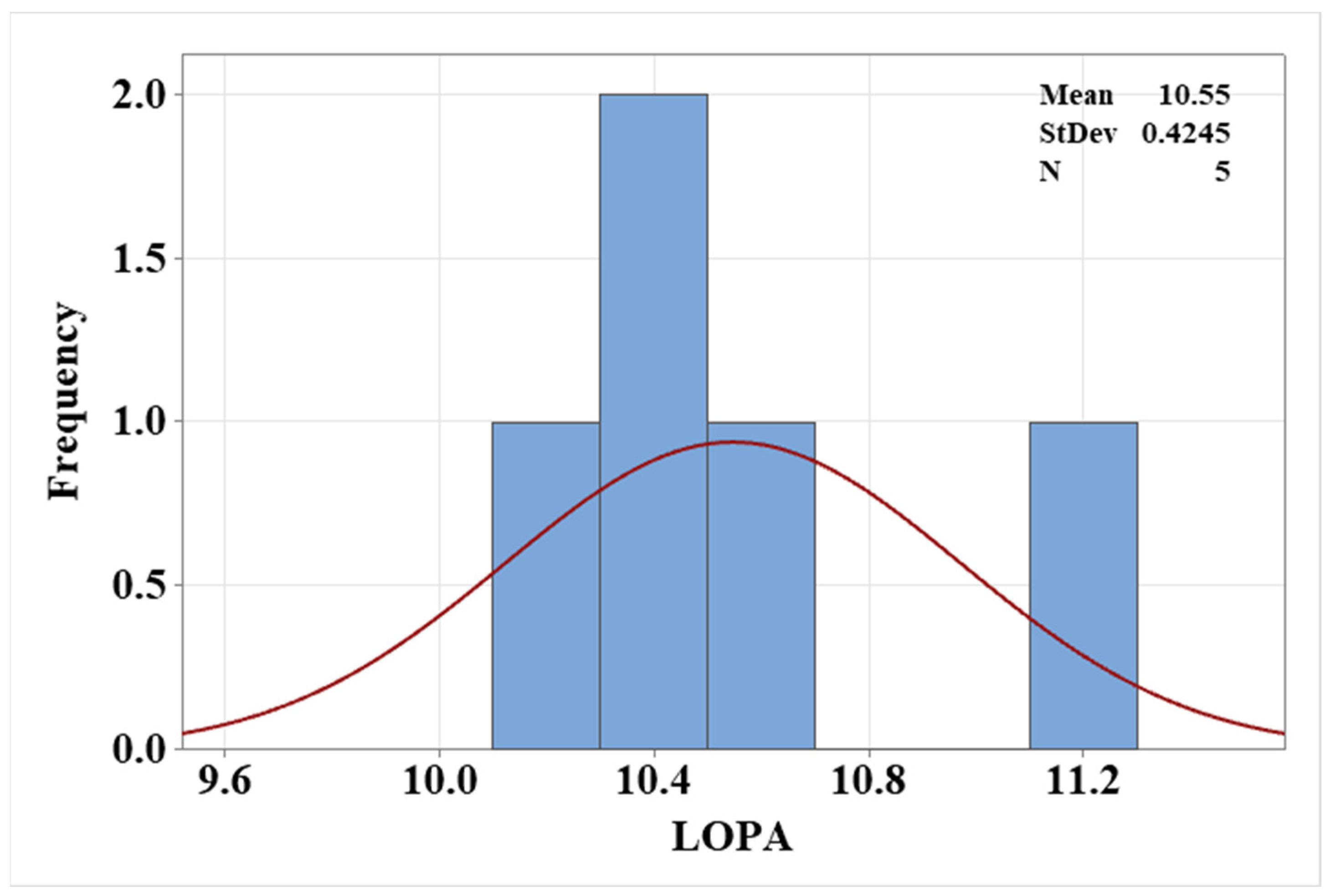
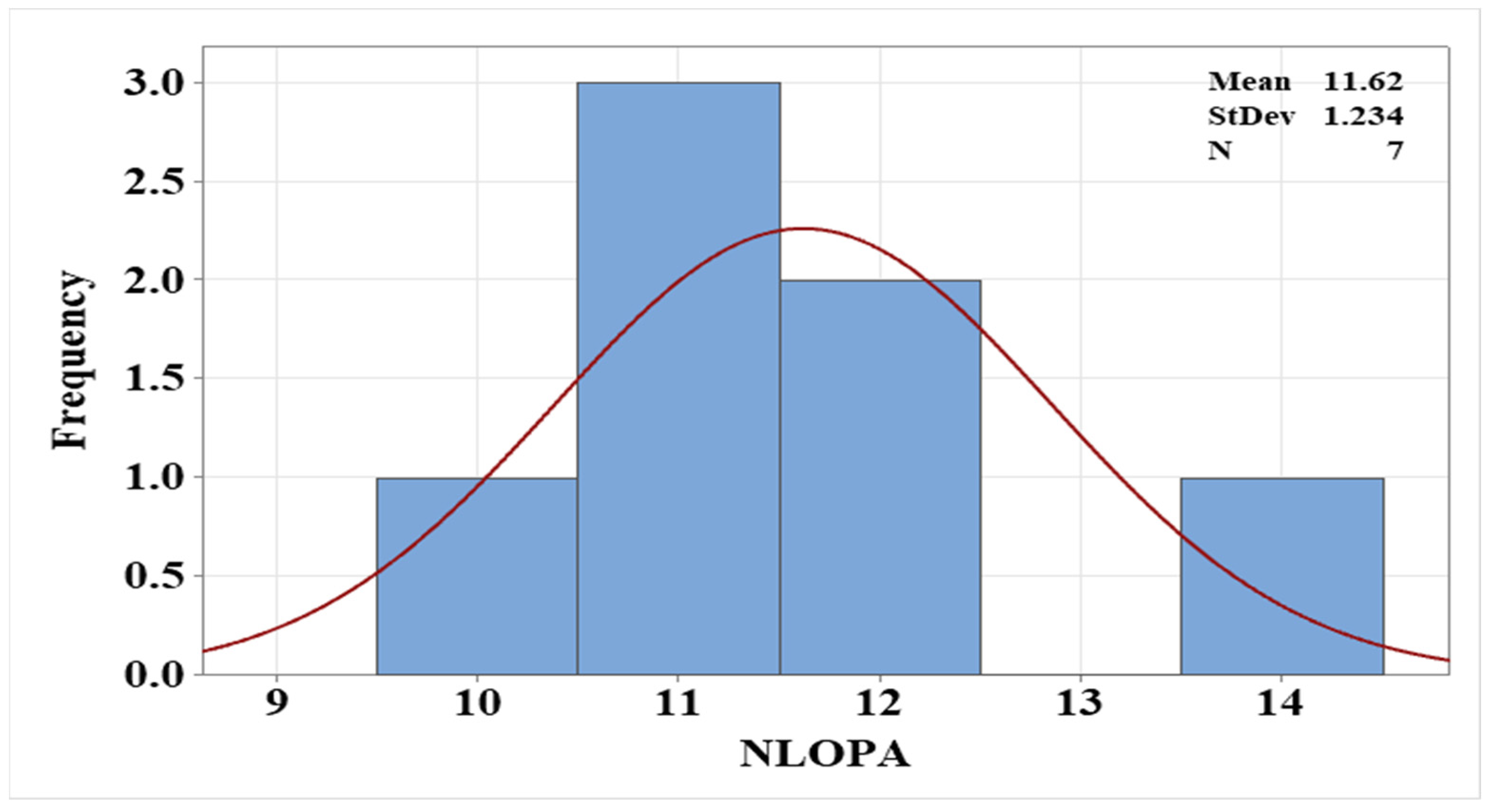
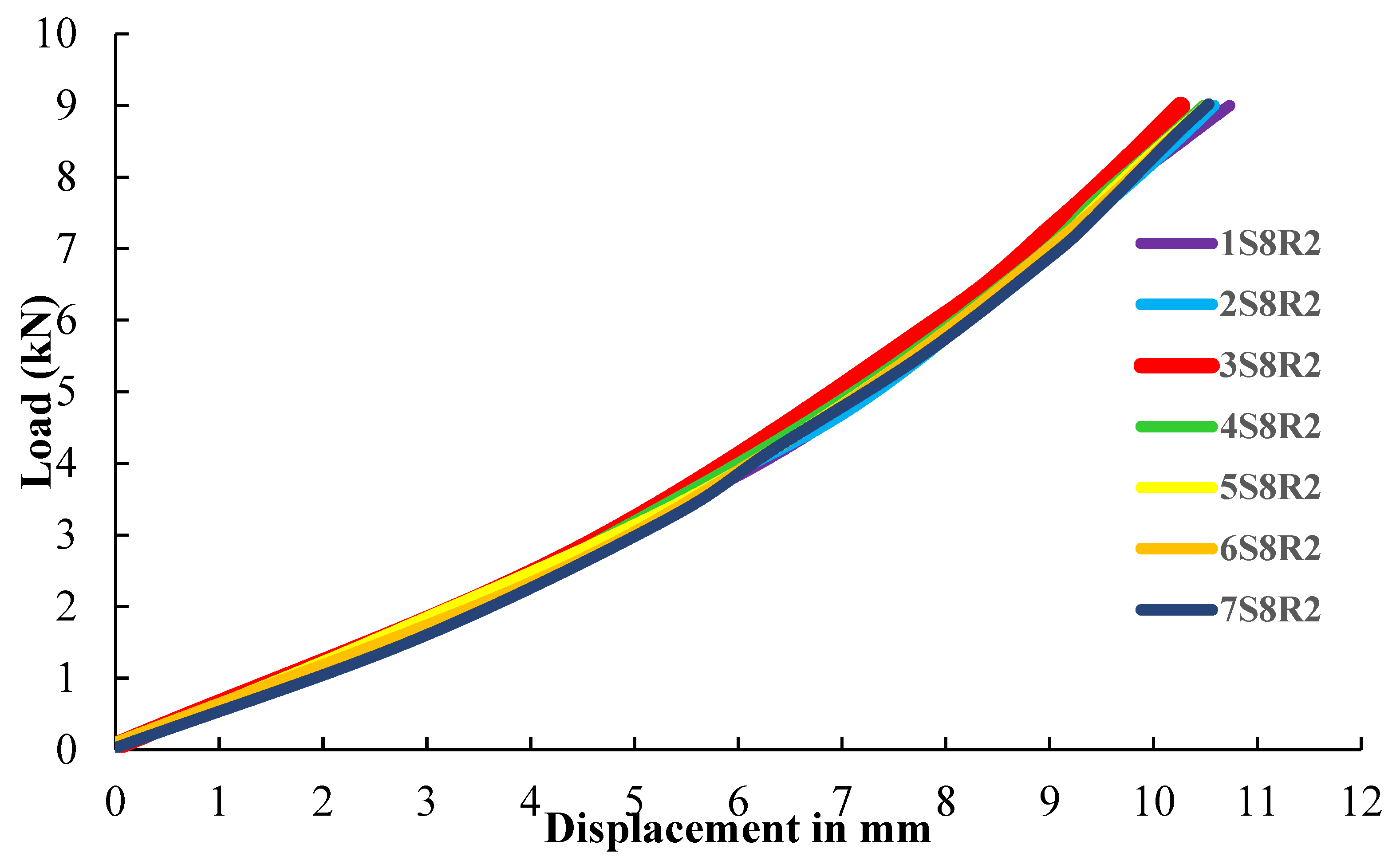
3.3. PSI Optimization—Experimental Study

The PSI was optimized using an analytical study, which was then compared with the results from the experimental study. The displacements were measured using LVDTs, and their values were then plotted. Figure 11 shows the comparison of all the varying PSIs on all the floors. The All 8P model had the smallest displacement compared with the other variations. This result correlates with the analytical study, and the trend was also the same here. Increasing the PSI above 8PSI increased the displacement: All 10P produced results that were more similar to those of All 8P and All 2P produced a greater displacement. Thus, the analytical results were validated by the experimental work.

3.4. Story Optimization—Experimental Study

The nonlinear optimization of pressure was performed experimentally by varying the pressures in each story, which was mentioned in Section 3.2. The pressures were controlled by pneumatic regulators, as shown in Figure 6. Here, the 3S8P model also had a better displacement when compared to the other story 8PSI variations, which are clearly pictured in Figure 12. The fixing of 8PSI at the third story restricted the plastic hinge formation at the early loads. These will act as a bare frame effect so that the crack initiation is minimized. The load transfer from the third story to the second and fourth stories is evident in the stress distribution shown in Figure 4b. This experimental study also validated the analytical model by correlating them with each other. Application of 8PSI to the top stories increased the displacement, which is also consistent with the results of the analytical work. There was a difference of 0.31% between 1S8R2 and 3S8R2, which shows the gap between the analytical study and the experimental study.

4. Comparative Study

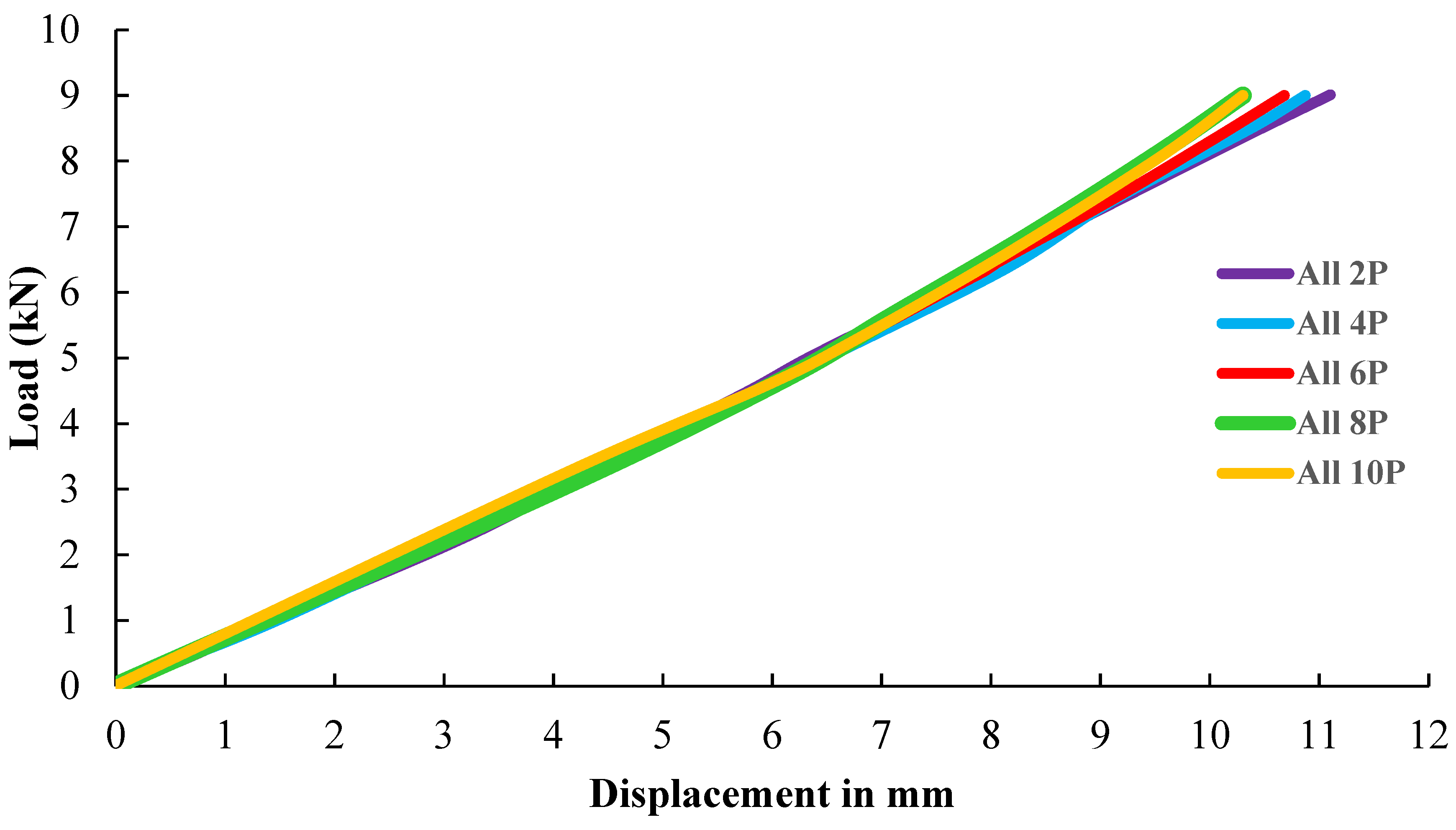
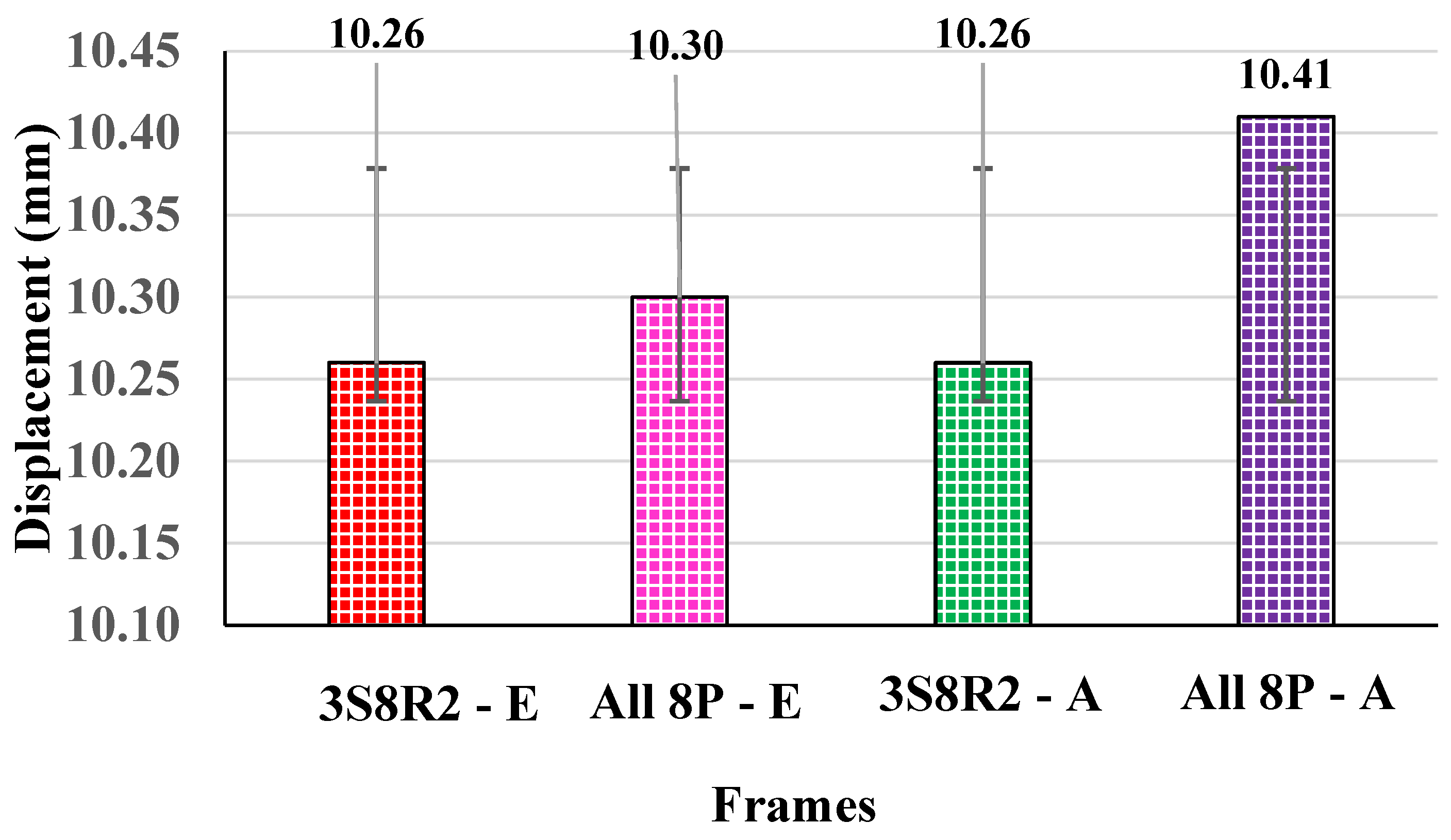
4.1. Displacement Study

The experimental and analytical results of both the linear and nonlinear patterns were compared. Figure 13 clearly shows that there was a small difference between fixing 8PSI in all the stories and fixing 8PSI at the third and 2PSI in the others. The difference was approximately 0.53% in the analytical study and 0.37% in the experimental work. This optimization process conserves energy in the remaining six stories. The error percentage for the experimental and analytical models was 0.61%, which is negligible. This effect is due to the critical position in which the plastic hinge formation occurs at the third story of the frame. Therefore, the pressure was given at the third story to resist the lateral load, which directly reduces the displacement when compared to the other pressure patterns.

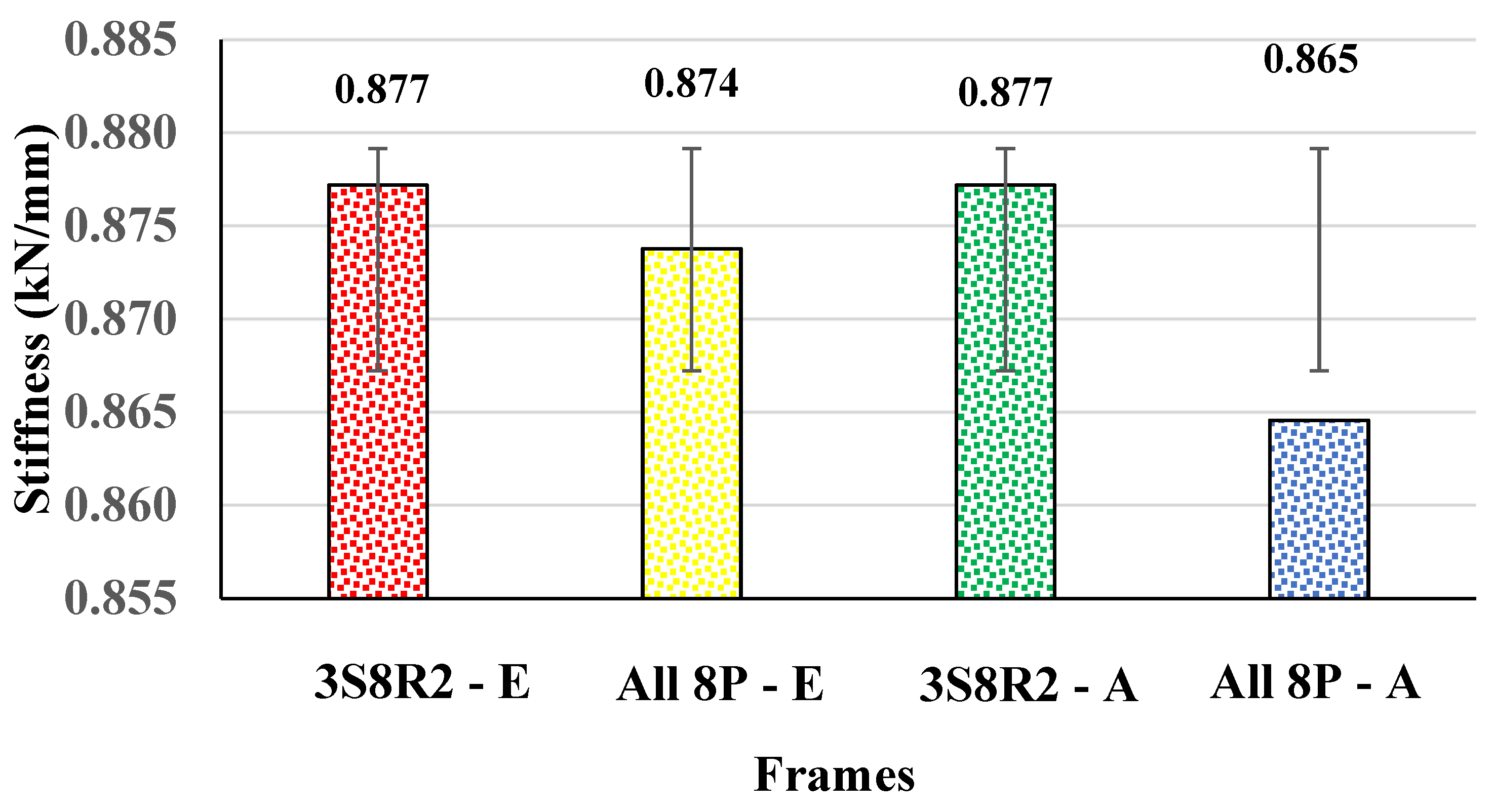
4.2. Stiffness Study

When comparing the stiffness of the linear and nonlinear pattern frames from the experimental and analytical studies, there was a higher stiffness in 3S8R2 than in All 8P in both the experimental and analytical studies. The 3S8R2 frame had a 0.34% higher stiffness than the All 8P frame experimentally, which is plotted in Figure 14. The stiffness was increased in the 3S8R2 pressure pattern frame compared to the other patterns due to the resistance of the lateral load by the pressure applied to the butyl rubber tubes. The plastic hinge formation location was found to be the third story and applying the pressure at that point improved the stiffness of the frame when a lateral load was applied to the frame.

4.3. Drift Study

The drift ratio is a quantitative measure that characterizes the relationship between the maximum lateral drift and the overall height of a given specimen. This method is employed to quantify the decrease in shear strength that transpires during the application of loads and the subsequent amplification of lateral drift. The story drift ratio is a valuable metric that can be employed to establish restrictions on story drift, expressed as a percentage of the story height, during seismic loading. The drift ratio for the optimized pressure patterns was calculated for both linear and nonlinear pressure patterns shown in Figure 15. The drift ratios prove that there was a significant decrease in the drift of the 3S8R2 pressure pattern frame when compared to the All 8P in both the experimental and analytical work. There was an improvement in stiffness that directly reflects a decreasing drift ratio, which causes the frame to not collapse and be more durable. The lower drift ratio causes twisting of the frame and allows the frame to be more stable.

5. Conclusions

Seven-story frames were tested by previous studies but the openings for windows were not specified. Moreover, ductile detailing was also added in this study. A 50% window opening was adopted in this study, which is the optimized size from previous research. A pneumatic interface was introduced in this study between the RC frame and infill panel. Optimizing the pressures in the pneumatic tubes was the main theme of this study. The optimization patterns followed linear and nonlinear patterns, such as the same pressures in all stories and varying pressures in all stories. The difference in displacement was due to the production of a plastic hinge on the third level of the frame, which is the site of the initial point of failure. This plastic hinge was the source of the initial point of failure. Because the butyl rubber tube was utilized as an interface material with pressure, the stress distribution at the third level was prevented. This led the frame to be displaced less than it would have if the pressure was applied in the interface medium at other levels. This method of optimization helps to conserve energy throughout the remaining six stories. The outcomes obtained from this study can be summarized as follows:
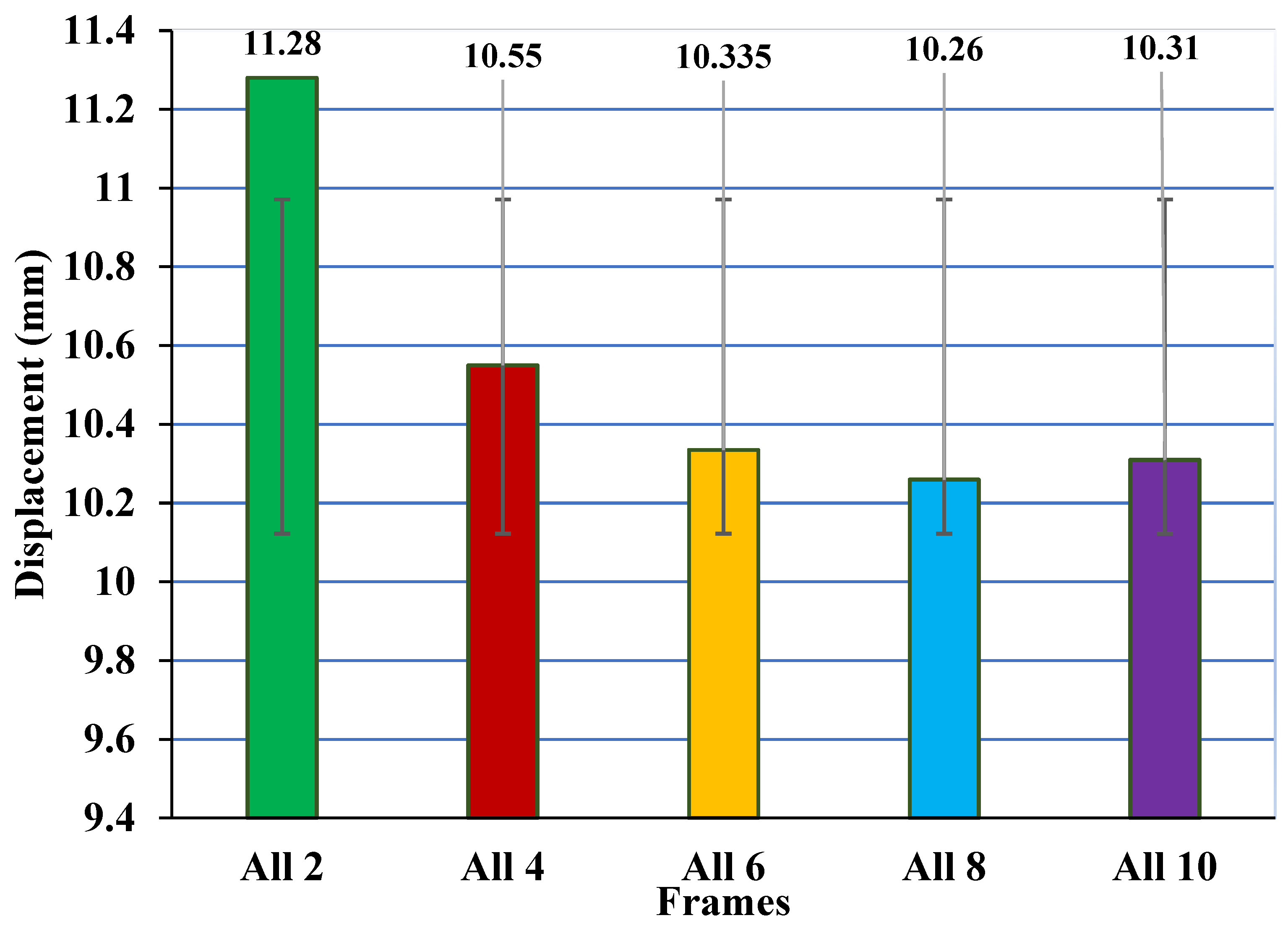
  • Maintaining 8 PSI at all seven stories showed the least displacement when compared to other PSI dosages.
  • There was a 0.73% difference between 6 PSI and 8 PSI and a 0.48% difference between 8 PSI and 10 PSI.
  • The next smallest displacement profile was obtained with 3S8P, so the pressure at the third story alone was set to 8 PSI, and the other stories were set as 2 PSI for this study. There was a gradual increase in displacement of frames when the pressure was moved to the top story, which behaved as a conventional frame.
  • The 3S8P and All 8P patterns achieve the least displacement when compared to the other variations. The difference was approximately 0.53% in the analytical study and 0.37% in the experimental work.
  • The frame 3S8P achieved the minimum displacement; this was due to the critical position in which the plastic hinge formation occurs at the third story of the frame. Therefore, the pressure was applied at the third story to resist the lateral load, which directly reduced the displacement when compared to the other pressure patterns.
  • The optimization was performed using both an experimental model and an analytical model, which had an error percentage of 0.61%.
  • There was a higher stiffness in 3S8R2 than in All 8P in both the experimental and analytical studies. The 3S8R2 frame was 0.34% times higher in stiffness than the All 8P frame experimentally.
  • The stiffness was increased in the 3S8R2 pressure pattern frame compared to the other patterns due to the resistance of the lateral load by the pressure applied to the butyl rubber tubes.
  • The drift ratios prove that there was a significant decrease in the drift of the 3S8R2 pressure pattern frame when compared to All 8P in both the experimental and analytical work. There was an improvement in stiffness that directly reflects a decreasing drift ratio, which caused the frame to not collapse and be more durable.

Author Contributions

Conceptualization, P.K.G., T.V. and Y.O.Ö.; Methodology, P.K.G., T.V. and Y.O.Ö.; Software, P.K.G. and S.K.S.; Validation, S.K.S.; Formal analysis, P.K.G., S.K.S. and I.Y.H.; Investigation, T.V. and I.Y.H.; Resources, I.Y.H.; Writing—original draft, P.K.G.; Writing—review & editing, P.K.G. and Y.O.Ö. All authors have read and agreed to the published version of the manuscript.

Funding

No funding involved in this research.

Data Availability Statement

The data underlying this study are openly available.

Acknowledgments

The authors are thankful to the Deanship of Scientific Research at Najran University for funding this work, under the Research Groups Funding program (grant code NU/RG/SERC/12/11). The authors are also grateful for the support from the Structural Engineering Laboratory SRMIST and Bentley LAB SRMIST.

Conflicts of Interest

There is no conflict of interest in this research.

References

  1. Palyvou, C. Akrotiri Thera: Building Technics and Morphology in Late Cycladic Architecture. Ph.D. Thesis, School of Architecture, National Technical University of Athens, Athens, Greece, 1988. (In Greek). [Google Scholar]
  2. Tsakanika, E. The Structural Role of Timber in Masonry of the Palatial Architecture of Minoan Crete. Ph.D. Thesis, School of Architecture, National Technical University of Athens, Athens, Greece, 2007. (In Greek). [Google Scholar]
  3. Fang, B.; Hu, Z.; Shi, T.; Liu, Y.; Wang, X.; Yang, D.; Zhu, K.; Zhao, X.; Zhao, Z. Research progress on the properties and applications of magnesium phosphate cement. Ceram. Int. 2022, 49, 4001–4016. [Google Scholar] [CrossRef]
  4. Shi, T.; Liu, Y.; Hu, Z.; Cen, M.; Zeng, C.; Xu, J.; Zhao, Z. Deformation Performance and Fracture Toughness of Carbon Nanofiber Modified Cement-Based Materials. ACI Mater. J. 2022, 119, 119–128. [Google Scholar] [CrossRef]
  5. Shi, T.; Liu, Y.; Zhao, X.; Wang, J.; Zhao, Z.; Corr, D.J.; Shah, S.P. Study on mechanical properties of the interfacial transition zone in carbon nanofiber-reinforced cement mortar based on the PeakForce tapping mode of atomic force microscope. J. Build. Eng. 2022, 61, 105248. [Google Scholar] [CrossRef]
  6. Jin, M.; Ma, Y.; Li, W.; Huang, J.; Yan, Y.; Zeng, H.; Lu, C.; Liu, J. Multi-scale investigation on composition-structure of C-(A)-S-H with different Al/Si ratios under attack of decalcification action. Cem. Concr. Res. 2023, 172, 107251. [Google Scholar] [CrossRef]
  7. Wang, M.; Yang, X.; Wang, W. Establishing a 3D aggregates database from X-ray CT scans of bulk concrete. Constr. Build. Mater. 2022, 315, 125740. [Google Scholar] [CrossRef]
  8. Tang, H.; Yang, Y.; Li, H.; Xiao, L.; Ge, Y. Effects of chloride salt erosion and freeze–thaw cycle on interface shear behavior between ordinary concrete and self-compacting concrete. Structures 2023, 56, 104990. [Google Scholar] [CrossRef]
  9. Zhou, S.; Lu, C.; Zhu, X.; Li, F. Preparation and Characterization of High-Strength Geopolymer Based on BH-1 Lunar Soil Simulant with Low Alkali Content. Engineering 2021, 7, 1631–1645. [Google Scholar] [CrossRef]
  10. Cai, J.; Pan, J.; Li, G.; Elchalakani, M. Behaviors of eccentrically loaded ECC-encased CFST columns after fire exposure. Eng. Struct. 2023, 289, 116258. [Google Scholar] [CrossRef]
  11. Li, D.; Nie, J.-H.; Wang, H.; Yan, J.-B.; Hu, C.-X.; Shen, P. Damage location, quantification and characterization of steel-concrete composite beams using acoustic emission. Eng. Struct. 2023, 283, 115866. [Google Scholar] [CrossRef]
  12. Özkılıç’, Y.O.; Beskopylny, A.N.; Stel’makh, S.A.; Shcherban’, E.M.; Mailyan, L.R.; Meskhi, B.; Chernil’nik, A.; Ananova, O.; Aksoylu, C.; Madenci, E. Lightweight Expanded-Clay Fiber Concrete with Improved Characteristics Reinforced with Short Natural Fibers. Case Stud. Constr. Mater. 2023, 19, e02367. [Google Scholar] [CrossRef]
  13. Huang, Y.; Zhang, W.; Liu, X. Assessment of Diagonal Macrocrack-Induced Debonding Mechanisms in FRP-Strengthened RC Beams. J. Compos. Constr. 2022, 26, 4022056. [Google Scholar] [CrossRef]
  14. Wei, J.; Xie, Z.; Zhang, W.; Luo, X.; Yang, Y.; Chen, B. Experimental study on circular steel tube-confined reinforced UHPC columns under axial loading. Eng. Struct. 2021, 230, 111599. [Google Scholar] [CrossRef]
  15. Huang, H.; Huang, M.; Zhang, W.; Guo, M.; Liu, B. Progressive collapse of multistorey 3D reinforced concrete frame structures after the loss of an edge column. Struct. Infrastruct. Eng. 2022, 18, 249–265. [Google Scholar] [CrossRef]
  16. Zhang, W.; Liu, X.; Huang, Y.; Tong, M.-N. Reliability-based analysis of the flexural strength of concrete beams reinforced with hybrid BFRP and steel rebars. Arch. Civ. Mech. Eng. 2022, 22, 171. [Google Scholar] [CrossRef]
  17. Özkılıç, Y.O.; Aksoylu, C.; Arslan, M.H. Numerical evaluation of effects of shear span, stirrup spacing and angle of stirrup on reinforced concrete beam behaviour. Struct. Eng. Mech. Int’L J. 2021, 79, 309–326. [Google Scholar]
  18. Barros, M.; Cavaco, E.; Neves, L.; Júlio, E. Effect of non-structural masonry brick infill walls on the robustness of a RC framed building severely damaged due to a landslide. Eng. Struct. 2019, 180, 274–283. [Google Scholar] [CrossRef]
  19. Sousa, L.; Monteiro, R. Seismic retrofit options for non-structural building partition walls: Impact on loss estimation and cost-benefit analysis. Eng. Struct. 2018, 161, 8–27. [Google Scholar] [CrossRef]
  20. Polyakov, S.V. On the Interaction between Masonry Filler Walls and Enclosing Frame when Loaded in the Plane of the Wall; Translation in Earthquake Engineering; EERI: San Fransisco, CA, USA, 1960. [Google Scholar]
  21. Lu, Y. Comparative study of the seismic behavior of multi-storeyed reinforced concrete framed structures. J. Struct. Eng. ASCE 2002, 128, 169–178. [Google Scholar] [CrossRef]
  22. Papia, M.; Cavaleri, L.; Fossetti, M. Infilled frames: Developments in the evaluation of the stiffening effect of infills. Struct. Eng. Mech. 2003, 16, 675–693. [Google Scholar] [CrossRef]
  23. Ozturk, M.S. Effects of Masonry Infill Walls on the Seismic Performance of Buildings. Master’s Thesis, Middle East Technical University, Ankara, Turkey, 2005. [Google Scholar]
  24. Erdem, I.; Akyuz, U.; Ersoy, U.; Ozcebe, G. An experimental study on two different strengthening techniques for RC frames. Eng. Struct. 2006, 28, 1843–1851. [Google Scholar] [CrossRef]
  25. Flanagan, R.D.; Bennett, R.M.; Barclay, G.A. In-plane behavior of structural clay tile infilled frames. J. Struct. Eng. ASCE 1999, 125, 590–599. [Google Scholar] [CrossRef]
  26. Basil Gnanappa, S. Behaviour of Multi-Bay R.C. Frames with Various Infills under Cyclic Loading. Ph.D. Thesis, Bharathiar University, Coimbatore, India, 2002. [Google Scholar]
  27. Basil Gnanappa, S.; Murugesan, R.; Perumal Pillai, E.B. Seismic Analysis in High Rise Structures with VARIOUS infills; International Seminar on Industrial Structures (ISIS): Coimbatore, India, 2003. [Google Scholar]
  28. Prabavathy, S.; Palanichamy, M.S.; Santhakumar, A.R. Behaviour of reinforced hollow block masonry infill in multistorey RC frames under lateral loading. Indian Concr. J. Sept. 2006, 80, 27–32. [Google Scholar]
  29. Altin, S.; Anil, O.; Kara, M.E. Strengthening of RC Nonductile frames with RC infills: An experimental study. Cem. Concr. Compos. 2008, 30, 612–621. [Google Scholar] [CrossRef]
  30. Altin, S.; Anil, O.; Kara, M.E.; Kaya, M. An experimental study on the strengthening of masonry infilled RC frames using diagonal CFRP strips. Compos. Part B Eng. 2008, 39, 680–693. [Google Scholar] [CrossRef]
  31. Furtado, A.; Rodrigues, H.; Arêde, A.; Varum, H. Influence of the in Plane and Out-of-Plane Masonry Infill Walls’ Interaction in the Structural Response of RC Buildings. Procedia Eng. 2015, 114, 722–729. [Google Scholar] [CrossRef]
  32. Fardis, M.N.; Schetakis, A.; Strepelias, E. RC buildings retro- fitted by converting frame bays into RC walls. Bull. Earthq. Eng. 2013, 11, 1541–1561. [Google Scholar] [CrossRef]
  33. Higashi, Y.; Endo, T.; Shimizu, Y. Experimental studies on retrofitting of RC building frames. In Proceedings of the 8th World Conference on Earthquake Engineering, San Francisco, CA, USA, 21–28 July 1984; National Information Centre of Earthquake Engineering at Indian Institute of Technology: Kanpur, India, 1984; Volume 4, pp. 477–484. [Google Scholar]
  34. Strepelias, E.; Palios, X.; Bousias, S.N.; Fardis, M.N. Experimental investigation of concrete frames infilled with RC for seismic rehabilitation. J. Struct. Eng. 2014, 140, 04013033. [Google Scholar] [CrossRef]
  35. Pulido, C.; Saiidi, M.S.; Sanders, D.; Itani, A.; El-Azazy, S. Seismic performance of two-column bents-Part II: Retrofit with infill walls. ACI Struct. J. 2004, 101, 642–649. [Google Scholar]
  36. Elgawady, M.; Lestuzzi, P.; Badoux, M. A review of conventional seismic retrofitting techniques for URM. In Proceedings of the 13th International Brick and Block Masonry Conference, Amsterdam, Holland, 4–7 July 2004; pp. 1–10. [Google Scholar]
  37. Koutas, L.; Bousias, S.N.; Triantafillou, T.C. Seismic strengthening of masonry-infilled RC frames with TRM: Experimental study. J. Compos. Constr. 2015, 19, 04014048. [Google Scholar] [CrossRef]
  38. Vögeli, C.; Mojsilovi’c, N.; Stojadinovi’c, B. Masonry wallettes with a soft layer bed joint: Behaviour under static-cyclic loading. Eng. Struct. 2015, 86, 16–32. [Google Scholar] [CrossRef]
  39. Ahmadi, H.; Dusi, A.; Gough, J. A rubber-based system for damage reduction in infill masonry walls. In Proceedings of the 16th World Conference on Earthquake Engineering, Santiago, Chile, 9–13 January 2017; Volume 4347, pp. 9–13. [Google Scholar]
  40. Mojsilovi´c, N.; Petrovi´c, M.; Anglada, X.R. Masonry elements with multi-layer bed joints: Behaviour under monotonic and static-cyclic shear. Constr. Build. Mater. 2015, 100, 149–162. [Google Scholar] [CrossRef]
  41. Calabria, A.; Guidi, G.; da Porto, F.; Modena, C. Innovative systems for masonry infill walls based on the use of rubber joints: Finite element modelling and comparison with in-plane tests. In Brick Block Mason; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar] [CrossRef]
  42. Petrovi´c, M.; Mojsilovi´c, N.; Stojadinovi´c, B. Masonry walls with a multi-layer bed joint subjected to in-plane cyclic loading: An experimental investigation. Eng. Struct. 2017, 143, 189–203. [Google Scholar] [CrossRef]
  43. Petrovi´c, M.; Stojadinovi´c, B.; Mojsilovi´c, N. I-shaped unreinforced masonry wallettes with a soft-layer bed joint: Behavior under static-cyclic shear. J. Struct. Eng. 2017, 143, 1–20. [Google Scholar] [CrossRef]
  44. EU Project INSYSME. INnovative SYStems for Earthquake Resistant Masonry Enclosures in Reinforced Concrete Buildings. 2016. Available online: www.insysme.eu (accessed on 27 July 2023).
  45. Kubalski, T.; Marinkovi´c, M.; Butenweg, C. Numerical investigation of masonry infilled R.C. frames. In Brick Block Mason; CRC Press: Boca Raton, FL, USA, 2016; pp. 1219–1226. [Google Scholar] [CrossRef]
  46. Okail, H.; Abdelrahman, A.; Abdelkhalik, A.; Metwaly, M. Experimental and analytical investigation of the lateral load response of confined masonry walls. HBRC J. 2016, 12, 33–46. [Google Scholar] [CrossRef]
  47. Nasiri, E.; Liu, Y. Development of a detailed 3D FE model for analysis of the in-plane behaviour of masonry infilled concrete frames. Eng. Struct. 2017, 143, 603–616. [Google Scholar] [CrossRef]
  48. Pantò, B.; Caliò, I.; Lourenço, P.B. Seismic safety evaluation of reinforced concrete masonry infilled frames using macro modelling approach. Bull. Earthq. Eng. 2017, 15, 3871–3895. [Google Scholar] [CrossRef]
  49. Breveglieri, M.; Camata, G.; Spacone, E. Strengthened infilled RC frames: Continuum and macro modeling in nonlinear finite element analysis. Compos. Part B Eng. 2018, 151, 78–91. [Google Scholar] [CrossRef]
  50. Penava, D.; Sarhosis, V.; Kožar, I.; Guljaš, I. Contribution of RC columns and masonry wall to the shear resistance of masonry infilled RC frames containing different in size window and door openings. Eng. Struct. 2018, 172, 105–130. [Google Scholar] [CrossRef]
  51. Prem Kumar, G.; Thirumurugan, V.; Satyanarayanan, K.S. Artificial neural network prediction of window openings and positions in reinforced concrete infilled frames with pneumatic interface. Asian J. Civ. Eng. 2023, 24, 1915–1925. [Google Scholar] [CrossRef]
  52. Aguilar, G.; Meli, R.; Diaz, R.; Vasquez-del-Mercado, A.R. Influence of horizontal reinforcement on the behavior of confined masonry walls. In Proceedings of the 11th World Conference on Earthquake Engineering, Acapulco, Mexico, 23–28 June 1996. [Google Scholar]
  53. Meli, R. Behavior of masonry walls under lateral loads. In Proceedings of the 5th World Conference on Earthquake Engineering, Rome, Italy, 25–29 June 1973. [Google Scholar]
  54. Tomazevic, M.; Klemenc, I. Seismic Behavior of Confined Masonry Walls. Earthq. Eng. Struct. Dyn. 1997, 26, 1059–1071. [Google Scholar] [CrossRef]
  55. Yoshimura, K.; Kikuchi, K.; Okamoto, Z.; Sanchez, T. Effect of vertical and horizontal wall reinforcement on seismic behavior of confined masonry walls. In Proceedings of the 11th World Conference on Earthquake Engineering, Acapulco, Mexico, 23–28 June 1996. [Google Scholar]
  56. Yoshimura, K.; Kikuchi, K.; Kuroki, M.; Nonaka, H.; Tae Kim, K.; Wangdi, R.; Osikata, A. Experimental study for developing higher seismic performance of brick masonry walls. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
  57. Brzev, S.; Astroza, M.; Moroni, O. Performance of Confined Masonry Buildings in the February 27, 2010 Chile Earthquake; Earthq Eng Research Inst.: Oakland, CA, USA, 2010. [Google Scholar]
  58. Alcocer, S.M.; Arias, J.G.; Vazquez, A. Response assessment of Mexican confined masonry structures through shake table tests. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
  59. Yáñez, F.; Astroza, M.; Holmberg, A.; Ogaz, O. Behavior of confined masonry shear walls with large openings. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
  60. Tomazavic, M. Earthquake-Resistant Design of Masonry Buildings, 1st ed.; Imperial College Press: London, UK, 1999. [Google Scholar]
  61. Singhal, V.; Rai, D.C. Behavior of confined masonry walls with openings under inplane and out-of-plane loads. Earthq. Spectra 2018, 34, 817–841. [Google Scholar] [CrossRef]
  62. Kumar, G.P.; Thirumurugan, V.; Satyanarayanan, K.S. An analytical study on the behaviour of infilled RC frame with opening in infill. Mater. Today Proc. 2022, 50, 331–334. [Google Scholar] [CrossRef]
  63. Anbarasan, S.; Varatharajan, T.; Srinivasan, S.K. Monitoring the behaviour of seven storeyed RC frame subjected to reversed cyclic loading by nonlinear NDT. Case Stud. Constr. Mater. 2022, 17, e01693. [Google Scholar] [CrossRef]
  64. Selvakumar, A.; Thirumurugan, V.; Satyanarayanan, K.S. Structural significance of Pneumatic Interface in Masonry infilled RC frames. Mater. Today Proc. 2021, 50, 282–286. [Google Scholar] [CrossRef]
  65. Thirumurugan, V.; Ganesan, T.P.; Satyanarayanan, K.S.; Parthasarathi, N.; Prakash, M. Influence of pneumatic interface pressure in reinforced concrete infilled frames. Mater. Today Proc. 2021, 34, 395–403. [Google Scholar] [CrossRef]
  66. Shakor, P.; Gowripalan, N.; Rasouli, H. Experimental and numerical analysis of 3D printed cement mortar specimens using inkjet 3DP. Archiv. Civ. Mech. Eng. 2021, 21, 58. [Google Scholar] [CrossRef]
  67. Liu, Y.; Li, J.; Lin, G. Seismic performance of advanced three-dimensional base-isolated nuclear structures in complex-layered sites. Eng. Struct. 2023, 289, 116247. [Google Scholar] [CrossRef]
  68. Zhai, S.-Y.; Lyu, Y.-F.; Cao, K.; Li, G.-Q.; Wang, W.-Y.; Chen, C. Seismic behavior of an innovative bolted connection with dual-slot hole for modular steel buildings. Eng. Struct. 2023, 279, 115619. [Google Scholar] [CrossRef]
  69. Yang, Y.; Lin, B.; Zhang, W. Experimental and numerical investigation of an arch–beam joint for an arch bridge. Arch. Civ. Mech. Eng. 2023, 23, 101. [Google Scholar] [CrossRef]
  70. Jiang, J.; Ye, M.; Chen, L.Y.; Zhu, Z.W.; Wu, M. Study on static strength of Q690 built-up K-joints under axial loads. Structures 2023, 51, 760–775. [Google Scholar] [CrossRef]
  71. Liu, C.; Cui, J.; Zhang, Z.; Liu, H.; Huang, X.; Zhang, C. The role of TBM asymmetric tail-grouting on surface settlement in coarse-grained soils of urban area: Field tests and FEA modelling. Tunn. Undergr. Space Technol. 2021, 111, 103857. [Google Scholar] [CrossRef]
  72. ABAQUS (2014) Analysis User’s Manual, Version 6.14; Dassault Systemes Simulia, Inc.: Johnston, RI, USA, 2014.
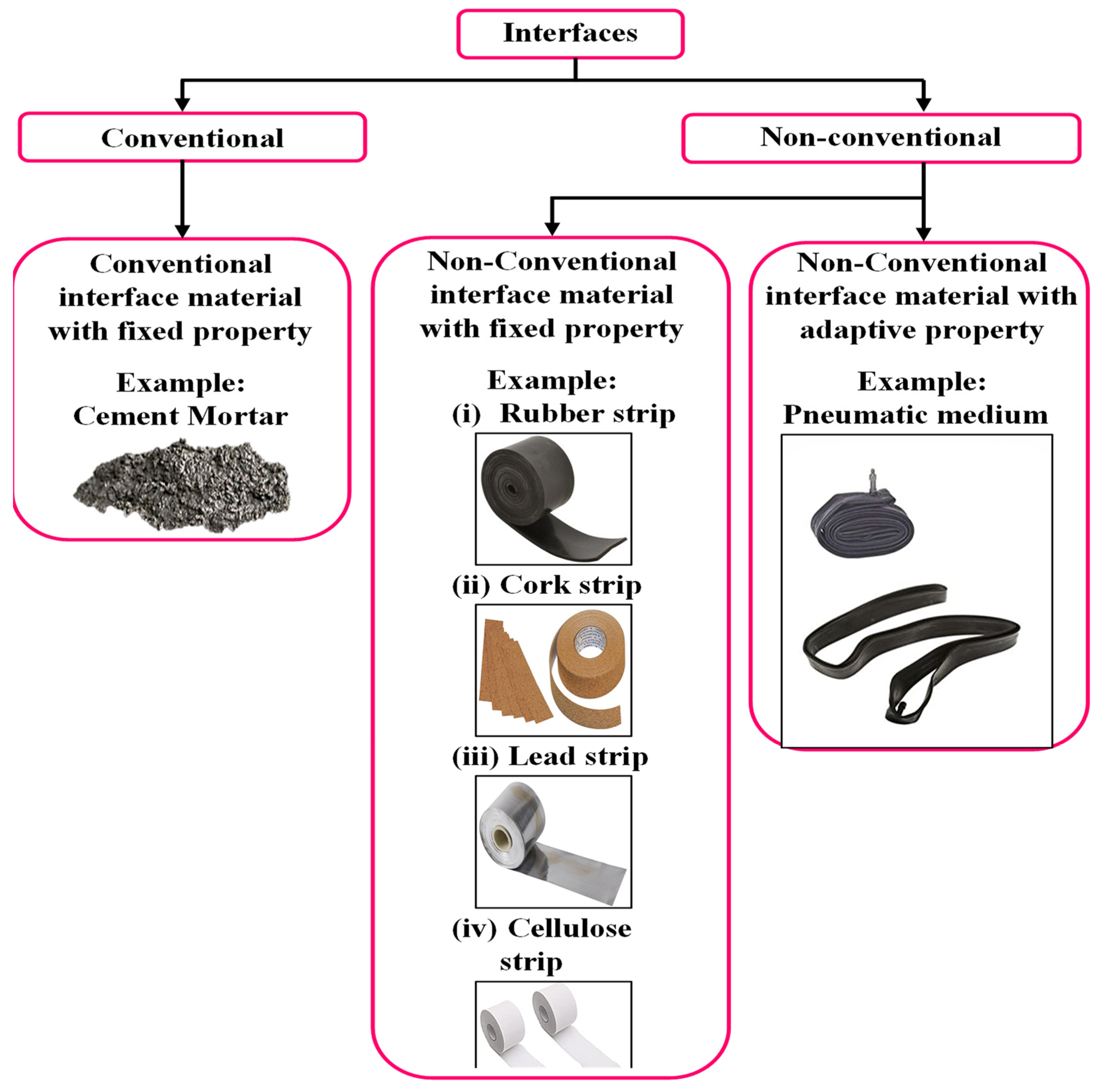
Buildings 13 02376 g001
Figure 1. Interface materials.
Figure 1. Interface materials.
Buildings 13 02376 g001
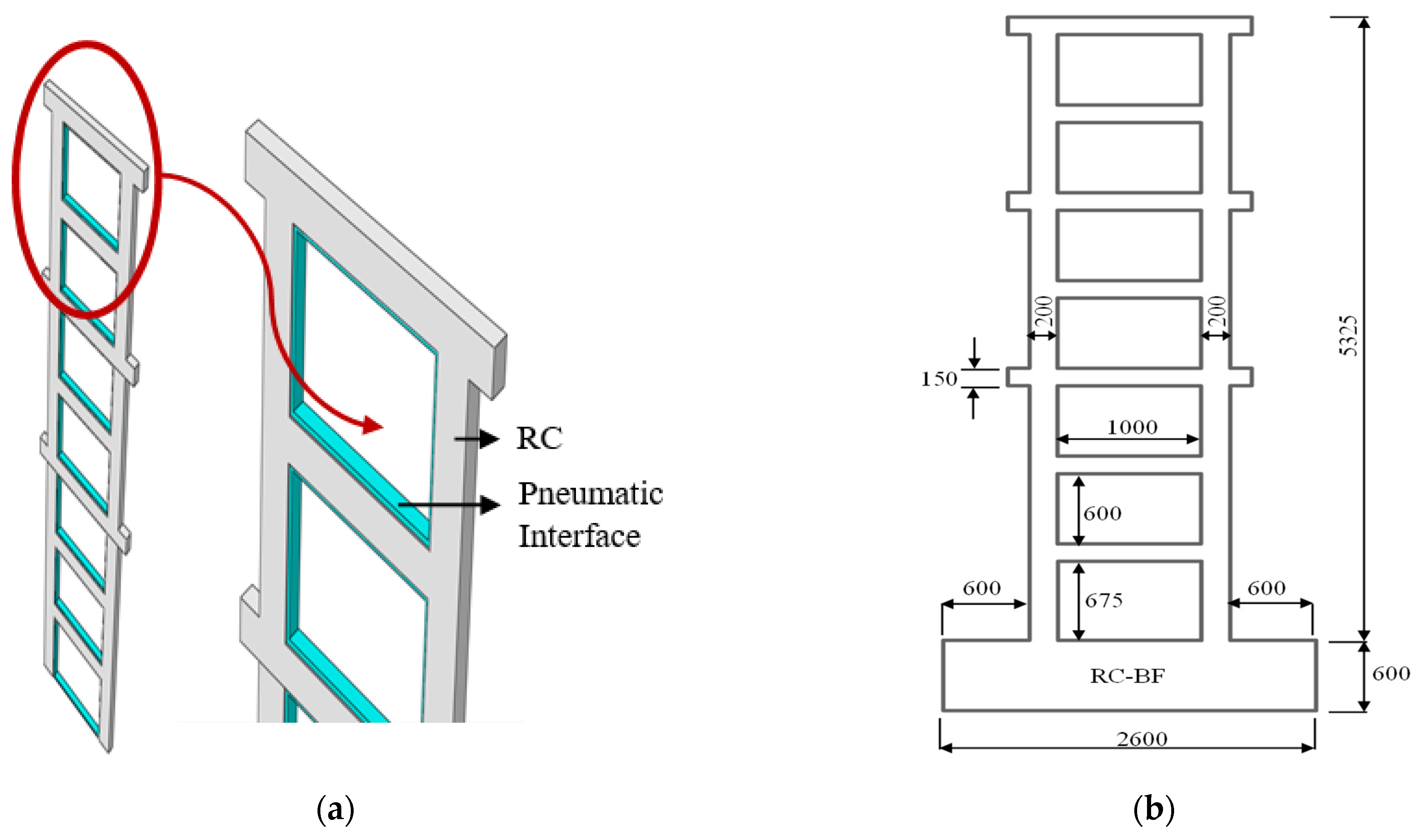
Buildings 13 02376 g002
Figure 2. (a) Orientation of the pneumatic interface in the infilled frame. (b) Dimensions of the reinforced concrete infilled frame (mm).
Figure 2. (a) Orientation of the pneumatic interface in the infilled frame. (b) Dimensions of the reinforced concrete infilled frame (mm).
Buildings 13 02376 g002
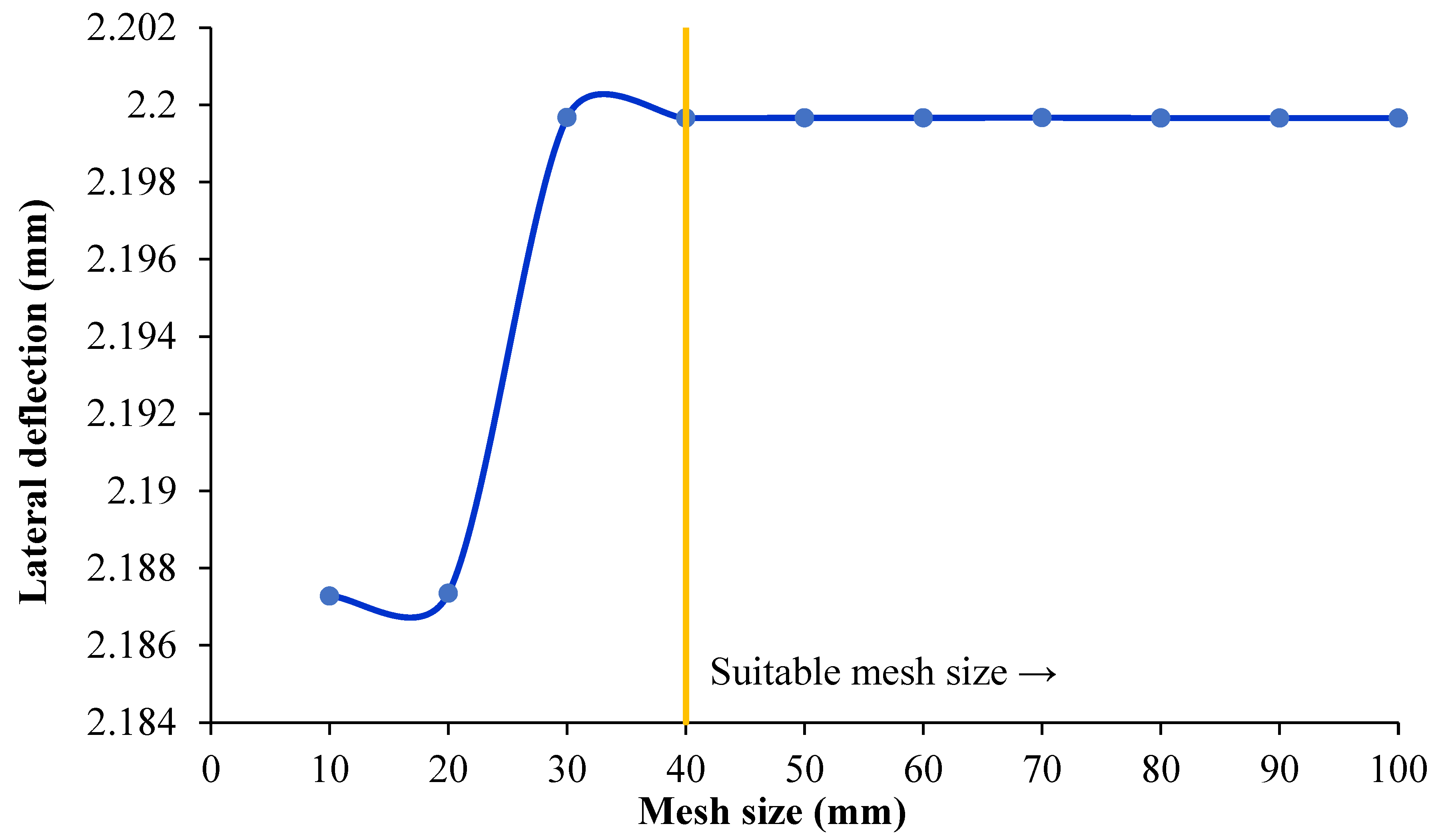
Buildings 13 02376 g003
Figure 3. Mesh size convergence for the RC frame.
Figure 3. Mesh size convergence for the RC frame.
Buildings 13 02376 g003
Buildings 13 02376 g004
Figure 4. Seven-story analytical model. (a) Displacement profile; (b) stress distribution.
Figure 4. Seven-story analytical model. (a) Displacement profile; (b) stress distribution.
Buildings 13 02376 g004
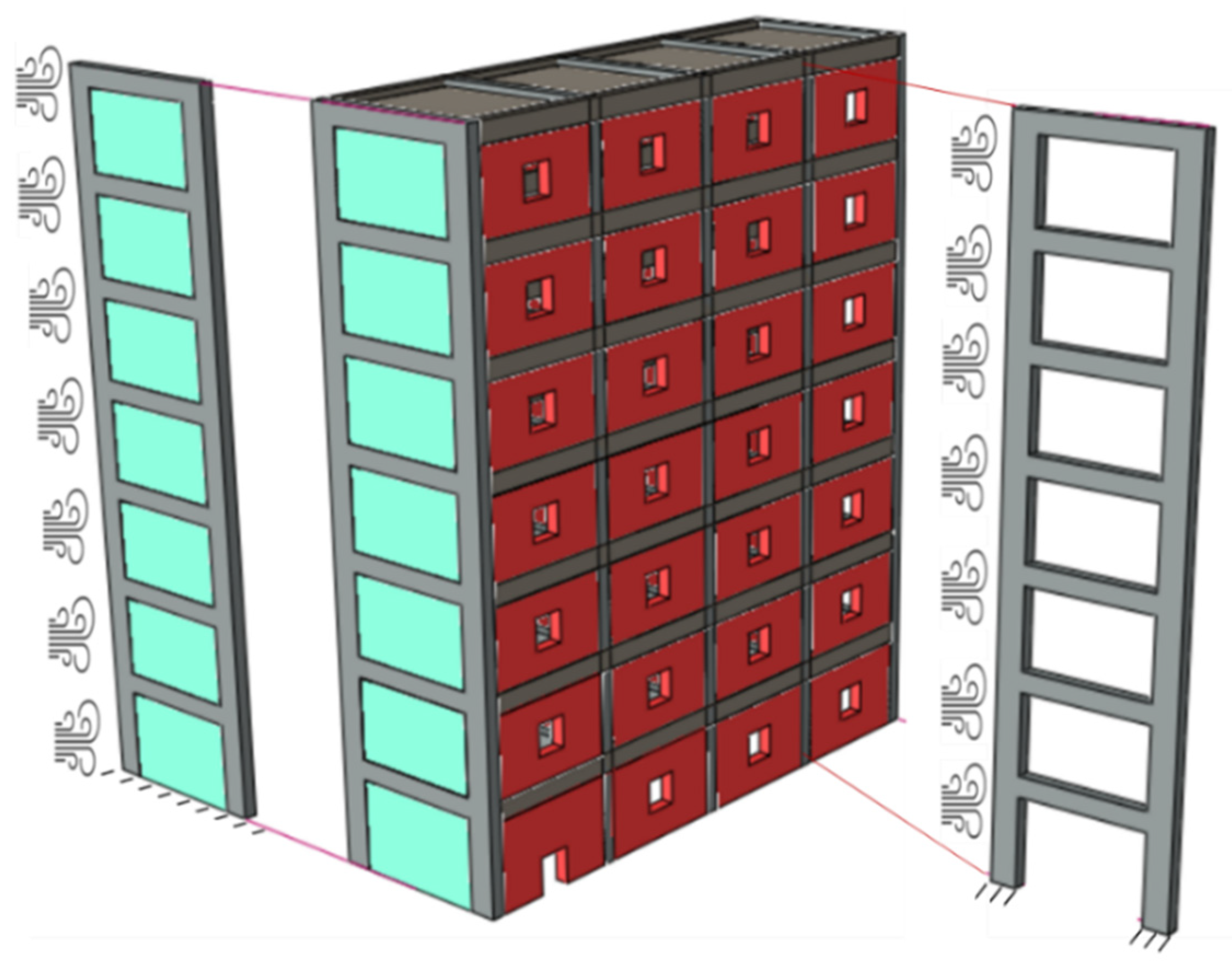
Buildings 13 02376 g005
Figure 5. Evaluation of the single bay seven-story frame model from a seven-story high-rise building.
Figure 5. Evaluation of the single bay seven-story frame model from a seven-story high-rise building.
Buildings 13 02376 g005
Buildings 13 02376 g006
Figure 6. Seven-story frame experimental setup.
Figure 6. Seven-story frame experimental setup.
Buildings 13 02376 g006
Buildings 13 02376 g007
Figure 7. Analytical linear optimization of pressure.
Figure 7. Analytical linear optimization of pressure.
Buildings 13 02376 g007
Buildings 13 02376 g008
Figure 8. Standard deviation for analytical linear optimization of pressure (LOPA).
Figure 8. Standard deviation for analytical linear optimization of pressure (LOPA).
Buildings 13 02376 g008
Buildings 13 02376 g009
Figure 9. Analytical non-linear optimization of pressure (NLOPA).
Figure 9. Analytical non-linear optimization of pressure (NLOPA).
Buildings 13 02376 g009
Buildings 13 02376 g010
Figure 10. Standard deviation for analytical non-linear optimization of pressure (NLOPA).
Figure 10. Standard deviation for analytical non-linear optimization of pressure (NLOPA).
Buildings 13 02376 g010
Buildings 13 02376 g011
Figure 11. Experimental optimization of pressure.
Figure 11. Experimental optimization of pressure.
Buildings 13 02376 g011
Buildings 13 02376 g012
Figure 12. Experimental non-linear optimization of pressure.
Figure 12. Experimental non-linear optimization of pressure.
Buildings 13 02376 g012
Buildings 13 02376 g013
Figure 13. Displacement comparison of linear and nonlinear optimization models.
Figure 13. Displacement comparison of linear and nonlinear optimization models.
Buildings 13 02376 g013
Buildings 13 02376 g014
Figure 14. Stiffness comparison of linear and nonlinear optimization models.
Figure 14. Stiffness comparison of linear and nonlinear optimization models.
Buildings 13 02376 g014
Buildings 13 02376 g015
Figure 15. Drift comparison of linear and nonlinear optimization models.
Figure 15. Drift comparison of linear and nonlinear optimization models.
Buildings 13 02376 g015
Table 1. Modeling features of ABAQUS.
Table 1. Modeling features of ABAQUS.
FeaturesModeling Technique
Concrete8 nodded 3D cubic continuum solid sections
Steel as reinforcement3D beam wire section
Masonry infill8 nodded 3D right rectangular solid prism
InterfaceEquivalent pressure homogeneous element
Concrete–steel interactionEmbedded region
Concrete–interface interactionSurface-to-surface interaction (used in concrete and butyl rubber tube)
Interface–masonry infill interactionSurface-to-surface interaction
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

George, P.K.; Varatharajan, T.; Srinivasan, S.K.; Hakeem, I.Y.; Özkılıç, Y.O. Pressure Optimization in Pneumatic Interfaces Using a Single-Bay Seven-Story Infilled Reinforced Concrete Frame: Experimental and Numerical Investigation. Buildings 2023, 13, 2376. https://doi.org/10.3390/buildings13092376

AMA Style

George PK, Varatharajan T, Srinivasan SK, Hakeem IY, Özkılıç YO. Pressure Optimization in Pneumatic Interfaces Using a Single-Bay Seven-Story Infilled Reinforced Concrete Frame: Experimental and Numerical Investigation. Buildings. 2023; 13(9):2376. https://doi.org/10.3390/buildings13092376

Chicago/Turabian Style

George, Prem Kumar, Thirumurugan Varatharajan, Satyanarayanan Kachabeswara Srinivasan, Ibrahim Y. Hakeem, and Yasin Onuralp Özkılıç. 2023. "Pressure Optimization in Pneumatic Interfaces Using a Single-Bay Seven-Story Infilled Reinforced Concrete Frame: Experimental and Numerical Investigation" Buildings 13, no. 9: 2376. https://doi.org/10.3390/buildings13092376

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop