Reliability-Based Proof Load Factors for Assessment of Bridges
Abstract
:1. Introduction
Hypothesis and Research Scope
- Can the target proof load be determined based on load modeling and without input from a resistance model while ensuring sufficient reliability (safety) of an existing bridge structure after a successful proof load test?
- Can advanced real-time monitoring be applied in a simplified and selective way for stop criteria evaluation?
2. State of the Art
2.1. Reliability-Based Methods
2.2. Load Modeling
- Legislation and demands for heavy vehicles: What are the requirements for the considered bridge and associated traffic?
- Administration of the legislation and demands. How are the legislation and demands handled? In Denmark, for instance, heavy special vehicles must apply for a specific permit and have the full route of transport approved by the authorities.
- Check and verification of vehicles. How efficiently is it checked that vehicles do carry an illegal overload?
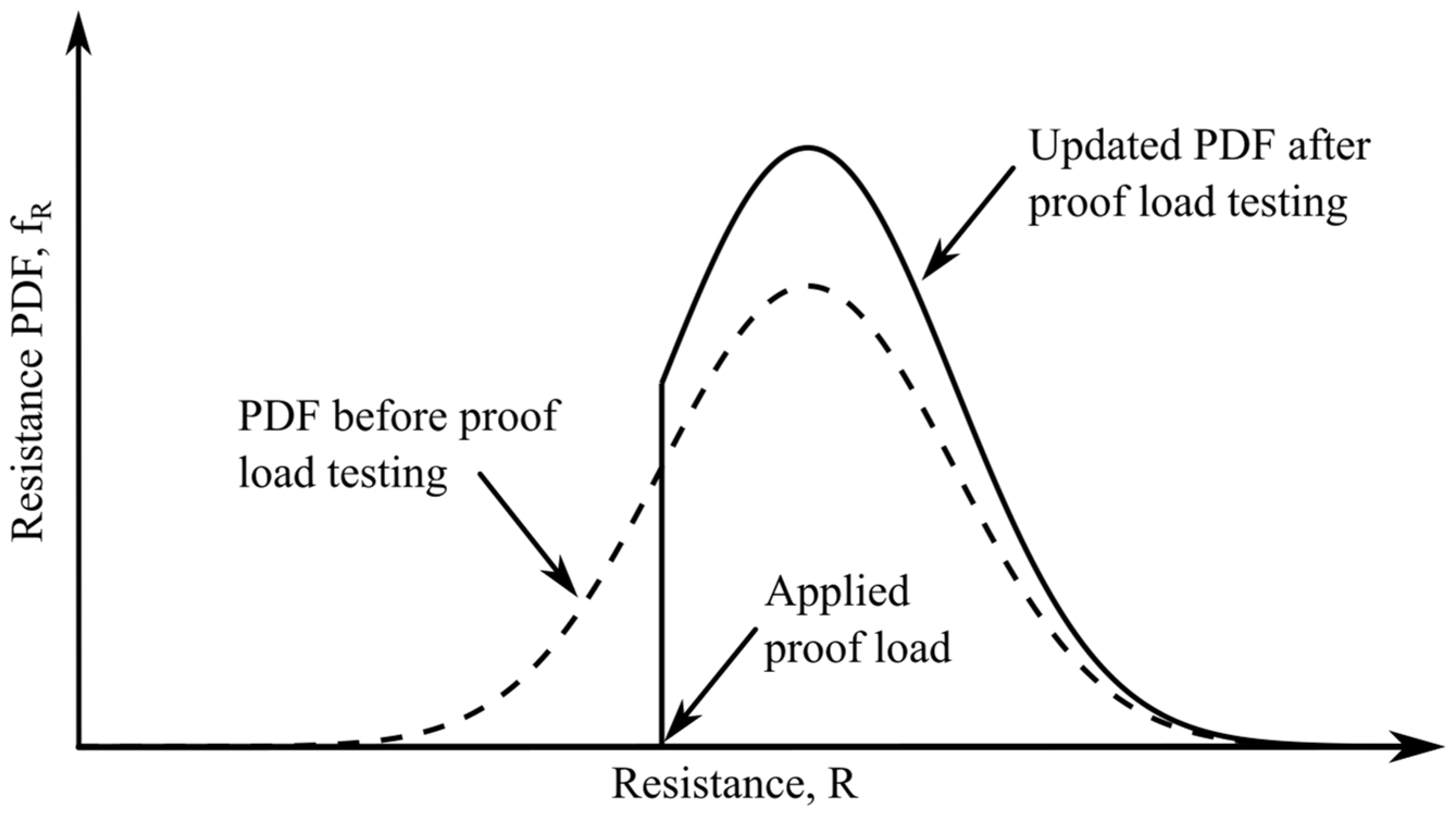
2.3. Proof Loading, Target Load, and Stop Criteria
3. A Different Approach to Proof Loading and Target Load
- Sufficient skill and care appropriate to the circumstances are exercised in the assessment; this is based on the knowledge and good practice generally available at the time.
- The assessment of the structure is performed by appropriately qualified and experienced personnel.
- Adequate supervision and quality control are provided during the assessment process.
3.1. Proof Loading Factors Based on Load Model
- is the annual extreme vehicle weight (characteristic value (): 98% quantile).
- is the traffic load model uncertainty.
- is the dynamic factor (characteristic value (Ks,k) depends on bridge geometry; Ks,k = 1.25 is used [21]).
- is the proof loading factor.
- is the distribution function for the annual extreme vehicle weight.
- is the normal distribution of vehicle weight for individual vehicles.
- is the number of vehicles in the reference period (1 year).
- is the dynamic supplement, which is normally distributed with N(41.5/W,41.5/W) for global effects [23].
- W is the weight of the vehicle in kN.
- The characteristic annual extreme vehicle weight, (98% quantile), is determined by solving for “x” in Equation (5).
- An appropriate number of simulations are run. In this example, 108 is applied to identify a failure probability of .
- In each simulation, realizations of the stochastic variables are obtained by simulating realizations of the cumulative distribution function as uniformly distributed between 0 and 1. Statistically independent realizations are applied to each of the variables.
- The annual extreme vehicle weight, , may be determined in the same way as .
- The dynamic supplement, , and the model uncertainty, , may similarly be determined by solving for x in the cumulative distribution function; however, the mean and standard deviation of are dependent on the vehicle weight. It is important to note that the vehicle weight, , in this case, refers to the realizations of the annual extreme vehicle weight, , which was determined in the previous point for each specific simulation.
- A value is guessed for the proof load factor, , and the product of Equation (4) is determined.
- Negative values represent a failure event. The simulated failure probability, , is determined as the sum of failure events over the number of simulations.
- The value of the proof load factor is changed until the simulated failure probability is equal to the target failure probability, .
3.2. Conservative or Not?
3.3. Proof Loading Recommendations
- A test should consider all plausible and relevant failure modes.
- The loading may be applied in three load levels with smaller increments. Large increments at the beginning and smaller when nearing the target load.
- Before testing, criteria should be specified to control and monitor the behavior of the structure during the test in order to avoid permanent damage to the structure.
- A detailed monitoring plan should be prepared prior to testing.
- During testing, time should be dedicated between load increments for the registration and evaluation of measurements.
- Deflection of the bridge (L/400 = 16.25 mm).
- Crack identification and width monitoring (0.2 mm).
- The degree of non-linearity of the response as a function of the deflection of the structure (25% stiffness change or engineering judgment).
- Settling of the foundation (Engineering judgment).
4. Proof Loading Pilot Project and Case Study
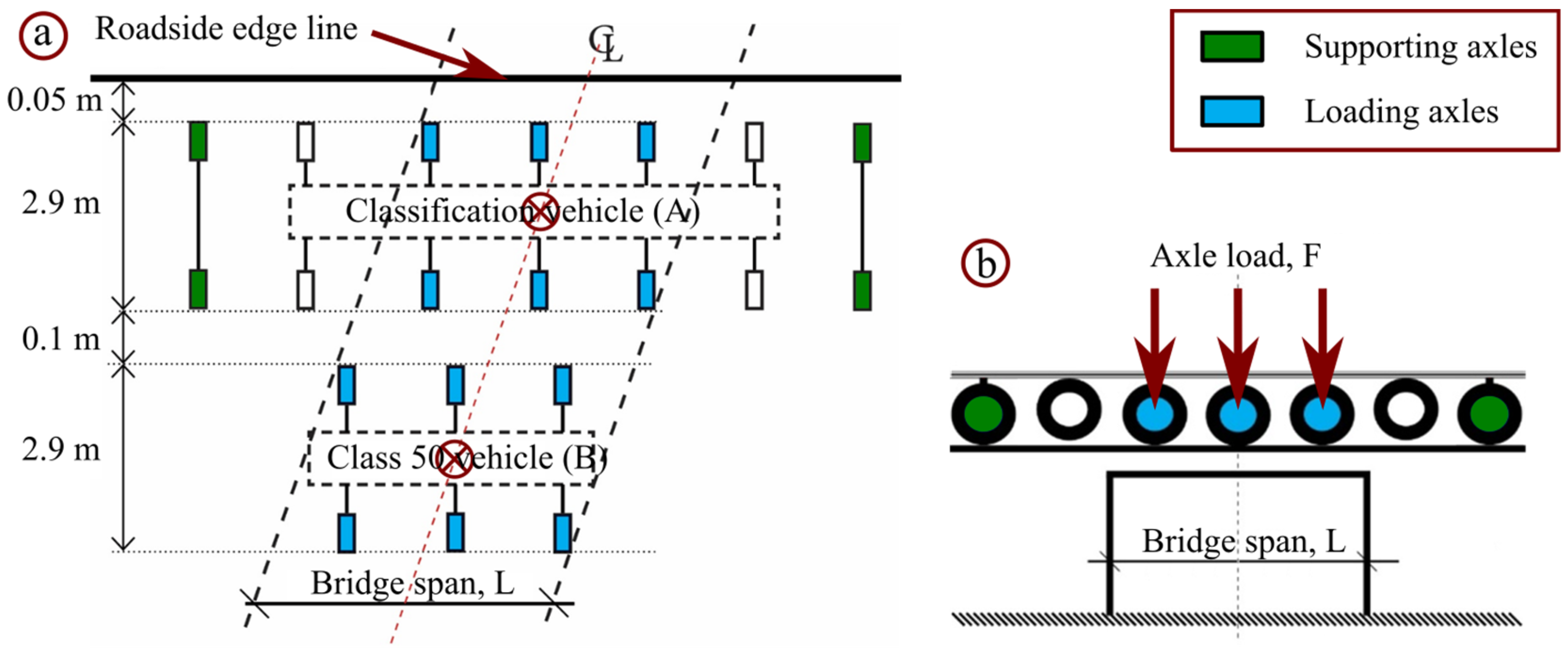
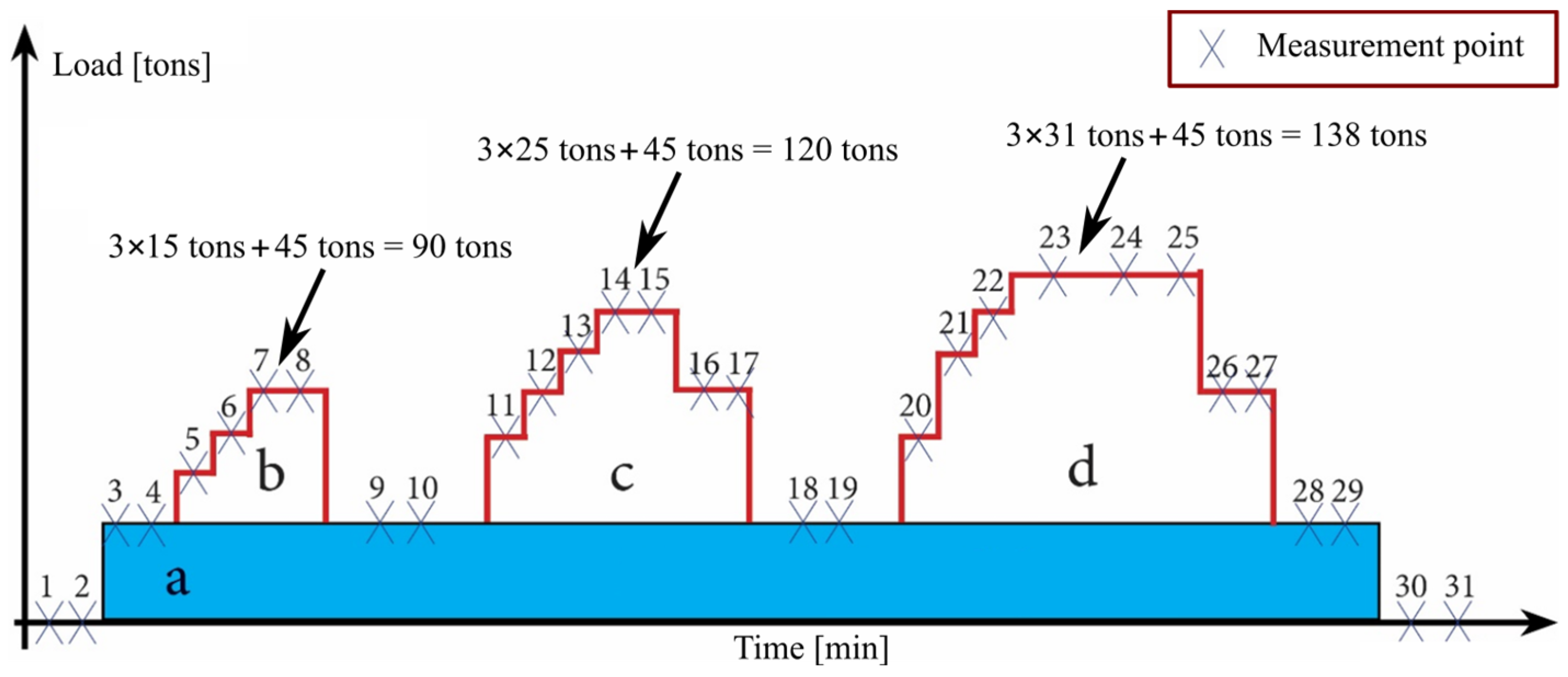
4.1. Loading with Special Transport Vehicles
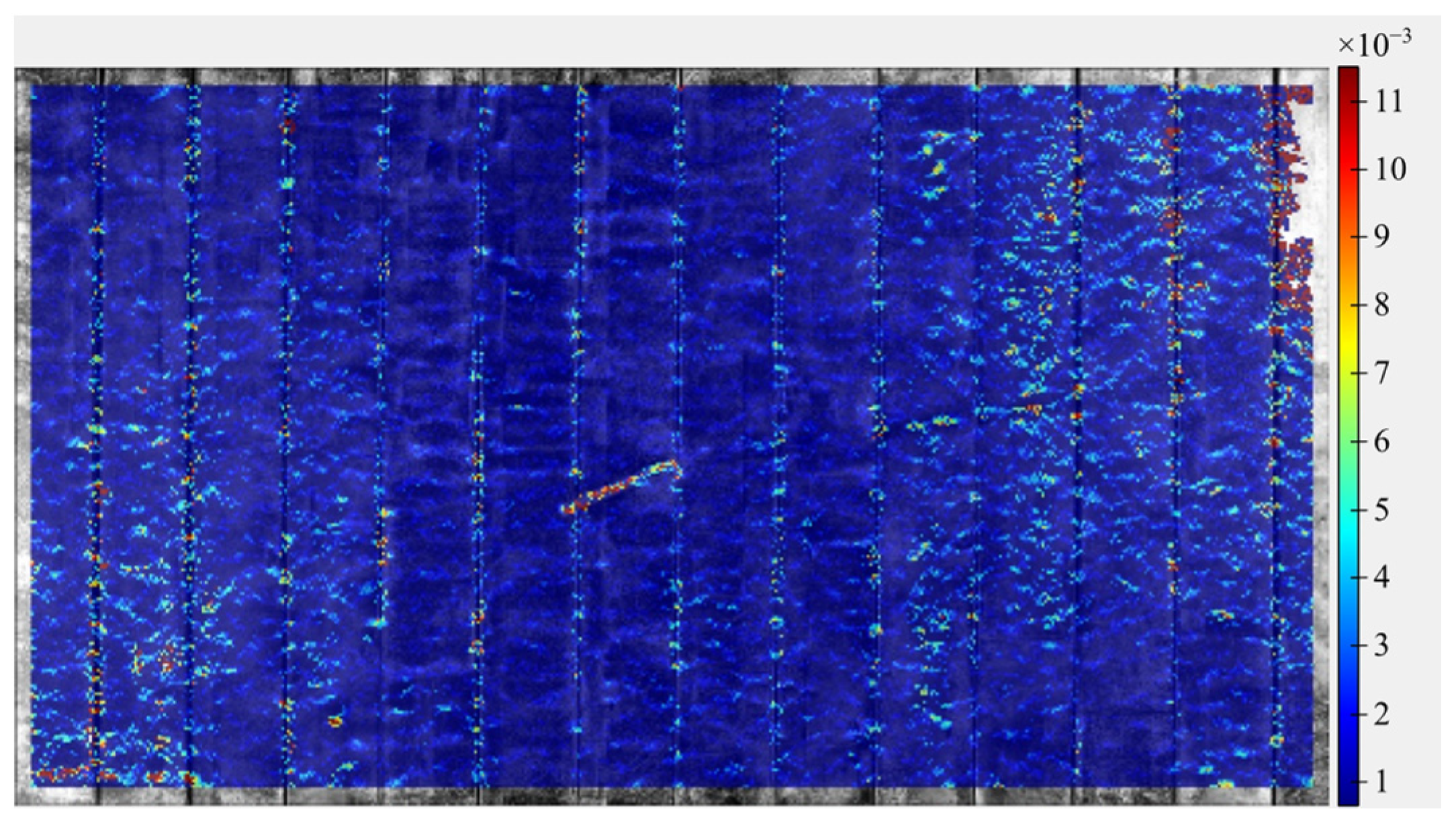
4.2. Monitoring
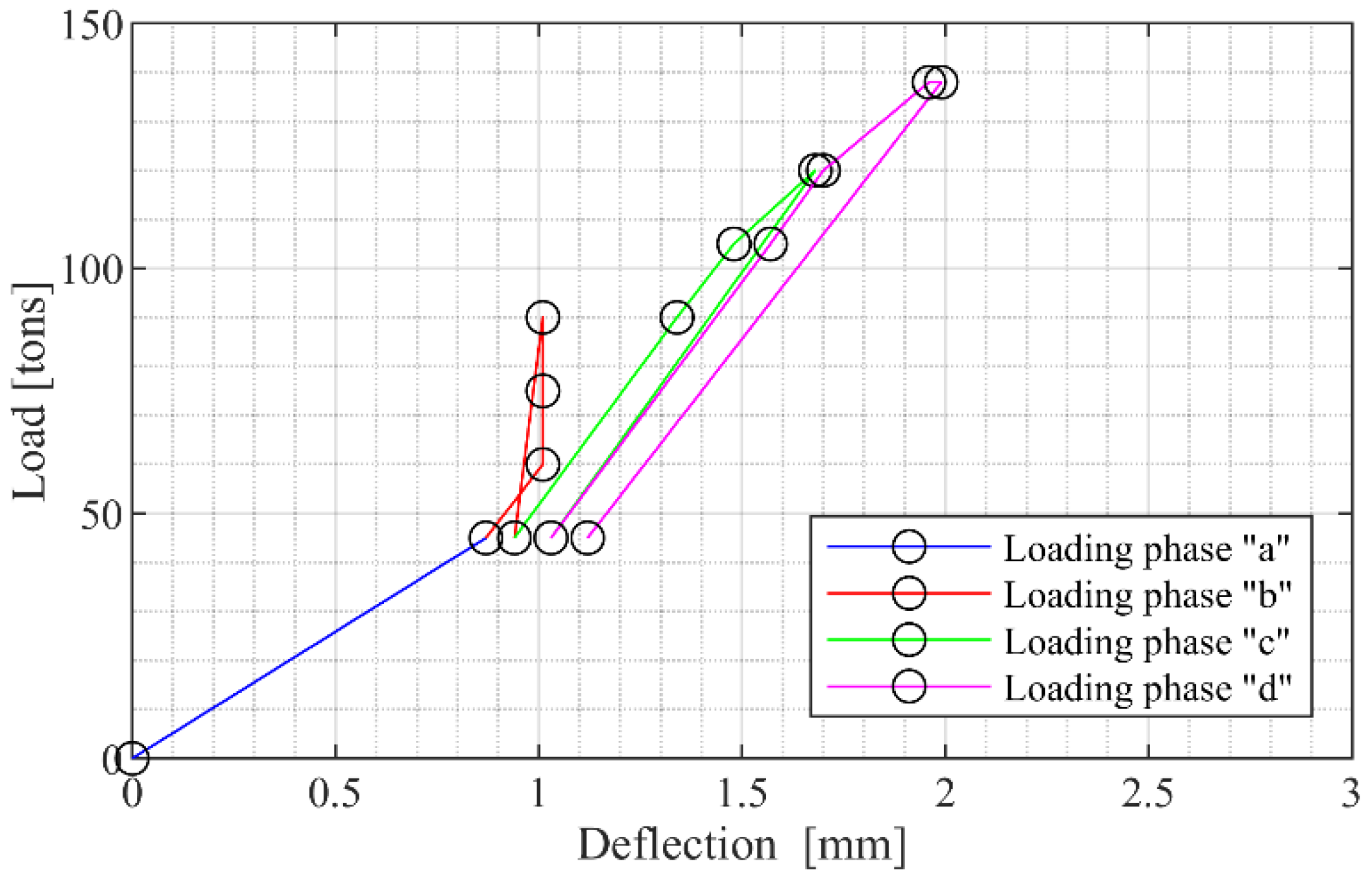
4.3. Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aguilar, C.V.; Jáuregui, D.V.; Newtson, C.M.; Weldon, B.D.; Cortez, T.M. Load rating a prestressed concrete double t-beam bridge without plans by field testing. Transp. Res. Rec. 2015, 2522, 90–99. [Google Scholar] [CrossRef]
- Lantsoght, E.O.L.; Koekkoek, R.T.; Hordijk, D.; de Boer, A. Towards standardisation of proof load testing: Pilot test on viaduct zijlweg. Struct. Infrastruct. Eng. 2017, 14, 365–380. [Google Scholar] [CrossRef]
- Faber, M.H.; Val, D.V.; Stewart, M.G. Proof load testing for bridge assessment and upgrading. Eng. Struct. 2000, 22, 1677–1689. [Google Scholar] [CrossRef]
- Halicka, A.; Lantsoght, E.O.L.; Hordijk, D.A. Rating of Concrete Road Bridges with Static Proof Load Tests; ACI Symposium Publication: Farmington Hills, MA, USA, 2017; Volume 323, pp. 3.1–3.6. [Google Scholar] [CrossRef]
- Schmidt, J.W.; Halding, P.S.; Jensen, T.W.; Engelund, S. High magnitude loading of concrete bridges. ACI Struct. J. 2018, 323, 9.1–9.20. [Google Scholar]
- Saraf, V.; Sokolik, A.F.; Nowak, A.S. Proof load testing of highway bridges. Transp. Res. Rec. J. Transp. Res. Board 1996, 1541, 51–57. [Google Scholar] [CrossRef]
- Gosbell, K.B.; Stevens, L.K. Test Loading of a Full Scale Bridge. In Proceedings of the A.R.R.B Proceedings; ARRB Transport Research: Victoria, VA, Canada, 1968; Volume 4, pp. 2018–2041. [Google Scholar]
- Goodpasture, D.W.; Burdette, E.G. Full scale tests to failure of four highway bridges. Am. Railw. Eng. Assoc. 1973, 74, 454–473. [Google Scholar]
- Isaksen, H.R.; Kanstad, T.; Olsen, P.-E. Prøvebelastning Av Bru Nr 02-1234 Smedstua Bru; Statens Vegvesen: Vegdirektoratet, Oslo, Norway, 1998. [Google Scholar]
- Zhang, J.; Peng, H.; Cai, C.S. Field study of overload behavior of an existing reinforced concrete bridge under simulated vehicle loads. J. Bridg. Eng. 2011, 16, 226–237. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, H.; Cai, C.S. Destructive testing of a decommissioned reinforced concrete bridge. J. Bridg. Eng. 2013, 18, 564–569. [Google Scholar] [CrossRef]
- Casas, J.R.; Gómez, J.D. Load rating of highway bridges by proof-loading. KSCE J. Civ. Eng. 2013, 17, 556–567. [Google Scholar] [CrossRef]
- Bakht, B.; Jaeger, L.G. Bridge testing—A surprise every time. J. Struct. Eng. 1990, 116, 1370–1383. [Google Scholar] [CrossRef]
- Saraf, V.; Nowak, A.S. Proof load testing of deteriorated steel girder bridges. J. Bridg. Eng. 1998, 3, 82–89. [Google Scholar] [CrossRef]
- Minervino, C.; Sivakumar, B.; Moses, F.; Mertz, D.; Edberg, W. New AASHTO guide manual for load and resistance factor rating of highway bridges. J. Bridg. Eng. 2004, 9, 43–54. [Google Scholar] [CrossRef]
- Barker, M.G. Quantifying field-test behavior for rating steel girder bridges. J. Bridg. Eng. 2001, 6, 254–261. [Google Scholar] [CrossRef]
- Moses, F.; Lebet, J.P.; Bez, R. Applications of field testing to bridge evaluation. J. Struct. Eng. 1994, 120, 1745–1762. [Google Scholar] [CrossRef]
- Lantsoght, E.O.L.; van der Veen, C.; de Boer, A.; Hordijk, D.A. State-of-the-art on load testing of concrete bridges. Eng. Struct. 2017, 150, 231–241. [Google Scholar] [CrossRef]
- Fujino, Y.; Lind, N.C. Proof-Load Factors and Reliability. ASCE J. Struct. Div. 1977, 103, 853–870. [Google Scholar] [CrossRef]
- prEN 1990-2; Eurocode—Basis of Assessment and Retrofitting of Existing Structures: General Rules and Actions. Project Team CEN/TC 250/WG 2/WG2.T2; Ver. November 2021. CEN: Brussels, Belgium, 2021.
- Vejdirektoratet (The Danish Road Directorate). DS/EN 1991-2 DK NA:2017, Annex A: Lastmodeller for Klassificering Og Bæreevnevurdering (Models of Special Vehicles for Road Bridges); The Danish Road Directorate: Copenhagen, Denmark, 2017. [Google Scholar]
- Vejdirektoratet (The Danish Road Directorate). Vejledning Til Belastnings—Og Beregningsgrundlag; The Danish Road Directorate: Copenhagen, Denmark, 2010. [Google Scholar]
- Vejdirektoratet (The Danish Road Directorate). Guideline for Reliability-Based Classification of the Load Carrying Capacity of Existing Bridges; The Danish Road Directorate: Copenhagen, Denmark, 2004. [Google Scholar]
- Thoft-Christensen, P.; Baker, M.J. Structural Reliability Theory and Its Applications; Springer: Berlin/Heidelberg, Germany, 1982. [Google Scholar]
- Box, G.E.P.; Tiao, G.C. Bayesian Inference in Statistical Analysis; Wiley: Hoboken, NJ, USA, 1992. [Google Scholar]
- Saraf, V.K. Reliability-Based Criteria for Proof Load Testing of Bridges; ProQuest Dissertations Publishing: Ann Arbor, MI, USA, 1997; ISBN 978-0-591-61868-6. [Google Scholar]
- Lantsoght, E.O.L.; van der Veen, C.; Hordijk, D.A.; de Boer, A. Reliability Index after Proof Load Testing: Viaduct de Beek. In Proceedings of the Safety and Reliability—Theory and Applications—Proceedings of the 27th European Safety and Reliability Conference, ESREL 2017, Portoroz, Slovenia, 18–22 June 2017. [Google Scholar]
- Nowak, A.S.; Tharmabala, T. Bridge reliability evaluation using load tests. J. Struct. Eng. 1988, 114, 2268–2279. [Google Scholar] [CrossRef]
- Kapoor, M.; Christensen, C.O.; Schmidt, J.W.; Sørensen, J.D.; Thöns, S. Decision analytic approach for the reclassification of concrete bridges by using elastic limit information from proof loading. Reliab. Eng. Syst. Saf. 2023, 232, 109049. [Google Scholar] [CrossRef]
- Ditlevsen, O.; Madsen, H.O. Stochastic vehicle-Queue-Load model for large bridges. J. Eng. Mech. 1994, 120, 1829–1847. [Google Scholar] [CrossRef]
- Gómez, J.D.; Casas, J.R. Assessment of Bridge Capacity through Proof Load Testing. In Proceedings of the Life-Cycle Civil Engineering—Proceedings of the 1st International Symposium on Life-Cycle Civil Engineering, IALCCE ’08, Varenna, Italy, 11–14 June 2008. [Google Scholar]
- Schmidt, J.W.; Thöns, S.; Kapoor, M.; Christensen, C.O.; Engelund, S.; Sørensen, J.D. Challenges related to probabilistic decision analysis for bridge testing and reclassification. Front. Built Env. 2020, 6. [Google Scholar] [CrossRef]
- ICE. Guidelines for the Supplementary Load Testing of Bridges; The Institution of Civil Engineers—National Steering Commitee for the Load Testing of Bridges: London, UK, 1998. [Google Scholar]
- DAfStb. DAfStb-Guideline: Load Tests on Concrete Structures; Deutscher Ausschuss für Stahlbeton: Berlin, Germany, 2000. [Google Scholar]
- Ministerio de Fomento. Instrucción de Acciones a Considerar En Puentes de Ferrocarril (IAPF); Ministerio de Fomento: Madrid, Spain, 2010. [Google Scholar]
- SIA. Existing Structures—Bases for Examination and Interventions; SIA: Singapore, 2011. [Google Scholar]
- NCHRP. Manual for Bridge Rating through Load Testing; NCHRP: Washington, DC, USA, 1998. [Google Scholar]
- Research Institute of Roads and Bridges. The Rules for Road Bridges Proof Loadings (In Polish) (Zalecenia Dotyczace Wykonywania Badan Pod Próbnym Obciazeniem Drogowych Obiektów Mostowych); Research Institute of Roads and Bridges: Warsaw, Poland, 2008. [Google Scholar]
- Lantsoght, E.O.L. Load Testing of Bridges: Current Practice and Diagnostic Load Testing, 1st ed.; Lantsoght, E.O.L., Ed.; CRC Press: Boca Raton, FL, USA, 2019; ISBN 9780367210823. [Google Scholar]
- AASHTO. The Manual for Bridge Evaluation, 2nd ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2011. [Google Scholar]
- ACI Commitee 437. Code Requirements for Load Testing of Existing Concrete Structures (ACI 437.2M-13); ACI Commitee 437: Farmington Hills, MA, USA, 2013. [Google Scholar]
- NRA. Load Testing for Bridge Assessment; NRA: Dublin, Ireland, 2014. [Google Scholar]
- Slovak Standardization Institute. Loading Tests of Bridges (ZataŽovacie Skúšky Mostov); Slovak Standardization Institute: Bratislava, Slovakia, 1979. [Google Scholar]
- Czech Normalization Institute. Loading Tests of Bridges; Czech Normalization Institute: Prague, Czech Republic, 1996. [Google Scholar]
- Hungarian Chamber of Engineers. Guidelines for Interventions in Hungary; Hungarian Chamber of Engineers: Budapest, Hungary, 2013. (In Hungarian) [Google Scholar]
- Ministerio de Fomento. Recomendaciones Para la Realizacion de Pruebas de Carga de Recepcion en Puentes de Carretera; Ministerio de Fomento—Direccion General de Carreteras: Madrid, Spain, 1999. [Google Scholar]
- Ministerio de Fomento. Instrucciones Para La Puesta En Carga de Estructuras (Pruebas de Carga Provisionales); Ministerio de Fomento: Tokyo, Japan, 2009. [Google Scholar]
- Alampalli, S.; Frangopol, D.M.; Grimson, J.; Kosnik, D.; Halling, M.; Lantsoght, E.; Weidner, J.S.; Yang, D.Y.; Zhou, Y.E. Primer on Bridge Load Testing; Transport; Transportation Research Board (TRB): Washington, DC, USA, 2019; ISBN 0097-8515. [Google Scholar]
- Fu, G.; Tang, J. Risk-based proof-load requirements for bridge evaluation. J. Struct. Eng. 1995, 121, 542–556. [Google Scholar] [CrossRef]
- Lantsoght, E.O.L.; Boer, A.; van der Veen, C.; Hordijk, D.A. Modelling of the Proof Load Test on Viaduct De Beek. In Proceedings of the Computational Modelling of Concrete Structures—Proceedings of the Conference on Computational Modelling of Concrete and Concrete Structures, EURO-C 2018, Bad Hofgastein, Austria, 26 February–1 March 2018; CRC Press/Balkema: Boca Raton, FL, USA, 2018; pp. 535–544. [Google Scholar]
- AASHTO. Guide Manual for Condition Evaluation and Load and Resistance Factor Rating (LRFR) of Highway Bridges; AASHTO: Washington, DC, USA, 2003. [Google Scholar]
- Lantsoght, E.O.L.; van der Veen, C.; de Boer, A.; Hordijk, D.A. Required proof load magnitude for probabilistic field assessment of viaduct de beek. Eng. Struct. 2017, 148, 767–779. [Google Scholar] [CrossRef]
- Lantsoght, E.; Veen, C.V.D.; Hordijk, D.A.; Boer, A. De development of recommendations for proof load testing of reinforced concrete slab bridges. Eng. Struct. 2017, 152, 202–210. [Google Scholar] [CrossRef]
- ISIS. Guidelines for Structural Health Monitoring-Design Manual N 2; ISIS: Mayadin, Syria, 2001. [Google Scholar]
- Lantsoght, E.O.L.; Yang, Y.; Veen, C.V.D.; Hordijk, D.A. Stop criteria for flexure for proof load testing of reinforced concrete structures. Front. Built Environ. 2019, 5. [Google Scholar] [CrossRef]
- Benitez, K.; Lantsoght, E.O.L.; Yang, Y. Development of a Stop Criterion for Load Tests Based on the Critical Shear Displacement Theory. In Life Cycle Analysis and Assessment in Civil Engineering: Towards an Integrated VisionLife; CRC Press: Boca Raton, FL, USA, 2018; pp. 145–152. [Google Scholar]
- Christensen, C.O.; Schmidt, J.W.; Halding, P.S.; Kapoor, M.; Goltermann, P. Digital image correlation for evaluation of cracks in reinforced concrete bridge slabs. Infrastructures 2021, 6, 99. [Google Scholar] [CrossRef]
- prEN 1990-2; Load Testing, Background Document for: prEN 1990-2 (CEN/TC 250/WG 2/WG2.T2). Project Team CEN/TC 250/WG 2/WG2.T2; Ver. November 2021. CEN: Brussels, Belgium, 2021.
- CEN/TC 250; EN 1990-1: Eurocode 0—Basis of Structural Design. European Committee for Standardization: Bruxelles, Belgium, 2002.
- Vejdirektoratet (The Danish Road Directorate). Vejledning for Prøvebelastning Af Broer (Guideline for Proof-Loading of Bridges); Vejdirektoratet (The Danish Road Directorate): Copenhagen, Denmark, 2021. [Google Scholar]
- Garnica, G.I.Z.; Zhang, F.; Yang, Y.; van der Veen, C.; Lantsoght, E.O.L.; Naaktgeboren, M.; Fennis, S.A.A.M. Monitoring Structural Responses during Proof Load Testing of Reinforced Concrete Bridges: A Review. In Proceedings of the Bridge Maintenance, Safety, Management, Life-Cycle Sustainability and Innovations, IABMAS 2020, Japan (Online), 11–18 April 2021. [Google Scholar]
- Jensen, T.W.; Poulsen, P.N.; Hoang, L.C. Finite element limit analysis of slabs including limitations on shear forces. Eng. Struct. 2018, 174, 896–905. [Google Scholar] [CrossRef]
- Lantsoght, E.O.L. (Ed.) Load Testing of Bridges Proof Load Testing and the Future of Load Testing, 1st ed; CRC Press: London, UK, 2019; ISBN 9780429265969. [Google Scholar]
- Steffens, K.; Opitz, H.; Quade, J.; Schwesinger, P. The loading truck BELFA for loading tests on concrete bridges and sewers. Bautechnik 2001, 78, 391–397. [Google Scholar] [CrossRef]
- Christensen, C.O.; Halding, P.S.; Schmidt, J.W.; Goltermann, P. Large-Scale OT-Slab Tests Laboratory Measurements and Evaluation. In Proceedings of the 11th International Conference on Bridge Maintenance, Safety and Management, Barcelona, Spain, 11–15 July 2022; pp. 2099–2106. [Google Scholar] [CrossRef]
- Halding, P.S.; Schmidt, J.W.; Jensen, T.W.; Henriksen, A.H. Structural Response of Full-Scale Concrete Bridges Subjected to High Load Magnitudes. In Proceedings of the Fourth Conference on Smart Monitoring, Assessment and Rehabilitation of Civil Structures, Zürich, Switzerland, 13–15 September 2017. [Google Scholar]
- Halding, P.S.; Schmidt, J.W.; Christensen, C.O. DIC-Monitoring of Full-Scale Concrete Bridge Using High-Resolution Wide-Angle Lens Camera. In Proceedings of the Maintenance, Safety, Risk, Management and Life-Cycle Performance of Bridges, Melbourne, Australia, 9–13 July 2018; pp. 1492–1499. [Google Scholar] [CrossRef]
- Halding, P.S.; Christensen, C.O.; Schmidt, J.W. Surface Rotation Correction and Strain Precision of Wide-Angle 2D DIC for Field Use. J. Bridg. Eng. 2019, 24, 04019008. [Google Scholar] [CrossRef]
- Christensen, C.O.; Lantsoght, E.O.L.; Schmidt, J.W. Quantification of Digital Image Correlation Applicability Related to In-Situ Proof Load Testing of Bridges. In Proceedings of the Fifth Conference on Smart Monitoring, Assessment and Rehabilitation of Civil Structures, Potsdam, Germany, 27–29 August 2019; pp. 1–8. [Google Scholar]
- Christensen, C.O.; Zhang, F.; Garnica, G.Z.; Lantsoght, E.O.L.; Goltermann, P.; Schmidt, J.W. Identification of stop criteria for large-scale laboratory slab tests using digital image correlation and acoustic emission. Infrastructures 2022, 7, 36. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Christensen, C.O.; Damsgaard, K.D.S.; Sørensen, J.D.; Engelund, S.; Goltermann, P.; Schmidt, J.W. Reliability-Based Proof Load Factors for Assessment of Bridges. Buildings 2023, 13, 1060. https://doi.org/10.3390/buildings13041060
Christensen CO, Damsgaard KDS, Sørensen JD, Engelund S, Goltermann P, Schmidt JW. Reliability-Based Proof Load Factors for Assessment of Bridges. Buildings. 2023; 13(4):1060. https://doi.org/10.3390/buildings13041060
Chicago/Turabian StyleChristensen, Christian Overgaard, Kenneth Dahl Schiøttz Damsgaard, John Dalsgaard Sørensen, Svend Engelund, Per Goltermann, and Jacob Wittrup Schmidt. 2023. "Reliability-Based Proof Load Factors for Assessment of Bridges" Buildings 13, no. 4: 1060. https://doi.org/10.3390/buildings13041060








