Sectional Model Wind Tunnel Test and Research on the Wind-Induced Vibration Response of a Curved Beam Unilateral Stayed Bridge
Abstract
:1. Introduction
2. Engineering Background and Sectional Model Wind Tunnel Tests
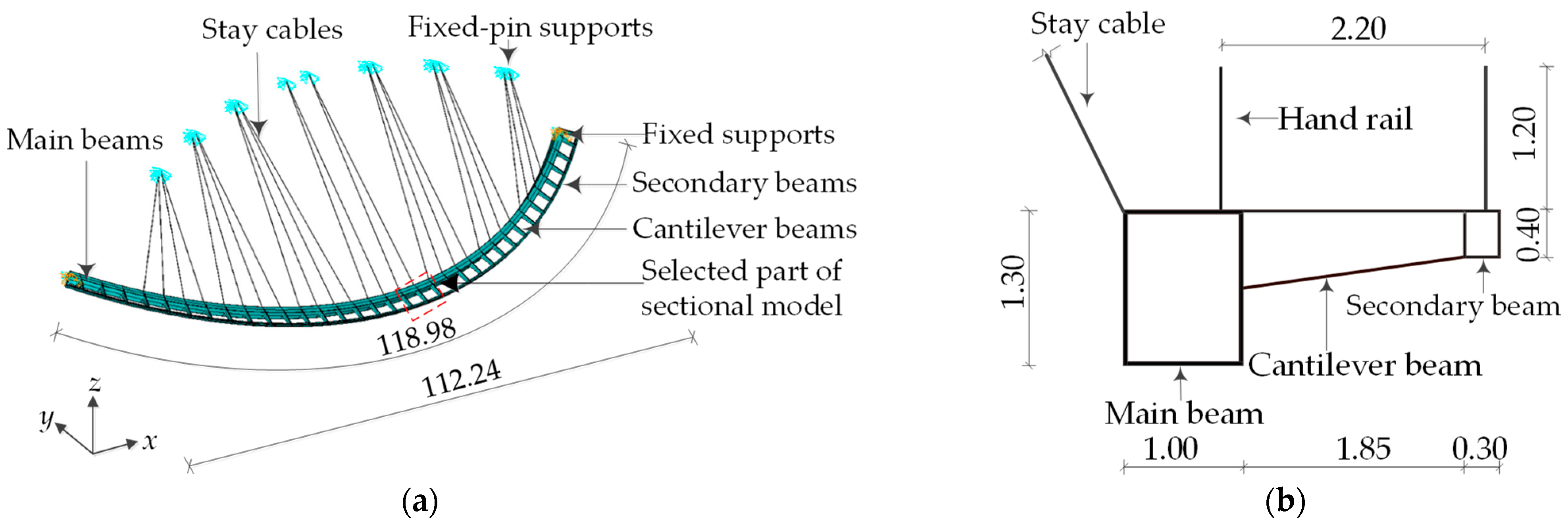
2.1. Background in Engineering and Laboratory
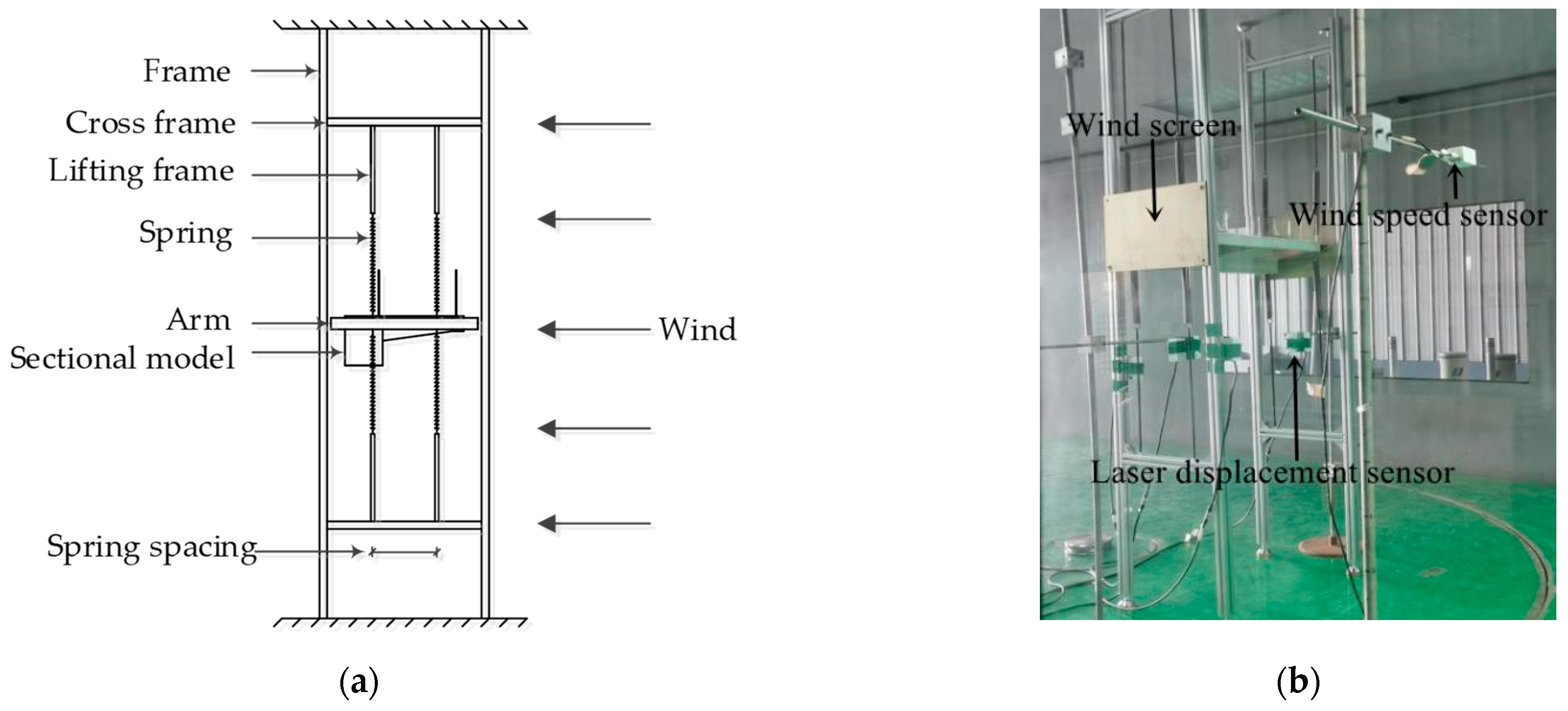
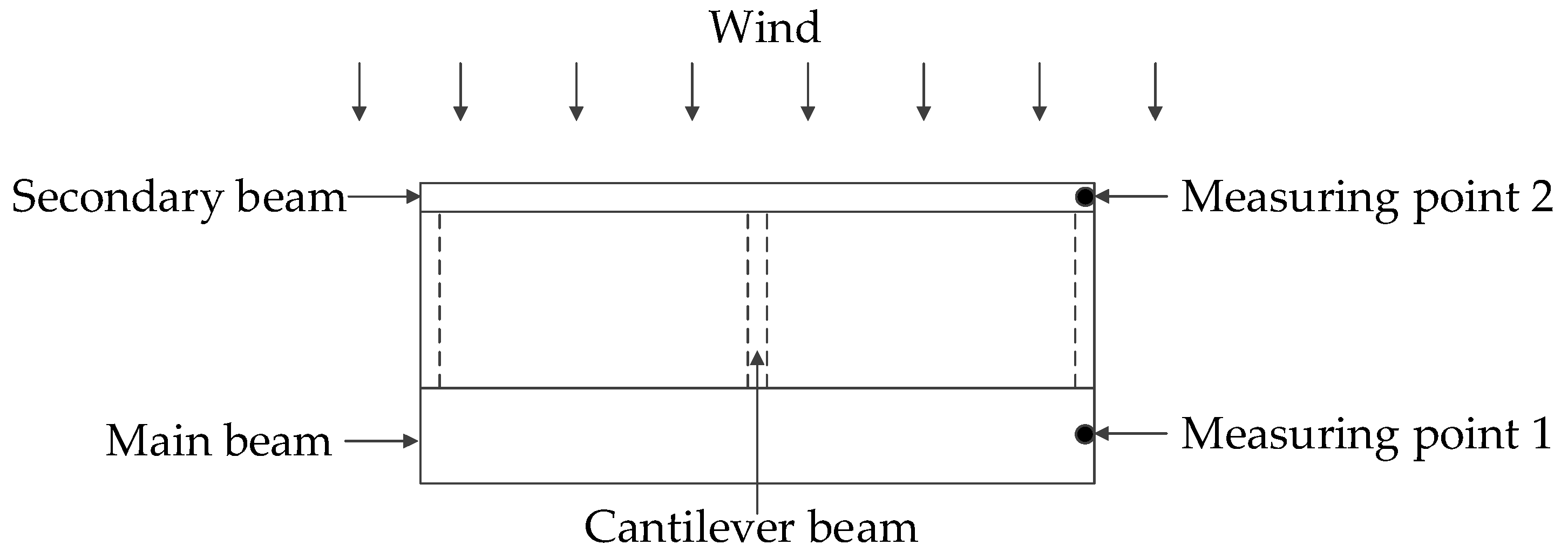
2.2. Design and Fabrication of Section Model and Vibration Test System
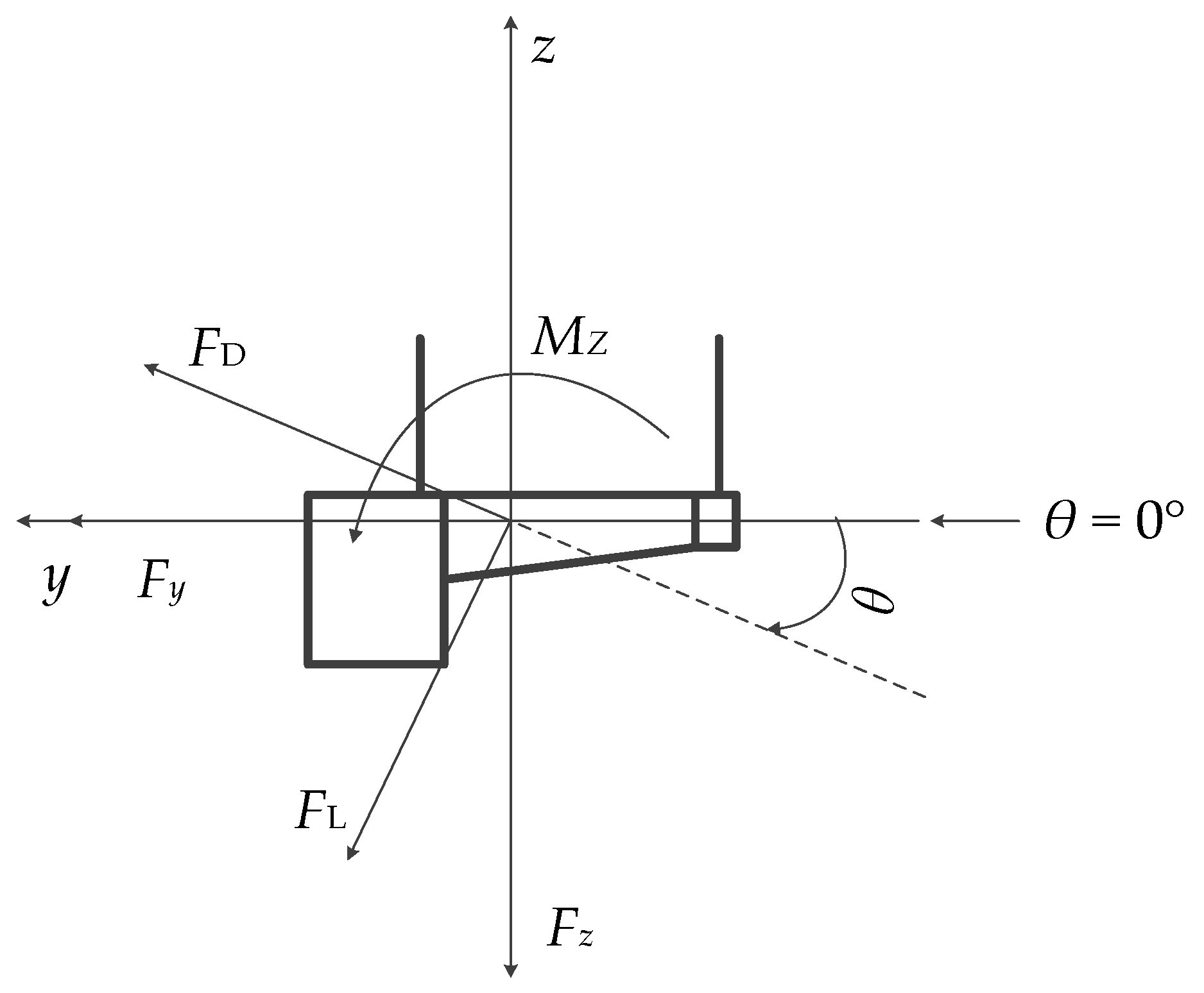
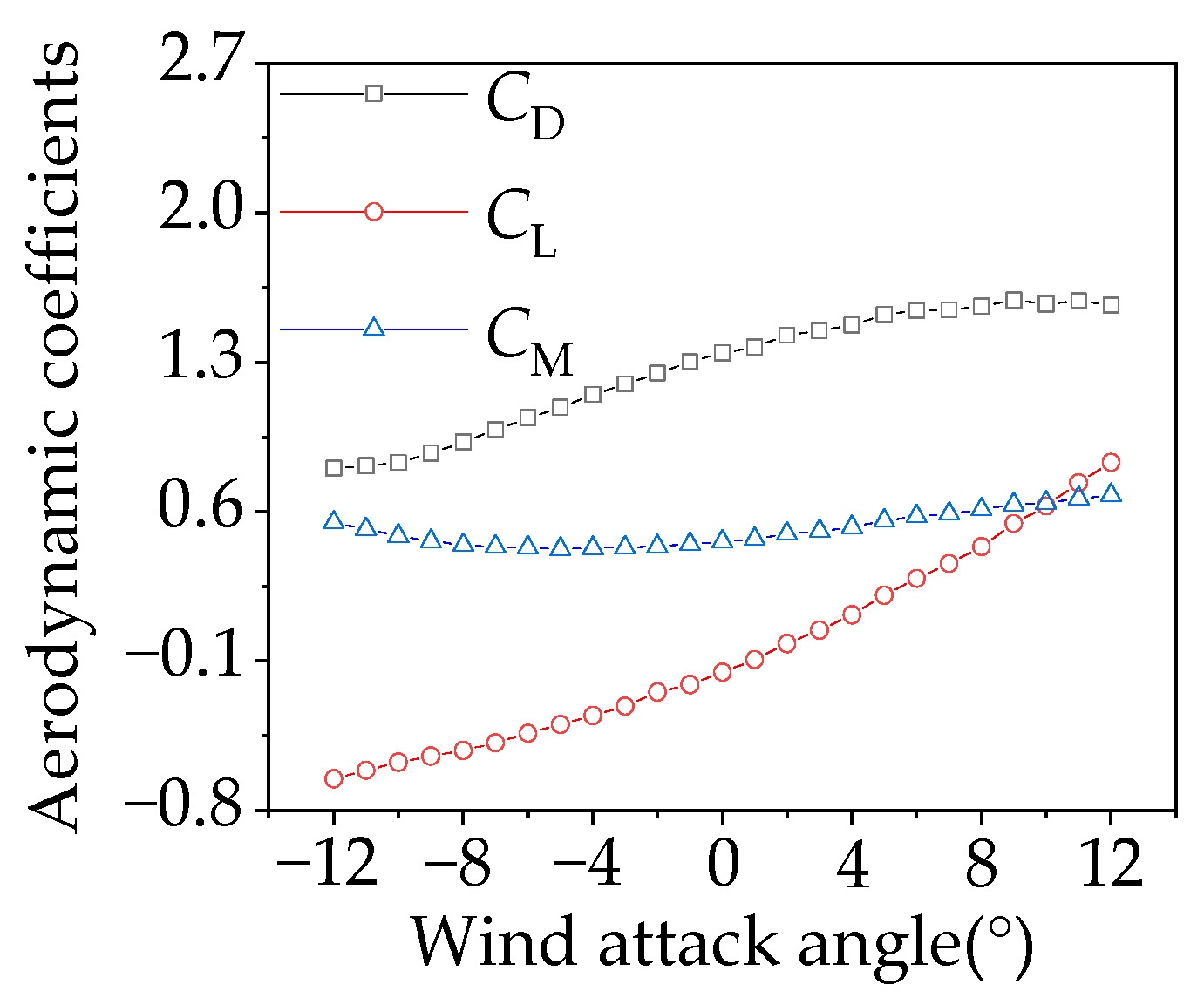
2.3. Aerostatic Force Tests of CBUSB
2.4. Sectional Model Vibration Tests of CBUSB
3. Numerical Analysis of CBUSB Wind-Induced Vibration Response
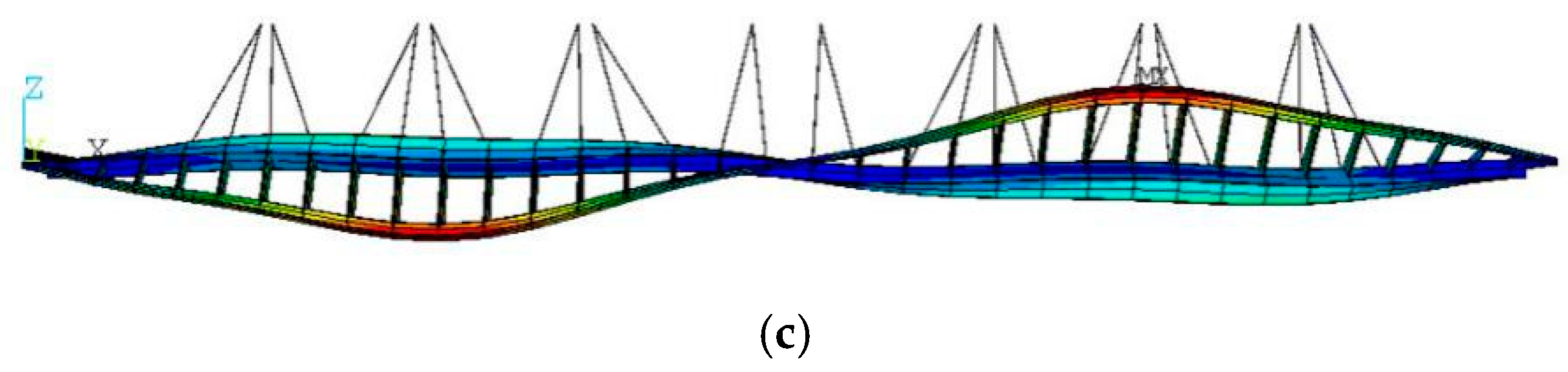
3.1. Establishment and Verification of Finite Element Model
3.2. Numerical Simulation and Characteristic Verification of Wind Field
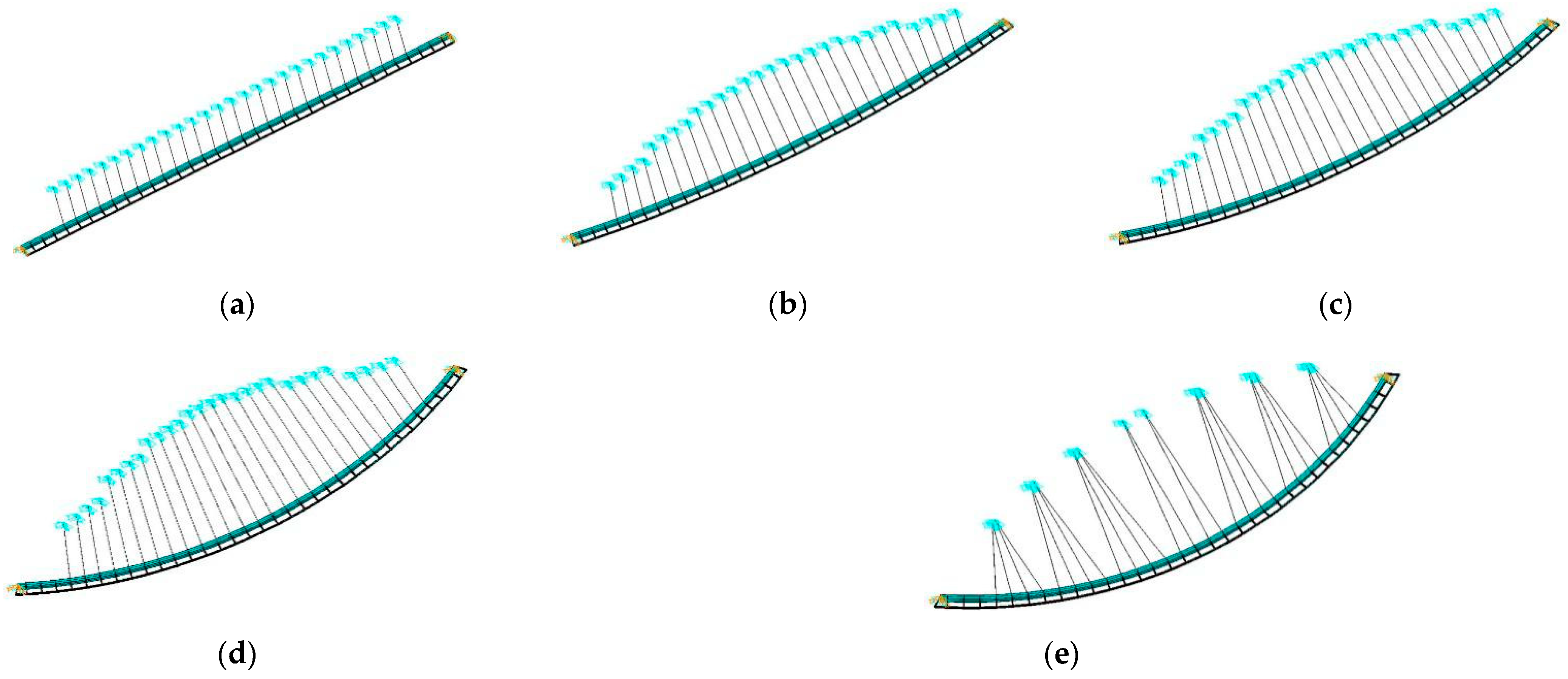
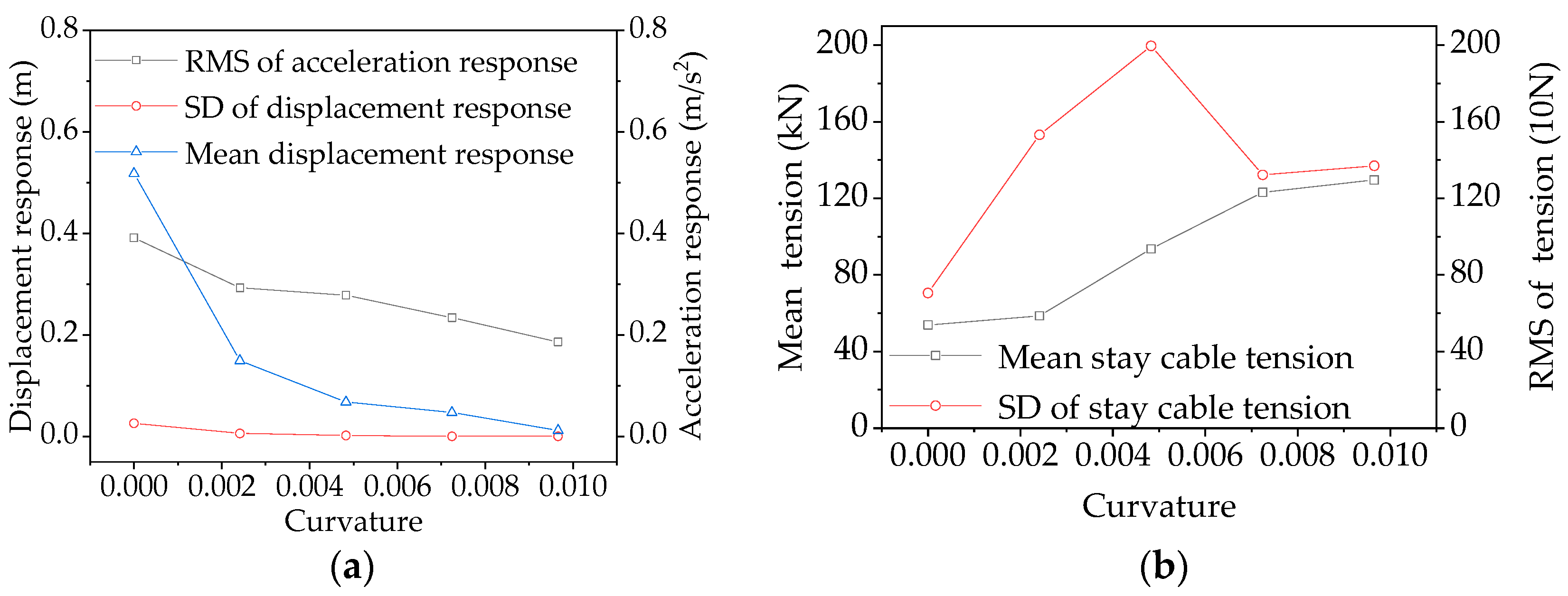
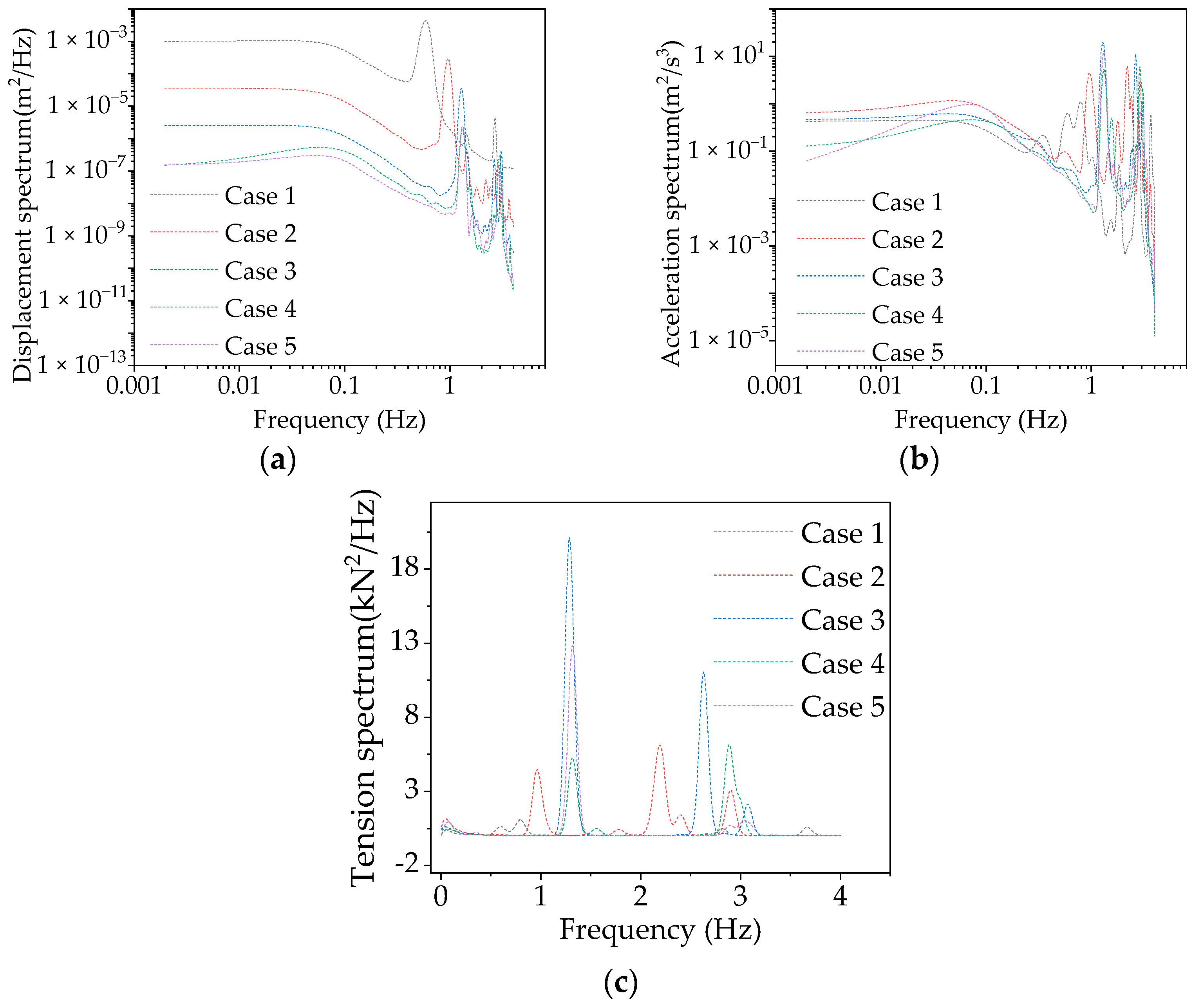
3.3. CBUSB Parametric Analysis of Curvature Variation
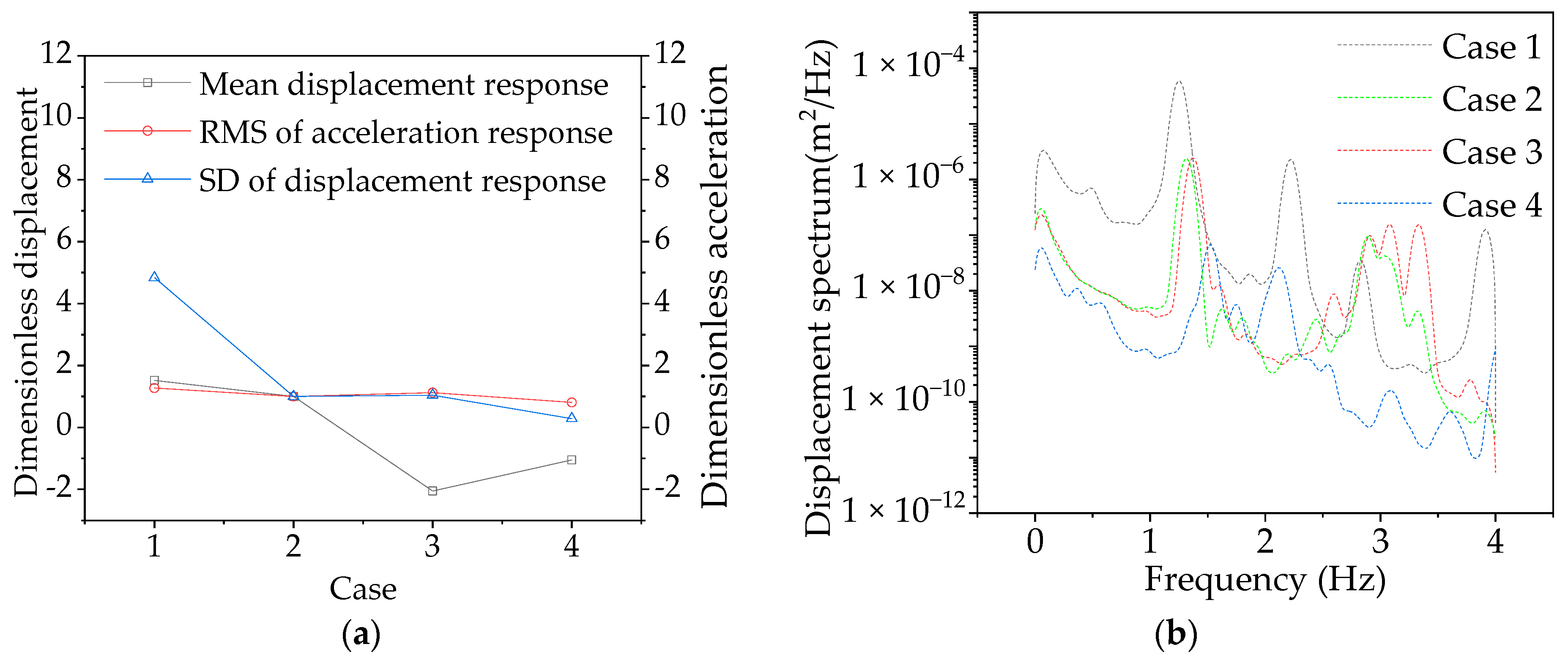
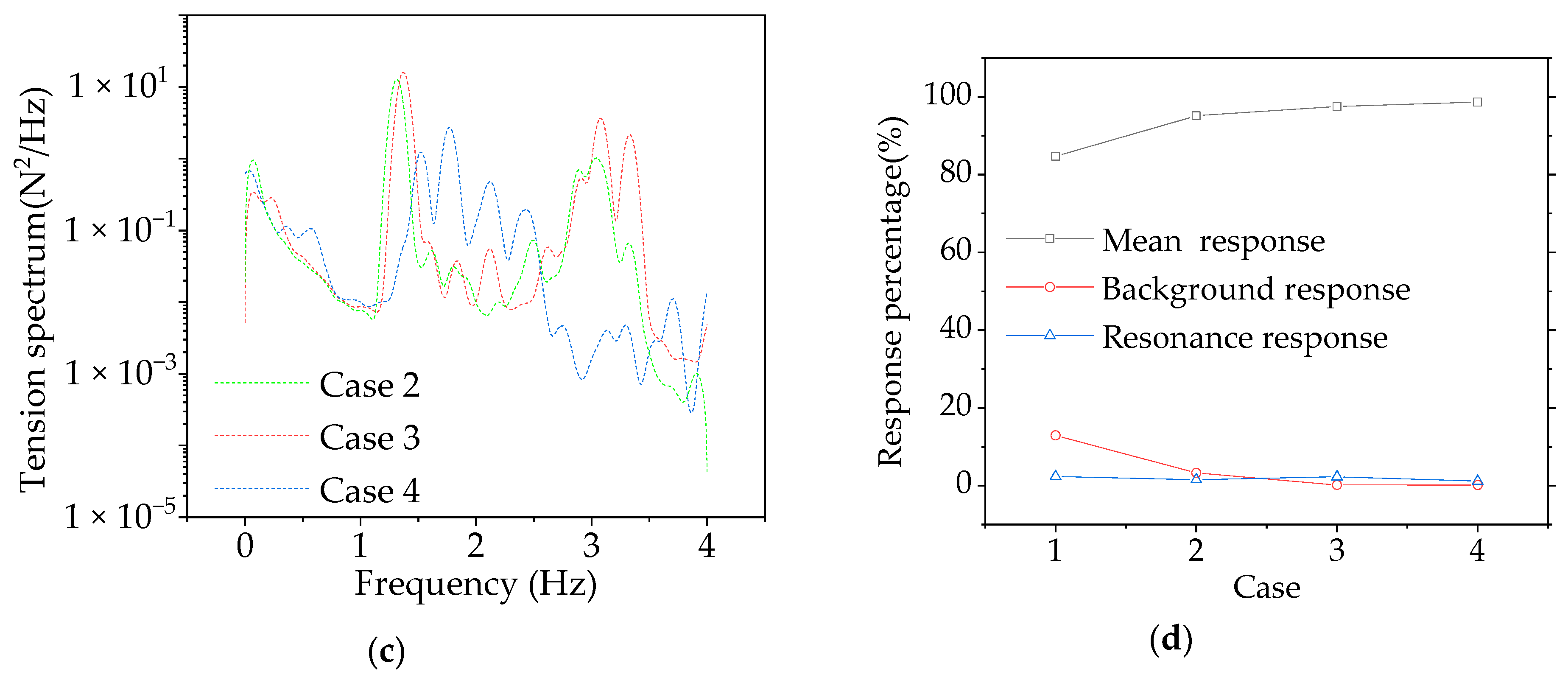
3.4. CBUSB Parametric Analysis of Stay Cable Layout Scheme
4. Conclusions
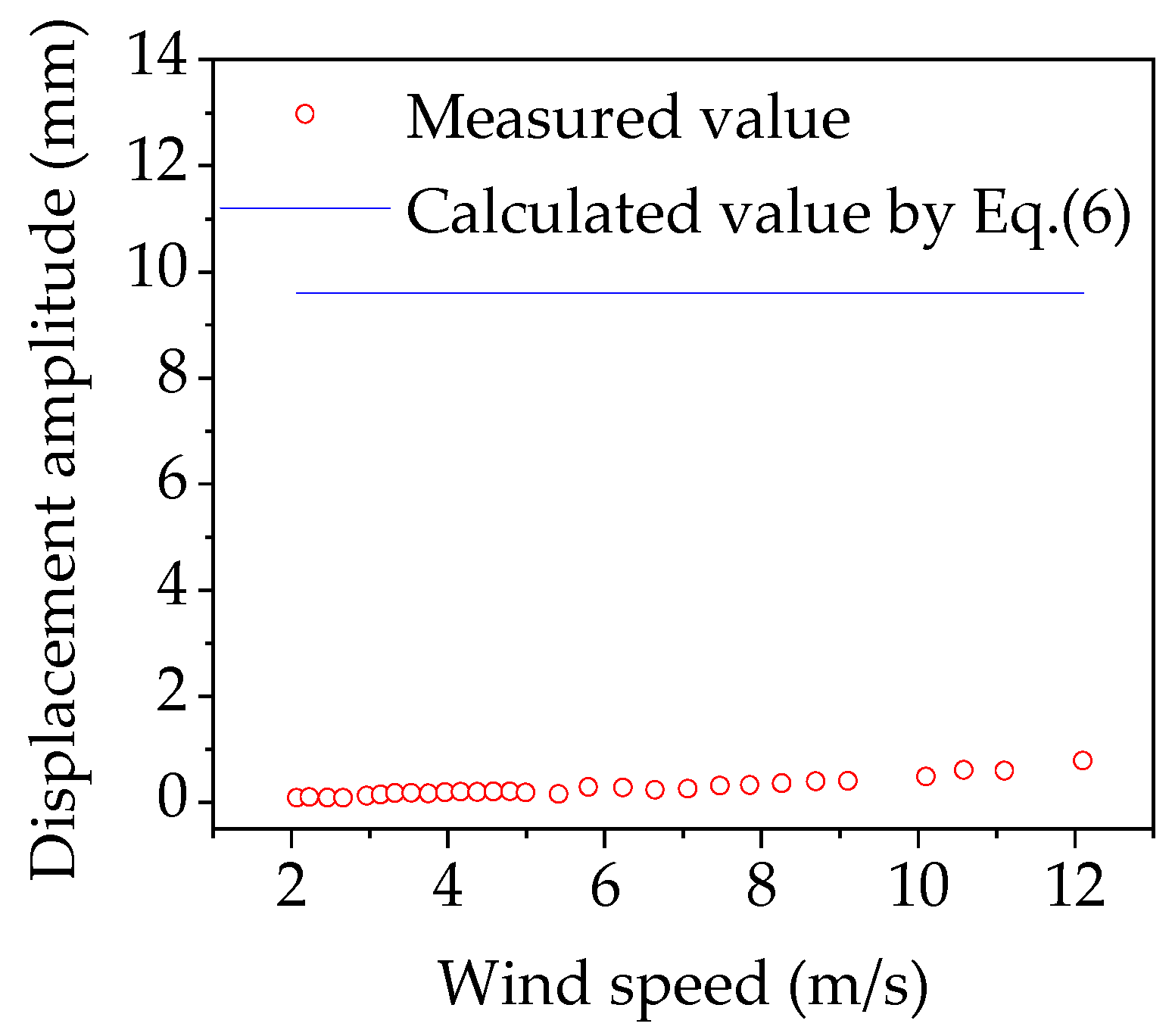
- The aerodynamic force coefficients were obtained through aerostatic force tests and slopes of the CL-θ and CM-θ were positive in various θ, indicating that the main beam had the necessary conditions for aerodynamic stability. Each test value in the sectional model vibration test met the code requirements, indicating that the CBUSB had good vortex vibration stability;
- With increasing curvature, the resonance energy excited by the wind load decreased at a certain wind speed, and the high-order modal resonance response was excited, indicating that high-frequency vibration reduction should be considered for pedestrian comfort control at high wind speeds, and a broadband vibration reduction method can be used. As the curvature increase, the resonance acceleration energy distribution gradually changes from sparse to dense, potentially resulting in modal coupling vibration. When the curvature is 0.0048, the resonance response regarding the fluctuating response is high, so fatigue failure of cables may occur; thus, further study on cable fracture for CBUSB is required;
- CBUSB is dominated by mean response under wind loads. The arrangement of cables can increase the proportion of mean displacement response in the total response and increase the natural frequency of the curved beam bridge. The arrangement of cables on the side close to the center of curvature helps to reduce the proportion of resonance response. The arrangement of cables on both sides can reduce the peak acceleration in the transverse direction of the bridge, which is conducive to the control of pedestrian comfort, and cause the distribution of high-order and low-order resonance energy to be closer, which may result in modal coupling vibration. The arrangement of cables on the side away from the center of curvature can significantly increase the proportion of resonance response and increase the possibility of resonance failure of the bridge under high wind speed. Therefore, when CBUSB arranges the cable, it should be arranged inside the curvature center as far as possible to reduce the possibility of resonance damage. Affected by the interaction between cable and bridge, the cable and Bridge transmit their own vibration to each other, both of which contain the response components of each other.
Author Contributions
Funding
Conflicts of Interest
References
- Cermak, J.E. Wind-tunnel development and trends in applications to civil engineering. J. Wind Eng. Ind. Aerodyn. 2003, 91, 355–370. [Google Scholar] [CrossRef]
- Gao, G.Z.; Zhu, L.D. Nonlinearity of mechanical damping and stiffness of a spring-suspended sectional model system for wind tunnel tests. J. Vib. Control. 2008, 318, 850–857. [Google Scholar] [CrossRef]
- Huang, M.H.; Lo, Y.L. A refined method of multi-target equivalent static wind loads: A bridge case. J. Wind Eng. Ind. Aerodyn. 2021, 212, 104609. [Google Scholar] [CrossRef]
- Xu, K.; Ge, Y.J.; Zhao, L. Quantitative evaluation of empirical models of vortex-induced vibration of bridge decks through sectional model wind tunnel testing. Eng. Struct. 2020, 219, 110860. [Google Scholar] [CrossRef]
- Zasso, A.; Belloli, M.; Muggiasca, S. Wind tunnel study on the Pescara footbridge. Eur. Afr. Conf. Wind. Eng. 2009, 10, 2309062. [Google Scholar]
- Li, H.; Piekarski, B.; DeVoe, D.L.; Balachandran, B. Nonlinear oscillations of piezoelectric microresonators with curved cross-sections. Sens. Actuator A Phys. 2008, 144, 194–200. [Google Scholar] [CrossRef]
- Yang, F.; Sedaghatia, R.; Esmailzadehb, E. Free in-plane vibration of general curved beams using finite element method. J. Vib. Control. 2008, 318, 850–857. [Google Scholar] [CrossRef]
- Swapan, K.C.; Sidney, S. Thin-walled curved beam finite element. J. Eng. Mech. 1977, 103, 921–937. [Google Scholar]
- Hu, J.; Ou, J.P. Comparison between field measurement and theoretical analysis results for a long-span suspension bridge’s wind-induced vibration responses. J. Vib. Shock. 2013, 32, 149–154. [Google Scholar]
- Arzoumanidis, S.G.; Bienie, M.P. Finite element analysis of suspension bridges. Comput. Struct. 1985, 21, 1237–1253. [Google Scholar] [CrossRef]
- Law, S.S.; Chan, T.H.T.; Wu, D. Super element with semi-rigid joints in model updating. J. Sound. Vib. 2001, 239, 19–39. [Google Scholar] [CrossRef]
- Lee, Y.Y.; Poon, W.Y.; Ng, C.F. Anti-symmetric mode vibration of a curved beam subject to auto parametric excitation. J. Sound. Vib. 2006, 290, 48–64. [Google Scholar] [CrossRef]
- Li, S.H.; Ren, J.Y. Analytical study on dynamic responses of a curved beam subjected to three-directional moving loads. Appl. Math. Model. 2018, 58, 355–387. [Google Scholar] [CrossRef]
- Yang, Y.B.; Wu, C.M.; Yau, J.D. Dynamic response of a horizontally curved beam subjected to vertical and horizontal moving loads. J. Sound. Vib. 2001, 242, 519–537. [Google Scholar] [CrossRef]
- Bao, Y.L.; Xiang, H.Y.; Li, Y.L.; Hou, G.Y. Dynamic effects of turbulent crosswinds on a suspended monorail vehicle–curved bridge coupled system. J. Vib. Control. 2021, 28, 1135–1147. [Google Scholar] [CrossRef]
- Lin, M.K.; Shi, J.Q. Analysis of Torsional vibration frequency of steel box-concrete composite beams with curved wavy webs. J. Lanzhou Jiaotong Univ. 2022, 41, 1–7. [Google Scholar]
- Xie, T.; Mohamed, A.M.S.; Elchalakani, M.; David, M. Experimental and analytical study of ultrahigh-performance fiber-reinforced concrete curved beams. J. Struct. Eng. 2020, 146, 91–92. [Google Scholar] [CrossRef]
- Arco, D.C.; Aparicio, Á.C. Improving suspension bridge wind stability with aerodynamic appendages. J. Struct. Eng. 1999, 125, 1357–1375. [Google Scholar] [CrossRef]
- Fenerci, A.; Oiseth, O.; Ronnquist, A. Long-term monitoring of wind field characteristics and dynamic response of a long-span suspension bridge in complex terrain. Eng. Struct. 2017, 147, 269–284. [Google Scholar] [CrossRef]
- Zhao, G.H.; Wang, Z.C.; Zhu, S.; Hao, J.M.; Wang, J. Experimental study of mitigation of wind-induced vibration in asymmetric cable-stayed bridge using sharp wind fairings. Appl. Sci. 2021, 12, 242. [Google Scholar] [CrossRef]
- Zhou, H.J.; Xu, Y.L. Wind–rain-induced vibration and control of stay cables in a cable-stayed bridge. J. Bridge. Eng. 2007, 303, 330–342. [Google Scholar] [CrossRef]
- Xing, C.X.; Wang, H.; Li, A.Q.; Xu, Y. Study on wind-induced vibration control of a long-span cable-stayed bridge using TMD-type counterweight. J. Brigde Eng. 2014, 19, 141–148. [Google Scholar] [CrossRef]
- Wu, B.; Zhang, L.L.; Yang, Y.; Liu, L.J.; Ni, Z.J. Refined time-domain buffeting analysis of a long-span suspension bridge in mountainous urban terrain. Adv. Civ. Eng. 2020, 2020, 4703169. [Google Scholar] [CrossRef]
- Montoya, M.C.; Hernández, S.; Nieto, F.; Kareem, A. Aero-structural design of bridges focusing on the buffeting response: Formulation, parametric studies and deck shape tailoring. J. Wind Eng. Ind. Aerodyn. 2020, 204, 104243. [Google Scholar] [CrossRef]
- He, B.; Zhao, M.X.; Feng, W.T.; Xiu, Y.P.; Wang, Y.; Feng, L.J.; Qin, Y.J.; Wang, C.K. A method for analyzing stability of tower-line system under strong winds. Adi. Eng. Softw. 2019, 127, 1–7. [Google Scholar] [CrossRef]
- Zhao, S.; Yan, Z.T.; Li, Z.L.; Dong, J.Y.; Zhong, Y.L. Investigation on wind tunnel tests of an aeroelastic model of 1000 kV sutong long span transmission tower-line system. Proc. CSEE 2018, 38, 5257–5265. [Google Scholar]
- Zhao, S.; Yue, J.H.; Savory, E.; Yan, Z.T.; Chen, J.H.; Zhang, B.; Peng, L.L. Dynamic windage yaw angle and dynamic wind load factor of a suspension insulator string. J. Vib. Shock. 2022, 2022, 6822689. [Google Scholar] [CrossRef]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Standard for Wind Tunnel Test of Buildings and Structures; JGJ/T 338-2014; China Architecture and Building Press: Beijing, China, 2014. [Google Scholar]
- Nussbaumer, H.J. The Fast Fourier Transform and Convolution Algorithms; Springer: Heidelberg, Germany, 1981; pp. 80–111. [Google Scholar]
- Ministry of Transport of the People’s Republic of China. Wind-Resistant Design Specification for Highway Bridges; JTG/T 3360-01-2018; China Communication Press: Beijing, China, 2018. [Google Scholar]
- Stolarski, T.; Nakasone, Y.; Yoshimoto, S. Engineering Analysis with ANSYS Software; Butterworth-Heinemann: London, UK, 2018; pp. 37–207. [Google Scholar]
- Hutchinson, J.R. Shear Coefficients for Timoshenko Beam Theory. J. Appl. Mech. 2001, 68, 87–92. [Google Scholar] [CrossRef]
- Hay, G.E. The finite displacement of thin rods. Trans. Am. Math. Soc. 1942, 51, 65–102. [Google Scholar] [CrossRef] [Green Version]
- Deodatis, G. Simulation of ergodic multivariate stochastic processes. J. Eng. Mech. 1996, 122, 778–787. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhao, N.; Peng, L.L.; Liu, S.Y.; Xin, J.Z. Fast simulation of fully non-stationary wind fields using a new matrix factorization assisted interpolation method. Mech. Syst. Signal. Process. 2022, 172, 108973. [Google Scholar] [CrossRef]
- Zhao, S.; Yan, Z.T.; Savory, E. Design wind loads for transmission towers with cantilever cross-arms based on the inertial load method. J. Wind Eng. Ind. Aerodyn. 2020, 205, 104286. [Google Scholar] [CrossRef]
- Lawrence, J.C.; Terry, J.F. The Band Pass Filter. Int. Econ. Rev. 2003, 44, 435–465. [Google Scholar]





| Parameters | Sectional Model |
|---|---|
| Length (mm) | 702.00 |
| width (mm) | 315.00 |
| Main beam height (mm) | 130.00 |
| Mass per unit length (kg/m) | 16.53 |
| Mass moment of inertia per unit length (kgm2/m) | 2.78 |
| Vertical frequency fv (Hz) | 4.101 |
| Torsional frequency (Hz) | 36.541 |
| Parameters | Sectional Model (pm) | Similarity Ratio (rs) | Finite Element Model (pf) | Error (e) |
|---|---|---|---|---|
| Mass moment of inertia per unit (kg·m2/m) | 2.78 | 1:104 | 27176.24 | 1.6% |
| Mass per unit (kg/m) | 16.53 | 1:102 | 1653.14 | 0.1% |
| Vertical frequency (Hz) | 4.101 | 1.318 | 1.6% | |
| Torsional frequency (Hz) | 36.541 | 11.589 | 3.0% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, S.; Chen, J.; Yue, J.; Yan, Z.; Liu, J.; Zhang, B.; Chen, J. Sectional Model Wind Tunnel Test and Research on the Wind-Induced Vibration Response of a Curved Beam Unilateral Stayed Bridge. Buildings 2022, 12, 1643. https://doi.org/10.3390/buildings12101643
Zhao S, Chen J, Yue J, Yan Z, Liu J, Zhang B, Chen J. Sectional Model Wind Tunnel Test and Research on the Wind-Induced Vibration Response of a Curved Beam Unilateral Stayed Bridge. Buildings. 2022; 12(10):1643. https://doi.org/10.3390/buildings12101643
Chicago/Turabian StyleZhao, Shuang, Jiahao Chen, Jiahao Yue, Zhitao Yan, Jun Liu, Bin Zhang, and Jianfeng Chen. 2022. "Sectional Model Wind Tunnel Test and Research on the Wind-Induced Vibration Response of a Curved Beam Unilateral Stayed Bridge" Buildings 12, no. 10: 1643. https://doi.org/10.3390/buildings12101643
APA StyleZhao, S., Chen, J., Yue, J., Yan, Z., Liu, J., Zhang, B., & Chen, J. (2022). Sectional Model Wind Tunnel Test and Research on the Wind-Induced Vibration Response of a Curved Beam Unilateral Stayed Bridge. Buildings, 12(10), 1643. https://doi.org/10.3390/buildings12101643








