Physical-Mechanism Exploration of the Low-Cycle Unified Creep-Fatigue Formulation
Abstract
:1. Introduction
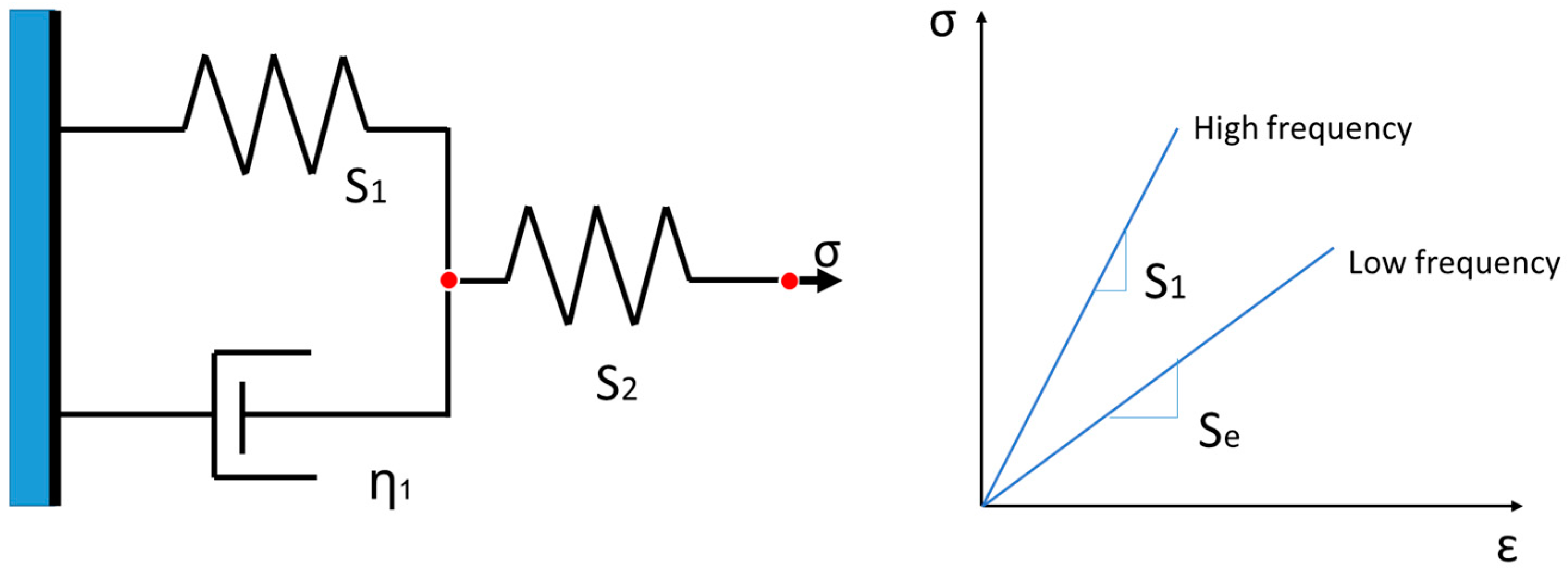
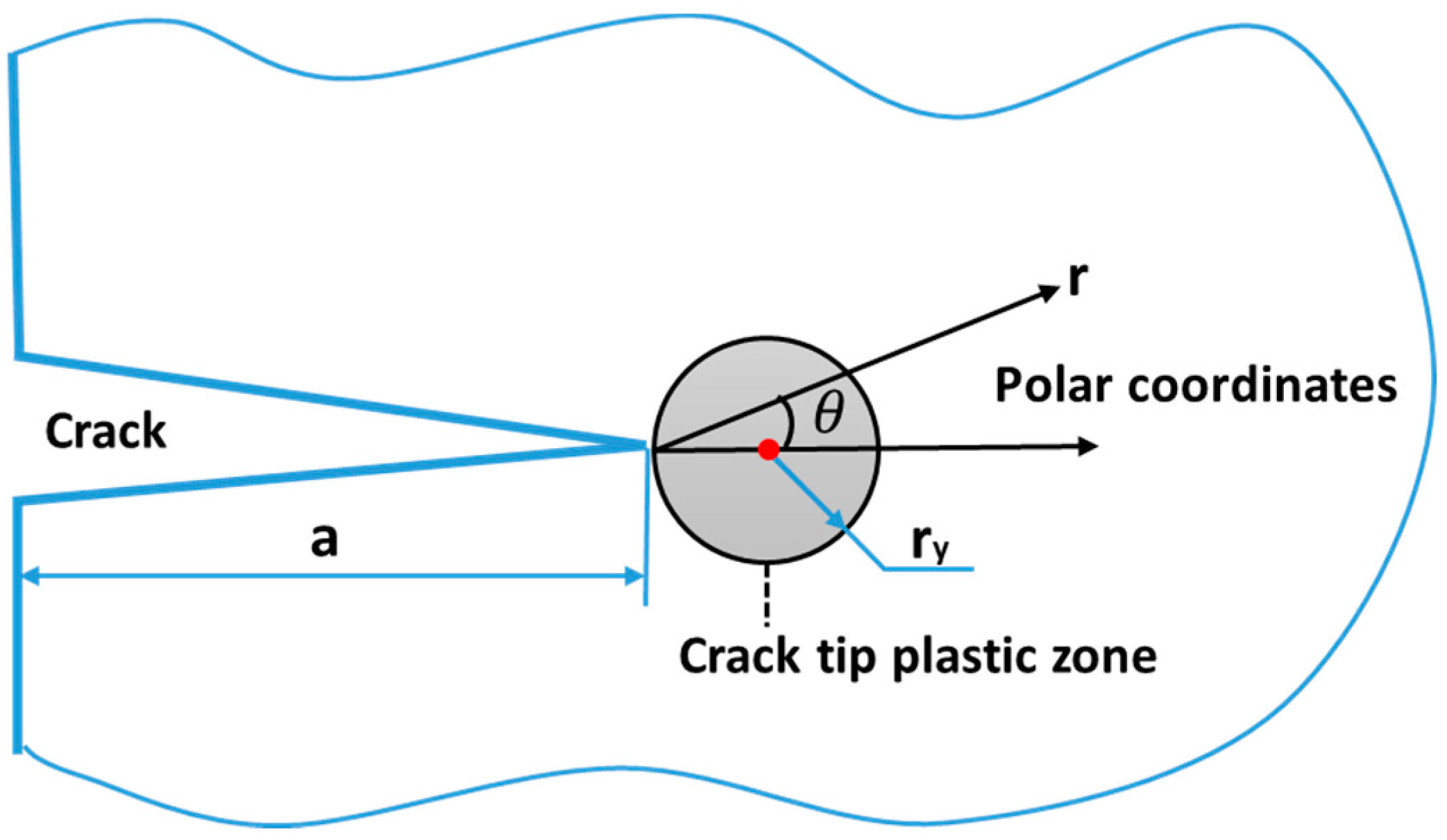
2. Brief Description of the Unified Model
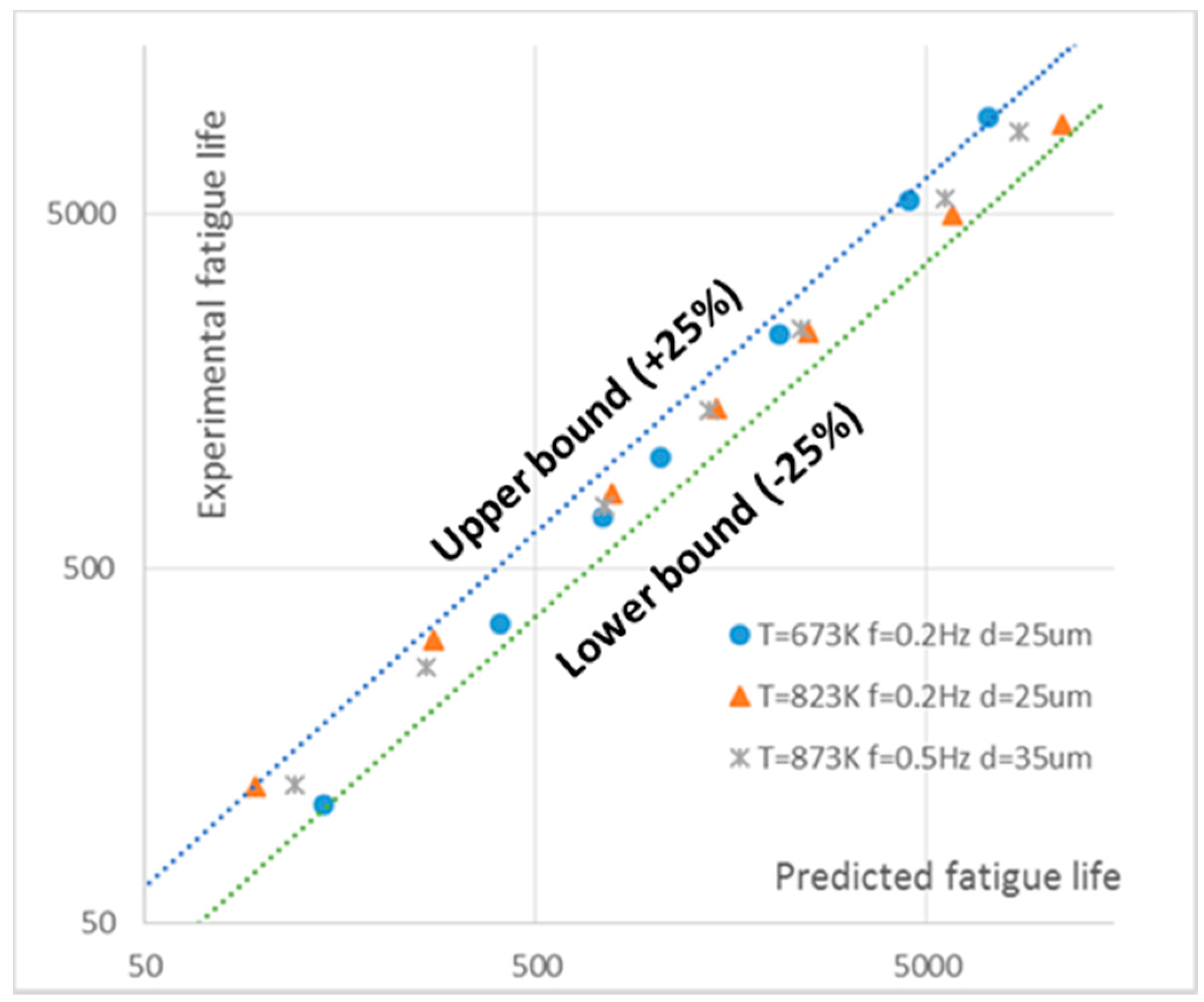
3. Influence of Relevant Variables on Creep-Fatigue Behavior
3.1. Temperature Dependency
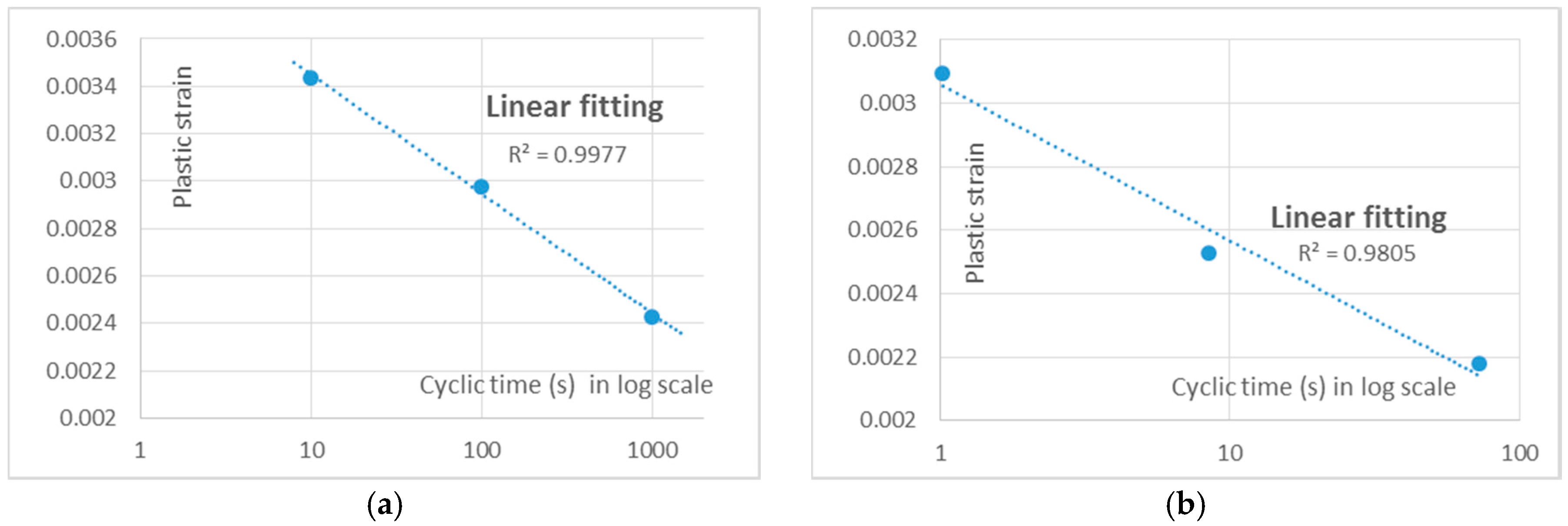
3.2. Frequency/Cyclic Time Dependence
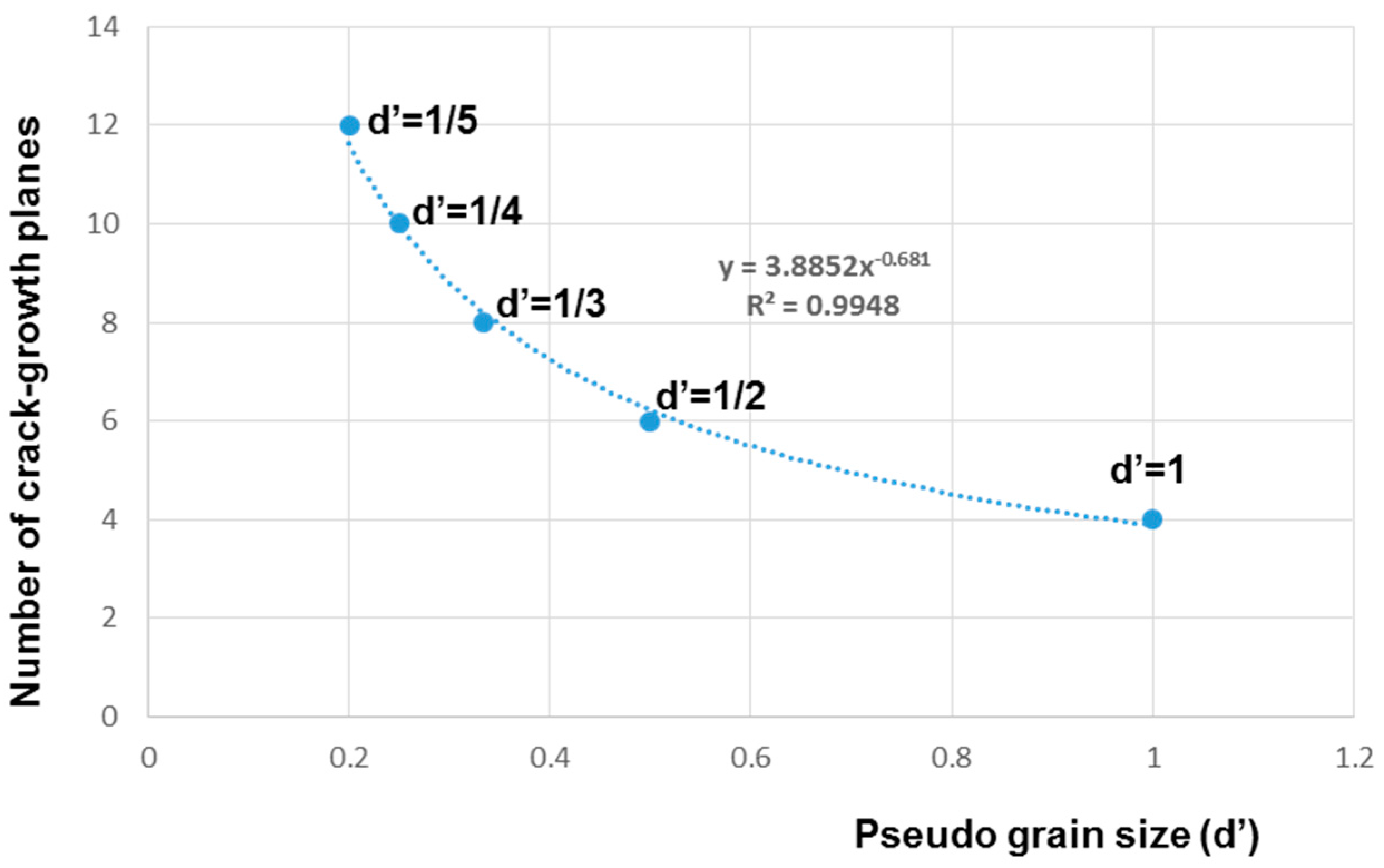
3.3. Grain-Size Dependence
4. Consistency between the Unified Formulation and Physical Phenomena
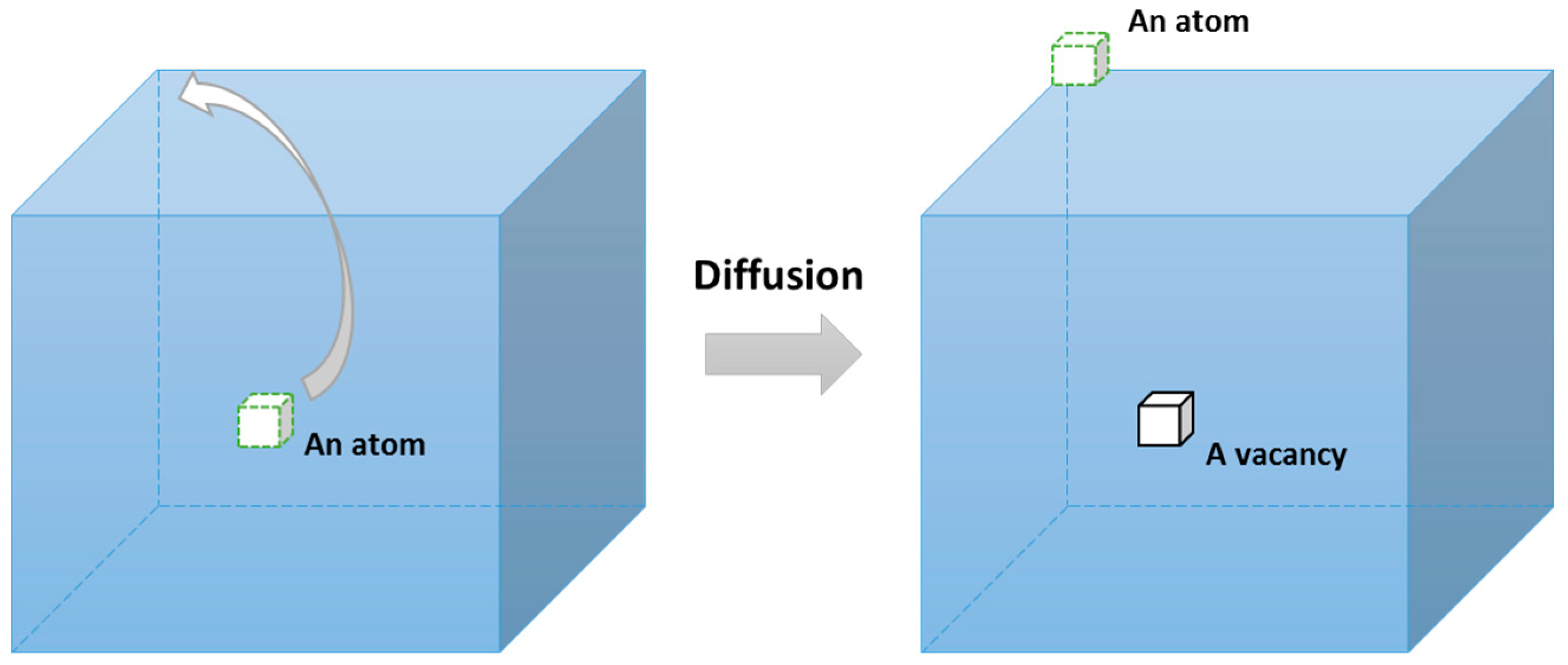
4.1. Linear Relationship between Temperature and Strain
4.2. Logarithmical Relation between Temperature and Cyclic Time
4.3. Power-Law Relation between Grain Size and Strain
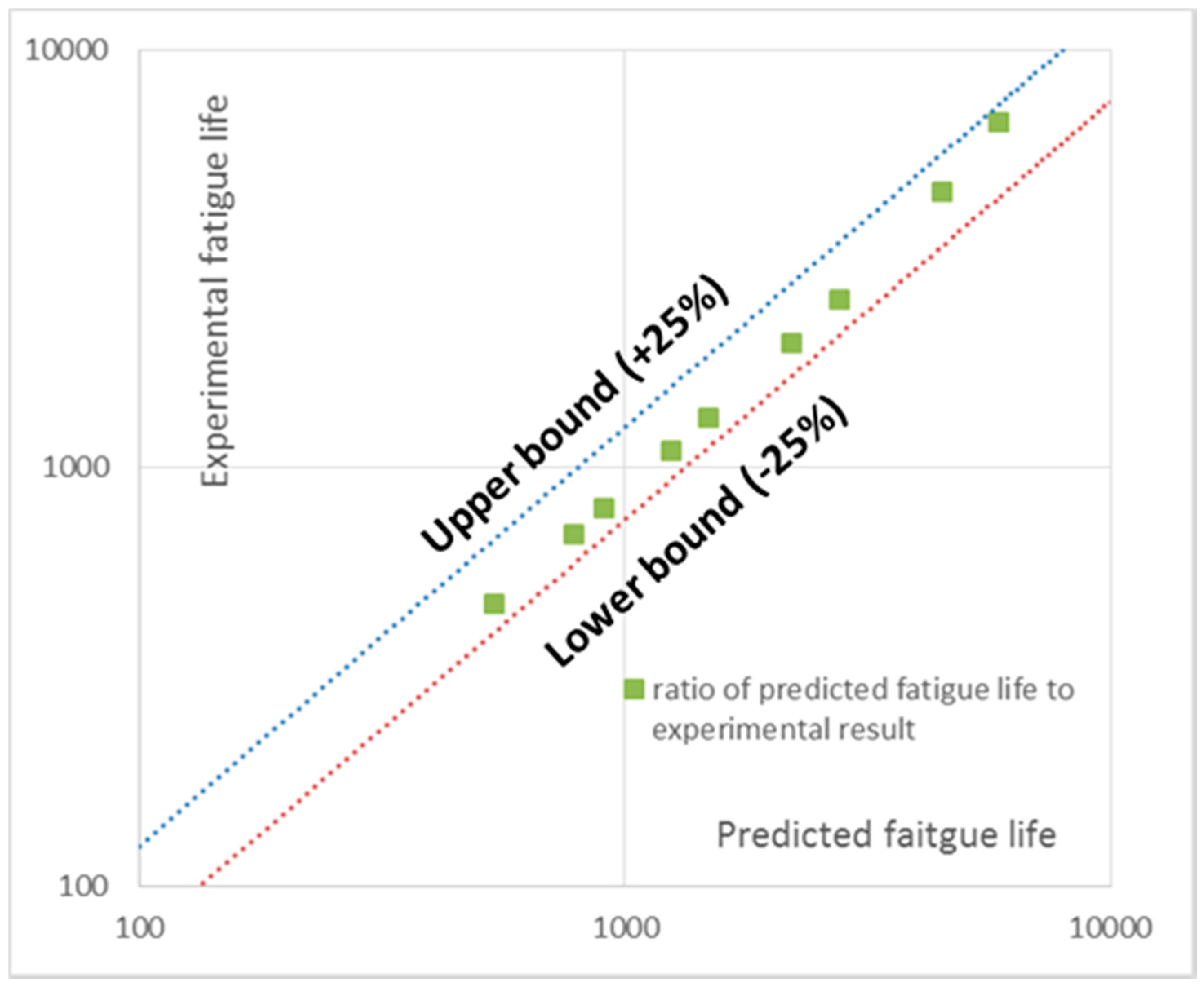
4.4. Power-Law Relation between Life and Strain
4.5. Numerical Presentation of Creep Effect on Fatigue Capacity
5. Discussion
5.1. Summary
5.2. Limitations and Future Work
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Miner, M.A. Cumulative damage in fatigue. J. Appl. Mech. 1945, 12, 159–164. [Google Scholar]
- Palmgren, A. Die lebensdauer von kugellagern. Z. Ver. Dtsch. Ing. 1924, 68, 339–341. [Google Scholar]
- Paris, P.; Erdogan, F. A critical analysis of crack propagation laws. J. Basic Eng. 1963, 85, 528–533. [Google Scholar] [CrossRef]
- Takahashi, Y. Study on creep-fatigue evaluation procedures for high-chromium steels—Part I: Test results and life prediction based on measured stress relaxation. Int. J. Press. Vessel. Pip. 2008, 85, 406–422. [Google Scholar] [CrossRef]
- Takahashi, Y.; Dogan, B.; Gandy, D. Systematic evaluation of creep-fatigue life prediction methods for various alloys. J. Press. Vessel. Technol. 2013, 135, 061204. [Google Scholar] [CrossRef]
- Payten, W.M.; Dean, D.W.; Snowden, K.U. A strain energy density method for the prediction of creep-fatigue damage in high temperature components. Mater. Sci. Eng. 2010, 527, 1920–1925. [Google Scholar] [CrossRef]
- Neu, R.; Sehitoglu, H. Thermomechanical fatigue, oxidation, and creep: Part II. Life prediction. Metall. Trans. A 1989, 20, 1769–1783. [Google Scholar] [CrossRef]
- Ainsworth, R.; Ruggles, M.; Takahashi, Y. Flaw assessment procedure for high-temperature reactor components. J. Press. Vessel. Technol. 1992, 114, 166–170. [Google Scholar] [CrossRef]
- Cailletaud, G.; Nouailhas, D.; Grattier, J.; Levaillant, C.; Mottot, M.; Tortel, J.; Escavarage, C.; Héliot, J.; Kang, S. A review of creep-fatigue life prediction methods: Identification and extrapolation to long term and low strain cyclic loading. Nucl. Eng. Des. 1984, 83, 267–278. [Google Scholar] [CrossRef]
- June, W. A continuum damage mechanics model for low-cycle fatigue failure of metals. Eng. Fract. Mech. 1992, 41, 437–441. [Google Scholar] [CrossRef]
- Chaboche, J.L. Une loi Différentielle D’endommagement de Fatigue avec Cumulation non Linéaire; Office Nationale d’Etudes et de Recherches Aérospatiales: Palaiseau, France, 1974.
- Metzger, M.; Nieweg, B.; Schweizer, C.; Seifert, T. Lifetime prediction of cast iron materials under combined thermomechanical fatigue and high cycle fatigue loading using a mechanism-based model. Int. J. Fatigue 2013, 53, 58–66. [Google Scholar] [CrossRef]
- Seifert, T.; Riedel, H. Mechanism-based thermomechanical fatigue life prediction of cast iron. Part I: Models. Int. J. Fatigue 2010, 32, 1358–1367. [Google Scholar] [CrossRef]
- Charkaluk, E.; Bignonnet, A.; Constantinescu, A.; Dang Van, K. Fatigue design of structures under thermomechanical loadings. Fatigue Fract. Eng. Mater. Struct. 2002, 25, 1199–1206. [Google Scholar] [CrossRef]
- Constantinescu, A.; Charkaluk, E.; Lederer, G.; Verger, L. A computational approach to thermomechanical fatigue. Int. J. Fatigue 2004, 26, 805–818. [Google Scholar] [CrossRef]
- Basquin, O. The Exponential Law of Endurance Tests; ASTM International: West Conshohocken, PA, USA, 1910; pp. 625–630. [Google Scholar]
- Coffin, L.F., Jr. A Study of the Effects of Cyclic Thermal Stresses on a Ductile Metal; Knolls Atomic Power Lab.: Niskayuna, NY, USA, 1953. [Google Scholar]
- Manson, S.S. Behavior of Materials under Conditions of Thermal Stress; Lewis Flight Propulsion Lab.: Cleveland, OH, USA, 1954. [Google Scholar]
- Coffin, L. Fatigue at high temperature. In Fatigue at Elevated Temperatures; ASTM International: West Conshohocken, PA, USA, 1973. [Google Scholar]
- Solomon, H. Fatigue of 60/40 solder. IEEE Trans. Compon. Hybrids Manuf. Technol. 1986, 9, 423–432. [Google Scholar] [CrossRef]
- Shi, X.; Pang, H.; Zhou, W.; Wang, Z. Low cycle fatigue analysis of temperature and frequency effects in eutectic solder alloy. Int. J. Fatigue 2000, 22, 217–228. [Google Scholar] [CrossRef]
- Jing, H.; Zhang, Y.; Xu, L.; Zhang, G.; Han, Y.; Wei, J. Low cycle fatigue behavior of a eutectic 80 au/20 sn solder alloy. Int. J. Fatigue 2015, 75, 100–107. [Google Scholar] [CrossRef]
- Engelmaier, W. Fatigue life of leadless chip carrier solder joints during power cycling. IEEE Trans. Compon. Hybrids Manuf. Technol. 1983, 232–237. [Google Scholar] [CrossRef]
- Wong, E.; Mai, Y.-W. A unified equation for creep-fatigue. Int. J. Fatigue 2014, 68, 186–194. [Google Scholar] [CrossRef]
- Liu, D.; Pons, D. Development of a unified creep-fatigue equation including heat treatment. Fatigue Fract. Eng. Mater. Struct. 2017. [Google Scholar] [CrossRef]
- Liu, D.; Pons, D.; Wong, E.-H. The unified creep-fatigue equation for stainless steel 316. Metals 2016, 6, 219. [Google Scholar] [CrossRef]
- Liu, D.; Pons, D.; Wong, E.-H. Creep-integrated fatigue equation for metals. Int. J. Fatigue 2017, 98, 167–175. [Google Scholar] [CrossRef]
- Manson, S.; Haferd, A. A Linear Time-Temperature Relation for Extrapolation of Creep and Stress-Rupture Data; Lewis Flight Propulsion Lab.: Cleveland, OH, USA, 1953. [Google Scholar]
- Tabuchi, M.; Hongo, H.; Li, Y.; Watanabe, T.; Takahashi, Y. Evaluation of microstructures and creep damages in the haz of p91 steel weldment. J. Press. Vessel. Technol. 2009, 131, 021406. [Google Scholar] [CrossRef]
- Mroziński, S.; Golański, G. Low cycle fatigue of gx12crmovnbn9–1 cast steel at elevated temperature. J. Achiev. Mater. Manuf. Eng. 2011, 49, 7–16. [Google Scholar]
- Liu, D.; Pons, D. A unified creep-fatigue equation with application to engineering design. InTechOpen 2017. under review. [Google Scholar]
- Dowling, N.E. Mechanical Behavior of Materials: Engineering Methods for Deformation, Fracture, and Fatigue; Pearson Education (US): London, UK, 2012. [Google Scholar]
- Shigley, J.E.; Mischke, C.R. Mechanical Engineering Design; McGraw-Hill: New York, NY, USA, 2003. [Google Scholar]
- Ashby, M.F.; Shercliff, H.; Cebon, D. Materials: Engineering, Science, Processing and Design; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Callister, W.D.; Rethwisch, D.G. Materials Science and Engineering; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Finnie, I.; Heller, W.R. Creep of Engineering Materials; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Kassner, M.E. Fundamentals of Creep in Metals and Alloys; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Poirier, J.-P. Creep of Crystals: High-Temperature Deformation Processes in Metals, Ceramics and Minerals; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Shewmon, P. Diffusion in Solids; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Prokoshkina, D.; Esin, V.; Wilde, G.; Divinski, S. Grain boundary width, energy and self-diffusion in nickel: Effect of material purity. Acta Mater. 2013, 61, 5188–5197. [Google Scholar] [CrossRef]
- Dai, C.; Zhang, B.; Xu, J.; Zhang, G. On size effects on fatigue properties of metal foils at micrometer scales. Mater. Sci. Eng. 2013, 575, 217–222. [Google Scholar] [CrossRef]
- Hanlon, T.; Kwon, Y.-N.; Suresh, S. Grain size effects on the fatigue response of nanocrystalline metals. Scr. Mater. 2003, 49, 675–680. [Google Scholar] [CrossRef]
- Cocks, A.; Pontern, A. Mechanics of Creep Brittle Materials 1; Springer Science & Business Media: Berlin, Germany, 1989. [Google Scholar]
- Ejaz, N.; Qureshi, I.; Rizvi, S. Creep failure of low pressure turbine blade of an aircraft engine. Eng. Fail. Anal. 2011, 18, 1407–1414. [Google Scholar] [CrossRef]
- Král, P.; Dvořák, J.; Kvapilová, M.; Svoboda, M.; Sklenička, V. Creep damage of al and al-sc alloy processed by ecap. In Proceedings of the Acta Metallurgica Slovaca-Conference, Košice, Slovakia, 2012. [Google Scholar]
- Hatanaka, K.; Yamada, T. Effect of grain size on low cycle fatigue in low carbon steel. Bull. JSME 1981, 24, 1692–1699. [Google Scholar] [CrossRef]
- Hattori, H.; Kitagawa, M.; Ohtomo, A. Effect of grain size on high temperature low-cycle fatigue properties of inconel 617. Tetsu-To-Hagane 1982, 68, 2521–2530. [Google Scholar] [CrossRef]
- Pieraggi, B.; Uginet, J. Fatigue and Creep Properties in Relation; The Minerals, Metals & Materials Society: Pittsburgh, PA, USA, 1994. [Google Scholar]
- Thébaud, L.; Villechaise, P.; Cormier, J.; Crozet, C.; Devaux, A.; Béchet, D.; Franchet, J.-M.; Organista, A.; Hamon, F. Relationships between microstructural parameters and time-dependent mechanical properties of a new nickel-based superalloy ad730™. Metals 2015, 5, 2236–2251. [Google Scholar] [CrossRef]
- Fredriksson, H. Solidification and Crystallization Processing in Metals and Alloys; John Wiley & Sons: New York, NY, USA, 2012. [Google Scholar]
- Kanazawa, K.; Yoshida, S. Effect of Temperature and Strain Rate on the High Temperature Low-Cycle Fatigue Behavior of Austenitic Stainless Steels; IAEA: Vienna, Austria, 1975. [Google Scholar]
- Weertman, J. Fatigue crack propagation theories. In Fatigue and Microstructure; ASM: Metals Park, OH, USA, 1979; pp. 279–306. [Google Scholar]
- You, C.; He, B.; Achintha, M.; Reed, P. Numerical modelling of the fatigue crack shape evolution in a shot-peened steam turbine material. Int. J. Fatigue 2017, 104, 120–135. [Google Scholar] [CrossRef]
- Liang, R.; Ji, Y.; Wang, S.; Liu, S. Effect of microstructure on fracture toughness and fatigue crack growth behavior of ti17 alloy. Metals 2016, 6, 186. [Google Scholar] [CrossRef]
- Paggi, M. Crack propagation in honeycomb cellular materials: A computational approach. Metals 2012, 2, 65–78. [Google Scholar] [CrossRef] [Green Version]
- Xiang, Y.; Lu, Z.; Liu, Y. Crack growth-based fatigue life prediction using an equivalent initial flaw model. Part I: Uniaxial loading. Int. J. Fatigue 2010, 32, 341–349. [Google Scholar] [CrossRef]
- Manson, S. A modified universal slopes equation for estimation of fatigue characteristics of metals. J. Eng. Mater. Technol. 1988, 110, 55. [Google Scholar]
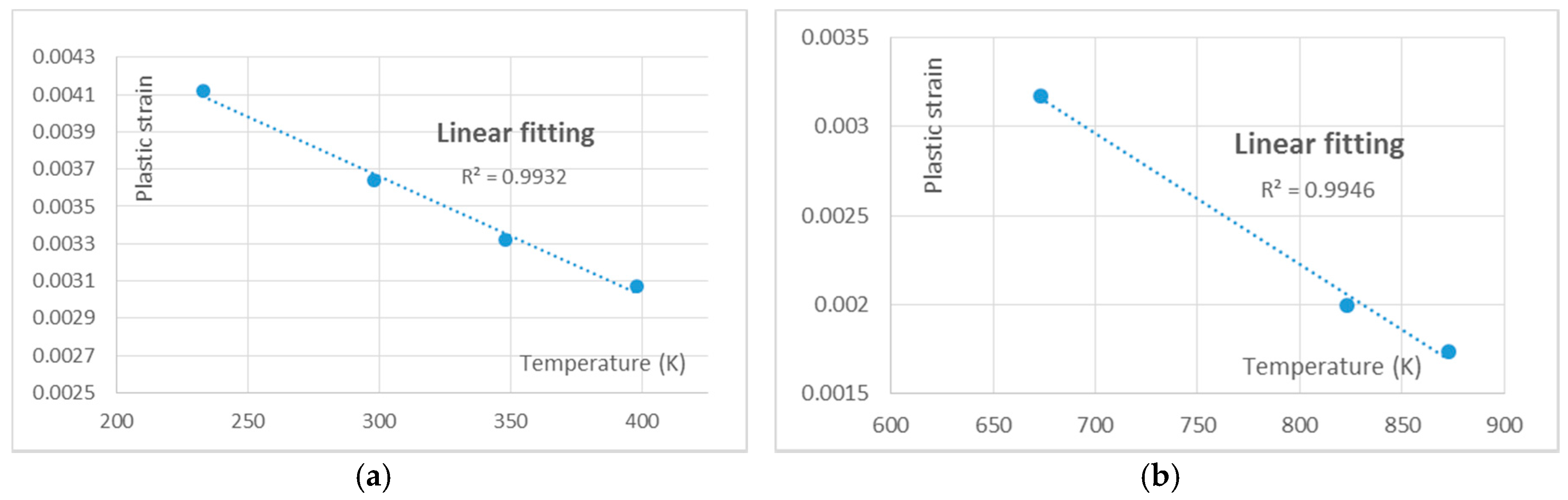

| Materials | Temperature (K) | Strain | Cyclic Time (s) | Life (Cycles) |
|---|---|---|---|---|
| 63Sn37Pb | 233 | 0.00412 | 1 | 5000 |
| 298 | 0.00364 | |||
| 248 | 0.00332 | |||
| 398 | 0.00307 | |||
| GP91 Casting Steel | 673 | 0.00317 | 20 | 5000 |
| 823 | 0.00199 | |||
| 873 | 0.00174 |
| Materials | Cyclic Time (s) | Strain | Temperature (K) | Life (Cycles) |
| 63Sn37Pb | 10 | 0.00344 | 298 | 5000 |
| 100 | 0.00298 | |||
| 1000 | 0.00243 | |||
| Materials | Strain Rate (%/min) | Strain | Temperature (K) | Life (Cycles) |
| Stainless Steel 316 | 0.4 | 0.00218 | 973 | 5000 |
| 4 | 0.00253 | |||
| 40 | 0.00309 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, D.; Pons, D.J. Physical-Mechanism Exploration of the Low-Cycle Unified Creep-Fatigue Formulation. Metals 2017, 7, 379. https://doi.org/10.3390/met7090379
Liu D, Pons DJ. Physical-Mechanism Exploration of the Low-Cycle Unified Creep-Fatigue Formulation. Metals. 2017; 7(9):379. https://doi.org/10.3390/met7090379
Chicago/Turabian StyleLiu, Dan, and Dirk John Pons. 2017. "Physical-Mechanism Exploration of the Low-Cycle Unified Creep-Fatigue Formulation" Metals 7, no. 9: 379. https://doi.org/10.3390/met7090379





