Experimental and Numerical Modeling of the Stress Rupture Behavior of Nickel-Based Single Crystal Superalloys Subject to Multi-Row Film Cooling Holes
Abstract
:1. Introduction
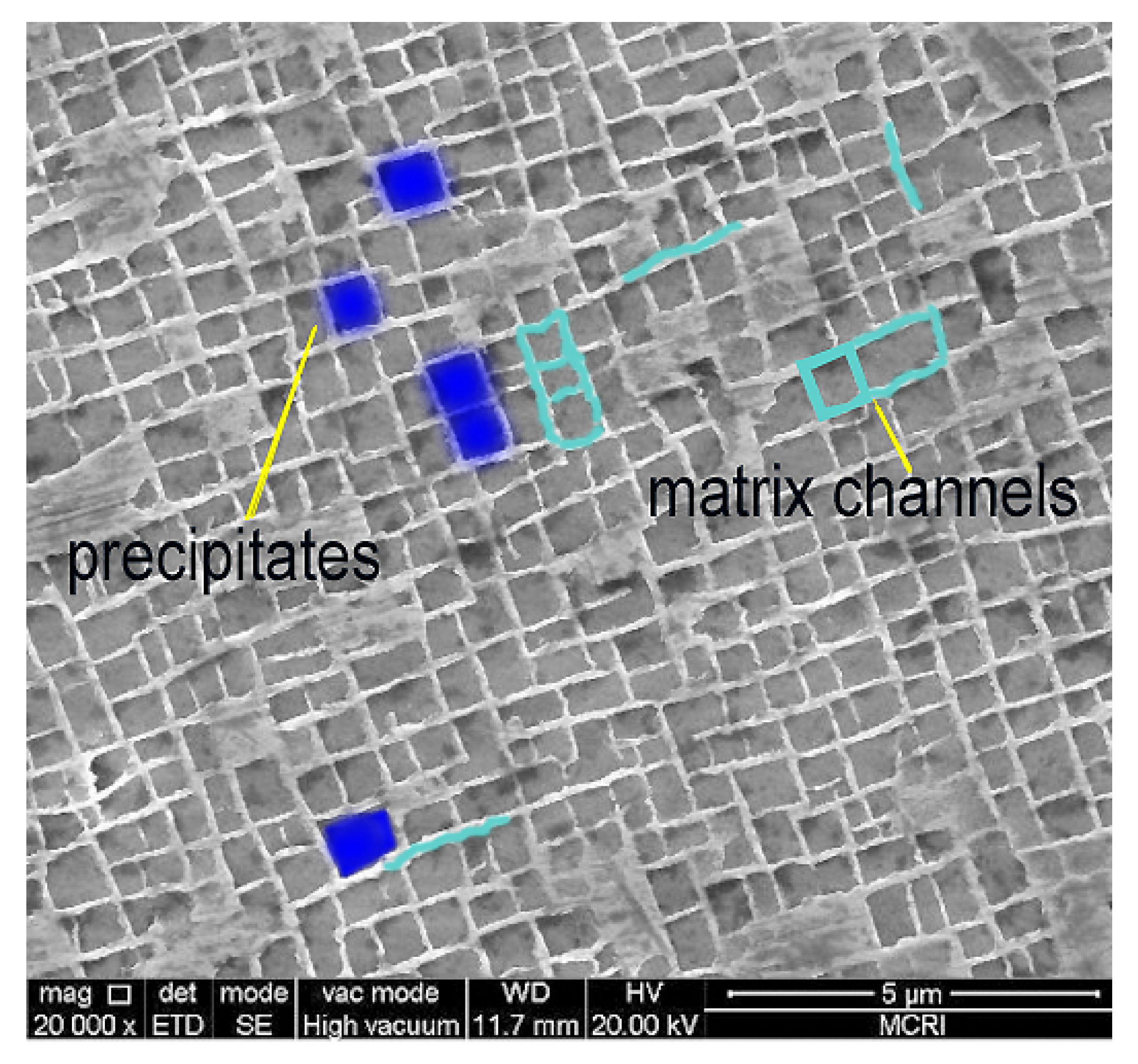
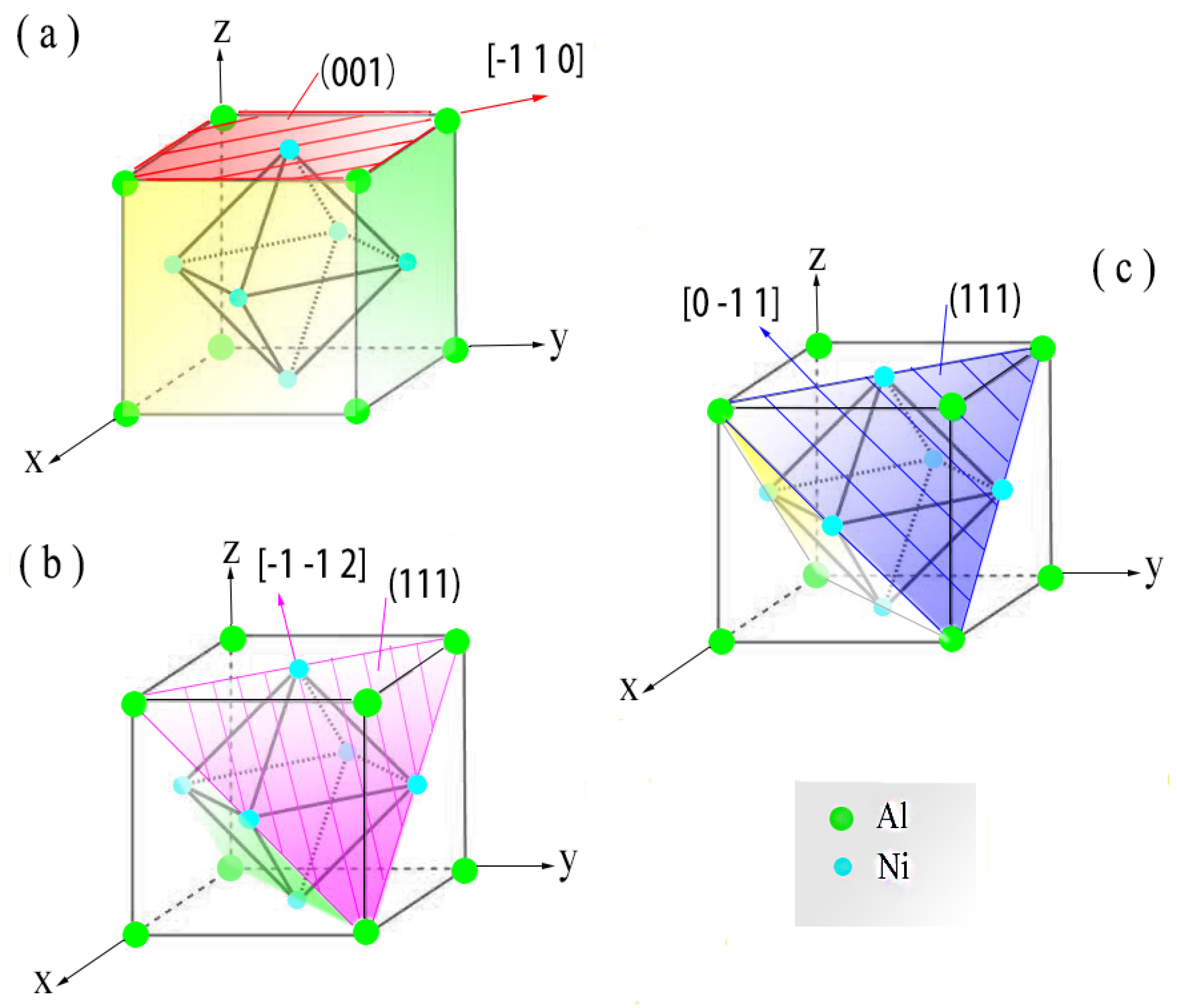
2. Materials
3. Methods
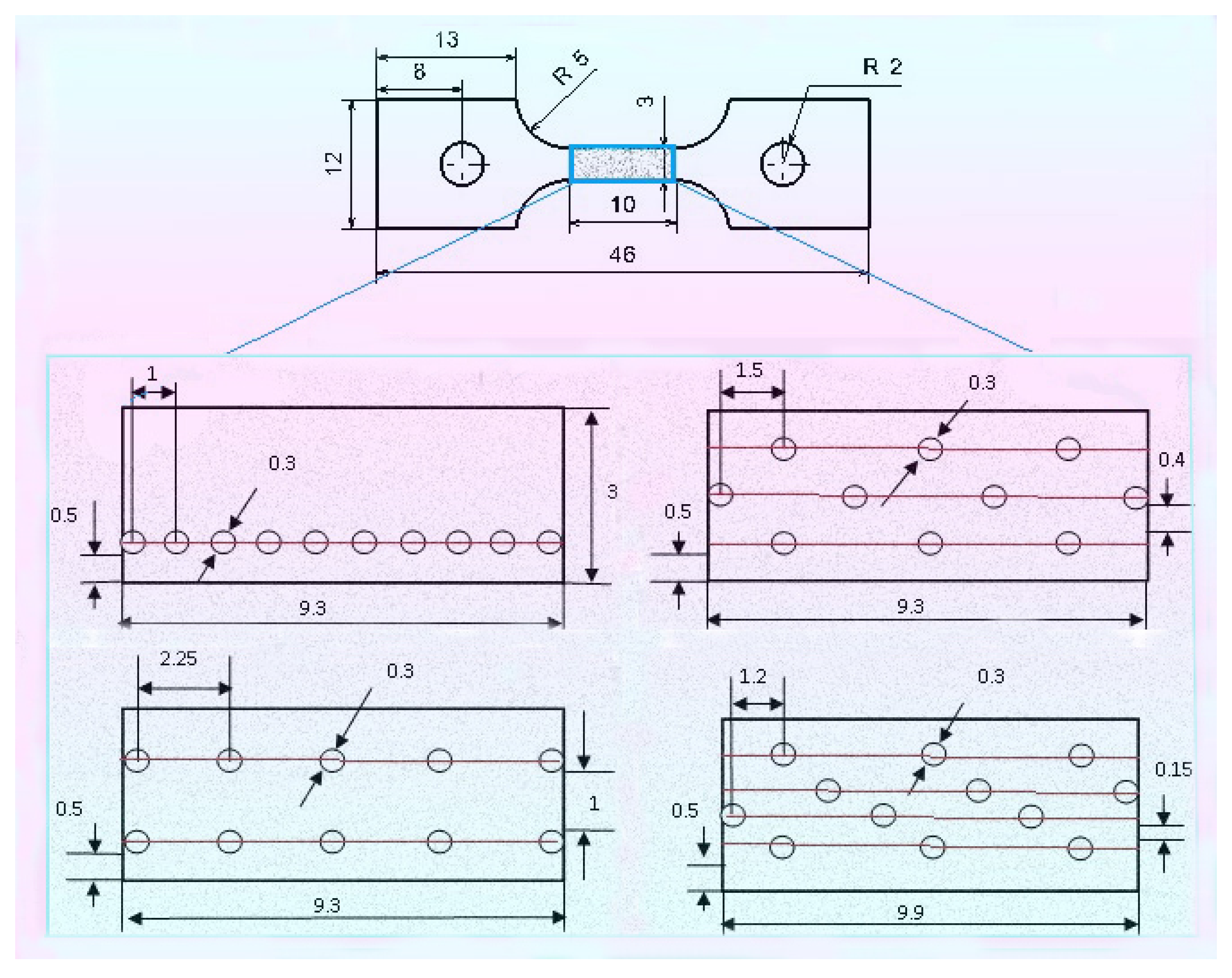
3.1. Experimental Setup
3.2. Numerical Modeling
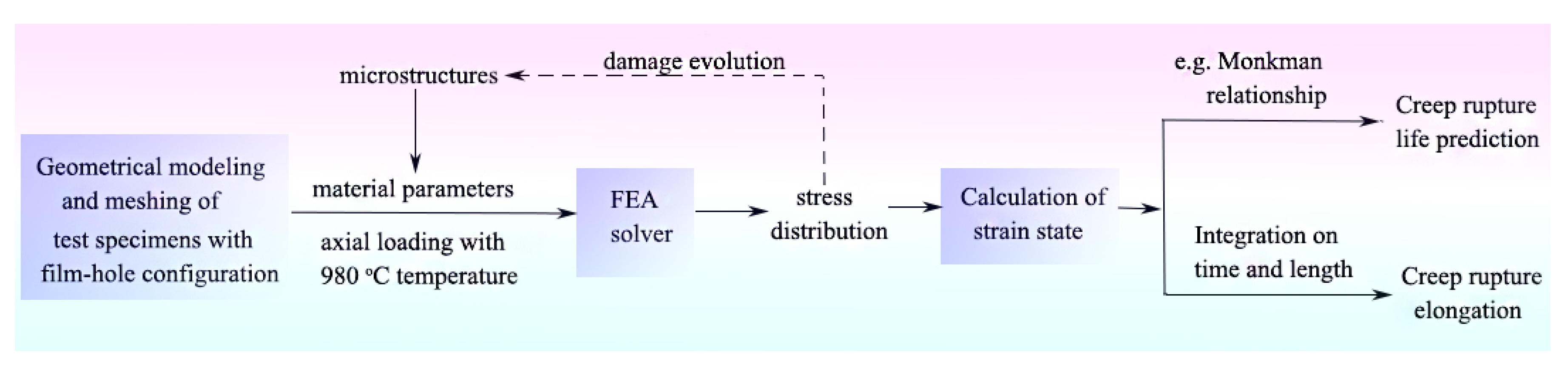
3.2.1. The Overall Procedure
3.2.2. Constitutive Relationship
3.2.3. Meshing
4. Results
4.1. Stress Rupture Lives of Specimens with Different Film-Hole Configurations
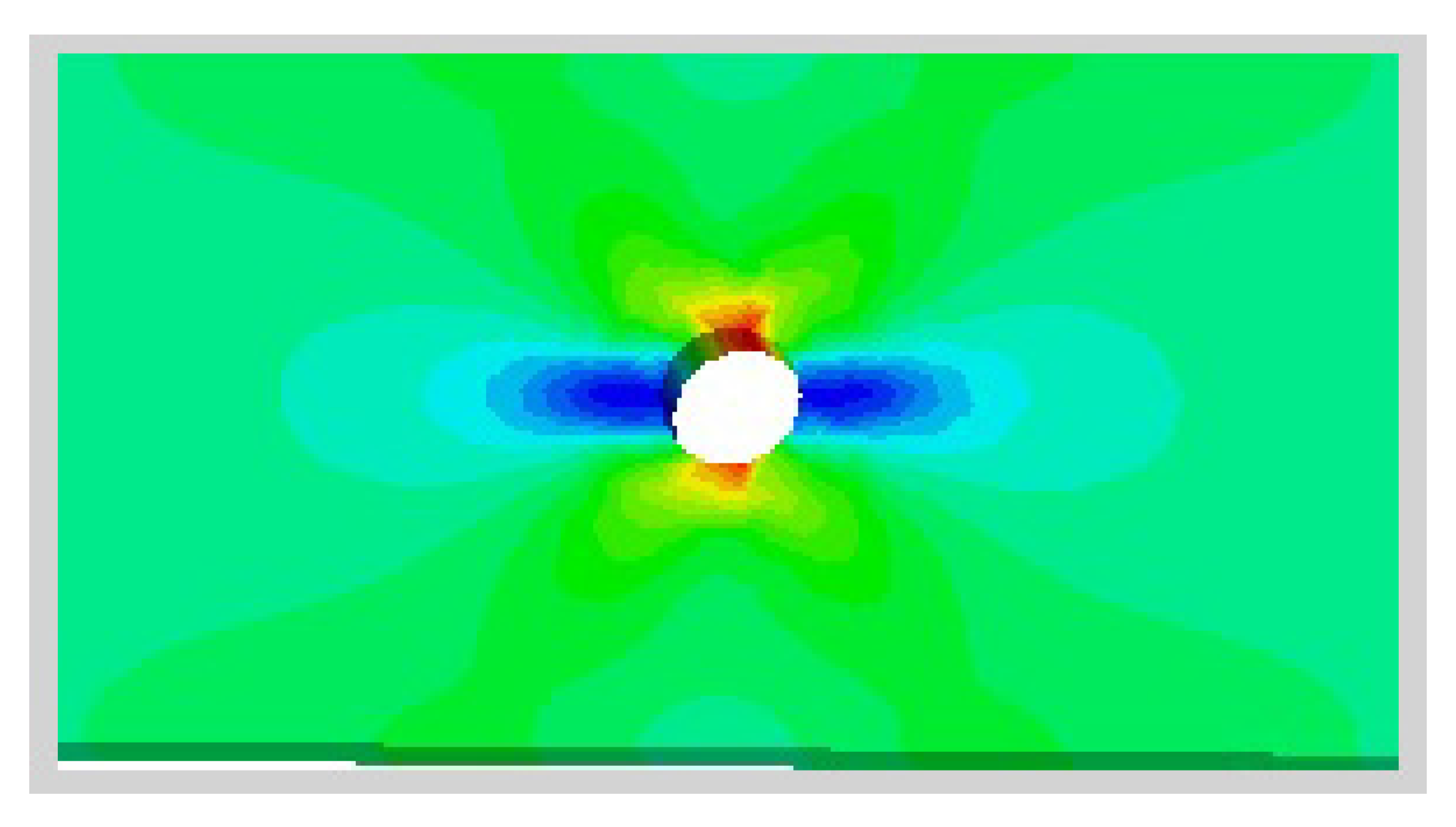
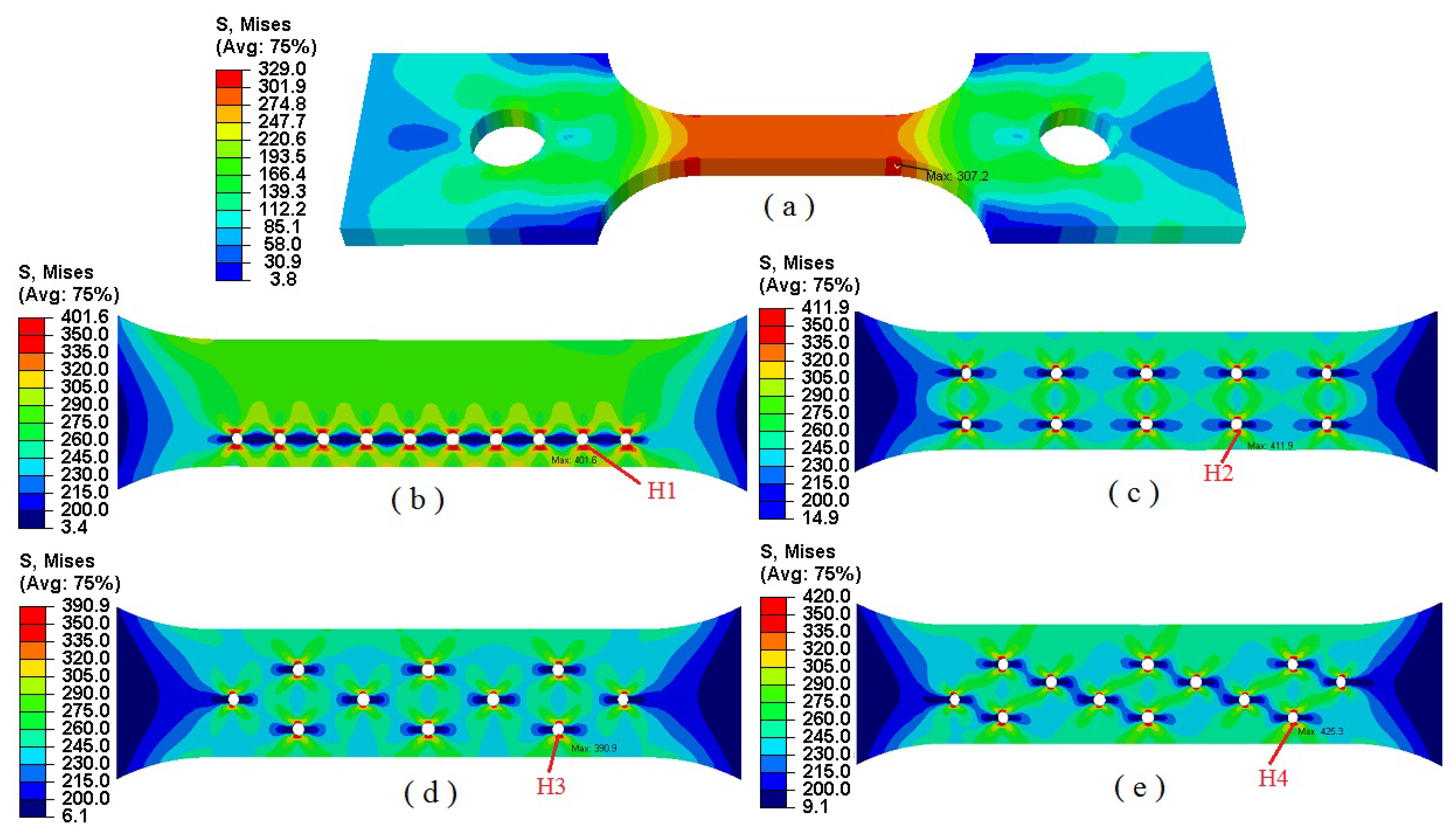
4.2. The Global Stress Distributions of Specimens
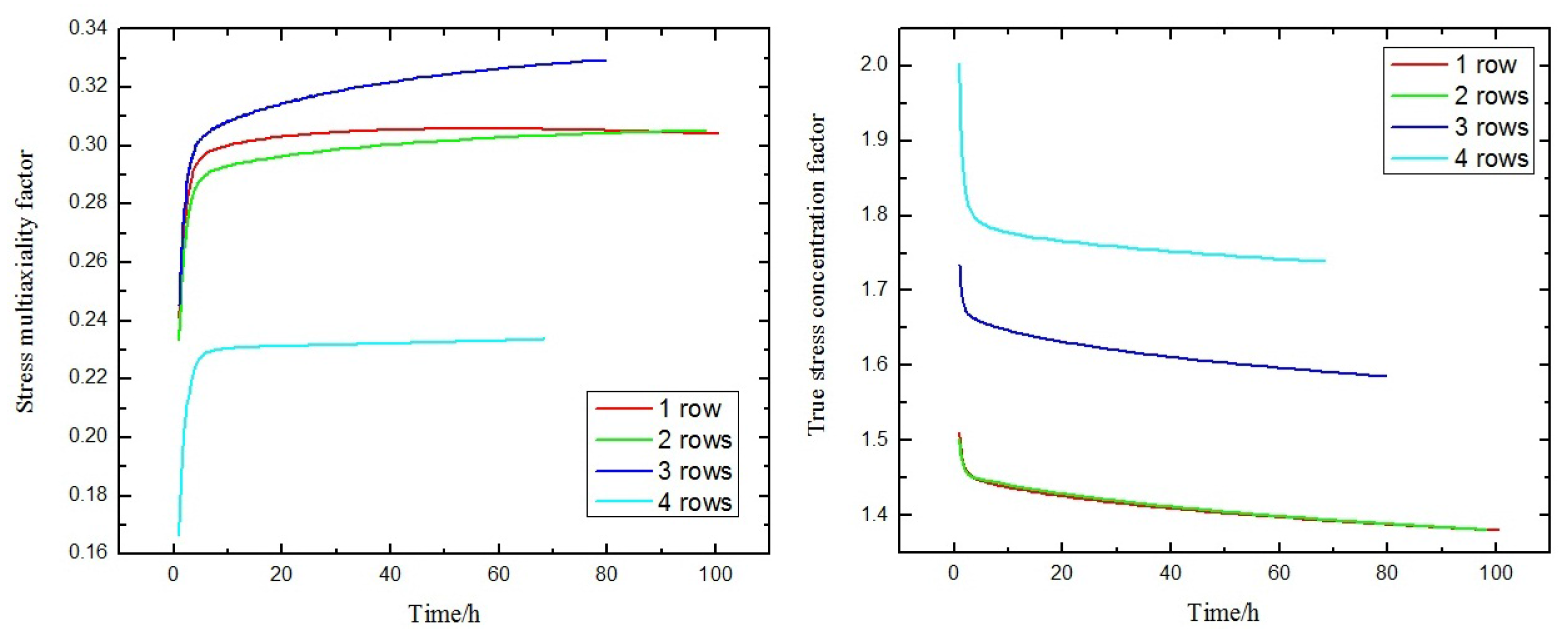
4.3. Stress State Characterization with Principal Stresses
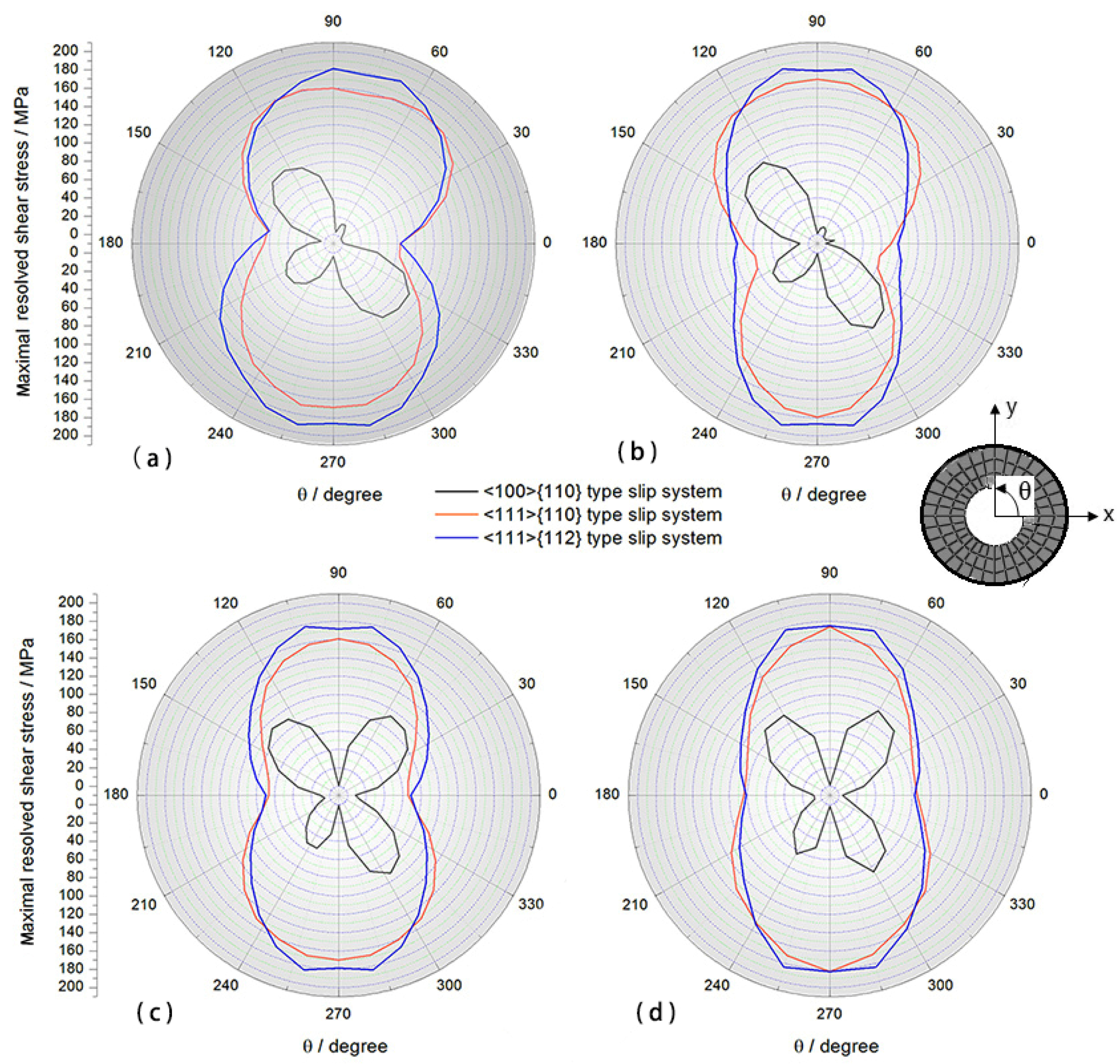
4.4. Maximal Resolved Shear Stress
4.5. Comparison between Simulation and Test on Rupture Positions and Shapes
5. Discussion
5.1. Stress Rupture Behavior
5.2. Discussion on the Effects of Film-Hole Configuration
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Asaro, R.J.; Rice, J. Strain localization in ductile single crystals. J. Mech. Phys. Solids 1977, 25, 309–338. [Google Scholar] [CrossRef]
- Hill, R. Generalized constitutive relations for incremental deformation of metal crystals by multislip. J. Mech. Phys. Solids 1966, 14, 95–102. [Google Scholar] [CrossRef]
- Mandel, J. Generalisation de la theorie de plasticite de WT koiter. Int. J. Solids Struct. 1965, 1, 273–295. [Google Scholar] [CrossRef]
- Simo, J.C.; Taylor, R.L. Consistent tangent operators for rate-independent elastoplasticity. Comput. Methods Appl. Mech. Eng. 1985, 48, 101–118. [Google Scholar] [CrossRef]
- Asaro, R.J.; Needleman, A. Texture development and strain hardening in rate dependent polycrystals. Acta Metall. 1985, 33, 923–953. [Google Scholar] [CrossRef]
- Peirce, D.; Asaro, R.J.; Needleman, A. An analysis of nonuniform and localized deformation in ductile single crystals. Acta Metall. 1982, 30, 1087–1119. [Google Scholar] [CrossRef]
- Hutchinson, J. Bounds and self-consistent estimates for creep of polycrystalline materials. Proc. R. Soc. Lond. Ser. A 1976, 348, 101–127. [Google Scholar] [CrossRef]
- Qi, W.; Bertram, A. Anisotropic continuum damage modeling for single crystals at high temperatures. Int. J. Plast. 1999, 15, 1197–1215. [Google Scholar] [CrossRef]
- MacLachlan, D.W.; Wright, L.W.; Gunturi, S.; Knowles, D.M. Constitutive modelling of anisotropic creepdeformation in single crystal blade alloysSRR99 and CMSX-4. Int. J. Plast. 2001, 17, 441–467. [Google Scholar] [CrossRef]
- MacLachlan, D.W.; Knowles, D.M. Modelling and prediction of the stress rupture behaviour of single crystal superalloys. Mater. Sci. Eng. A 2001, 302, 275–285. [Google Scholar] [CrossRef]
- MacLachlan, D.W.; Gunturi, G.S.K.; Knowles, D.M. Modelling the uniaxial creep anisotropy of nickel base single crystal superalloys CMSX-4 and RR2000 at 1023 K using a slip system based finite element approach. Comput. Mater. Sci. 2002, 25, 129–141. [Google Scholar] [CrossRef]
- Xu, B.X.; Wang, X.M.; Zhao, B.; Yue, Z.F. Study of crystallographic creep parameters of nickel-based single crystal superalloys by indentation method. Mater. Sci. Eng. A 2008, 478, 187–194. [Google Scholar] [CrossRef]
- Svoboda, J.; Lukas, P. Model of creep in 001 oriented superalloy single crystals. Acta Mater. 1998, 46, 925–953. [Google Scholar] [CrossRef]
- Svoboda, J.; Lukas, P. Creep deformation modelling of superalloy single crystals. Acta Mater. 2000, 48, 2519–2528. [Google Scholar] [CrossRef]
- Ma, A.; Dye, D.; Reed, R.C. A model for the creep deformation behaviour of single-crystal superalloy CMSX-4. Acta Mater. 2008, 56, 1657–1670. [Google Scholar] [CrossRef]
- Zhu, Z.; Basoalto, H.; Warnken, N.; Reed, R.C. A model for the creep deformation behaviour of nickel-based single crystal superalloys. Acta Mater. 2012, 60, 4888–4900. [Google Scholar] [CrossRef]
- MacKay, R.A.; Gabb, T.P.; Nathal, M.V. Microstructure-sensitive creep models for nickel-base superalloy single crystals. Mater. Sci. Eng. A 2013, 582, 397–408. [Google Scholar] [CrossRef]
- Graverend, J.B.L.; Cormier, J.; Gallerneau, F.; Villechaise, P.; Kruch, S.; Mendez, J. A microstructure-sensitive constitutive modeling of the inelastic behavior of single crystal nickel-based superalloys at very high temperature. Int. J. Plast. 2014, 59, 55–83. [Google Scholar] [CrossRef]
- Zhou, C.; Beyerlein, I.J.; LeSar, R. Plastic deformation mechanisms of fcc single crystals at small scales. Acta Mater. 2011, 59, 7673–7682. [Google Scholar] [CrossRef]
- Keshavarz, S.; Ghosh, S. Multi-scale crystal plasticity finite element model approach to modeling nickel-based superalloys. Acta Mater. 2013, 61, 6549–6561. [Google Scholar] [CrossRef]
- Mukherjee, S.; Zhou, B.; Dasgupta, A.; Bieler, T.R. Multiscale modeling of the anisotropic transient creep response of heterogeneous single crystal SnAgCu solder. Int. J. Plast. 2016, 78, 1–25. [Google Scholar] [CrossRef]
- Tian, S.; Su, Y.; Qian, B.; Yu, X.; Liang, F.; Li, A. Creep behavior of a single crystal nickel-based superalloy containing 4.2% Re. Mater. Des. 2012, 37, 236–242. [Google Scholar] [CrossRef]
- Sass, V.; Glatzel, U.; Feller-Kniepmeier, M. Anisotropic creep properties of the nickel base superalloy CMSX-4. Acta Mater. 1996, 44, 1967–1977. [Google Scholar] [CrossRef]
- Tian, C.; Han, G.; Cui, C.; Sun, X. Effects of stacking fault energy on the creep behaviors of Ni-base superalloy. Mater. Des. 2014, 64, 316–323. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, J.; Harada, H.; Koizumi, Y. The effect of lattice misfit on the dislocation motion in superalloys during high-temperature low-stress creep. Acta Mater. 2005, 53, 4623–4633. [Google Scholar] [CrossRef]
- MacLachlan, D.W.; Williams, S.; Knowles, D.M. Damage Mechanics Approach to Stress Rupture and Creep of Single Crystal Blade Alloys. In Proceedings of the Seventh International Conference on Creep and Fracture of Engineering Materials and Structures (TMS), Warrendale, PA, USA, 1997; p. 707. [Google Scholar]
- MacLachlan, D.W.; Knowles, D.M. Creep-behavior modeling of the single-crystal superalloy CMSX-4. Metall. Mater. Trans. A 2000, 31, 1401–1411. [Google Scholar] [CrossRef]
- Pearson, D.D.; Lemkey, F.D.; Kear, B.H. Stress Coarsening of γ’ and Its Influence on Creep Properties of a Single Crystal Superalloy. In Superalloys; ASM: Materials Park, OH, USA, 1980; pp. 513–520. [Google Scholar]
- Schneider, W.; Hammer, J.; Mughrabi, H. Creep Deformation and Rupture Behaviour of the Monocrystalline Superalloy CMSX-4: A Comparison with the Alloy SRR 99. In Superalloys; The Minerals, Metals & Materials Society (TMS): Warrendale, PA, USA, 1992; pp. 589–598. [Google Scholar]
- Hammer, J.; Mughrabi, H. High-Temperature Creep and Microstructure of the Monocrystalline Nickel-base Superalloy SRR 99. In Proceedings of the Advanced Materials and Processes, European Conference on Advanced Materials and Processes (EUROMAT89), DGM, Oberursel, Germany, 22–24 October 1989; p. 445. [Google Scholar]
- Caron, P.; Henderson, P.J.; Khan, T.; McLean, M. On the effects of heat treatments on the creep behaviour of a single crystal superalloy. Scr. Metall. 1986, 20, 875–880. [Google Scholar] [CrossRef]
- Cassenti, B.; Staroselsky, A. The effect of thickness on the creep response of thin-wall single crystal components. Mater. Sci. Eng. A 2009, 508, 183–189. [Google Scholar] [CrossRef]
- Lukas, P.; Preclik, P.; Cadek, J. Notch effects on creep behaviour of CMSX-4 superalloy single crystals. Mater. Sci. Eng. A 2001, 298, 84–89. [Google Scholar] [CrossRef]
- Mao, H.Z.; Wen, Z.X.; Yue, Z.F.; Wang, B.Z. The evolution of plasticity for nickel-base single crystal cooled blade with film cooling holes. Mater. Sci. Eng. A 2013, 587, 79–84. [Google Scholar] [CrossRef]
- Yu, Q.M.; Yue, Z.F.; Wen, Z.X. Creep damage evolution in a modeling specimen of nickel-based single crystal superalloys air-cooled blades. Mater. Sci. Eng. A 2008, 477, 319–327. [Google Scholar] [CrossRef]
- Liang, J.; Wen, Z.X.; Yue, Z.F. Numerical Simulation on the Creep Damage Evolution of Nickel-Based Single Crystal Specimens with Slant-Angled Film Cooling Holes. Rare Met. Mater. Eng. 2015, 44, 2656–2660. [Google Scholar]
- Wen, Z.X.; Zhang, D.X.; Li, S.W.; Yue, Z.F.; Gao, J.Y. Anisotropic creep damage and fracture mechanism of nickel-base single crystal superalloy under multiaxial stress. J. Alloys Compd. 2016, 692, 301–312. [Google Scholar] [CrossRef]
- Liu, Y.; Peng, Z.F. Estimation of structural volume fraction of phase and relationship between phase amounts in multi-phase alloys. Acta Metall. Sin. 2003, 39, 22–26. [Google Scholar]
- Taylor, G.I.; Elam, C.F. The Plastic Extension and Fracture of Aluminium Crystals. Proc. R. Soc. Lond. 1925, 108, 25–28. [Google Scholar] [CrossRef]
- Abaqus, version 6.4; Users Manual; ABAQUS Inc.: Pawtucket, RI, USA, 2004.
- Yin, Z.Y.; Yue, Z.F.; Yang, Z.G.; Cheng, X.M. Strength and Life Analysis of Nickel-Based Single Crystal Superalloys; Defense Industry Press: Beijing, China, 2003. [Google Scholar]


| Co | W | Ta | Al | Cr | Re | Mo | Nb | Hf | Ni |
|---|---|---|---|---|---|---|---|---|---|
| 9 | 8 | 7.5 | 5.6 | 4.3 | 2 | 2 | 0.5 | 0.1 | Balance |
| Film-Hole Rows | 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|---|
| Raw data of stress rupture life/h | NO.1 | 97 | 134 | 88 | 89 | 72 |
| NO.2 | 77 | 163 | 105 | 92 | 78 | |
| NO.3 | 90 | 83 | 95 | 85 | 77 | |
| NO.4 | 96 | 84 | 91 | 78 | 70 | |
| NO.5 | 97 | 83 | 108 | - | 72 | |
| NO.6 | 83 | 77 | - | - | 43 | |
| Statistic results | Average life/h | 89.66 | 99.55 | 97.09 | 85.84 | 67.40 |
| Confidence level | >95% | >80% | >95% | >95% | >90% | |
| Hole Rows | Nominal Stress/MPa | /MPa | /MPa | /MPa | /MPa | ||
|---|---|---|---|---|---|---|---|
| 0 | 300 | 300 | 312.0 | 9.4 | 5.9 | 0.025 | 1.014 |
| 1 | 300 | 270 | 523.0 | 205.4 | 112.7 | 0.304 | 1.380 |
| 2 | 300 | 240 | 467.0 | 182.0 | 103.1 | 0.305 | 1.381 |
| 3 | 300 | 240 | 542.7 | 242.9 | 114.7 | 0.330 | 1.585 |
| 4 | 300 | 240 | 521.2 | 191.4 | 52.1 | 0.234 | 1.738 |
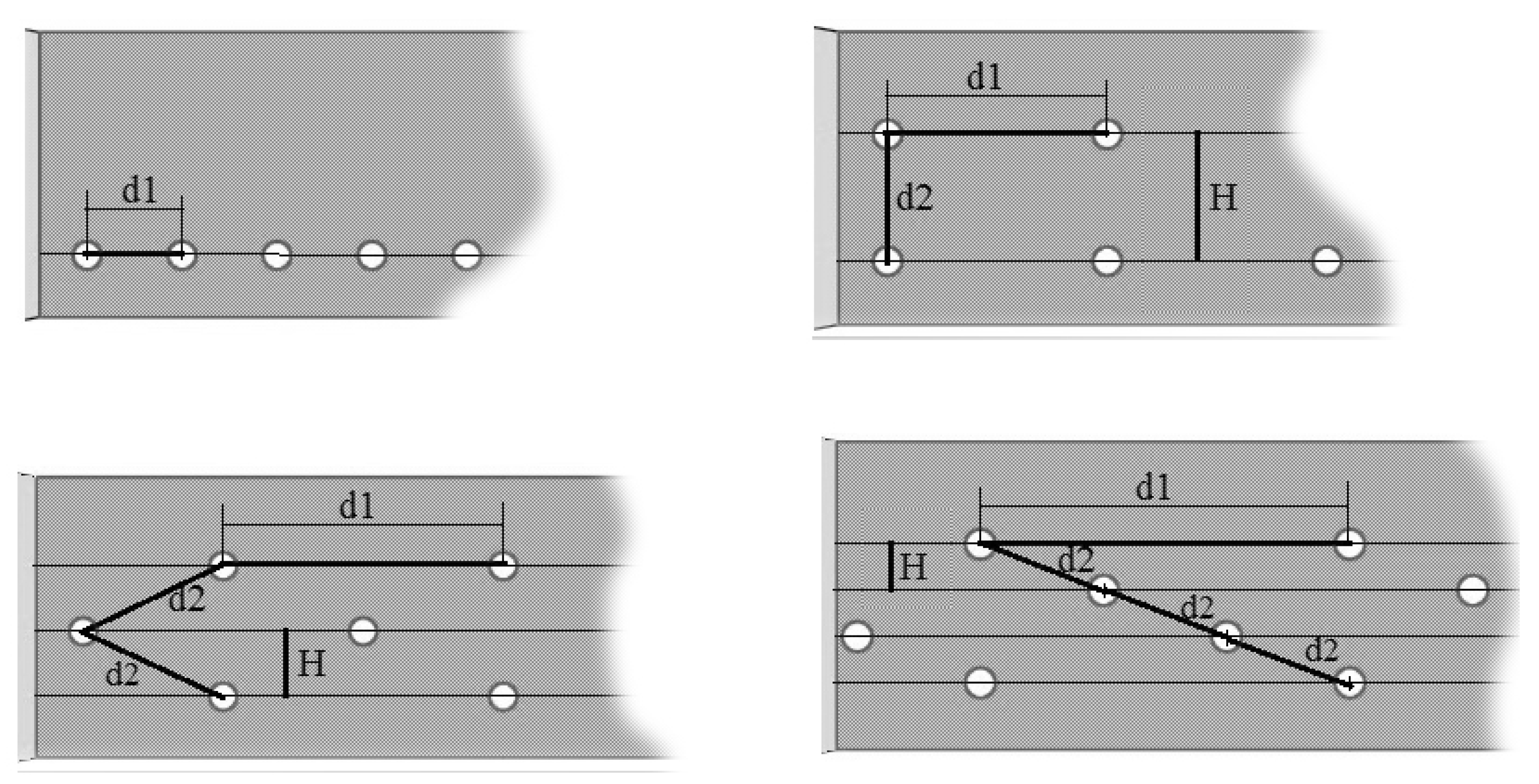
| Hole Rows | Main Parameters/mm | ||
|---|---|---|---|
| d1 | d2 | H | |
| 1 | 1 | - | - |
| 2 | 2.25 | 1.3 | 1.3 |
| 3 | 3 | 1.655 | 0.7 |
| 4 | 3.6 | 1.282 | 0.45 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Sun, W.; Dai, W.; Hu, C.; Liu, X.; Zhang, W. Experimental and Numerical Modeling of the Stress Rupture Behavior of Nickel-Based Single Crystal Superalloys Subject to Multi-Row Film Cooling Holes. Metals 2017, 7, 340. https://doi.org/10.3390/met7090340
Xu Y, Sun W, Dai W, Hu C, Liu X, Zhang W. Experimental and Numerical Modeling of the Stress Rupture Behavior of Nickel-Based Single Crystal Superalloys Subject to Multi-Row Film Cooling Holes. Metals. 2017; 7(9):340. https://doi.org/10.3390/met7090340
Chicago/Turabian StyleXu, Yuanming, Weikang Sun, Wei Dai, Chunyan Hu, Xinling Liu, and Weifang Zhang. 2017. "Experimental and Numerical Modeling of the Stress Rupture Behavior of Nickel-Based Single Crystal Superalloys Subject to Multi-Row Film Cooling Holes" Metals 7, no. 9: 340. https://doi.org/10.3390/met7090340





