A Modified Johnson-Cook Model for Hot Deformation Behavior of 35CrMo Steel
Abstract
:1. Introduction
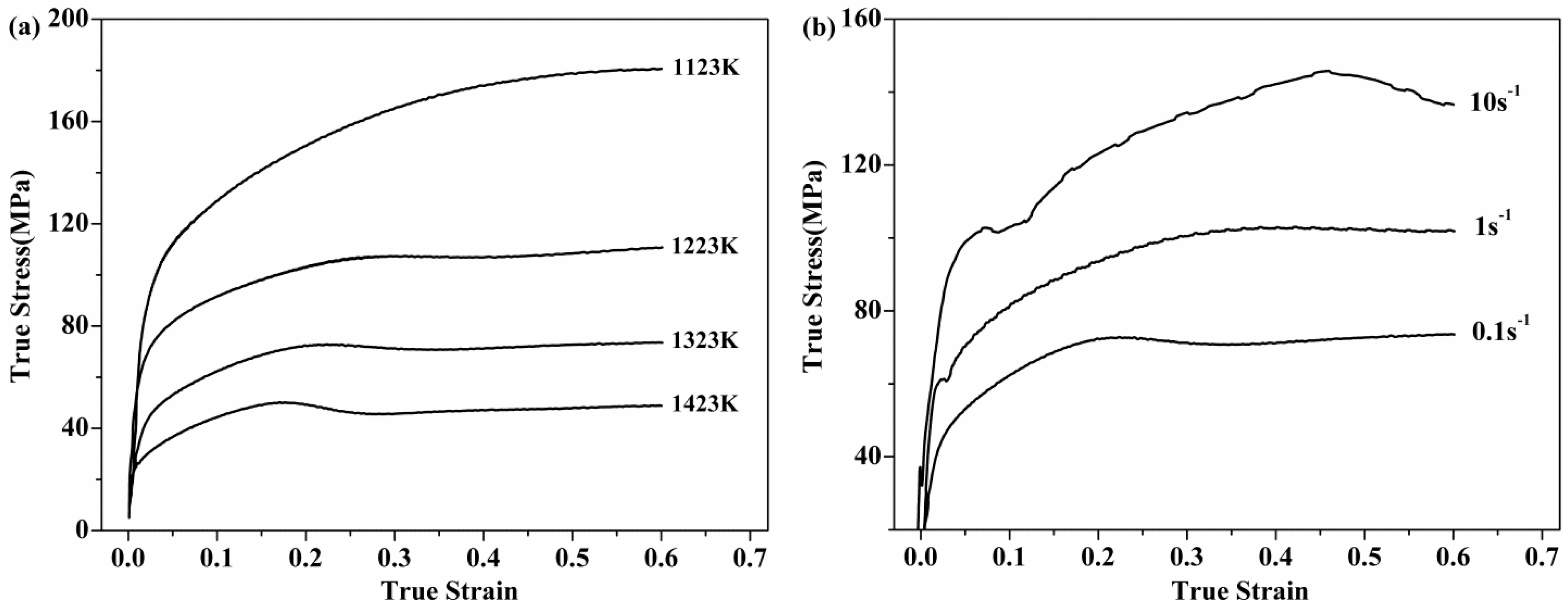
2. Experiments and Results
3. The Original JC Model and Its Modified Equation
4. Results and Discussion
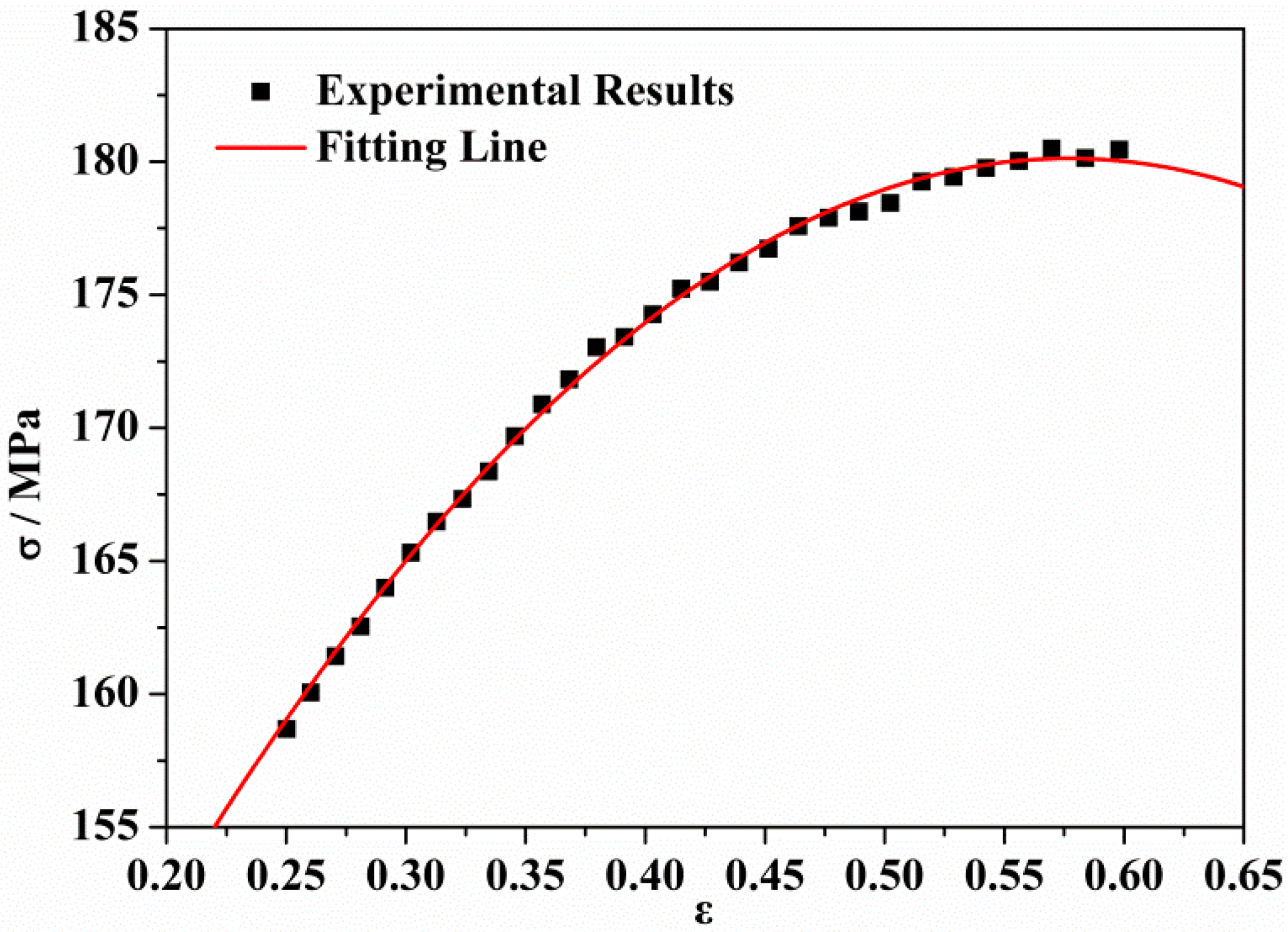
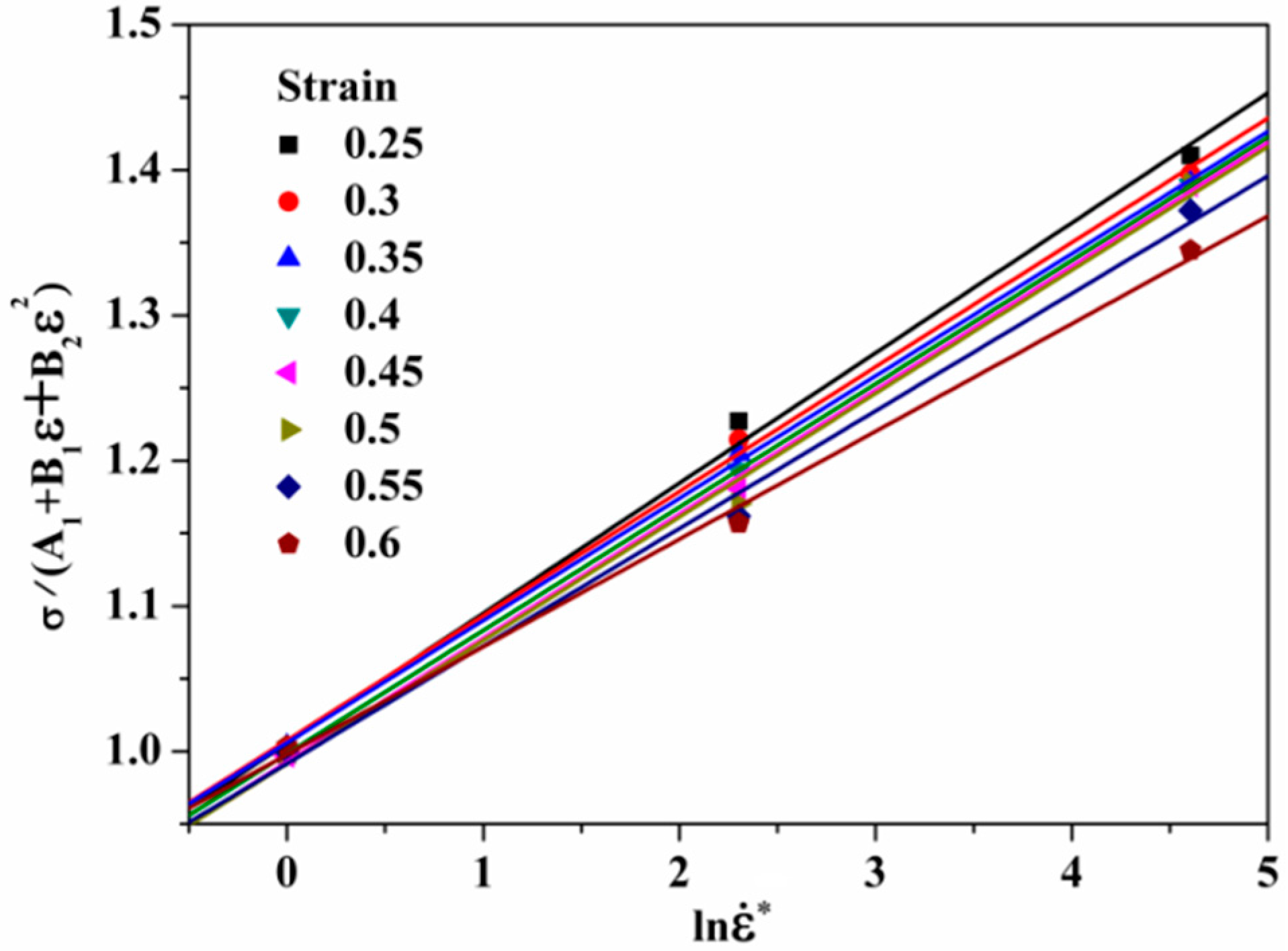
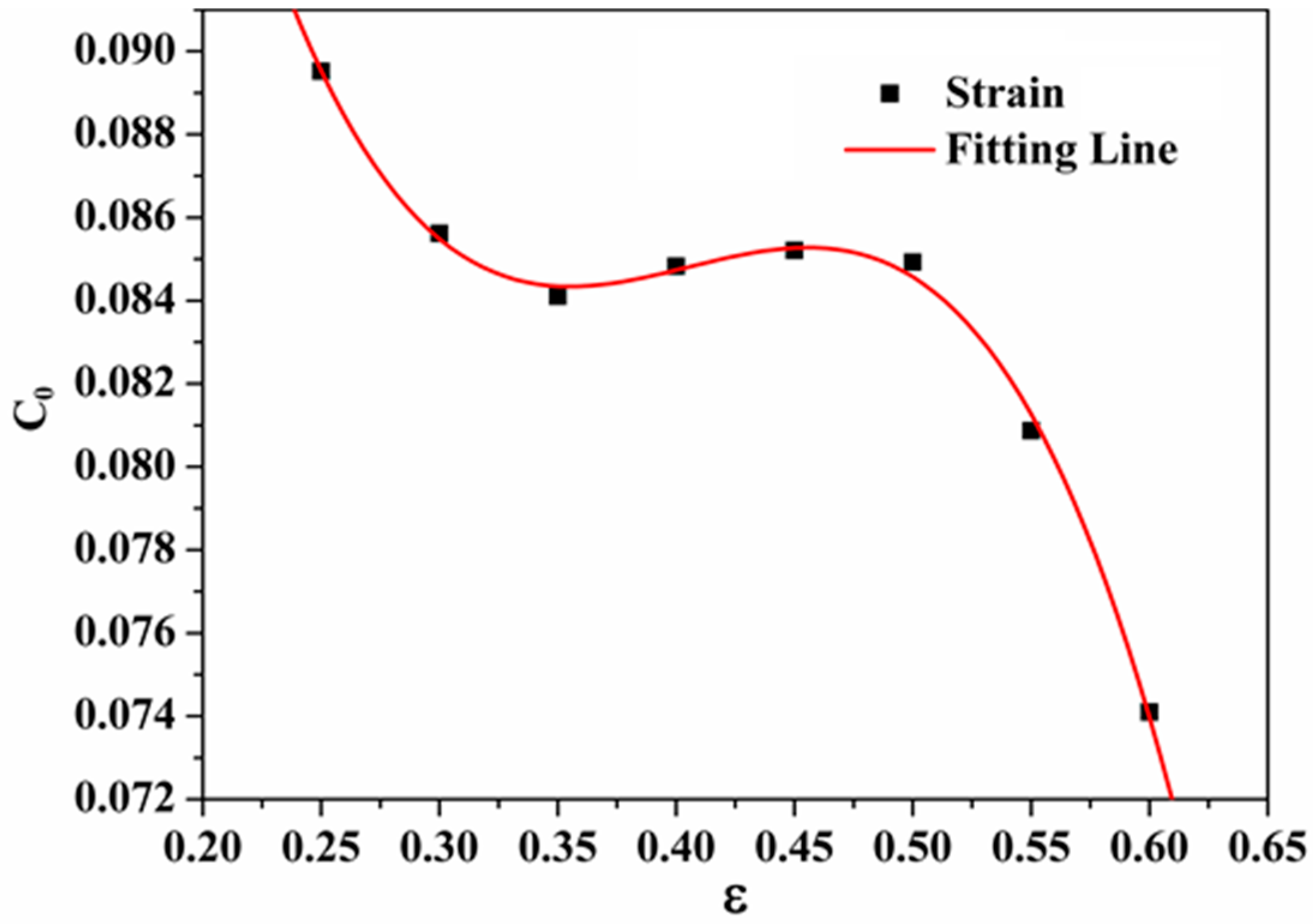
4.1. The Modified JC Model
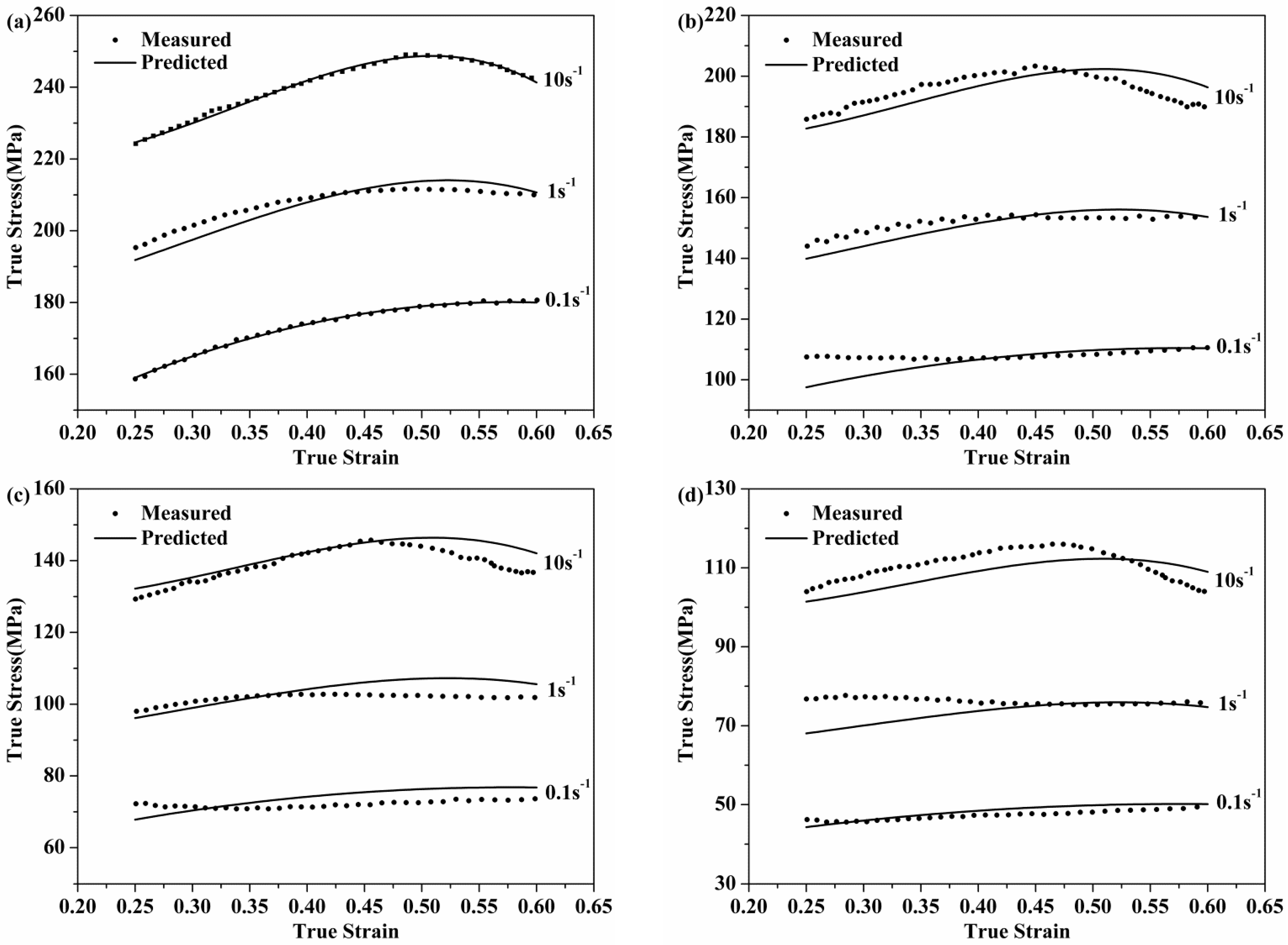
4.2. Error Analysis of Prediction Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yue, W.; Sun, X.; Wang, C.; Fu, Z.; Liu, Y.; Liu, J. A comparative study on the tribological behaviors of nitrided and sulfur-nitrided 35CrMo steel lubricated in PAO base oil with MoDTC additive. Tribol. Int. 2011, 44, 2029–2034. [Google Scholar] [CrossRef]
- Zhang, J.W.; Lu, L.T.; Shiozawa, K.; Zhou, W.N.; Zhang, W.H. Effect of nitrocarburizing and post-oxidation on fatigue behavior of 35CrMo alloy steel in very high cycle fatigue regime. Int. J. Fatigue 2011, 33, 880–886. [Google Scholar] [CrossRef]
- Zhang, J.W.; Lu, L.T.; Wu, P.B.; Ma, J.J.; Wang, G.G.; Zhang, W.H. Inclusion size evaluation and fatigue strength analysis of 35CrMo alloy railway axle steel. Mater. Sci. Eng. A 2013, 562, 211–217. [Google Scholar] [CrossRef]
- Xiao, Z.B.; Huang, Y.C.; Liu, Y. Plastic deformation behavior and processing maps of 35CrMo steel. J. Mater. Eng. Perform. 2016, 25, 1219–1227. [Google Scholar] [CrossRef]
- Liang, G.; Shi, C.; Zhou, Y.; Mao, D. Effect of ultrasonic treatment on the solidification microstructure of die-cast 35CrMo steel. Metals 2016, 6, 260. [Google Scholar] [CrossRef]
- Tavares, S.S.M.; Pardal, J.M.; Ponzio, E.; Loureiro, A.; De Souza, J.A. Influence of microstructure on the corrosion resistance of hyperduplex stainless steel. Mater. Corros. 2015, 61, 313–317. [Google Scholar] [CrossRef]
- Moura, V.S.; Lima, L.D.; Pardal, J.M.; Kina, A.Y.; Corte, R.R.A.; Tavares, S.S.M. Influence of microstructure on the corrosion resistance of the duplex stainless steel UNS S31803. Mater. Charact. 2008, 59, 1127–1132. [Google Scholar] [CrossRef]
- Johnson, G.; Cook, W. A Constitutive Model and Data for Metals Subjected to Large Strains, High Strain Rates and High Temperatures. In Proceedings of the 7th International Symposium on Ballistics, The Hague, The Netherlands, 19–21 April 1983; pp. 541–547. [Google Scholar]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Zener, C.; Hollomon, J.H. Effect of strain rate upon plastic flow of steel. J. Appl. Phys. 1944, 15, 22–32. [Google Scholar] [CrossRef]
- Sellars, C.M.; Mctegart, W.J. On the mechanism of hot deformation. Acta Metall. 1966, 14, 1136–1138. [Google Scholar] [CrossRef]
- Lin, Y.C.; Liu, G. A new mathematical model for predicting flow stress of typical high-strength alloy steel at elevated high temperature. Comput. Mater. Sci. 2010, 48, 54–58. [Google Scholar] [CrossRef]
- Haghdadi, N.; Zarei-Hanzaki, A.; Abedi, H.R. The flow behavior modeling of cast A356 aluminum alloy at elevated temperatures considering the effect of strain. Mater. Sci. Eng. A 2012, 535, 252–257. [Google Scholar] [CrossRef]
- Yin, F.; Hua, L.; Mao, H.; Han, X. Constitutive modeling for flow behavior of GCr15 steel under hot compression experiments. Mater. Des. 2013, 43, 393–401. [Google Scholar] [CrossRef]
- Haj, M.; Mansouri, H.; Vafaei, R.; Ebrahimi, G.R.; Kanani, A. Hot compression deformation behavior of AISI 321 austenitic stainless steel. Int. J. Miner. Metall. Mater. 2013, 20, 529–534. [Google Scholar] [CrossRef]
- Zou, D.N.; Wu, K.; Han, Y.; Zhang, W.; Cheng, B.; Qiao, G.J. Deformation characteristic and prediction of flow stress for as-cast 21Cr economical duplex stainless steel under hot compression. Mater. Des. 2013, 51, 975–982. [Google Scholar] [CrossRef]
- Wu, H.Y.; Zhu, F.J.; Wang, S.C.; Wang, W.R.; Wang, C.C.; Chiu, C.H. Hot deformation characteristics and strain-dependent constitutive analysis of Inconel 600 superalloy. J. Mater. Sci. 2012, 47, 3971–3981. [Google Scholar] [CrossRef]
- Samantaray, D.; Phaniraj, C.; Mandal, S.; Bhaduri, A.K. Strain dependent rate equation to predict elevated temperature flow behavior of modified 9Cr-1Mo (P91) steel. Mater. Sci. Eng. A 2011, 528, 1071–1077. [Google Scholar] [CrossRef]
- Li, H.Y.; Wei, D.D.; Li, Y.H.; Wang, X.F. Application of artificial neural network and constitutive equations to describe the hot compressive behavior of 28CrMnMoV steel. Mater. Des. 2012, 35, 557–562. [Google Scholar] [CrossRef]
- Fazilat, H.; Ghatarband, M.; Mazinani, S.; Asadi, Z.A.; Shiri, M.E.; Kalaee, M.R. Predicting the mechanical properties of glass fiber reinforced polymers via artificial neural network and adaptive neuro-fuzzy inference system. Comput. Mater. Sci. 2012, 58, 31–37. [Google Scholar] [CrossRef]
- Haghdadi, N.; Zarei-Hanzaki, A.; Khalesian, A.R.; Abedi, H.R. Artificial neural network modeling to predict the hot deformation behavior of an A356 aluminum alloy. Mater. Des. 2013, 49, 386–391. [Google Scholar] [CrossRef]
- Lin, Y.C.; Zhang, J.; Zhong, J. Application of neural networks to predict the elevated temperature flow behavior of a low alloy steel. Comput. Mater. Sci. 2008, 43, 752–758. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, M.S.; Zhong, J. Prediction of 42CrMo steel flow stress at high temperature and strain rate. Mech. Res. Commun. 2008, 35, 142–150. [Google Scholar] [CrossRef]
- Zerilli, F.J.; Armstrong, R.W. Dislocation-mechanics-based constitutive relations for material dynamics calculations. J. Appl. Phys. 1987, 61, 1816–1825. [Google Scholar] [CrossRef]
- Chiou, S.T.; Cheng, W.C.; Lee, W.S. Strain rate effects on the mechanical properties of a Fe-Mn-Al alloy under dynamic impact deformations. Mater. Sci. Eng. A 2005, 392, 156–162. [Google Scholar] [CrossRef]
- Follansbee, P.S.; Kocks, U.F. A constitutive description of the deformation of copper based on the use of the mechanical threshold stress as an internal state variable. Acta Metall. 1988, 36, 81–93. [Google Scholar] [CrossRef]
- Goetz, R.L.; Seetharaman, V. Modeling dynamic recrystallization using cellular automata. Scr. Mater. 1998, 38, 405–413. [Google Scholar] [CrossRef]
- Bodner, S.R.; Partom, Y. Constitutive equations for elastic-viscoplastic strain-hardening materials. J. Appl. Mech. 1975, 42, 385–389. [Google Scholar] [CrossRef]
- Donahue, E.G.; Odette, G.R.; Lucas, G.E. A physically based constitutive model for a V-4Cr-4Ti alloy. J. Nucl. Mater. 2000, 283–287, 637–641. [Google Scholar] [CrossRef]
- Wei, H.L.; Liu, G.Q.; Zhang, M.H. Physically based constitutive analysis to predict flow stress of medium carbon and vanadium microalloyed steels. Mater. Sci. Eng. A 2014, 602, 127–133. [Google Scholar] [CrossRef]
- Mirzadeh, H. A comparative study on the hot flow stress of Mg-Al-Zn magnesium alloys using a simple physically-based approach. J. Magnes. Alloys 2014, 2, 225–229. [Google Scholar] [CrossRef]
- Dorogoy, A.; Rittel, D. Determination of the Johnson–Cook material parameters using the SCS specimen. Exp. Mech. 2009, 49, 881–885. [Google Scholar] [CrossRef]
- Prawoto, Y.; Fanone, M.; Shahedi, S.; Ismail, M.S.; Nik, W.B.W. Computational approach using Johnson–Cook model on dual phase steel. Comput. Mater. Sci. 2012, 54, 48–55. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.P.; Han, C.J.; Wang, C.; Li, S.K. A modified Johnson–Cook model for 30Cr2Ni4MoV rotor steel over a wide range of temperature and strain rate. J. Mater. Sci. 2011, 46, 2922–2927. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, X.; Liu, G. A modified Johnson–Cook model for tensile behaviors of typical high-strength alloy steel. Mater. Sci. Eng. A 2010, 527, 6980–6986. [Google Scholar] [CrossRef]
- He, A.; Xie, G.; Zhang, H.; Wang, X. A comparative study on Johnson–Cook, modified Johnson–Cook and Arrhenius-type constitutive models to predict the high temperature flow stress in 20CrMo alloy steel. Mater. Des. 2013, 52, 677–685. [Google Scholar] [CrossRef]
- Song, W.; Ning, J.; Mao, X.; Tang, H. A modified Johnson–Cook model for titanium matrix composites reinforced with titanium carbide particles at elevated temperatures. Mater. Sci. Eng. A 2013, 576, 280–289. [Google Scholar] [CrossRef]
- Li, H.; He, L.; Zhao, G.; Zhang, L. Constitutive relationships of hot stamping boron steel B1500HS based on the modified Arrhenius and Johnson–Cook model. Mater. Sci. Eng. A 2013, 580, 330–348. [Google Scholar] [CrossRef]
- Umbrello, D.; M’Saoubi, R.; Outeiro, J.C. The influence of Johnson–Cook material constants on finite element simulation of machining of AISI 316L steel. Int. J. Mach. Tools Manuf. 2007, 47, 462–470. [Google Scholar] [CrossRef]
- Bobbili, R.; Madhu, V. Effect of strain rate and stress triaxiality on tensile behavior of Titanium alloy Ti-10-2-3 at elevated temperatures. Mater. Sci. Eng. A 2016, 667, 33–41. [Google Scholar] [CrossRef]
- Zhang, D.N.; Shangguan, Q.Q.; Xie, C.J.; Liu, F. A modified Johnson-Cook model of dynamic tensile behaviors for 7075-T6 aluminum alloy. J. Alloys Compd. 2015, 619, 186–194. [Google Scholar] [CrossRef]
- Wang, J.; Chen, J.; Zhang, B.; Zhao, Z.; Ruan, X.Y. The flow stress model of 35CrMo structural steel during hot forming. J. Shanghai Jiaotong Univ. 2005, 39, 1784–1791. [Google Scholar]
- Zhang, B.; Zhang, H.B.; Ruan, X.Y.; Zhang, Y. Hot deformation behavior and dynamic recrystallization model of 35CrMo steel. Acta Metall. Sin. 2003, 16, 183–191. [Google Scholar]
- Joshi, M.; Mason, T.D. Effect of initial microstructure on plastic flow behaviour during isothermal forging of Ti-10V-2Fe-3Al. Mater. Sci. Eng. A 2009, 501, 248–254. [Google Scholar]
- Huang, Y.; Wang, S.; Xiao, Z.; Liu, H. Critical condition of dynamic recrystallization in 35CrMo steel. Metals 2017, 7, 161. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, M.S.; Zhong, J. Constitutive modeling for elevated temperature flow behavior of 42CrMo steel. Comput. Mater. Sci. 2008, 42, 470–477. [Google Scholar] [CrossRef]
- Tan, J.Q.; Zhan, M.; Liu, S.; Huang, T.; Guo, J.; Yang, H. A modified Johnson-Cook model for tensile flow behaviors of 7050-T7451 aluminum alloy at high strain rates. Mater. Sci. Eng. A 2015, 631, 214–219. [Google Scholar] [CrossRef]
- Sun, Y.; Ye, W.H.; Hu, L.X. Constitutive modeling of high-temperature flow behavior of Al-0.62Mg-0.73Si aluminum alloy. J. Mater. Eng. Perform. 2016, 25, 1621–1630. [Google Scholar] [CrossRef]
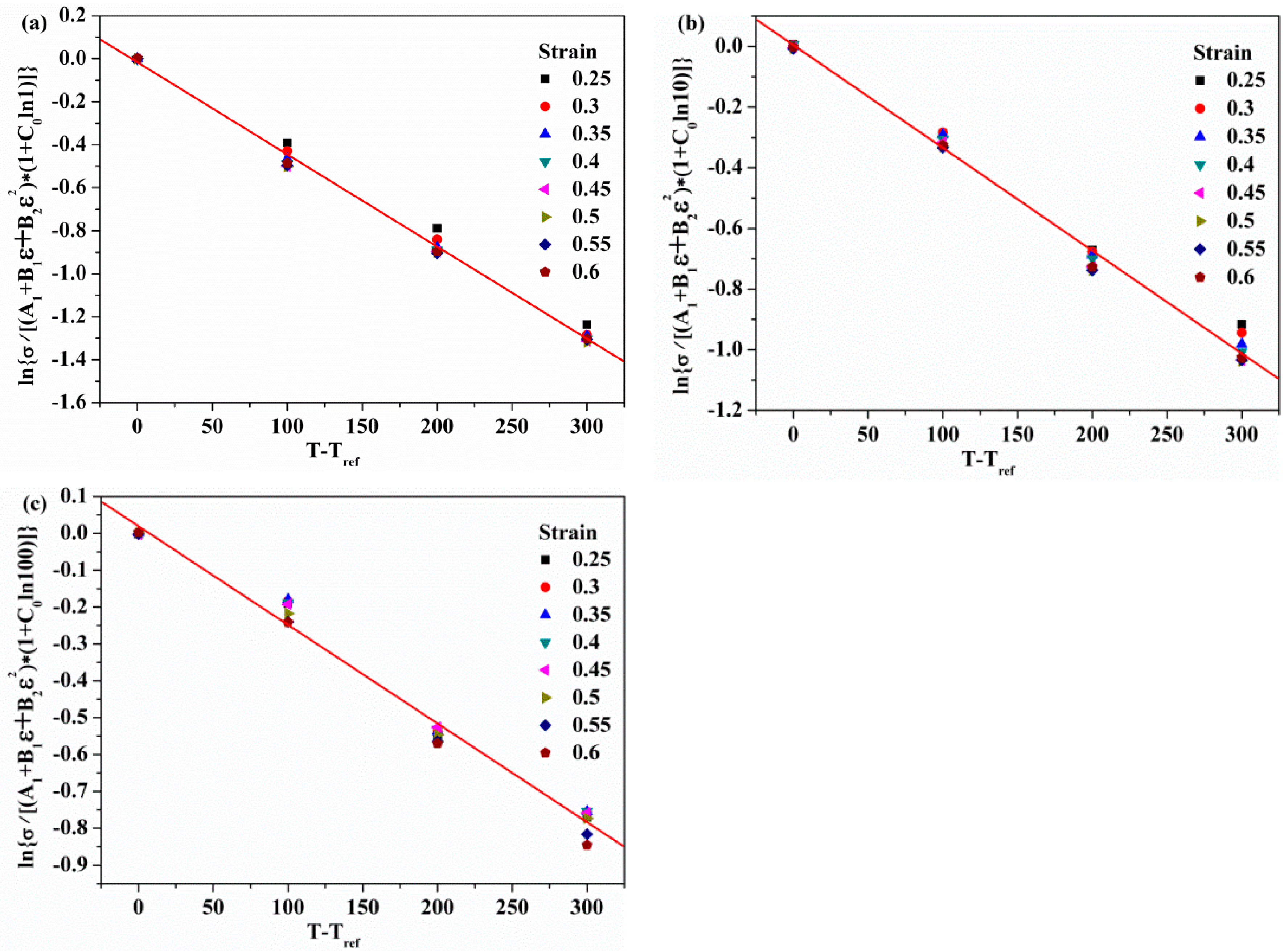
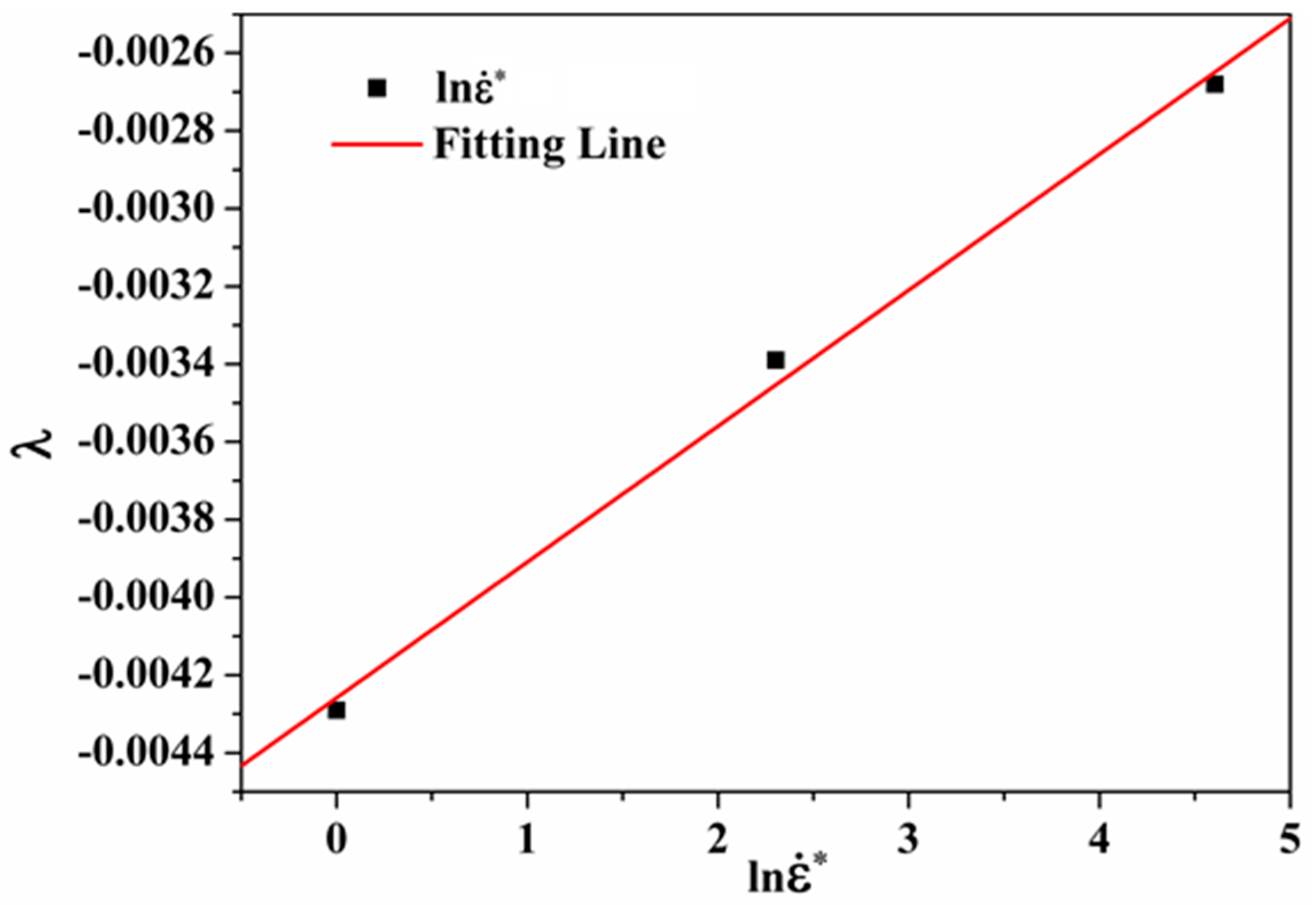

| ε | 0.25 | 0.30 | 0.35 | 0.40 | 0.45 | 0.50 | 0.55 | 0.60 |
| C0 | 0.08952 | 0.08562 | 0.08411 | 0.08483 | 0.08521 | 0.08493 | 0.08087 | 0.0741 |
| Parameters | A1 | B1 | B2 | C1 | C2 | C3 | C4 | λ1 | λ2 |
|---|---|---|---|---|---|---|---|---|---|
| Value | 114.45 | 227.75 | 197.47 | 0.2017 | −0.89301 | 2.23743 | −1.8398 | −0.00426 | 0.000349607 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Huang, Y.; Xiao, Z.; Liu, Y.; Liu, H. A Modified Johnson-Cook Model for Hot Deformation Behavior of 35CrMo Steel. Metals 2017, 7, 337. https://doi.org/10.3390/met7090337
Wang S, Huang Y, Xiao Z, Liu Y, Liu H. A Modified Johnson-Cook Model for Hot Deformation Behavior of 35CrMo Steel. Metals. 2017; 7(9):337. https://doi.org/10.3390/met7090337
Chicago/Turabian StyleWang, Sanxing, Yuanchun Huang, Zhengbing Xiao, Yu Liu, and Hui Liu. 2017. "A Modified Johnson-Cook Model for Hot Deformation Behavior of 35CrMo Steel" Metals 7, no. 9: 337. https://doi.org/10.3390/met7090337





