Method to Evaluate the Kinetics of Bainite Transformation in Low-Temperature Nanobainitic Steel Using Thermal Dilatation Curve Analysis
Abstract
:1. Introduction
2. Materials and Experimental Procedure
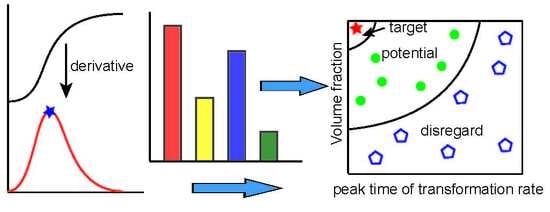
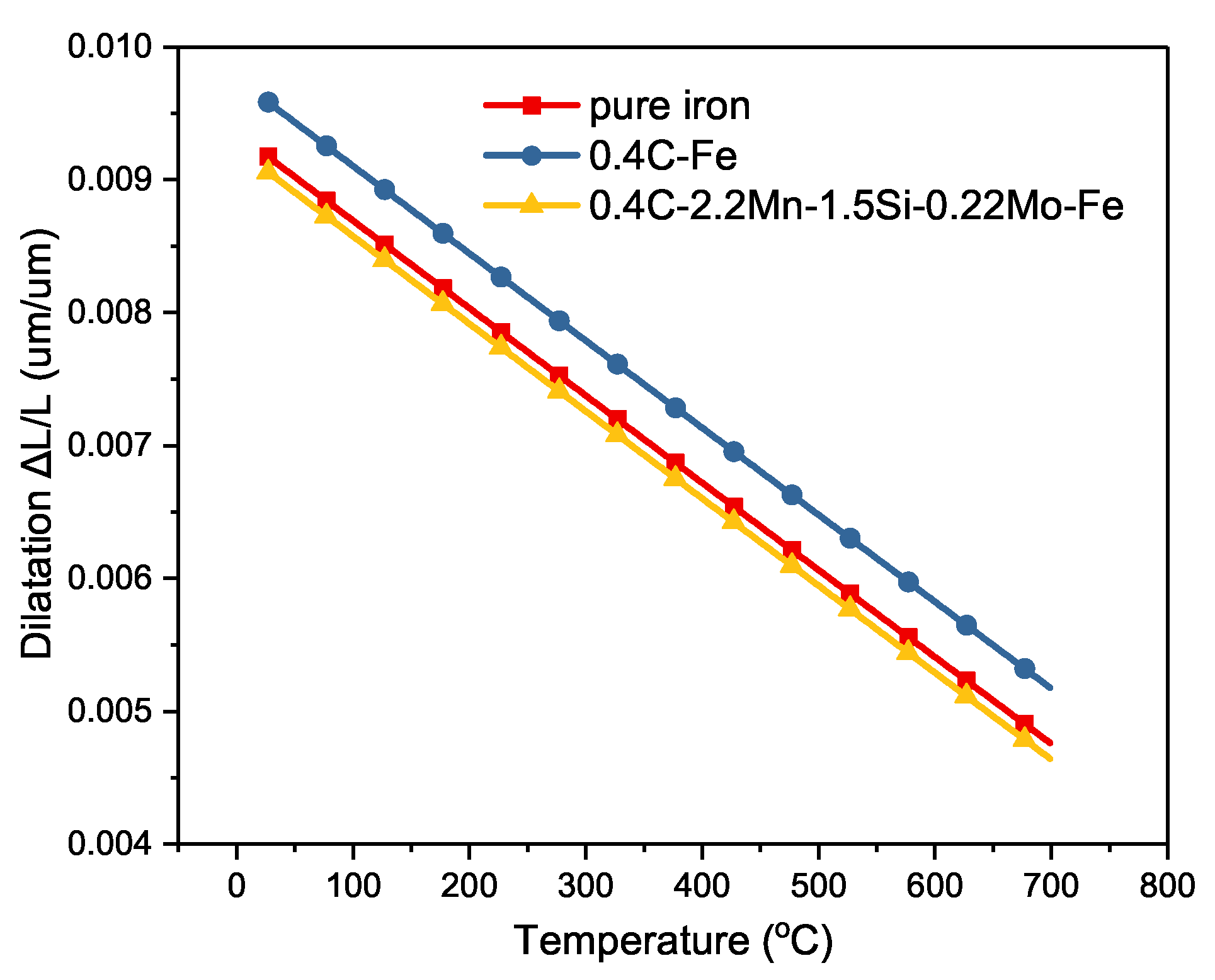
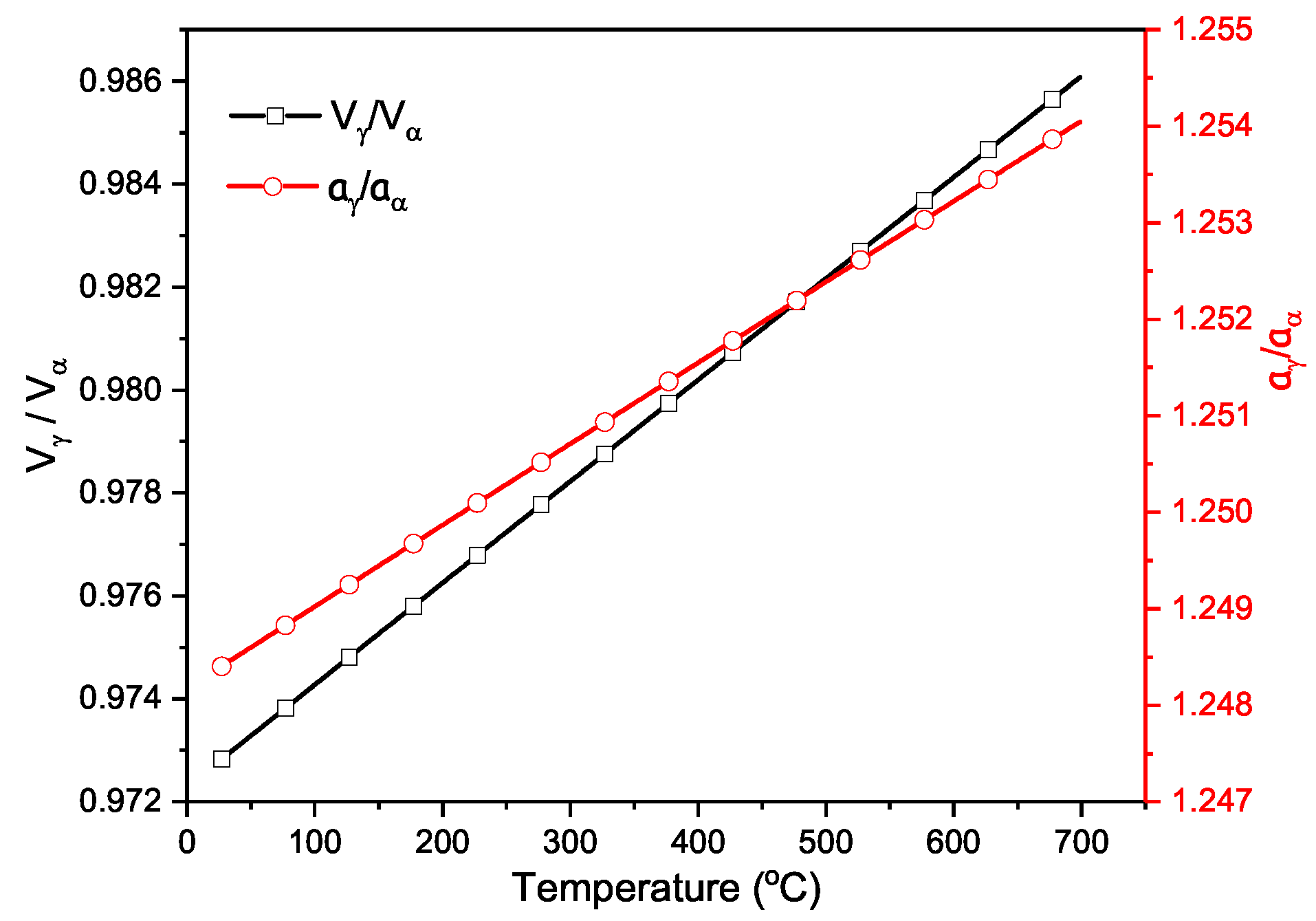
3. Method
4. Results and Discussion
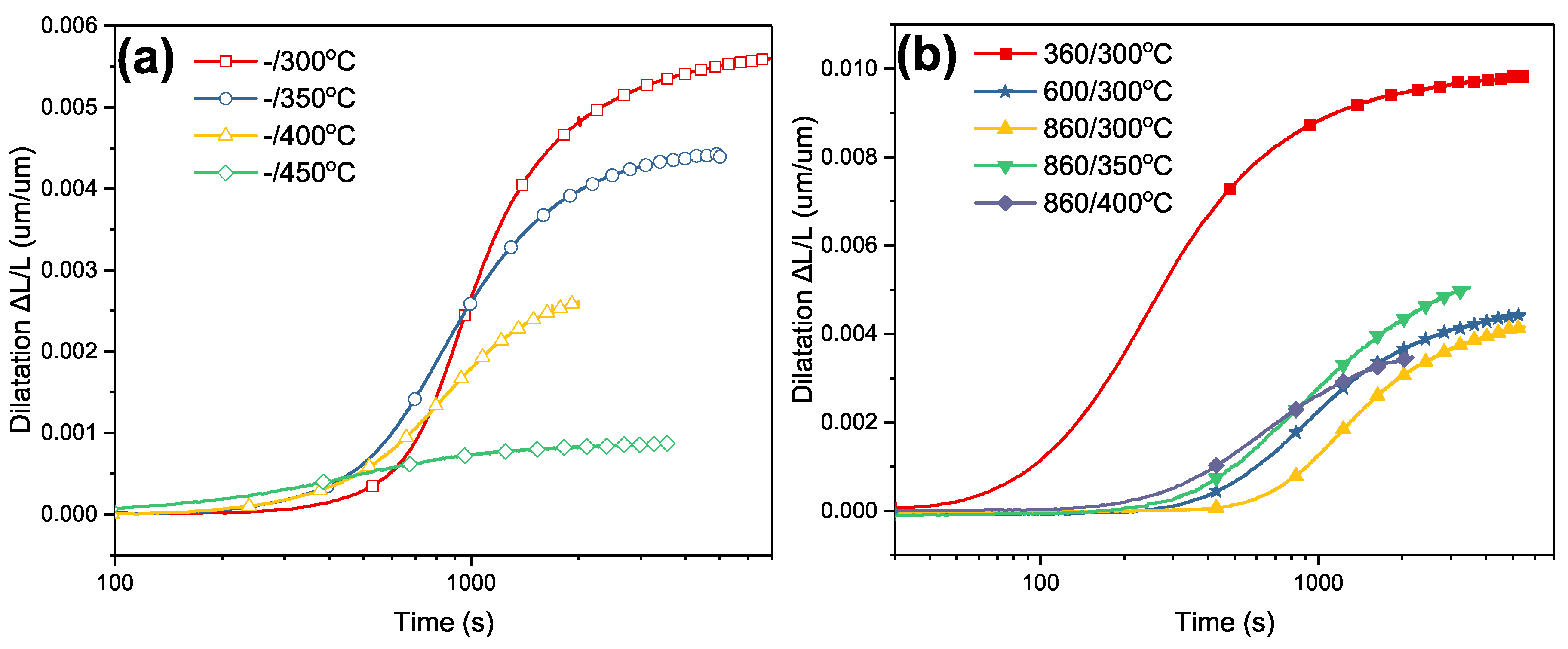
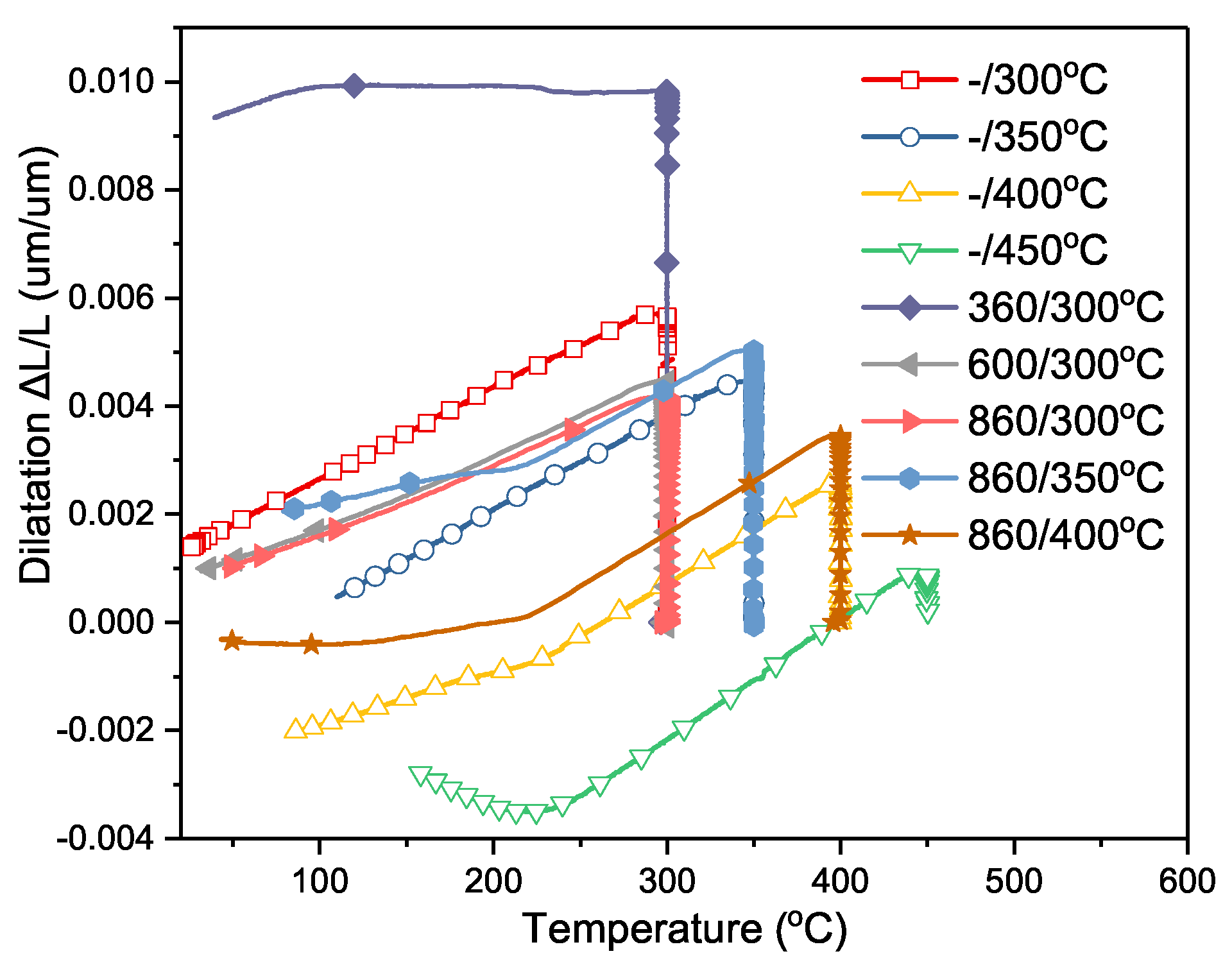
4.1. Isothermal Transformation
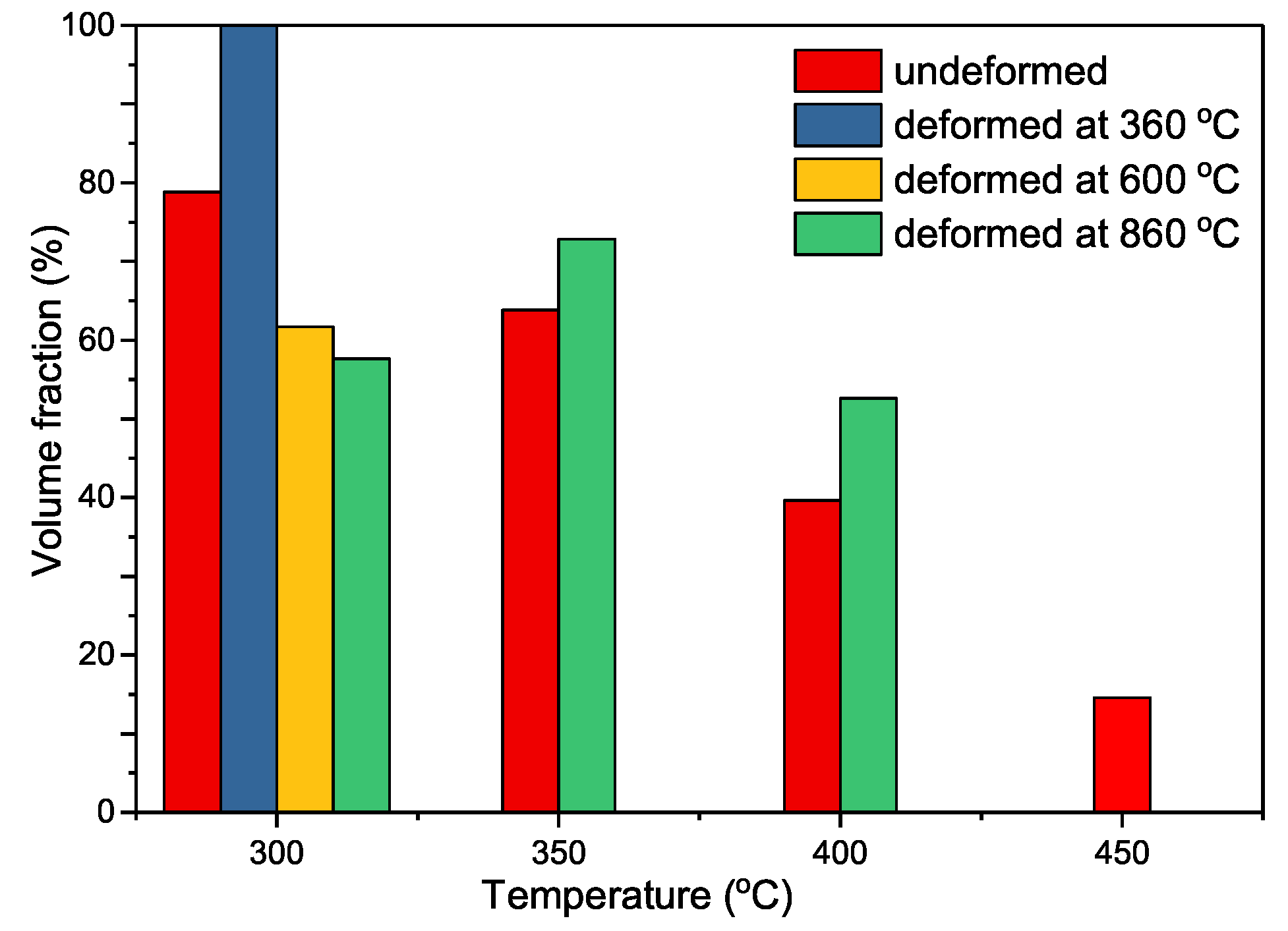
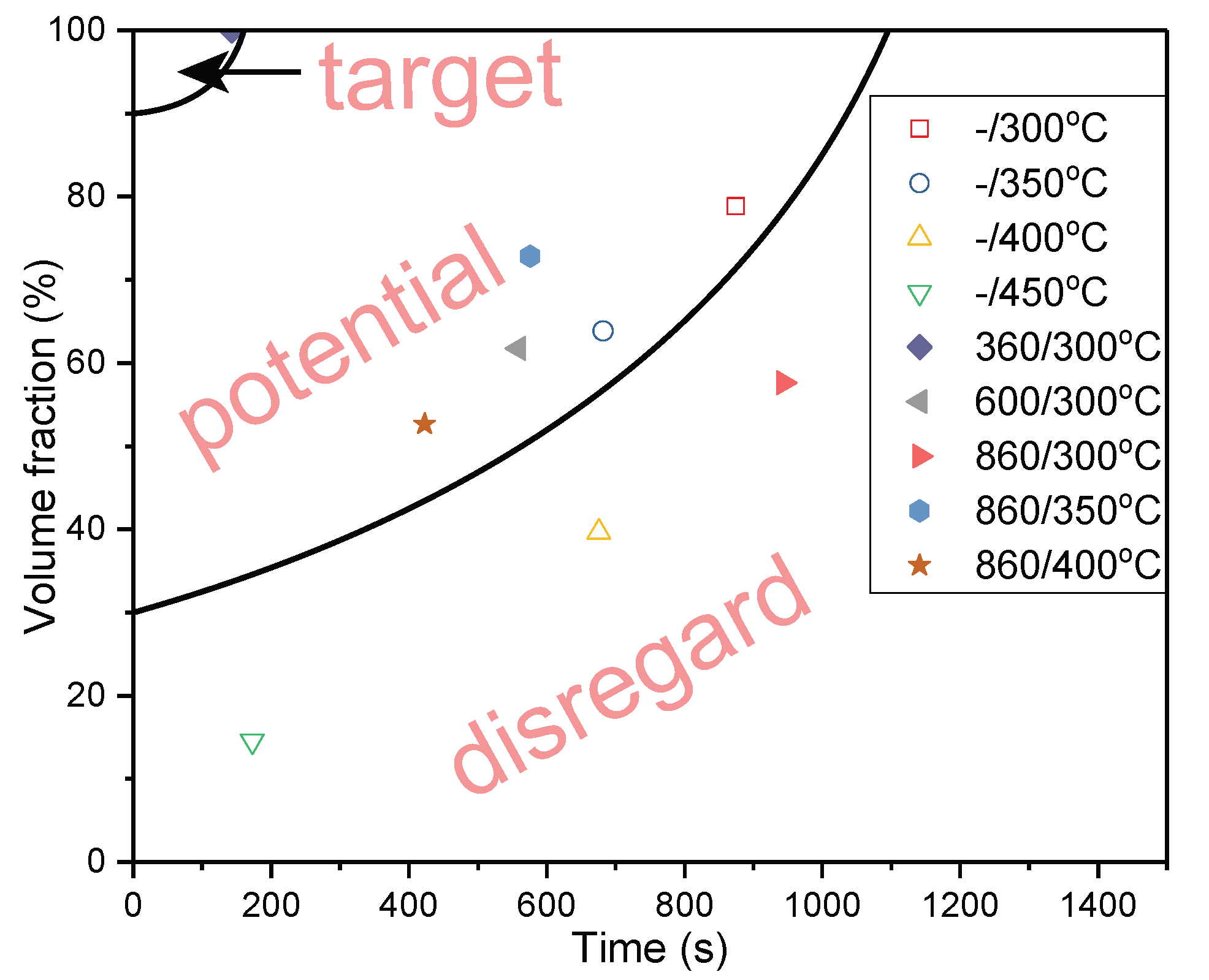
4.2. Volume Fraction of Phase Transformation
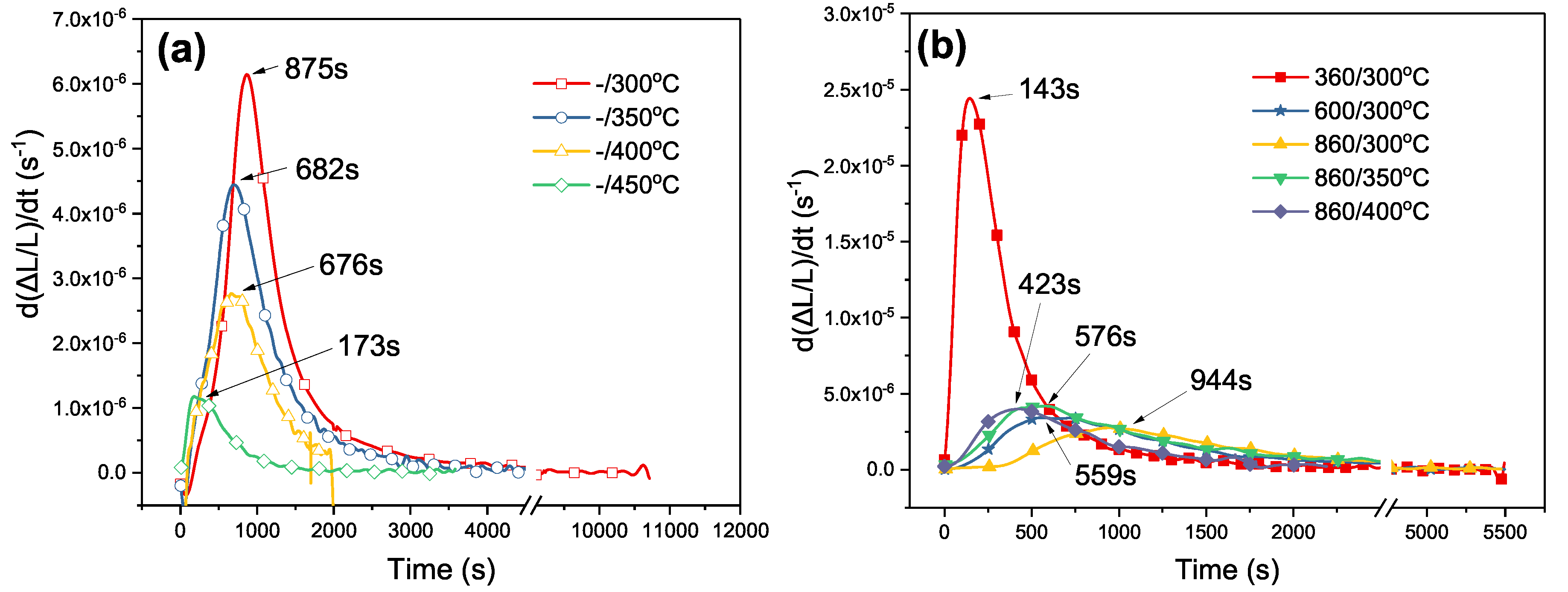
4.3. Evaluation of Bainitic Transformation
5. Conclusions
- The relative change due to phase transformation is temperature-dependent and can be calculated theoretically.
- The peak time of transformation rate (PTTR) which was obtained by taking a derivative of the dilatation curve with respect to time can serve as a clear and effective parameter that accounts for the information of transformation time.
- By making a volume fraction versus PTTR graph, the bainite transformation was evaluated clearly and concisely, and can be used to optimize preparation techniques.
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| PTTR | peak time of transformation rate |
References
- Onink, M.; Tichelaar, F.D.; Brakman, C.M.; Mittemeijer, E.J.; Van der Zwaag, S. Quantitative analysis of the dilatation by decomposition of Fe-C austenites; Calculation of volume change upon transformation. Z. Für Metallkd. 1996, 87, 24–32. [Google Scholar]
- García de Andrés, C.; Caballero, F.G.; Capdevila, C.; Bhadeshia, H.K.D.H. Modelling of kinetics and dilatometric behavior of non-isothermal pearlite-to-austenite transformation in an eutectoid steel. Scr. Mater. 1998, 39, 791–796. [Google Scholar] [CrossRef]
- Reed, R.C.; Akbay, T.; Shen, Z.; Robinson, J.M.; Root, J.H. Determination of reaustenitisation kinetics in a Fe-0.4C steel using using dilatometry and neutron diffraction. Mater. Sci. Eng. A 1998, 256, 152–165. [Google Scholar] [CrossRef]
- Caballero, F.G.; Capdevila, C.; Andrés, C.G.d. Kinetics and dilatometric behaviour of non-isothermal ferrite-austenite transformation. Mater. Sci. Technol. 2001, 17, 1114–1118. [Google Scholar] [CrossRef] [Green Version]
- Gómez, M.; Medina, S.F.; Caruana, G. Modelling of phase transformation kinetics by correction of dilatometry results for a ferritic Nb-microalloyed steel. ISIJ Int. 2003, 43, 1228–1237. [Google Scholar] [CrossRef] [Green Version]
- Choi, S. Model for estimation of transformation kinetics from the dilatation data during a cooling of hypoeutectoid steels. Mater. Sci. Eng. A 2003, 363, 72–80. [Google Scholar] [CrossRef]
- San Martín, D.; Rivera-Díaz-del Castillo, P.E.J.; García-de Andrés, C. In situ study of austenite formation by dilatometry in a low carbon microalloyed steel. Scr. Mater. 2008, 58, 926–929. [Google Scholar] [CrossRef] [Green Version]
- Kamyabi-Gol, A.; Clark, S.J.; Gibbs, J.W.; Sridhar, S.; Mendez, P.F. Quantification of evolution of multiple simultaneous phase transformations using dilation curve analysis (DCA). Acta Mater. 2016, 102, 231–240. [Google Scholar] [CrossRef]
- Xu, G.; Liu, F.; Wang, L.; Hu, H. A new approach to quantitative analysis of bainitic transformation in a superbainite steel. Scr. Mater. 2013, 68, 833–836. [Google Scholar] [CrossRef]
- Bhadeshia, H.; Edmonds, D. Bainite in silicon steels: New composition-property approach Part 1. Metal Sci. 1983, 17, 411–419. [Google Scholar] [CrossRef]
- Caballero, F.G.; Bhadeshia, H.K.D.H. Very strong bainite. Curr. Opin. Solid State Mater. Sci. 2004, 8, 251–257. [Google Scholar] [CrossRef]
- Caballero, F.; Bhadeshia, H.; Mawella, K.; Jones, D.; Brown, P. Very strong low temperature bainite. Mater. Sci. Technol. 2002, 18, 279–284. [Google Scholar] [CrossRef] [Green Version]
- Gong, W.; Tomota, Y.; Adachi, Y.; Paradowska, A.M.; Kelleher, J.F.; Zhang, S.Y. Effects of ausforming temperature on bainite transformation, microstructure and variant selection in nanobainite steel. Acta Mater. 2013, 61, 4142–4154. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, Y.H.; Zheng, C.L.; Zhang, F.C.; Wang, T.S. Effects of ausforming on isothermal bainite transformation behaviour and microstructural refinement in medium-carbon Si-Al-rich alloy steel. Mater. Des. 2014, 62, 168–174. [Google Scholar] [CrossRef]
- He, J.; Zhao, A.; Zhi, C.; Fan, H. Acceleration of nanobainite transformation by multi-step ausforming process. Scr. Mater. 2015, 107, 71–74. [Google Scholar] [CrossRef]
- Hu, H.; Zurob, H.S.; Xu, G.; Embury, D.; Purdy, G.R. New insights to the effects of ausforming on the bainitic transformation. Mater. Sci. Eng. A 2015, 626, 34–40. [Google Scholar] [CrossRef]
- Hu, F.; Wu, K.M.; Zheng, H. Influence of Co and Al on bainitic transformation in super bainitic steels. Steel Res. Int. 2013, 84, 1060–1065. [Google Scholar] [CrossRef]
- Zhao, L.; Qian, L.; Meng, J.; Zhou, Q.; Zhang, F. Below-Ms austempering to obtain refined bainitic structure and enhanced mechanical properties in low-C high-Si/Al steels. Scr. Mater. 2016, 112, 96–100. [Google Scholar] [CrossRef]
- Kang, J.Y.; Park, S.J.; Suh, D.W.; Han, H.N. Estimation of phase fraction in dual phase steel using microscopic characterizations and dilatometric analysis. Mater. Charact. 2013, 84, 205–215. [Google Scholar] [CrossRef]
- Dyson, D.; Holmes, B. Effect of alloying additions on the lattice parameter of austenite. J. Iron Steel Inst. 1970, 208, 469–474. [Google Scholar]
- Babu, S.S.; Specht, E.D.; David, S.A.; Karapetrova, E.; Zschack, P.; Peet, M.; Bhadeshia, H.K.D.H. In-situ observations of lattice parameter fluctuations in austenite and transformation to bainite. Metall. Mater. Trans. A 2005, 36, 3281–3289. [Google Scholar] [CrossRef]
- Bhadeshia, H.; David, S.; Vitek, J.; Reed, R. Stress induced transformation to bainite in Fe-Cr-Mo-C pressure vessel steel. Mater. Sci. Technol. 1991, 7, 686–698. [Google Scholar] [CrossRef]
- van Bohemen, S.M.C. The nonlinear lattice expansion of iron alloys in the range 100–1600 K. Scr. Mater. 2013, 69, 315–318. [Google Scholar] [CrossRef]
- Onink, M.; Brakman, C.; Tichelaar, F.; Mittemeijer, E.; Van der Zwaag, S.; Root, J.; Konyer, N. The lattice-parameters of austenite and ferrite in Fe-C alloys as functions of carbon concentration and temperature. Scr. Metall. Mater. 1993, 29, 1011–1016. [Google Scholar] [CrossRef]
- Zhou, M.-X.; Xu, G.; Wang, L.; Xue, Z.-L.; Hu, H.-J. Comprehensive analysis of the dilatation during bainitic transformation under stress. Metals Mater. Int. 2015, 21, 985–990. [Google Scholar] [CrossRef]
- Suh, D.W.; Oh, C.S.; Han, H.N.; Kim, S.J. Dilatometric analysis of austenite decomposition considering the effect of non-isotropic volume change. Acta Mater. 2007, 55, 2659–2669. [Google Scholar] [CrossRef]
- Park, B.J.; Choi, J.M.; Lee, K.J. Analysis of phase transformations during continuous cooling by the first derivative of dilatation in low carbon steels. Mater. Charact. 2012, 64, 8–14. [Google Scholar] [CrossRef]
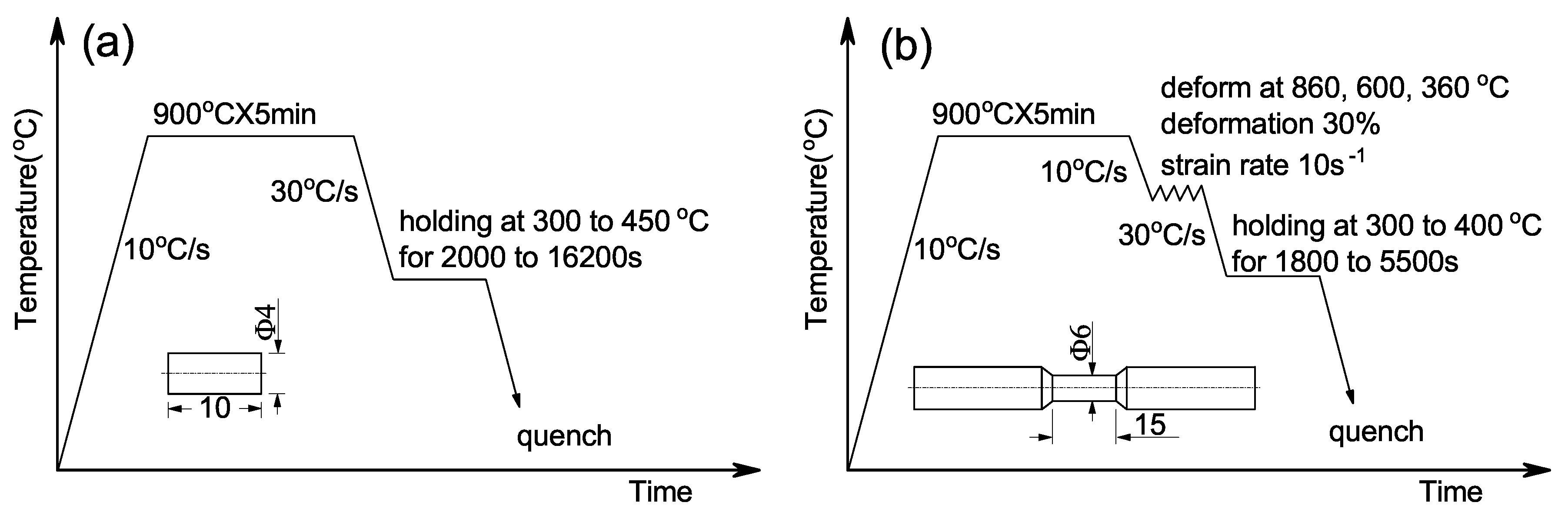


| C | Si | Mn | Al | P | S | Mo |
|---|---|---|---|---|---|---|
| 0.4 | 1.5 | 2.2 | 0.033 | 0.008 | 0.001 | 0.22 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Xu, G.; Mao, X.; Zhao, G.; Bao, S. Method to Evaluate the Kinetics of Bainite Transformation in Low-Temperature Nanobainitic Steel Using Thermal Dilatation Curve Analysis. Metals 2017, 7, 330. https://doi.org/10.3390/met7090330
Xu Y, Xu G, Mao X, Zhao G, Bao S. Method to Evaluate the Kinetics of Bainite Transformation in Low-Temperature Nanobainitic Steel Using Thermal Dilatation Curve Analysis. Metals. 2017; 7(9):330. https://doi.org/10.3390/met7090330
Chicago/Turabian StyleXu, Yaowen, Guang Xu, Xinping Mao, Gang Zhao, and Siqian Bao. 2017. "Method to Evaluate the Kinetics of Bainite Transformation in Low-Temperature Nanobainitic Steel Using Thermal Dilatation Curve Analysis" Metals 7, no. 9: 330. https://doi.org/10.3390/met7090330