Processing Map of NiTiNb Shape Memory Alloy Subjected to Plastic Deformation at High Temperatures
Abstract
:1. Introduction
2. Materials and Methods
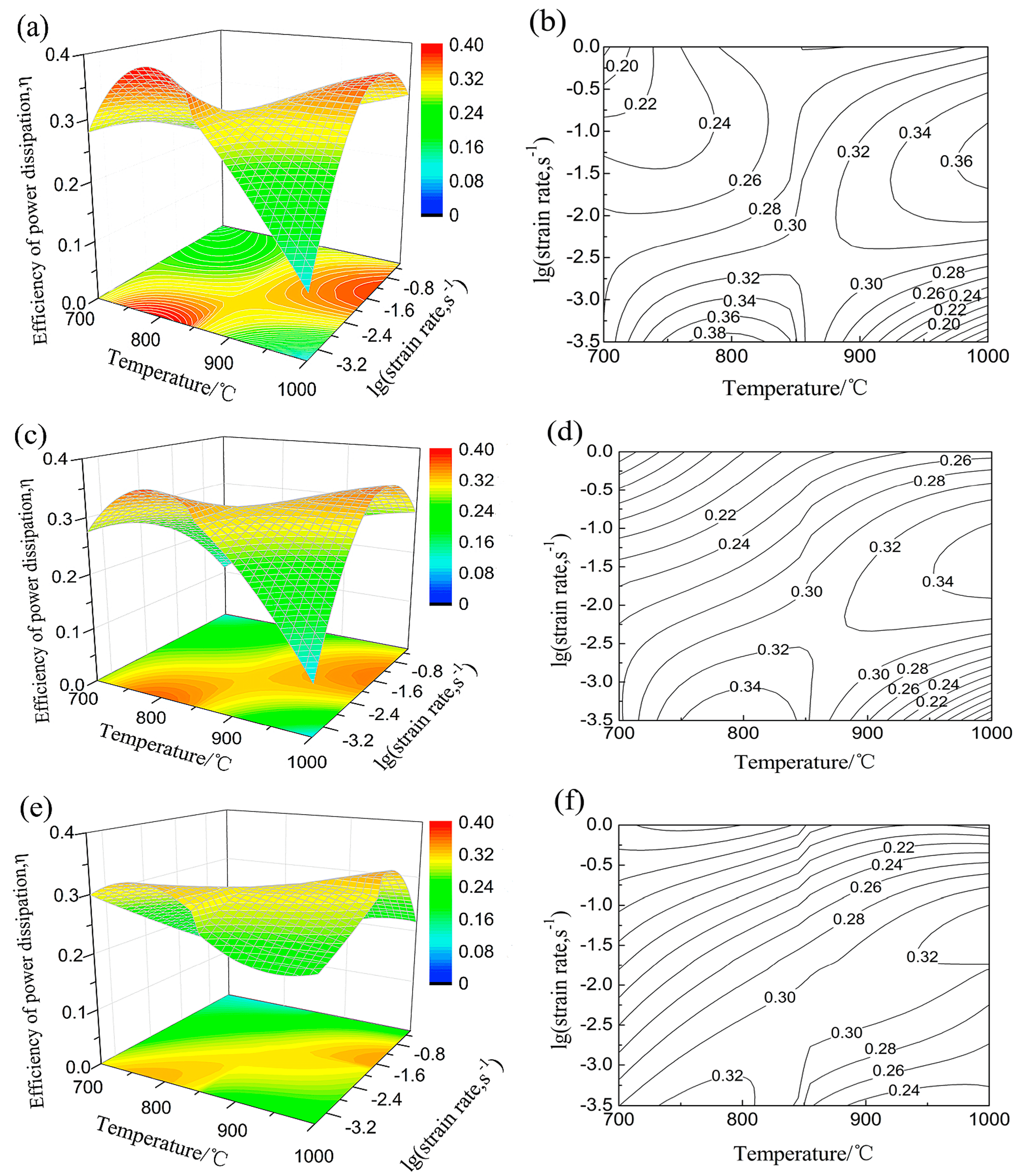
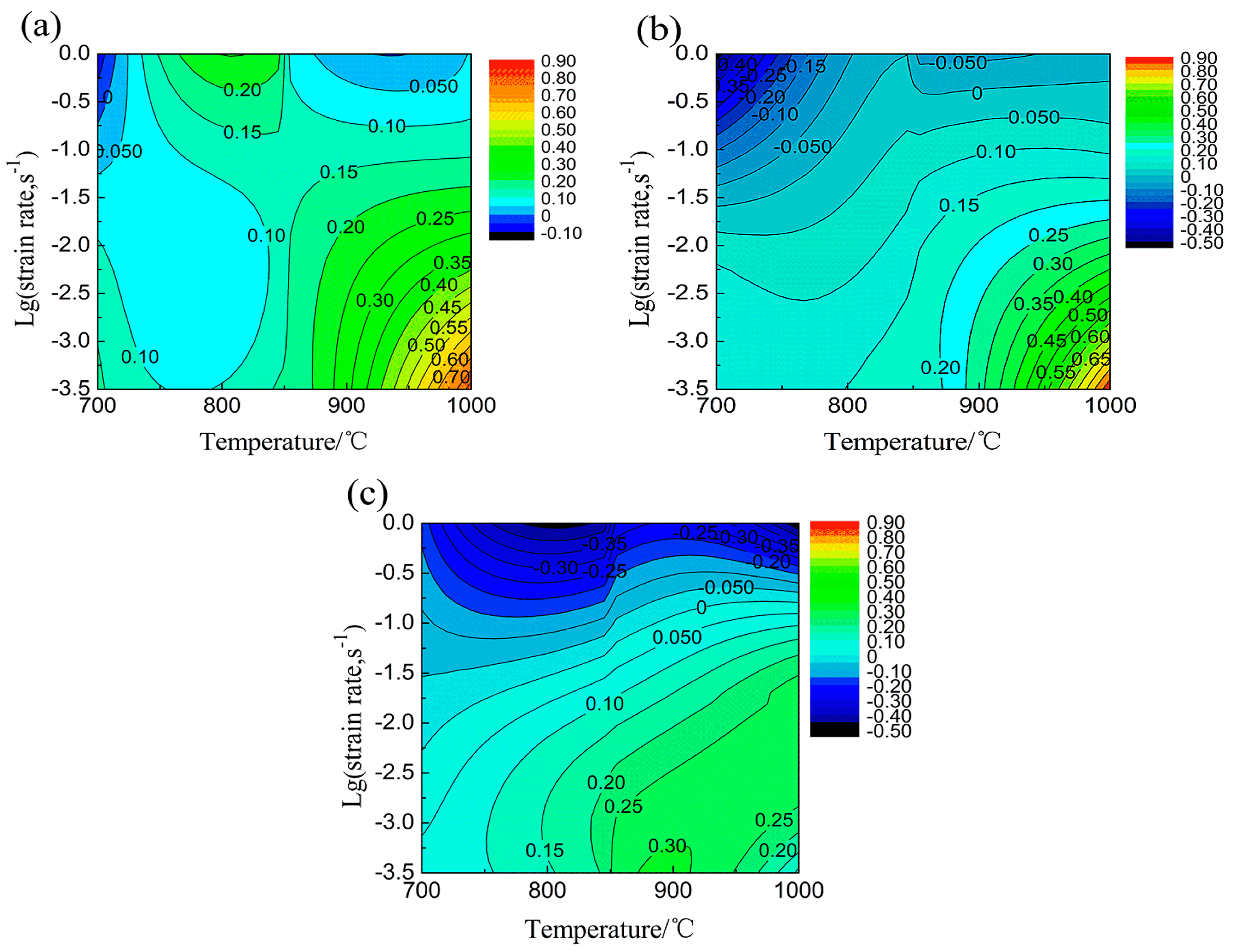
3. Principle for the Processing Map
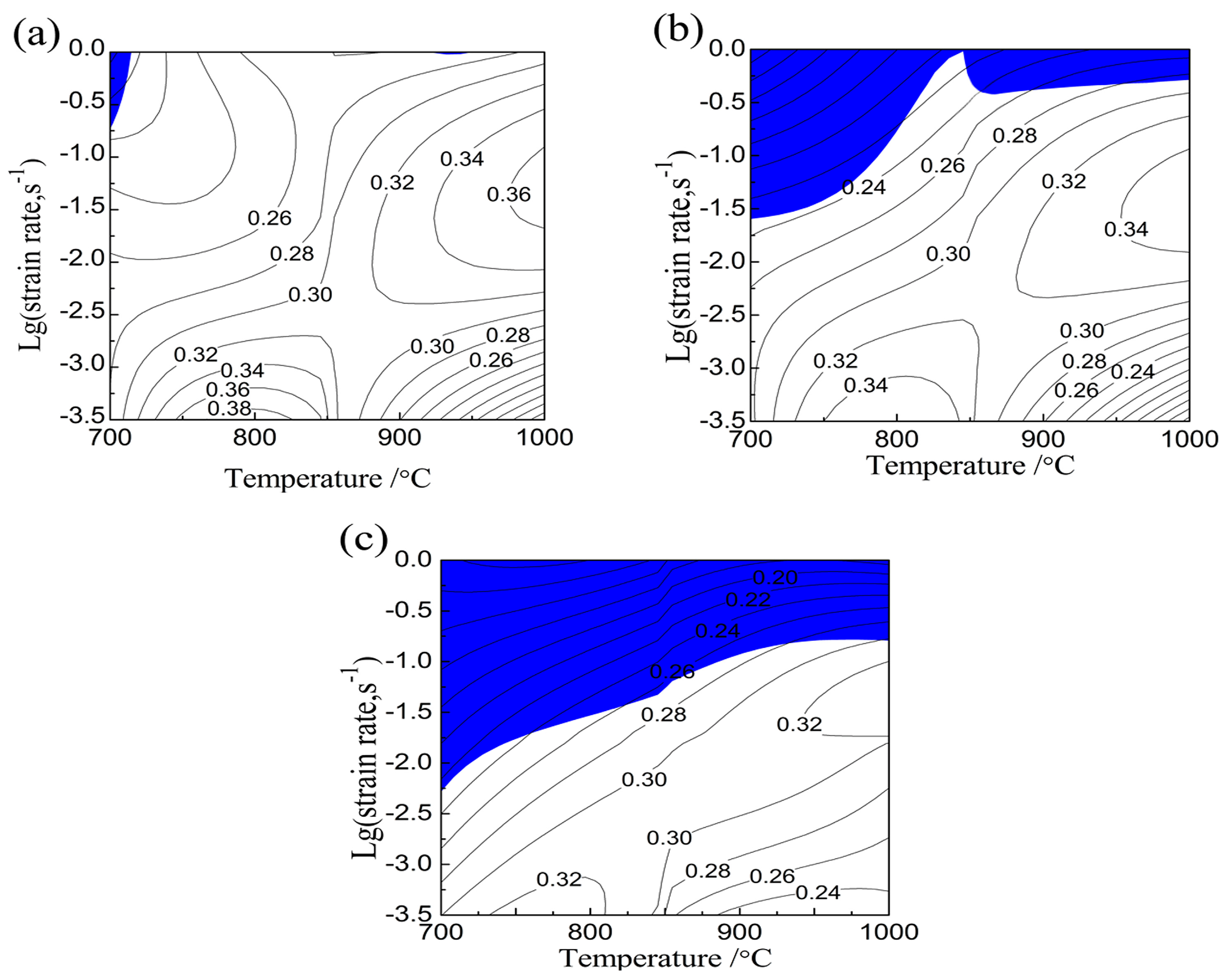
4. Results and Discussion
5. Conclusions
- (1)
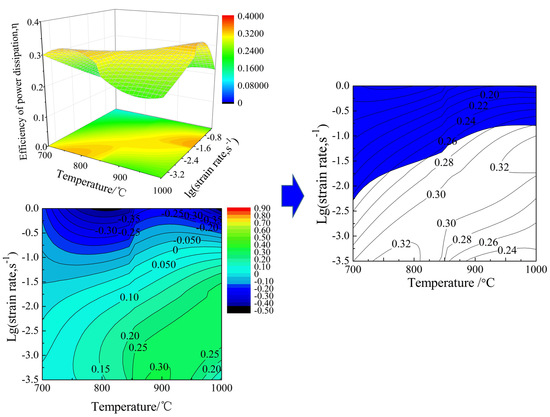
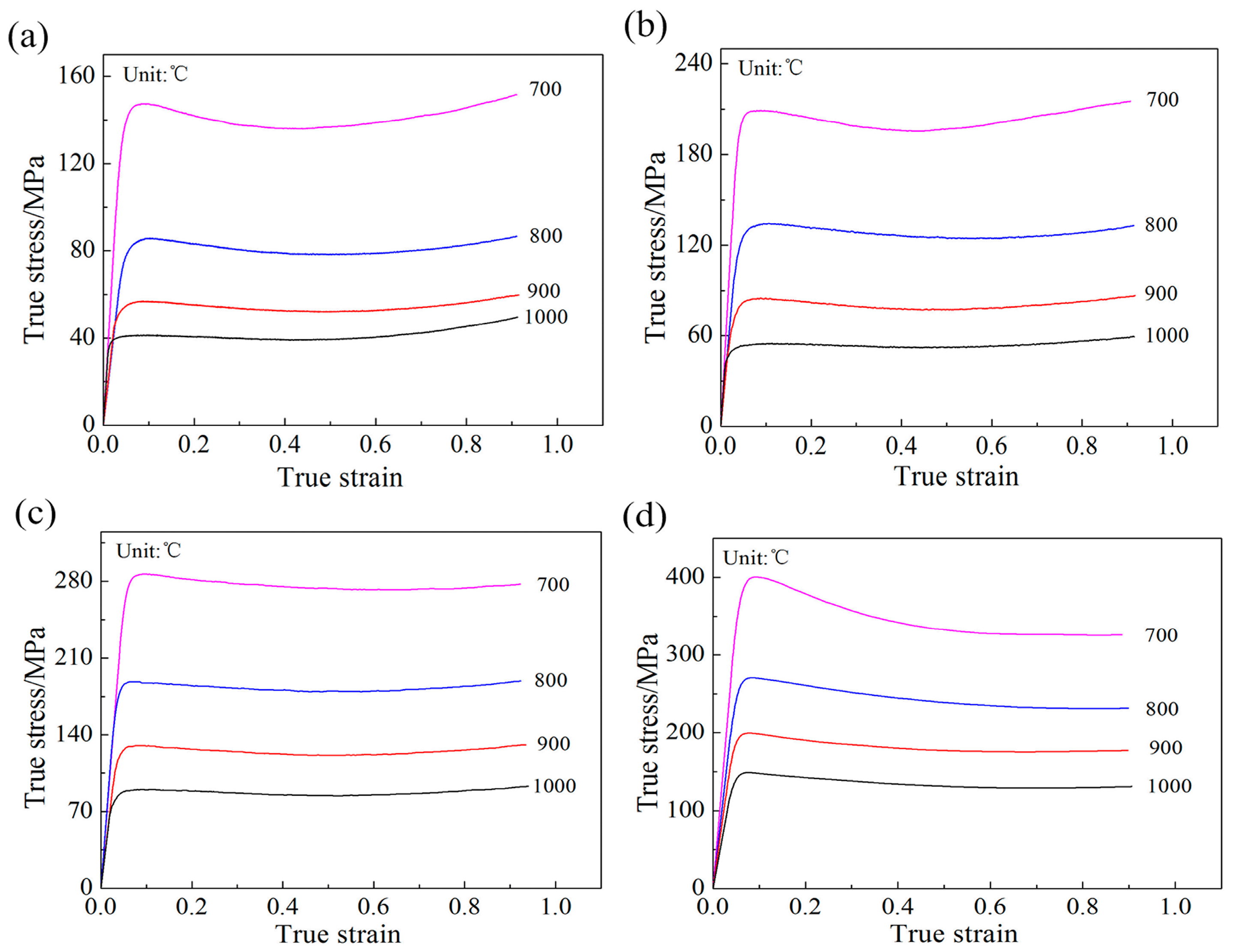
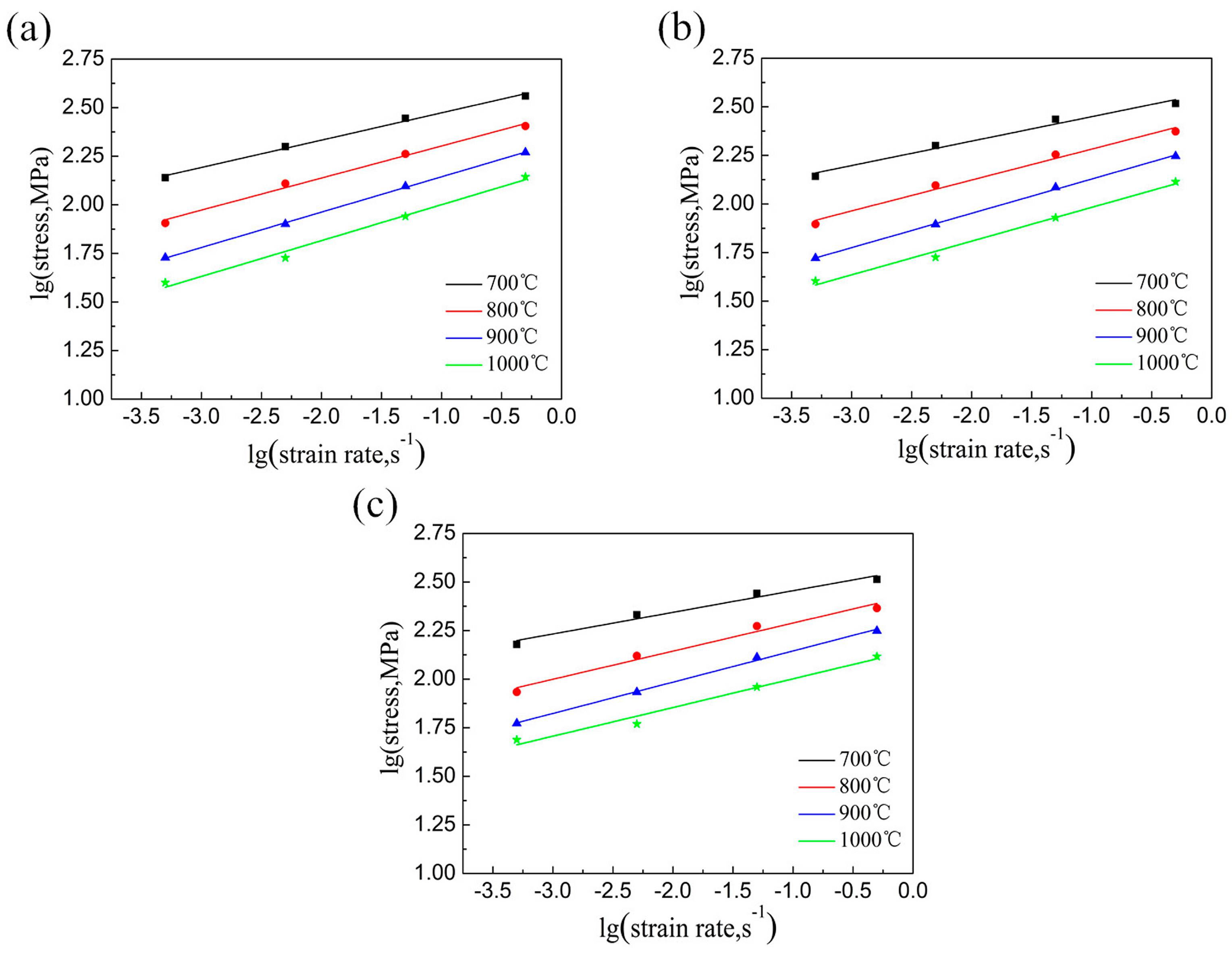
- Flow stress of NiTiNb SMA is dependent upon the strain rate and temperature. In the case of a constant strain rate, flow stress decreases with increasing temperature. In the case of a constant temperature, flow stress increases with the increasing strain rate. The instability region of NiTiNb SMA increases with the increasing true strain and it mainly focuses on the region with high strain rate. The workability of NiTiNb SMA becomes worse and worse with increasing plastic strain, as well as decreasing the deformation temperature.
- (2)
- There exist two stability zones which are suitable for hot working of NiTiNb SMA. One is the region where NiTiNb SMA experiences hot working in the temperature range of 750–840 °C, as well as at the strain rate range of 0.0003–0.001 s−1. The other is the region where NiTiNb SMA is subjected to hot working in the temperature range of 930–1000 °C, as well as at the strain rate range of 0.016–0.1 s−1. The processing map lays the foundation for optimizing the hot working parameters of NiTiNb SMA.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jani, J.M.; Leary, M.; Subic, A.; Gibson, M.A. A review of shape memory alloy research, applications and opportunities. Mater. Des. 2014, 56, 1078–1113. [Google Scholar] [CrossRef]
- Elibol, C.; Wagner, M.F.X. Investigation of the stress-induced martensitic transformation in pseudoelastic NiTi under uniaxial tension, compression and compression-shear. Mater. Sci. Eng. A 2015, 621, 76–81. [Google Scholar] [CrossRef]
- Kuang, C.H.; Chien, C.; Wu, S.K. Multistage martensitic transformation in high temperature aged Ti48Ni52 shape memory alloy. Intermetallics 2015, 67, 12–18. [Google Scholar] [CrossRef]
- Jones, N.G.; Dye, D. Influence of applied stress on the transformation behaviour and martensite evolution of a Ti-Ni-Cu shape memory alloy. Intermetallics 2013, 32, 239–249. [Google Scholar] [CrossRef]
- Basu, R.; Eskandari, M.; Upadhayay, L.; Mohtadi-Bonab, M.A.; Szpunar, J.A. A systematic investigation on the role of microstructure on phase transformation behavior in Ni-Ti-Fe shape memory alloys. J. Alloys Compd. 2015, 645, 213–222. [Google Scholar] [CrossRef]
- Mohammad Sharifi, E.; Kermanpur, A.; Karimzadeh, F. The effect of thermomechanical processing on the microstructure and mechanical properties of the nanocrystalline TiNiCo shape memory alloy. Mater. Sci. Eng. A 2014, 598, 183–189. [Google Scholar] [CrossRef]
- Jiang, P.C.; Zheng, Y.F.; Tong, Y.X.; Chen, F.; Tian, B.; Li, L.; Gunderov, D.V.; Valiev, R.Z. Transformation hysteresis and shape memory effect of an ultrafine-grained TiNiNb shape memory alloy. Intermetallics 2014, 54, 133–135. [Google Scholar] [CrossRef]
- Choi, E.; Hong, H.K.; Kim, H.S.; Chung, Y.S. Hysteretic behavior of NiTi and NiTiNb SMA wires under recovery or pre-stressing stress. J. Alloys Compd. 2013, 577, 444–447. [Google Scholar] [CrossRef]
- Zhao, L.C.; Duerig, T.W.; Justi, S. The study of niobium-rich precipitates in a Ni-Ti-Nb shape memory alloy. Scr. Metall. Mater. 1990, 24, 221–226. [Google Scholar] [CrossRef]
- Dong, Z.Z.; Zhou, S.L.; Liu, W.X. A study of NiTiNb shape-memory alloy pipe-joint with improved properties. Mater. Sci. Forum 2002, 394–395, 107–110. [Google Scholar] [CrossRef]
- Uchida, K.; Shigenaka, N.; Sakuma, T.; Sutou, Y.; Yamauchi, K. Effect of Nb content on martensitic transformation temperatures and mechanical properties of Ti-Ni-Nb shape memory alloys for pipe joint applications. Mater. Trans. 2007, 48, 445–450. [Google Scholar] [CrossRef]
- Korostelev, A.B. Properties of a Ti-Ni-Nb Alloy for producing thermomechanical couplings. Russ. Metall. 2011, 2011, 576–578. [Google Scholar] [CrossRef]
- Etaati, A.; Dehghani, K. A study on hot deformation behavior of Ni-42.5Ti-7.5Cu alloy. Mater. Chem. Phys. 2013, 140, 208–215. [Google Scholar] [CrossRef] [Green Version]
- Mirzadeh, H.; Parsa, M.H. Hot deformation and dynamic recrystallization of NiTi intermetallic compound. J. Alloys Compd. 2014, 614, 56–59. [Google Scholar] [CrossRef]
- Yeom, J.T.; Kim, J.H.; Hong, J.K.; Kim, S.W.; Park, C.H.; Nam, T.H.; Lee, K.Y. Hot forging design of as-cast NiTi shape memory alloy. Mater. Res. Bull. 2014, 58, 234–238. [Google Scholar] [CrossRef]
- Morakabati, M.; Kheirandish, S.; Aboutalebi, M.; Taheri, A.K.; Abbasi, S.M. The effect of Cu addition on the hot deformation behavior of NiTi shape memory alloys. J. Alloys Compd. 2010, 499, 57–62. [Google Scholar] [CrossRef]
- Morakabati, M.; Aboutalebi, M.; Kheirandish, S.; Taheri, A.K.; Abbasi, S.M. Hot tensile properties and microstructural evolution of as cast NiTi and NiTiCu shape memory alloys. Mater. Des. 2011, 32, 406–413. [Google Scholar] [CrossRef]
- Shamsolhodaei, A.; Zarei-hanzaki, A.; Ghambari, M.; Moemeni, S. The high temperature flow behavior modeling of NiTi shape memory alloy employing phenomenological and physical based constitutive models: A comparative study. Intermetallics 2014, 53, 140–149. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Jiang, S.Y.; Zhao, Y.N.; Liu, S.W. Constitutive equation and processing map of equiatomic NiTi shape memory alloy under hot plastic deformation. Trans. Nonferr. Met. Soc. 2016, 26, 2152–2161. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, S.; Chen, C.; Hu, L.; Zhu, X. Hot workability of a NiTiCu shape memory alloy with acicular martensite phase based on processing maps. Intermetallics 2017, 86, 94–103. [Google Scholar] [CrossRef]
- Gangolu, S.; Gourav Rao, A.; Sabirov, I.; Kashyap, B.P.; Prabhu, N.; Deshmukh, V.P. Development of constitutive relationship and processing map for Al-6.65Si-0.44Mg alloy and its composite with B4C particulates. Mater. Sci. Eng. A 2016, 655, 256–264. [Google Scholar] [CrossRef]
- Rastegari, H.; Kermanpur, A.; Najafizadeh, A.; Somani, M.C.; Porter, D.A.; Ghassemali, E.; Jarfors, A.E.W. Determination of processing maps for the warm working of vanadium microalloyed eutectoid steels. Mater. Sci. Eng. A 2016, 658, 167–175. [Google Scholar] [CrossRef]
- Rajput, S.K.; Chaudhari, G.P.; Nath, S.K. Characterization of hot deformation behavior of a low carbon steel using processing maps, constitutive equations and Zener-Hollomon parameter. J. Mater. Process. Technol. 2016, 237, 113–125. [Google Scholar] [CrossRef]
- Momeni, A.; Dehghani, K. Hot working behavior of 2205 austenite-ferrite duplex stainless steel characterized by constitutive equations and processing maps. Mater. Sci. Eng. A 2011, 528, 1448–1454. [Google Scholar] [CrossRef]
- Prasad, Y.V.R.K.; Sasidhara, S. Hot Working Guide: A Compendium of Processing Maps; ASM International: Materials Park, OH, USA, 1997. [Google Scholar]
- Wu, H.; Wu, C.; Yang, J.; Lin, M. Hot workability analysis of AZ61 Mg alloys with processing maps. Mater. Sci. Eng. A 2014, 607, 261–268. [Google Scholar] [CrossRef]
- Shang, X.; Zhou, J.; Wang, X.; Luo, Y. Optimizing and identifying the process parameters of AZ31 magnesium alloy in hot compression on the base of processing maps. J. Alloys Compd. 2015, 629, 155–161. [Google Scholar] [CrossRef]
- Wu, H.; Wen, S.P.; Huang, H.; Gao, K.Y.; Wu, X.L.; Wang, W.; Nie, Z.R. Hot deformation behavior and processing map of a new type Al-Zn-Mg-Er-Zr alloy. J. Alloys Compd. 2016, 685, 869–880. [Google Scholar] [CrossRef]
- Zeng, W.D.; Zhou, Y.G.; Zhou, J.; Yu, H.Q.; Zhang, X.M.; Xu, B. Recent development of processing map theory. Rare Met. Mater. Eng. 2006, 35, 673–677. [Google Scholar]
- Ziegler, H.; Sneedon, I.N.; Hill, R. Progress in Solid Mechanics; Wiley: New York, NY, USA, 1963. [Google Scholar]
- Łukaszek-Solek, A.; Krawczyk, J. The analysis of the hot deformation behaviour of the Ti-3Al-8V-6Cr-4Zr-4Mo alloy, using processing maps, a map of microstructure and of hardness. Mater. Des. 2015, 65, 165–173. [Google Scholar] [CrossRef]


| 700 | 800 | 900 | 1000 | ||
|---|---|---|---|---|---|
| 0.3 | 0.0005 | 137.8010 | 80.4978 | 53.4650 | 39.7838 |
| 0.005 | 199.2236 | 128.6067 | 79.6107 | 53.3478 | |
| 0.05 | 278.4276 | 182.6738 | 124.5443 | 87.1276 | |
| 0.5 | 362.9075 | 254.1071 | 185.9302 | 139.1716 | |
| 0.6 | 0.0005 | 138.6029 | 78.6816 | 52.6534 | 40.1727 |
| 0.005 | 199.7022 | 124.5523 | 78.5104 | 53.1897 | |
| 0.05 | 272.5415 | 179.6717 | 121.7723 | 85.0241 | |
| 0.5 | 328.3940 | 236.2028 | 176.2441 | 130.1123 | |
| 0.9 | 0.0005 | 150.7980 | 85.8143 | 59.2176 | 48.7737 |
| 0.005 | 214.5237 | 131.7976 | 85.6582 | 58.8096 | |
| 0.05 | 276.0619 | 187.4464 | 129.4072 | 91.1164 | |
| 0.5 | 325.8891 | 231.8062 | 177.1036 | 130.8063 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Jiang, S.; Zhang, Y. Processing Map of NiTiNb Shape Memory Alloy Subjected to Plastic Deformation at High Temperatures. Metals 2017, 7, 328. https://doi.org/10.3390/met7090328
Wang Y, Jiang S, Zhang Y. Processing Map of NiTiNb Shape Memory Alloy Subjected to Plastic Deformation at High Temperatures. Metals. 2017; 7(9):328. https://doi.org/10.3390/met7090328
Chicago/Turabian StyleWang, Yu, Shuyong Jiang, and Yanqiu Zhang. 2017. "Processing Map of NiTiNb Shape Memory Alloy Subjected to Plastic Deformation at High Temperatures" Metals 7, no. 9: 328. https://doi.org/10.3390/met7090328