Peculiar Spatiotemporal Behavior of Unstable Plastic Flow in an AlMgMnScZr Alloy with Coarse and Ultrafine Grains
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Microstructure before and after ECAP
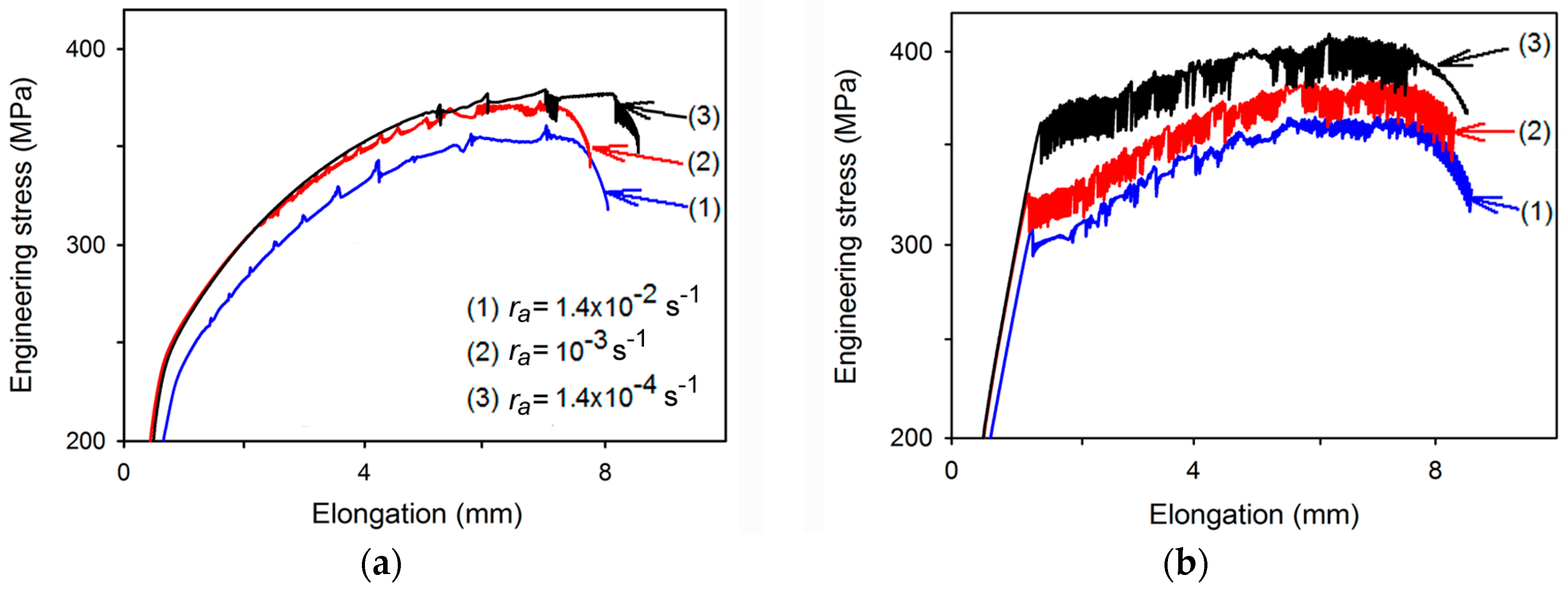
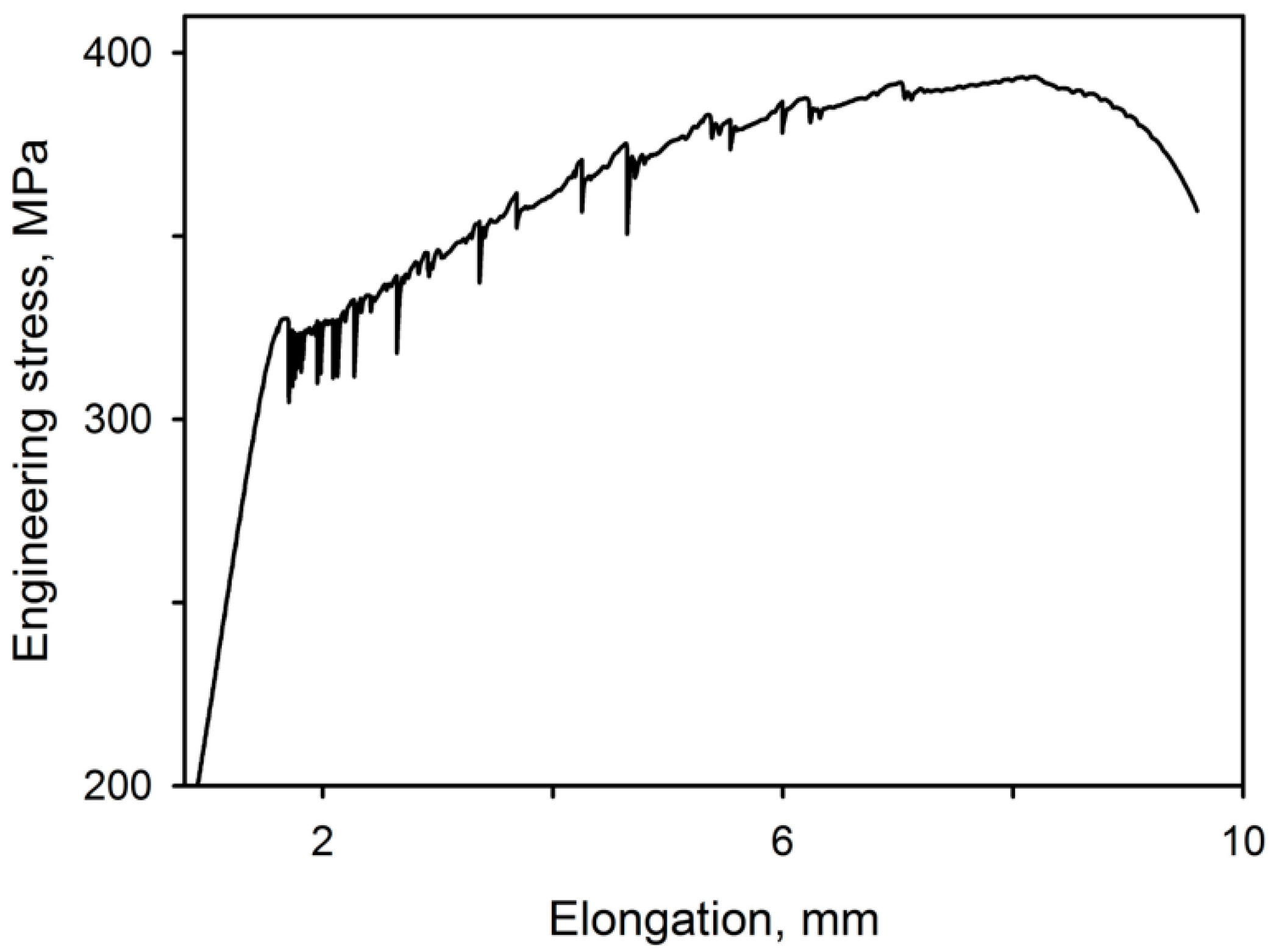
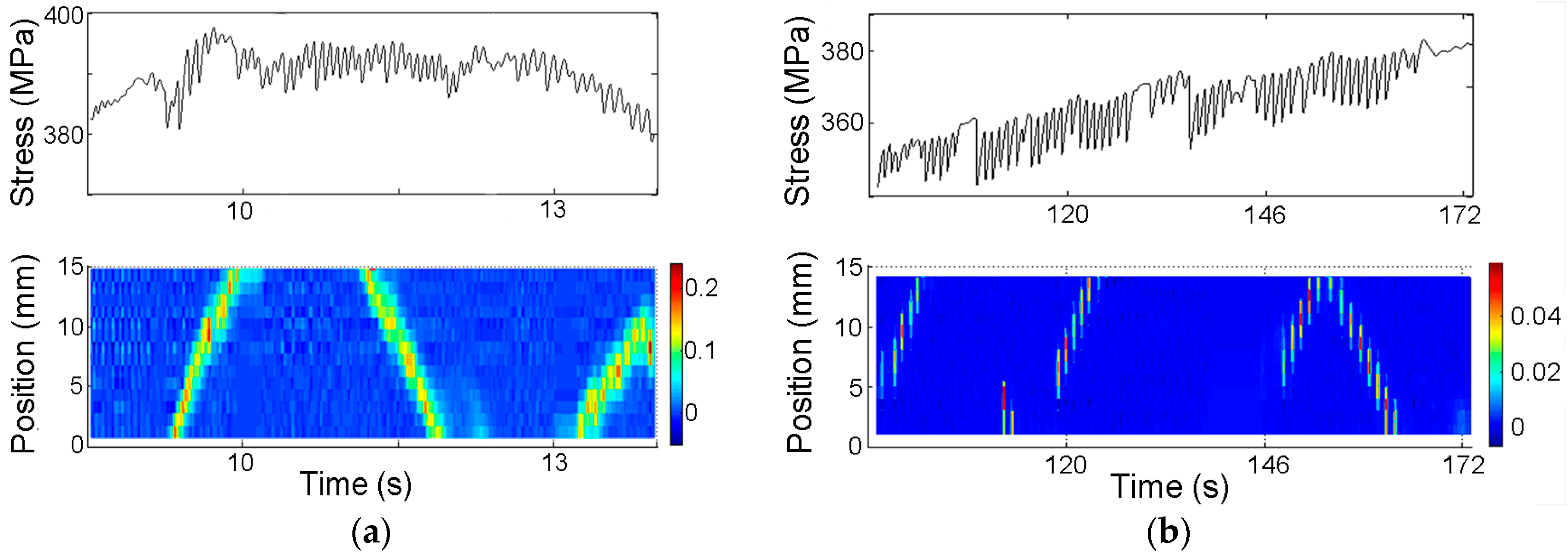
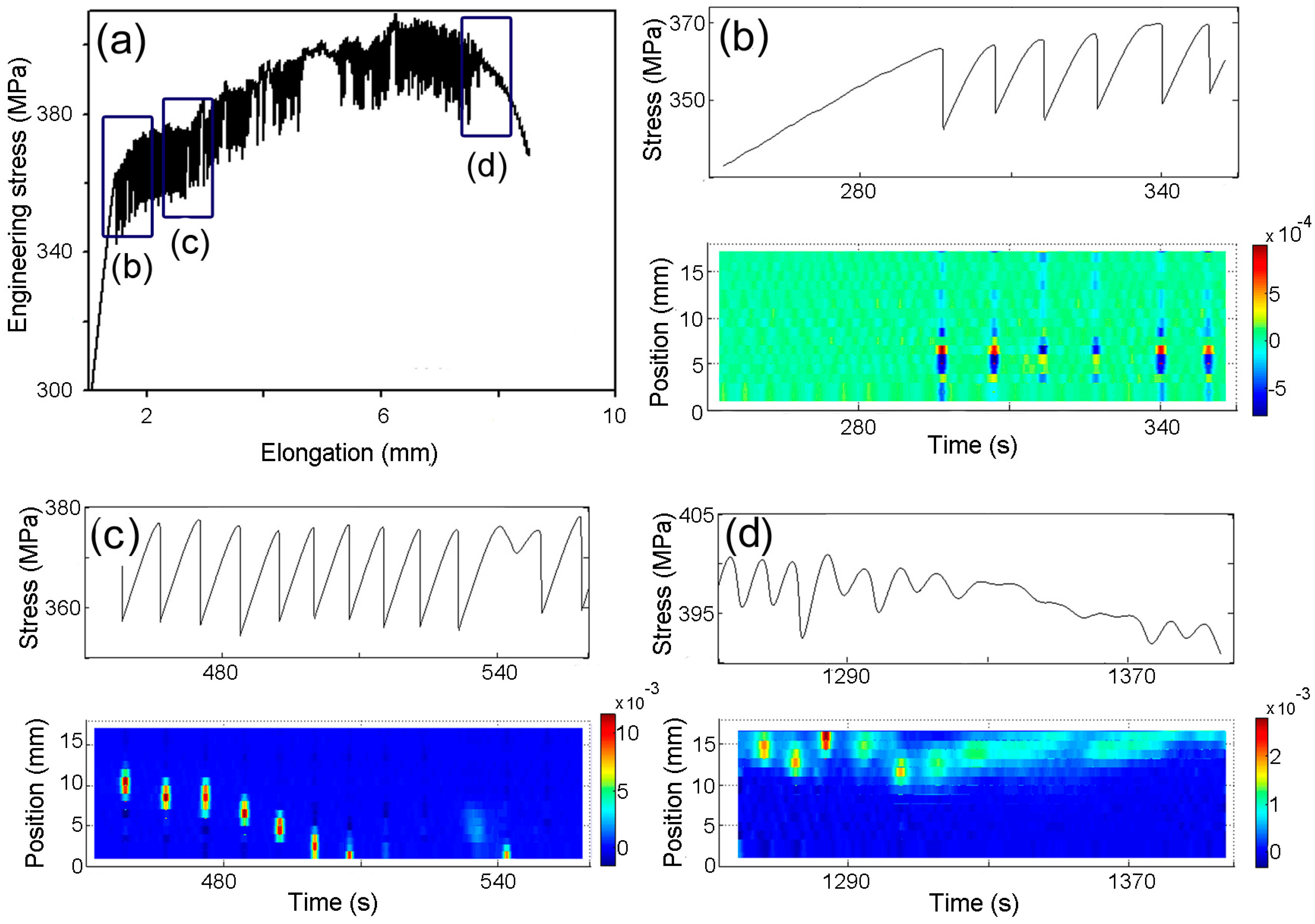
3.2. Stress Serrations Patterns
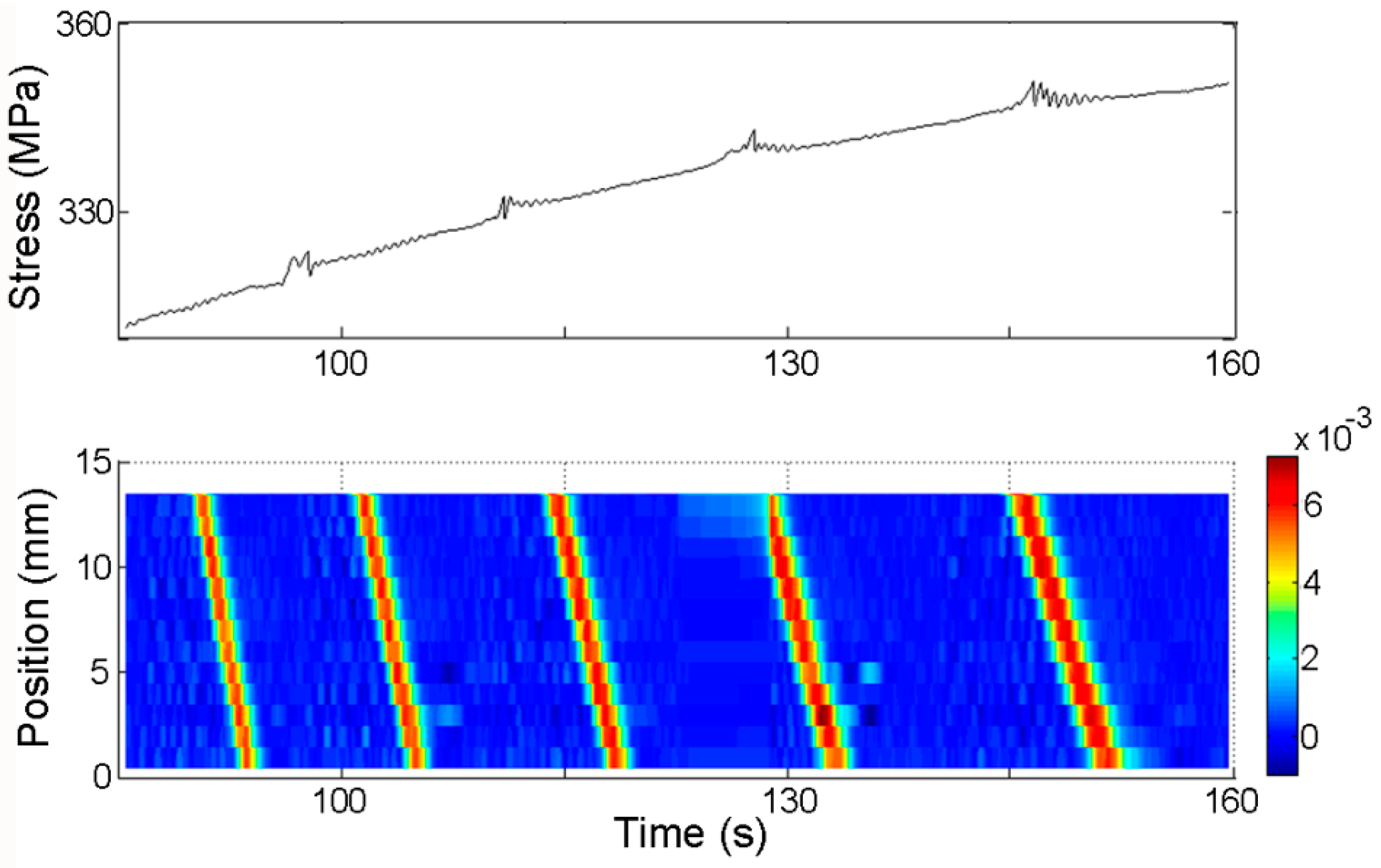
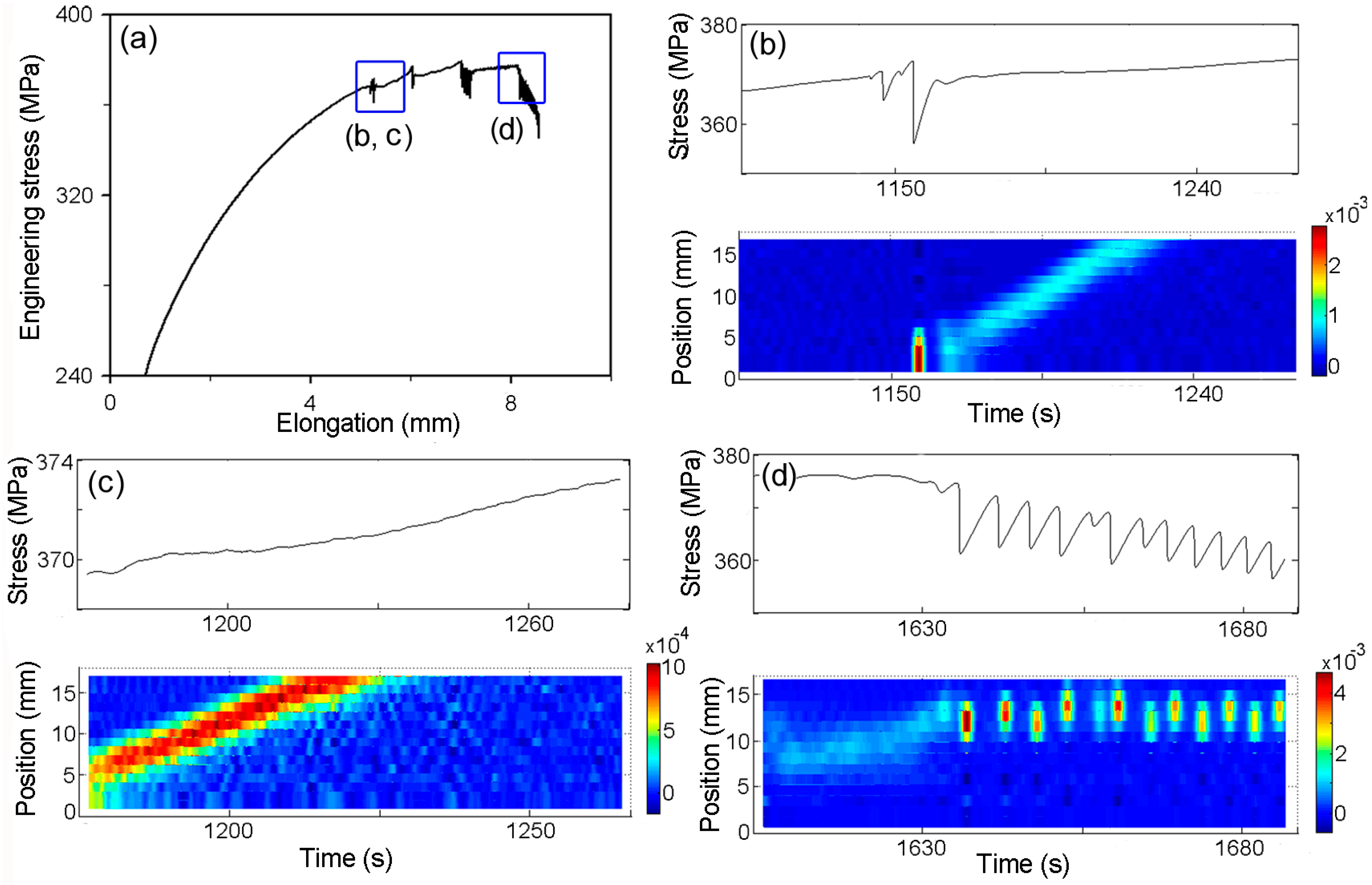
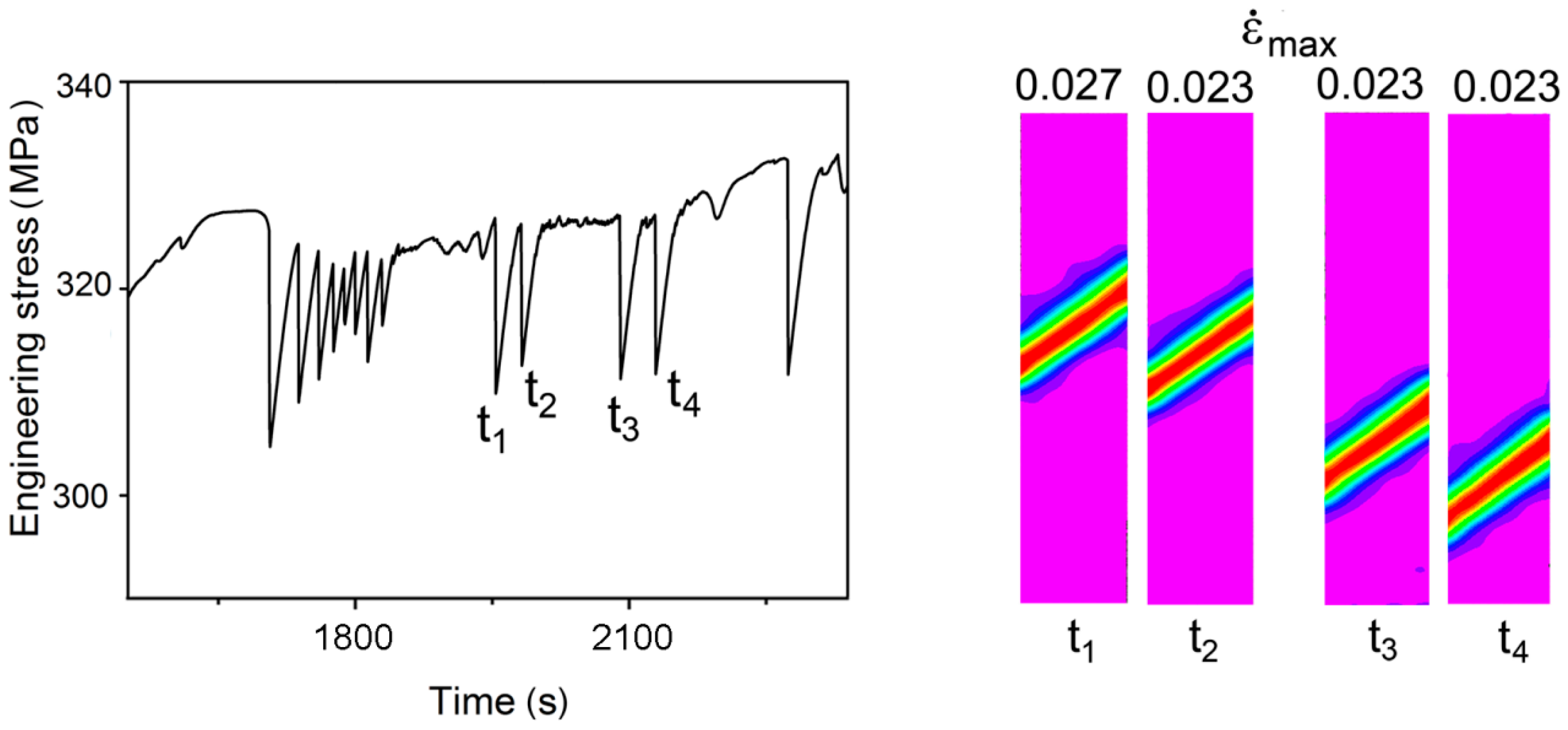
3.3. PLC Bands Patterns
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Portevin, A.; Le Chatelier, F. Sur un Phénomène Observé lors de L’essai de Traction d’Alliages en Cours de Transformation. C. R. Acad. Sci. Paris 1923, 176, 507–510. [Google Scholar]
- Rodriguez, P. Serrated plastic flow. Bull. Mater. Sci. 1984, 6, 653–663. [Google Scholar] [CrossRef]
- Van den Beukel, A. Theory of the effect of dynamic strain ageing on mechanical properties. Phys. Status Solidi 1975, 30, 197–206. [Google Scholar] [CrossRef]
- Kubin, L.P.; Estrin, Y. The Portevin-Le Chatelier effect in deformation with constant stress rate. Acta Metall. 1985, 33, 397–407. [Google Scholar] [CrossRef]
- Robinson, J.M.; Shaw, M.P. Microstructural and Mechanical Influences on Dynamic Strain Aging Phenomena. Int. Mater. Rev. 1994, 39, 113–122. [Google Scholar] [CrossRef]
- Picu, R.C. A mechanism for the negative strain-rate sensitivity of dilute solid solutions. Acta Mater. 2004, 52, 3447–3458. [Google Scholar] [CrossRef]
- Aboulfadl, H.; Deges, J.; Choi, P.; Raabe, D. Dynamic strain aging studied at the atomic scale. Acta Mater. 2015, 86, 34–42. [Google Scholar] [CrossRef]
- Lebyodkin, M.; Dunin-Barkowskii, L.; Brechet, Y.; Estrin, Y.; Kubin, L.P. Spatio-temporal dynamics of the Portevin-Le Chatelier effect: Experiment and modelling. Acta Mater. 2000, 48, 2529–2541. [Google Scholar] [CrossRef]
- Bharathi, M.S.; Lebyodkin, M.; Ananthakrishna, G.; Fressengeas, C.; Kubin, L.P. The hidden order behind jerky flow. Acta Mater. 2002, 50, 2813–2824. [Google Scholar] [CrossRef]
- Robinson, J.M. Serrated flow in aluminium base alloys. Int. Mater. Rev. 1994, 39, 217–227. [Google Scholar] [CrossRef]
- Balik, J.; Lukac, P. Portevin-Le Chatelier instabilities in Al-3Mg alloy conditioned by strain rate and strain. Acta Metall. Mater. 1993, 41, 1447–1454. [Google Scholar] [CrossRef]
- Chihab, K.; Estrin, Y.; Kubin, L.P.; Vergnol, J. The kinetics of the Portevin-Le Chatelier bands in an Al-5at%Mg alloy. Scr. Mater. 1987, 21, 203–208. [Google Scholar] [CrossRef]
- Horvath, G.; Chinh, N.Q.; Gubicza, J.; Lendvai, J. Plastic instabilities and dislocation densities during plastic deformation in Al-Mg alloys. Mater. Sci. Eng. A 2007, 445–446, 186–192. [Google Scholar] [CrossRef]
- Halim, H.; Wilkinson, D.S.; Niewczas, M. The Portevin-Le Chatelier (PLC) effect and shear band formation in an AA5754 alloy. Acta Mater. 2007, 55, 4151–4160. [Google Scholar] [CrossRef]
- Louche, H.; Vacher, P.; Arrieux, R. Thermal observations associated with the Portevin-Le Chatelier effect in an Al-Mg alloy. Mater. Sci. Eng. A 2005, 404, 188–196. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, Q.; Chen, X.; Chen, Z.; Jiang, Z.; Wu, X.; Fan, J. Three types of Portevin-Le Chatelier effect: Experiment and modeling. Acta Mater. 2007, 55, 2219–2228. [Google Scholar] [CrossRef]
- Lebyodkin, M.A.; Lebedkina, T.A. Multifractality and randomness in the unstable plastic flow near the lower strain-rate boundary of instability. Phys. Rev. E 2008, 77, 026111. [Google Scholar] [CrossRef] [PubMed]
- Kok, S.; Beaudoin, A.J.; Tortorelli, D.A.; Lebyodkin, M. A finite element model for the Portevin-Le Chatelier effect based on polycrystal plasticity. Model. Simul. Mater. Sci. Eng. 2002, 10, 745–763. [Google Scholar] [CrossRef]
- Polmear, I.J. Light Alloys: From Traditional Alloys to Nanocrystals, 4th ed.; Butterworth-Heinemann/Elsevier: Oxford, UK, 2006; pp. 205–235. ISBN 978-0-75-066371-7. [Google Scholar]
- Filatov, Y.A.; Yelagin, V.I.; Zakharov, V.V. New Al-Mg-Sc alloys. Mater. Sci. Eng. A 2000, 280, 97–101. [Google Scholar] [CrossRef]
- Zhemchuzhnikova, D.A.; Lebyodkin, M.A.; Lebedkina, T.A.; Kaibyshev, R.O. Unusual behavior of the Portevin-Le Chatelier effect in an AlMg alloy containing precipitates. Mater. Sci. Eng. A 2015, 639, 37–41. [Google Scholar] [CrossRef]
- Estrin, Y.; Vinogradov, A. Extreme grain refinement by severe plastic deformation: A wealth of challenging science. Acta Mater. 2013, 61, 782–817. [Google Scholar] [CrossRef]
- Sabirov, I.; Murashkin, M.Y.; Valiev, R.Z. Nanostructured aluminium alloys produced by severe plastic deformation: New horizons in development. Mater. Sci. Eng. A 2013, 560, 1–24. [Google Scholar] [CrossRef]
- Malopheyev, S.; Kaibyshev, R. Strengthening mechanisms in a Zr-modified 5083 alloy deformed to high strains. Mater. Sci. Eng. A 2015, 620, 246–252. [Google Scholar] [CrossRef]
- Mogucheva, A.; Yuzbekova, D.; Kaibyshev, R.; Lebedkina, T.; Lebyodkin, M. Effect of grain refinement on jerky flow in Al-Mg-Sc alloy. Metall. Mater. Trans. A 2016, 47, 2093–2106. [Google Scholar] [CrossRef]
- Lebedkina, T.A.; Lebyodkin, M.A.; Lamark, T.T.; Janecek, M.; Estrin, Y. Effect of equal channel angular pressing on the Portevin-Le Chatelier effect in an Al3Mg alloy. Mater. Sci. Eng. A 2014, 615, 7–13. [Google Scholar] [CrossRef]
- Zhao, S.; Meng, C.; Mao, F.; Hu, W.; Gottstein, G. Influence of severe plastic deformation on dynamic strain aging of ultrafine grained Al-Mg alloys. Acta Mater. 2014, 76, 54–67. [Google Scholar] [CrossRef]
- Mogucheva, A.; Babich, E.; Ovsyannikov, B.; Kaibyshev, R. Microstructural evolution in a 5024 aluminum alloy processed by ECAP with and without back pressure. Mater. Sci. Eng. A 2013, 560, 178–192. [Google Scholar] [CrossRef]
- Valiev, R.Z.; Langdon, T.G. Principles of equal-channel angular pressing as a processing tool for grain refinement. Prog. Mater. Sci. 2006, 51, 881–981. [Google Scholar] [CrossRef]
- Lebedkina, T.A.; Lebyodkin, M.A.; Château, J.-P.; Jacques, A.; Allain, S. On the mechanism of unstable plastic flow in an austenitic FeMnC TWIP steel. Mater. Sci. Eng. A 2009, 519, 147–154. [Google Scholar] [CrossRef]
- Cai, Y.L.; Yang, S.L.; Wang, Y.H.; Fu, S.H.; Zhang, Q.C. Characterization of the deformation behaviors associated with the serrated flow of a 5456 Al-based alloy using two orthogonal digital image correlation systems. Mater. Sci. Eng. A 2016, 664, 155–164. [Google Scholar] [CrossRef]
- Lebedkina, T.A.; Lebyodkin, M.A. Effect of deformation geometry on the intermittent plastic flow associated with the Portevin-Le Chatelier effect. Acta Mater. 2008, 56, 5567–5574. [Google Scholar] [CrossRef]
- Kral, R.; Lukac, P. Modelling of strain hardening and its relation to the onset of Portevin-Le Chatelier effect in Al-Mg alloys. Mater. Sci. Eng. A 1997, 234–236, 786–789. [Google Scholar] [CrossRef]
- Schwab, R.; Ruff, V. On the nature of the yield point phenomenon. Acta Mater. 2013, 61, 1798–1808. [Google Scholar] [CrossRef]
- Antolovich, S.D.; Armstrong, R.W. Plastic strain localization in metals: Origins and consequences. Prog. Mater. Sci. 2014, 59, 1–160. [Google Scholar] [CrossRef]
- Kubin, L.P.; Estrin, Y. Evolution of dislocation densities and the critical conditions for the Portevin-Le Chatelier effect. Acta Metall. Mater. 1990, 38, 697–708. [Google Scholar] [CrossRef]
- Nijs, O.; Holmedal, B.; Friis, J.; Nes, E. Sub-structure strengthening and work hardening of an ultra-fine grained aluminium-magnesium alloy. Mater. Sci. Eng. A 2008, 483–484, 51–53. [Google Scholar] [CrossRef]
- Coër, J.; Manach, P.Y.; Laurent, H.; Oliveira, M.C.; Menezes, L.F. Piobert-Lüders plateau and Portevin-Le Chatelier effect in an Al-Mg alloy in simple shear. Mech. Res. Commun. 2013, 48, 1–7. [Google Scholar] [CrossRef]
- Klusemann, B.; Fischer, G.; Böhlke, T.; Svendsen, G.B. Thermomechanical characterization of Portevin-Le Chatelier bands in AlMg3 (AA5754) and modeling based on a modified Estrin-McCormick approach. Int. J. Plast. 2015, 67, 192–216. [Google Scholar] [CrossRef]
- Ait-Amokhtar, H.; Vacher, P.; Boudrahem, S. Kinematics fields and spatial activity of Portevin-Le Chatelier bands using the digital image correlation method. Acta Mater. 2006, 54, 4365–4371. [Google Scholar] [CrossRef]
- Yuzbekova, D.; Mogucheva, A.; Zhemchuzhnikova, D.; Lebedkina, T.; Lebyodkin, M.; Kaibyshev, R. Effect of microstructure on continuous propagation of the Portevin-Le Chatelier deformation bands. Int. J. Plast. 2017, 96, 210–226. [Google Scholar] [CrossRef]
- Zuev, L.B. On the waves of plastic flow localization in pure metals and alloys. Ann. Phys. 2007, 16, 286–310. [Google Scholar] [CrossRef]
- Mudrock, R.N.; Lebyodkin, M.A.; Kurath, P.; Beaudoin, A.J.; Lebedkina, T.A. Strain-rate fluctuations during macroscopically uniform deformation of a solution-strengthened alloy. Scr. Mater. 2011, 65, 1093–1096. [Google Scholar] [CrossRef]
- Fressengeas, C.; Beaudoin, A.J.; Entemeyer, D.; Lebedkina, T.; Lebyodkin, M.; Taupin, V. Dislocation transport and intermittency in the plasticity of crystalline solids. Phys. Rev. B 2009, 7, 014108. [Google Scholar] [CrossRef]
- Lebyodkin, M.A.; Kobelev, N.P.; Bougherira, Y.; Entemeyer, D.; Fressengeas, C.; Gornakov, V.S.; Lebedkina, T.A.; Shashkov, I.V. On the similarity of plastic flow processes during smooth and jerky flow: Statistical analysis. Acta Mater. 2012, 60, 3729–3740. [Google Scholar] [CrossRef]
- Pérez, C.J.; Corral, Á.; Díaz-Guilera, A.; Christensen, K.; Arenas, A. On self-organized criticality and synchronization in lattice models of coupled dynamical systems. Int. J. Mod. Phys. B 1996, 10, 1111–1151. [Google Scholar] [CrossRef]
- Zhemchuzhnikova, D.A.; Lebyodkin, M.A.; Lebedkina, T.A.; Kaibyshev, R.O. The Portevin-Le Chatelier Effect and Kinematics of Deformation Bands in an Al-Mg-Sc Alloy: Effect of Grain Size. Mater. Sci. Forum 2016, 879, 2268–2273. [Google Scholar] [CrossRef]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhemchuzhnikova, D.; Lebyodkin, M.; Lebedkina, T.; Mogucheva, A.; Yuzbekova, D.; Kaibyshev, R. Peculiar Spatiotemporal Behavior of Unstable Plastic Flow in an AlMgMnScZr Alloy with Coarse and Ultrafine Grains. Metals 2017, 7, 325. https://doi.org/10.3390/met7090325
Zhemchuzhnikova D, Lebyodkin M, Lebedkina T, Mogucheva A, Yuzbekova D, Kaibyshev R. Peculiar Spatiotemporal Behavior of Unstable Plastic Flow in an AlMgMnScZr Alloy with Coarse and Ultrafine Grains. Metals. 2017; 7(9):325. https://doi.org/10.3390/met7090325
Chicago/Turabian StyleZhemchuzhnikova, Daria, Mikhail Lebyodkin, Tatiana Lebedkina, Anna Mogucheva, Diana Yuzbekova, and Rustam Kaibyshev. 2017. "Peculiar Spatiotemporal Behavior of Unstable Plastic Flow in an AlMgMnScZr Alloy with Coarse and Ultrafine Grains" Metals 7, no. 9: 325. https://doi.org/10.3390/met7090325




