Ultrasound Assisted Casting of an AM60 Based Metal Matrix Nanocomposite, Its Properties, and Recyclability
Abstract
:1. Introduction
2. Materials and Methods
3. Results
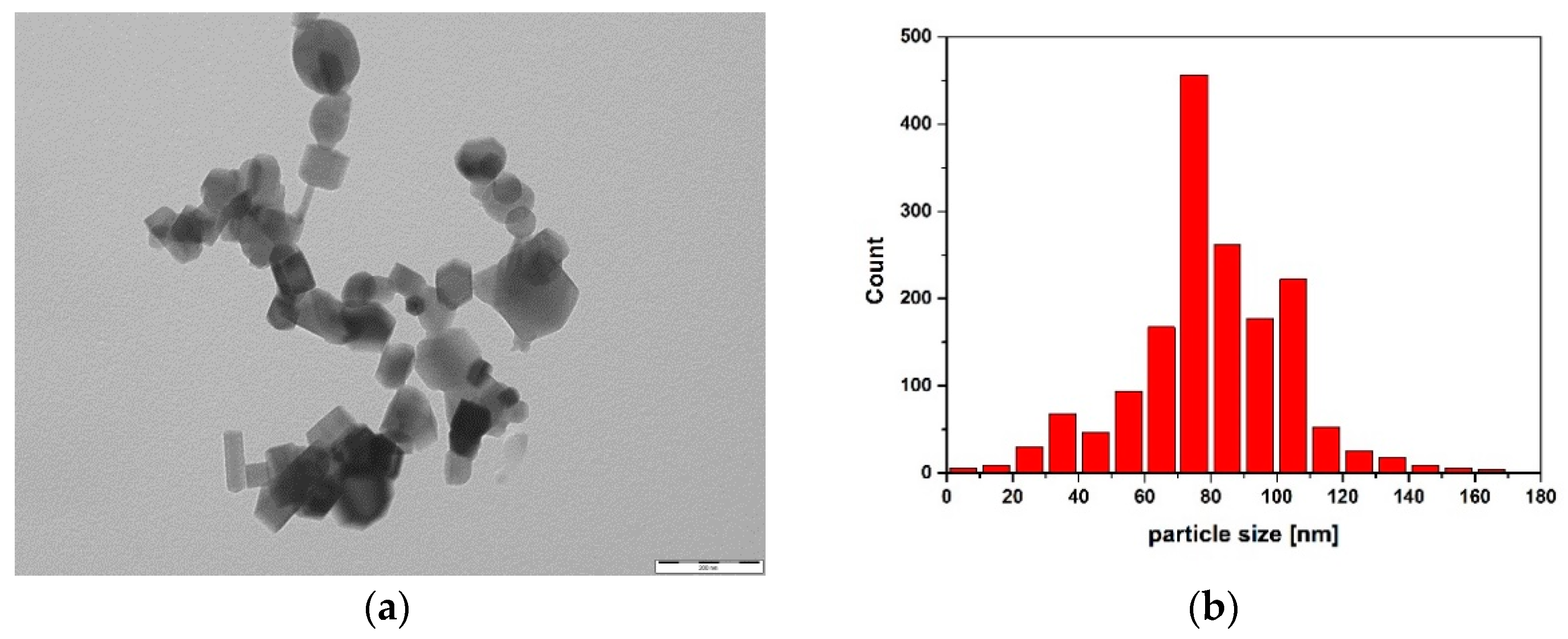
3.1. Microstructure
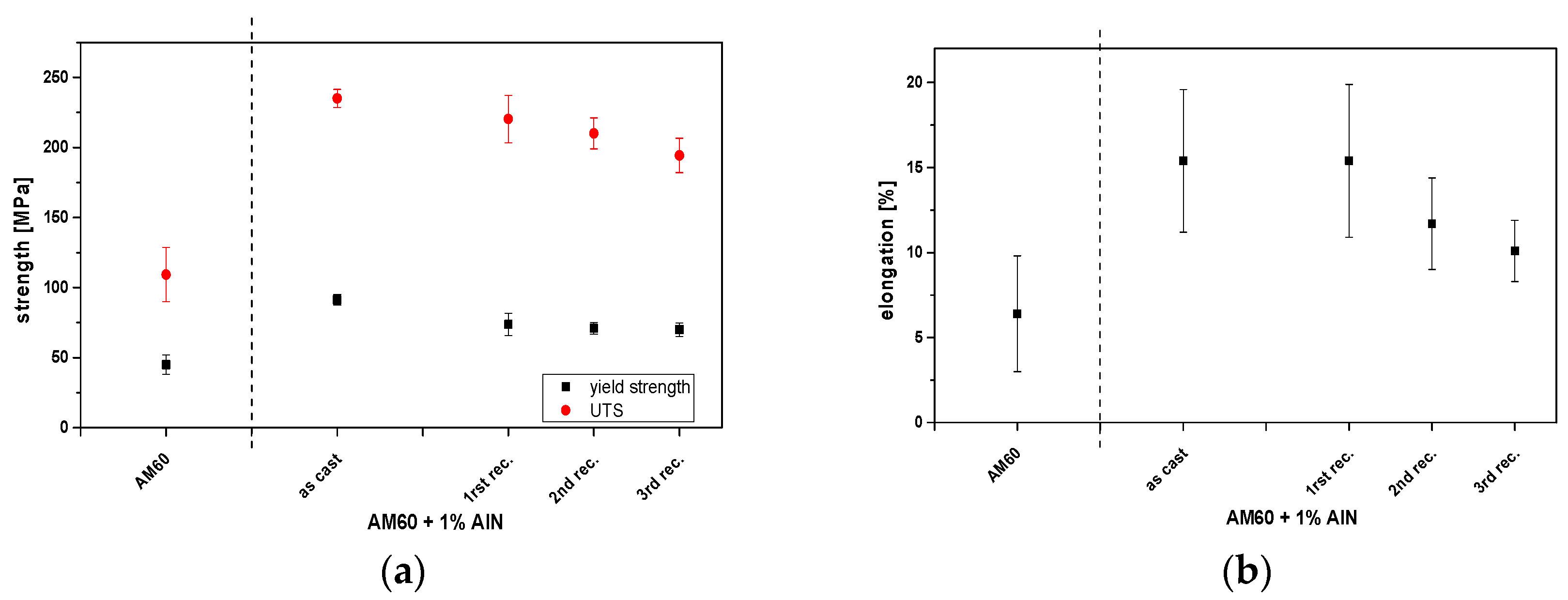
3.2. Mechanical Properties
4. Discussion
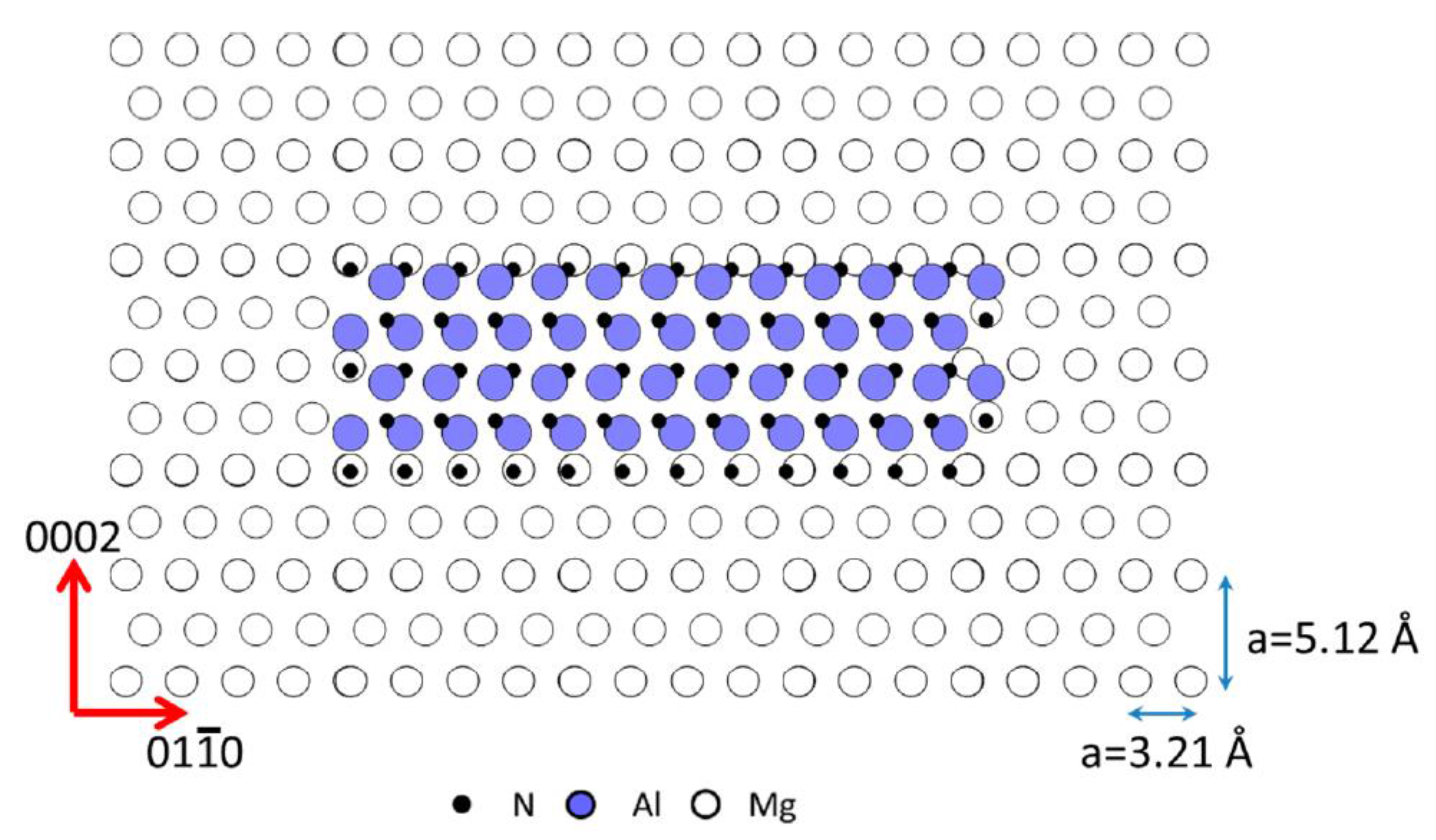
4.1. Microstructure
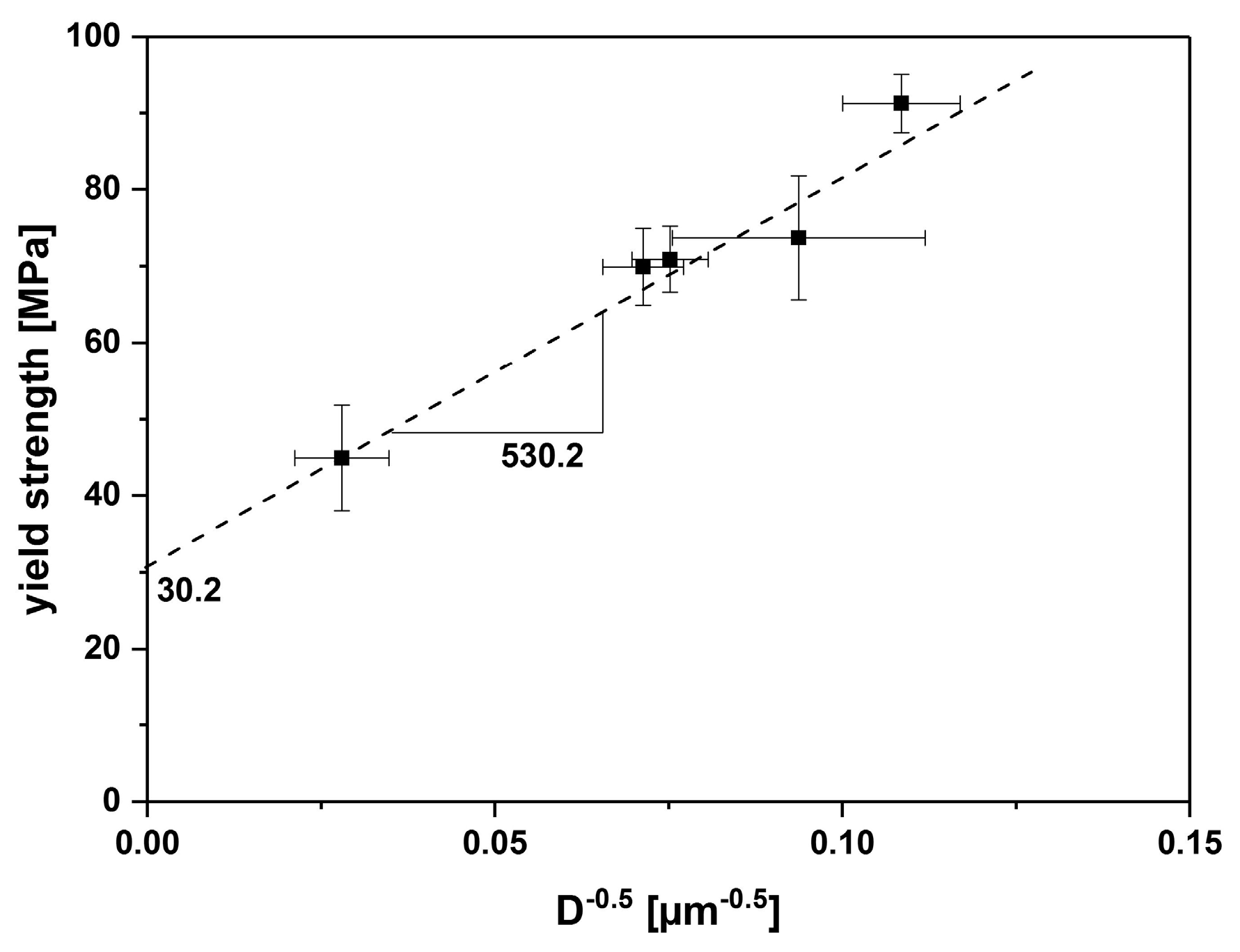
4.2. Mechanical Properties
4.3. Comparison of Yield Strength Prediction by Models
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Gavras, S.; Zhu, S.M.; Nie, J.F.; Gibson, M.A.; Easton, M.A. On the microstructural factors affecting creep resistance of die-cast Mg-La-rare earth (Nd, Y or Gd) alloys. Mater. Sci. Eng. 2016, 675, 65–75. [Google Scholar] [CrossRef]
- Zhu, S.M.; Gibson, M.A.; Easton, M.A.; Nie, J.F. The relationship between microstructure and creep resistance in die-cast magnesium-rare earth alloys. Scr. Mater. 2010, 63, 698–703. [Google Scholar] [CrossRef]
- Moreno, I.P.; Nandy, T.K.; Jones, J.W.; Allison, J.E.; Pollock, T.M. Microstructural stability and creep of rare-earth containing magnesium alloys. Scr. Mater. 2003, 48, 1029–1034. [Google Scholar] [CrossRef]
- Deming, H.; Yungui, C.; Yongbai, T.; Hongmei, L.; Gao, N. Indentation creep behavior of AE42 and Ca-containing AE41 alloys. Mater. Lett. 2007, 61, 1015–1019. [Google Scholar] [CrossRef]
- Wan, X.; Sun, Y.; Xue, F. Microstructure and mechanical properties of ZA62 based magnesium alloys with calcium addition. Trans. Nonferr. Met. Soc. China 2010, 20, 757–762. [Google Scholar] [CrossRef]
- Dargusch, M.S.; Zhu, S.M.; Nie, J.F.; Dunlop, G.L. Microstructural analysis of the improved creep resistance of a die-cast magnesium-aluminium-rare earth alloy by strontium additions. Scr. Mater. 2009, 60, 116–119. [Google Scholar] [CrossRef]
- Zhao, P.; Wang, Q.; Zhai, C.; Zhu, Y. Effects of strontium and titanium on the microstructure, tensile properties and creep behavior of AM50 alloys. Mater. Sci. Eng. 2007, 444, 318–326. [Google Scholar] [CrossRef]
- Mahmudi, R.; Moeendarbari, S. Effects of Sn additions on the microstructure and impression creep behaviour of AZ91magnesium alloy. Mater. Sci. Eng. 2013, 566, 30–39. [Google Scholar] [CrossRef]
- Huang, Y.; Dieringa, H.; Kainer, K.U.; Hort, N. Understanding effects of microstructural inhomogeneity on creep response—New approaches to improve the creep resistance in magnesium alloys. J. Magnes. Alloys 2014, 2, 124–132. [Google Scholar] [CrossRef]
- Dieringa, H.; Huang, Y.; Wittke, P.; Klein, M.; Walther, F.; Dikovits, M.; Poletti, C. Compression creep response of magnesium alloy DieMag422 containing barium compared with the commercial creep-resistant alloys AE42 and MRI230D. Mater. Sci. Eng. 2013, 585, 430–438. [Google Scholar] [CrossRef]
- Trojanova, Z.; Szaraz, Z.; Labar, J.; Lukac, P. Deformation behaviour of an AS21 alloy reinforced by short Saffil fibres and SiC particles. J. Mater. Proc. Technol. 2005, 162–163, 131–138. [Google Scholar] [CrossRef]
- Zhang, X.; Fang, L.; Xiong, B.; Hu, H. Microstructure and Tensile Properties of Mg (AM60)/Al2O3 Metal Matrix Composites with Varying Volume Fractions of Fiber Reinforcement. J. Mater. Eng. Perform. 2015, 24, 4601–4611. [Google Scholar] [CrossRef]
- Mondal, A.K.; Kumar, S. Dry sliding wear behaviour of magnesium alloy based hybrid composites in the longitudinal direction. Wear 2009, 267, 458–466. [Google Scholar] [CrossRef]
- Sklenicka, V.; Pahutova, M.; Kucharova, K.; Svoboda, M.; Langdon, T.G. Creep Processes in Magnesium Alloys and their Composites. Metall. Mater. Trans. 2002, 33, 883–889. [Google Scholar] [CrossRef]
- Sklenicka, V.; Svoboda, M.; Pahutova, M.; Kucharova, K.; Langdon, T.G. Microstructural processes in creep of an AZ 91 magnesium-based composite and its matrix alloy. Mater. Sci. Eng. 2001, 319–321, 741–745. [Google Scholar] [CrossRef]
- Viswanath, A.; Dieringa, H.; Ajith Kumar, K.K.; Pillai, U.T.S.; Pai, B.C. Investigation on mechanical properties and creep behavior of stir cast AZ91-SiCp composites. J. Magnes. Alloys 2015, 3, 16–22. [Google Scholar] [CrossRef]
- Ochi, Y.; Masaki, K.; Matsumura, T.; Wadasako, M. Effects of volume fraction of alumina short fibers on high cycle fatigue properties of Al and Mg alloy composites. Mater. Sci. Eng. 2007, 468–470, 230–236. [Google Scholar] [CrossRef]
- Huang, Y.D.; Hort, N.; Dieringa, H.; Maier, P.; Kainer, K.U. Investigations on thermal fatigue of aluminum- and magnesium-alloy based composites. Int. J. Fatigue 2006, 28, 1399–1405. [Google Scholar] [CrossRef]
- Fu, H.M.; Zhang, M.-X.; Qiu, D.; Kelly, P.M.; Taylor, J.A. Grain refinement by AlN particles in Mg-Al based alloys. J. Alloys Compd. 2009, 478, 809–812. [Google Scholar] [CrossRef]
- Kim, C.-S.; Sohn, I.; Nezafati, M.; Ferguson, J.B.; Schultz, B.F.; Bajestani-Gohari, Z.; Rohatgi, P.K.; Cho, K. Prediction models for the yield strength of particle-reinforced unimodal pure magnesium (Mg) metal matrix nanocomposites (MMNCs). J. Mater. Sci. 2013, 48, 4191–4204. [Google Scholar] [CrossRef]
- Paramsothy, M.; Gupta, M. The opposing nanoscale and macroscale effects of selected nanoparticle addition to AZ91/ZK60A hybrid magnesium alloy. J. Nanopart. Res. 2013, 15, 1938–1950. [Google Scholar] [CrossRef]
- Paramsothy, M.; Chan, J.; Kwok, R.; Gupta, M. Nitride nanoparticle addition to beneficially reinforce hybrid magnesium alloys. Metall. Mater. Trans. 2013, 44, 1123–1138. [Google Scholar] [CrossRef]
- Dieringa, H. Properties of magnesium alloys reinforced with nanoparticles and carbon nanotubes: A review. J. Mater. Sci. 2011, 46, 289–306. [Google Scholar] [CrossRef]
- Tan, X.; How, W.C.K.; Weng, J.C.K.; Onn, R.K.W.; Gupta, M. Development of high-performance quaternary LPSO Mg-Y-Zn-Al alloys by Disintegrated Melt Deposition technique. Mater. Des. 2015, 83, 443–450. [Google Scholar]
- Hassan, S.; Gupta, M. Development of a novel magnesium-copper based composite with improved mechanical properties. Mater. Res. Bull. 2002, 37, 377–389. [Google Scholar] [CrossRef]
- Chen, L.-Y.; Xu, J.; Choi, H.; Pozuelo, M.; Ma, X.; Bhowmick, S.; Yang, J.; Mathaudhu, S.; Li, X. Processing and properties of magnesium containing a dense uniform dispersion of nanoparticles. Nature 2015, 528, 539–543. [Google Scholar] [CrossRef] [PubMed]
- Sillekens, W.H.; Jarvis, D.J.; Vorozhtsov, A.; Bojarevics, V.; Badini, C.F.; Pavese, M.; Terzi, S.; Salvo, L.; Katsarou, L.; Dieringa, H. The ExoMet Project: EU/ESA Research on High-Performance Light-Metal Alloys and Nanocomposites. Metall. Mater. Trans. 2014, 45, 3349–3361. [Google Scholar] [CrossRef]
- Katsarou, L.; Mounib, M.; Lefebvre, W.; Vorozhtsov, S.; Pavese, M.; Badini, C.; Molina-Aldareguia, J.M.; Cepeda Jimenez, C.; Pérez Prado, M.T.; Dieringa, H. Microstructure, mechanical properties and creep of magnesium alloy Elektron21 reinforced with AlN nanoparticles by ultrasound-assisted stirring. Mater. Sci. Eng. 2016, 659, 84–92. [Google Scholar] [CrossRef]
- Lerner, M.; Vorozhtsov, A.; Guseinov, S.; Storozhenko, P. Metal Nanopowders Production. In Metal Nanopowders: Production, Characterization, and Energetic Applications; Gromov, A.A., Teipel, U., Eds.; Wiley-VCH: Hoboken, NJ, USA, 2014; pp. 79–106. ISBN 9783527680726. [Google Scholar]
- Pearson’s—Crystal Structure Database for Inorganic Compounds (on CD-ROM); Villars, P.; Cenzual, K. (Eds.) Release 2015/16.
- Somekawa, H.; Mukai, T. Effect of grain refinement on fracture toughness in extruded pure magnesium. Scr. Mater. 2005, 53, 1059–1064. [Google Scholar] [CrossRef]
- Kang, S.H.; Lee, Y.S.; Lee, J.H. Effect of grain refinement of magnesium alloy AZ31 by severe plastic deformation on material characteristics. J. Mater. Proc. Technol. 2008, 201, 436–440. [Google Scholar] [CrossRef]
- Mukai, T.; Yamanoi, M.; Watanabe, H.; Ishikawa, K.; Higashi, K. Effect of grain refinement on tensile ductility in ZK60 magnesium allyo under dynamic loading. Mater. Trans. 2001, 42, 1177–1181. [Google Scholar] [CrossRef]
- StJohn, D.H.; Prasad, A.; Easton, M.A.; Qian, M. The contribution of constitutional supercooling to nucleation and grain formation. Metall. Mater. Trans. 2015, 46, 4868–4885. [Google Scholar] [CrossRef]
- Greer, A.L.; Bunn, A.M.; Tronche, A.; Evans, P.V.; Bristow, D.J. Modelling of inoculation of metallic melts: Application to grain refinement of aluminium by AlTiB. Acta Mater. 2000, 48, 2823–2835. [Google Scholar] [CrossRef]
- StJohn, D.H.; Qian, M.; Easton, M.A.; Cao, P. The Interdependence Theory: The relationship between grain formation and grain selection. Acta Mater. 2011, 59, 4907–4921. [Google Scholar] [CrossRef]
- Poirier, D.R. Density, viscosity, and diffusion coefficients in hypoeutectic Al-Si liquid alloys: An assessment of available data. Metall. Mater. Trans. 2014, 45, 1345–1354. [Google Scholar] [CrossRef]
- Goh, C.S.; Wei, J.; Lee, L.C.; Gupta, M. Properties and deformation behaviour of Mg-Y2O3 nanocomposites. Acta Mater. 2007, 55, 5115–5121. [Google Scholar] [CrossRef]
- Dai, L.H.; Ling, Z.; Bai, Y.L. Size-dependent inelastic behavior of particle-reinforced metal-matrix composites. Compos. Sci. Technol. 2001, 61, 1057–1063. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, D.L. Consideration of Orowan strengthening effect in particulate-reinforced metal matrix nanocomposites: A model for predicting their yield strength. Scr. Mater. 2006, 54, 1321–1326. [Google Scholar] [CrossRef]
- Vogt, R.; Zhang, Z.; Li, Y.; Bonds, M.; Browning, N.D.; Lavernia, E.J.; Schoenung, J.M. The absence of thermal expansion mismatch strengthening in nanostructured metal-matrix composites. Scr. Mater. 2009, 61, 1052–1055. [Google Scholar] [CrossRef]
- Redsten, A.M.; Klier, E.M.; Brown, A.M.; Dunand, D.C. Mechanical properties and microstructure of cast oxide-dispersion-strengthened aluminium. Mater. Sci. Eng. 1995, 201, 88–102. [Google Scholar] [CrossRef]
- Dunand, D.C.; Mortensen, A. On plastic relaxation of thermal stresses in reinforced metals. Acta Metall. Mater. 1991, 39, 127–139. [Google Scholar] [CrossRef]
- Hall, E.O. The deformation and Ageing of mild steel: III Discussion of Results. Phys. Soc. 1951, 64, 747–753. [Google Scholar] [CrossRef]
- Petch, N.J. The Cleavage Strength of Polycrystals. J. Iron Steel Inst. 1953, 174, 25–28. [Google Scholar]
| Property | AM60 | AM60 + AlN | 1st Recycling | 2nd Recycling | 3rd Recycling |
|---|---|---|---|---|---|
| Grain size (µm) | 1277.0 ± 301.3 | 84.9 ± 6.2 | 113.8 ± 22.1 | 176.8 ± 12.9 | 196.4 ± 16.0 |
| Hardness (HV5) | 48.0 ± 4.0 | 46.4 ± 6.0 | 50.9 ± 1.1 | 47.8 ± 1.0 | 48.5 ± 2.6 |
| Density (g/cm3) | 1.7848 ± 0.0004 | 1.783 ± 0 | 1.7842 ± 0.00075 | 1.7852 ± 0.0004 | 1.785 ± 0 |
| Porosity (%) | - | 0.919 | 0.853 | 0.797 | 0.808 |
| Yield strength (MPa) | 44.9 ± 6.9 | 91.2 ± 3.8 Δ = 46.3 | 73.7 ± 8.1 Δ = 28.8 | 70.9 ± 4.3 Δ = 26.0 | 69.9 ± 5.0 Δ = 25.0 |
| UTS (MPa) | 109.3 ± 19.2 | 235.1 ± 6.4 | 220.3 ± 16.8 | 210.0 ± 11.0 | 194.3 ± 12.3 |
| Elongation (%) | 6.4 ± 3.4 | 15.4 ± 4.2 | 15.4 ± 4.5 | 11.7 ± 2.7 | 10.1 ± 1.8 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dieringa, H.; Katsarou, L.; Buzolin, R.; Szakács, G.; Horstmann, M.; Wolff, M.; Mendis, C.; Vorozhtsov, S.; StJohn, D. Ultrasound Assisted Casting of an AM60 Based Metal Matrix Nanocomposite, Its Properties, and Recyclability. Metals 2017, 7, 388. https://doi.org/10.3390/met7100388
Dieringa H, Katsarou L, Buzolin R, Szakács G, Horstmann M, Wolff M, Mendis C, Vorozhtsov S, StJohn D. Ultrasound Assisted Casting of an AM60 Based Metal Matrix Nanocomposite, Its Properties, and Recyclability. Metals. 2017; 7(10):388. https://doi.org/10.3390/met7100388
Chicago/Turabian StyleDieringa, Hajo, Lydia Katsarou, Ricardo Buzolin, Gábor Szakács, Manfred Horstmann, Martin Wolff, Chamini Mendis, Sergey Vorozhtsov, and David StJohn. 2017. "Ultrasound Assisted Casting of an AM60 Based Metal Matrix Nanocomposite, Its Properties, and Recyclability" Metals 7, no. 10: 388. https://doi.org/10.3390/met7100388







