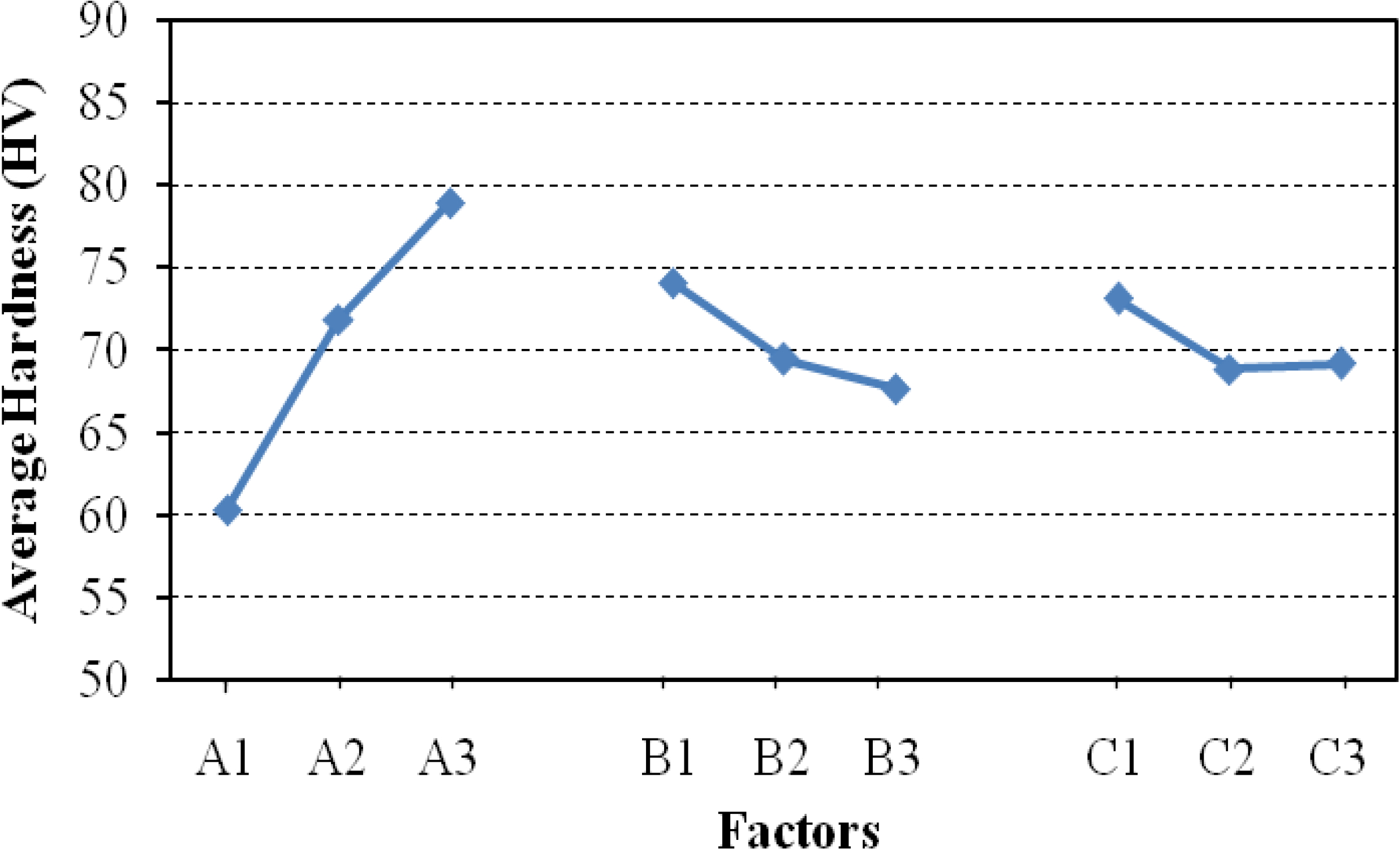
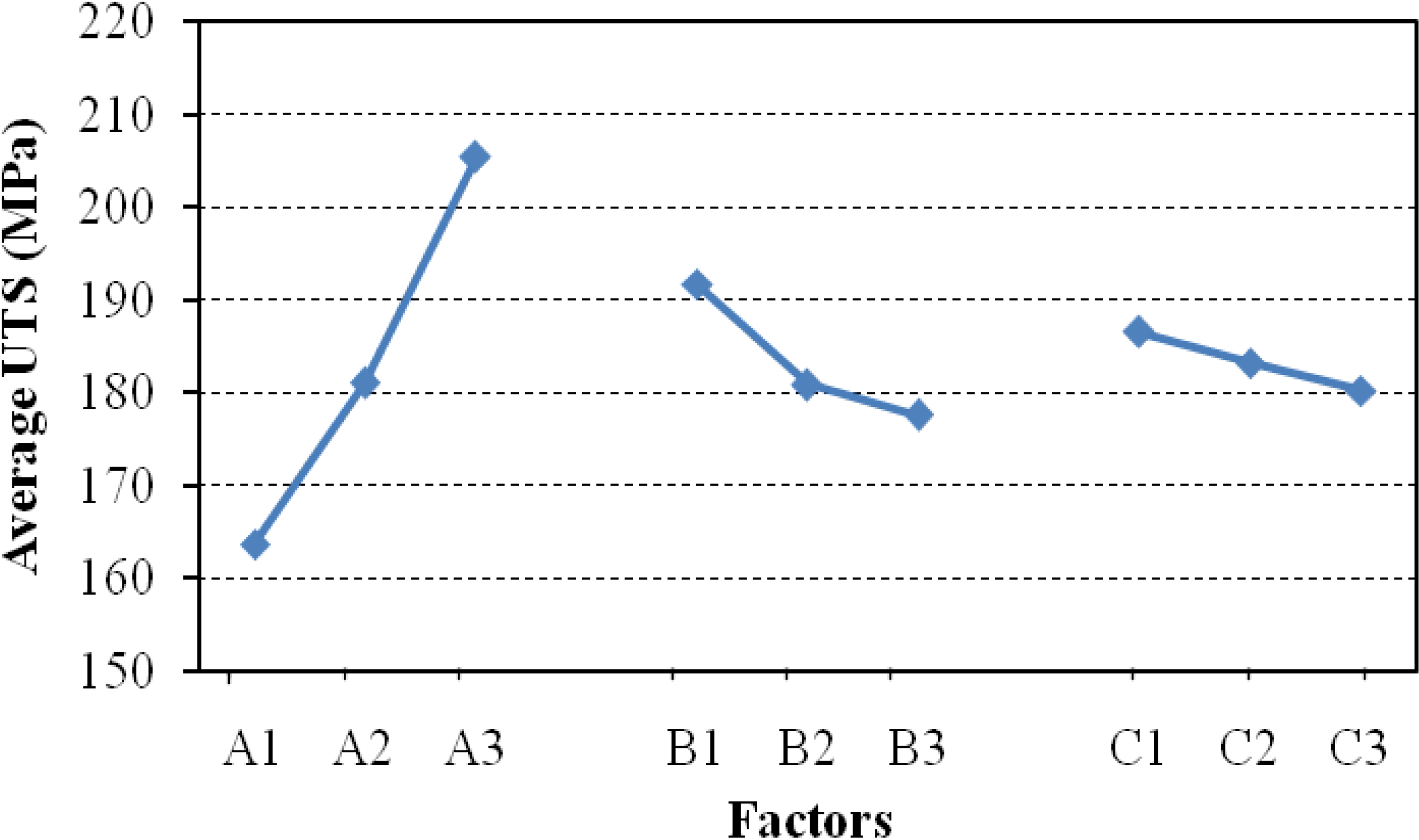
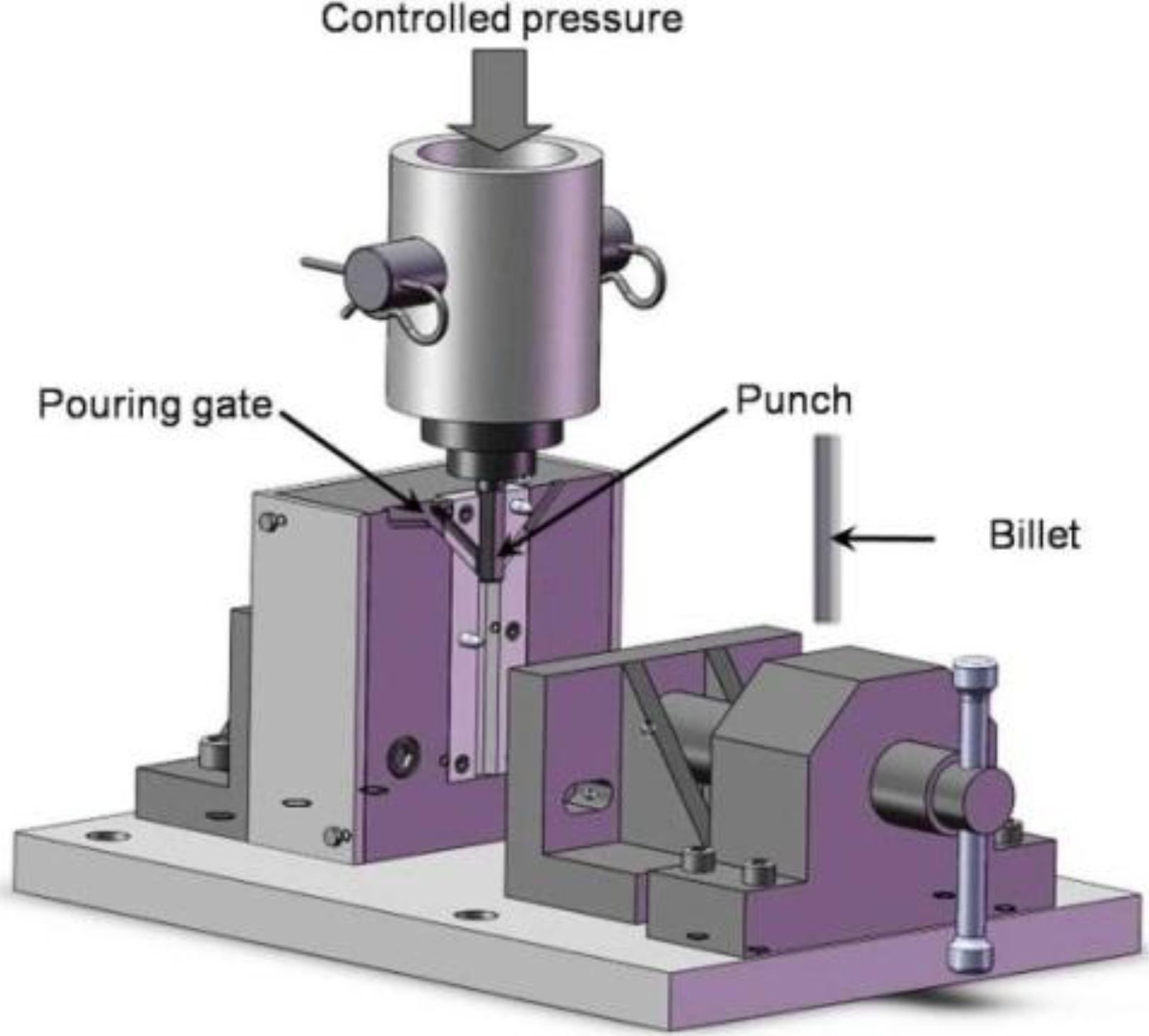
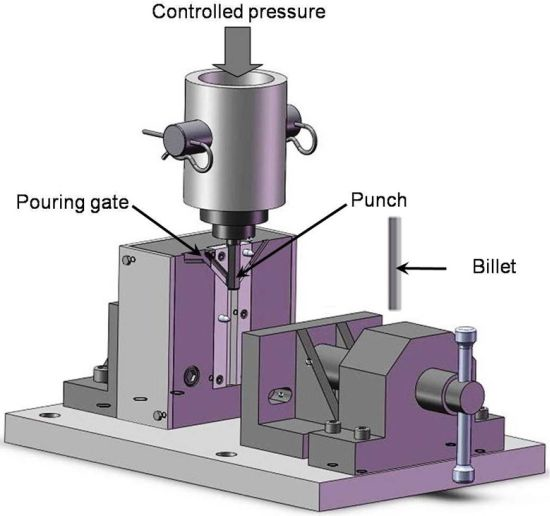
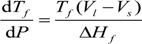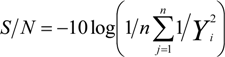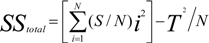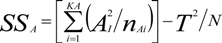The squeeze casting process parameters namely squeeze pressure (A), melt temperature (B) and die temperature (C) at three levels are listed in
Table 1. To ensure the accuracy of the results, three samples were fabricated for each of the parameter combinations. The averages were computed for ultimate tensile strength (UTS) and hardness in each of the nine experimental conditions. In the latter, main effect, variance analysis (ANOVA) and signal-to-noise (S/N) ratio are analyzed to find ranking and optimum levels of the process parameters.
2.2. Analysis of Variance (ANOVA)
The analysis of variance (ANOVA) was used to investigate which parameters significantly affected the quality characteristic and to determine the percentage contribution of the parameters at 95% confidence level. The F ratio value named Fisher test was used to see which process parameters have a significant effect. Usually, when the F-values of experimental trials are higher than 5.32 (from the F table), it means that the change in the process parameter has significant effect on the quality characteristic. In addition, the percentage contribution expresses the importance of the process parameters for the response.
ANOVA analysis for UTS and hardness was carried out using Equations (2)–(6) and the resulting data is given in
Table 4 and
Table 5, respectively. The significance and importance of the parameters were determined by the
F-value and percentage contribution, respectively. The
F-value in
Table 4 and
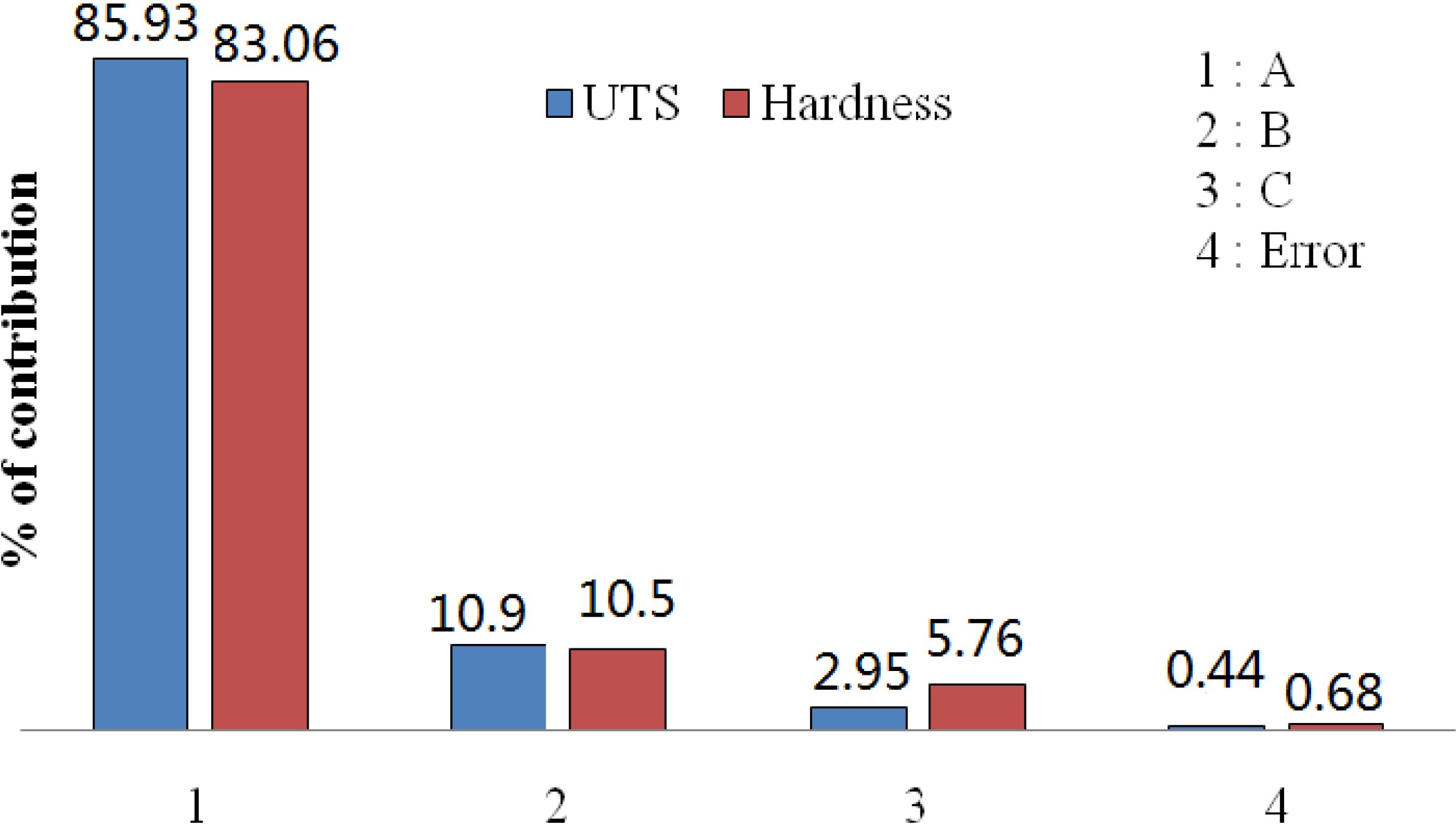
Table 5 shows that the considered process parameters are highly significant factors affecting the mechanical properties of 2017A Al alloy in the order of squeeze pressure (parameter A), melt temperature (parameter B) and die temperature (parameter C). However, squeeze pressure has the most significant effect on UTS and hardness as shown by much higher
F-value (
i.e., 197.74 and 122.33) and also percent contribution (
i.e., 85.93 and 83.06). The percentage contribution of significant factors on the quality characteristic is shown in
Figure 3.
Table 4.
Variance (ANOVA) Table for ultimate tensile strength (UTS).
| Source | Degrees of freedom (DOF) | Sum of squares (SS) | Variance (V) | F ratio | Percent contribution (P) |
|---|
| A | 2 | 5.9391 | 2.9695 | 197.74 | 85.93 |
| B | 2 | 0.7591 | 0.3795 | 25.28 | 10.98 |
| C | 2 | 0.1831 | 0.0915 | 6.10 | 2.65 |
| Error | 2 | 0.0300 | 0.0150 | | 0.44 |
| Total | 8 | 6.9114 | | | 100.00 |
Table 5.
Variance (ANOVA) Table for hardness.
| Source | Degrees of freedom (DOF) | Sum of squares (SS) | Variance (V) | F ratio | Percent contribution (P) |
|---|
| A | 2 | 8.4730 | 4.2364 | 122.33 | 83.06 |
| B | 2 | 1.0712 | 0.5356 | 15.47 | 10.50 |
| C | 2 | 0.5875 | 0.2937 | 8.48 | 5.76 |
| Error | 2 | 0.0693 | 0.0346 | | 0.68 |
| Total | 8 | 10.2009 | | | 100.00 |
Figure 3.
Percentage contribution of significant control factors.
2.3. Signal to Noise Ratio (S/N)
The next analysis was investigated by using analysis of signal-to-noise ratio (S/N). According to the data presented in
Table 1 and Equation (6), the average response and S/N ratio of UTS and hardness for the nine experiments were calculated on the basis of the following procedure. Typically, the average effect for level 1 of the squeeze pressure is computed using data from experiments 1–3 of
Table 6. Similarly, the average effects for levels 2 and 3 of squeeze pressure were computed using data from experiments 4–6 and 7–9, respectively. The level 3 for squeeze pressure (90 MPa, see No.7–9) has the highest S/N ratio value, which indicates that the casting performance at such level produces the minimum variation of the UTS and hardness due to uncontrollable factors. However, a maximum of S/N ratio corresponds to better quality characteristics [
23]. It can also be seen from
Table 6 that experiment number 7 possesses the largest S/N ratio when squeeze pressure at 90 MPa, melt temperature at 700 °C and die temperature at 300 °C; therefore, the combination of parameters and their levels is A3 B1 C3 as shown in
Table 3.
Table 6.
Computation of S/N ratio for ultimate tensile strength (UTS) and hardness.
| No | Average UTS | Average hardness | S/N ratio of UTS | S/N ratio of hardness |
|---|
| 1 | 174.667 | 66.000 | 44.839 | 36.377 |
| 2 | 162.667 | 59.000 | 44.220 | 35.394 |
| 3 | 153.667 | 56.000 | 43.727 | 34.952 |
| 4 | 188.333 | 73.666 | 45.473 | 37.246 |
| 5 | 175.000 | 69.000 | 44.858 | 36.739 |
| 6 | 180.000 | 73.000 | 45.098 | 37.180 |
| 7 | 212.333 | 82.666 | 46.537 | 38.334 |
| 8 | 205.000 | 80.333 | 46.232 | 38.081 |
| 9 | 199.000 | 74.000 | 45.974 | 37.359 |
| Mean | Y1=183.407 | Y2=70.407 | | |
The combination shown above differs from the previously mentioned one in main effects. It sheds light on the optimum combination of parameters and their levels. However, it shows that, in the present case study, the combination of parameters and their levels A3 B1 C3 yield optimum mechanical properties with minimum variance from the target value.
2.4. Estimation of Predicted Mean and Confirmation Test
The purpose of estimation of predicted means is to validate the squeeze casting condition at the optimal levels of parameters, which is A3 B1 C1 for mechanical properties. The predicted mean (μ) for UTS and hardness was estimated using the following two equations [
24]:
where, A3 is the average UTS and hardness at third level of squeeze pressure (
Table 2), B1 is the average UTS and hardness at first level of melt temperature (
Table 2), C1 is the average UTS and hardness at first level of die temperature (
Table 2),
Y1 and
Y2 are the means of UTS and hardness (
Table 6). Substituting the values of various terms in Equations (1) and (2), then
Three confirmation tests are conducted at the optimum settings of squeeze casting parameters recommended by the investigation. The average values of UTS and hardness obtained at the optimum settings of the process parameters are 219.333 MPa and 86.666 HV, respectively. We notice that the difference between the estimated results and the experimental results is negligible. Therefore, the experimental values are within the confidence interval of the predicted optimal of mechanical properties.
2.5.Effect of the Squeeze Pressure on Microstructure and Mechanical Properties
The influence of squeeze pressure (the most significant factor) on the microstructure and the mechanical properties has been analyzed on the basis of the statistical analysis developed in
Section 2.1 (at pouring and die temperatures of 700 °C and 200 °C, respectively).
Figure 4a–d illustrates the microstructure of the 2017 A Al alloy squeeze cast under various pressure levels.
Figure 4.
Optical micrographs of the squeeze cast sample (a) 15 MPa; (b) 30 MPa; (c) 60 MPa; and (d) 90 MPa applied pressure.
These micrographs show that the microstructures prepared under higher applied pressures are much finer and smaller α-primary dendrites. It is clear that the squeezing pressure has significant influence on the microstructure of the alloy [
7]. Furthermore, the inter-metallic phases in the alloy with no applied pressure are coarser than those under high squeezing pressure. This effect is a result of the change in phase diagram according to the Clausius-Clapeyron Equation [
6]:
where
Tf is the equilibrium freezing temperature,
P is the applied pressure,
Vl and
Vs are the specific volumes of the liquid and solid, respectively, and Δ
Hf is the latent heat of fusion. During the solidification process, both Δ
Hf and
(Vl − Vs) are normally negative due to the heat release and shrinkage of metals, respectively. Thus, d
Tf/d
P is positive, which indicates that the applied pressure will increase the melting point of a metal having a volume decrease tendency during solidification. Increasing the freezing point causes undercooling in the alloy that is already superheated. However, such change in freezing temperature with the increasing pressure is expected due to the reduction in interatomic distance and thus the restriction of atomic movement [
6]. The higher freezing point brings about the larger undercooling in the initially superheated alloy and thus elevates the nucleation frequency, resulting in a more fine-grained structure. Apart from the changes in undercooling of the molten alloy caused by applied pressure, greater cooling rates for the solidifying alloy can be realized due to reduction in the air gap between the alloy and the die wall and thus larger effective contact area. Obviously, the increase of cooling rate and heat-transfer coefficient will result in the refinement of the grain size of squeeze casting alloy.
The mechanical properties of squeeze cast specimens such as ultimate tensile strength (UTS) and hardness (HV) are compiled in
Figure 5. It shows that an increase in squeeze pressure from 15–90 MPa enhances the UTS with 46% increment from 150 MPa (15 MPa) to 219.66 MPa (90 MPa). Also, there is a 58% increase in hardness over the 15 MPa squeeze pressure.
Evidently the improvement of mechanical properties by increasing the pressure up to 90 MPa seems to be attributed, in part, to the refinement of the α-primary dendrites and, in part, to material densification.
Figure 5.
Ultimate tensile strength (UTS) and hardness of 2017 A Al alloy manufactured in various conditions.