Transformation Volume Effects on Shape Memory Alloys
Abstract
:1. Introduction
2. Quantitative Theory of Thermoelastic Behavior of SMAs
2.1. Symmetry Conforming Approach to the Problem
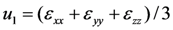
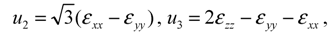
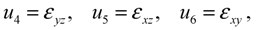
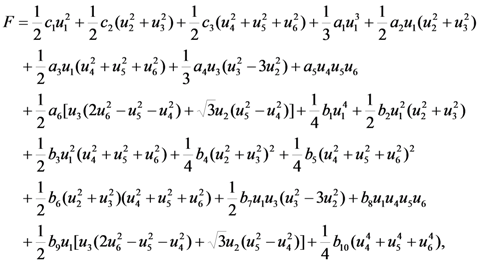
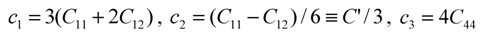
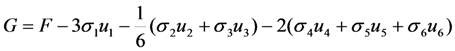
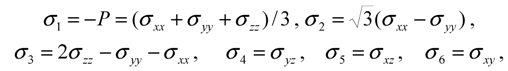
 type (n = 1,2,3) the cubic-tetragonal MT is not possible, because the extremum conditions for the Gibbs potential show that in the course of phase transformation characterized by the two-component order parameter u2,3 the concomitant nondiagonal strains
type (n = 1,2,3) the cubic-tetragonal MT is not possible, because the extremum conditions for the Gibbs potential show that in the course of phase transformation characterized by the two-component order parameter u2,3 the concomitant nondiagonal strains  must appear. The appearance of these strains leads to the appropriate lowering of tetragonal symmetry of the product phase. In presence of the energy terms of
must appear. The appearance of these strains leads to the appropriate lowering of tetragonal symmetry of the product phase. In presence of the energy terms of  type the phase transformation characterized by the three-component order parameter is accompanied by the appearance of the concomitant strains
type the phase transformation characterized by the three-component order parameter is accompanied by the appearance of the concomitant strains  and the appropriate lowering of rhombohedral symmetry of the product phase.
and the appropriate lowering of rhombohedral symmetry of the product phase. type. As so, the cubic-tetragonal phase transition is characterized by the appearance of the concomitant component
type. As so, the cubic-tetragonal phase transition is characterized by the appearance of the concomitant component  , while the concomitant component
, while the concomitant component  arises in the course of the cubic-rhombohedral phase transition. The role of concomitant components is especially important for the purview of this article, because the value of 3u1 is the trace of strain tensor, and therefore, it is related to the volume change of the alloy as
arises in the course of the cubic-rhombohedral phase transition. The role of concomitant components is especially important for the purview of this article, because the value of 3u1 is the trace of strain tensor, and therefore, it is related to the volume change of the alloy as
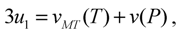
2.2. Cubic-Tetragonal MT
 and therefore, the energy terms
and therefore, the energy terms  ,
,  and
and  can be considered small as compared with
can be considered small as compared with  and
and  . In that case the equation for the Gibbs potential takes the following form
. In that case the equation for the Gibbs potential takes the following form
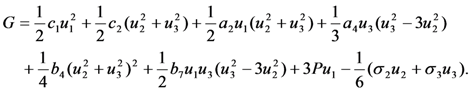
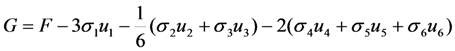
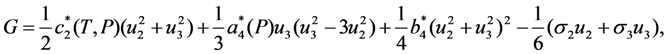
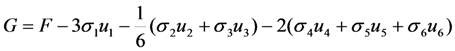
 result in the equations describing the dependencies of the order parameter components on the temperature and pressure. A zero solution of these equations corresponds to the high-temperature (cubic) phase. The nonzero solutions correspond to three equivalent variants of tetragonal lattice, which are usually referred to as the x- y- and z-variants of martensitic phase. The principal axis (c-axis) of x-variant is parallel to the crystallographic direction [100] of cubic phase, the principal axes of y- and z-variants are aligned with [010] and [001] directions, respectively (for more details see [39,40]).
result in the equations describing the dependencies of the order parameter components on the temperature and pressure. A zero solution of these equations corresponds to the high-temperature (cubic) phase. The nonzero solutions correspond to three equivalent variants of tetragonal lattice, which are usually referred to as the x- y- and z-variants of martensitic phase. The principal axis (c-axis) of x-variant is parallel to the crystallographic direction [100] of cubic phase, the principal axes of y- and z-variants are aligned with [010] and [001] directions, respectively (for more details see [39,40]).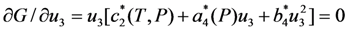
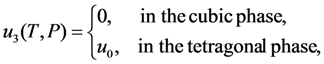
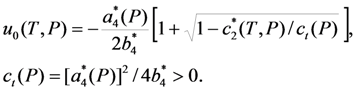
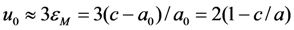
 . The solution describing the low-temperature (martensitic) phase is stable if
. The solution describing the low-temperature (martensitic) phase is stable if  . If the coefficients, Equation 12, are known, the equations
. If the coefficients, Equation 12, are known, the equations
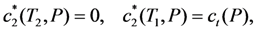
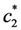 is the increasing function of temperature, so the inequality T1 > T2 is held.
is the increasing function of temperature, so the inequality T1 > T2 is held.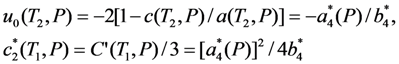
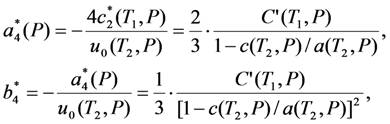
 value is independent of pressure. As so, the Equation 19 predicts that the shear modulus of cubic phase measured just before the start of MT depends on the pressure as the second power of MT strain measured just after the finish of MT. This prediction can be verified experimentally.
value is independent of pressure. As so, the Equation 19 predicts that the shear modulus of cubic phase measured just before the start of MT depends on the pressure as the second power of MT strain measured just after the finish of MT. This prediction can be verified experimentally.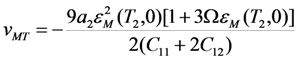
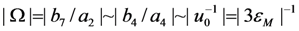 . In this case the order of magnitude of the energy coefficient a2 can be determined from the approximate relationship
. In this case the order of magnitude of the energy coefficient a2 can be determined from the approximate relationship
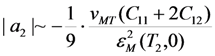
2.3. Cubic-Rhombohedral MT
 . Due to this, the energy terms
. Due to this, the energy terms  ,
,  and
and  can be considered negligibly small as compared with
can be considered negligibly small as compared with  and
and  , respectively. In this case the expression for the Gibbs potential, Equation 4, is reduced to the form
, respectively. In this case the expression for the Gibbs potential, Equation 4, is reduced to the form
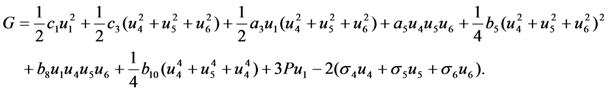
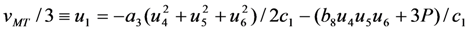
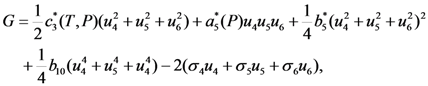
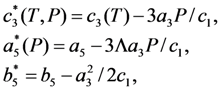
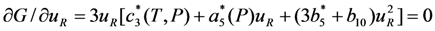
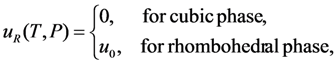
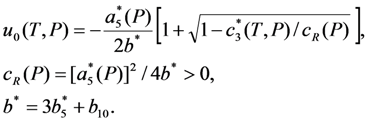
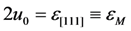
 . The solution describing the low-temperature phase is stable if
. The solution describing the low-temperature phase is stable if  . In the case when the Landau expansion coefficients are determined from the equations Equation 25, the conditions
. In the case when the Landau expansion coefficients are determined from the equations Equation 25, the conditions
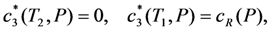
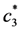 is the increasing function of temperature and the inequality T1 > T2 holds.
is the increasing function of temperature and the inequality T1 > T2 holds.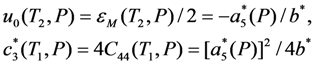
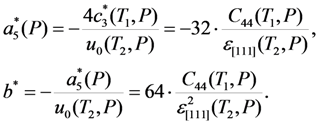
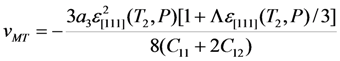
 is valid and the energy coefficient a3 can be estimated by the order of magnitude from the relationship
is valid and the energy coefficient a3 can be estimated by the order of magnitude from the relationship
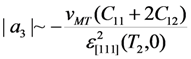
2.4. Summary of Basic Points and Preview of Applications of the Theory
3. Martensite Stabilization/Destabilization under Hydrostatic Pressure
3.1. Interrelation between the Volume Change during MT and Pressure Effects
- a)
- b)
- an increase/decrease of the soft elastic modulus of martensite.
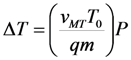
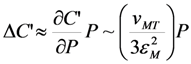
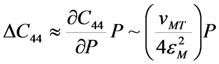
3.2. Landau Expansion Coefficients Estimated from the Shear Modulus of Ti-Ni Alloy
 , which describes the elastic response of alloy in the austenitic state to the mechanical loading in [111] crystallographic direction. In the presence of stress σ = σ[111], Equation 26 is modified as
, which describes the elastic response of alloy in the austenitic state to the mechanical loading in [111] crystallographic direction. In the presence of stress σ = σ[111], Equation 26 is modified as
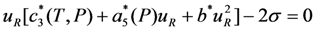
 . The substitution of the values
. The substitution of the values  and
and  into Equation 39 leads to the formula that interrelates the MT strain and the difference of shear modules characterizing the martensitic and austenitic states of an alloy:
into Equation 39 leads to the formula that interrelates the MT strain and the difference of shear modules characterizing the martensitic and austenitic states of an alloy:
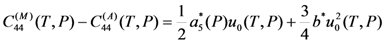
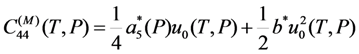
 (see Equation 31) into Equation 41, one can derive the relationships
(see Equation 31) into Equation 41, one can derive the relationships
- (i)
- a theoretical evaluation of the shear modulus from the experimental temperature dependencies of lattice parameters in the martensitic phase;
- (ii)
- a restoring of the temperature dependence of MT strain from the temperature dependence of the shear modulus.

 and b* = 2.9 × 107 GPa can be found from Equation 32 using experimental value ε[111] = 2u0(T2) ≈ −1% [48] and estimation νMT ≈ −5 × 10−4 resulting from the Clausius-Clapeyron relationship (for more details see [28]). To describe an influence of the hydrostatic pressure, a dimensionless parameter Λ that is involved in the renormalized energy coefficients, Equation 25, should be estimated to be
and b* = 2.9 × 107 GPa can be found from Equation 32 using experimental value ε[111] = 2u0(T2) ≈ −1% [48] and estimation νMT ≈ −5 × 10−4 resulting from the Clausius-Clapeyron relationship (for more details see [28]). To describe an influence of the hydrostatic pressure, a dimensionless parameter Λ that is involved in the renormalized energy coefficients, Equation 25, should be estimated to be  (see the last paragraph of Section 2.3). The estimated values enable calculation of the ratio a3/c1 and coefficients c3(T,P),
(see the last paragraph of Section 2.3). The estimated values enable calculation of the ratio a3/c1 and coefficients c3(T,P),  from Equations 33 and 25. Due to this, a quantitative description of the transformational behavior of the single-crystalline sample under the action of uniaxial mechanical loading becomes possible (the appropriate theoretical procedure is described in [49]).
from Equations 33 and 25. Due to this, a quantitative description of the transformational behavior of the single-crystalline sample under the action of uniaxial mechanical loading becomes possible (the appropriate theoretical procedure is described in [49]).3.3. The Influence of Pressure on the MT Strain and MT Temperature
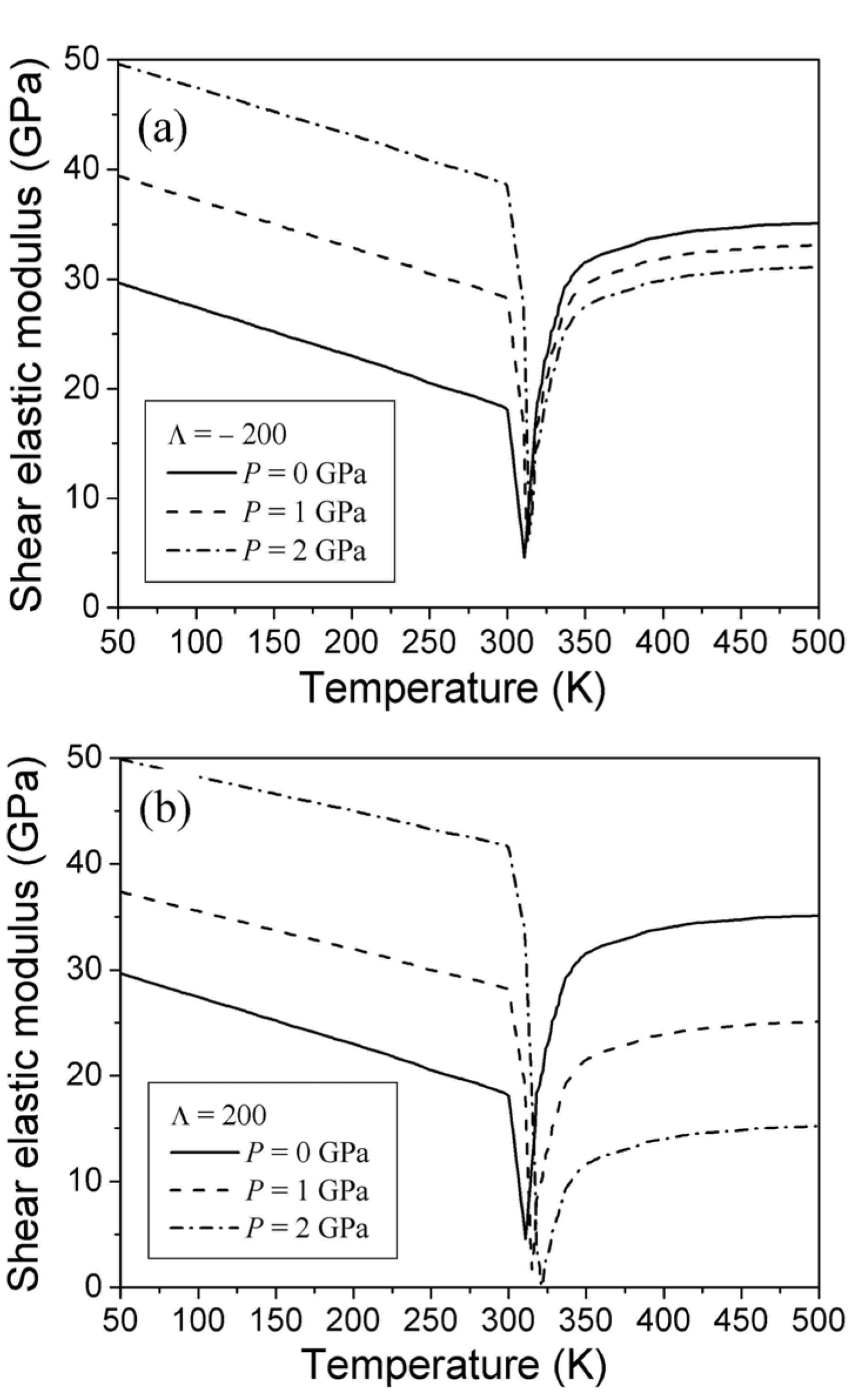
 , b*, and function C44 (T,0) are known. The energy coefficients were determined above for the Ti49.5Ni50.5 alloy. The C44 (T,0) function must coincide with experimental temperature dependence obtained for the austenitic and martensitic phases of this alloy and satisfy Equation 42. This function is shown in Figure 1 by the solid line. The figure demonstrates that experimental temperature dependence of shear modulus does not satisfy the condition of Equation 42. A disagreement between theory and experiment is obviously caused by the appearance of mixed two-phase state in the temperature range of T2 < T < T1.
, b*, and function C44 (T,0) are known. The energy coefficients were determined above for the Ti49.5Ni50.5 alloy. The C44 (T,0) function must coincide with experimental temperature dependence obtained for the austenitic and martensitic phases of this alloy and satisfy Equation 42. This function is shown in Figure 1 by the solid line. The figure demonstrates that experimental temperature dependence of shear modulus does not satisfy the condition of Equation 42. A disagreement between theory and experiment is obviously caused by the appearance of mixed two-phase state in the temperature range of T2 < T < T1.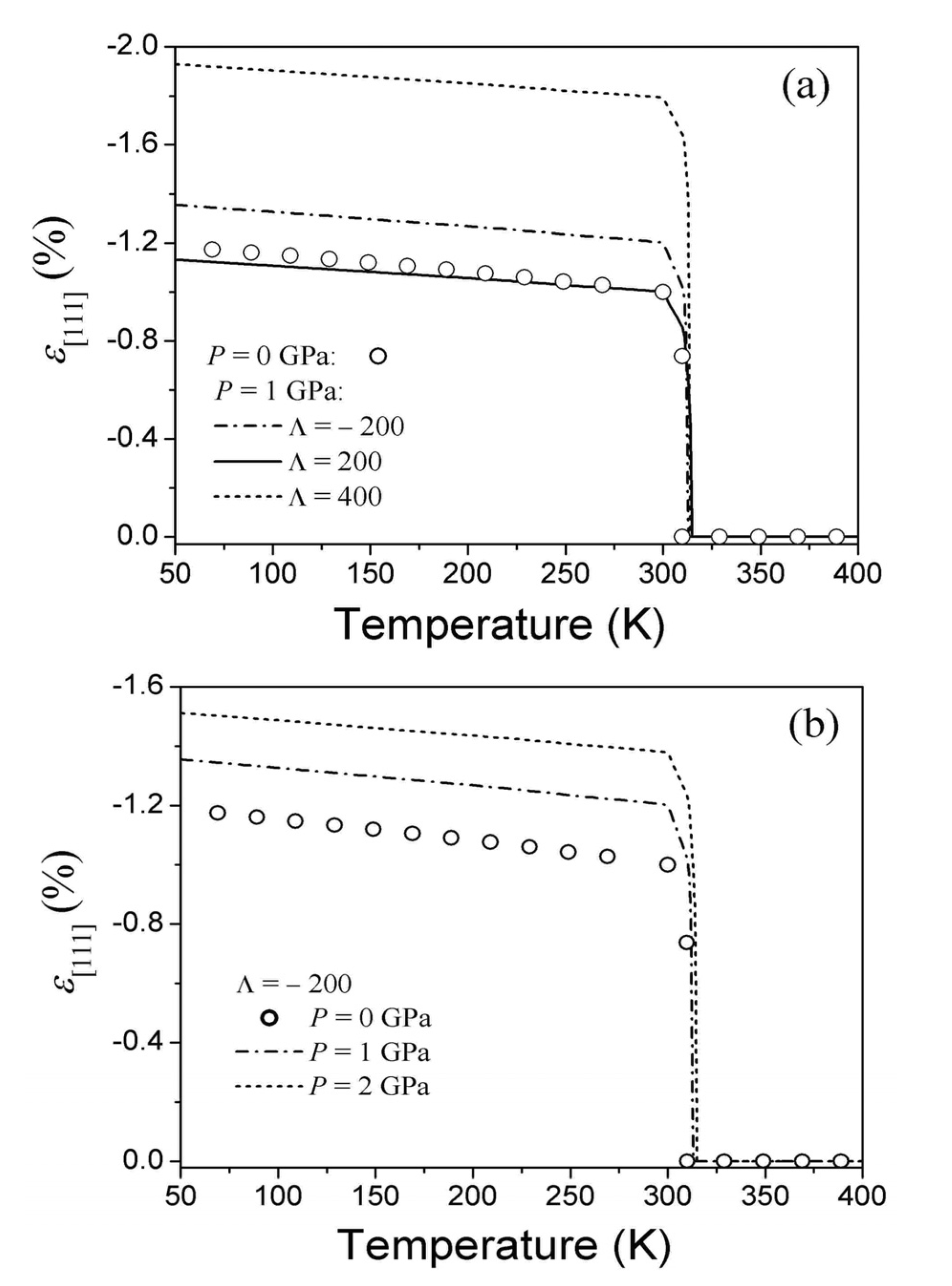

3.4. The Influence of Pressure on the Shear Elastic Modulus
4. Stabilization of Martensitic Phase by Its Aging
4.1. Isotropic Mechanism of Martensite Stabilization
- (i)
- (ii)
- a gradual change of the lattice parameters during martensite aging [54];
- (iii)
 corresponds to the symmetry of crystal lattice in this phase. Secondly, the theory takes into account that the tendency of the crystal with defects to the ground state is accompanied by a volume change.
corresponds to the symmetry of crystal lattice in this phase. Secondly, the theory takes into account that the tendency of the crystal with defects to the ground state is accompanied by a volume change. describes an influence of defects on the crystal lattice, and therefore, depends on time t due to a slow reconfiguration of the defect subsystem during martensite aging. This tensor can be subdivided into the isotropic and axial parts as
describes an influence of defects on the crystal lattice, and therefore, depends on time t due to a slow reconfiguration of the defect subsystem during martensite aging. This tensor can be subdivided into the isotropic and axial parts as
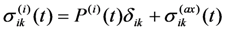
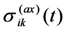 , the trace of this tensor is equal to zero.
, the trace of this tensor is equal to zero. . It means that the larger is a ratio of the volume change during MT to the MT strain (other parameters being equal), the more pronounced are aging effects.
. It means that the larger is a ratio of the volume change during MT to the MT strain (other parameters being equal), the more pronounced are aging effects. 4.2. Martensite Stabilization in Au-Cd Alloys
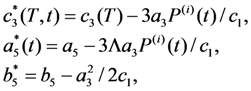
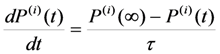
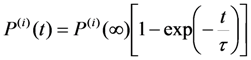
 can be chosen (see below). With known shear modulus, the transformation strain and volume change enable us to evaluate the coefficients a3/c1, a5(0) = 1.6 × 105 GPa and b*(0) = 4 × 107 GPa from Equations 31–34. The Clausius–Clapeyron relationship with the values q ≈ 1 J g−1 and m≈ 14 g cm−3 [28] results in the characteristic temperature value of T1 = 306.8 K.
can be chosen (see below). With known shear modulus, the transformation strain and volume change enable us to evaluate the coefficients a3/c1, a5(0) = 1.6 × 105 GPa and b*(0) = 4 × 107 GPa from Equations 31–34. The Clausius–Clapeyron relationship with the values q ≈ 1 J g−1 and m≈ 14 g cm−3 [28] results in the characteristic temperature value of T1 = 306.8 K.  coefficient whose temperature dependence leads to the phase transformation. As a consequence, the characteristic MT temperatures determined from the Equation 30 prove to be time-dependent.
coefficient whose temperature dependence leads to the phase transformation. As a consequence, the characteristic MT temperatures determined from the Equation 30 prove to be time-dependent. and
and  . The value
. The value  is the temperature range for the two-phase region, that represents a mixture of austenitic-martensitic structures. These temperature differences were computed using the aforementioned set of physical values and Equations 46 and 47. The relaxation time of τ = 50 min and the saturation value of internal pressure P(i)(∞) = 3.8 GPa were determined by fitting ΔAF(t) theoretical curve to the experimental values reported in [57]. The results of computations are shown in Figure 5 together with the austenite finish temperature changes experimentally observed in [57].
is the temperature range for the two-phase region, that represents a mixture of austenitic-martensitic structures. These temperature differences were computed using the aforementioned set of physical values and Equations 46 and 47. The relaxation time of τ = 50 min and the saturation value of internal pressure P(i)(∞) = 3.8 GPa were determined by fitting ΔAF(t) theoretical curve to the experimental values reported in [57]. The results of computations are shown in Figure 5 together with the austenite finish temperature changes experimentally observed in [57].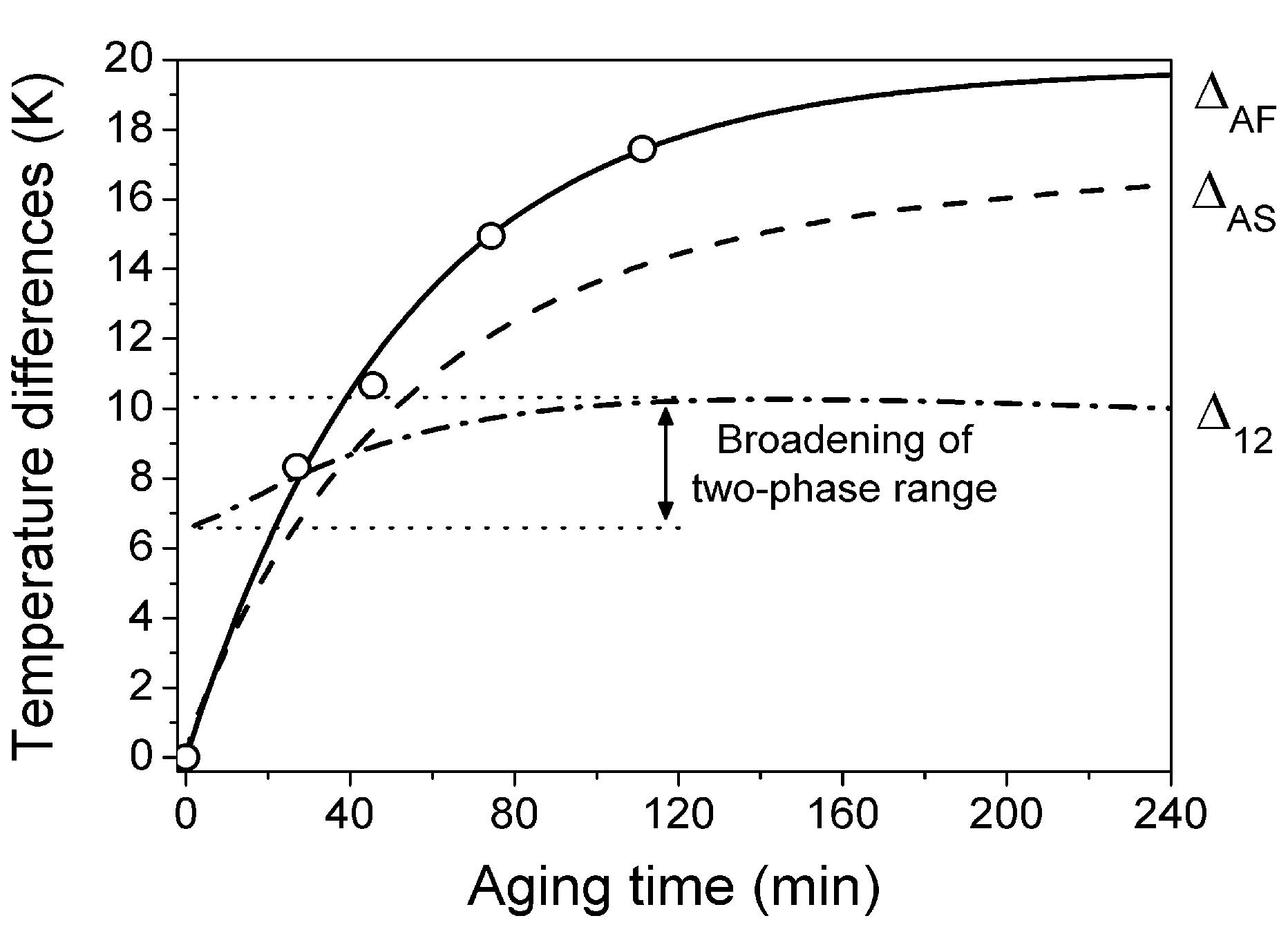
 . The negative value of Λ was used for obtaining results presented in Figure 5. The negative value was chosen because in this case the theory shows that the martensite aging causes broadening of the two-phase temperature range of the reverse MT (see two-side arrow in Figure 5). This feature of the transformational behavior of aged alloys is indirectly confirmed by the experiments in [67,68,69,70].
. The negative value of Λ was used for obtaining results presented in Figure 5. The negative value was chosen because in this case the theory shows that the martensite aging causes broadening of the two-phase temperature range of the reverse MT (see two-side arrow in Figure 5). This feature of the transformational behavior of aged alloys is indirectly confirmed by the experiments in [67,68,69,70]. , which prescribes that MT must be the first-order phase transition. According to Equation 45 and argumentation presented in Section 2.4, we have:
, which prescribes that MT must be the first-order phase transition. According to Equation 45 and argumentation presented in Section 2.4, we have:
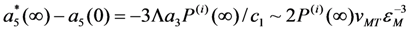
 . This estimation shows that the jumps of physical values observed in the course of MT would be enlarged by factor of 1.4 if the stabilizing pressure of the order of 4 GPa should appear.
. This estimation shows that the jumps of physical values observed in the course of MT would be enlarged by factor of 1.4 if the stabilizing pressure of the order of 4 GPa should appear.- (i)
- The time evolution of the crystal defects subsystem leads to a gradual volume change of the SMA aged in the martensitic state.
- (ii)
- According to the general principles of thermodynamics, the time-dependent internal pressure can be defined as the thermodynamic value, which is conjugated to the volume change.
- (iii)
- The internal pressure contributes to the martensite stabilization effect but does not change the symmetry of the crystal lattice; therefore, the gradual volume change of the alloy, held in the martensitic phase, provides the isotropic mechanism of martensite stabilization, which is extrinsic to the commonly known SC-SRO principle formulated in [44,53].
- (iv)
5. Destabilization of Martensitic Phase by Thermomechanical Cycling
5.1. Introductory Statement
5.2. Experiment
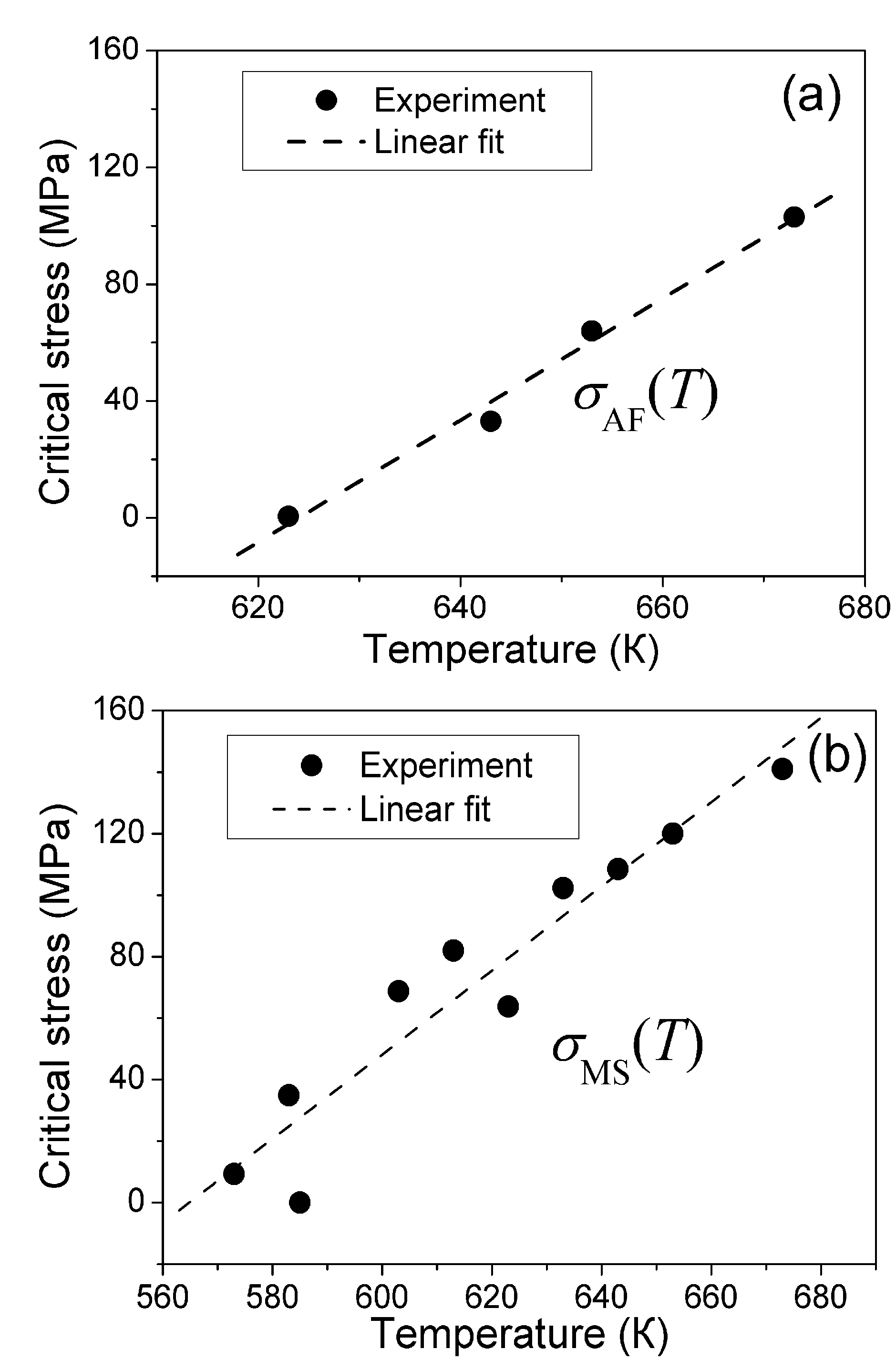
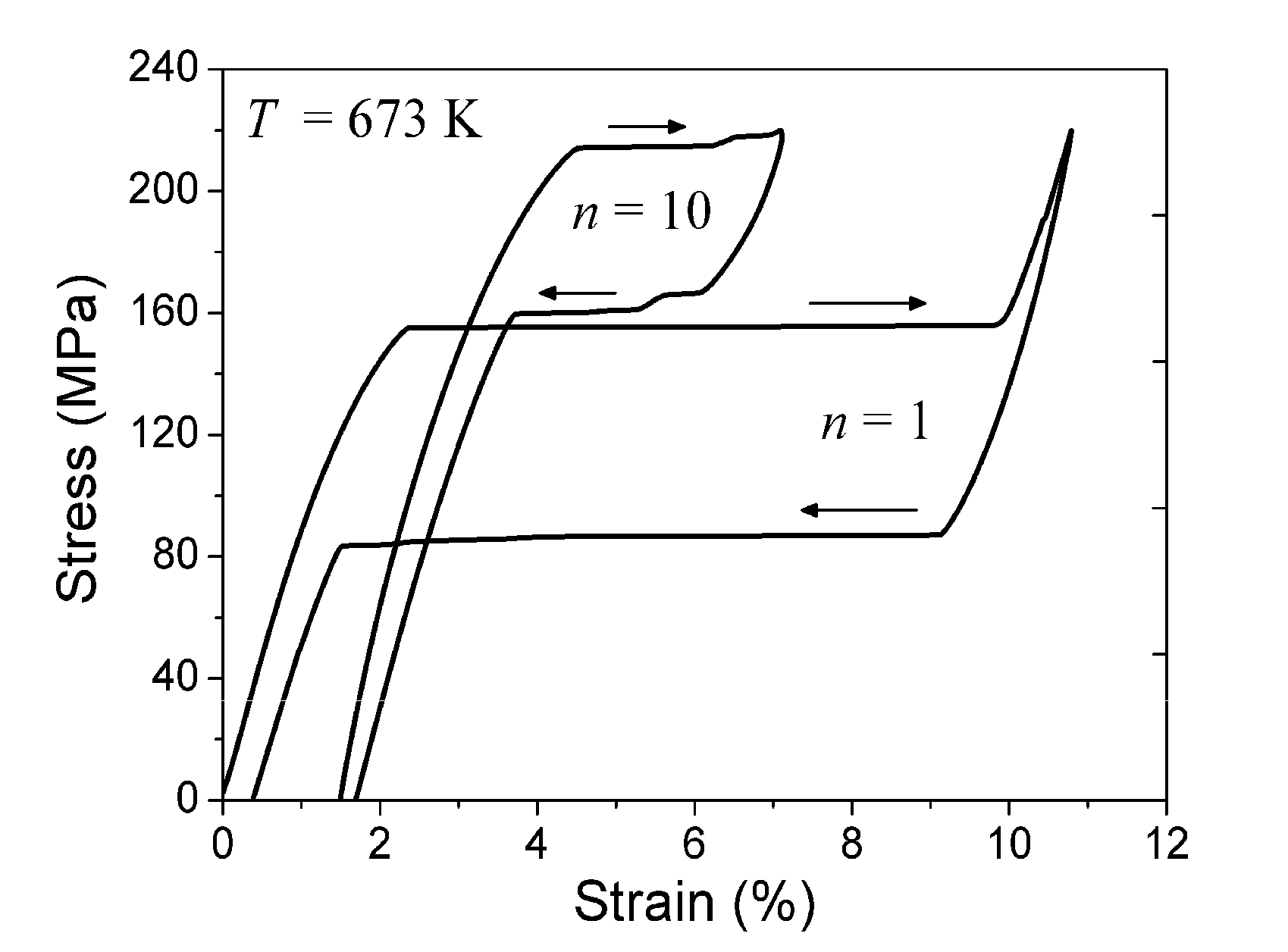

5.3. Qualitative Explanation of Experimental Results
5.4. Quantitative Description of the Martensite Destabilization Effects
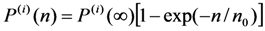
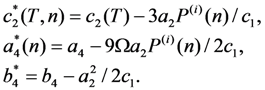
 , whereas the martensitic phase is stable for
, whereas the martensitic phase is stable for  . The equations
. The equations  and
and  prescribe the values of the lability temperatures T1(n) and T2(n). The shear elastic modulus of austenitic phase
prescribe the values of the lability temperatures T1(n) and T2(n). The shear elastic modulus of austenitic phase  is related to the coefficient of the second-order energy term as
is related to the coefficient of the second-order energy term as
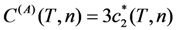
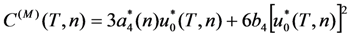
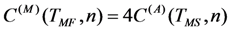
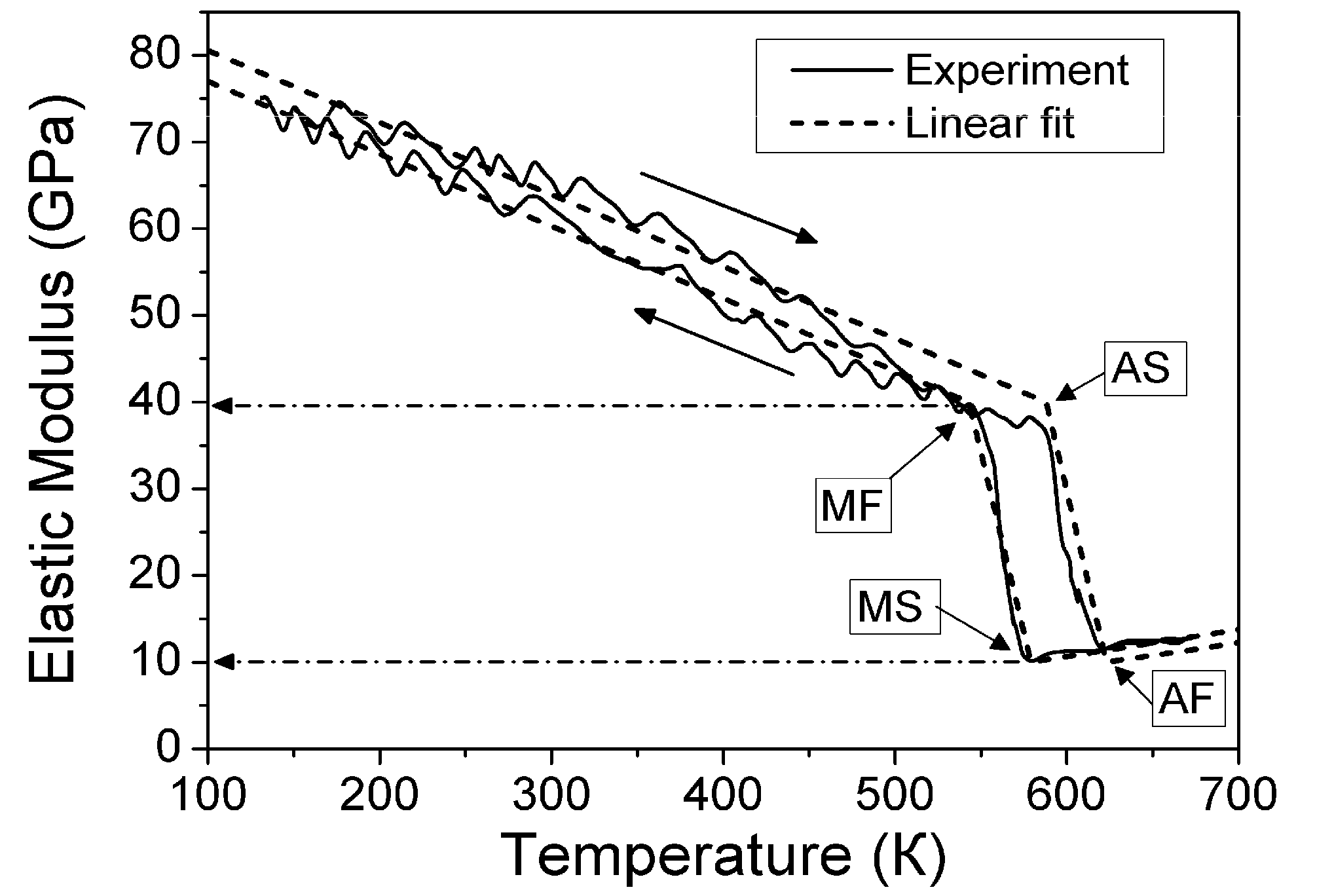
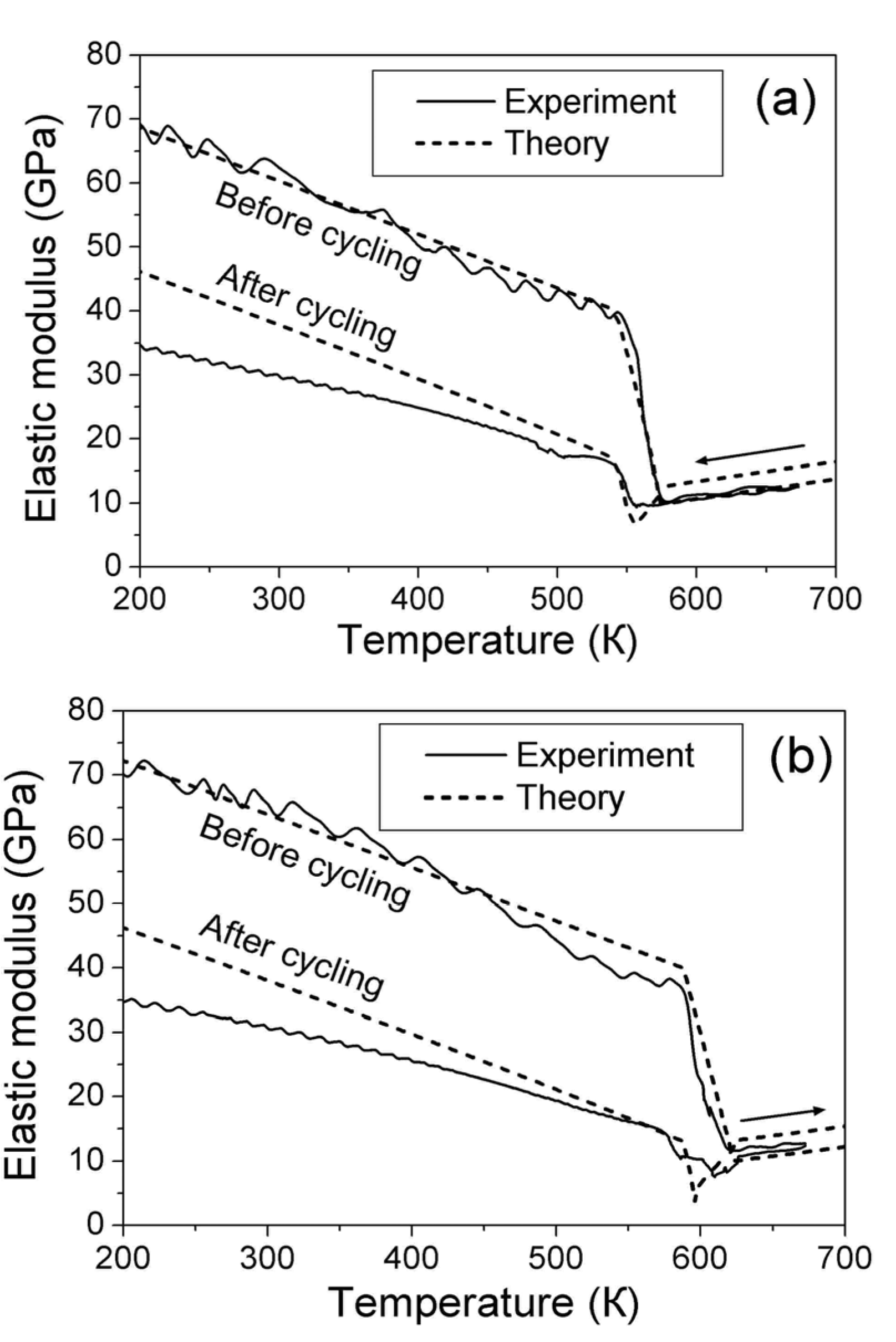
 correspond to the state of the real crystal before cycling (that is to zero value of destabilizing stress). To evaluate these coefficients, the experimental dependencies of elastic modulus were approximated by the straight dashed lines shown in Figure 6 and Equations 18 and 19 with C' (T1,2) ≈ E(TMS,MF)/3 were used. The approximation was made taking into account Equation 53. In addition, the experimental values of tetragonality ratio c/a = 1.22 and the volume change vMT ≈ −0.5% [78] were used for computations. These experimental values give rise to the estimations u0(TMF) = 2(c/a-1) = 0.44, a4 = −10.1 GPa,
correspond to the state of the real crystal before cycling (that is to zero value of destabilizing stress). To evaluate these coefficients, the experimental dependencies of elastic modulus were approximated by the straight dashed lines shown in Figure 6 and Equations 18 and 19 with C' (T1,2) ≈ E(TMS,MF)/3 were used. The approximation was made taking into account Equation 53. In addition, the experimental values of tetragonality ratio c/a = 1.22 and the volume change vMT ≈ −0.5% [78] were used for computations. These experimental values give rise to the estimations u0(TMF) = 2(c/a-1) = 0.44, a4 = −10.1 GPa,  and a2/c1 = 0.017, which are the same for both forward and reverse MTs. Note, that the procedure of obtaining these estimations is similar to that described in Section 3.3, Section 4.2. The difference between the forward and reverse MTs arises when the different experimental temperature dependencies of the elastic modulus (see Figure 6) and correspondent characteristic temperatures (T1 = TMS, T2 = TMF for the forward MT, and T1 = TAF, T2 = TAS for the reverse MT) are substituted into Equations 51 and 52.
and a2/c1 = 0.017, which are the same for both forward and reverse MTs. Note, that the procedure of obtaining these estimations is similar to that described in Section 3.3, Section 4.2. The difference between the forward and reverse MTs arises when the different experimental temperature dependencies of the elastic modulus (see Figure 6) and correspondent characteristic temperatures (T1 = TMS, T2 = TMF for the forward MT, and T1 = TAF, T2 = TAS for the reverse MT) are substituted into Equations 51 and 52. and
and  were calculated for theoretical description of the influence of thermomechanical cycling on the temperature dependence of elastic modulus of Sample 1. The expression for
were calculated for theoretical description of the influence of thermomechanical cycling on the temperature dependence of elastic modulus of Sample 1. The expression for  involves a dimensionless parameter Ω. According to argumentation presented in Section 2.2, the value
involves a dimensionless parameter Ω. According to argumentation presented in Section 2.2, the value  was accepted. For the sake of definiteness, the value n0 = 4 was used for computations. Characteristic values of the internal pressure P(i)(∞) = −6 GPa (for the forward MT) and P(i)(∞) = −7.5 GPa (for the reverse MT) were adjusted to achieve a reasonable agreement between the theoretical and experimental temperature dependencies of the elastic modulus. Figure 8 shows that an agreement between the experimental and theoretical dependencies takes place in rather wide temperature interval, ~100 K, below the martensite finish (for the forward MT) and austenite start (for the reverse MT) temperatures.
was accepted. For the sake of definiteness, the value n0 = 4 was used for computations. Characteristic values of the internal pressure P(i)(∞) = −6 GPa (for the forward MT) and P(i)(∞) = −7.5 GPa (for the reverse MT) were adjusted to achieve a reasonable agreement between the theoretical and experimental temperature dependencies of the elastic modulus. Figure 8 shows that an agreement between the experimental and theoretical dependencies takes place in rather wide temperature interval, ~100 K, below the martensite finish (for the forward MT) and austenite start (for the reverse MT) temperatures.5.5. Summary of Destabilization Effects
6. Quasi-Second-Order Martensitic Transformations
6.1. General Considerations
 and a5u4u5u6, which are proportional to the third power of the order parameters of the cubic-tetragonal and cubic-rhombohedral MTs. It means that the martensitic transformations must be the first-order phase transition and the jumps of the values of lattice parameters and elastic modules at MT temperature must be predetermined by a4 or a5 values (for the alloys exhibiting cubic-tetragonal or cubic-rhombohedral MT, respectively).
and a5u4u5u6, which are proportional to the third power of the order parameters of the cubic-tetragonal and cubic-rhombohedral MTs. It means that the martensitic transformations must be the first-order phase transition and the jumps of the values of lattice parameters and elastic modules at MT temperature must be predetermined by a4 or a5 values (for the alloys exhibiting cubic-tetragonal or cubic-rhombohedral MT, respectively).  and
and  , see Equations 45 and 50, respectively. Using the Equations 20 and 33, the renormalized coefficients can be expressed through the volume effect of MT and MT strain as follows:
, see Equations 45 and 50, respectively. Using the Equations 20 and 33, the renormalized coefficients can be expressed through the volume effect of MT and MT strain as follows:
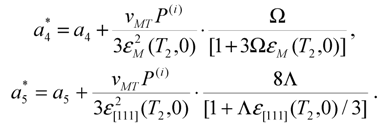
 or
or  . If so, the values a4 and Ω or a5 and Λmust be of the opposite signs. In the same time, the signs of parameters
. If so, the values a4 and Ω or a5 and Λmust be of the opposite signs. In the same time, the signs of parameters  and
and  are opposite to the signs of MT strains (see Equations 15 and 28). Therefore, the parameter Ω or Λ must be of the same sign as the strain arising in the course of cubic-tetragonal or cubic-rhombohedral MT. The martensite stabilization accompanies the martensite aging. Therefore, the martensite aging denotes an increase of
are opposite to the signs of MT strains (see Equations 15 and 28). Therefore, the parameter Ω or Λ must be of the same sign as the strain arising in the course of cubic-tetragonal or cubic-rhombohedral MT. The martensite stabilization accompanies the martensite aging. Therefore, the martensite aging denotes an increase of  or
or  magnitude and makes the first-order character of MT more pronounced.
magnitude and makes the first-order character of MT more pronounced.  or
or  magnitudes and glosses over the first-order character of MT. The destabilizing internal pressure is of the same sign as the spontaneous volume change vMT. It may be possible to observe a quasi-second order MT in presence of destabilizing internal pressure, which considerably reduces the absolute values of the coefficients
magnitudes and glosses over the first-order character of MT. The destabilizing internal pressure is of the same sign as the spontaneous volume change vMT. It may be possible to observe a quasi-second order MT in presence of destabilizing internal pressure, which considerably reduces the absolute values of the coefficients  and
and  .
.6.2. Application to the Ni-Mn-Ga and Au-Cd Alloys
 has been evaluated for Ni-Mn-Ga alloy with a/c < 1 (u0 ≈ −0.12) in [41]. The reported in this work data show that the destabilizing internal pressure of about of −3 GPa reduces the
has been evaluated for Ni-Mn-Ga alloy with a/c < 1 (u0 ≈ −0.12) in [41]. The reported in this work data show that the destabilizing internal pressure of about of −3 GPa reduces the  value by one order of magnitude if the values Ω = 2u0−1 and vMT = −0.5% are accepted for estimations. The choice of Ω value is explained in Section 2.3. The values of volume changes during MTs in the Ni-Mn-Ga alloys with c/a < 1 are disputed: the X-ray diffraction data result in the large value vMT ≈ −2·10−2, while the values estimated from thermodynamic measurements are smaller by almost one order of magnitude (see [28] and references therein). In view of this ambiguity, the ratio
value by one order of magnitude if the values Ω = 2u0−1 and vMT = −0.5% are accepted for estimations. The choice of Ω value is explained in Section 2.3. The values of volume changes during MTs in the Ni-Mn-Ga alloys with c/a < 1 are disputed: the X-ray diffraction data result in the large value vMT ≈ −2·10−2, while the values estimated from thermodynamic measurements are smaller by almost one order of magnitude (see [28] and references therein). In view of this ambiguity, the ratio  is presented in Figure 11 for the low (0.1%), intermediate (0.5%) and high (2%) volume changes.
is presented in Figure 11 for the low (0.1%), intermediate (0.5%) and high (2%) volume changes.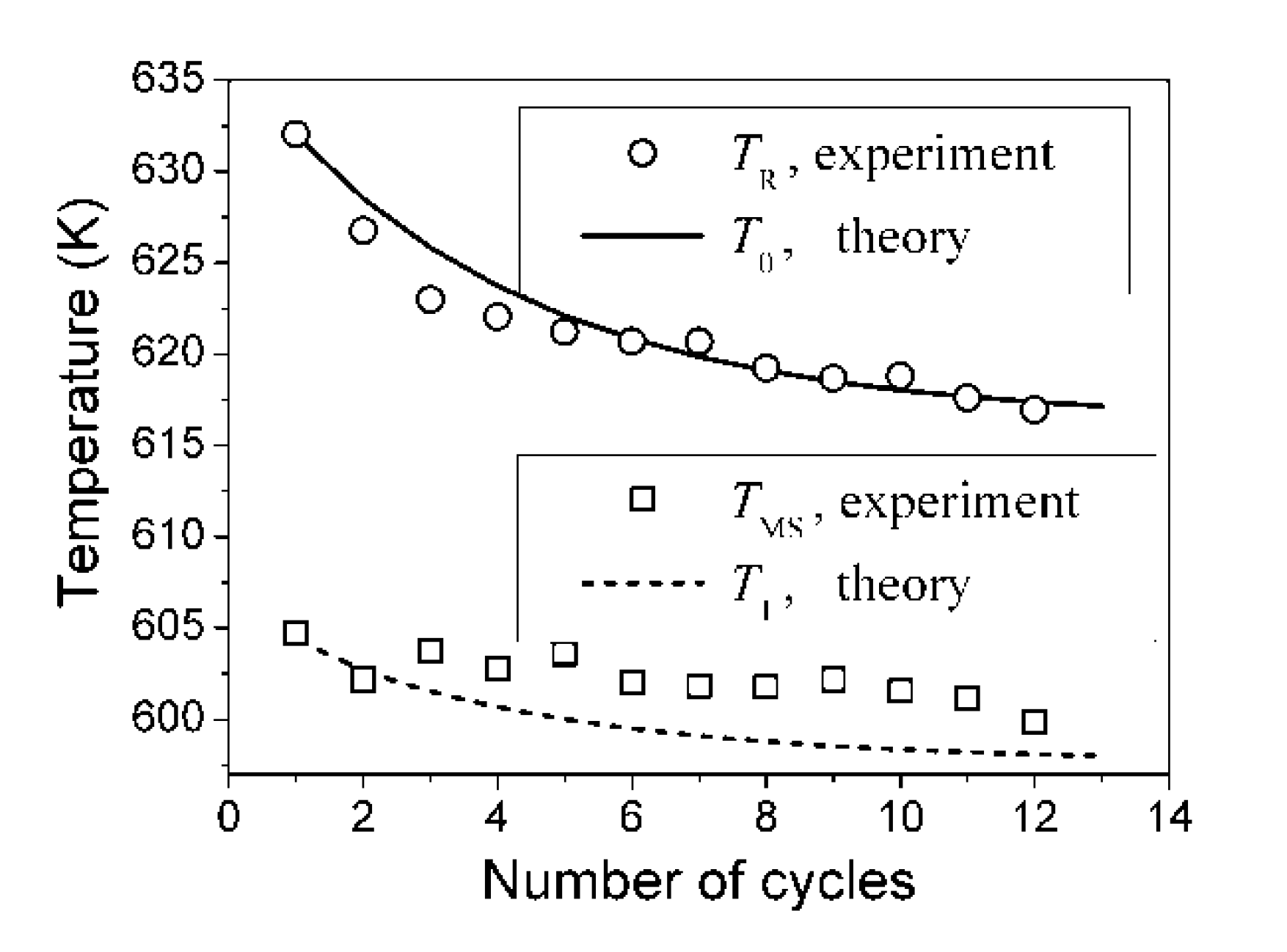
 value by one order of magnitude. In this case the MT in the alloy considered in [41] may bear resemblance to the second-order phase transition. It should be noticed that the theoretical analysis of aging effects in Ni-Mn-Ga martensite with c/a < 1 gave a comparatively low value of stabilizing pressure P(i)(t) < 1 GPa [35], but larger in the absolute value destabilizing pressure can be induced by the thermomechanical cycling of alloy specimens or some other mode of treatment.
value by one order of magnitude. In this case the MT in the alloy considered in [41] may bear resemblance to the second-order phase transition. It should be noticed that the theoretical analysis of aging effects in Ni-Mn-Ga martensite with c/a < 1 gave a comparatively low value of stabilizing pressure P(i)(t) < 1 GPa [35], but larger in the absolute value destabilizing pressure can be induced by the thermomechanical cycling of alloy specimens or some other mode of treatment.
 coefficient by factor of 0.55.
coefficient by factor of 0.55. value by factor of 0.93 only. The weak renormalization of the
value by factor of 0.93 only. The weak renormalization of the  coefficient follows from the large value εM ≈ 15% being inherent to the considered Ni-Mn-Ga martensites: according to Equation 54, the renormalization of
coefficient follows from the large value εM ≈ 15% being inherent to the considered Ni-Mn-Ga martensites: according to Equation 54, the renormalization of  is proportional to the ratio of the dimensionless values
is proportional to the ratio of the dimensionless values  , which is approximately equal to 300 for the Ni-Mn-Ga alloys with c/a > 1 and is of the order of −104 for the Ni-Mn-Ga alloys with c/a < 1.
, which is approximately equal to 300 for the Ni-Mn-Ga alloys with c/a > 1 and is of the order of −104 for the Ni-Mn-Ga alloys with c/a < 1.7. Volume Changes Contributing to the Entropy in Magnetic Shape Memory Alloys
7.1. Elastic and Magnetic Components of the Entropy Change during MT
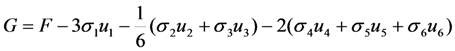
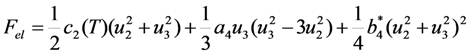
 is the sum of spin-exchange and magnetic anisotropy energies expressed through the magnetization vector components Mk as
is the sum of spin-exchange and magnetic anisotropy energies expressed through the magnetization vector components Mk as
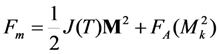
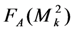 .
.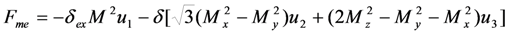
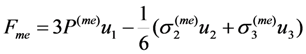
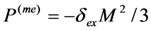
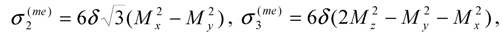
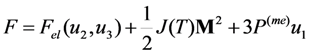
 of free energy has to be calculated considering that the order parameter is temperature-independent. At the second step, the equilibrium values of the order parameter that are inherent to the austenitic and martensitic phases have to be substituted into the obtained expression for the entropy and the difference of the resultant entropy values ΔS ≡ SA − SM has to be calculated.
of free energy has to be calculated considering that the order parameter is temperature-independent. At the second step, the equilibrium values of the order parameter that are inherent to the austenitic and martensitic phases have to be substituted into the obtained expression for the entropy and the difference of the resultant entropy values ΔS ≡ SA − SM has to be calculated.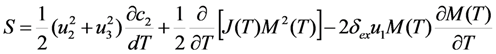
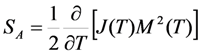
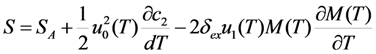
 is substituted in Equation 65 by the value Equation 64, which is inherent to the cubic ferromagnetic phase.
is substituted in Equation 65 by the value Equation 64, which is inherent to the cubic ferromagnetic phase.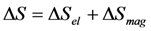
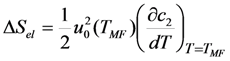
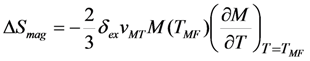
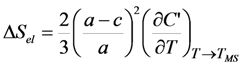
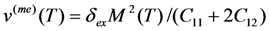
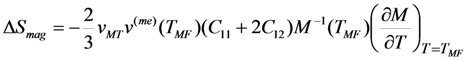
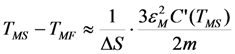
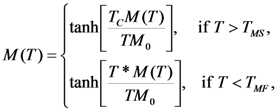
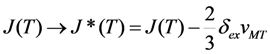
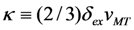
- I)
- The entropy change during MT is inversely proportional to the width of the temperature interval of mixed (austenitic-martensitic) state.
- II)
- The magnetoelastic energy of a deformable magnetic solid, such as FSMA, is the difference between the magnetic energies of its deformed and undeformed states.
- III)
- The magnetic contribution to the total entropy change caused by the deformation of magnetic solid is the partial temperature derivative of magnetoelastic energy taken with the opposite sign.
- IV)
- The ordinary magnetostriction of FSMA is substantially smaller than the MT strain vMT, and the axial magnetostriction is much smaller than the spontaneous volume magnetostriction v(me) in the case if the Curie temperature is of the order of room temperature. In this case the magnetic entropy change is directly proportional to the product vMTv(me)(TMF).
- V)
7.2. Magnetic Entropy Change during MT of Ni-Mn-Ga Alloy
 is valid [83], thus the Equation 76 gives the value κ = 150. In this case the numeric computation of M(T) function and its derivative results in the estimation ΔSmag = 14.3 J kg−1K−1. This entropy change corresponds to the heat exchange qmag = T0ΔSmag = 4.07 J g−1. It is astonishing that the theoretical estimation of the “magnetic” heat exchange is very close to the experimental value of total transformation heat q ≈ 4.2 J g−1 reported for Alloy 1 [78,86]. The experimental value of transformation heat corresponds to the total entropy change of 14.7 J kg−1K−1.
is valid [83], thus the Equation 76 gives the value κ = 150. In this case the numeric computation of M(T) function and its derivative results in the estimation ΔSmag = 14.3 J kg−1K−1. This entropy change corresponds to the heat exchange qmag = T0ΔSmag = 4.07 J g−1. It is astonishing that the theoretical estimation of the “magnetic” heat exchange is very close to the experimental value of total transformation heat q ≈ 4.2 J g−1 reported for Alloy 1 [78,86]. The experimental value of transformation heat corresponds to the total entropy change of 14.7 J kg−1K−1.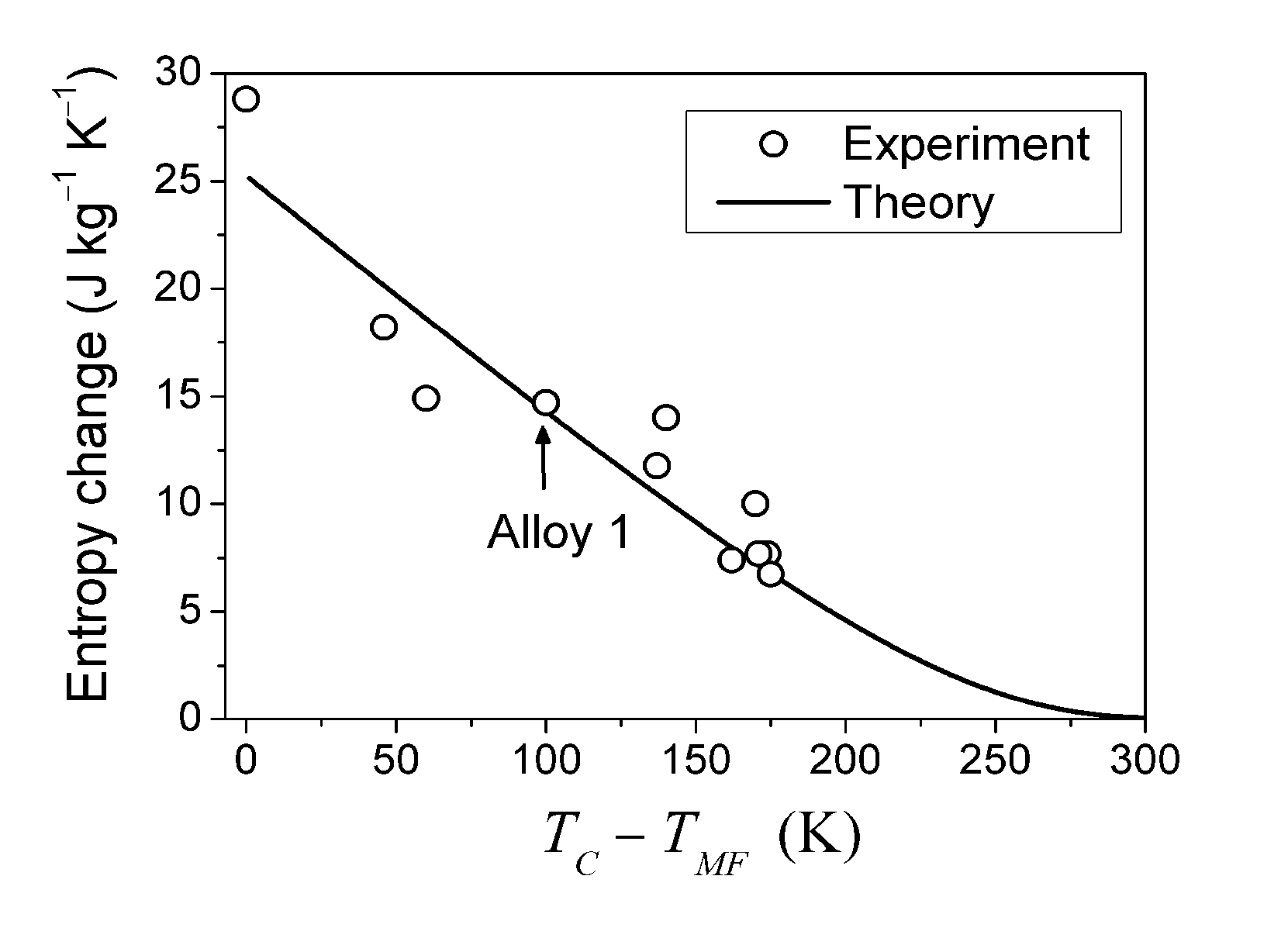
7.3. Magnetic Entropy Change during MT of a Quasi-Stoichiometric Ni-Fe-Ga Alloy

7.4. Summary on the Entropy Change
- (i)
- The total entropy change during MT is inversely proportional to the width of the temperature interval of mixed two-phase state.
- (ii)
- The elastic part of the entropy change is proportional to the value of temperature derivative of the shear elastic modulus. This feature illustrates that the cubic-tetragonal MT is caused by the instability of crystal lattice with respect to the vibrations corresponding to the TA2 [110] phonon mode and to the softening of this phonon mode which leads to a decrease of C′ value in the vicinity of MT. In practice, the evaluation of ΔSel from the temperature dependencies of shear modules of SMAs is hampered by an uncertainty in the experimental values of these modules.
- (iii)
- The elastic part of the entropy change is proportional to the squared tetragonal distortion of the unit cell, (1−c/a)2), which is about of 4 × 10−2 for the Ni-Mn-Ga alloys with c/a > 1, TMS > TC and 3 × 10−3 for the alloys withc/a < 1, TMS < TC. This feature is in line with the fact that the observed in [91] entropy change is noticeably larger for the Ni-Mn-Ga alloys with TMS > TC than for those with TMS < TC.
- (iv)
- In the case of FSMAs with TMS < TC, the Landau theory confirms a crucial role of the interaction between the magnetic and elastic subsystems in the formation of thermodynamic characteristics of the MT. The magnetic part of the entropy change estimated from M(T) curves for Ni-Mn-Ga alloy (Alloy 1) appeared to be close in value to the experimentally observed total entropy change. In this connection, the entropy change demonstrates a sharp decrease when the MT temperature of the alloy moves away from the Curie temperature. The experiments show that this is a common feature of the Ni-Mn-Ga, Ni-Mn-In and Ni-Mn-In-Co alloy systems [32]. Recently, a pronounced dependence of ΔS on TC−TMF has been observed also in Ni-Mn-Ga-Co alloys [95].
- (v)
- The computations illustrate that the evaluation of the magnetic entropy change from the temperature dependence of magnetization is very sensitive to the character of this dependence (see Figure 14). Moreover, it occurs that the standard equations corresponding to the Bragg–Williams approximation do not describe the magnetization of Ni-Fe-Ga alloys. It can be concluded, therefore, that the careful study of the magnetic structure and magnetization of every alloy system must be carried out for the correct evaluation of magnetic entropy change.
- (vi)
- Equation 71 shows that the magnetic entropy change is proportional to the volume magnetostriction. Therefore, a careful theoretical analysis of the effect of spontaneous and forced magnetostriction on the characteristic MT temperatures will be very important.
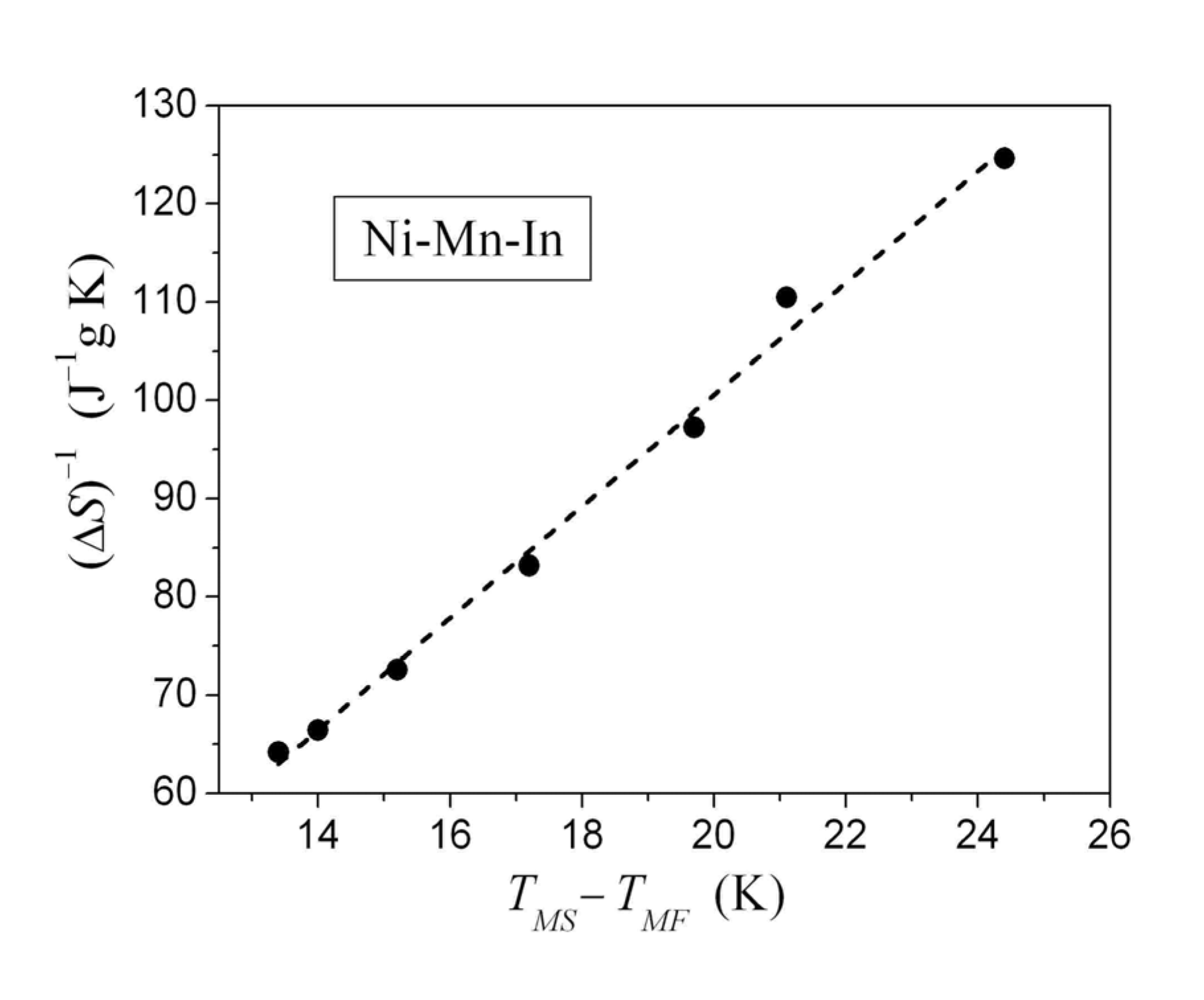
 [83,84] and volume change of the order of 1% directly given for Ni-Mn-Ga alloys by the X-ray data, while the Clausius–Clapeyron relationship results in a value for the volume change of about 0.1% estimated from the shift of MT temperature by the hydrostatic compression of Ni-Mn-Ga. The reduction of the volume change by one order of magnitude can be compensated only by the proportional increase of the magnetoelastic constant. The value
[83,84] and volume change of the order of 1% directly given for Ni-Mn-Ga alloys by the X-ray data, while the Clausius–Clapeyron relationship results in a value for the volume change of about 0.1% estimated from the shift of MT temperature by the hydrostatic compression of Ni-Mn-Ga. The reduction of the volume change by one order of magnitude can be compensated only by the proportional increase of the magnetoelastic constant. The value  was reported in [85].
was reported in [85].8. Discussion
Acknowledgments
References
- Christian, J.W. Theory of Phase Transformations in Metals and Alloys; Pergamon Press: New York, NY, USA, 1975; pp. 1–973. [Google Scholar]
- Khachaturyan, A.G. Theory of Structural Transformations in Solids; Wiley: New York, NY, USA, 1983; pp. 1–574. [Google Scholar]
- Otsuka, K.; Wayman, C.M. Shape Memory Materials; Cambridge University Press: Cambridge, UK, 1998; pp. 1–267. [Google Scholar]
- Lagoudas, C. Shape Memory Alloys: Modeling and Engineering Applications; Springer-Verlag: New York, NY, USA, 2007; pp. 1–435. [Google Scholar]
- Kohl, M. Shape Memory Microactuators; Springer-Verlag: Berlin, Germany, 2004; pp. 1–245. [Google Scholar]
- Hannula, S.-P.; Söderberg, O.; Jämsä, T.; Lindroos, V.K. Shape memory alloys for biomedical applications. Adv. Sci. Technol. 2006, 49, 109–118. [Google Scholar] [CrossRef]
- Humbeeck, J.V. Non-Medical applications of shape memory alloys. Mater. Sci. Eng. 1999, 273–275, 134–148. [Google Scholar] [CrossRef]
- O’Handley, R.C.; Allen, S.M. Shape-Memory Alloys, Magnetically Activated Ferromagnetic Shape-Memory Materials. In Encyclopedia of Smart Materials; Schwartz, M., Ed.; Wiley: New York, NY, USA, 2002; pp. 936–951. [Google Scholar]
- Söderberg, O.; Ge, Y.; Sozinov, A.; Hannula, S.-P.; Lindroos, V.K. Giant Magnetostrictive Materials. In Handbook of Magnetic Materials; Buschow, J., Ed.; Elsevier Science: Amsterdam, the Netherlands, 2006; pp. 1–39. [Google Scholar]
- Chernenko, V.A. Advances in Shape Memory Materials; TTP: Zurich, Switzerland, 2008; pp. 1–302. [Google Scholar]
- Chernenko, V.A. Advances in Shape Memory Materials; TTP: Zurich, Switzerland, 2011; pp. 1–231. [Google Scholar]
- Entel, P.; Buchelnikov, V.D.; Khovailo, V.V.; Zayak, A.T.; Adeagbo, W.A.; Gruner, M.E.; Herper, H.C.; Wassermann, E.F. Modelling the phase diagram of magnetic shape memory Heusler alloys. J. Phys. D Appl. Phys. 2006, 39, 865–889. [Google Scholar] [CrossRef]
- Acet, M.; Manosa, L.; Planes, A. Magnetic-Field-Induced Effects in Martensitic Heusler-Based Magnetic Shape Memory Alloys. In Handbook of Magnetic Materials; Buschow, J., Ed.; Elsevier Science: Amsterdam, the Netherlands, 2011; pp. 232–282. [Google Scholar]
- Entel, P.; Siewert, M.; Gruner, M.E.; Herper, H.C.; Comtesse, D.; Arroyave, R.; Singh, N.; Talapatra, A.; Sokolovskiy, V.V.; Buchelnikov, V.D.; Albertini, F.; et al. Complex magnetic ordering as a driving mechanism of multifunctional properties of Heusler alloys from first principles. Eur. Phys. J. B 2013, 86, 65–75. [Google Scholar] [CrossRef]
- Murray, S.J.; Marioni, M.; Allen, S.M.; O’Handley, R.C.; Lograsso, T.A. 6% magnetic-field-induced strain by twin-boundary motion in ferromagnetic Ni–Mn–Ga. Appl. Phys. Lett. 2000, 77, 886–888. [Google Scholar] [CrossRef]
- Heczko, O.; Sozinov, A.; Ullakko, K. Giant field-induced reversible strain in magnetic shape memory NiMnGa alloy. IEEE Trans. Magn. 2000, 36, 3266–3268. [Google Scholar] [CrossRef]
- Sozinov, A.; Lanska, N.; Soroka, A.; Zou, W. 12% magnetic field-induced strain in Ni-Mn-Ga-based non-modulated martensite. Appl. Phys. Lett. 2013, 102, 021902:1–021902:5. [Google Scholar]
- Warlimont, H.; Delaey, L. Martersitic. Transformations in Copper-,Silver- and Gold-Based Alloys; Pergamon Press: New York, NY, USA, 1974; pp. 1–379. [Google Scholar]
- Kokorin, V.V.; Samsonov, Yu.I.; Khshanovskiy, L.F.; Chernenko, V.A.; Shevchenko, O.M. Volume change during γ–α transformation in iron-nickel base alloys. Phys. Met. Metall. 1991, 71, 141–146. [Google Scholar]
- Maki, T.; Kobayashi, K.; Minato, M.; Tamura, I. Thermoelastic martensite in an ausaged Fe-Ni-Ti-Co alloy. Scripta. Met. 1984, 18, 1105–1109. [Google Scholar] [CrossRef]
- Maki, T.; Furutani, S.; Tamura, I. Shape memory effect related to thin plate martensite with large thermal hysteresis in ausaged Fe-Ni-Co-Ti alloy. ISIJ Int. 1989, 29, 438–445. [Google Scholar] [CrossRef]
- Kokorin, V.V.; Chernenko, V.A. Reversion stress evaluation in Fe-Ni-Co-Ti alloys. In Proceedings of the Second International Conference on Shape Memory and Superelastic Technologies, Pacific Grove, CA, USA, 1997; pp. 119–124.
- Jost, N.; Escher, K.; Donner, P.; Sade, M.; Halter, K.; Hornbogen, E. Steels with shape memory. WIRE 1990, 40, 639–640. [Google Scholar]
- Gefen, Y.; Halwany, A.; Rosen, M. Effect of hydrostatic pressure on the cubic-orthorhombic phase transformation in Au-47.5 at% Cd alloy. Phil. Mag. 1973, 28, 1–9. [Google Scholar] [CrossRef]
- Kakeshita, T.; Yoshirnura, Y.; Shimizu, K.; Endo, S.; Akahama, Y.; Fujita, F.E. Effect of hydrostatic pressure on martensitic transformations of Cu-Al-Ni shape memory alloy. Trans. Jpn. Inst. Metals 1988, 29, 781–789. [Google Scholar]
- Kakeshita, T.; Shimizu, K. Effects of hydrostatic pressure on martensitic transformations. Mat. Trans. JIM 1997, 38, 668–681. [Google Scholar]
- Zakrevskiy, I.G.; Kokorin, V.V.; Chernenko, V.A. Baroelastic martensitic transformation in Fe-Ni-Co-Ti alloy. Soviet Phys. Dokl. 1989, 34, 73–74. [Google Scholar]
- Chernenko, V.A.; L'vov, V.A. Thermodynamics of martensitic transformations affected by hydrostatic pressure. Phil. Mag. A 1996, 73, 999–1008. [Google Scholar] [CrossRef]
- Aseguinolaza, I.R.; Reyes-Salazar, I.; Svalov, A.V.; Wilson, K.; Knowlton, W.B.; Mullner, P.; Barandiaran, J.M.; Villa, E.; Chernenko, V.A. Transformation volume strain in Ni-Mn-Ga thin films. Appl. Phys. Lett. 2012, 101, 241912:1–241912:4. [Google Scholar]
- Khovailo, V.V.; Takagi, T.; Tani, J.; Levitin, R.Z.; Cherechukin, A.A.; Matsumoto, M.; Note, R. Magnetic properties of Ni2.18Mn0.82Ga Heusler alloys with a coupled magnetostructural transition. Phys. Rev. B 2002, 65, 092410:1–092410:4. [Google Scholar]
- Ito, W.; Imano, Y.; Kainuma, R.; Sutou, Y.; Oikawa, K.; Ishida, K. Martensitic and magnetic transformation behaviors in Heusler-type NiMnIn and NiCoMnIn metamagnetic shape memory alloys. Metall. Mater. Trans. A 2007, 38, 759–766. [Google Scholar] [CrossRef]
- Kustov, S.; Corró, M.L.; Pons, J.; Cesari, E. Entropy change and effect of magnetic field on martensitic transformation in a metamagnetic Ni–Co–Mn–In shape memory alloy. Appl. Phys. Lett. 2009, 94, 191901:1–191901:3. [Google Scholar]
- L’vov, V.A.; Cesari, E.; Recarte, V.; Pérez-Landazábal, J.I. Entropy change of martensitic transformation in ferromagnetic shape memory alloys. Acta Mater. 2013, 61, 1764–1772. [Google Scholar] [CrossRef]
- Xu, X.; Ito, W.; Umetsu, R.Y.; Koyama, K.; Kainuma, K.; Ishida, K. Kinetic arrest of martensitic transformation in Ni33:0Co13:4Mn39:7Ga13:9 metamagnetic shape memory alloy. Mater. Trans. 2010, 51, 469–471. [Google Scholar] [CrossRef]
- L'vov, V.A.; Kosogor, A.; Söderberg, O.; Hannula, S.-P. The symmetry-conforming theory of martensite aging. Mater. Sci. Forum 2010, 635, 13–19. [Google Scholar]
- Kosogor, A.; L’vov, V.A.; Soderberg, O.; Hannula, S.-P. Stabilizing internal stress as the thermodynamic factor of martensite aging effects. Acta Mater. 2011, 59, 3593–3601. [Google Scholar] [CrossRef]
- L’vov, V.A.; Kosogor, A.; Barandiaran, J.M.; Chernenko, V.A. Destabilization of Ni–Mn–Ga martensite: Experiment and theory. Acta Mater. 2012, 60, 1587–1593. [Google Scholar] [CrossRef]
- Liakos, J.K.; Saunders, G.A. Application of the Landau theory to elastic phase transitions. Philos. Mag. A 1982, 46, 217–242. [Google Scholar] [CrossRef]
- Gomonaj, E.V.; L'vov, V.A. Martensitic phase transition with two-component order parameter in a stressed cubic crystal. Phase Trans. 1994, 47, 9–21. [Google Scholar] [CrossRef]
- Barsch, G.R.; Krumhansl, J.A. Twin boundaries in ferroelastic media without interface dislocations. Phys. Rev. Lett. 1984, 53, 1069–1072. [Google Scholar]
- Danilevich, A.G.; L’vov, V.A. Strong influence of ferromagnetic ordering and internal pressure on the elastic modulus of shape memory alloy. JMMM 2013, 333, 108–113. [Google Scholar] [CrossRef]
- Patel, J.R.; Cohen, M. Criterion for the action of applied stress in the martensitic transformation. Acta Metall. 1953, 1, 531–538. [Google Scholar] [CrossRef]
- Rohde, R.W.; Graham, R.A. The effect of hydrostatic pressure on the martensitic reversal of an iron-nickel-carbon alloy. Trans. Met. Soc. AIME 1969, 245, 2441–2445. [Google Scholar]
- Otsuka, K.; Ren, X. Mechanism of martensite aging effects and new aspects. Mater. Sci. Eng. A 2001, 312, 207–218. [Google Scholar] [CrossRef]
- Pelegrina, J.L.; Ahlers, M. Influence of a constant stress during isothermal β phase ageing on the martensitic transformation in a Cu–Zn–Al shape memory alloy. Scr. Mater. 2004, 50, 423–427. [Google Scholar] [CrossRef]
- Cahn, R.W. Metallic rubber bounces back. Nature 1995, 374, 120–121. [Google Scholar] [CrossRef]
- Picornell, C.; Pons, J.; Cesari, E. Effect of aging under compressive stress along [100] in Co–Ni–Ga single crystals. Funct. Mater. Lett. 2009, 2, 83–86. [Google Scholar]
- Otsuka, K.; Ren, X. Physical metallurgy of Ti-Ni based shape memory alloys. Prog. Mater. Sci. 2005, 50, 511–678. [Google Scholar] [CrossRef]
- L’vov, V.A.; Glavatska, N.; Aaltio, I.; Söderberg, O.; Glavatskyy, I.; Hannula, S.-P. The role of anisotropic thermal expansion of shape memory alloys in their functional properties. Acta Mater. 2009, 57, 5605–5612. [Google Scholar] [CrossRef]
- Brill, T.M.; Mittelbach, S.; Assmus, W.; Mullner, M.; Luthi, B. Elastic properties of NiTi. J. Phys. Condens. Matter. 1991, 3, 9621–9627. [Google Scholar] [CrossRef]
- Chernenko, V.A.; Homenko, D.V.; L’vov, V.A.; Barandiaran, J.M. Specific heat of shape memory alloys with soft elastic moduli. J. Appl. Phys. 2011, 109, 013526:1–013526:6. [Google Scholar]
- Lapshin, V.P.; Grishkov, V.N.; Lotkov, A.I. On certain anharmonic characteristics of B2-Phase Ti(Ni, Fe) alloys under hydrostatic pressure. Russ. Phys. J. 2000, 43, 999–1002. [Google Scholar]
- Ren, X.; Otsuka, K. Origin of rubber-like behaviour in metal alloys. Nature 1997, 389, 579–582. [Google Scholar] [CrossRef]
- Ishibashi, H.; Kogachi, M.; Ohba, T.; Ren, X.; Otsuka, K. Vacancy migration and long-range ordering due to ageing in AuCd shape memory alloys. Mater. Sci. Eng. A 2002, 329–331, 568–572. [Google Scholar] [CrossRef]
- Tadaki, K.; Otsuka, K.; Shimizu, K. Shape memory alloys. Ann. Rev. Mater. Sci. 1988, 18, 25–45. [Google Scholar] [CrossRef]
- Otsuka, K.; Ren, X. Mechanism of martensite aging effect. Scr. Mater. 2004, 50, 207–212. [Google Scholar] [CrossRef]
- Murakami, Y.; Nakajima, Y.; Otsuka, K.; Ohba, T.; Matsuo, R.; Ohshima, K. Characteristics and mechanism of martensite ageing effect in Au-Cd alloys. Mater. Sci. Eng. A 1997, 237, 87–101. [Google Scholar] [CrossRef]
- Ohta, T. Theory of rubber-like elasticity in shape memory alloys. Mater. Sci. Eng. A 2001, 312, 57–65. [Google Scholar] [CrossRef]
- Ren, X.; Otsuka, K. Universal symmetry property of point defects in crystals. Phys. Rev. Lett. 2000, 85, 1016–1019. [Google Scholar] [CrossRef]
- Xue, D.; Zhou, Y.; Ding, X.; Otsuka, K.; Sun, J.; Ren, X. Martensite aging effects on the dynamic properties of Au–Cd shape memory alloys: Characteristics and modelling. Acta Mater. 2011, 59, 4999–5011. [Google Scholar]
- Xue, D.; Zhou, Y.; Ding, X.; Lookman, T.; Sun, J.; Ren, X. Aging and deaging effects in shape memory alloys. Phys. Rev. B 2012, 86, 184109:1–184109:11. [Google Scholar]
- Kosogor, A.; Xue, D.; Zhou, Y.; Ding, X.; Otsuka, K.; L’vov, V.A.; Sun, J.; Ren, X. Impact of the volume change on the aging effects in Cu-Al-Ni martensite: experiment and theory. J. Phys. Condens. Matter 2013. submitted for publication. [Google Scholar]
- Otsuka, K.; Ren, X.; Murakami, Y.; Kawano, T.; Ishii, T.; Ohba, T. Composition dependence of the rubber-like behavior in ζ2′-martensite of AuCd alloys. Mater. Sci. Eng. A 1999, 273, 558–563. [Google Scholar]
- Ren, X.; Otsuka, K. The role of softening in elastic constant c44 in martensitic transformation. Scr. Mater. 1998, 38, 1669–1675. [Google Scholar]
- Otsuka, K.; Ren, X. Martensitic transformations in nonferrous shape memory alloys. Mater. Sci. Eng. A 1999, 273–275, 89–105. [Google Scholar] [CrossRef]
- Otsuka, K.; Shimizu, K. Morphology and crystallography of thermoelastic Cu-Al-Ni martensite analyzed by the phenomenological theory. Mat. Trans. JIM 1974, 15, 103–108. [Google Scholar]
- Van Humbeeck, J.; Janssen, J.; Mwamba, N.; Delaey, L. The stabilisation of step-quenched copper-zinc-aluminum martensite part I: The reverse transformation temperatures. Scr. Metall. 1984, 18, 893–898. [Google Scholar] [CrossRef]
- Nakata, Y.; Yamamoto, O.; Shimizu, K. Effect of aging in Cu-Zn-Al shape memory alloys. Mat. Trans. JIM 1993, 34, 429–437. [Google Scholar]
- Kokorin, V.V.; Kozlova, L.E.; Titenko, A.N. Temperature hysteresis of martensite transformation in aging Cu–Mn–Al alloy. Scr. Mater. 2002, 47, 499–502. [Google Scholar] [CrossRef]
- Kustov, S.; Pons, J.; Cesari, E.; Van Humbeeck, J. Pinning-induced stabilization of martensite: Part I. Stabilization due to static pinning of interfaces. Acta Mater. 2004, 52, 3075–3081. [Google Scholar] [CrossRef]
- Chernenko, V.A.; Pons, J.; Cesari, E.; Zasimchuk, I.K. Transformation behaviour and martensite stabilization in the ferromagnetic Co–Ni–Ga Heusler alloy. Scr. Mater. 2004, 50, 225–229. [Google Scholar] [CrossRef]
- Chernenko, V.A.; Villa, E.; Besseghini, S.; Barandiaran, J.M. Giant two-way shape memory effect in high-temperature Ni–Mn–Ga single crystal. Phys. Proced. 2010, 10, 94–98. [Google Scholar] [CrossRef]
- Hsieh, S.F.; Chang, W.K. Martensitic transformation of an aged/thermal-cycled Ti30.5Ni49.5Zr10Hf10 Shape Memory Alloy. J. Mater. Sci. 2007, 37, 2851–2856. [Google Scholar] [CrossRef]
- Wayman, C.M.; Cornelis, I.; Shimizu, K. Transformation behavior and the shape memory effect in thermally cycled TiNi. Scr. Metall. 1972, 6, 115–122. [Google Scholar] [CrossRef]
- Miyazaki, S.; Igo, Y.; Otsuka, K. Effect of thermal cycling on the transformation temperatures of Ti-Ni alloys. Acta Metall. 1986, 34, 2045–2051. [Google Scholar] [CrossRef]
- Hsieh, S.F.; Wu, S.K.; Lin, H.C. Martensitic transformation of a Ti-rich Ti51Ni47Si2 shape memory alloy. J. Alloys Compd. 2002, 335, 254–261. [Google Scholar] [CrossRef]
- Perkins, J.; Muesing, W.E. Martensitic transformation cycling effects in Cu-Zn-Al shape memory alloys. Met. Trans. A 1983, 14, 33–36. [Google Scholar] [CrossRef]
- Chernenko, V.A.; Kokorin, V.V.; Babii, O.M.; Zasimchuk, I.K. Phase diagrams in the Ni-Mn-Ga system under compression. Intermetallics 1998, 6, 29–34. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Course of Theoretical Physics; Volume 5 Statistical Physics; Pergamon Press: New York, NY, USA, 1980. [Google Scholar]
- L’vov, V.A.; Matsishin, N.; Glavatska, N. Thermoelastic behaviour of martensitic alloy in the vicinity of critical point in the stress–temperature phase diagram. Phase Trans. 2010, 83, 293–301. [Google Scholar]
- Kosogor, A.; Matsishin, N.J.; L'vov, V.A. Modelling of hysteresis loops taken during the stress- and temperature-induced martensitic transformations. Phase Trans. 2013, in press. [Google Scholar]
- L’vov, V.A.; Gomonaj, E.V.; Chernenko, V.A. A phenomenological model of ferromagnetic martensite. J. Phys. Condens. Mat. 1998, 10, 4587–4596. [Google Scholar] [CrossRef]
- Chernenko, V.A.; L'vov, V.A.; Pasquale, M.; Besseghini, S.; Sasso, C.; Polenur, D.A. Magnetoelastic behavior of Ni-Mn-Ga martensitic alloys. Int. J. Appl. Electromagn. Mech. 2000, 12, 3–8. [Google Scholar]
- Chernenko, V.A.; L’vov, V.A.; Zagorodnyuk, S.P.; Takagi, T. Ferromagnetism of thermoelastic martensites: Theory and experiment. Phys. Rev. B 2003, 67, 064407:1–064407:6. [Google Scholar]
- Buchelnikov, V.D.; Khovailo, V.V.; Takagi, T. The thermal expansion coefficient and volume magnetostriction of Heusler Ni2MnGa alloys. JMMM 2006, 300, e459–e461. [Google Scholar] [CrossRef]
- Chernenko, V.A.; Amengual, A.; Cesari, E.; Kokorin, V.V.; Zasimchuk, I.K. Thermal and magnetic properties of stress-induced martensites in Ni2MnGa alloys. J. Phys. IV 1995, 5, 95–98. [Google Scholar]
- Fukuda, T.; Maeda, H.; Yasui, M.; Kakeshita, T. Influence of magnetocrystalline anisotropy on martensitic transformation under magnetic field of single-crystalline Ni2MnGa. Scr. Mater. 2009, 60, 261–263. [Google Scholar] [CrossRef]
- Seguí, C.; Chernenko, V.A.; Pons, J.; Cesari, E. Low-Temperature-Induced intermartensitic phase transformations in Ni–Mn–Ga single crystal. JMMM 2005, 290, 811–815. [Google Scholar]
- Seguí, C.; Chernenko, V.A.; Pons, J.; Cesari, E. Two-Step martensitic transformation in Ni-Mn-Ga alloys. J. Phys. IV 2003, 112, 903–906. [Google Scholar]
- Chernenko, V.A.; Cesari, E.; Pons, J.; Seguí, C. Phase transformations in rapidly quenched Ni–Mn–Ga alloys. Mat. J. Res. 2000, 15, 1496–1504. [Google Scholar] [CrossRef]
- Chernenko, V.A.; Cesari, E.; Kokorin, V.V.; Vitenko, I.N. The development of new ferromagnetic shape memory alloys in Ni-Mn-Ga system. Scr. Met. Mat. 1995, 33, 1239–1244. [Google Scholar] [CrossRef]
- Cesari, E.; Salas, D.; Kustov, S. Entropy changes in ferromagnetic shape memory alloys. Mat. Sci. Forum 2011, 684, 49–60. [Google Scholar] [CrossRef]
- Recarte, V.; Pérez-Landazábal, J.I.; Gómez-Polo, C.; Sánchez-Alarcos, V.; Cesari, E.; Pons, J. Vibrational and magnetic contributions to the entropy change associated with the martensitic transformation of Ni–Fe–Ga ferromagnetic shape memory alloys. J. Phys. Condens. Matter 2010, 22, 416001:1–416001:7. [Google Scholar]
- Liu, Z.H.; Hu, H.N.; Liu, G.D.; Cui, Y.T.; Zhang, M.; Chen, J.L.; Wu, G.H. Electronic structure and ferromagnetism in the martensitic-transformation material Ni2FeGa. Phys. Rev. B 2004, 69, 134415. [Google Scholar]
- Seguí, C.; Cesari, E. Composition and atomic order effects on the structural and magnetic transformations in ferromagnetic Ni–Co–Mn–Ga shape memory alloys. J. Appl. Phys. 2012, 111, 043914:1–043914:7. [Google Scholar]
- Barandiaran, J.M.; Chernenko, V.A.; Cesari, E.; Salas, D.; Lazpita, P.; Gutierrez, J.; Orue, I. Magnetic influence on the martensitic transformation entropy in Ni-Mn-In metamagnetic alloy. Appl. Phys. Lett. 2013, 102, 071904:1–071904:4. [Google Scholar]
- Gruner, M.E.; Entel, P. Impact of local lattice distortions on the structural stability of Fe-Pd magnetic shape-memory alloys. Phys. Rev. B 2011, 83, 214415:1–214415:11. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chernenko, V.A.; L'vov, V.A.; Cesari, E.; Kosogor, A.; Barandiaran, J.M. Transformation Volume Effects on Shape Memory Alloys. Metals 2013, 3, 237-282. https://doi.org/10.3390/met3030237
Chernenko VA, L'vov VA, Cesari E, Kosogor A, Barandiaran JM. Transformation Volume Effects on Shape Memory Alloys. Metals. 2013; 3(3):237-282. https://doi.org/10.3390/met3030237
Chicago/Turabian StyleChernenko, Volodymyr A., Victor A. L'vov, Eduard Cesari, Anna Kosogor, and Jose M. Barandiaran. 2013. "Transformation Volume Effects on Shape Memory Alloys" Metals 3, no. 3: 237-282. https://doi.org/10.3390/met3030237




