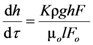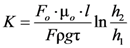1. Introduction
Open-pore metal sponges offer a wide range of possible applications, such as heat-exchangers, fuel cells, filtering processes,
etc. Accordingly, many state-of-the-art technologies are used for obtaining such permeable materials [
1,
2].
Replication casting can provide the advanced performances such as stability and repeatability of foam structure. Briefly, the process can be described by the following steps. The porous bed of preheated NaCl particles is infiltrated with molten metal. The resulting composite after solidification can be shaped into the desirable form, and then salt is subsequently removed by dissolution in water. Infiltration can be actuated by vacuum suction [
3] or under high gas pressure [
4]. Sodium chloride can be preheated either in the mold before the infiltration [
4], or separately [
5].
A similar technology was applied commercially by Composite Materials Ltd. (Ekaterinburg, Russia). Here, granular sodium chloride is preheated in a special furnace and is then cast into the mold. Molten aluminum infiltrates the salt bed by vacuum suction. The technology reduces production costs significantly and facilitates the manufacture of a variety of porous cast aluminum items, mainly filter cells and pneumatic silencers.
The main characteristic that determines the dimensions and features (wall thickness, surface area) of porous casting is permeability
K in an integrated form of Darcy’s law:
where
Q (m
3/s) is an average volumetric flow rate through the porous medium, Δ
P is the pressure drop experienced by a fluid of dynamic viscosity μ traversing through the porous medium,
l is the thickness of the porous medium along the direction of fluid flow,
F is the average cross-section area (m
2) of the porous medium perpendicularly to the direction of fluid flow.
The permeability K is determined by porous medium structure, which is the result of capillary interaction between molten metal and solid salt granules.
2. Theory
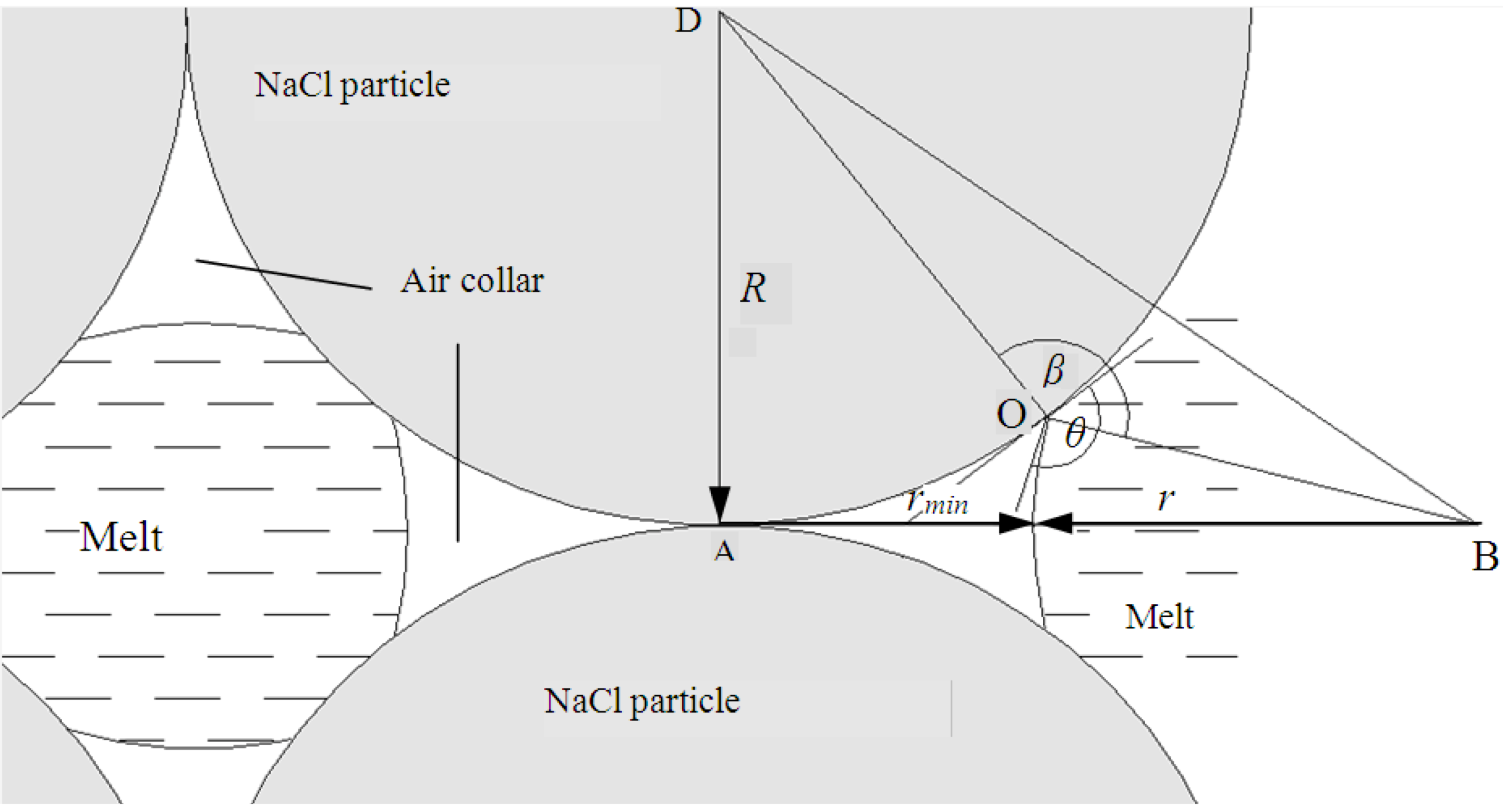
Let us assume that NaCl granules are of spherical shape with the uniform radius
R. Consequently poor wettability of NaCl by molten aluminum at the contact between nearest NaCl granules leads to the formation of air pockets or “air collars” (
Figure 1).
After solidification of the metal and dissolution of NaCl, the porous medium consists of cavities, shaped by parent NaCl granules connected through the air collars (
Figure 2). Thereby, the replicated metal foam structure is described by two defined pore sizes: the maximum is equal to 2
R and the minimum is equal to 2
rmin where
rmin is the internal radius of an air collar (see
Figure 1).
Figure 1.
Air collars formation due to infiltration of melted metal into the layer of NaCl granules.
Figure 2.
Porous structure model.
The shape of the air collar is described by Laplace’s Equation:
where σ is the surface tension of the molten metal,
r is the external radius of the air collar,
P is the pressure on the surface of the air collar determined as a vector sum of external pressures:
where
Pat is theatmospheric pressure and
Pac is the pressure of air entrapped during melt filtration in the air collar, ρ is the melt density,
h is the height of liquid column.
Since the radii of the air collar’s curvatures are in mutually perpendicular planes, Laplace’s Equation (2) can be rearranged to:
The angle β (
Figure 1) is equal to the wetting angle θ that can be geometrically defined from
Figure 1. We have found the length of the segment DB applying Pythagorean theorem to triangle АDB, and the cosine theorem to triangle DОB. Simple algebraic manipulations yield:
The simultaneous solution of Equations (4) and (5) gives the equation for the minimum pore radius of replicated aluminum foam:
We used the model of thermal conductivity of a granular medium in vacuum [
6] to predict the permeability of replicated foam. The model shows that the main resistance concentrates at contact spots between grains, which form the minimal pore in the structure of replicated foam. Thereby, the main assumption of the permeability model consists in concentration of flow resistance at circular aperture of radius
rmin [
5].
A similar “bottleneck” model was applied to derive the permeability of replicated aluminum foam in [
4].
We can consider the pressure drop Δ
Pr at this aperture (presented as aperture in a thin plane) by the following expression:
where
q is the flow rate through one aperture of radius
rmin.
We can divide the porous media into slabs of thickness 2R along the average flow direction.
Because the air collar is located in the zone of contact between grains, the number of apertures of radius
rmin for one grain defined as coordination number
N, is described by Equation [
7]:
where Δ is the porosity of the NaCl bed. Due to the large ratio between maximum and minimum pore sizes, the porosity of replicated aluminum foam is close to (1 − Δ).
Each sphere is in contact with
N adjoining spheres, so that the direction of each mutually perpendicular axis corresponds to
N/3 contacts and each of the opposite directions along one axis corresponds to
N/6 contacts. The physical meaning of this proposition consists in a numerical value of the flow rate vector
![Metals 03 00049 i006]()
through one aperture of radius
rmin in one slab along the macroscopic flow direction:
The number of spheres contained in one slab is given by:
Let us suppose that isobars are corresponding with planes, perpendicular to the direction of filtration. Then the loss of pressure in each slab is ΔPn, and the flow rate through one slab is equal to the flow rate through the porous medium Q. Therefore, the flow rate through one slab is given by the joint solution of Equations (7), (9) and (10).
We assume a homogeneous distribution of the pressure loss along the flow direction. Then, we calculate the combined loss of pressure through a porous medium (contained
l/2
R slabs) as:
The solution of Equations (1), (8) and (12) leads to the expression for permeability of replicated aluminum foam:
3. Experimental Procedures and Results
Replicated aluminum foam was produced by the process described in Reference [
3,
5]. Pure sodium chloride of spherical shape was sieved to obtain the following fractions: 0.32–0.63 mm, 0.63–0.8 mm, 0.8–1.0 mm. Fraction 1.0–1.5 mm had a fragmental shape. Then sodium chloride was heated to 700 °C in an electric furnace and was poured into a metal mold of 80 mm diameter and 140 mm height, preheated to 500 °C. Molten metal (99.95% Al) was poured over the surface of the NaCl bed and then infiltrated with vacuum suction.
The porosity of NaCl bed varied from 50% up to 65% (in case of the compaction by vibration). The gauge DV8009-Kc of the membrane type with an error of 2.5% was used to estimate the pressure vacuum.
The resulting Al-NaCl composite with monolithic Al casting head was extracted from the mold after solidification. The total height of castings ranged from 120 to 140 mm with 20–40 mm metal head. In fact the height of metal head is irrelevant to the determination of the hydrostatic pressure. Samples of one inch diameter and 10 mm height were cut from the bottom part of the composite (10 mm from bottom surface). Sodium chloride was subsequently removed by dissolution in water. The hydrostatic pressure was determined individually for each casting. The contribution of the hydrostatic pressure is in the range of 2% to 14%.
The photomicrograph of the flat surface of replicated foam (
Figure 3) was examined by SIAMS (System of Image Analysis and Modeling Structures, SIAMS Ltd., Ekaterinburg, Russia) based on SIMAGIS software for image analysis [
8]. The error of pore’s size determination in this case doesn’t exceed 0.5% so it complicates the showing of error bars on the
Figure 4.
Figure 3.
Photomicrograph of flat surface of replicated foam.
Figure 4.
Relation between aperture radius and NaCl particle size (P = 25 kPa).
The aperture radius between the big pores corresponding to the radius of the air collar and the minimum pore radius of replicated aluminum foam was calculated using
rmin=
![Metals 03 00049 i012]()
,where
S is the average area of 10 apertures in one sample.
Figure 4 shows the results of experimental
rmin in comparison with theoretical calculations by Equation (5). Data of capillary interaction of molten aluminum alloys with inorganic salts are given in [
9]. According to [
9], the wetting angle θ for system of NaCl and pure aluminum is equal to 140 degrees and the surface tension σ is 945 MJ/m
2.
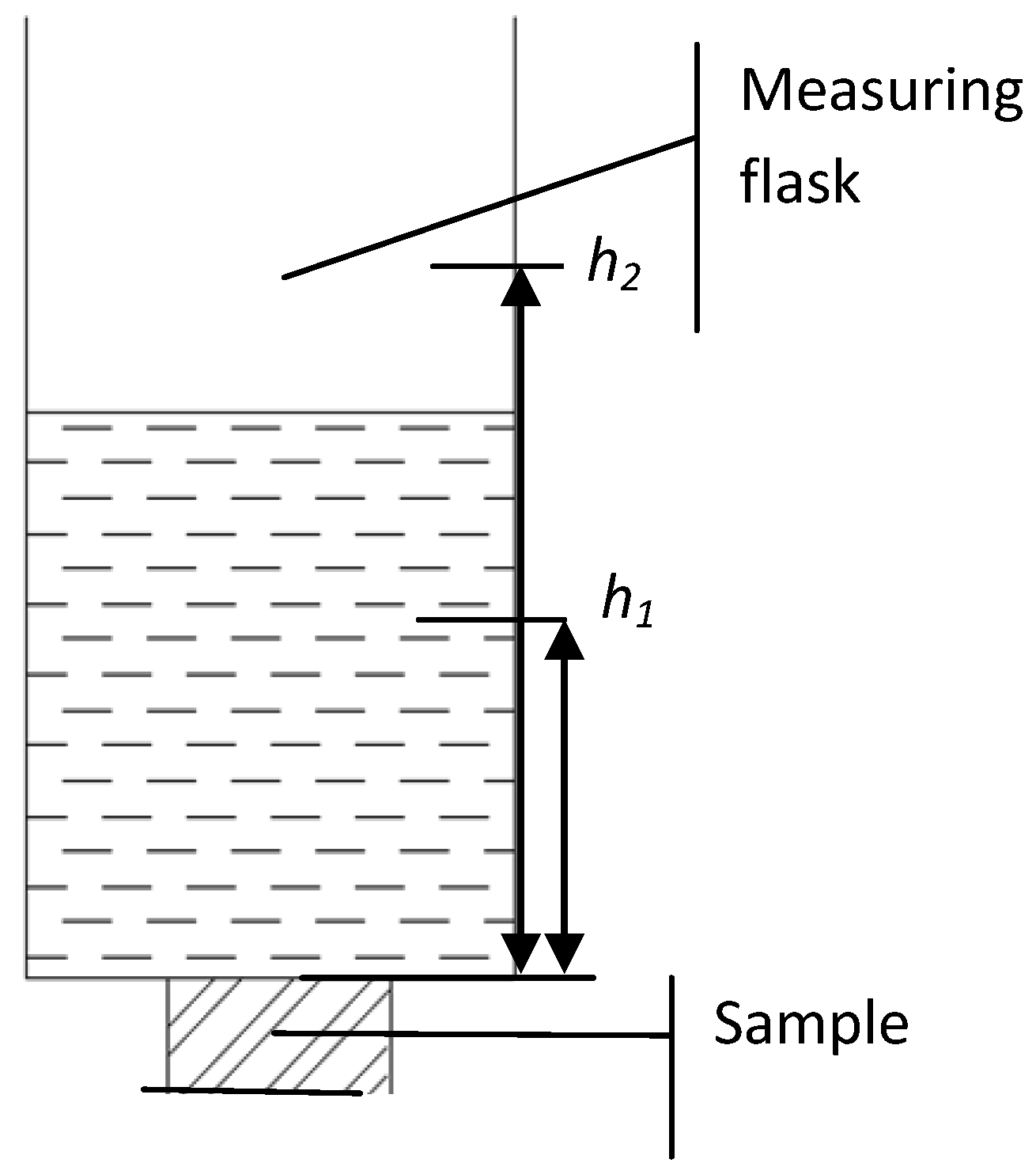
The set up for measuring the permeability of replicated aluminum foam is shown in
Figure 5. The liquid (transformer oil of viscosity μ
o from a standard measuring flask) flowed through the porous sample. The measured value of viscosity of the oil was 0.0216 Pa·s ± 2.5% (at 20 °С). The height of the liquid column changed from
h2 to
h1 during filtration. Minimum filtration time was equal to 100 s at the highest value of permeability and was measured three times for each experimental condition.
Figure 5.
Set up for measuring the permeability of porous sample.
The reduction of the liquid column according to Darcy’s law is given by the Equation (1) in the differential form:
where
h is the height of the liquid column, ρ is the density of filtrated liquid,
Fo is the sectional area of the measuring flask. After this, Equation (14) is integrated:
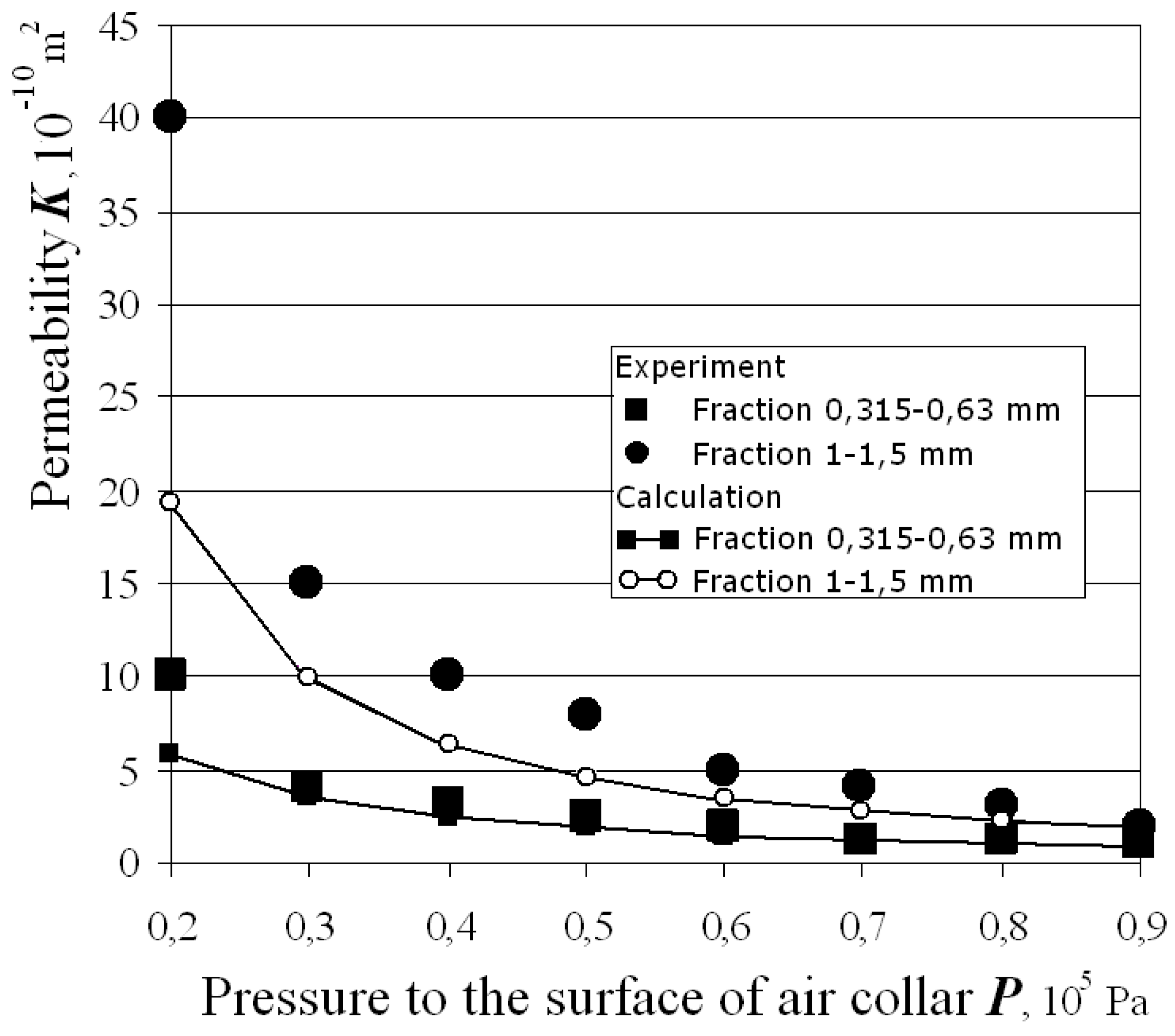
Figure 6 shows experimental results of
K observation in comparison with theoretical calculations by Equation (13). The porosity of replicated aluminum foam (1 − Δ) was about 60% in this case. Finally the micrograph of real foam is given in
Figure 7. The total instrument’s error did not exceed 3.5% in all experiments.
Figure 6.
Permeability of replicated aluminum.
Figure 7.
Micrograph of real foam samples.
4. Discussion
Measured values of average minimum pore size are close to theoretically predicted ones, regardless of the particle shape. Because of their fragmental shape some particles are interconnected with sharp angle to flat, others with flat to flat angle. Subsequently, the minimum pore size varies over a wide range, but the average value is close to that calculated by Equation (6). Therefore, Equation (6) can be applied easily for the estimation of the minimum pore size of replicated aluminum foam. Equations (6) and (13) are consequently solved. Predictions of Equation (13) are in compliance with experiment (
Figure 6), especially for the samples produced at higher pressure drop. We notice significant discrepancy between experimental data and results of theoretical calculations at low pressure drop. The explanation can be found in the impossibility to represent the pore of minimum radius as an aperture in a thin plate. In case of low pressure drop the proportion between minimum and maximum size of pores is more than one quarter, and the flow of liquid is close to the modified Cozeny-Carman formula that connects the permeability with the average capillary radius (
K =
f (
R + rmin)
2) [
10]. Therefore, the permeability at low pressure drop differs from that calculated by Equation (13). Nevertheless, we use Equation (13) to design porous castings because they are usually produced for industrial applications at higher pressure drop.
The agreement with experiments is found to be very satisfying, especially due to the consecutive application of two models.
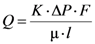

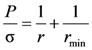
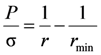
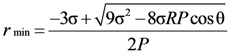
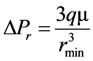
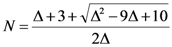
 through one aperture of radius rmin in one slab along the macroscopic flow direction:
through one aperture of radius rmin in one slab along the macroscopic flow direction:
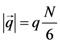
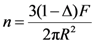
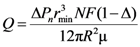
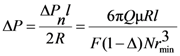
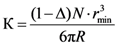


 ,where S is the average area of 10 apertures in one sample.
,where S is the average area of 10 apertures in one sample.