Structural Irreversibility and Enhanced Brittleness under Fatigue in Zr-Based Amorphous Solids
Abstract
:1. Introduction
2. Results and Discussion
2.1. Specific Heat
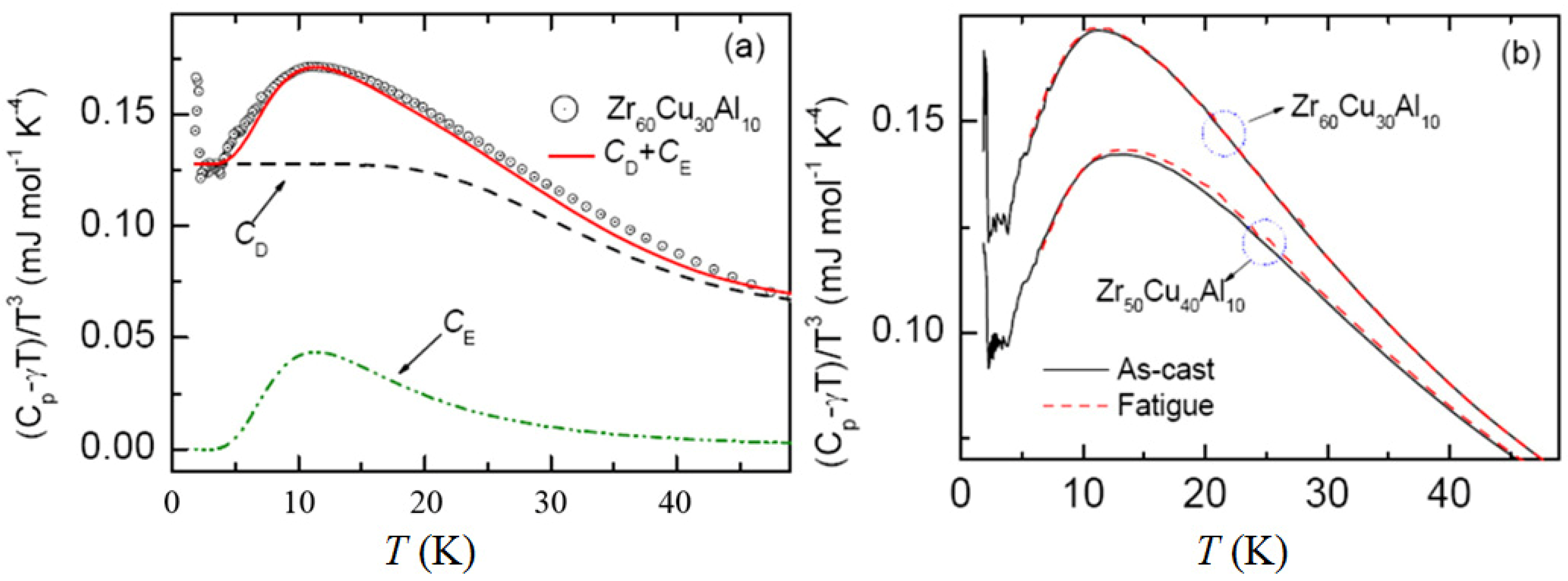
2.2. Inelastic Neutron Scattering
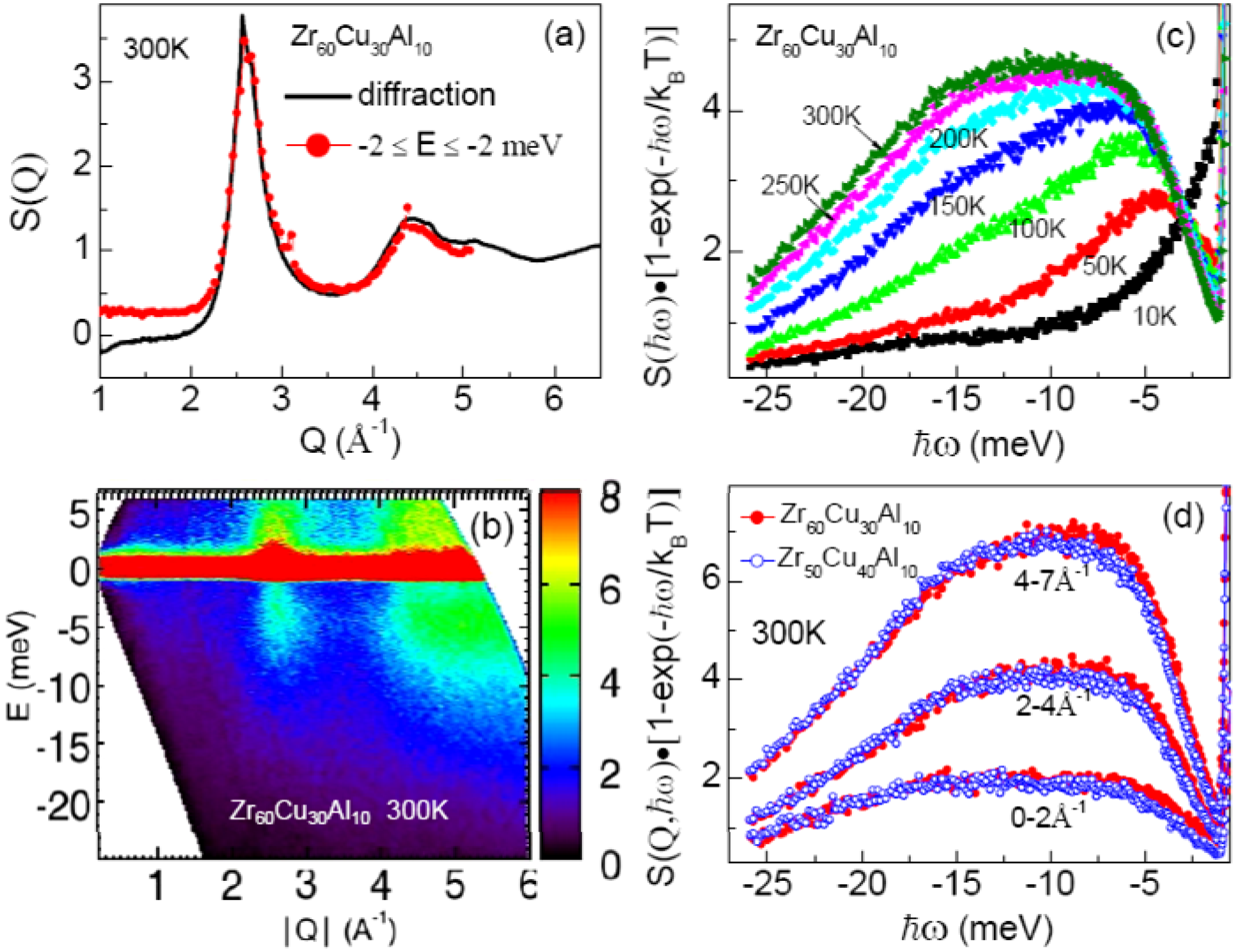
2.3. Vibrational Density of States under Fatigue
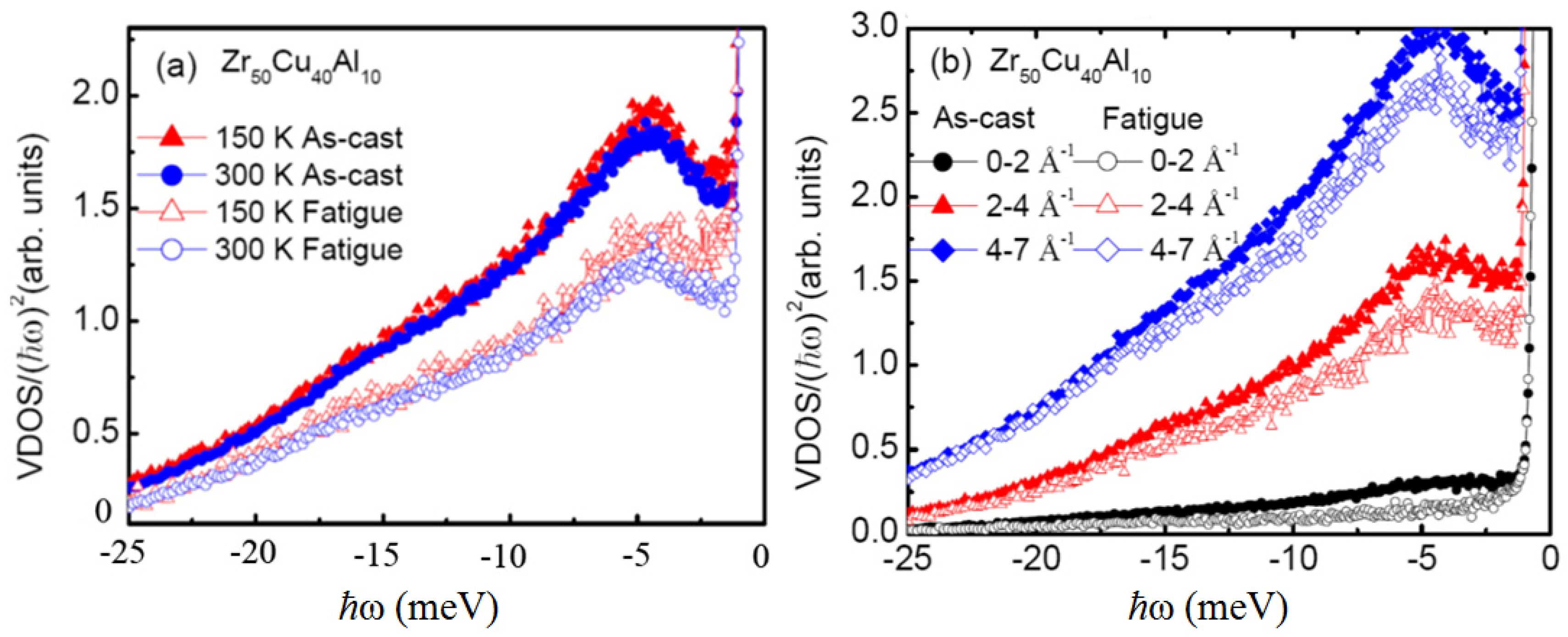
2.4. Local Structure under Fatigue
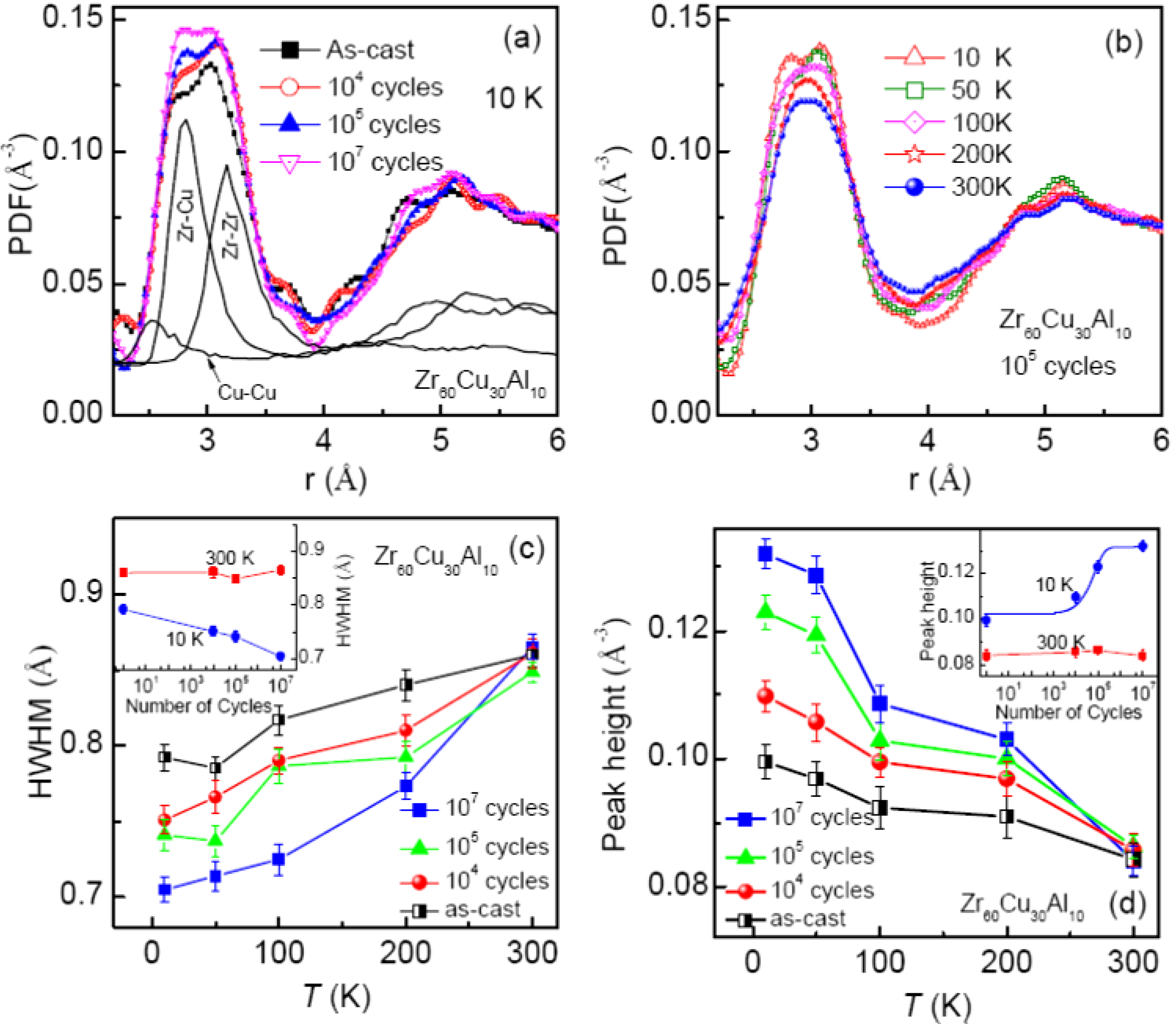
3. Experimental Section
4. Conclusions
Acknowledgments
Conflict of Interest
References
- Debenedetti, P.G.; Stillinger, F.H. Supercooled liquids and the glass transition. Nature 2001, 410, 259–267. [Google Scholar] [CrossRef]
- Spaepen, F. A microscopic mechanism for steady state inhomogeneous flow in metallic glasses. Acta Mater. 1977, 25, 407–415. [Google Scholar] [CrossRef]
- Argon, A.S. Plastic deformation in metallic glasses. Acta Mater. 1979, 27, 47–58. [Google Scholar] [CrossRef]
- Masumoto, T.; Maddin, R. Structural stability and mechanical properties of amorphous metals. Mater. Sci. Eng. 1975, 19, 1–24. [Google Scholar] [CrossRef]
- Greer, A.L.; Ma, E. Bulk metallic glasses: At the cutting edge of metals research. MRS Bull. 2007, 32, 611–615. [Google Scholar] [CrossRef]
- Chen, M.; Inoue, A.; Zhang, W.; Sakurai, T. Extraordinary plasticity of ductile bulk metallic glasses. Phys. Rev. Lett. 2006, 96, 245502:1–245502:4. [Google Scholar]
- Scopigno, T.; Ruocco, G.; Sette, F.; Monaco, G. Is the fragility of a liquid embedded in the properties of its glass? Science 2003, 302, 849–852. [Google Scholar] [CrossRef]
- Das, J.; Tang, M.B.; Kim, K.B.; Theissmann, R.; Baier, F.; Wang, W.H.; Eckert, J. “Work-hardenable” ductile bulk metallic glass. Phys. Rev. Lett. 2005, 94, 205501:1–205501:4. [Google Scholar]
- Greer, A.L. Metallic glasses. Science 1995, 267, 1947–1953. [Google Scholar]
- Freels, M.; Wang, G.Y.; Zhang, W.; Liaw, P.K.; Inoue, A. Cyclic compression behavior of a Cu-Zr-Al-Ag bulk metallic glass. Intermetallics 2011, 19, 1174–1183. [Google Scholar] [CrossRef]
- Wang, G.Y.; Liaw, P.K.; Jin, X.Q.; Yokoyama, Y.; Huang, E.W.; Jiang, F.; Keer, L.M.; Inoue, A. Fatigue initiation and propagation behavior in bulk metallic glasses under a bending load. J. Appl. Phys. 2010, 108, 113512:1–113512:7. [Google Scholar]
- Wang, G.Y.; Qiao, D.C.; Yokoyama, Y.; Freels, M.; Inoue, A.; Liaw, P.K. Effects of loading modes on the fatigue behavior of Zr-based bulk metallic glasses. J. Alloys Comp. 2009, 483, 143–145. [Google Scholar] [CrossRef]
- Buchenau, U.; Nucker, N.; Dianoux, A.J. Neutron scattering study of the low-frequency vibrations in vitreous Silica. Phys. Rev. Lett. 1984, 53, 2316:1–2316:4. [Google Scholar]
- Sette, F.; Krisch, M.H.; Masciovecchio, C.; Ruocco, G.; Monaco, G. Dynamics of glasses and glass-forming liquids studies by inelastic x-ray scattering. Science 1998, 280, 1550–1555. [Google Scholar] [CrossRef]
- Shintani, H.; Tanaka, H. Universal link between the boson peak and transverse phonons in glass. Nature Mat. 2008, 7, 870–877. [Google Scholar] [CrossRef]
- Sokolov, A.P.; Calemczuk, R.; Salce, B.; Kisliuk, A.; Quitmann, D.; Duval, E. Low temperature anomalies in strong and fragile glass formers. Phys. Rev. Lett. 1997, 78, 2405:1–2405:1. [Google Scholar]
- Duval, E.; Boukenter, A.; Achibat, T. Vibrational dynamics and the structure of glasses. J. Phys. Condens. Matter. 1990, 2, 10227–10234. [Google Scholar] [CrossRef]
- Klinger, M.I.; Kosevich, A.M. Soft-mode-dynamics model of acoustic-like high-frequency excitations in boson-peak spectra of glasses. Phys. Lett. A 2001, 280, 365–370. [Google Scholar] [CrossRef]
- Chumakov, A.I.; Monaco, G.; Monaco, A.; Crichton, W.A.; Bosak, A.; Rüffer, R.; Meyer, A.; Kargl, F.; Comez, L.; Fioretto, D.; et al. Equivalence of the Boson peak in glasses to the transverse acoustic van hove singularity in crystals. Phys. Rev. Lett. 2011, 106, 225501:1–225501:4. [Google Scholar]
- Schirmacher, W.; Diezemann, G.; Ganter, C. Harmonic vibrational excitations in disordered solids and the “Boson peak”. Phys. Rev. Lett. 1998, 81, 136:1–136:4. [Google Scholar]
- Taraskin, S.N.; Loh, Y.L.; Natarajan, G.; Elliott, S.R. Origin of the Boson peak in systems with lattice disorder. Phys. Rev. Lett. 2001, 86, 1255:1–1255:4. [Google Scholar]
- Novikov, V.N.; Sokolov, A.P. Poisson’s ratio and the fragility of glass-forming liquids. Nature 2004, 431, 961–963. [Google Scholar] [CrossRef]
- Johnson, W.L. Bulk Glass-Forming Metallic Alloys: Science and Technology. In Bulk Metallic Glasses, Proceedings of Materials Research Society Symposium, Boston, MA, USA, December 1–3, 1998; Johnson, W.L., Inoue, A., Liu, C.T., Eds.; Materials Research Society: Warrendale, PA, USA, 1999; 554, pp. 191–196. [Google Scholar]
- Inoue, A. Bulk Amorphous Alloys: Practical Characteristics and Applications; Trans Tech Publications: Zurich, Switzerland, 1999. [Google Scholar]
- Pacard, C.E.; Homer, E.R.; Al-Aqeeli, N.; Schuh, C.A. Cyclic hardening of metallic glasses under Hertzian contacts: Experiments and STZ dynamics simulations. Philos. Mag. 2010, 90, 1373–1390. [Google Scholar] [CrossRef]
- Packard, C.E.; Witmer, L.M.; Schuh, C.A. Hardening of a metallic glass during cyclic loading in elastic range. Appl. Phys. Lett. 2008, 92, 171911:1–171911:3. [Google Scholar]
- Li, Y.; Bai, H.Y.; Wang, W.H.; Samwer, K. Low-temperature specific heat anomalies associated with the boson peak in CuZr-based bulk metallic glasses. Phys. Rev. B 2006, 74, 052201:1–052201:4. [Google Scholar]
- Inoue, A. Stabilization of metallic supercooled liquid and bulk amorphous alloys. Acta Mater. 2000, 48, 279–306. [Google Scholar] [CrossRef]
- Wang, G.Y.; Liaw, P.K.; Peter, W.H.; Yang, B.; Yokoyama, Y.; Benson, M.L.; Green, B.A.; Kirkham, M.J.; White, S.A.; Saleh, T.A.; et al. Fatigue behavior of bulk metallic glasses. Intermetallics 2004, 12, 885–892. [Google Scholar] [CrossRef]
- Qiao, D.C.; Huang, L.; Jiang, W.; Fan, C.; Liaw, P.K. Fatigue softening of (Zr58Ni13.6Cu18Al10.4)99Nb1 bulk metallic glass. Metall. Mat. Trans. A 2010, 41, 1787–1791. [Google Scholar] [CrossRef]
- Tang, M.B.; Bai, H.Y.; Pan, M.X.; Zhao, D.Q.; Wang, W.H. Einstein oscillator in highly-random-packed bulk metallic glass. Appl. Phys. Lett. 2005, 86, 021910:1–021910:3. [Google Scholar]
- Keppens, V.; Mandrus, D.; Sales, B.C.; Chakoumakos, B.C.; Dai, P.; Coldea, R.; Maple, M.B.; Gajewski, D.A.; Freeman, E.J.; Bennington, S. Localized vibrational modes in metallic solids. Nature 1998, 395, 876–878. [Google Scholar]
- Hermann, R.P. Einstein oscillators in thallium filled antimony skutterudites. Phys. Rev. Lett. 2003, 90, 135505:1–135505:1. [Google Scholar]
- Grigera, T.S.; Martin-Mayor, V.; Parisi, G.; Verrocchio, P. Phonon interpretation of the “Boson peak” in supercooled liquids. Nature 2003, 422, 289–292. [Google Scholar]
- Malinovsky, V.K.; Sokolov, A.P. The nature of boson peak in Raman spectra in glasses. Solid State Comm. 1986, 57, 757–761. [Google Scholar] [CrossRef]
- Yannopoulos, S.N.; Andrikopoulos, K.S.; Ruocco, G. On the analysis of the vibrational Boson peak and low-energy excitations in glasses. J. Non-Cryst. Solids 2006, 352, 4541–4551. [Google Scholar] [CrossRef]
- Kazimirov, V.Y.; Louca, D.; Widom, M.; Gu, X.-J.; Poon, S.J.; Shiflet, G.J. Local organization and atomic clustering in multicomponent amorphous steels. Phys. Rev. B 2008, 78, 054112:1–054112:5. [Google Scholar]
- Daw, M.S.; Baskes, M.I. Semiempirical, quantum mechanical calculation of hydrogen embrittlement in metals. Phys. Rev. Lett. 1983, 50, 1285:1–1285:4. [Google Scholar]
- Cheng, Y.Q.; Ma, E.; Sheng, H.W. Atomic level structure in multicomponent bulk metallic glass. Phys. Rev. Lett. 2009, 102, 245501:1–245501:4. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Tong, P.; Louca, D.; Wang, G.; Liaw, P.K.; Yokoyama, Y.; Llobet, A.; Kawaji, H.; Qiu, Y.; Shi, Y. Structural Irreversibility and Enhanced Brittleness under Fatigue in Zr-Based Amorphous Solids. Metals 2012, 2, 529-539. https://doi.org/10.3390/met2040529
Tong P, Louca D, Wang G, Liaw PK, Yokoyama Y, Llobet A, Kawaji H, Qiu Y, Shi Y. Structural Irreversibility and Enhanced Brittleness under Fatigue in Zr-Based Amorphous Solids. Metals. 2012; 2(4):529-539. https://doi.org/10.3390/met2040529
Chicago/Turabian StyleTong, Peng, Despina Louca, Gongyao Wang, Peter K. Liaw, Yoshihiko Yokoyama, Anna Llobet, Hiroshi Kawaji, Yiming Qiu, and Yunfeng Shi. 2012. "Structural Irreversibility and Enhanced Brittleness under Fatigue in Zr-Based Amorphous Solids" Metals 2, no. 4: 529-539. https://doi.org/10.3390/met2040529





