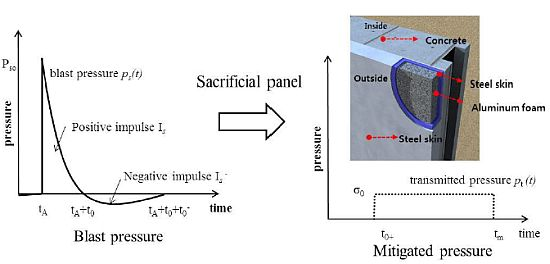
Mitigation of Blast Effects on Protective Structures by Aluminum Foam Panels
Abstract
:1. Introduction
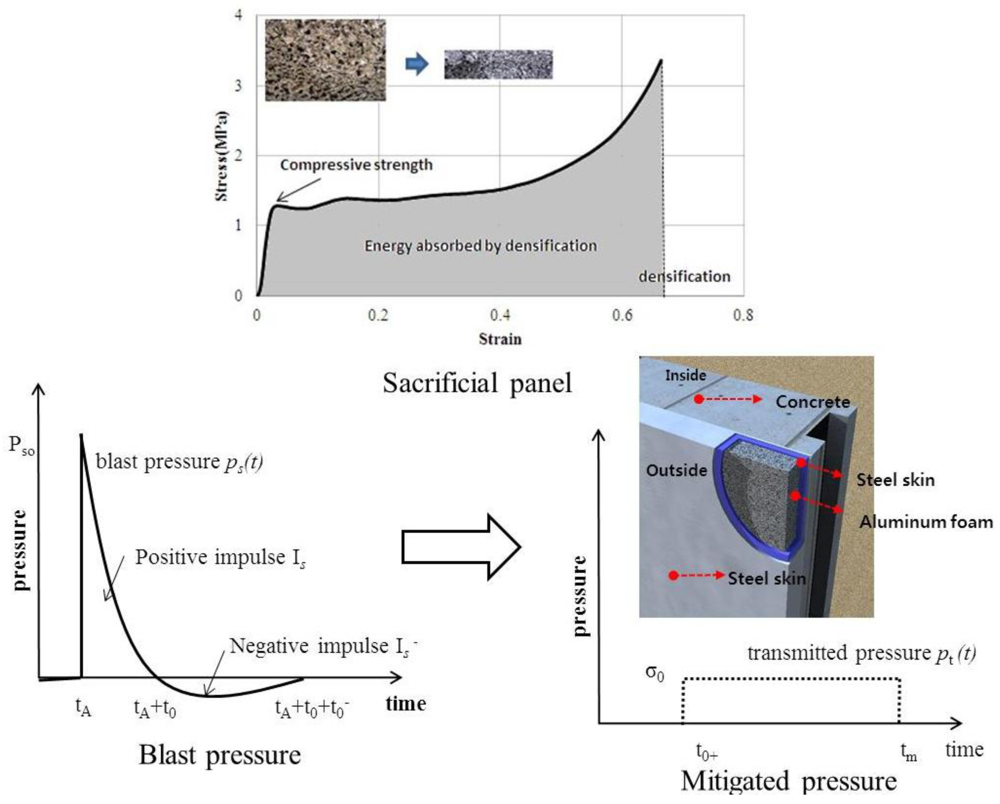
2. Material Models
2.1. Mechanical Properties of Aluminum Foams

| Density | Yield strength (Z) | Yield strength (X, Y) | densification strain | Energy absorption capacity (20% strain) | Energy absorption capacity (50% strain) |
|---|---|---|---|---|---|
| 200 kg/m3 | 0.8 MPa | 0.9 MPa | 70% | 0.24 MJ/m3 | 0.61 MJ/m3 |
| 370 kg/m3 | 1.9 MPa | 2.2 MPa | 65% | 0.52 MJ/m3 | 1.28 MJ/m3 |
2.2. Material Models for Explicit Analysis
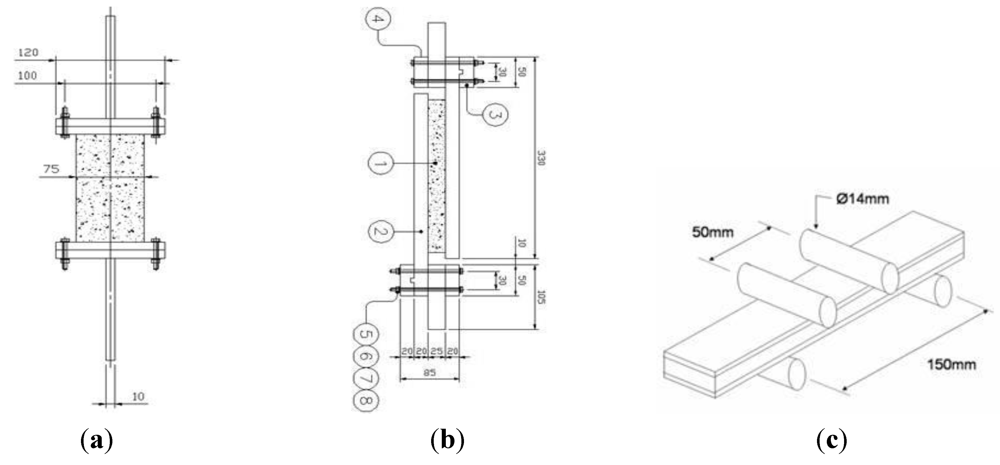
3. Blast Tests and Analyses
3.1. Test Setup and Specimens
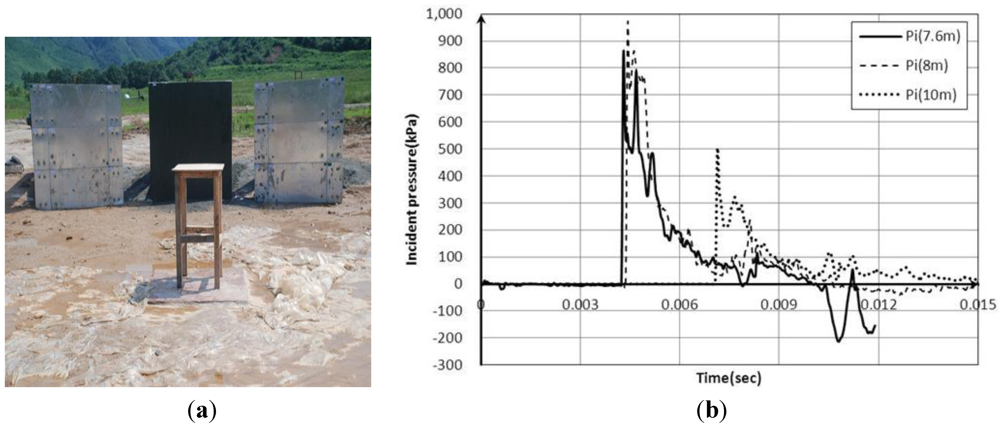
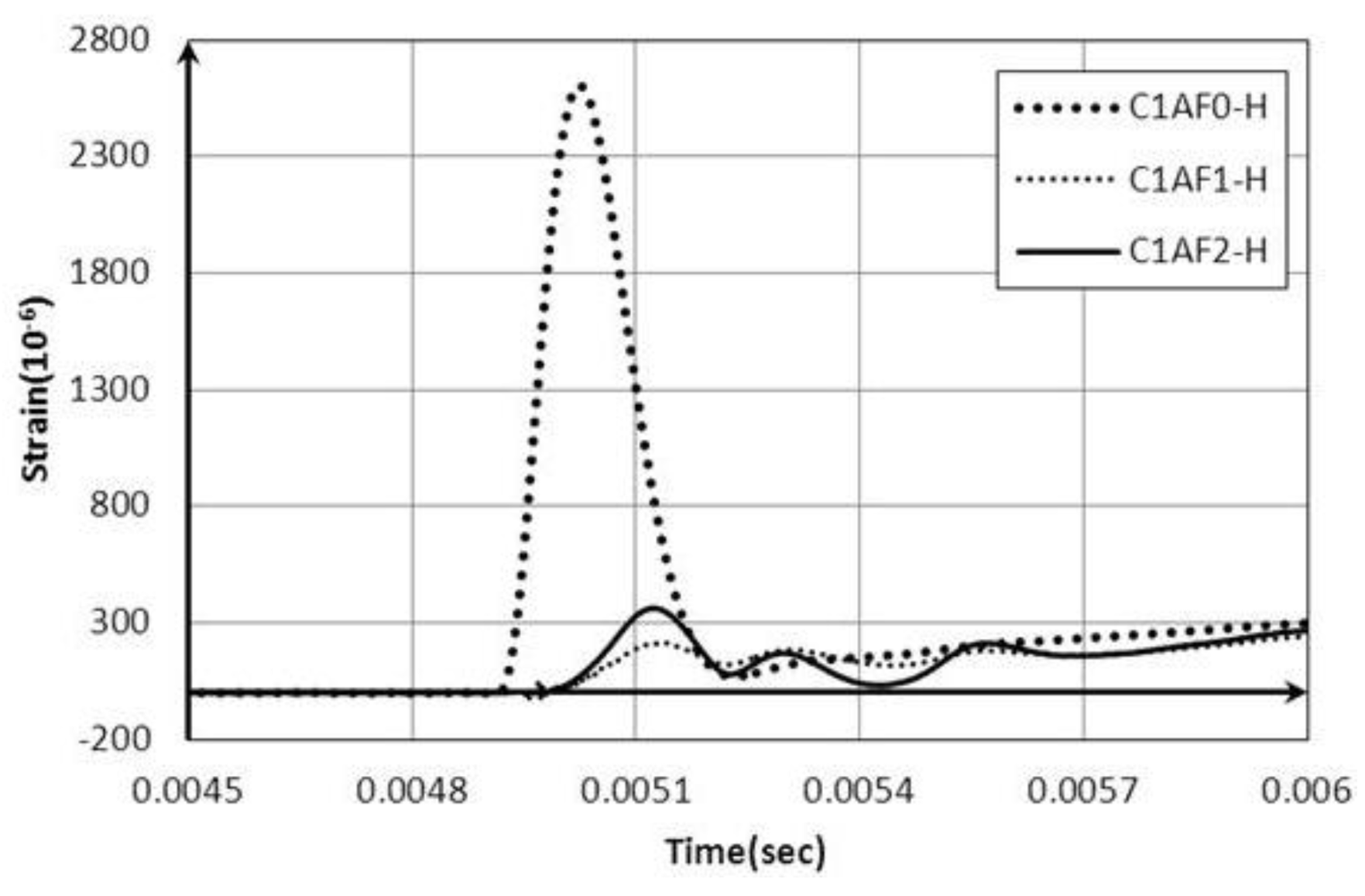
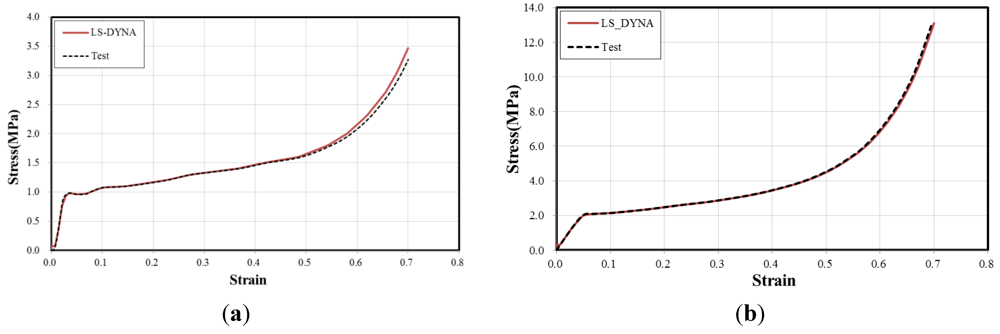
3.2. Explicit Finite Element Analyses
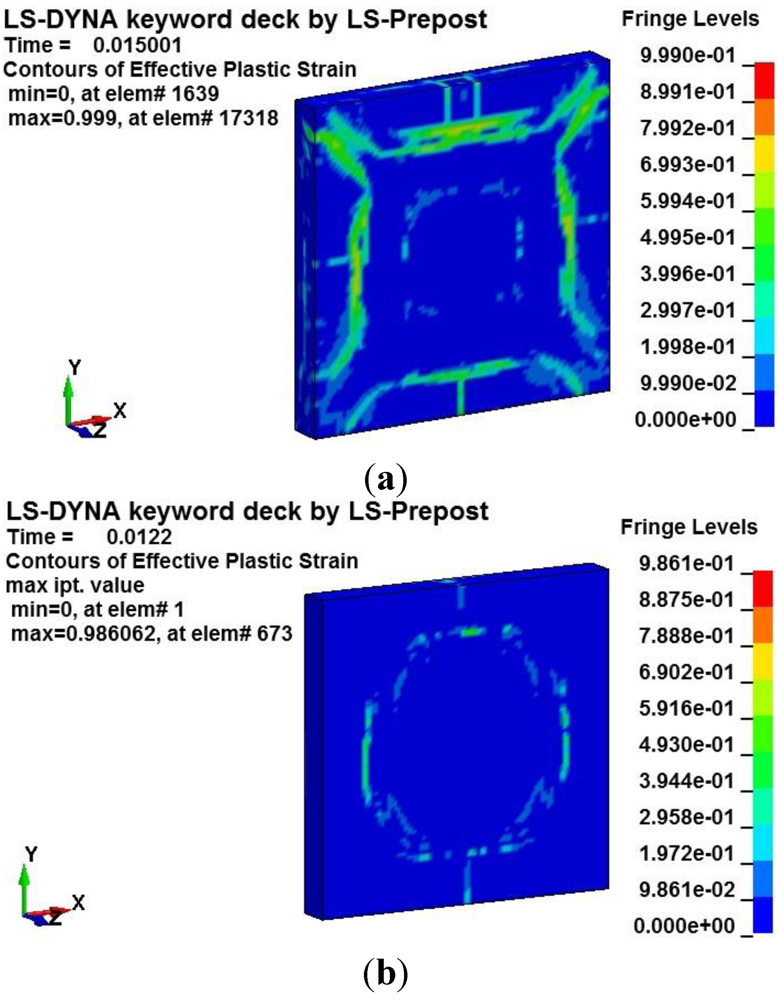
4. Conclusions
Acknowledgments
Conflict of Interest
References
- Dannemann, K.A.; Lankford, J., Jr. High strain rate compression of closed-cell aluminum foams. J. Mater. Sci. A 2000, 293, 157–164. [Google Scholar] [CrossRef]
- Sadot, O.; Anteby, I.; Harush, S.; Levintant, O.; Nizri, E.; Ostraich, B.; Schenker, A.; Gal, E.; Kivity, Y.; Ben-Dor, G. Experimental investigation of dynamic properties of aluminum foams. J. Struct. Eng. 2005, 131, 1226–1232. [Google Scholar]
- Shim, C.; Yun, N. Evaluation of close-range blast pressure mitigation using a sacrificial member. J. Earthq. Eng. Soc. Korea 2010, 14, 11–23. [Google Scholar] [CrossRef]
- Hanssen, A.G.; Enstock, L.; Langseth, M. Close range blast loading of aluminium foam panels. Int. J. Impact Eng. 2002, 27, 593–618. [Google Scholar] [CrossRef]
- Mukai, T.; Kanahashi, H.; Miyoshi, T.; Mabuchi, M.; Nieh, T.G.; Higashi, K. Experimental studyof energy absorption in closed-cell aluminum foam under dynamic loading. Scripta Met. 1999, 40, 921. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Fleck, N.A. Isotropic constitutive models for metallic foams. J. Mech. Phys. Solids 2000, 48, 1253–1283. [Google Scholar]
- Langdon, G.S.; Karagiozova, D.; Theobald, M.D.; Nurick, G.N.; Lu, G.; Merrett, R.P. Fracture of aluminum foam core sacrificial cladding subjected to air-blast loading. Int. J. Impact Eng. 2010, 37, 638–651. [Google Scholar] [CrossRef]
- Hanssen, A.G.; Hopperstad, O.S.; Langseth, M.; Ilstad, H. Validation of constitutive models applicable to aluminium foams. Int. J. Mech. Sci. 2002, 44, 359–406. [Google Scholar] [CrossRef]
- Hanssen, A.G.; Girard, Y.; Olovsson, L.; Berstad, T.; Langseth, M. A numerical model for bird strike of aluminium foam-based sandwich panels. Int. J. Impact Eng. 2006, 32, 1127–1144. [Google Scholar] [CrossRef]
- Shahbeyk, S.; Petrinic, N.; Vafai, A. Numerical modelling of dynamically loaded metal foam-filled square columns. Int. J. Impact Eng. 2007, 34, 573–586. [Google Scholar] [CrossRef]
- LS-DYNA Keyword User’s Manual; Livermore Software Technology Corporation: Livermore, CA, USA, 2006.
- Standard Test Method for Flatwise Compressive Properties of Sandwich Cores; ASTM C365-03; American Society for Testing and Materials: West Conshohocken, PA, USA, 2003.
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Shim, C.; Yun, N.; Yu, R.; Byun, D. Mitigation of Blast Effects on Protective Structures by Aluminum Foam Panels. Metals 2012, 2, 170-177. https://doi.org/10.3390/met2020170
Shim C, Yun N, Yu R, Byun D. Mitigation of Blast Effects on Protective Structures by Aluminum Foam Panels. Metals. 2012; 2(2):170-177. https://doi.org/10.3390/met2020170
Chicago/Turabian StyleShim, Changsu, Nuri Yun, Robin Yu, and Doyeon Byun. 2012. "Mitigation of Blast Effects on Protective Structures by Aluminum Foam Panels" Metals 2, no. 2: 170-177. https://doi.org/10.3390/met2020170