Thermal Conductivity Computations of Sintered Hollow Sphere Structures
Abstract
:1. Introduction
2. Methodology and Material
2.1. Numerical Modeling

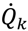 perpendicular to the surfaces with the constant temperature is calculated by the finite element analysis. The total heat flux
perpendicular to the surfaces with the constant temperature is calculated by the finite element analysis. The total heat flux  is the sum of the single nodal heat fluxes
is the sum of the single nodal heat fluxes 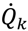 through one of the boundary surfaces. Within this study, the thermal radiation effect on heat transfer is neglected since its contribution is very low for the relevant temperature range which is below 700 K [24]. The influence of thermal convection is also disregarded because sintered HSS represents mainly a closed-cell structure with a low volume fraction of interconnected porosity [2]. In this study, pores are assumed to be filled with air. Due to the low thermal conductivity of the gas mixture, conductive heat transfer inside the pore space is negligible. These assumptions simplify the mathematical description of the heat transfer and the effective thermal conductivity can be calculated according to Equation (1) with Fourier’s law.
through one of the boundary surfaces. Within this study, the thermal radiation effect on heat transfer is neglected since its contribution is very low for the relevant temperature range which is below 700 K [24]. The influence of thermal convection is also disregarded because sintered HSS represents mainly a closed-cell structure with a low volume fraction of interconnected porosity [2]. In this study, pores are assumed to be filled with air. Due to the low thermal conductivity of the gas mixture, conductive heat transfer inside the pore space is negligible. These assumptions simplify the mathematical description of the heat transfer and the effective thermal conductivity can be calculated according to Equation (1) with Fourier’s law. 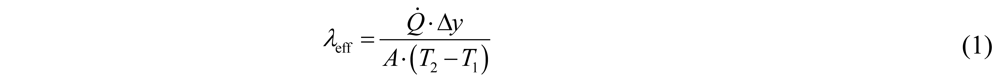
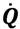 = heat flux, Δy = spatial distance between two opposing boundary surfaces, A = projected area, T1 = temperature on the top, T2 = temperature on the bottom. The geometry shown in Figure 1 consists of approximately 5 cells per edge length and consequently possesses about 53 = 125 cells in total. This number exceeds the approximately 100 cells required for a representative volume [15]. The model size is 18 × 18 × 18 mm and is represented by 4003 voxels resulting in a resolution of 0.045 mm/voxel. The FE-model consists of roughly five million elements (i.e., hexahedral-, tetrahedral- and pentahedral elements).
= heat flux, Δy = spatial distance between two opposing boundary surfaces, A = projected area, T1 = temperature on the top, T2 = temperature on the bottom. The geometry shown in Figure 1 consists of approximately 5 cells per edge length and consequently possesses about 53 = 125 cells in total. This number exceeds the approximately 100 cells required for a representative volume [15]. The model size is 18 × 18 × 18 mm and is represented by 4003 voxels resulting in a resolution of 0.045 mm/voxel. The FE-model consists of roughly five million elements (i.e., hexahedral-, tetrahedral- and pentahedral elements).2.2. Material


3. Numerical Results
3.1. Convergence Analysis
| Elements | Nodes | Mesh density | V3D | VFE | |ΔV| | λ |
|---|---|---|---|---|---|---|
| [−] | [−] | [Elements/Vvoxels] | [−] | [−] | [−] | [%] |
| 212941 | 90151 | 0.30 | 0.149 | 0.15 | 0.00671 | 9.15 |
| 343344 | 154412 | 0.49 | 0.149 | 0.15 | 0.00671 | 9.14 |
| 622385 | 311255 | 0.88 | 0.149 | 0.149 | 0 | 9.05 |
| 1489933 | 790252 | 2.13 | 0.149 | 0.149 | 0 | 9.05 |
| 2509508 | 1424344 | 3.57 | 0.149 | 0.149 | 0 | 9.03 |
| 5114321 | 3136257 | 7.14 | 0.149 | 0.149 | 0 | 9.03 |
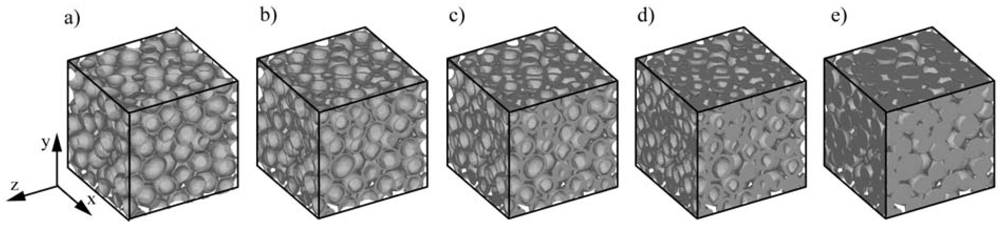
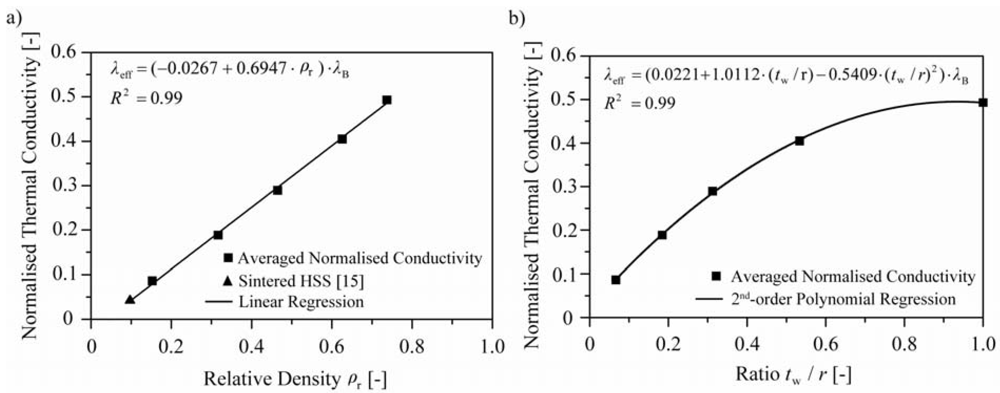
3.2. Results and Discussion

4. Conclusions
Acknowledgments
References
- Gibson, L.J.; Ashby, M.F.; Harley, A.B. Cellular Materials in Nature and Medicine; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
- Gibson, L.J.; Ashby, M.F. Cellular Solids-Structure and Properties, 2nd ed; Cambridge University Press: New York, NY, USA, 2001. [Google Scholar]
- Ashby, M.F.; Evans, A.; Fleck, N.A.; Gibson, L.J.; Hutchinson, J.W.; Wadley, H.N.G. Metal Foams: A Design Guide; Butterworth-Heinemann: Oxford, UK, 2000. [Google Scholar]
- Fiedler, T. Numerical and Experimental Investigation of Hollow Sphere Structures in Sandwich Panels; Trans Tech Publications: Stafa, Zurich, 2008. [Google Scholar]
- Stephani, G.; Quadbeck, P.; Andersen, O. New multifunctional lightweight materials based on cellular metals-manufacturing, properties and applications. In Proceedings of the International Conference on Advanced Structural and Functional Materials Design, Osaka, Japan, 10–12 November 2008.
- Banhart, J. Manufacture, characterisation and application of cellular metals and metal foams. Prog. Mater. Sci. 2001, 46, 559–632. [Google Scholar]
- Lösch Cellular Engineering Ziviltechniker GesmbH Home Page. Available online: http://lce.co.at (accessed on 15 May 2012).
- Studnitzky, T.; Andersen, O. Control of the carbon content in metal hollow sphere structures by variation of the debindering condtions. In Proceedings of the Symposium on Cellular Metals and Polymers, Fürth, Germany, 12–14 October 2004.
- Veyhl, C.; Belova, I.V.; Murch, G.E.; Fiedler, T. Finite element analysis of the mechanical properties of cellular aluminium based on micro-computed tomography. Mater. Sci. Eng. A 2011, 528, 4550–4555. [Google Scholar] [CrossRef]
- Öchsner, A.; Augustin, C. Multifunctional Metallic Hollow Sphere Structures; Springer: Berlin, Germany, 2009. [Google Scholar]
- Evans, A.G.; Hutchinson, J.W.; Ashby, M.F. Cellular metals. Curr. Opin. Solid State Mater. Sci. 1998, 3, 288–303. [Google Scholar] [CrossRef]
- Solórzano, E.; Rodríguez-Perez, M.A.; de Saja, J.A. Thermal conductivity of metallic hollow sphere structures: An experimental, analytical and comparative study. Mater. Lett. 2009, 63, 1128–1130. [Google Scholar] [CrossRef]
- Fiedler, T.; Solórzano, E.; Öchsner, A. Numerical and experimental analysis of the thermal conductivity of metallic hollow sphere structures. Mater. Lett. 2008, 62, 1204–1207. [Google Scholar] [CrossRef]
- Öchsner, A.; Tane, M.; Nakajima, H. Prediction of the thermal properties of lotus-type and quasi-isotropic porous metals: Numerical and analytical methods. Mater. Lett. 2006, 60, 2690–2694. [Google Scholar] [CrossRef]
- Fiedler, T.; Löffler, R.; Bernthaler, T.; Winkler, R.; Belova, I.V.; Murch, G.E.; Öchsner, A. Numerical analyses of the thermal conductivity of random hollow sphere structures. Mater. Lett. 2009, 63, 1125–1127. [Google Scholar]
- Fiedler, T.; Belova, I.V.; Murch, G.E. Theoretical and Lattice Monte Carlo analyses on thermal conduction in cellular metals. Comput. Mater. Sci. 2010, 50, 503–509. [Google Scholar] [CrossRef]
- Fiedler, T.; Solórzano, E.; Garcia-Moreno, F.; Öchsner, A.; Belova, I.V.; Murch, G.E. Computed tomography based finite element analysis of the thermal properties of cellular aluminium. Mater. Sci. Eng. Technol. 2009, 40, 139–143. [Google Scholar]
- Veyhl, C.; Belova, I.V.; Murch, G.E.; Öchsner, A.; Fiedler, T. Thermal analysis of aluminium foam based on micro-computed tomography. Mater. Sci. Eng. Technol. 2011, 42, 350–355. [Google Scholar] [Green Version]
- Fiedler, T.; Öchsner, A. Influence of the morphology of joining on the heat transfer properties of periodic metal hollow sphere structures. Mater. Sci. Forum 2007, 553, 45–50. [Google Scholar] [CrossRef]
- Fiedler, T.; Öchsner, A. On the thermal conductivity of adhesivley bonded and sintered hollow sphere structures (HSS). Mater. Sci. Forum 2007, 553, 39–44. [Google Scholar] [CrossRef]
- Vesenjak, M.; Žunič, Z.; Öchsner, A.; Hribersek, M.; Ren, Z. Heat conduction in closed-cell cellular metals. Mater. Sci. Eng. Technol. 2005, 36, 608–612. [Google Scholar]
- Vesenjak, M.; Žunič, Z.; Ren, Z.; Öchsner, A. Computational study of heat transfer in honeycomb structures accounting for gaseous pore filler. Defect Diffus. Forum 2008, 273–276, 699–706. [Google Scholar] [CrossRef]
- Veyhl, C.; Belova, I.V.; Murch, G.E.; Öchsner, A.; Fiedler, T. On the mesh dependence of non-linear mechanical finite element analysis. Finite Elem. Anal. Des. 2010, 46, 371–378. [Google Scholar] [CrossRef]
- Lu, T.J.; Chen, C. Thermal transport and fire retardance properties of cellular aluminium alloys. Acta Mater. 1999, 47, 1469–1485. [Google Scholar] [CrossRef]
- Maxwell, J.C. A Treatise on Electricity and Magnetism; Clarendon Press: Calfornia, CA, USA; p. 1892.
- Jaeger, H.M.; Nagel, S.R. Physics of granular state. Science 1992, 255, 1523–1531. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Veyhl, C.; Fiedler, T.; Herzig, T.; Öchsner, A.; Bernthaler, T.; Belova, I.V.; Murch, G.E. Thermal Conductivity Computations of Sintered Hollow Sphere Structures. Metals 2012, 2, 113-121. https://doi.org/10.3390/met2020113
Veyhl C, Fiedler T, Herzig T, Öchsner A, Bernthaler T, Belova IV, Murch GE. Thermal Conductivity Computations of Sintered Hollow Sphere Structures. Metals. 2012; 2(2):113-121. https://doi.org/10.3390/met2020113
Chicago/Turabian StyleVeyhl, Christoph, Thomas Fiedler, Tobias Herzig, Andreas Öchsner, Timo Bernthaler, Irina V. Belova, and Graeme E. Murch. 2012. "Thermal Conductivity Computations of Sintered Hollow Sphere Structures" Metals 2, no. 2: 113-121. https://doi.org/10.3390/met2020113





