First-Principles Study of Cu Addition on Mechanical Properties of Ni₃Sn₄-Based Intermetallic Compounds

Abstract

Ni–Cu under-bump metallisation (UBM) can reduce stress and improve wetting ability in technology for electronic packaging technology advances with three-dimensional integrated circuit (3D IC) devices. The bond between the Sn-based solder and Ni–Cu UBM is affected by the formation of intermetallic compounds (IMCs), specifically Ni₃Sn₄ and (Ni,Cu)₃Sn₄. This paper investigates the mechanical properties of IMCs, which are critical in assessing the longevity of solder joints. First-principles calculations were carried out to investigate the phase stability, mechanical properties and electronic structures of Ni₃Sn₄, Ni_2.5Cu_0.5Sn₄, Ni_2.0Cu_1.0Sn₄, and Ni_1.5Cu_1.5Sn₄ IMCs. The calculated formation enthalpies show that the doping of Cu atoms leads to a decrease in the stability of the phases and a reduction in the mechanical properties of the Ni₃Sn₄ crystal structure. As the concentration of Cu atoms in the Ni₃Sn₄ cells increases, the bulk modulus values of (Ni,Cu)₃Sn₄ formed with different compositions decrease from 107.78 GPa to 87.84 GPa, the shear modulus decreases from 56.64 GPa to 45.08 GPa, and the elastic modulus decreases from 144.59 GPa to 115.48 GPa, indicating that the doping of Cu atoms into the Ni₃Sn₄ cells may adversely affect their mechanical properties and increase the possibility of microcracking at the interface during actual service. The anisotropy of (Ni,Cu)₃Sn₄ is more significant than that of Ni₃Sn₄, with Ni_2.0Cu_1.0Sn₄ showing the highest anisotropy. After evaluating the electronic structures, the metallic properties of Ni₃Sn₄ and the Ni_2.5Cu_0.5Sn₄, Ni_2.0Cu_1.0Sn₄, and Ni_1.5Cu_1.5Sn₄ phases are revealed by electronic structure analysis. The total density of states (TDOS) for (Ni,Cu)₃Sn₄ structures is mainly influenced by Ni-d and Cu-d states. The addition of Cu atoms can increase the brittleness of Ni₃Sn₄. In addition, the region where d and p hybridisation occurs gradually increases with increasing Cu content. The electronic properties suggest that the binding energy between Ni and Sn atoms weakens with the addition of Cu atoms, resulting in a decrease in the elastic modulus. This research can serve as a valuable reference and theoretical guide for future applications of these materials.

1. Introduction

Three-dimensional electronic packaging technology can meet the high-density assembly performance requirements of today’s electronic products while also providing high reliability, fast transmission speeds, low power consumption, low cost, and light weight [1,2,3]. At the same time, there can be concerns about the reliability of solder joints as they become smaller and smaller [4]. The reliability of microelectronic brazed interconnects is primarily influenced by the wetting behaviour of the solder bump, as well as the interfacial reactions between the solder and the metal layer beneath the bump during production and service, and electron migration. The bonding of the Sn-based solder/UBM interface during the soldering process is influenced by the physicochemical properties of the interacting materials, in particular the diffusion process and the resulting formation of various intermetallic compounds (IMCs) [5,6]. Meanwhile, the changes in the interfacial microstructure and mechanical properties of solder joints are usually the cause of serious reliability problems. Thick IMC layers have been found to weaken the mechanical properties and cause reliability problems, while thin IMC layers can increase the strength of the joint [7]. As the demand for smaller electronic devices increases, solder joints are shrinking in size. This decrease in solder volume increases the volume fraction of IMCs in the total solder joint volume, making the interface behaviour more important. In fact, the mechanical properties of IMCs largely determine the failure mechanisms of solder joints, which have emerged as a critical issue in solder reliability [8,9,10]. Therefore, it is crucial to understand the mechanical properties of IMCs in order to assess the reliability of solder joints in electronic packaging.

For example, due to the difference in ductility between the IMC layer and substrate, the stress distribution within solder joints is altered during reflow and ageing. To achieve slower reaction rates or more stable IMCs, the composition of UBM films can be adjusted. Compared to copper (Cu) UBM, nickel (Ni) UBM exhibits a reduced interfacial reaction with solders, as shown in previous research [11,12,13,14]. Ni and Ni-based alloys are known to have favourable magnetic properties, excellent mechanical properties and excellent corrosion and abrasion resistance. A variety of Ni-based UBMs have been used in industry to improve reliability [15]. These include widely used UBMs such as electroplated Ni, sputtered Ni(V) and electroless Ni(P)/Au. However, Ni UBM has a notable disadvantage in the form of inherent stress generation during the plating process [16,17]. After investigating the detrimental effects of Ni film and considering the potential of Ni–Cu to reduce stress and improve wetting, the use of Ni–Cu UBM as a replacement for Ni UBM is a viable option.

For this reason, interfacial reactions and IMC growth between Sn-based and Ni–Cu substrates have been the subject of much interest. Sn-based solders react with Ni coatings, primarily forming the intermetallic compound Ni₃Sn₄ [18,19,20]. In addition, Sn–Ag–Cu ternary lead-free solders are considered to be some of the best candidates for replacing conventional Sn–Pb solders in electronic packaging due to their desirable properties. It has also been observed by other researchers that Cu atoms can also replace Ni atoms in sublattice positions of Ni₃Sn₄ to form a ternary intermetal, (Ni,Cu)₃Sn₄. It is possible that the mechanical properties of Ni₃Sn₄ can be altered by doping with Cu atoms. However, most research on (Ni,Cu)₃Sn₄ has been experimental. Few studies have focused on the mechanical properties of (Ni,Cu)₃Sn₄ [21,22]. Further studies are needed to investigate the stability of (Ni,Cu)₃Sn₄ in more detail. The initial stage of first-principles calculations involves identifying the most stable geometric structure corresponding to the lowest energy, as well as determining the electronic, thermodynamic, and optical properties of a material through self-consistent calculations based on the laws of quantum mechanics and its constituent atoms [23,24]. In this paper, first-principles calculations are used as a convenient scheme to derive the essential properties of materials. The effect of Cu additions on the mechanical properties of Ni₃Sn₄ IMCs is investigated in this work. We will perform first-principles calculations on Ni₃Sn₄, Ni_2.5Cu_0.5Sn₄, Ni_2.0Cu_1.0Sn₄, and Ni_1.5Cu_1.5Sn₄ to derive their structural, elastic, thermodynamic and electronic properties. The results of our systematic research will complement the physical property data and facilitate the discovery of intermetallic structural stability and mechanical properties.

2. First-Principles Calculation Details

The initial model for this study was taken from the experimental crystal structure of Ni₃Sn₄ [25]. Figure 1a shows the primitive structure of the Ni₃Sn₄ phase, which was a monoclinic structure in the C2/m space group and contained six Ni and eight Sn atoms per cell. It can be seen that the Ni atoms occupy two different positions, 2a (Ni₁) and 4i (Ni₂). Ni₁ is located at the eight top angles of the hexahedron and the face centre position of the xy plane, while Ni₂ is located in the interior of the hexahedron and the xz plane [26]. The formation enthalpy calculations show that Ni_2.5Cu_0.5Sn₄(2a) has a value of −219.65 meV/atom and Ni_2.5Cu_0.5Sn₄ (4i) has a value of −226.19 meV/atom. This suggests that Cu has a greater tendency to occupy the 4i site [27]. In this paper, only the substitution of the Ni 4i position is discussed. It was found that during reflow and ageing, the diffusion of Cu atoms to the interface gradually decreases with the increasing addition of Ni. When using SAC-1Ni as the soldering material, the resulting IMC (Ni,Cu)₃Sn₄ contains 10.17–27.2% Cu [28,29]. According to the formulas of Ni_2.5Cu_0.5Sn₄, Ni_2.0Cu_1.0Sn₄ and Ni_1.5Cu_1.5Sn₄, different amounts of Cu (7.14 at.%, 14.3 at.% and 21.4 at.%, respectively) were added to the Ni₃Sn₄ phase, which are shown in Figure 1b–d.

In this study, first-principles calculations using density functional theory (DFT) were performed using the Cambridge Sequential Total Energy Package (CASTEP, 2017, Dassault Systèmes is located in Paris, France) [30]. To ensure the accuracy of subsequent calculations and to obtain the most stable crystal structure, strict total energy convergence tests were implemented. An energy threshold of 400 eV and 3 × 9 × 7 Monkhorst-Pack k-points were used to calculate the lattice parameters and elastic constants (C_ij) for the Ni₃Sn₄, Ni_2.5Cu_0.5Sn₄, Ni_2.0Cu_1.0Sn₄, and Ni_1.5Cu_1.5Sn₄ phases.

The Generalised Gradient Approximation (GGA) was used to treat the exchange and correlation function in terms of the Perdew–Burke–Ernzerhof (PBE) exchange–correlation energy [31]. The stability of intermetallic compounds can be determined by comparing their formation energies. In general, a compound will only form if its energy is less than the sum of the energies of the individual crystals. Therefore, the more negative the formation energy, the more stable the resulting compound will be. In order to study the thermodynamic stability, the heats of formation for Ni₃Sn₄, Ni_2.5Cu_0.5Sn₄, Ni_2.0Cu_1.0Sn₄, and Ni_1.5Cu_1.5Sn₄ were calculated using the following formula:

$$\Delta H=E_{total}(N{i}_{x}C{u}_{y}S{n}_z)-[x{E}_{total}(Ni)+y{E}_{total}(Cu)+z{E}_{total}(Sn)]$$

(1)

in which E_total(Ni_xCu_ySn_z) is the calculated total energy of Ni_xCu_ySn_z at equilibrium lattice constants. The energies of the isolated Ni, Cu and Sn atoms are given as E_total(Ni), E_total(Cu)and E_total(Sn), respectively. In Ni_xCu_ySn_z, x, y and z denote the number of Ni, Cu and Sn atoms, respectively.

3. Results and Discussion

3.1. Structure Optimisation

For Ni₃Sn₄, Ni_2.5Cu_0.5Sn₄, Ni_2.0Cu_1.0Sn₄, and Ni_1.5Cu_1.5Sn₄, the optimised structural parameters calculated are shown in

Table 1. The lattice constants a, b and c (Å), angle β (°) and the heat of formation (ΔH, meV/atom) of Ni₃Sn₄, Ni_2.5Cu_0.5Sn₄, Ni_2.0Cu_1.0Sn₄, and Ni_1.5Cu_1.5Sn₄ obtained from Refs. [26,27,32,33] and this paper.

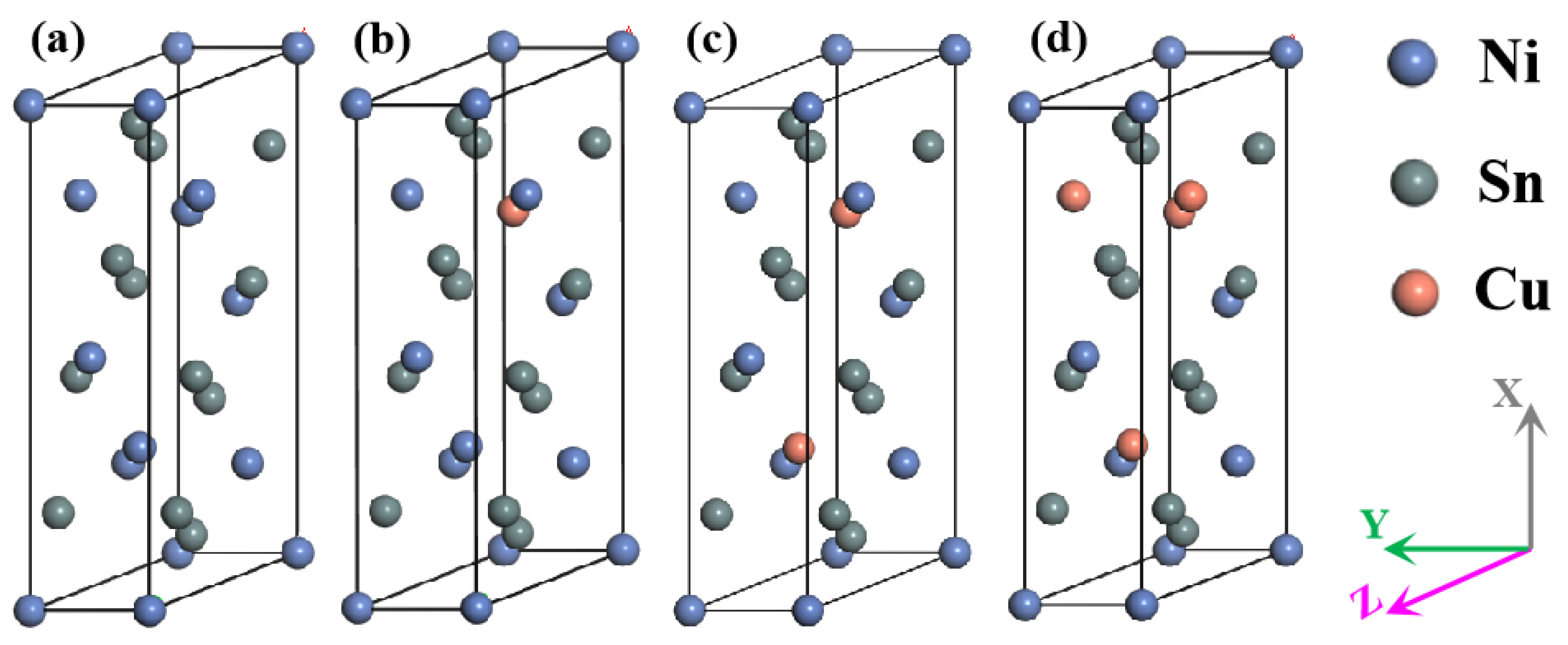
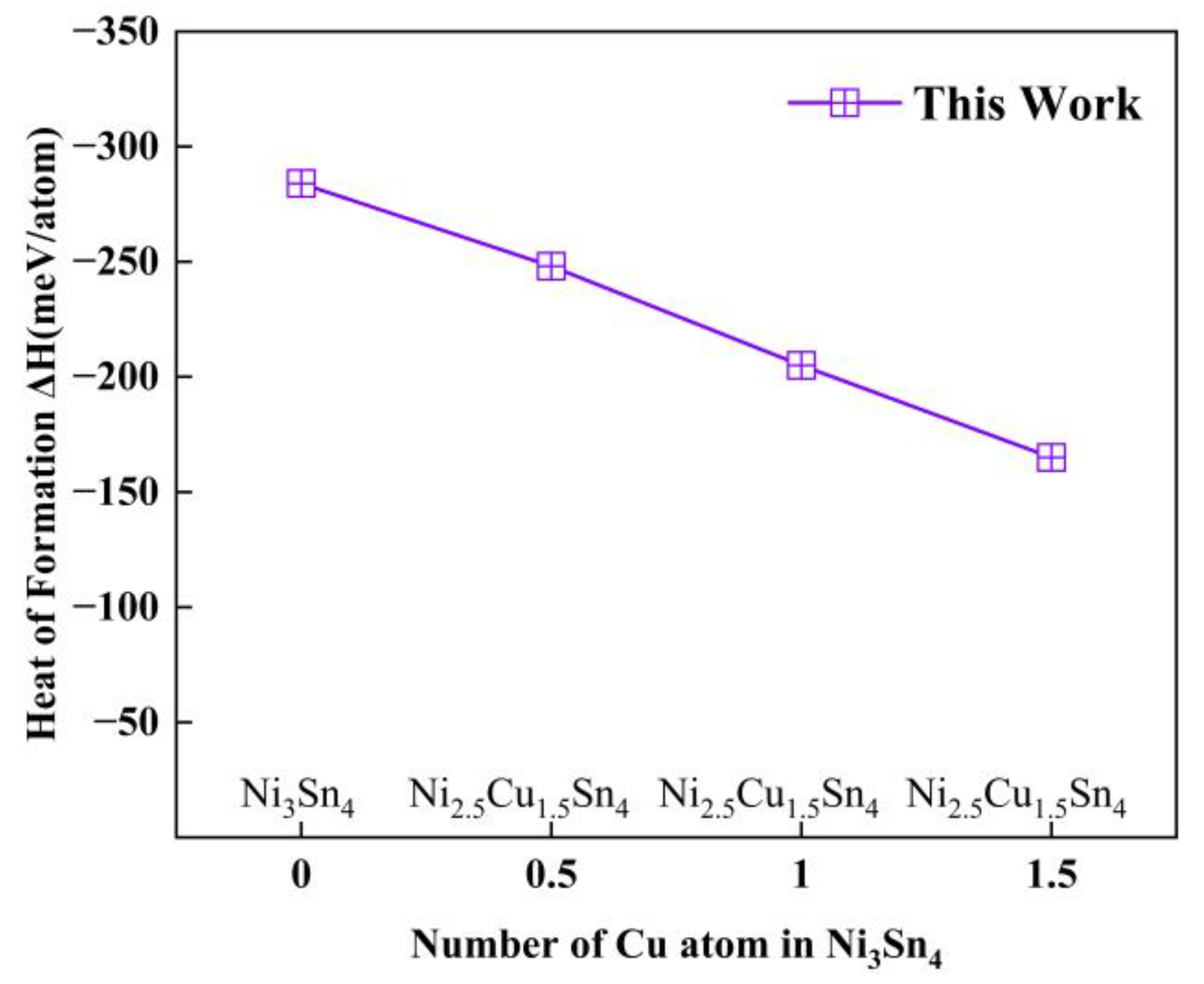
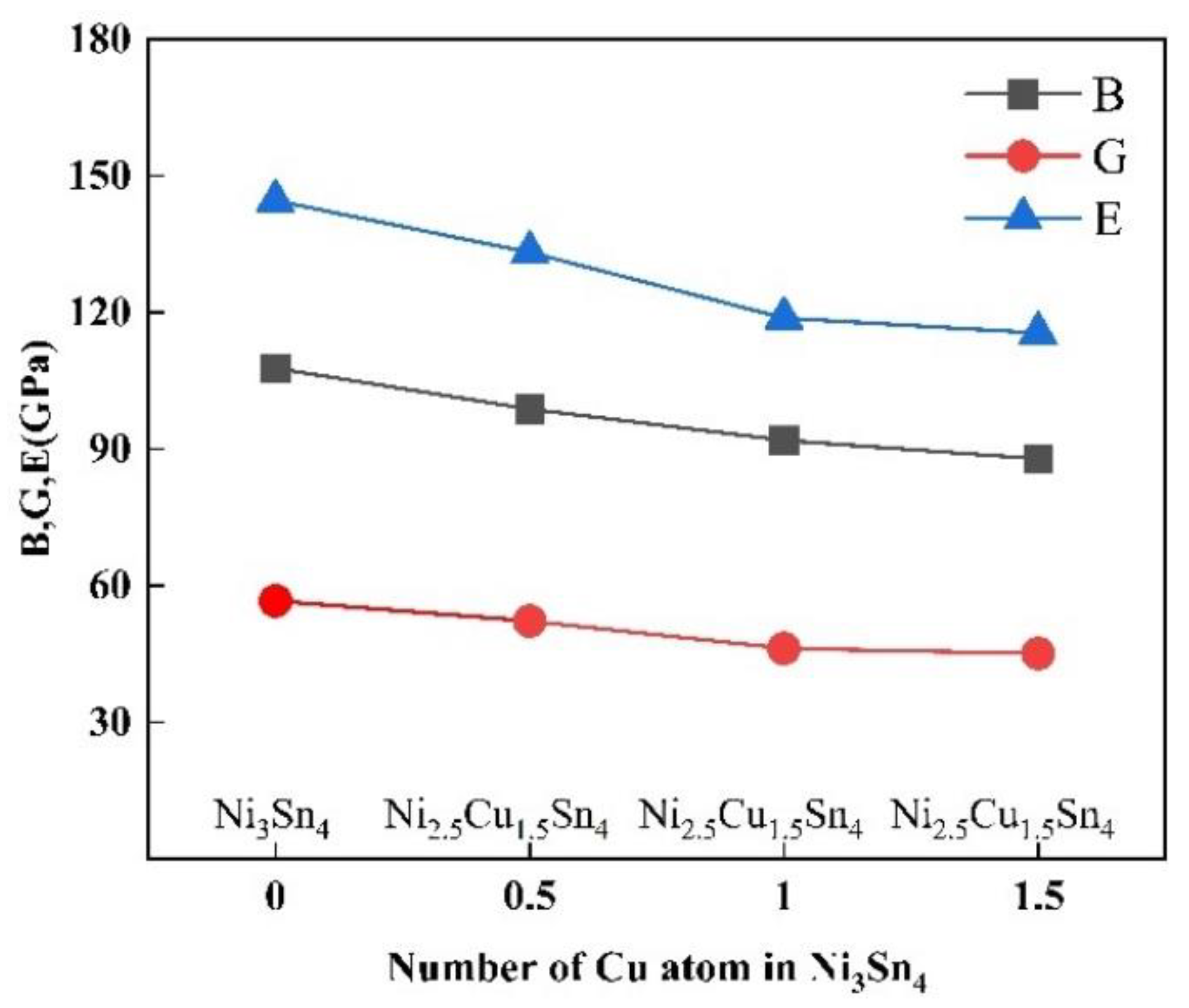
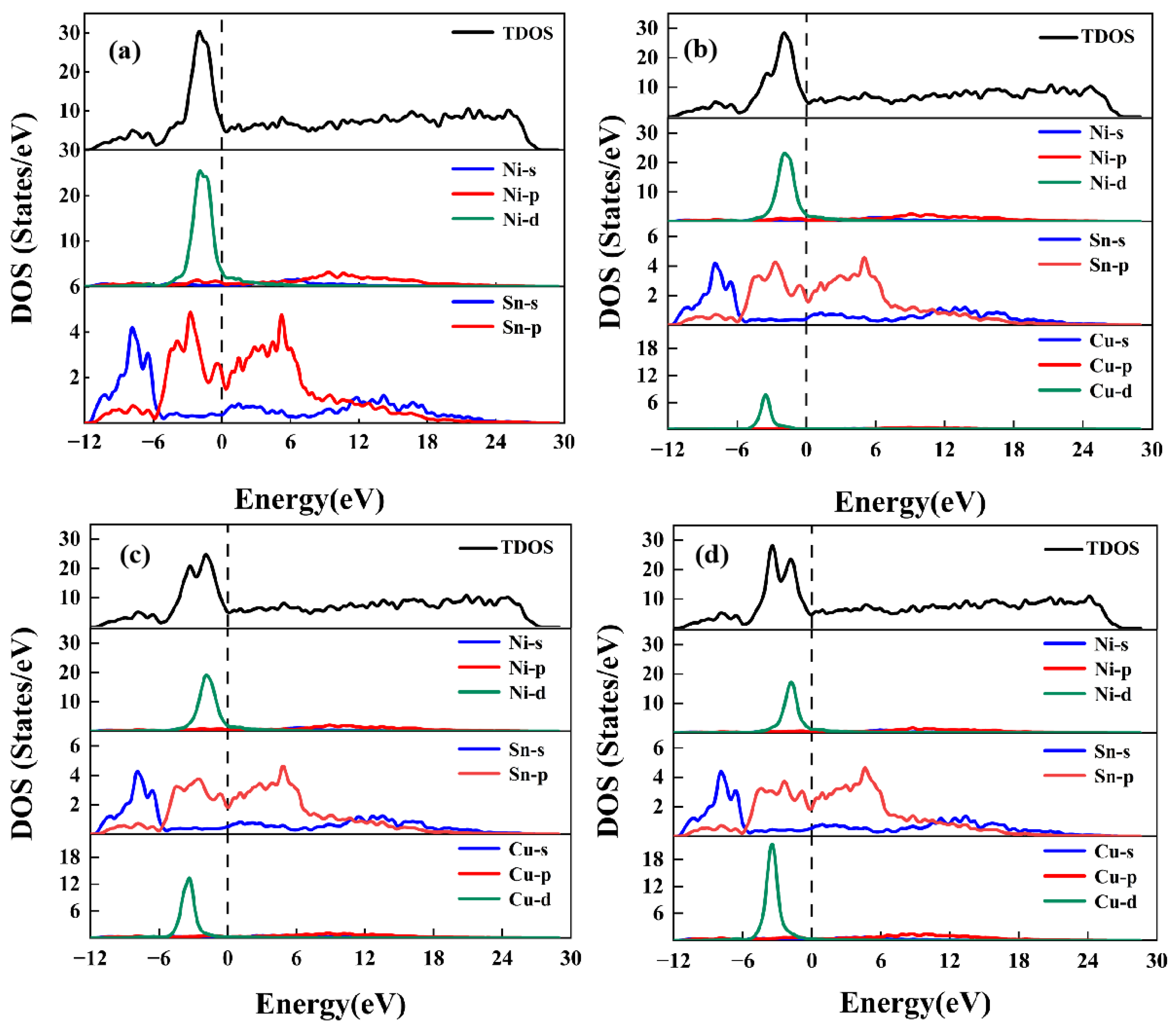
Phases	Reference	a	b	c	β	ΔH
Ni3Sn4	This work	12.323	4.119	5.303	105.416	−284
	[26]	12.299	4.084	5.288	105.190	−260
	[32]	12.418	4.111	4.315	105.480	−267
	[33]	12.334	4.100	5.325	105.010	−269
Ni2.5Cu0.5Sn4	This work	12.419	4.146	5.291	105.555	−248
	[26]	12.357	4.102	5.307	105.150	−219
	[32]	12.426	4.101	5.363	105.690	−193
Ni2.0Cu1.0Sn4	This work	12.434	4.149	5.365	105.541	−205
	[26]	12.420	4.128	5.331	105.150	−179
	[27]	12.422	4.133	5.331	105.160	−188
Ni1.5Cu1.5Sn4	This work	12.538	4.173	5.382	105.958	−165
	[26]	12.495	4.145	5.381	105.16	−135
	[27]	12.507	4.146	5.382	105.07	−144

. These results are discussed in this paper along with other literature [26,32,33]. Our analysis showed that the structural parameters calculated in this work have minimal deviations from the existing literature, and the deviations are less than 1.0%. This demonstrates the validity of the theoretical approaches used. It was observed that the lattice constants remained largely unaffected by the addition of Cu to all phases. This indicates that there were no changes in the crystal structures following the introduction of Cu atoms into the Ni₃Sn₄ phase. To determine the effect of Cu additions on the phase stability of Ni₃Sn₄, the heat of formation (ΔH, meV/atom) for Ni₃Sn₄, Ni_2.5Cu_0.5Sn₄, Ni_2.0Cu_1.0Sn₄, and Ni_1.5Cu_1.5Sn₄ at zero temperature, we calculated the heat of formation using Equation (1). The results are given in Table 1. A negative ΔH indicates the stability of the studied phase and a larger negative energy implies a more stable structure. The heat of formation of Ni₃Sn₄ in this work was −284 meV/atom, close to the previously calculated results of −260, −267, and −269 meV/atom. As shown in Figure 2, when Cu atoms were added to the Ni₃Sn₄ structure, the heat of formation increased slightly, with ΔH = −248 meV/atom for Ni_2.5Cu_0.5Sn₄, ΔH = −205 meV/atom for Ni_2.0Cu_1.0Sn₄, and ΔH = −165 meV/atom for Ni_1.5Cu_1.5Sn₄. The structure of Ni₃Sn₄ was found to be more stable than that of (Ni,Cu)₃Sn₄ IMCs. In simple terms, the introduction of Cu atoms reduced the structural integrity of the Ni₃Sn₄ IMC. Increasing the number of Cu atoms leads to a decrease in the stability of the structure.

3.2. Mechanical Properties

This study investigates the effect of Cu addition on the mechanical properties of Ni₃Sn₄. The elastic constant (C_ij) of Ni₃Sn₄-based structures was calculated. The elastic constant (C_ij) characterises the elasticity of a material and is represented by the quadratic coefficient in the case of small strains [34]. The matrix of elastic constants can be summarised in 13 variables, based on the symmetry of monoclinic structures [35].

The C_ij results obtained are listed in

Table 2. The calculated elastic constants C_ij (GPa) for Ni₃Sn₄, Ni_2.5Cu_0.5Sn₄, Ni_2.0Cu_1.0Sn₄, and Ni_1.5Cu_1.5Sn₄ obtained from Refs. [26,32,33] and this paper.

Phases	Reference	C11	C12	C13	C22	C23	C33	C44	C55	C66	C15	C25	C35	C46
Ni3Sn4	This work	165.96	74.58	72.13	183.59	68.85	191.67	62.35	64.28	55.35	−17.26	12.83	−5.70	9.67
	[26]	176.60	64.30	57.40	146.00	76.10	169.70	60.80	49.50	46.70	−22.90	7.00	−9.60	6.90
	[32]	155.48	70.68	69.34	164.33	68.26	149.86	62.74	59.99	59.95	−21.97	13.99	−8.73	4.90
	[33]	153.09	68.22	63.25	144.31	75.37	176.53	57.42	57.35	53.84	−22.70	12.94	−11.11	9.09
Ni2.5Cu0.5Sn4	This work	153.70	67.24	63.10	165.94	63.53	186.08	48.84	59.64	57.98	−21.22	12.00	−4.30	9.61
	[32]	146.95	71.79	64.07	176.30	73.29	154.47	57.86	55.11	55.41	−21.79	11.93	−6.18	8.22
Ni2.0Cu1.0Sn4	This work	138.64	63.51	62.15	156.72	60.21	166.06	45.23	47.76	56.05	−20.92	10.26	−4.43	8.55
Ni1.5Cu1.5Sn4	This work	134.58	53.68	59.37	146.62	69.75	148.91	54.13	40.93	55.57	−14.66	8.82	−4.51	7.93

. The mechanical stability of the crystal structure could be determined by using independent elastic constants, while for a monoclinic structure composed of Ni₃Sn₄-based IMCs, the conditions required for mechanical stability can be defined as follows:

$$C_{ii}>0\left(i=1–6\right)$$

(2)

$$\left[C_{11}+C_{22}+C_{33}+2(C_{12}+C_{13}+C_{23})\right]>0$$

(3)

$$(C_{33}{C}_{55}-C_{35}{}^2)>0,(C_{44}{C}_{66}-C_{46}{}^2)>0,(C_{22}+C_{33}-2C_{23})>0$$

(4)

Table 2 shows the calculated elastic constants (C_ij) for all Ni₃Sn₄-based structures. The elastic constants (C_ij) of Ni₃Sn₄ are close to the other calculations [26,32,33]. C₁₁ represents the elastic deformation resistance of the crystal structures in the [100] direction [36]. It can be observed that the value of C₁₁ for Ni₃Sn₄ is 165.96 GPa, which is higher than that of (Ni,Cu)₃Sn₄. This suggests that Ni₃Sn₄ exhibits the highest resistance to elastic deformation. From Table 2, the elastic constants (C_ij) were calculated for all the Ni₃Sn₄-based structures; (Ni,Cu)₃Sn₄ structures typically have lower elastic constants (C_ij) than Ni₃Sn₄. And the corresponding criteria listed in Equations (2)–(4) were easily satisfied, indicating that the Ni₃Sn₄-based structures studied are mechanically stable at 0 K.

In order to further approximate the Young modulus of Ni₃Sn₄-based ternary structures in the polycrystalline state [37], Voight–Reuss–Hill (VRH) [38] can be applied. The Voigt (V) and Reuss (R) for bulk and shear modulus can be calculated as follows:

$$B_V=\frac{1}{9}\left[C_{11}+C_{22}+C_{33}+2(C_{12}+C_{13}+C_{23})\right]$$

(5)

$$G_V=\frac{1}{15}\left[C_{11}+C_{22}+C_{33}+3(C_{44}+C_{55}+C_{66})-(C_{12}+C_{13}+C_{23})\right]$$

(6)

$$B_R=\Omega {\left[\begin{array}{l}a(C_{11}+C_{22}-2C_{12})+b(2C_{12}-2C_{11}-C_{23})+c(C_{15}-2C_{25})+\\ d(2C_{12}+2C_{23}-C_{13}-2C_{22})+2e(C_{25}-C_{15})+f\end{array}\right]}^{-1}$$

(7)

$$G_R=15{\left\{4\left[\frac{\begin{array}{l}a(C_{11}+C_{22}+C_{12})+b(C_{11}-C_{12}-C_{23})\\ +c(C_{15}+C_{25})+d(C_{22}-C_{12}-C_{23}-C_{13})\\ +e(C_{15}-C_{25})+f\end{array}}{\Omega }\right]+3\left[\frac{g}{\Omega }+\frac{(C_{44}+C_{66})}{(C_{44}{C}_{66}-C_{46}{}^2)}\right]\right\}}^{-1}$$

(8)

$$a=C_{33}{C}_{55}-C_{35}{}^2$$

(9)

$$b=C_{23}{C}_{55}-C_{25}{C}_{35}$$

(10)

$$c=C_{13}{C}_{35}-C_{15}{C}_{33}$$

(11)

$$d=C_{13}{C}_{55}-C_{15}{C}_{35}$$

(12)

$$e=C_{13}{C}_{25}-C_{15}{C}_{23}$$

(13)

$$\begin{array}{l}f=C_{11}\left(C_{22}{C}_{55}-C_{25}{}^2\right)-C_{12}\left(C_{12}{C}_{55}-C_{15}{C}_{25}\right)+C_{15}\left(C_{12}{C}_{25}-C_{15}{C}_{22}\right)\\ +C_{25}\left(C_{23}{C}_{35}-C_{25}{C}_{33}\right)\end{array}$$

(14)

$$\Omega =2\left[\begin{array}{l}{C}_{15}{C}_{25}\left(C_{33}{C}_{12}-C_{13}{C}_{23}\right)+C_{15}{C}_{35}\left(C_{22}{C}_{13}-C_{12}{C}_{23}\right)\\ +C_{25}{C}_{35}\left(C_{11}{C}_{23}-C_{12}{C}_{13}\right)-C_{15}{}^2\left(C_{22}{C}_{33}-C_{23}{}^2\right)\\ +C_{25}{}^2\left(C_{11}{C}_{33}-C_{13}{}^2\right)+C_{35}{}^2\left(C_{11}{C}_{22}-C_{12}{}^2\right)\end{array}\right]+g{C}_{55}$$

(15)

The following equations were used to calculate the bulk modulus (B), shear modulus (G), Young modulus (E) and Poisson ratio (ν). where B_V, B_R, G_V and G_R are the bulk and shear modulus in VRH.

$$B=\frac{(B_V+B_R)}{2}$$

(16)

$$G=\frac{(G_V+G_R)}{2}$$

(17)

$$E=\frac{9BG}{(3B+G)}$$

(18)

$$v=\frac{(3B-2G)}{\left[2(3B+G)\right]}$$

(19)

The values for B, G, E, ν and B/G of Ni₃Sn₄-based IMCS can be obtained using Equations (16)–(19). The results are shown in Figure 3 and

Table 3. The calculated bulk modulus (B, GPa), shear modulus (G, GPa), Young modulus (E, GPa) and Poisson ratio (ν) for Ni₃Sn₄, Ni_2.5Cu_0.5Sn₄, Ni_2.0Cu_1.0Sn₄, and Ni_1.5Cu_1.5Sn₄ obtained from Refs. [23,26,27,32,33] and this paper.

Phases	Reference	B	G	E	ν	B/G
Ni3Sn4	This work	107.78	56.64	144.59	0.276	1.90
	[23]	102.10	54.10	127.20	0.250	1.89
	[26]	97.90	49.08	126.11	0.285	2.00
	[32]	98.01	53.96	136.78	0.287	1.82
	[33]	98.30	49.27	126.65	0.290	2.00
Ni2.5Cu0.5Sn4	This work	98.79	52.23	133.21	0.275	1.89
	[27]	94.25	49.07	125.43	0.278	1.92
	[32]	98.45	49.62	127.45	0.284	1.95
Ni2.0Cu1.0Sn4	This work	91.93	46.24	118.80	0.285	1.99
Ni1.5Cu1.5Sn4	This work	87.84	45.08	115.48	0.281	1.95

. The B, G, E, ν and B/G of Ni₃Sn₄ are 107.78 GPa, 56.64 GPa, 144.59 GPa, 0.276 and 1.90, respectively, which are close to the results of other references.

Bulk modulus values for different compositions are documented as 107.78 GPa (Ni₃Sn₄), 98.79 GPa (Ni_2.5Cu_0.5Sn₄), 91.93 GPa (Ni_2.0Cu_1.0Sn₄), and 87.84 GPa (Ni_1.5Cu_1.5Sn₄). In addition, the shear modulus and Young modulus of Ni₃Sn₄ were 56.64 GPa and 144.59 GPa, respectively. After the addition of Cu to the Ni₃Sn₄ structure, the shear modulus and Young’s modulus were significantly reduced. It can be observed that Cu addition had a significant effect on the mechanical properties of the studied Ni₃Sn₄-based alloys. For Ni_2.5Cu_0.5Sn₄, the values were G = 52.23 GPa and E = 133.21 GPa; for Ni_2.0Cu_1.0Sn₄, the values were G = 46.24 GPa and E = 118.80 GPa; and for Ni_1.5Cu_1.5Sn₄, the values were G = 45.08 GPa and E = 115.48 GPa. The incorporation of Cu atoms into Ni₃Sn₄ crystals is predicted to reduce the binding energy in structures containing Ni₃Sn₄. This could lead to a lower shear modulus and Young modulus.

According to Pugh’s criterion [39], the B/G ratio is proposed as a condition to distinguish between brittle and ductile materials. If the value exceeds 1.75, the material has ductile properties, otherwise it is brittle. The B/G ratios for Ni₃Sn₄, Ni_2.5Cu_0.5Sn₄, Ni_2.0Cu_1.0Sn₄, and Ni_1.5Cu_1.5Sn₄ are 1.90, 1.89, 1.99 and 1.95, respectively. Therefore, all phases based on Ni₃Sn₄ can be classified as ductile, with the Ni₃Sn₄ IMC exhibiting the highest ductility of all the structures investigated. In addition, the Poisson ratio (ν) can be considered as a parameter to represent the ductile or brittle behaviour of materials when ν is above or below 0.25 [40].

From the Poisson ratio shown in Table 3, it was expected that all phases based on Ni₃Sn₄ would exhibit ductility. It is possible to predict the Young modulus of IMCs using first-principles calculations. Nevertheless, the plastic properties of materials are influenced by various factors such as crystal structure, microstructure and experimental conditions. It is widely accepted that material mechanics are strongly influenced by the growth and progression of microcracks. During the manufacture and use of solder joints, the anisotropic plastic deformation of intermetallic compounds leads to the formation of microcracks, which affect the reliability of electronic products [41]. To investigate the effect of the introduction of Cu on the elastic anisotropy of a Ni₃Sn₄ IMC, the universal anisotropy index (A^U) was used. A higher value of A^U indicates a greater structural anisotropy of the materials.

A^U could be expressed as the following:

$$A^U=5\frac{G_V}{G_R}+\frac{B_V}{B_R}-6>0$$

(20)

If A^U has a value of zero, a crystal structure should be isotropic. A higher value of A^U indicates greater anisotropy for a material. The values of A^U for Ni₃Sn₄-based IMCs can be obtained using Equation (20). The results are given in Figure 4 and

Table 4. The calculated bulk modulus (GPa) and shear modulus (Gpa) in VRH approximations and the universal anisotropy index (A^U) for Ni₃Sn₄, Ni_2.5Cu_0.5Sn₄, Ni_2.0Cu_1.0Sn₄, and Ni_1.5Cu_1.5Sn₄ obtained from Refs. [32,33] and this paper.

IMCs	Reference	GV	GR	BV	BR	GV/GR	BV/BR	AU
Ni3Sn4	This work	58.11	55.17	108.04	107.53	1.053	1.005	0.271
	[32]	53.96	49.42	98.47	97.56	1.092	1.001	0.461
	[33]	51.79	46.74	99.07	97.53	1.108	1.016	0.556
Ni2.5Cu0.5Sn4	This work	54.08	50.38	99.27	98.31	1.077	1.010	0.378
	[32]	51.58	47.66	99.56	97.33	1.082	1.013	0.423
Ni2.0Cu1.0Sn4	This work	48.18	44.30	92.57	91.28	1.088	1.014	0.454
Ni1.5Cu1.5Sn4	This work	46.61	43.54	88.41	87.26	1.071	1.013	0.366

. The atomic unit (A^U) of Ni₃Sn₄ is 0.271, which is close to other references. Obviously, both Ni₃Sn₄ and (Ni,Cu)₃Sn₄ must be considered anisotropic materials. The addition of copper would increase the mechanical anisotropy of the Ni₃Sn₄ intermetallic compound. The increase in elastic anisotropy resulted in a greater propensity for microcracking in Ni₃Sn₄, which reduced the shear strength of brazed joints. In order to gain further insight into the elastic anisotropy of Ni₃Sn₄-based phases, 3D surface plots of the bulk modulus and Young modulus were made in the present study.

As shown in Figure 5, the ability of a material to resist deformation is expressed by its bulk modulus, B, which is determined by the strength and compressibility of the chemical bonds. The higher the bulk modulus of a material, the higher the corresponding strength of the material. Where the greater deviation from the spherical shape indicates greater anisotropy, it can be seen that the bulk modulus anisotropy of (Ni,Cu)₃Sn₄ is overall greater than that of undoped Ni₃Sn₄ as the copper atom content increases. As indicated in Figure 6, it was observed that for all structures based on Ni₃Sn₄, 3D surface plots displayed some deviations from a spherical shape. This is indicative of the elastic anisotropies of Ni₃Sn₄ and (Ni,Cu)₃Sn₄. Moreover, after the Cu doping, the shape of the directional modulus was further away from the sphere, indicating the stronger elastic anisotropy of (Ni,Cu)₃Sn₄. And the Ni_2.0Cu_1.0Sn₄ had the strongest anisotropy.

3.3. Electronic Structures

The stability and bonding characteristics of a material are closely related to its electronic structure. In order to reveal the fundamental chemical bonding of the Ni₃Sn₄-based IMCs, the total density of states (TDOS) and partial density of states (PDOS) were performed and are shown in Figure 7. The Fermi levels are shown at zero energy in both TDOS and PDOS. Any non-zero states observed in the Fermi levels indicate the metallic nature of these IMCs. The electronic property indicates that the Ni₃Sn₄, Ni_2.5Cu_0.5Sn₄, Ni_2.0Cu_1.0Sn₄, and Ni_1.5Cu_1.5Sn₄ phases exhibit metallic properties.

As shown in Figure 7a, the TDOS in the energy range of about −12 to −6 eV is predominantly contributed by the Sn-s state. In the region from about −6 eV to the Fermi level, the dominant parts of the TDOS are the Ni-d state and the Sn-p state. It is evident that the Ni-d states, which have undergone a slight hybridisation with the Sn-p states, form the primary component close to the Fermi level in Ni₃Sn₄. Compared to the Ni₃Sn₄ phase, the peak of the TDOS from −6 eV to the Fermi level has a reduced height as shown in Figure 7b–d. The Fermi level reflects the stability of the material. Material stability decreases as the TDOS value increases [42]. The TDOS for (Ni,Cu)₃Sn₄ structures is primarily influenced by Ni-d and Cu-d states. The relationship between the electronic structure and the ductility and brittleness of crystal structures is well established [43]. The strength of atomic interactions can be inferred from the overlap region of d- and p-hybridised orbitals. The addition of Cu atoms can increase the brittleness of Ni₃Sn₄. Furthermore, the d- and p-hybridised area gradually increases with the increase in Cu content.

This suggests that the hybridisation between the Ni-d and Sn-p electrons was weakened after Cu replaced Ni in Ni₃Sn₄. In addition, a new peak appears from −6 eV to 0 eV, which is mainly dominated by Cu-d electrons. The peak position of the Cu-d state corresponded to the position of the Sn-p saddle point at an energy level of about −4 eV. Therefore, the doped Cu atoms could not adapt to the loss of bonding between Sn and Ni. In short, the binding energy of Ni₃Sn₄ exceeded that of Ni₃Sn₄-based IMCs. It is well known that a higher binding energy corresponds to a stronger charge interaction [44], which leads to an increase in structural stability. The results may explain the difference in elastic properties observed between Ni₃Sn₄ and Ni_2.5Cu_0.5Sn₄, Ni_2.0Cu_1.0Sn₄, and Ni_1.5Cu_1.5Sn₄.

4. Conclusions

In this study, Ni₃Sn₄-based IMCs are modelled by first-principles calculations to investigate the crystal structures and mechanical properties, as well as the electronic properties of the substitution of Cu for Ni in Ni₃Sn₄. We use the predictions of the systematic work calculated from first principles. As the concentration of Cu atoms in the Ni₃Sn₄ cells increases, the bulk modulus values of (Ni,Cu)₃Sn₄ formed with different compositions decrease from 107.78 GPa to 87.84 GPa, the shear modulus decreases from 56.64 GPa to 45.08 GPa, and the elastic modulus decreases from 144.59 GPa to 115.48 GPa, indicating that the doping of Cu atoms into the Ni₃Sn₄ cells may adversely affect their mechanical properties and increase the possibility of microcracking at the interface during actual service. It is also found that the anisotropy of (Ni,Cu)₃Sn₄ is more pronounced than that of Ni₃Sn₄, with the highest anisotropy observed in Ni_2.0Cu_1.0Sn₄. The metallic properties of Ni₃Sn₄ and the Ni_2.5Cu_0.5Sn₄, Ni_2.0Cu_1.0Sn₄, and Ni_1.5Cu_1.5Sn₄ phases are revealed by electronic structure analysis. The total density of states (TDOS) for (Ni,Cu)₃Sn₄ structures is mainly influenced by Ni-d and Cu-d states. The addition of Cu atoms can increase the brittleness of Ni₃Sn₄. In addition, the region where d and p hybridisation occurs gradually increases with increasing Cu content. The electronic properties suggest that the binding energy between Ni and Sn atoms weakens with the addition of Cu atoms, resulting in a decrease in the elastic modulus. This research can serve as a valuable reference and theoretical guide for future applications of these materials.