Forming and Microstructure Evolution Mechanism of Asymmetric Molten Pool in Laser Cladding
Abstract
:1. Introduction
2. Experimental Procedures
3. Results and Discussion
3.1. Laser Energy Distribution and Attenuation Model
3.1.1. Laser Attenuation Rate Model
3.1.2. Laser Energy Density Model
3.2. Powder Catchment Efficiency
3.3. Analysis on Forming of Single-Pass Cladding
3.4. Analysis of Microstructures
4. Conclusions
- (1)
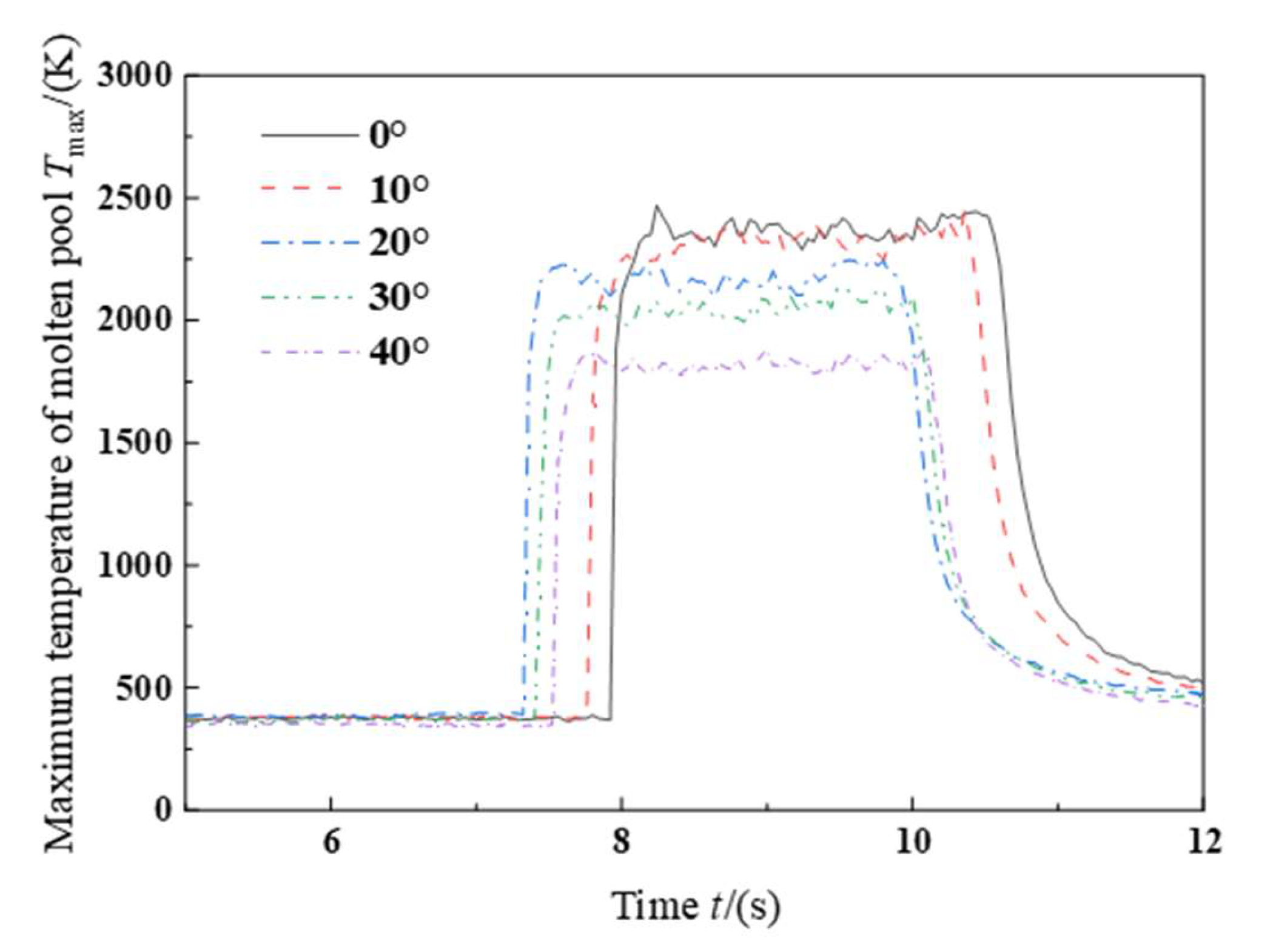
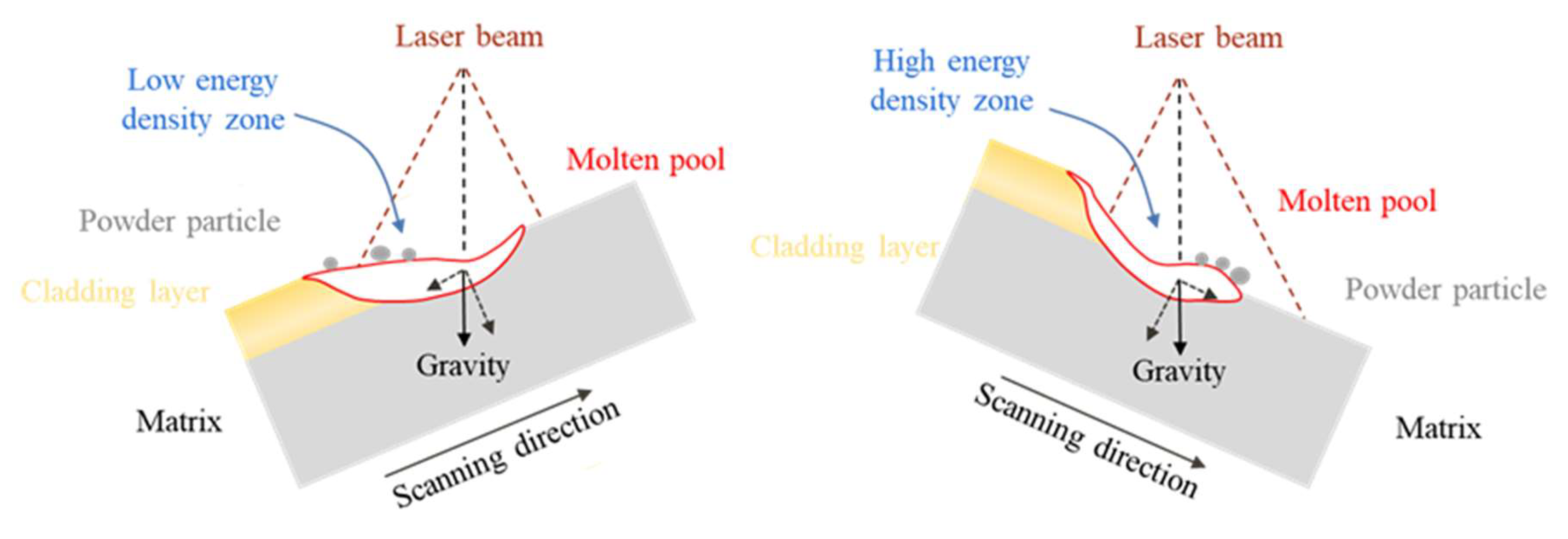
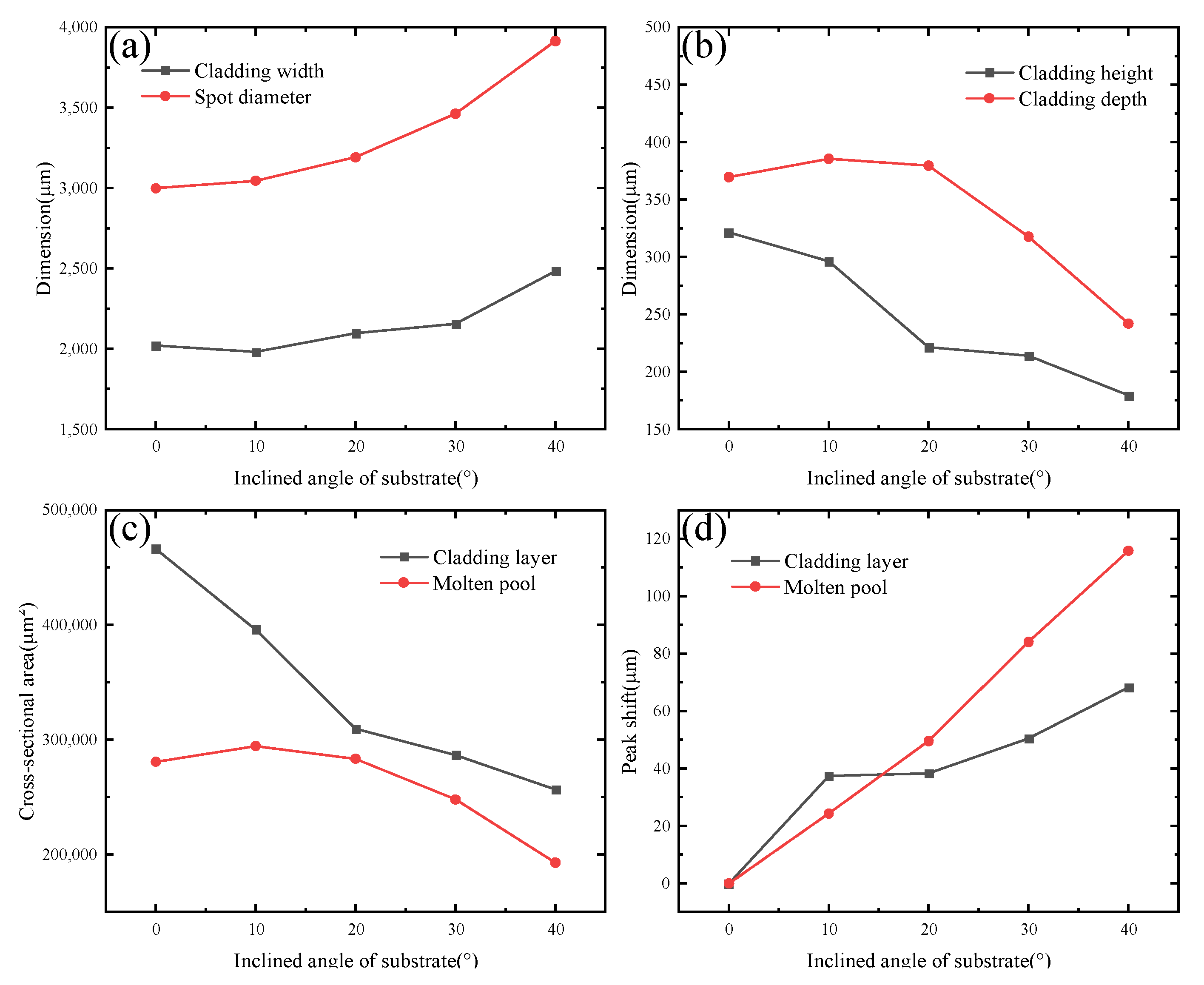
- The introduction of the extinction coefficient Kexc in the calculation of laser energy attenuation reveals its inverse proportionality to the carrier gas flow rate and direct proportionality to the powder feeding rate. The projection of the laser spot on the tilted substrate changes from a circular shape to an elongated ellipse along the inclined direction, resulting in a decrease in laser energy density and a gradual dispersion of its distribution, with the symmetrical center shifting toward the upper edge of the inclined surface. The melt pool temperature at different tilt angles is monitored using an infrared thermal forming system, confirming the inverse proportionality between substrate thermal input and tilt angle and validating the numerical model of laser energy density.
- (2)
- The powder utilization rate decreases as the matrix inclination angle increases under all three scanning modes. The increase in angle results in a reduction in heat input to the matrix, making it more challenging to form a molten pool in the edge region. Additionally, the asymmetry of powder flow intensifies collisions and rebounds between the powder and matrix, further diminishing the powder utilization rate.
- (3)
- Laser-based cladding on non-horizontal surfaces results in an asymmetric melt pool, which becomes increasingly flattened with larger tilt angles, exhibiting a wider width on the downhill side and a narrower width on the uphill side of the cladding layer. With an increase in tilt angle, the melting width, the highest point of the cladding layer, and the deepest point of the melt pool show a decreasing trend, while the melting height, depth, and cross-sectional area exhibit an increasing trend.
- (4)
- The melt pool experiences asymmetry due to the influence of gravity, while the pressure of the shielding gas and internal viscous shear can to some extent inhibit the effect of gravity. Under larger tilt angles, gravity weakens the asymmetrical internal flow field of the melt pool, prolongs the solidification time, and promotes the grain growth.
- (5)
- Under the 40° scanning mode, the lower half of the asymmetric melt pool exhibits smaller temperature gradients, a greater amount of material participating in flow circulation, and denser and more chaotic velocity vectors. Therefore, the grain size in the lower half is larger and the growth direction is more random compared to the upper half.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nanamuthun, D.S. Cladding: America. U.S. Patent US3952180A, 20 April 1976. [Google Scholar]
- Schopphoven, T.; Gasser, A.; Backes, G. EHLA: Extreme High-speed Laser Material Deposition-economical and Effective Protection against Corrosion and Wear. Laser Technol. J. 2017, 14, 26–29. [Google Scholar] [CrossRef]
- Takemura, S.; Koike, R.; Kakinuma, Y.; Sato, Y.; Oda, Y. Design of powder nozzle for high resource efficiency in directed energy deposition based on computational fluid dynamics simulation. Int. J. Adv. Manuf. Technol. 2019, 105, 4107–4121. [Google Scholar] [CrossRef]
- Wang, H.Z.; Cheng, Y.H.; Song, W.; Yang, J.Y.; Liang, X.B. Research on the influence of laser scanning speed on Fe-based amorphous coating organization and performance. Intermetallics 2021, 136, 107266. [Google Scholar] [CrossRef]
- Zhou, J.L.; Cheng, Y.H.; Yang, J.Y.; Wang, Q.Q.; Liang, X.B. Effects of WS2 and Ti3AlC2 additions on the high temperature wear properties of laser cladding YW1/NiCoCrAlY tool coating. Ceram. Int. 2021, 47, 35124–35133. [Google Scholar] [CrossRef]
- Lee, Y.S.; Farson, D.F. Surface tension-powered build dimension control in laser additive manufacturing process. Int. J. Adv. Manuf. Technol. 2016, 85, 1035–1044. [Google Scholar] [CrossRef]
- Bruna-Rosso, C.; Demir, A.G.; Previtali, B. Selective laser melting finite element modeling: Validation with high-speed imaging and lack of fusion defects prediction. Mater. Des. 2018, 156, 143–153. [Google Scholar] [CrossRef]
- Li, Z.; Yu, G.; He, X.; Li, S.; Tian, C.; Dong, B. Analysis of surface tension driven flow and solidification behavior in laser linear welding of stainless steel. Opt. Laser Technol. 2020, 123, 105914. [Google Scholar] [CrossRef]
- Chai, Q.; Wang, Z.; Fang, C.; Xing, Y.; Qiu, X.; Zhou, Z. Numerical and experimental study on the profile of metal alloys formed on the inclined substrate by laser cladding. Surf. Coat. Technol. 2021, 422, 127494. [Google Scholar] [CrossRef]
- Lin, J.; Hwang, B.C. Coaxial laser cladding on an inclined substrate. Opt. Laser Technol. 1999, 31, 571–578. [Google Scholar] [CrossRef]
- Li, X.; Li, T.; Shi, B.; Wang, D.; Adnan, M.; Lu, H. The influence of substrate tilt angle on the morphology of laser cladding layer. Surf. Coat. Technol. 2020, 391, 125706. [Google Scholar] [CrossRef]
- Mohammadpour, M.; Yang, B.; Wang, H.P.; Forrest, J.; Poss, M.; Carlson, B.; Kovacevic, R. Influence of laser beam inclination angle on galvanized steel laser braze quality. Opt. Laser Technol. 2020, 129, 106303. [Google Scholar] [CrossRef]
- Huang, J.; Qi, L.; Luo, J.; Hou, X. Insights into the impact and solidification of metal droplets in ground-based investigation of droplet deposition 3D printing under microgravity. Appl. Therm. Eng. 2021, 183, 116176. [Google Scholar] [CrossRef]
- Xu, B.; Yuan, Z.; Wu, Y. Simulation analysis on surface morphology and hysteresis characteristics of molten Sn-3.0Ag-0.5Cu sitting on the inclined Ni substrate. Colloids Surf. A Physicochem. Eng. Asp. 2014, 441, 217–225. [Google Scholar] [CrossRef]
- Gu, H.; Li, L. Computational fluid dynamic simulation of gravity and pressure effects in laser metal deposition for potential additive manufacturing in space. Int. J. Heat Mass Transf. 2019, 140, 51–65. [Google Scholar] [CrossRef]
- Tan, H.; Fan, W.; Qian, Y.; Chen, Y.; Liu, S.; Lin, X. Influence of inclined substrate on process characteristics of directed energy deposition. Opt. Laser Technol. 2020, 129, 106288–106297. [Google Scholar] [CrossRef]
- Tan, H.; Shang, W.; Zhang, F.; Clare, A.T.; Lin, X.; Chen, J.; Huang, W. Process mechanisms based on powder flow spatial distribution in direct metal deposition. J. Mater. Process. Technol. 2018, 254, 361–372. [Google Scholar] [CrossRef]
- Yang, J.; Aiyiti, W.; Jiang, H.; Shan, J.; Zhang, Y. Evolution of molten pool morphology and prediction of inclined cladding layer morphology. Opt. Laser Technol. 2021, 142, 107164. [Google Scholar] [CrossRef]
- Cao, H.; Huang, R.; Yi, H.; Liu, M.; Jia, L. Asymmetric molten pool morphology in wire-arc directed energy deposition: Evolution mechanism and suppression strategy. Addit. Manuf. 2022, 59, 103113. [Google Scholar] [CrossRef]
- Khan, M.S.; Ali, S.; Westerbaan, D.; Duley, W.; Biro, E.; Zhou, Y.N. The effect of laser impingement angle on the optimization of melt pool geometry to improve process stability during high-speed laser welding of thin-gauge automotive steels. J. Manuf. Process. 2022, 78, 242–253. [Google Scholar] [CrossRef]
- Wang, D.; Li, T.; Shi, B.; Wang, H.; Xia, Z.; Cao, M.; Zhang, X. An analytical model of bead morphology on the inclined substrate in coaxial laser cladding. Surf. Coat. Technol. 2021, 410, 126944–126956. [Google Scholar] [CrossRef]
- Alya, S.; Vundru, C.; Ankamreddy, B.; Singh, R. Characterization and modeling of deposition geometry in directed energy deposition over inclined surfaces. Procedia Manuf. 2019, 34, 695–703. [Google Scholar] [CrossRef]
- Ghorbani, J.; Li, J.; Srivastava, A.K. Application of optimized laser surface re-melting process on selective laser melted 316L stainless steel inclined parts. J. Manuf. Process. 2020, 56, 726–734. [Google Scholar] [CrossRef]
- Le, K.Q.; Wong, C.H.; Chua, K.H.G.; Tang, C.; Du, H. Discontinuity of overhanging melt track in selective laser melting process. Int. J. Heat Mass Transf. 2020, 162, 120284. [Google Scholar] [CrossRef]
- He, Y.; Wei, J.; Liu, J.; Wang, X.; Wang, Y.; He, L. Experimental study on the fabrication profile and mechanical properties by substrate-inclined angle using laser melting deposition (LMD) integrating with the substrate of stainless steel. Opt. Laser Technol. 2020, 125, 106038–106044. [Google Scholar] [CrossRef]
- Hao, J.; Meng, Q.; Li, C.; Li, Z.; Wu, D. Effects of tilt angle between laser nozzle and substrate on bead morphology in multi-axis laser cladding. J. Manuf. Process. 2019, 43, 311–322. [Google Scholar] [CrossRef]
- Mahade, S.; Awe, S.A.; Björklund, S.; Lukáč, F.; Mušálek, R.; Joshi, S. Sliding wear behavior of a sustainable Fe-based coating and its damage mechanisms. Wear 2022, 500–501, 204375. [Google Scholar] [CrossRef]
- Olofsson, U.; Lyu, Y.; Åström, A.H.; Wahlström, J.; Dizdar, S.; Nogueira, A.P.G.; Gialanella, S. Laser Cladding Treatment for Refurbishing Disc Brake Rotors: Environmental and Tribological Analysis. Tribol. Lett. 2021, 69, 57. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, X.; Li, M.; Gong, P. Surface Morphology and Subsurface Microstructure Evolution When Form Grinding 20Cr2Ni4A Alloys. Materials 2023, 16, 425. [Google Scholar] [CrossRef]
- Li, L.; Shen, F.; Zhou, Y.; Tao, W. Comparative study of stainless steel AISI 431 coatings prepared by extreme-high-speed and conventional laser cladding. J. Laser Appl. 2019, 31, 042009. [Google Scholar] [CrossRef]
- Hoadley, A.; Rappaz, M. A thermal model of laser cladding by powder injection. Metall. Trans. B 1992, 23, 631–642. [Google Scholar] [CrossRef]
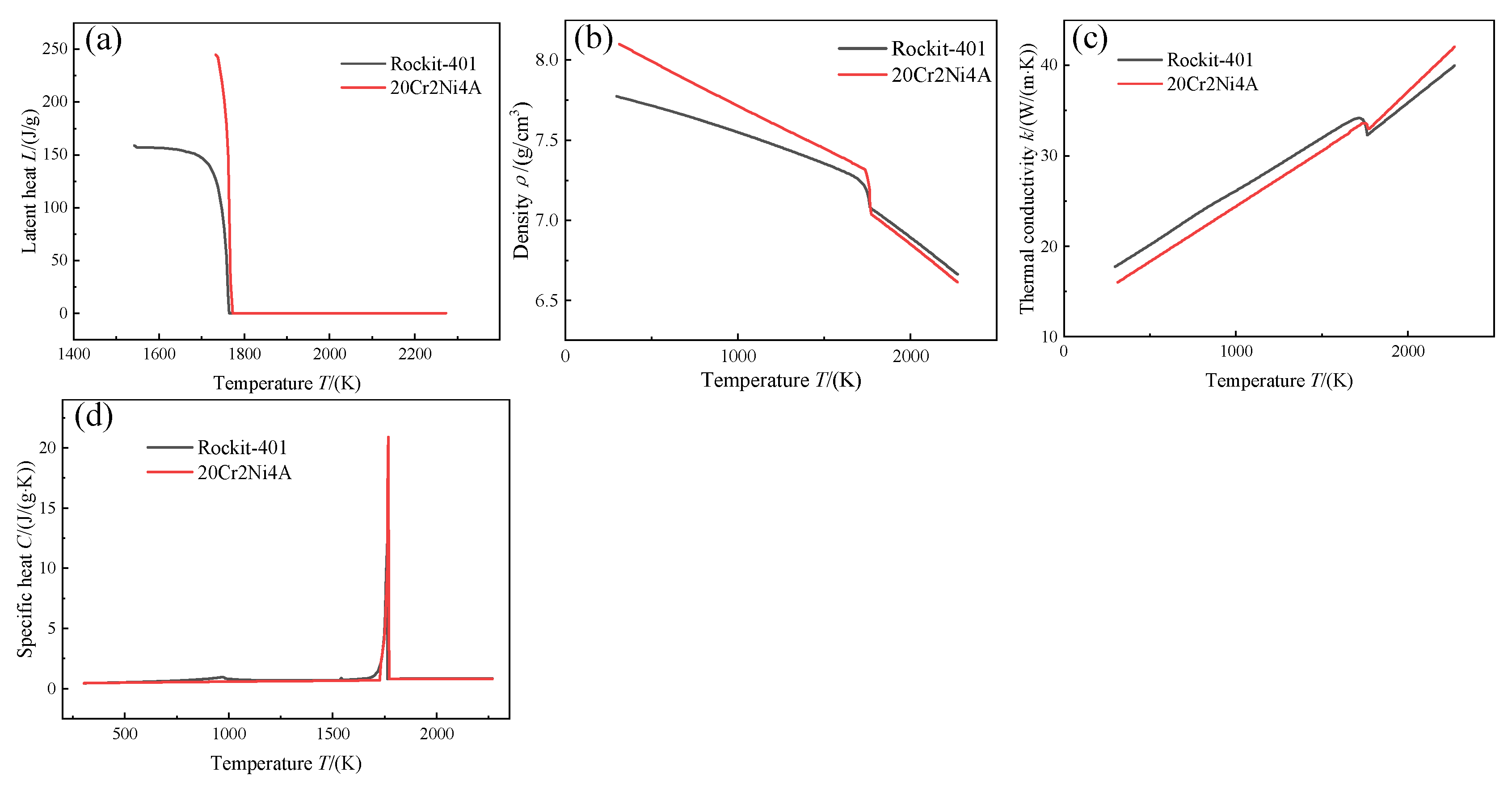
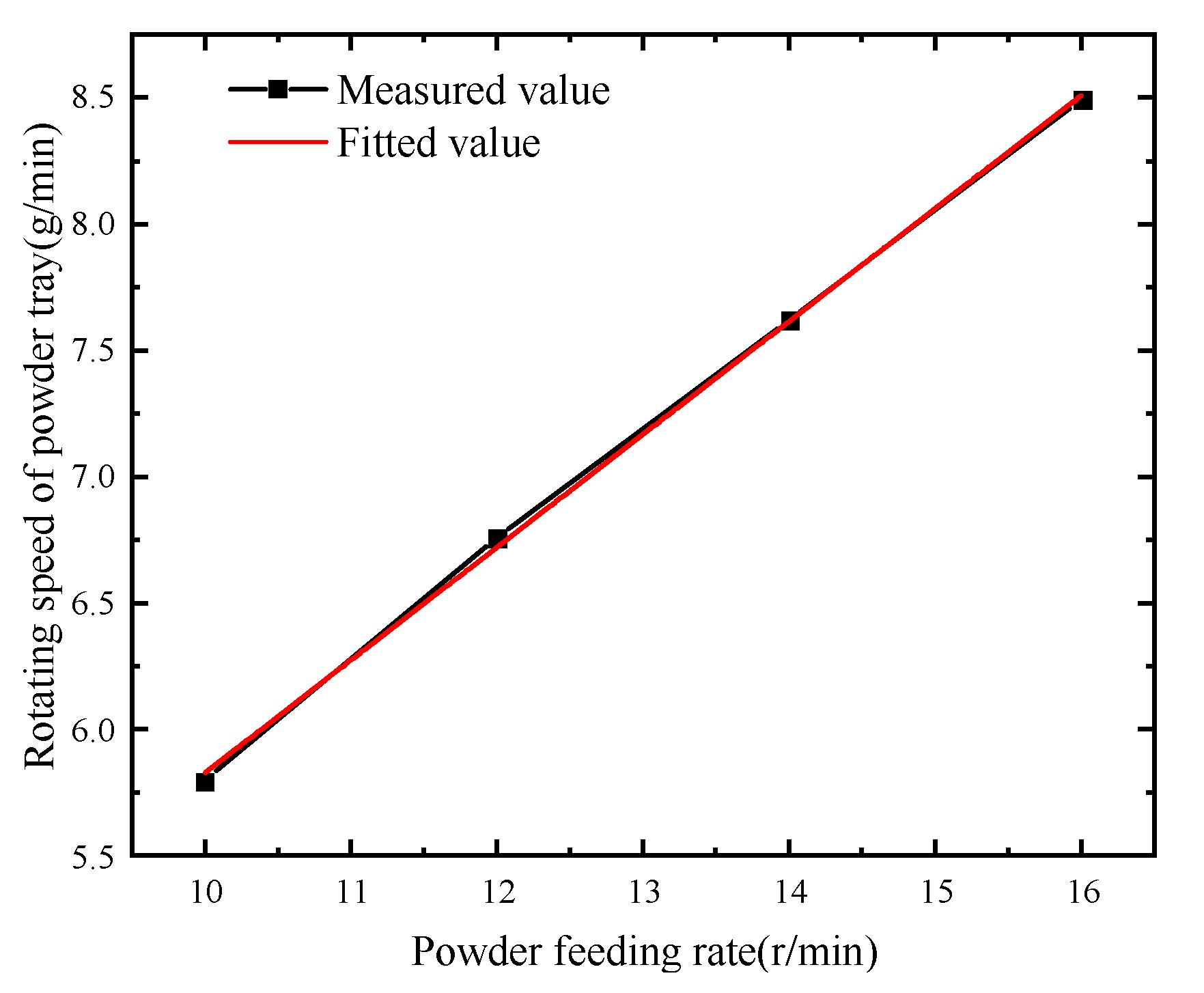








| Material | C | Si | Cr | Ni | Mo | Mn | Fe |
|---|---|---|---|---|---|---|---|
| Powder | 0.13 | - | 18 | 2.5 | 0.5 | - | Bal. |
| Substrate | 0.21 | 0.25 | 1.45 | 3.55 | - | 0.48 | Bal. |
| Parameter | Power P/(kW) | Scanning Velocity v/(mm/s) | Powder Feeding Rate Qp(g/min) | Inclined Angle θ/(°) |
|---|---|---|---|---|
| Value | 1.4 | 25 | 12.4 | 0, 10, 20, 30, 40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Zhang, X.; Wang, Y.; Zhou, J.; Ma, K.; Ma, F.; Cheng, Y.; Gao, C. Forming and Microstructure Evolution Mechanism of Asymmetric Molten Pool in Laser Cladding. Metals 2023, 13, 1970. https://doi.org/10.3390/met13121970
Wang H, Zhang X, Wang Y, Zhou J, Ma K, Ma F, Cheng Y, Gao C. Forming and Microstructure Evolution Mechanism of Asymmetric Molten Pool in Laser Cladding. Metals. 2023; 13(12):1970. https://doi.org/10.3390/met13121970
Chicago/Turabian StyleWang, Hong, Xiaofeng Zhang, Yunfei Wang, Jiali Zhou, Kai Ma, Fuwen Ma, Yanhai Cheng, and Chuwei Gao. 2023. "Forming and Microstructure Evolution Mechanism of Asymmetric Molten Pool in Laser Cladding" Metals 13, no. 12: 1970. https://doi.org/10.3390/met13121970





