A Computational Fluid Dynamics Study on Shearing Mechanisms in Thermal Elastohydrodynamic Line Contacts
Abstract
:1. Introduction
2. Methods
2.1. Governing Equations
2.2. Cavitation Modeling
2.3. Lubricant Properties
2.3.1. Density Equations
2.3.2. Viscosity Equations for Newtonian Fluid Behavior
2.3.3. Rheological Models
2.4. Surface Temperature
2.5. The Film Thickness Equation
2.6. Mesh Generation and Numerical Method
3. Results and Discussion
3.1. Mesh Verification Test
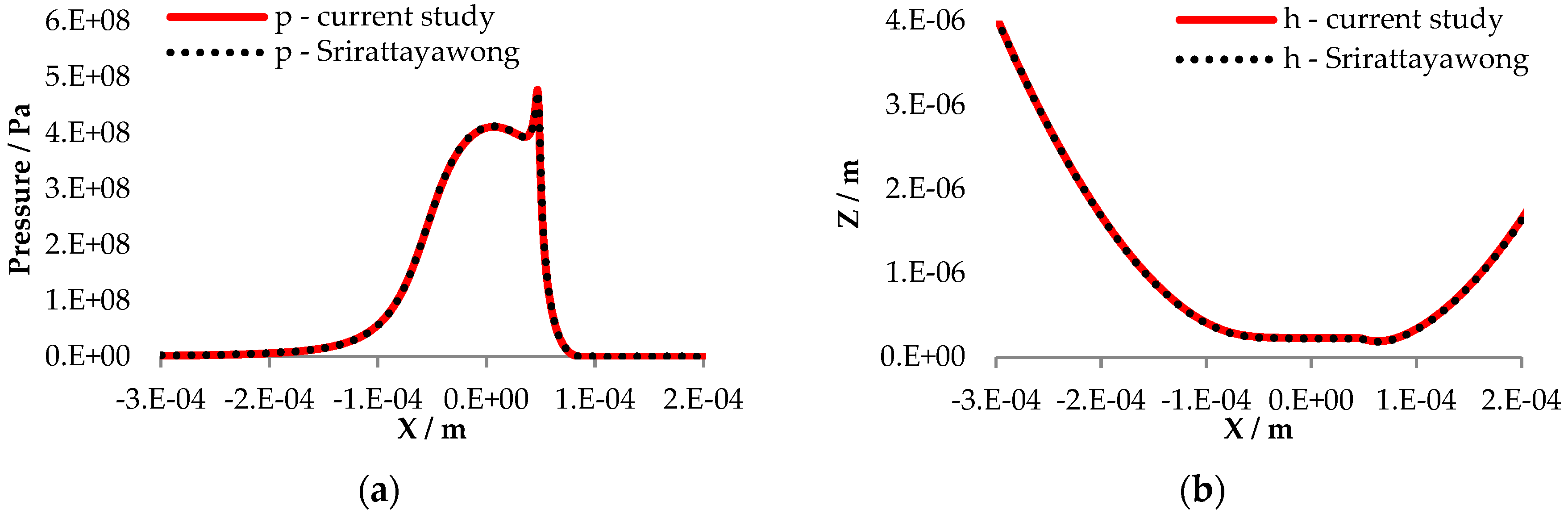
3.2. Isothermal Conditions, Newtonain Fluid Behavior, Low Pressure
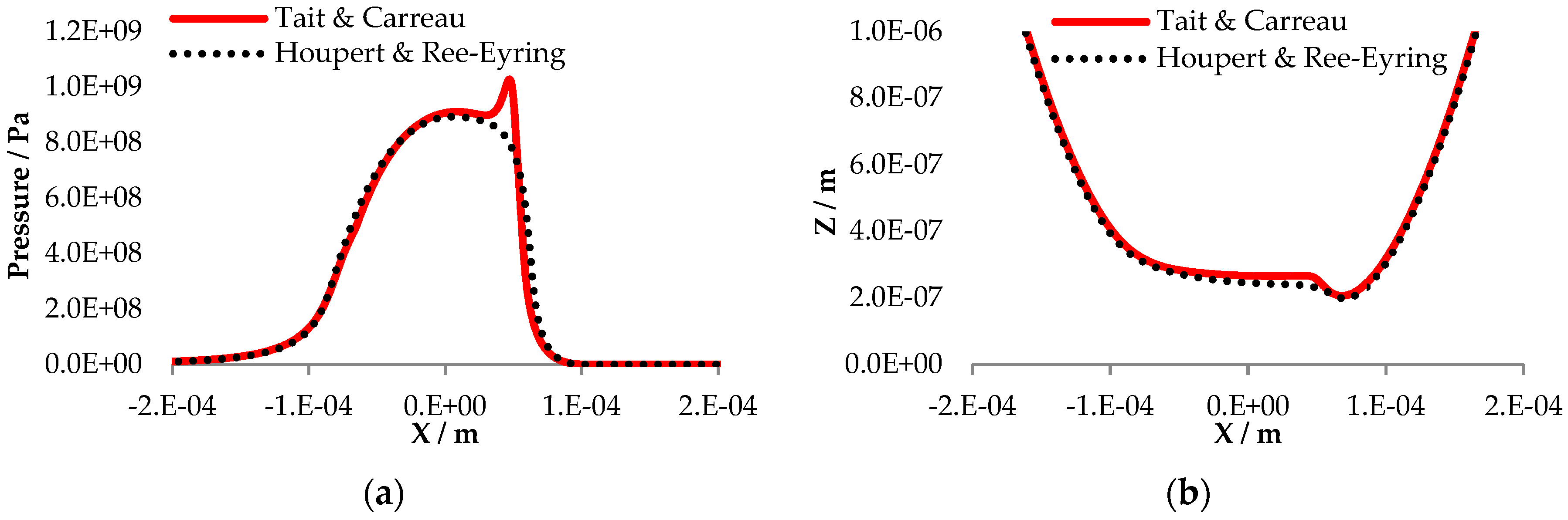
3.3. Thermal Conditions, Non-Newtonain Fluid Behavior, High Fluid Pressure
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Pressure–viscosity coefficient | ||
| Volume fraction of phase k | - | |
| Temperature–viscosity coefficient | ||
| Temperature coefficient of | ||
| Diffusion coefficient | ||
| Shear strain rate | ||
| Min. cell size in X-direction | ||
| Thermal expansion coefficient | ||
| Dynamic viscosity according to Carreau rheological model | ||
| Dynamic viscosity according to Houpert | ||
| Dynamic viscosity according to Roelands | ||
| Dynamic viscosity according to Ree–Eyring rheological model | ||
| Limiting stress pressure coefficient | - | |
| Relaxation time at ambient pressure and reference temperature | - | |
| Limiting low-shear viscosity | ||
| Dynamic viscosity at ambient pressure and reference temperature | ||
| Dynamic viscosity of phase k | ||
| Low shear viscosity at ambient pressure and reference temperature | ||
| Dynamic viscosity of vapor phase | ||
| Viscosity extrapolated to infinite temperature | ||
| Velocity | ||
| Poisson ratio | - | |
| Density | ||
| Density of phase k | ||
| Lubricant density at ambient pressure and reference temperature | ||
| Stress tensor | ||
| Limiting shear stress | ||
| Eyring stress | ||
| Dimensionless viscosity scaling parameter | - | |
| Viscosity scaling parameter for unbounded viscosity | - | |
| Thermal expansivity defined for volume linear with | ||
| Hertzian half width | ||
| Fragility parameter in the new viscosity equation | - | |
| Specific heat capacity | ||
| Modulus of elasticity | ||
| Reduced elastic modulus | ||
| Energy per unit mass of phase k | ||
| Thermodynamic interaction parameter | - | |
| Film thickness | ||
| Minimum gap between the solid surfaces in undeformed state | ||
| Unit tensor | - | |
| Thermal conductivity | ||
| Effective thermal conductivity | ||
| Isothermal bulk modulus at | ||
| Pressure rate of change of isothermal bulk modulus at | - | |
| at zero absolute temperature | ||
| Characteristic length scale | ||
| Power law exponent | - | |
| Pressure | ||
| Vapor pressure | ||
| Peclet number | - | |
| Heat flux from fluid to solid wall | ||
| Reduced radius of curvature | ||
| Time | ||
| Temperature | ||
| Surface temperature according to Carlaw-Jaeger | ||
| Reference temperature | ||
| Entrainment speed | ||
| Surface velocity | ||
| Fluid volume | ||
| Fluid volume at ambient pressure | ||
| Fluid volume at ambient pressure and reference temperature | ||
| Applied load | ||
| Coordinate | ||
| Relative coordinate | ||
| Coordinate | ||
| Roelands pressure–viscosity index | - |
References
- Johnson, K.L.; Roberts, A.D. Observations of viscoelastic behaviour of an elastohydrodynamic lubricant film. Proceed. R. Soc. London A Math. Phys. Sci. 1974, 20, 217–242. [Google Scholar] [CrossRef]
- Tevaarwerk, J.L.; Johnson, K.L. The influence of Fluid Rheology on the Performance of Traction Drives. ASME J. Lubr. Tech. 1979, 101, 266–273. [Google Scholar] [CrossRef]
- Evans, C.R.; Johnson, K.L. The rheological properties of elastohydrodynamic lubricants. Proceed. Inst. Mech. Eng. C J. Mech. Eng. Sci. 1986, 200, 303–312. [Google Scholar] [CrossRef]
- Spikes, H.; Jie, Z. History, Origins and Prediction of Elastohydrodynamic Friction. Tribol. Lett. 2014, 56, 1–25. [Google Scholar] [CrossRef] [Green Version]
- Spikes, H.; Jie, Z. Reply to the Comment by Scott Bair, Philippe Vergne, Punit Kumar, Gerhard Poll, Ivan Krupka, Martin Hartl, Wassim Habchi, Roland Larson on “History, Origins and Prediction of Elastohydrodynamic Friction” by Spikes and Jie in Tribology Letters. Tribol. Lett. 2015, 58, 1–6. [Google Scholar] [CrossRef]
- Bair, S.; Vergne, P.; Kumar, P.; Poll, G.; Krupka, I.; Hartl, M.; Habchi, W.; Larsson, R. Comment on “History, Origins and Prediction of Elastohydrodynamic Friction” by Spikes and Jie. Tribol. Lett. 2015, 58, 1–8. [Google Scholar] [CrossRef]
- Cann, P.M.; Spikes, H.A. Determination of the shear stresses of lubricants in elastohydrodynamic contacts. Tribol. Trans. 1989, 32, 414–422. [Google Scholar] [CrossRef]
- Glovnea, R.; Spikes, H.A. Mapping shear stress in elastohydrodynamic contacts. Tribol. Trans. 1995, 38, 932–940. [Google Scholar] [CrossRef]
- Spikes, H.A.; Anghel, V.; Glovnea, R.P. Measurement of the rheology of lubricant films within elastohydrodynamic contacts. Tribol. Lett. 2004, 17, 593–605. [Google Scholar] [CrossRef]
- Almqvist, T.; Larsson, R. The Navier–Stokes approach for thermal EHL line contact solutions. Tribol. Int. 2002, 35, 163–170. [Google Scholar] [CrossRef]
- Almqvist, T.; Larsson, R. Some Remarks on the Validity of Reynolds Equation in the Modeling of Lubricant Film Flows on the Surface Roughness Scale. J. Tribol. 2004, 126, 703–710. [Google Scholar] [CrossRef]
- Hartinger, M.; Dumont, M.L.; Ioannides, S.; Gosman, D.; Spikes, H. CFD Modeling of a Thermal and Shear-Thinning Elastohydrodynamic Line Contact. J. Tribol. 2008, 130, 1–16. [Google Scholar] [CrossRef]
- Lohner, T.; Ziegltrum, A.; Stemplinger, J.P.; Stahl, K. Engineering software solution for thermal elastohydrodynamic lubrication using multiphysics software. Adv. Tribol. 2016, 2016, 1–13. [Google Scholar] [CrossRef]
- Hajishafiee, A.; Kadiric, A.; Ioannides, S.; Dini, D. A coupled finite-volume CFD solver for two-dimensional elastohydrodynamic lubrication problems with particular application to rolling element bearings. Tribol. Int. 2017, 109, 258–273. [Google Scholar] [CrossRef]
- ANSYS Inc. ANSYS Fluent Theory Guide, Release 15.0; ANSYS Inc.: Canonsburg, PA, USA, 2013. [Google Scholar]
- Srirattayawong, S. CFD Study of Surface Roughness Effects on the Thermo-Elastohydrodynamic Lubrication Line Contact Problem. Ph.D. Thesis, University of Leicester, Leicester, UK, 2014. [Google Scholar]
- Singhal, A.K.; Athavale, M.M.; Li, H.; Jiang, Y. Mathematical Basis and Validation of the Full Cavitation Model. J. Fluid. Eng. 2002, 124, 617–624. [Google Scholar] [CrossRef]
- Dowson, D.; Higginson, G.R. Elasto-Hydrodynamic Lubrication: The Fundamentals of Roller and Gear Lubrication, 1st ed.; Pergamon Press: Oxford, UK, 1966. [Google Scholar]
- Bos, J. Frictional Heating of Tribological Contacts. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 1994. [Google Scholar]
- Habchi, W. A Full-System Finite Element Approach to Elastohydrodynamic Lubrication Problems: Application to Ultra-Low-Viscosity Fluids. Ph.D. Thesis, The Institut National des Sciences Appliquées de Lyon, Lyon, France, 2008. [Google Scholar]
- Björling, M.; Habchi, W.; Bair, S.; Larsson, R.; Marklund, P. Friction Reduction in Elastohydrodynamic Contacts by Thin-Layer Thermal Insulation. Tribol. Lett. 2014, 53, 477–486. [Google Scholar] [CrossRef] [Green Version]
- Roelands, C.J.A. Correlation Aspects of Viscosity-Temperature-Pressure Relationship of Lubricating Oils. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1966. [Google Scholar]
- Houpert, L. New Results of Traction Force Calculations in Elastohydrodynamic Contacts. J. Tribol. 1985, 107, 241–245. [Google Scholar] [CrossRef]
- Hartinger, M. CFD Modelling of Elastohydrodynamic Lubrication. Ph.D. Thesis, Imperial College London, London, UK, 2007. [Google Scholar]
- Hartinger, M.; Reddyhoff, T. CFD Modeling Compared to Temperature and Friction Measurements of an EHL Line Contact. Tribol. Int. 2018, 126, 144–152. [Google Scholar] [CrossRef]
- Korotkovskii, V.I.; Lebedev, A.V.; Ryshkova, O.S.; Bolotnikov, M.F.; Shevchenko, Y.E.; Neruchev, Y.A. Thermophysical Properties of Liquid Squalane C30H62 within the Temperature Range of 298.15–413.15 K at Atmospheric Pressure. High Temp. 2012, 50, 471–474. [Google Scholar] [CrossRef]
- Pettersson, A.; Larsson, R.; Norby, T.; Andersson, O. Properties of Base Fluids for Environmentally Adapted Lubricants. In Proceedings of the World Tribology Congress, Vienna, Austria, 3–7 September 2001. [Google Scholar]
- Pensado, A.S.; Comunas, M.J.P.; Lugo, L.; Fernandez, J. High-Pressure Characterization of Dynamic Viscosity and Derived Properties for Squalane and Two Pentaerythritol Ester Lubricants: Pentaerythritol Tetra-2-ethylhexanoate and Pentaerythritol Tetranonanoate. Ind. Eng. Chem. 2006, 45, 2394–2404. [Google Scholar] [CrossRef]
- Jadhaoa, V.; Robbins, M.O. Probing large viscosities in glass-formers with nonequilibrium simulations. Proc. Natl. Acad. Sci. USA 2017, 114, 7952–7957. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bair, S. Reference liquids for quantitative elastohydrodynamics. Tribol. Lett. 2006, 22, 197–206. [Google Scholar] [CrossRef]
- Habchi, W.; Bair, S.; Vergne, P. On friction regimes in quantitative elastohydrodynamics. Tribol. Int. 2013, 58, 107–117. [Google Scholar] [CrossRef]
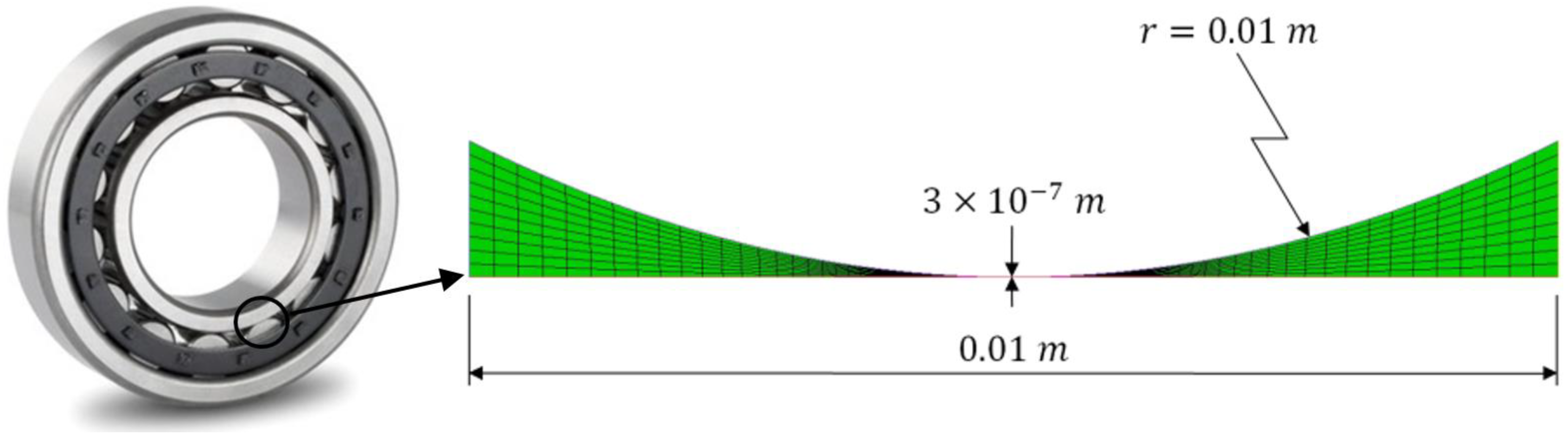
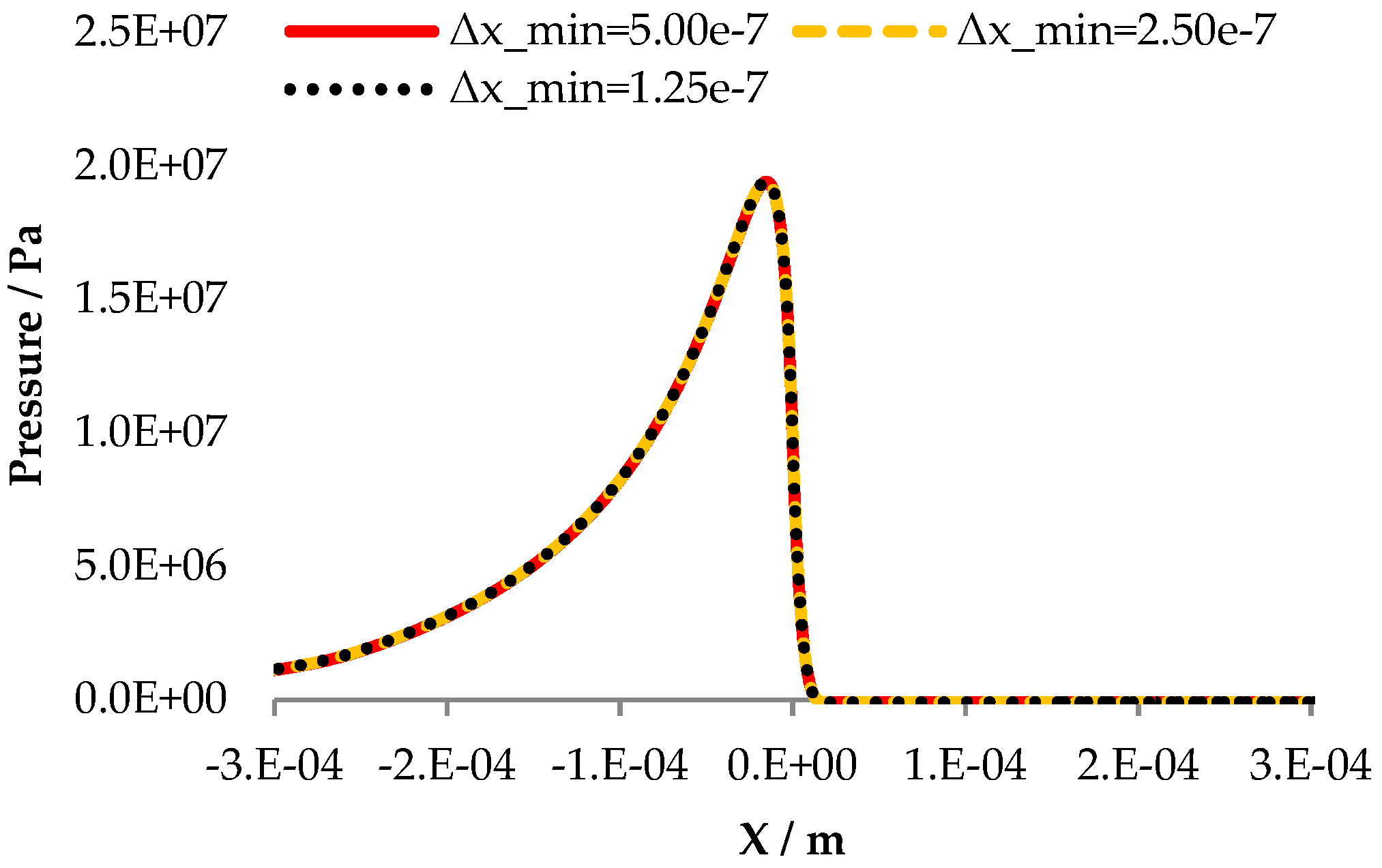


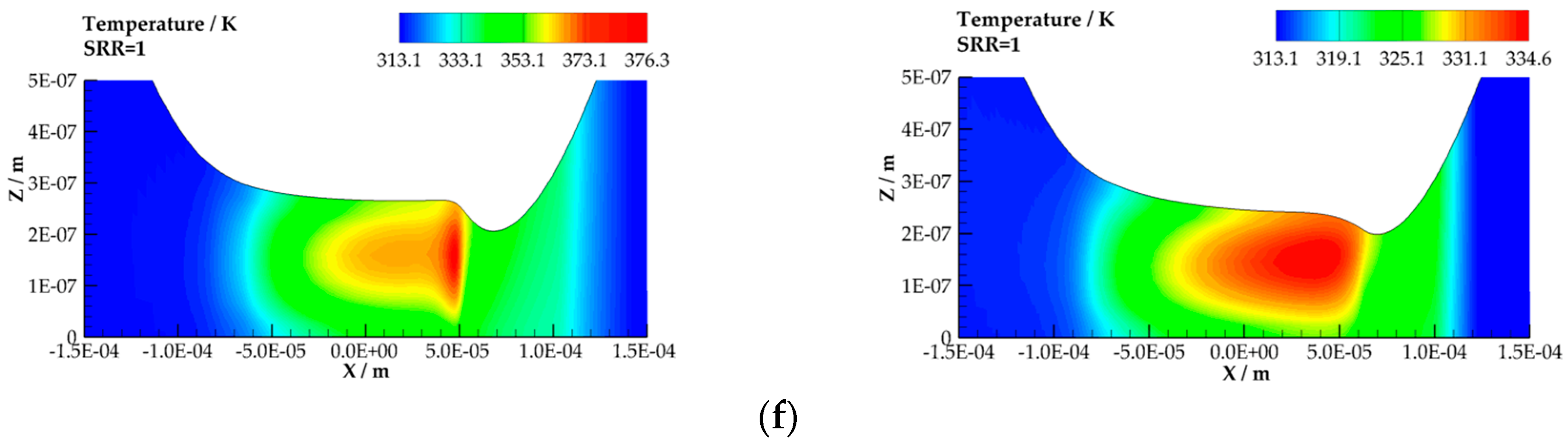

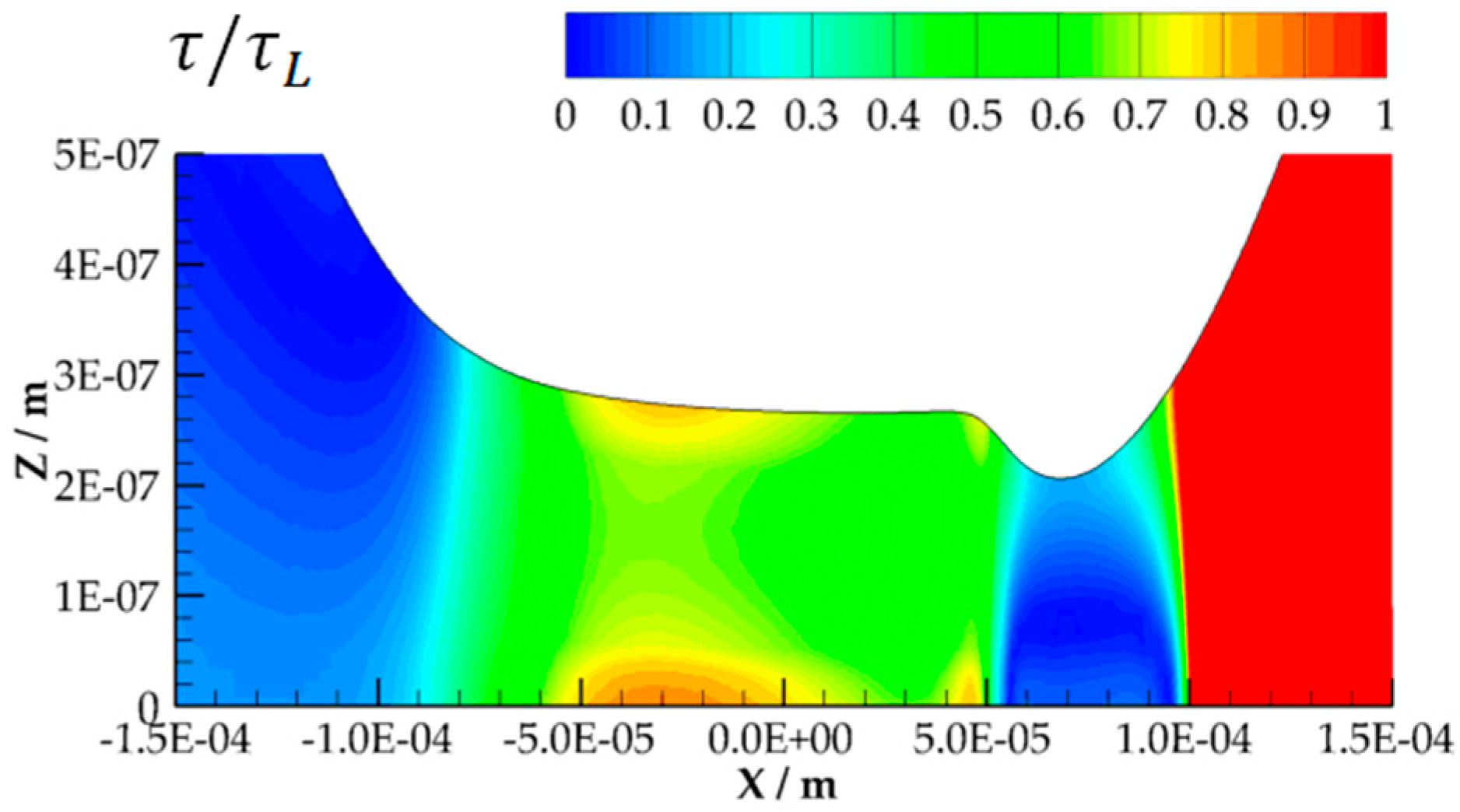

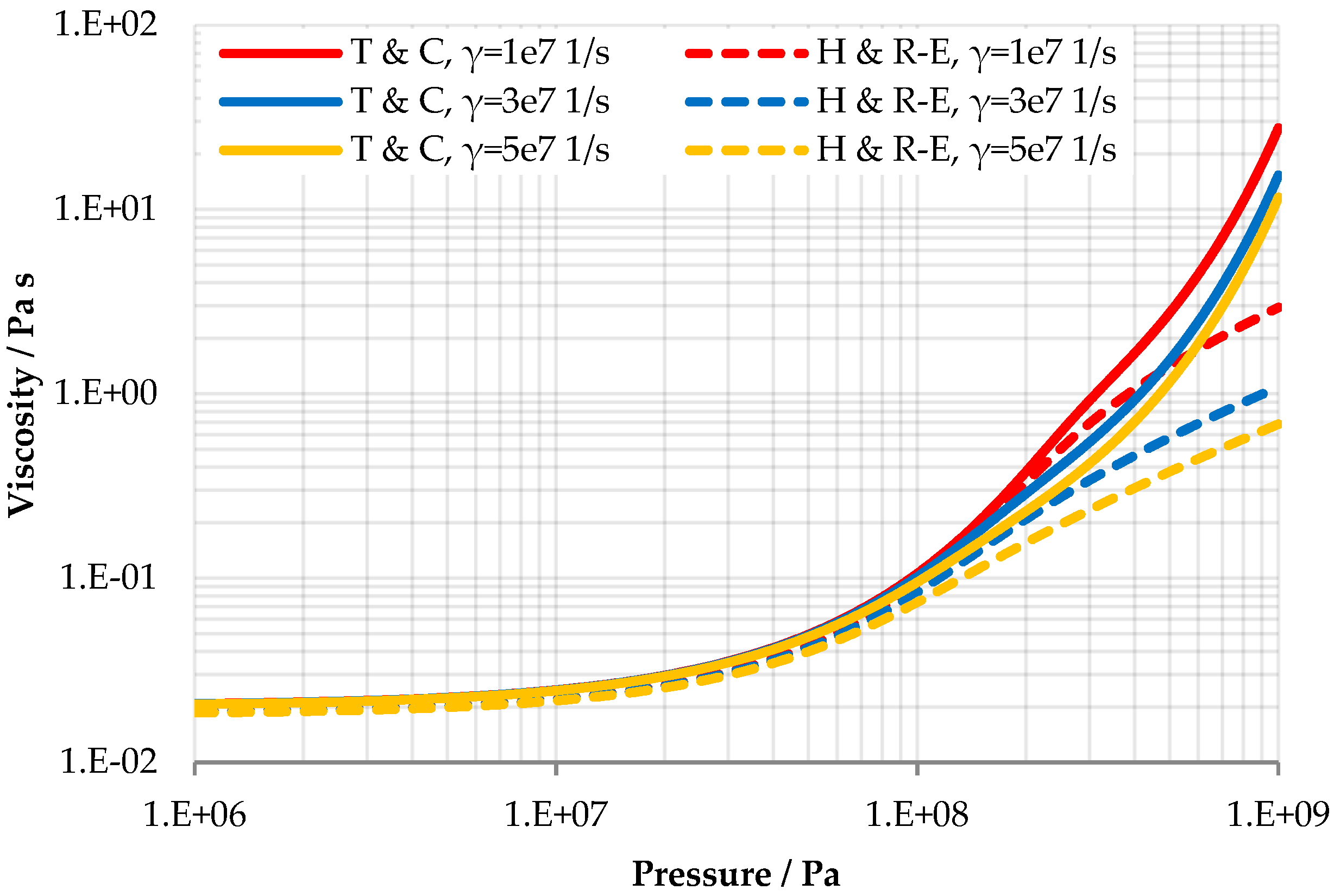
| Min. Cell Size of in X-dir. | Total no. of Cells | Max. Pressure in Pa | CPU Time in s |
|---|---|---|---|
| m | 13,480 | 304 | |
| m | 25,480 | 370 | |
| m | 49,480 | 496 |
| Parameter | Value | Unit | |
|---|---|---|---|
| Operating conditions | |||
| External load, | |||
| Entrainment speed, | |||
| Reference temperature, | |||
| Reduced radius of curvature, | |||
| Properties of solids | |||
| steel [16] | ceramics [16] | ||
| Modulus of elasticity, | |||
| Poisson ratio, | - | ||
| Density, | |||
| Specific heat capacity, | |||
| Thermal conductivity, | |||
| Properties of liquids | |||
| oil [16] | Squalane | ||
| Dynamic viscosity at ambient pressure and , | [21] | ||
| Density, | [26] | ||
| Dynamic viscosity of vapor phase, | 1 | ||
| Density of vapor phase, | 1 | ||
| Specific heat capacity, | - | [26] | |
| Thermal conductivity, | - | [27] 2 | |
| Thermal expansivity, | - | [21] | |
| Houpert and Ree–Eyring input parameters | |||
| oil [16] | Squalane | ||
| Temperature–viscosity coefficient, | - | [28] | |
| Eyring stress, | - | [29] 3 | |
| Roelands pressure–viscosity index, | 0.689 | 4 | - |
| Tait and Carreau input parameters | |||
| Squalane [21] | |||
| Pressure rate of change of isothermal bulk modulus at , | - | ||
| Thermal expansivity defined for volume linear with , | |||
| at zero absolute temperature, | |||
| Temperature coefficient of , | |||
| Thermodynamic interaction parameter, | - | ||
| Viscosity scaling parameter for unbounded viscosity, | - | ||
| Fragility parameter in the new viscosity equation, | - | ||
| Viscosity extrapolated to infinite temperature, | |||
| Relaxation time at and ambient pressure, | |||
| Power law exponent, | - | ||
| Limiting stress pressure coefficient, | - | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tošić, M.; Larsson, R.; Jovanović, J.; Lohner, T.; Björling, M.; Stahl, K. A Computational Fluid Dynamics Study on Shearing Mechanisms in Thermal Elastohydrodynamic Line Contacts. Lubricants 2019, 7, 69. https://doi.org/10.3390/lubricants7080069
Tošić M, Larsson R, Jovanović J, Lohner T, Björling M, Stahl K. A Computational Fluid Dynamics Study on Shearing Mechanisms in Thermal Elastohydrodynamic Line Contacts. Lubricants. 2019; 7(8):69. https://doi.org/10.3390/lubricants7080069
Chicago/Turabian StyleTošić, Marko, Roland Larsson, Janko Jovanović, Thomas Lohner, Marcus Björling, and Karsten Stahl. 2019. "A Computational Fluid Dynamics Study on Shearing Mechanisms in Thermal Elastohydrodynamic Line Contacts" Lubricants 7, no. 8: 69. https://doi.org/10.3390/lubricants7080069







