Exploring the Limits of Cell Adhesion under Shear Stress within Physiological Conditions and beyond on a Chip
Abstract
:1. Introduction
2. Materials and Methods
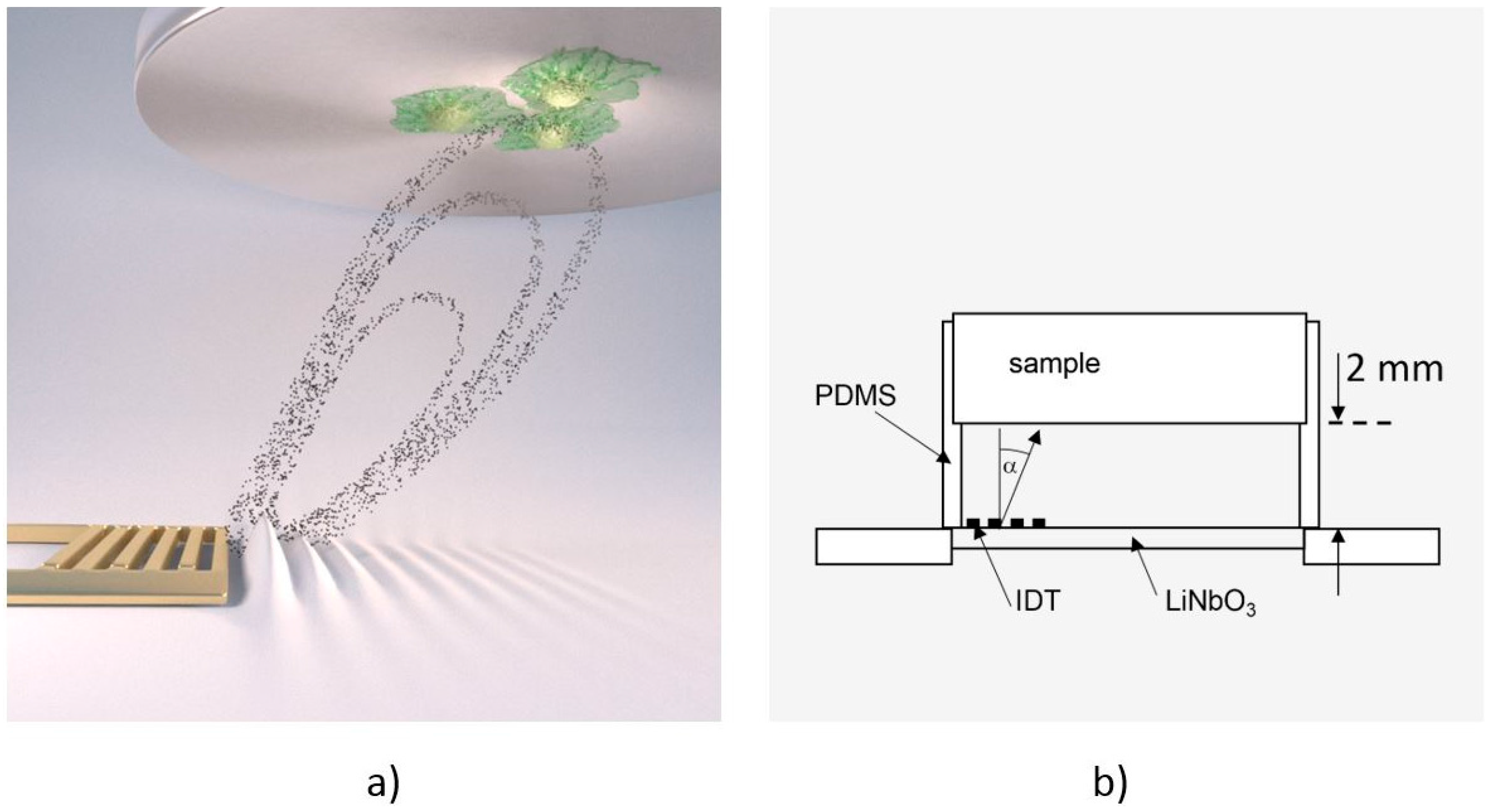
2.1. The De-Adhesion Number Investigator (DANI)
2.2. Scanning Particle Image Velocimetry
2.3. Sample Preparation
2.4. Cell Culture Lines
2.5. Cell Adhesion and Fluorescence Imaging
3. Results and Discussion
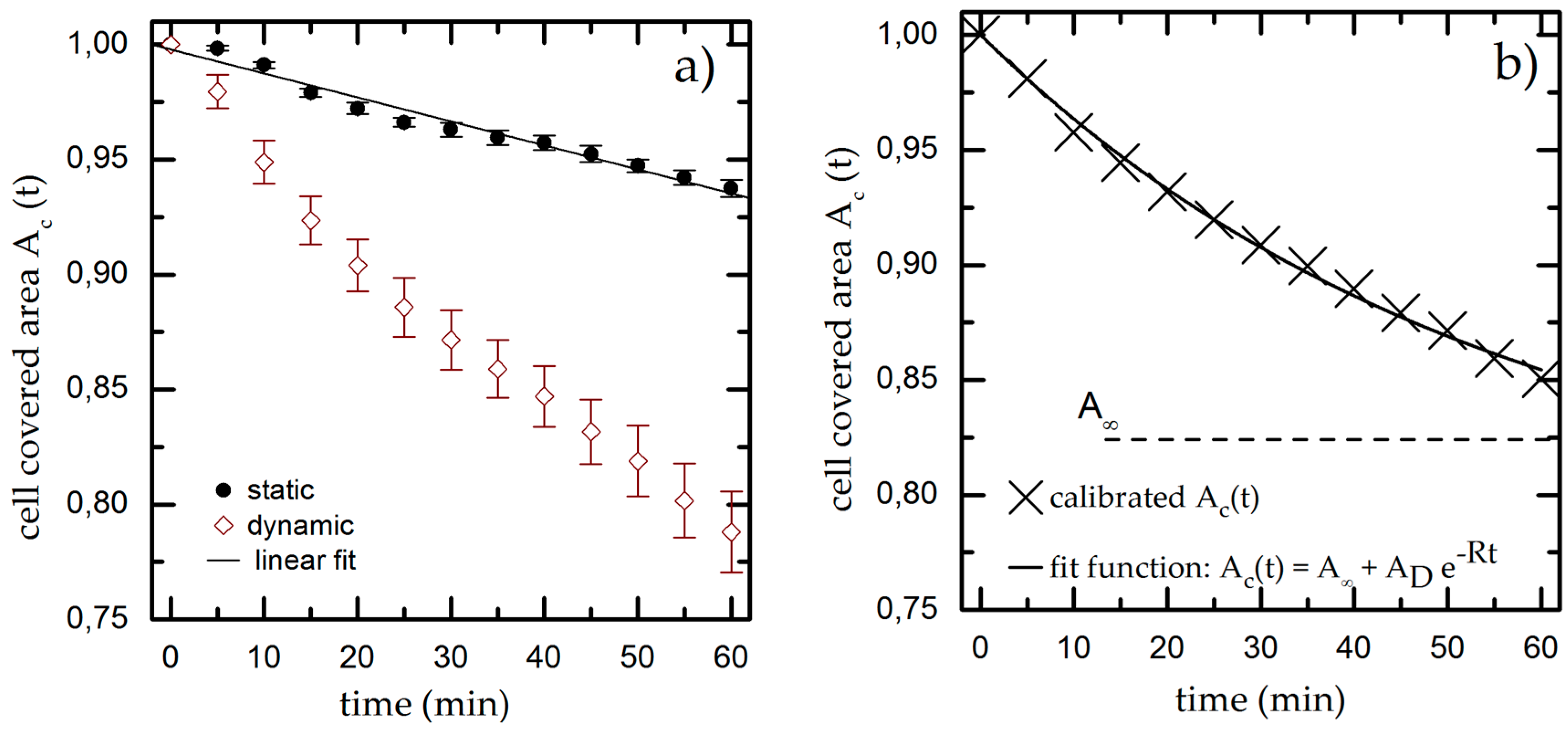
3.1. Time-Dependent Cell Detachment
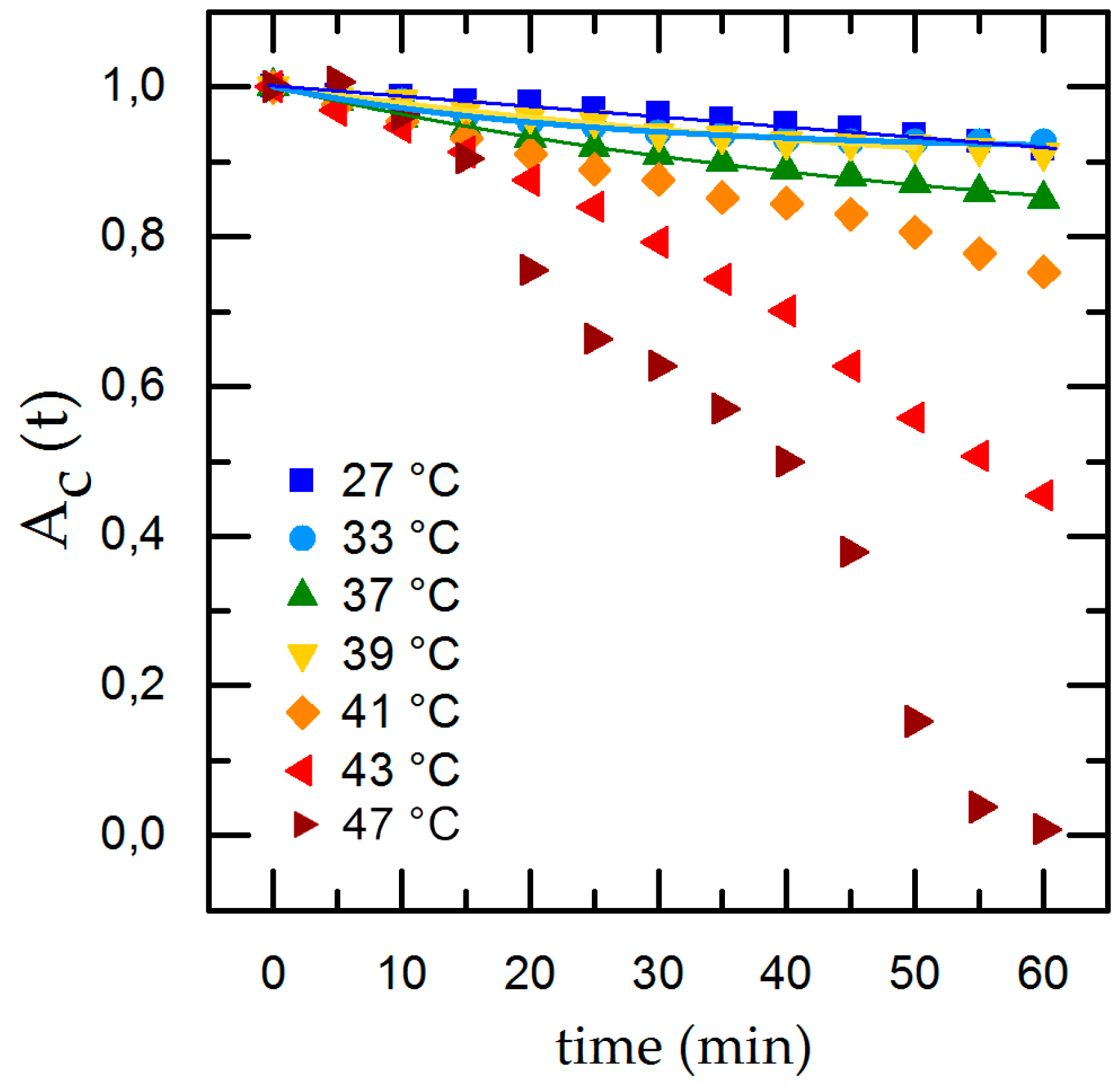
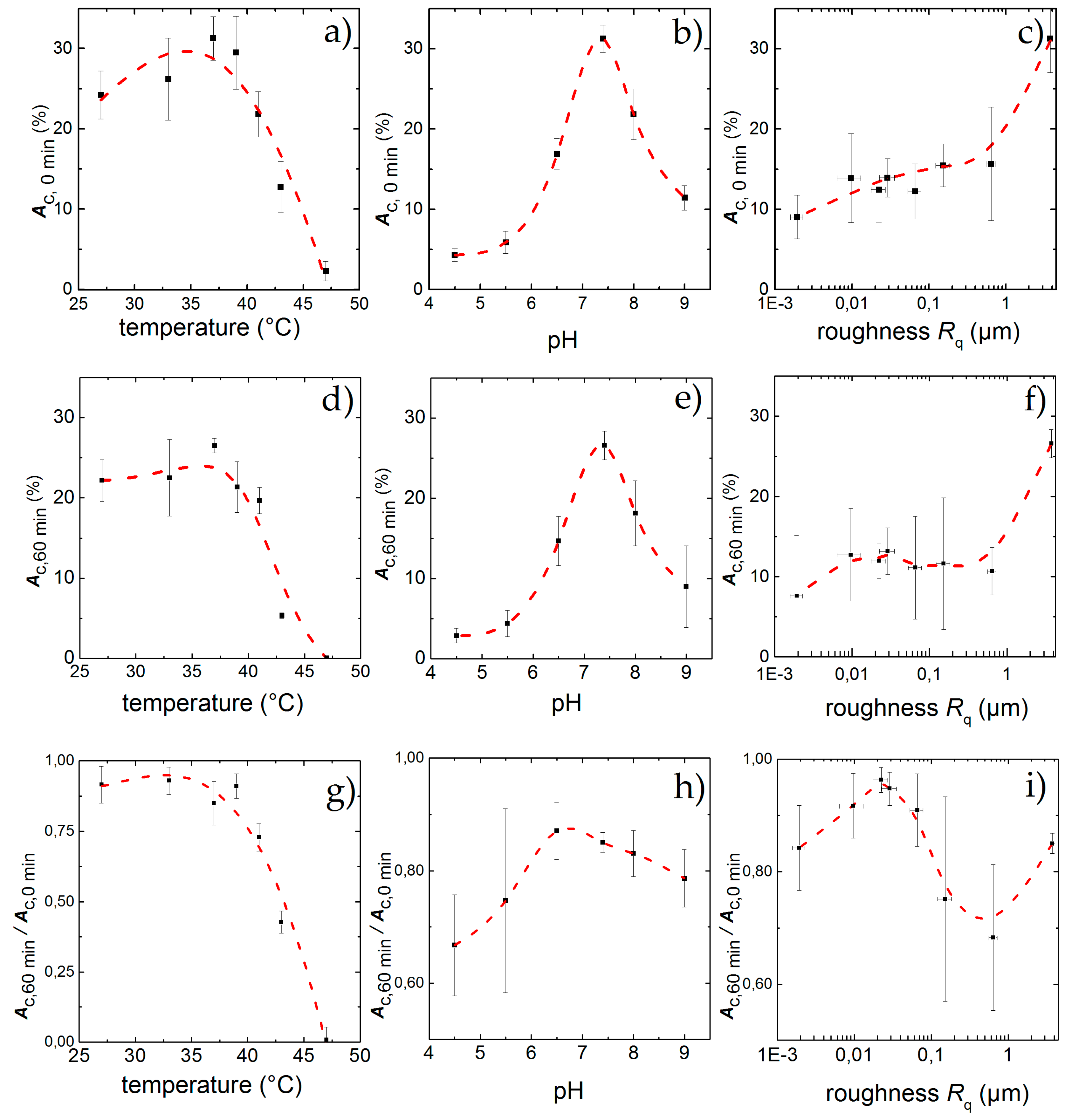
3.2. Influence of Temperature, pH and Surface Roughness on Cell Adhesion
4. Conclusions and Outlook
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| DANI | De-Adhesion Number Investigator |
| SPIV | scanning Particle Image Velocimetry |
| SAW | Surface Acoustic Waves |
| IDT | Inter Digital Transducer |
References
- OECD Indicators. Health at a Glance 2015; OECD Publishing: Paris, France, 2015. [Google Scholar]
- Kurtz, S.; Ong, K.; Lau, E.; Mowat, F.; Halpern, M. Projections of Primary and Revision Hip and Knee Arthroplasty in the United States from 2005 to 2030. J. Bone Jt. Surg. 2007, 89, 780–785. [Google Scholar] [CrossRef] [PubMed]
- Anselme, K.; Bigerelle, M.; Noel, B.; Dufresne, E.; Judas, D.; Iost, A.; Hardouin, P. Qualitative and quantitative study of human osteoblast adhesion on materials with various surface roughnesses. J. Biomed. Mater. Res. 2000, 49, 155–166. [Google Scholar] [CrossRef]
- Anselme, K. Osteoblast adhesion on biomaterials. Biomaterials 2000, 21, 667–681. [Google Scholar] [CrossRef]
- Khalili, A.; Ahmad, M. A Review of Cell Adhesion Studies for Biomedical and Biological Applications. Int. J. Mol. Sci. 2015, 16, 18149–18184. [Google Scholar] [CrossRef] [PubMed]
- Burridge, K. Focal Adhesions: Transmembrane Junctions between the Extracellular Matrix and the Cytoskeleton. Annu. Rev. Cell Dev. Biol. 1988, 4, 487–525. [Google Scholar] [CrossRef] [PubMed]
- Shyy, J.Y.J.; Chien, S. Role of integrins in endothelial mechanosensing of shear stress. Circ. Res. 2002, 91, 769–775. [Google Scholar] [CrossRef] [PubMed]
- Pellegrin, S.; Mellor, H. Actin stress fibres. J. Cell Sci. 2007, 120, 3491–3499. [Google Scholar] [CrossRef] [PubMed]
- Nine, M.J.; Choudhury, D.; Hee, A.C.; Mootanah, R.; Osman, N.A.A. Wear Debris Characterization and Corresponding Biological Response: Artificial Hip and Knee Joints. Materials 2014, 7, 980–1016. [Google Scholar] [CrossRef]
- Hirashima, Y.; Ishiguro, N.; Kondo, S.; Iwata, H. Osteoclast induction from bone marrow cells is due to pro-inflammatory mediators from macrophages exposed to polyethylene particles: A possible mechanism of osteolysis in failed THA. J. Biomed. Mater. Res. 2001, 56, 177–183. [Google Scholar] [CrossRef]
- Pye, A.D.; Lockhart, D.E.A.; Dawson, M.P.; Murray, C.A.; Smith, A.J. A review of dental implants and infection. J. Hosp. Infect. 2009, 72, 104–110. [Google Scholar] [CrossRef] [PubMed]
- Physiologie des Menschen, 22nd ed.; Schmidt, R.F.; Thews, G. (Eds.) Springer: Berlin/Heidelberg, Germany, 1997.
- Ducommun, P.; Ruffieux, P.-A.; Kadouri, A.; von Stockar, U.; Marison, I. W. Monitoring of temperature effects on animal cell metabolism in a packed bed process. Biotechnol. Bioeng. 2002, 77, 838–842. [Google Scholar] [CrossRef] [PubMed]
- Weiss, L. Cell contact phenomena. In Vitro 1970, 5, 48–78. [Google Scholar] [CrossRef] [PubMed]
- Usami, S.; Chen, H.-H.; Zhao, Y.; Chien, S.; Skalak, R. Design and construction of a linear shear stress flow chamber. Ann. Biomed. Eng. 1993, 21, 77–83. [Google Scholar] [CrossRef] [PubMed]
- Bussonnière, A.; Miron, Y.; Baudoin, M.; Bou Matar, O.; Grandbois, M.; Charette, P.; Renaudin, A. Cell detachment and label-free cell sorting using modulated surface acoustic waves (SAWs) in droplet-based microfluidics. Lab Chip 2014, 14, 3556–3563. [Google Scholar] [CrossRef] [PubMed]
- Stamp, M.E.M.; Brugger, M.S.; Wixforth, A.; Westerhausen, C. Acoustotaxis—In vitro stimulation in a wound healing assay employing surface acoustic waves. Biomater. Sci. 2016, 4, 1092–1099. [Google Scholar] [CrossRef] [PubMed]
- Hartmann, A.; Stamp, M.; Kmeth, R.; Buchegger, S.; Stritzker, B.; Saldamli, B.; Burgkart, R.; Schneider, M.F.; Wixforth, A. A novel tool for dynamic cell adhesion studies—The De-Adhesion Number Investigator DANI. Lab Chip 2014, 14, 542–546. [Google Scholar] [CrossRef] [PubMed]
- Frommelt, T.; Gogel, D.; Kostur, M.; Talkner, P.; Hänggi, P. Flow Patterns and Transport in Rayleigh Surface Acoustic Wave Streaming: Combined Finite Element Method and Raytracing Numerics versus Experiments. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2008, 55, 2298–2305. [Google Scholar] [CrossRef] [PubMed]
- Strobl, F.G.; Breyer, D.; Link, P.; Torrano, A.A.; Brauchle, C.; Schneider, M.F.; Wixforth, A. A surface acoustic wave-driven micropump for particle uptake investigation under physiological flow conditions in very small volumes. Beilstein J. Nanotechnol. 2015, 6, 414–419. [Google Scholar] [CrossRef] [PubMed]
- Thielicke, W.; Stamhuis, E.J. PIVlab—Towards User-friendly, Affordable and Accurate Digital Particle Image Velocimetry in MATLAB. J. Open Res. Softw. 2014, 2, e30. [Google Scholar] [CrossRef]
- Thielicke, W.; Stamhuis, E.J. PIVlab—Time-Resolved Digital Particle Image Velocimetry Tool for MATLAB (Version: 1.4). 2015. Available online: http://pivlab.blogspot.com/ (accessed on 19 October 2016).
- Thielicke, W. The Flapping Flight of Birds—Analysis and Application. Ph.D. Thesis, Rijksuniversiteit, Groningen, The Netherlands, 2014. [Google Scholar]
- Lindken, R.; Rossi, M.; Große, S.; Westerweel, J. Micro-Particle Image Velocimetry (µPIV): Recent developments, applications, and guidelines. Lab Chip 2009, 9, 2551–2567. [Google Scholar] [CrossRef] [PubMed]
- Davies, P.F.; Dewey, C.F.; Bussolari, S.R.; Gordon, E.J.; Gimbrone, M.A. Influence of hemodynamic forces on vascular endothelial function. In vitro studies of shear stress and pinocytosis in bovine aortic cells. J. Clin. Investig. 1984, 73, 1121–1129. [Google Scholar] [CrossRef] [PubMed]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef] [PubMed]
- Kaufmann, H.; Mazur, X.; Fussenegger, M.; Bailey, J.E. Influence of low temperature on productivity, proteome and protein phosphorylation of CHO cells. Biotechnol. Bioeng. 1999, 63, 573–582. [Google Scholar] [CrossRef]
- Goergen, J.L.; Marc, A.; Engasser, J.M. Determination of cell lysis and death kinetics in continuous hybridoma cultures from the measurement of lactate dehydrogenase release. Cytotechnology 1993, 11, 189–195. [Google Scholar] [CrossRef] [PubMed]
- Wust, P.; Rau, B.; Gellermann, J.; Pegios, W.; Löffel, J.; Riess, H.; Felix, R.; Schlag, P.M. Radiochemotherapy and Hyperthermia in the Treatment of Rectal Cancer. Recent Results Cancer Res. 1998, 146, 175–191. [Google Scholar] [PubMed]
- Hildebrandt, B.; Wust, P.; Ahlers, O.; Dieing, A.; Sreenivasa, G.; Kerner, T.; Felix, R.; Riess, H. The cellular and molecular basis of hyperthermia. Crit. Rev. Oncol. Hematol. 2002, 43, 33–56. [Google Scholar] [CrossRef]
- Holme, T.A. Denaturation. Available online: http://www.encyclopedia.com/topic/denaturation.aspx (accessed on 21 July 2016).
- Konings, A.W.T.; Ruifrok, A.C.C. Role of Membrane Lipids and Membrane Fluidity in Thermosensitivity and Thermotolerance of Mammalian Cells. Radiat. Res. 1985, 102, 86–98. [Google Scholar] [CrossRef] [PubMed]
- Majda, J.A.; Gerner, E.W.; Vanlandingham, B.; Gehlsen, K.R.; Cress, A.E. Heat Shock-Induced Shedding of Cell Surface Integrins in A549 Human Lung Tumor Cells in Culture. Exp. Cell Res. 1994, 210, 46–51. [Google Scholar] [CrossRef] [PubMed]
- Coss, R.A.; Linnemans, W.A.M. The effects of hyperthermia on the cytoskeleton: A review. Int. J. Hyperth. 1996, 12, 173–196. [Google Scholar] [CrossRef]
- Allgemeine und spezielle Pharmakologie und Toxikologie, 7th ed.; Forth, W.; Henschler, D.; Rummel, W.; Starke, K. (Eds.) Elsevier: Berlin, Germany, 1996. (In German)
- Punnia-Moorthy, A. Evaluation of pH changes in inflammation of the subcutaneous air pouch lining in the rat, induced by carrageenan, dextran and staphylococcus aureus. J. Oral Pathol. Med. 1987, 16, 36–44. [Google Scholar] [CrossRef] [PubMed]
- McQueen, A.; Bailey, J.E. Effect of ammonium ion and extracellular pH of hybridoma cell metabolism and antibody production. Biotechnol. Bioeng. 1990, 35, 1067–1077. [Google Scholar] [CrossRef] [PubMed]
- Tannock, I.; Rotin, D. Acid pH in tumors and its potential for therapeutic exploitation. Cancer Res. 1989, 49, 4373–4384. [Google Scholar] [PubMed]
- Modenaar, H. Effects of growth factors on intracellular pH regulation. Annu. Rev. Physiol. 1986, 48, 363–376. [Google Scholar]
- Serrano, C.V.; Fraticelli, A.; Paniccia, R.; Teti, A.; Noble, B.; Corda, S.; Faraggiana, T.; Ziegelstein, R.C.; Zweier, J.L.; Capogrossi, M.C. pH dependence of neutrophil-endothelial cell adhesion and adhesion molecule expression. Am. J. Physiol. 1996, 271, C962–C970. [Google Scholar] [PubMed]
- Crouch, C.F.; Fowler, H.W.; Spier, R.E. The adhesion of animal cells to surfaces: The measurement of critical surface shear stress permitting attachment or causing detachment. J. Chem. Technol. Biotechnol. Biotechnol. 1985, 35, 273–281. [Google Scholar] [CrossRef]
- Deligianni, D.D.; Katsala, N.D.; Koutsoukos, P.G.; Missirlis, Y.F. Effect of surface roughness of hydroxyapatite on human bone marrow cell adhesion, proliferation, differentiation and detachment strength. Biomaterials 2000, 22, 87–96. [Google Scholar] [CrossRef]
- Meyle, J.; Gültig, K.; Wolburg, H.; von Recum, A.F. Fibroblast anchorage to microtextured surfaces. J. Biomed. Mater. Res. 1993, 27, 1553–1557. [Google Scholar] [CrossRef] [PubMed]
- Boyan, B. Role of material surfaces in regulating bone and cartilage cell response. Biomaterials 1996, 17, 137–146. [Google Scholar] [CrossRef]
- Oakley, C.; Brunette, D.M. The sequence of alignment of microtubules, focal contacts and actin filaments in fibroblasts spreading on smooth and grooved titanium substrata. J. Cell Sci. 1993, 106, 343–354. [Google Scholar] [PubMed]
- Huang, H.H.; Ho, C.T.; Lee, T.H.; Lee, T.L.; Liao, K.K.; Chen, F.L. Effect of surface roughness of ground titanium on initial cell adhesion. Biomol. Eng. 2004, 21, 93–97. [Google Scholar] [CrossRef] [PubMed]
- Den Braber, E.T.; de Ruijter, J.E.; Smits, H.T.J.; Ginsel, L.A.; von Recum, A.F.; Jansen, J.A. Quantitative analysis of cell proliferation and orientation on substrata with uniform parallel surface micro-grooves. Biomaterials 1996, 17, 1093–1099. [Google Scholar] [CrossRef]
- Schmidt, C. Mechanical Stressing of Integrin Receptors Induces Enhanced Tyrosine Phosphorylation of Cytoskeletally Anchored Proteins. J. Biol. Chem. 1998, 273, 5081–5085. [Google Scholar] [CrossRef] [PubMed]
- Cavalcanti-Adam, E.A.; Volberg, T.; Micoulet, A.; Kessler, H.; Geiger, B.; Spatz, J.P. Cell Spreading and Focal Adhesion Dynamics Are Regulated by Spacing of Integrin Ligands. Biophys. J. 2007, 92, 2964–2974. [Google Scholar] [CrossRef] [PubMed]
- Heitmann, S. Messung des Intraossealen Blutflusses zur Bestimmung der Klärfunktion im Gesunden und im Heilenden Knochen Mittels Laser- Dopplerflussmessung im Kaninchenmodell. Ph.D. Thesis, Tierärztliche Hochschule Hannover, Hannover, Germany, 2008. [Google Scholar]
- Laroche, M. Intraosseous circulation from physiology to disease. Jt. Bone Spine 2002, 69, 262–269. [Google Scholar] [CrossRef]
- Cowin, S.C.; Cardoso, L. Blood and interstitial flow in the hierarchical pore space architecture of bone tissue. J. Biomech. 2015, 48, 842–854. [Google Scholar] [CrossRef] [PubMed]
- Buchegger, S.; Vogel, C.; Herrmann, R.; Stritzker, B.; Wixforth, A.; Westerhausen, C. Antibacterial metal ion release from diamond-like carbon modified surfaces for novel multifunctional implant materials. J. Mater. Res. 2016, 31, 2571–2577. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stamp, M.E.M.; Jötten, A.M.; Kudella, P.W.; Breyer, D.; Strobl, F.G.; Geislinger, T.M.; Wixforth, A.; Westerhausen, C. Exploring the Limits of Cell Adhesion under Shear Stress within Physiological Conditions and beyond on a Chip. Diagnostics 2016, 6, 38. https://doi.org/10.3390/diagnostics6040038
Stamp MEM, Jötten AM, Kudella PW, Breyer D, Strobl FG, Geislinger TM, Wixforth A, Westerhausen C. Exploring the Limits of Cell Adhesion under Shear Stress within Physiological Conditions and beyond on a Chip. Diagnostics. 2016; 6(4):38. https://doi.org/10.3390/diagnostics6040038
Chicago/Turabian StyleStamp, Melanie E. M., Anna M. Jötten, Patrick W. Kudella, Dominik Breyer, Florian G. Strobl, Thomas M. Geislinger, Achim Wixforth, and Christoph Westerhausen. 2016. "Exploring the Limits of Cell Adhesion under Shear Stress within Physiological Conditions and beyond on a Chip" Diagnostics 6, no. 4: 38. https://doi.org/10.3390/diagnostics6040038





