Bayesian Estimation of Combined Accuracy for Tests with Verification Bias
Abstract
: This presentation will emphasize the estimation of the combined accuracy of two or more tests when verification bias is present. Verification bias occurs when some of the subjects are not subject to the gold standard. The approach is Bayesian where the estimation of test accuracy is based on the posterior distribution of the relevant parameter. Accuracy of two combined binary tests is estimated employing either “believe the positive” or “believe the negative” rule, then the true and false positive fractions for each rule are computed for two tests. In order to perform the analysis, the missing at random assumption is imposed, and an interesting example is provided by estimating the combined accuracy of CT and MRI to diagnose lung cancer. The Bayesian approach is extended to two ordinal tests when verification bias is present, and the accuracy of the combined tests is based on the ROC area of the risk function. An example involving mammography with two readers with extreme verification bias illustrates the estimation of the combined test accuracy for ordinal tests.1. Introduction
This article introduces the reader to the methodology of measuring the accuracy of several medical tests that are administered to the patient. Our main focus is on measuring the accuracy of a combination of two or more tests. For example, to diagnose type 2 diabetes, the patient is given a fasting blood glucose test, which is followed by an oral glucose tolerance test. What is the accuracy (true and false positive fractions) of this combination of two tests? Or, in order to diagnose coronary artery disease, the subject's history of chest pain is followed by an exercise stress test. Still another example is for the diagnosis of prostate cancer, where a digital rectal exam is followed by measuring PSA (prostate specific antigen). The reader is referred to Johnson, Sandmire, and Klein [1] for a description of additional examples of multiple tests to diagnose a large number of diseases, including heart disease, diabetes, lung cancer, breast cancer, etc.
In many scenarios, it is common practice to administer one or more tests to diagnose a given condition and we will explore two avenues. One case where it is common to administer several tests is in standard medical practice, and the other is an experimental situation where one test is compared to a standard medical test. An example of the latter is that MRI is now being studied as an alternative to standard mammography, as a means to diagnose breast cancer.
There are many studies that assess the accuracy of the combination of two or more tests. Two tests for the diagnosis of a disease measure different aspects or characteristics of the same disease. In the case of diagnostic imaging, two modalities have different qualities (resolution, contrast, and noise), thus, although they are imaging the same scene, the information is not the same from the two sources. When this is the case, the accuracy of the combination of two modalities is of paramount importance. For example, the accuracy of the combination of mammography and scintimammography for suspected breast cancer has been reported by Buscombe, Cwikla, Holloway, and Hilson [2]. Another study for diagnosing breast cancer was performed by Berg, Gutierrez, et al. [3] who measured the accuracy of mammography, clinical examination, ultrasound, and MRI in a preoperative assessment of the disease, The accuracy of each modality and various combinations of the modalites were measured. When investigating metastasis to the lymph nodes in lung cancer, Van Iverhagen, Brakel, and Heijenbrok et al. [4] measured the accuracy of ultrasound and CT and the combination of two. Ultrasound conveys different information about metastasis compared to CT, but the combination of the two might provide a more accurate diagnosis than each separately. For an example of the diagnosis of head and neck cancer, Pauleit, Zimmerman, Stoffels et al. [5] used two nuclear medicine modalities, 18F-FET PET and 18F-FDG PET to assess the extent of the disease and estimated the accuracy of each and combined. On the other hand, Schaffler, Wolf, Schoelinast et al. [6] evaluated pleural abnormalities with CT and 18F-FDG PET and the combination of the two.
2. Measuring the Combined Accuracy of Two Binary Tests
What is the optimal way to measure the accuracy for combination of two binary tests? Pepe ([7], p. 207) presents two approaches: (1) believe the positive rule, or BP, where a positive test score on a subject occurs when one or the other of the two tests is scored positive; and (2) believe the negative rule, or BN, where a subject is scores positive if both tests are scored positive. Pepe also provides some properties about these rules, namely:
The BP rule increases sensitivity relative to the two binary tests, but increases the FPF (false positive fraction), but by no more than the sum of the two false positive fractions FPF1 + FPF2. The false positive fraction of test 1 and test 2 are denoted by FPF1 and FPF2 respectively;
The BN rule decreases the false positive rate relative to the false positive rates of the two tests, but at the same time, decreases the sensitivity, however, the sensitivity remains above TPF1 + TPF2 − 1. Note that the true positive fractions for the two tests are designated by TPF1 and TPF2.
Thus, with the BP rule the combined test is scored positive if one or the other or both of the two are scored positive, but, on the other hand, with the BN rule the combined test is scored positive if both tests are positive.
3. Verification Bias
Verification bias is present when some of the subjects are not subject to the gold standard, thus, the disease status of some of the patients is not known. Consider an example involving the exercise stress test to diagnose heart disease. Among those that test positive, some will undergo coronary angiography to confirm the diagnosis. On the other hand, among those that test negative, very few will be subject to the gold standard. Using only those cases that are verified will lead to biased estimates of test accuracy both of the true and false positive rates, thus, alternative methods based on the missing at random assumptions will be derived from a Bayesian viewpoint.
When assessing the accuracy of two tests, the design in many cases is paired. When two tests are used to assess the patient's condition, true and false positive fractions will be estimated assuming the BP (believe the positive) and BN (believe the negative) rules. For example, two modalities (e.g., CT and MRI) are imaging the same patients and the two images would be expected to be quite similar. Another case of a paired design is for two readers who are imaging the same set of patients with the same imaging device. One expects the information gained from the two paired sources to be highly correlated, and in the case of two paired readers, agreement between the two is also of interest. The experimental layout for a paired study when verification bias is present, namely:
A Good introduction to statistical methods for estimating test accuracy with verification bias is Zhou et al. ([8], p. 307), who use maximum likelihood estimation for the study below.
The two binary tests are Y1 and Y2, where 1 and 0 designate positive and negative tests respectively. For those subjects who are verified for disease V = 1, while those who are not verified are denoted with V = 0.
Note that the number of subjects verified under the gold standard, when both tests are positive, is s11 + r11, among which s11 had the disease and r11 did not have the disease, and also the number that were not verified under the gold standard when both tests are positive is u11 etc., also note that the total number of subjects is
4. Posterior Distribution of Combined Test Accuracy
The following derivation is based on the MAR assumption, namely
Thus, the probability a subject's disease status is verified depends only on the outcomes of the two tests, and not on other considerations. Derivations below follow to some extent Chapter 10 of Zhou, Obuchowski, and McClish8.
Suppose the unknown parameters are defined as follows:
Also let
The likelihood for the parameters is
Assuming an improper prior distribution for the parameters, the posterior distributions are
The improper prior imposed on the parameters is given by the density
Note that if a uniform prior is assumed, one should adjust the posterior distributions for the phis and thetas by adding a one to the beta and Dirichlet hyper parameters given in formulas (6) and (7).
The main parameters of interest are the true positive fraction and the false positive fraction for the two tests, thus for the first test
The main focus of this section is on measuring the accuracy of the combined test in the presence of verification bias of both tests using the BN (believe the negative) and BP (believe the positive) principles.
Assume the BP principle is in effect, then the true positive fraction for the combined test is
Formulas (16)–(19) measure the combined accuracy of two binary tests assuming MAR and assuming an improper prior. If a uniform prior distribution is assumed for the φij and θij, adjust the hyper parameters in formulas (6) and (7) accordingly. For additional information about estimating accuracy with verification bias see Zhou [9,10] and Zhou and Castelluccio [11].
5. Example of MRI and CT to Assess Risk of Lung Cancer
Consider the hypothetical results of two correlated binary tests when verification bias is present as given below. The first test Y1 give the results for a CT determination of lung cancer risk, where a 0 indicates a small risk and a 1 a high risk of lung cancer, while the second test Y2 is a determination of lung cancer risk using MRI. The patients where D = 0 do not have lung cancer.
Using BUGS CODE 1, an analysis that determines the accuracy of the CT and MRI separately and for the combined accuracy is executed with 45,000 observations, with a burn in of 5,000 and a refresh of 100. The list statement of the code gives the data for this example, assuming an improper prior distribution:
BUGS CODE 1
model; {
# two binary tests verification bias
# accuracy of combined tests
g00∼dgamma(m00,2)
g01∼dgamma(m01,2)
g10∼dgamma(m10,2)
g11∼dgamma(m11,2)
h<-g00+g01+g10+g11
th00<-g00/h
th01<-g01/h
th10<-g10/h
th11<-g11/h
ph00∼dbeta(s00,r00)
ph01∼dbeta(s01,r01)
ph10∼dbeta(s10,r10)
ph11∼dbeta(s11,r11)
s1.<-s11+s10
r1.<-r11+r10
s.1<-s01+s11
r.1<-r01+r11
r0.<-r00+r01
s0.<-s00+s01
s.0<-s00+s10
r.0<-r00+r10
ph1.∼dbeta(s1.,r1.)
ph.1∼dbeta(s.1,r.1)
ph0.∼dbeta(s0.,r0.)
ph.0∼dbeta(s.0,r.0)
th1.<-th11+th10
th.1<-th01+th11
th0.<-th01+th00
th.0<-th00+th10
# accuracy for test 1
tpf1<-ph1.*th1./pd1
fpf1<-(1-ph1.)*th1./(1-pd1)
# p[D-1]
pd1<-ph1.*th1.+ph0.*th0.
# accuracy for test 2
tpf2<-ph.1*th.1/pd2
fpf2<-(1-ph.1)*th.1/(1-pd2)
pd2<-ph.1*th.1+ph.0*th.0
# accuracy combined tests
# believe the positive, BP
tpfbp<-(ph11*th11+ph01*th01+ph10*th10)/pd
# P[d=1]
pd<-ph11*th11+ph10*th10+ph01*th01+ph00*th00
fpfbp<-((1-ph11)*th11+(1-ph10)*th10+(1-ph01)*th01)/(1-pd)
# believe the negative, BN
tpfbn<-ph11*th11/pd
fpfbn<- (1-ph11)*th11/(1-pd)}
# CT and MRI for lung cancer risk with improper prior
# for a uniform prior, add a one to the values in the list statement
list(s00=3,r00=18,s01=9,r01=13,s10=12,r10=9,s11=14,r11=4, m00=31,m01=31,m10=29,m11=25)
# activate initial values from the specification tool with the gen inits button
Note the above code closely follows the derivation given in formulas (1)–(19). This analysis can be executed by downloading the code from http://medtestacc.blogspot.com.
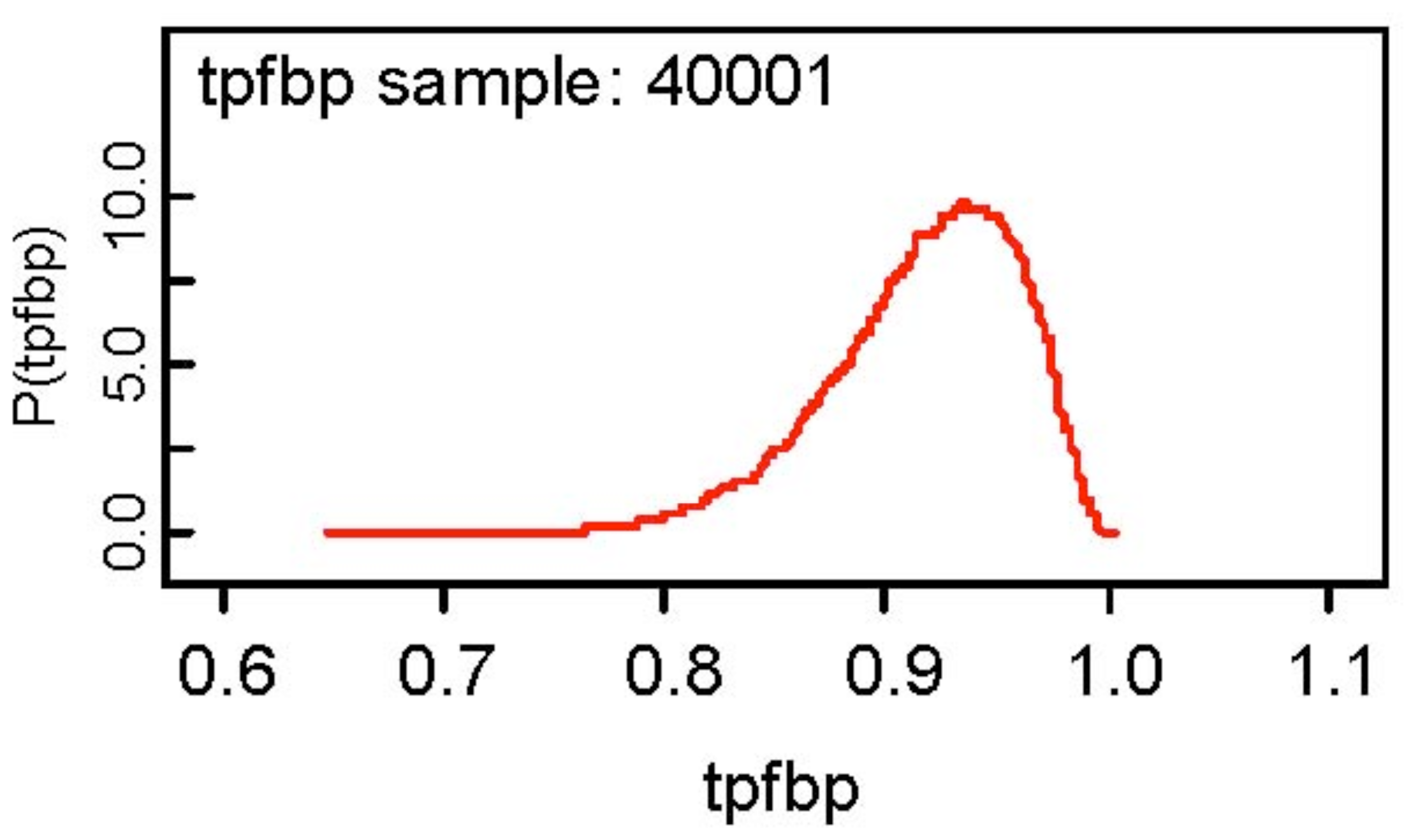
The results of the analysis show that the false positive fractions for the two modalities are fairly high being 0.286 and 0.38 for CT and MRI respectively, but on the other hand, the true positive fractions for the two modalities are somewhat low at 0.6755 and 0.60 respectively for CT and MRI. It is also observed that the MCMC errors for all parameters are less than 0.0001 and the posterior distributions of all parameters appear to be symmetric about the posterior mean. Assuming the BN rule, the true and false positive fractions are estimated as 0.3663 and 0.0880, but as for the BP rule, the corresponding estimates (based on the posterior mean) are 0.9165 and 0.5766! The fact that both modalities are not very accurate is reflected in the estimated combined accuracies for the BN and BP rules. At first glance, the BP rule is encouraging in that the true positive fraction is 0.9165, but the false positive fraction is also large as 0.5766. The BN rule gives a low estimate of 0.0880 for the false positive rate, but also a low estimate of 0.3663 for the true positive fraction. The posterior density of the true positive fraction for the BP rule is depicted below. Note what rule the user adopts depends on their personal preference.
6. Extreme Verification Bias
The reader is referred to Pepe ([7], p. 180) and Broemeling ([12], p. 166) for a description of many studies for those cases where when the test is positive, the subject is referred to the gold standard (verification of disease status), but if the test is negative the subject is not referred to the gold standard. In such situations, the true and false positive rates are not estimable. Consider the following hypothetical example given by above in Table 2, where MRI and CT are jointly used to detect lung cancer, where the results of CT are given by the first test and those of MRI given by Y2. Note when the subject is verified with D = 0, the patient does not have lung cancer.
The results of Table 2 have been modified so that all patients are referred to the gold standard (biopsy) except those where both tests are negative. There are 82 patients, of which 61 are verified for disease, namely the 18 who test positive when both CT and MRI are positive, 21 patients who test positive with CT but negative with MRI, and lastly 22 patients who test positive with MRI and negative with CT.
When both tests are negative, 21 patients are not subject to the gold standard. Since they were not verified, one does not know their disease status (D = 0 or D = 1), thus one does not know the fraction of patients with disease, and the true and false positive fractions cannot be estimated. This is a case where it is not possible to estimate the true and false positive fractions for either test. However, not all is lost because other measures of test accuracies for both tests can be estimated.
Consider the detection probability for CT namely P[Y1= 1, D = 1], then the estimated detection probability is 26/82 = 0.317, while the detection probability of MRI is estimated as 23/82 = 0.280. In lieu of the true and false positive fractions, the detection probability and the false referral probability for both tests aid in the estimation of the test accuracy of the combined tests. For example, the false referral probability for CT is P[Y1 = 1, D = 0] which is estimated as 13/82 = 0.158, and for MRI the false referral probability is estimated as 17/82 = 0.2073.
It is interesting to note that the detection probability of a test is expressed as
It is interesting to observe that the individual true and false positive fractions cannot be estimated, but that the true and false positive fractions of two tests can be compared for studies with extreme verification bias.
How is the accuracy of the combined tests estimated? Can one employ the BP (believe the positive) and BN rules to estimate the accuracy of the combined tests? The answer is no!
Consider the BP rule and refer to Table 4, where the true positive fraction of the combined tests is measured by P[Y1 =1orY2 =1|D = 1], however, the disease frequency cannot be estimated. On the other hand, the ratio of the true positive fraction for the BP rule relative to the true positive fraction of the BN rule can be measured by
From Table 4 for the CT-MRI study of lung cancer risk, a naïve estimate of this quantity is 35/14 = 2.5, which implies the true positive fraction for the BP rule is approximately 2.5 times larger than the true positive fraction for the BN rule.
In a similar way the false positive fraction for the BP rule relative to the false positive fraction of the BN rule can be measured as
Referring to Table 4 provides an estimate of 26/4 = 6.5 for comparing the false positive fractions for the two rules, implying the false positive rate for the BP rule is six and half times larger that of the BN rule.
Extreme verification bias does not provide sufficient information to estimate the usual measures of test accuracy, however, in lieu of those measures, it is possible to assess the accuracy of two binary tests (with extreme verification bias) by: (1) the detection probabilities; (2) the false referral probabilities and (3) the ratio of the true positive fraction for the BP rule relative to that of the BN rule, and (4) the ratio of the false positive fraction of the BP rule relative to that of the BN rule.
7. Bayesian Analysis for Extreme Verification Bias
The foundation of the Bayesian analysis given by formulas (1)–(19) which are now expanded to determine the posterior distribution of the detection probabilities and false referral probabilities of both tests.
With regard to estimating the combined accuracy of the two tests in the presence of extreme verification bias, the posterior distributions of the ratio of the true positive fraction of the BP relative to that of the BN rule is determined as is the ratio of the false positive fraction of the BP rule relative to that of the BN rule.
For the detection probability of the first test
8. Bayesian Analysis for Risk of Lung Cancer
BUGS CODE 1 is amended with the following WinBUGS® code.
For the detection probabilities, the statements are:
Refer to formula (30) for the ratio of the true positive fraction of the BP rule relative to that of the BN rule, thus the following:
The analysis for the CT-MRI determination of lung cancer risk with extreme verification bias is based on the amended BUGS CODE 1 by generating 55,000 samples from the posterior distributions of the detection and false referral probabilities of both CT and MRI. Also computed are the posterior distributions of the ratio of the true and false positive fractions of the BP rule relative to that of the BN rule. I used a burn in of 5,000 observations with a refresh of 100 to give.
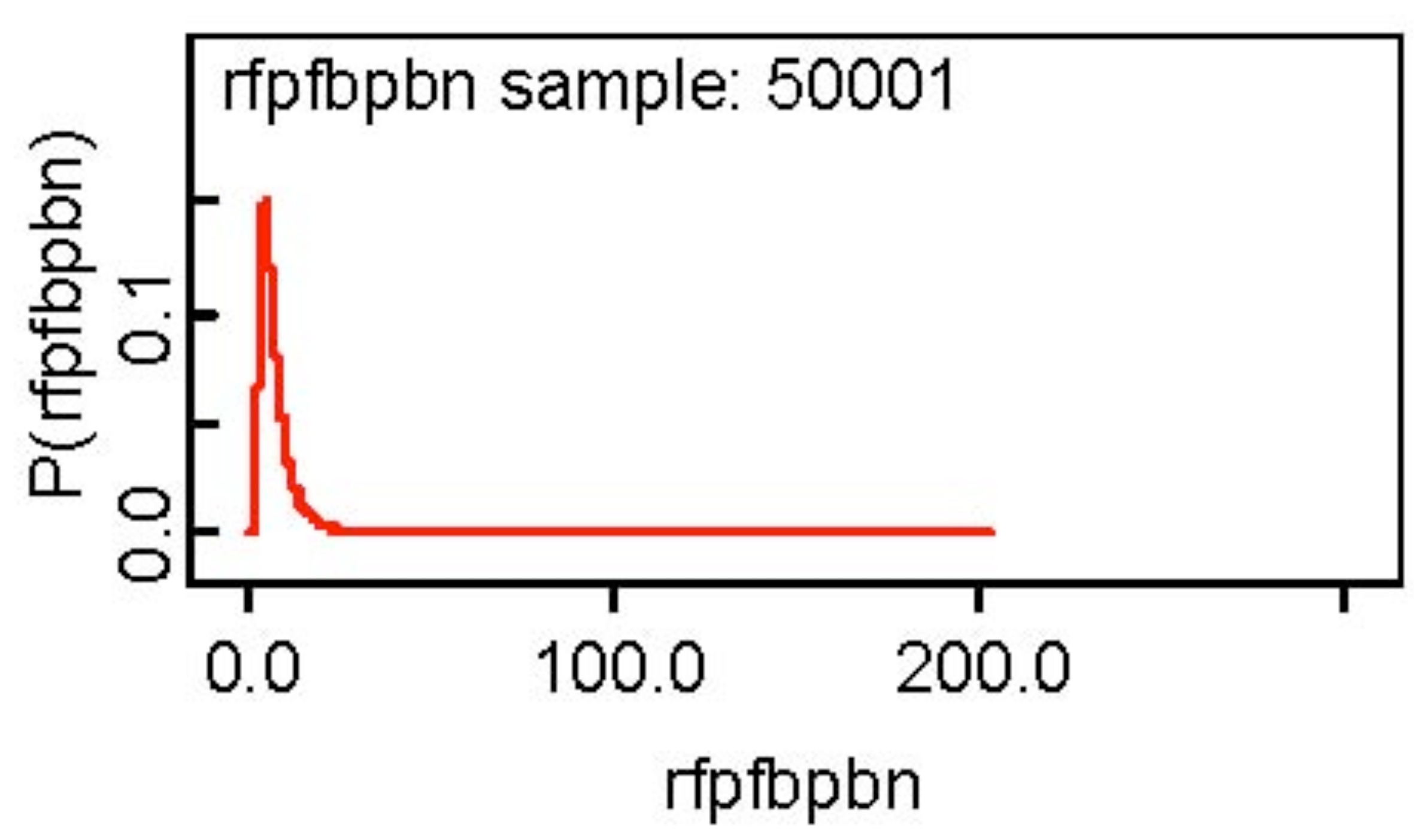
One notices the skewness of the posterior distribution of the ratio of the false positive fraction of the BP rule relative to the BN rule and the skewness is evident from Figure 2 below. I would use 6.902 the posterior median as a point estimate of the ratio.
The other posterior distributions appear to be symmetric about the posterior mean. The detection probability of the two tests are similar, but the false referral probability of CT is somewhat less than that of MRI and the TPF of the BP rule appears to be 2.61 times that of the BN rules. On the other hand, the false positive fraction of the BP rule is 6.9 times that of the BN rule.
Recall that the true and false positive fractions of the two rules are not known, thus, it is difficult to interpret these ratios. The detection probability of a test is somewhat related to the true positive fraction in that one would favor a test with a higher detection probability. Also, of course, one would favor a test with lower false referral probability, thus, the overall conclusion about test comparison is to favor the CT determination of lung cancer risk. As for the accuracy of the combined test, the two ratios one for the true positive fraction and one for the false positive fraction provide the relevant information. Should the accuracy be based on the BP or the BN rule? The BP rule gives a larger true positive fraction, but unfortunately a much larger false positive fraction.
9. Verification Bias for Two Ordinal Tests
When analyzing the accuracy of combined tests when the tests are ordinal, a somewhat different approach is taken, where the overall accuracy is measured by the area of the ROC curve of the risk score. The risk scores are the probability of disease of each patient, usually determined. An informative presentation of the risk score is given by Pepe ([7], p. 271).
Our general methodology is based on inverse probability weighting which transforms the original table of observations with verification (See Table), to an imputed table. Such ideas will be explained in a later section, but the reader is referred to Pepe ([7], p.172) and Broemeling ([13], p. 279) for additional details of the inverse probability weighting approach for estimating the accuracy of tests with verification bias.
The analysis of assessing the accuracy of two tests is now expanded to include two ordinal tests T1 and T2, where the general layout is given by Table 5. As before the si denote the number of patients for the 9 events when D = 1, while the ri represent the number of cases for the nine events when D = 0. The total number of observations is . Each test has three values, but of course the general situation has a similar scenario.
In what is to follow, the posterior distribution of the ROC area of the two ordinal tests is developed, which is to be followed by an explanation of inverse probability weighting, and lastly the use of the risk score to asses the accuracy of the combined tests is explained.
10. Posterior Distribution of the ROC Areas for Two Ordinal Tests with Verification Bias
Recall from formulas (1) and (2) that
The improper prior density used here is the reciprocal of the parameters over the relevant region of the parameter space.
If uniform prior is appropriate, add a 1 to the hyper parameters of the φi and θi for i = 1,2,3.
Note that
Of course, a similar expression holds for the ROC area of test 2. After determining the posterior distribution of the ROC areas of the two tests, the accuracy of the combined tests will be measured by the ROC area of the risk score. In order to illustrate Bayesian inference for estimating the accuracy of two ordinal tests, consider the following example, two readers are diagnosing breast cancer. They are both employed by a university cancer center and they both use a three–point scale to diagnose the disease, where a 1 indicates definitely no lesion is seen in the mammogram, a 2 denotes there is a possibility that a lesion is present, and a 3 signifies that a lesion is definitely present The diseased patients in fact have breast cancer and the non-diseased definitely do not have breast cancer.
The total number of patients is , and for each of the nine categories patients are not referred to the gold standard, for example. For example, when T1 = T2 = 1, 109 are referred to the gold standard and 2 are not, while if T1 = T2 = 2, 83 are not referred, while 153 are subject the gold standard. What are the ROC areas of the two tests? The following code is based on the previous development of the posterior distributions of the relevant parameters (given by formulas (36)–(50)) and appears below.
BUGS CODE 2
model;
# hypothetical data set
# two tests for staging melanoma
# one rater is a surgeon the other a dermatologist
# ratings are: stage 1, stage 2, stage 3
# similar to Zhou([8],p347) on CT and MRI
{
for (i in 1:9) {ph[i]∼dbeta(s[i],r[i])}
for (i in 1:9) {g[i]∼dgamma(m[i],2)}
ms<-sum(g[])
for (i in 1:9) {theta[i]<-g[i]/ms }
theta1.<- theta[1]+theta[2]+theta[3]
theta2.<- theta[4]+theta[5]+theta[6]
theta3.<- theta[7]+theta[8]+theta[9]
theta.1<- theta[1]+theta[4]+theta[7]
theta.2<- theta[2]+theta[5]+theta[8]
theta.3<- theta[3]+theta[6]+theta[9]
s1.<-s[1]+s[2]+s[3]
s2.<-s[4]+s[5]+s[6]
s3.<-s[7]+s[8]+s[9]
s.1<-s[1]+s[4]+s[7]
s.2<-s[2]+s[5]+s[8]
s.3<-s[3]+s[6]+s[9]
r1.<-r[1]+r[2]+r[3]
r2.<-r[4]+r[5]+r[6]
r3.<-r[7]+r[8]+r[9]
r.1<-r[1]+r[4]+r[7]
r.2<-r[2]+r[5]+r[8]
r.3<-r[3]+r[6]+r[9]
# the prob D=1 given Y1=1
ph1.∼dbeta(s1.,r1.)
ph2.∼dbeta(s2.,r2.)
ph3.∼dbeta(s3.,r3.)
ph.1∼dbeta(s.1,r.1)
ph.2∼dbeta(s.2,r.2)
ph.3∼dbeta(s.3,r.3)
# the prob the first test =1 given d=1
alpha1[1]<- ph1.*theta1./dalpha1
alpha1[2]<- ph2.*theta2./dalpha1
alpha1[3]<- ph3.*theta3./dalpha1
dalpha1<- ph1.*theta1.+ph2.*theta2.+ph3.*theta3.
# the prob the first test =1 given D=0
beta1[1]<-((1-ph1.)*theta1.)/dbeta1
beta1[2]<-((1-ph2.)*theta2.)/dbeta1
beta1[3]<-((1-ph3.)*theta3.)/dbeta1
dbeta1<-(1-ph1.)*theta1.+(1-ph2.)*theta2.+(1-ph3.)*theta3.
# the prob that the second test =1 given d=1
alpha2[1]<- ph.1*theta.1/dalpha2
alpha2[2]<- ph.2*theta.2/dalpha2
alpha2[3]<- ph.3*theta.3/dalpha2
dalpha2<- ph.1*theta.1+ph.2*theta.2+ph.3*theta.3
beta2[1]<-((1-ph.1)*theta.1)/dbeta2
beta2[2]<-((1-ph.2)*theta.2)/dbeta2
beta2[3]<-((1-ph.3)*theta.3)/dbeta2
dbeta2<-(1-ph.1)*theta.1+(1-ph.2)*theta.2+(1-ph.3)*theta.3
# area of test 1
A1<- A11+A12
A11<- alpha1[2]*beta1[1]+alpha1[3]*(beta1[1]+beta1[2])
A12<- (alpha1[1]*beta1[1]+alpha1[2]*beta1[2]+alpha1[3]*beta1[3])/2
# area of test 2
A2<- A21+A22
A21<- alpha2[2]*beta2[1]+alpha2[3]*(beta2[1]+beta2[2])
A22<- (alpha2[1]*beta2[1]+alpha2[2]*beta2[2]+alpha2[3]*beta2[3])/2
d<-A1-A2
}
# two readers
# assume an improper prior
# see Table 6
list(r = c(101,105,83,67,72,40,41,30,4), s = c(8,26,51,43,81,94,117,140,208), m= c(111,149,196,124,236,201,221,210,320))
# the initial values are activated from the specification tool by clicking on the gen inits button.
The code closely follows formulas (36)–(50), and the analysis is executed with 55,000 samples from the posterior distribution of the parameters, with a burn in of 5,000 and a refresh of 100 and the results are reported in Table 7.
Reader 1 appears more accurate that reader 2. It should be noted that the gold standard is biopsy of the tissue from the suspected lesion. The MCMC errors are quite “small” and give one confidence that the simulation is providing accurate estimates of the accuracy.
The main goal of the analysis is to estimate the combined accuracy of the two readers nd compare it the individual estimated ROC areas given by Table 7.
11. Inverse Probability Weighting
Pepe ([7], p. 171) describes an interesting variation on estimating test accuracy with verification bias by the inverse probability weighting technique, and for further information, see Begg and Greenes [14]. Briefly this method involves constructing an imputed data table from the observed data table with verification bias. Consider the observed data table (Table 6) with verification bias. For each pair of values (T1,T2), the cell entries for si and ri are multiplied by the inverse of the verification rate. For example, when (T1,T2) = (1,1) the verification rate is 109/111, thus for s1, 8 is replaced 8(111/109) = 8.146 and for r1, the number 101 is replaced by 101(111/109) = 102.85. If this is done for the remaining 8 events, the observed Table 6 is replaced by the selected table below:
The imputed table has no verification bias and the ROC areas of the two tests based on this table are the same as those based on Table 6, the table with verification bias. In general it can be shown for binary tests that the true and false positive fractions are the same, for those based on the observed table and those based on the selected table without verification bias. See Pepe ([7], p. 172), thus, inverse probability weighting is appropriate for two ordinal tests with verification bias. It is seen the effect of inverse probability weighting is to convert a table with verification bias into a table without. The presentation is continued by developing the risk score to assess the accuracy of two ordinal tests with verification bias, where the basic idea is to compute the ROC of the risk score. For additional information about estimating the test accuracy of ordinal tests with verification bias using the ROC area, see Gray et al. [15].
12. The Risk Score
The risk score is the probability that D = 1, which is the value assigned to all patients in the study. For example, for each of the 1,768 patients in the melanoma staging study portrayed in Table 8, the probability of disease is assigned and the ROC area computed. The ROC area of the risk score is the combined accuracy of the two ordinal tests with verification bias.
The risk score is defined as
The risk score (51) has the same ROC curve as the likelihood ratio and the same optimal properties. Observe that
Suppose the risk score is expressed as
the parameter λ can be estimated, even for retrospective designs in which the sampling depends on D, and
the function g is optimal for determining the ROC curve of the risk function.
From a practical point of view, logistic regression can be used to determine the ROC curve of the risk function, but it should be noted that finding a suitable function g can be a challenge. After all, g can be a complicated non-linear function of λ and/ or Y, but it would be convenient if g is linear in the test scores Y. In order to estimate the logistic regression function or risk score, Broemeling ([13], p. 474), takes a Bayesian approach.
For the example of Table 8, where two readers are diagnosing breast cancer, the risk score is computed by logistic regression using the following code.
BUGS CODE 3
model;
# logistic regression
{
for(i in 1:N){d[i]∼dbern(theta[i])}
for(i in 1:N){logit(theta[i])<-b[1]+b[2]*T1[i]+b[3]*T2[i]}
# prior distributions
for(i in 1:3){b[i]∼dnorm(0.000,.0001)}
}
In order to accommodate the data, a list statement must be added, which consists of three vectors, each of dimension 1,768, corresponding to the number of patients in the study: The vectors T1 and T2 will consist of the values 1,2, or 3 corresponding to Table 8, while a d vector will consists of zeros and ones, where a 1 indicates the patient has melanoma and a 0 indicates no melanoma, thus, the first 1,078 components of d consist of a one, while the remaining 690 consist of zeros. After execution of the BUGS CODE 3, with 45,000 samples from the posterior distribution, with a burn in of 5,000, and a refresh of 100, the posterior distribution of coefficients of the logistic regression is given in Table 9.
The posterior distributions indicate the coefficients are not zero and are important in determining the risk score of each patient, but the main interest is in the vector theta (of dimension 1,768) where the median of each component is used as the risk score. There were 9 distinct risk scores: 0.086, 0.187, 0.36, 0.336, 0.5542, 0.733, 0.7542, 0.8704, and 0.9426. Therefore, I computed the ROC using the basic formula from Broemeling ([12], p. 58) for the ROC area of a test with ordinal responses.
Using BUGS CODE 4, I computed the ROC area of the risk score via BUGS CODE 4 with posterior mean 0.842 with a 95% credible interval of (0.8238, 0.8608). (Also, the ROC area was computed with a non-parametric technique with SPSS with the same result as the Bayesian). Thus, using the risk score, the estimated ROC area is 0.842 compared to a ROC area of 0.78 for the surgeon and 0.63 for the dermatologist, thus, the accuracy of the combining results of two readers is more than the individual accuracies. Consider the posterior analysis:
Based on BUGS CODE 4, the analysis is executed with 55,000 observations with a burn in of 5,000 and a refresh of 100. A2 is the probability of a tie, and auc is the ROC area. Small MCMC errors for the parameters are evident, and the posterior distribution of all parameters appear to be symmetric. The code below is explained with explanatory remarks indicated by #.
BUGS CODE 4
# Area under the curve
# Ordinal values
# Nine values
model;
{
# generate Dirichlet distribution
g11∼dgamma(a11,2)
g12∼dgamma(a12,2)
g13∼dgamma(a13,2)
g14∼dgamma(a14,2)
g15∼dgamma(a15,2)
g16∼dgamma(a16,2)
g17∼dgamma(a17,2)
g18∼dgamma(a18,2)
g19∼dgamma(a19,2)
g01∼dgamma(a01,2)
g02∼dgamma(a02,2)
g03∼dgamma(a03,2)
g04∼dgamma(a04,2)
g05∼dgamma(a05,2)
g06∼dgamma(a06,2)
g07∼dgamma(a07,2)
g08∼dgamma(a08,2)
g09∼dgamma(a09,2)
g1<-g11+g12+g13+g14+g15+g16+g17+g18+g19
g0<-g01+g02+g03+g04+g05+g06+g07+g08+g09
# posterior distribution of probabilities for response of diseased patients
theta1<-g11/g1
theta2<-g12/g1
theta3<-g13/g1
theta4<-g14/g1
theta5<-g15/g1
theta6<-g16/g1
theta7<-g17/g1
theta8<-g18/g1
theta9<-g19/g1
# posterior distribution for probabilities of response of non-diseased patients
ph1<-g01/g0
ph2<-g02/g0
ph3<-g03/g0
ph4<-g04/g0
ph5<-g05/g0
ph6<-g06/g0
ph7<-g07/g0
ph8<-g08/g0
ph9<-g09/g0
# auc is area under ROC curve
#A1 is the P[Y>X]
#A2 is the P[Y=X]
auc<- A1+A2/2
A1<-theta2*ph1+theta3*(ph1+ph2)+theta4*(ph1+ph2+ph3)+
theta5*(ph1+ph2+ph3+ph4)+theta6*(ph1+ph2+ph3+ph4+ph5)+
theta7*(ph1+ph2+ph3+ph4+ph5+ph6)+
theta8*(ph1+ph2+ph3+ph4+ph5+ph6+ph7)+
theta9*(ph1+ph2+ph3+ph4+ph5+ph6+ph7+ph8)
A2<- theta1*ph1+theta2*ph2+theta3*ph3+theta4*ph4
+theta5*ph5+theta6*ph6+theta7*ph7+theta8*ph8+theta9*ph9
}
#see Table 8
# diagnosing breast cancer with two readers
# verification bias
# improper prior
list(a11=8,a12=30,a13=75,a14=48,a15=.125,a16=164,a17=141,a18=173,a19=314,a01=103,a02=119,a 03=121,a04=76,a05=111,a06=57,a07=60,a08=37,a09=6)
# initial values
list(g11=1,g12=1,g13=1,g14=1,g15=1,g16=1,g17=1,g18=1,g19=1,g01=1,g02=1,g03=1, g04=1,g05=1, g06=1,g07=1,g08=1,g09=1)
13. Comments and Conclusions
This presentation has reviewed the Bayesian methodology available for estimating the test accuracy when two or more tests are used to diagnose disease. The main focus is on tests that are subject to verification bias, that is, when some of the patients are not subject to the gold standard (are not verified for disease status). When verification bias occurs certain techniques are employed to correct for bias. If the usual estimators are calculated only for those patients that are verified for disease, the estimators are biased, thus, this article develops Bayesian procedures that “correct” for bias. By imposing the missing at random assumption, Bayesian estimators of the usual measures of test accuracy are developed. For two binary tests, the true and false positive fractions estimate the test accuracy, while for two ordinal tests the ROC area of the score function estimates the test accuracy of the combined tests. An interesting variation of verification bias is extreme verification bias, which is present when all of the patients that test negative with both tests are not verified for disease. In such a scenario, the true and false positive fractions cannot be estimated. However, other measures of the combined accuracy are available and easily estimated with Bayesian inference. Bayesian inference is illustrated with examples involving the diagnosis of breast and lung cancer.
There is a large literature on the subject of verification bias, and for additional recent information about the subject see [16-19]. Very little has appeared from a Bayesian viewpoint, however, Buzoianu and Kadane [20] present results on adjustment for verification bias. Broemeling [12,13] is the only book that focuses on the Bayesian approach to verification bias.
| Y1 = 1, 0 | ||||
| V = 1 | Y2 = 1 | Y2 = 0 | Y2 = 1 | Y2 = 0 |
| D = 1 | s11 | s10 | s01 | s00 |
| D = 0 | r11 | r10 | r01 | r00 |
| V = 0 | u11 | u10 | u01 | u00 |
| Total | m11 | m10 | m01 | m00 |
| Y1 = 1, 0 | ||||
| V = 1 | Y2 = 1 | Y2 = 0 | Y2 = 1 | Y2 = 0 |
| D = 1 | s11 = 14 | s10 = 12 | s01 = 9 | s00 = 3 |
| D = 0 | r11 = 4 | r10 = 9 | r01 = 13 | r00 = 18 |
| V = 0 | u11 = 7 | u10 = 8 | u01 = 9 | u00 = 10 |
| Total | m11 = 25 | m10 = 29 | m01 = 31 | m00 = 31 |
| Parameter | Mean | SD | Error | 2 1/2 | Median | 97 1/2 |
|---|---|---|---|---|---|---|
| fpf1 | 0.2864 | 0.06201 | <0.0001 | 0.1725 | 0.284 | 0.4141 |
| fpf2 | 0.3809 | 0.0668 | <0.0001 | 0.253 | 0.3799 | 0.5144 |
| fpfbn | 0.0880 | 0.0697 | <0.0001 | 0.0264 | 0.0829 | 0.1795 |
| fpfbp | 0.5766 | 0.0653 | <0.0001 | 0.4559 | 0.5777 | 0.7021 |
| tpf1 | 0.6755 | 0.0712 | <0.0001 | 0.5305 | 0.6779 | 0.8074 |
| tpf2 | 0.6007 | 0.0737 | <0.0001 | 0.4538 | 0.6018 | 0.7414 |
| tpfbn | 0.3663 | 0.0694 | <0.0001 | 0.2367 | 0.3645 | 0.5081 |
| tpfbp | 0.9165 | 0.0439 | <0.0001 | 0.8131 | 0.9233 | 0.9812 |
| Y1 = 1, 0 | ||||
| V = 1 | Y2 = 1 | Y2 = 0 | Y2 = 1 | Y2 = 0 |
| D = 1 | s11 = 14 | s10 = 12 | s01 = 9 | s00 = 0 |
| D = 0 | r11 = 4 | r10 = 9 | r01 = 13 | r00 = 0 |
| V = 0 | u11 = 0 | u10 = 0 | u01 = 0 | u00 = 21 |
| Total | m11 = 18 | m10 = 21 | m01 = 22 | m00 = 21 |
| Parameter | Mean | SD | Error | 2 1/2 | Median | 97 1/2 |
|---|---|---|---|---|---|---|
| DP1 | 0.3169 | 0.0508 | <0.0001 | 0.22 | 0.3155 | 0.4206 |
| DP2 | 0.2805 | 0.0493 | <0.0001 | 0.1891 | 0.2787 | 0.3823 |
| FRP1 | 0.1586 | 0.0400 | <0.0001 | 0.0882 | 0.1559 | 0.2411 |
| FRP2 | 0.2074 | 0.0446 | <0.0001 | 0.127 | 0.2051 | 0.3016 |
| Ratio TPF | 2.618 | 0.5922 | 0.0019 | 1.774 | 2.515 | 4.503 |
| Ratio FPF | 8.346 | 5.629 | 0.0168 | 3.187 | 6.902 | 22.01 |
| T1 = 1, 2, 3 | |||||||||
| T2 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
| D = 1 | s1 8 | s2 26 | s3 51 | s4 43 | s5 81 | s6 94 | s7 117 | s8 140 | s9 208 |
| D = 0 | r1 101 | r2 105 | r3 83 | r4 67 | r5 72 | r6 40 | r7 41 | r8 30 | r9 4 |
| V = 0 | u1 2 | u2 18 | u3 62 | u4 14 | u5 83 | u6 67 | u7 63 | u8 40 | u9 108 |
| Total | m1 111 | m2 149 | m3 196 | m4 224 | m5 236 | m6 201 | m7 221 | m8 210 | m9 320 |
| Parameter | Mean | SD | Error | 2 1/2 | Median | 97 1/2 |
|---|---|---|---|---|---|---|
| A1(reader 1) | 0.7867 | 0.0119 | <0.00001 | 0.763 | 0.787 | 0.8097 |
| A2(reader 2) | 0.6351 | 0.0145 | <0.00001 | 0.6062 | 0.6352 | 0.6633 |
| T1 = 1, 2, 3 | ||||||||
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
| s1 8 | s2 30 | s3 75 | s4 48 | s5 125 | s6 141 | s7 164 | s8 164 | s9 314 |
| r1 103 | r2 119 | r3 121 | r4 76 | r5 111 | r6 60 | r7 57 | r8 37 | r9 6 |
| u1 0 | u2 0 | u3 0 | u4 0 | u5 0 | u6 0 | u7 0 | u8 0 | u9 0 |
| m1 111 | m2 149 | m3 196 | m4 124 | m5 236 | m6 201 | m7 221 | m8 210 | m9 320 |
| Parameter | Mean | SD | Error | 2 1/2 | Median | 97 1/2 |
|---|---|---|---|---|---|---|
| b[1] | −4.947 | 0.2859 | 0.00173 | −5,515 | −4.943 | −4.395 |
| b[2] | 1.688 | 0.0851 | <0.0001 | 1.524 | 1.687 | 1.857 |
| b[3] | 0.8946 | 0.0804 | <0.0001 | 0.7373 | 0.894 | 1.053 |
| Parameter | Mean | SD | Error | 2 1/2 | Median | 97 1/2 |
|---|---|---|---|---|---|---|
| A1 | 0.8099 | 0.0106 | <0.00001 | 0.7885 | 0.8101 | 0.8308 |
| A2 | 0.0657 | 0.0030 | <0.00001 | 0.0599 | 0.0656 | 0.0716 |
| auc | 0.8428 | 0.0094 | <0.00001 | 0.8238 | 0.843 | 0.8608 |
References
- Johnson, D.; Sandmire, D.; Klein, D. Medical Tests that Can Save Your Life, Tests Your Doctor Won't Order Unless You Know To Ask; Rodale Inc.: Emmaus, PA, USA, 2004. [Google Scholar]
- Buscombe, J.R.; Cwikla, J.B.; Holloway, B.; Hilson, A.J.W. Prediction and usefulness of combined mammography and scintimmaography in suspected primary breast cancer using ROC curves. J. Nuclear Medicine 2001, 42, 3. [Google Scholar]
- Berg, W.A.; Gutierrez, L.; NessAlver, M.S.; Carter, W.B.; Bhargavan, M.; Lewis, R.S.; Loffe, O.B. Diagnostic accuracy of mammography, clinical examination, US and MR, imaging in preoperative assessment of breast cancer. Radiology 2004, 233, 830–849. [Google Scholar] [CrossRef] [PubMed]
- Van Overhagen, H.; Brakel, K.; Heijenbrok, M.W.; van Kasteren, J.H.L.M.; van de Moosdijk, C.N.F.; Roldann, A.C.; van Gils, A.P.; Hansen, B.E. Metastasis in supraclavicular lymph nodes in lung cancer: Assessment in palpation, US, and CT. Radiology 2004, 232, 75–80. [Google Scholar] [CrossRef] [PubMed]
- Pauleit, D.; Zimmerman, A.; Stoffels, G.; Bauer, D.; Risse, J.; Fluss, M.O.; Hamacher, K.; Coenene, H.H.; Langen, K.J. 18F-FET PET compared with 18F-FEG PET ad CT in patients with head and neck cancer. J. Nuclear Med. 2006, 47, 256–261. [Google Scholar]
- Schaffler, G.J.; Wolf, G.W.; Schoellnast, H.; Groell, R.; Maier, A.; Smolle-Juttner, F.M.; Woltsche, M.; Fasching, G.; Nicolletti, R.; Aigner, R.M. Non-small cell lung cancer: Evaluation of pleural abnormalities on CT scans with 18F-FET PET. Radiology 2004, 231, 858–865. [Google Scholar] [CrossRef] [PubMed]
- Pepe, M.S. The Statistical Evaluation of Medical Tests for Classification and Prediction; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Zhou, X.H.; Obuchowski, N.A.; McClish, D.K. Statistical Methods in DiagnosticMedicine; John Wiley & Sons Inc.: New York, NY, USA, 2002. [Google Scholar]
- Zhou, X.H. Maximum likelihood estimators of sensitivity and specificity corrected for verification bias. Commun. Stat. Theory Methods 1993, 22, 3177–3198. [Google Scholar] [CrossRef]
- Zhou, X.H. Nonparametric ML estimate of the ROC area corrected for verification bias. Biometrics 1996, 52, 310–316. [Google Scholar]
- Zhou, X.H.; Castelluccio, P. Nonparametric analysis for the ROC curves of two diagnostic tests in the presence of non ignorable verification bias. J. Stat. Plan. Infer. 2002, 115, 193–213. [Google Scholar]
- Broemeling, L.D. Bayesian Biostatistics and Diagnostic Medicine; Chapman & Hall/CRC Taylor & Francis: Boca Raton, FL, USA, 2007. [Google Scholar]
- Broemeling, L.D. Advanced Bayesian Methods for Medical Test Accuracy; Chapman & Hall/CRC Taylor & Francis: Boca Raton, FL, USA, 2011. [Google Scholar]
- Begg, C.B.; Greenes, R.A. Assessment of diagnostic tests when disease verification is subject to selection bias. Biometrics 1983, 39, 207–215. [Google Scholar] [CrossRef] [PubMed]
- Gray, R.; Begg, C.; Greenes, R. Construction of receiver operating characteristic curve when disease verification is subject to selection bias. Med. Decis. Making 1984, 4, 151–164. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Zhou, X.H. A model for adjusting for nonignorable verification bias in estimation of the ROC curve and its area with likelihood-based approach. Biometrics 2010, 66, 1119–1128. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z. Likelihood-based confidence sets for partially identified parameters. J. Stat. Plan. Infer. 2009, 139, 696–710. [Google Scholar] [CrossRef]
- Alonzo, T.A. Comparing accuracy in an unpaired post-market device study with incomplete disease assessment. Biom. J. 2009, 51, 491–503. [Google Scholar] [CrossRef] [PubMed]
- He, H.; Lyness, J.M.; McDermott, M.P. Direct estimation of the area under the receiver operating characteristic curve in the presence of verification bias. Stat. Med. 2009, 28, 361–376. [Google Scholar] [CrossRef] [PubMed]
- Buzoianu, M.; Kadane, J.B. Adjusting for verification bias in diagnostic test evaluation: A Bayesian approach. Stat. Med. 2008, 27, 2453–2473. [Google Scholar] [CrossRef] [PubMed]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Broemeling, L.D. Bayesian Estimation of Combined Accuracy for Tests with Verification Bias. Diagnostics 2011, 1, 53-76. https://doi.org/10.3390/diagnostics1010053
Broemeling LD. Bayesian Estimation of Combined Accuracy for Tests with Verification Bias. Diagnostics. 2011; 1(1):53-76. https://doi.org/10.3390/diagnostics1010053
Chicago/Turabian StyleBroemeling, Lyle D. 2011. "Bayesian Estimation of Combined Accuracy for Tests with Verification Bias" Diagnostics 1, no. 1: 53-76. https://doi.org/10.3390/diagnostics1010053




