Setting the Stage for Habitable Planets
Abstract
:1. Introduction
2. The CHZ, GHZ and CHA Concepts and Habitable Planet Formation
2.1. The Circumstellar Habitable Zone (CHZ)
2.2. The Galactic Habitable Zone (GHZ)
2.3. The Cosmic Habitable Age (CHA)
3. Learning from Exoplanets and the Solar System
3.1. Observed Trends among Exoplanets

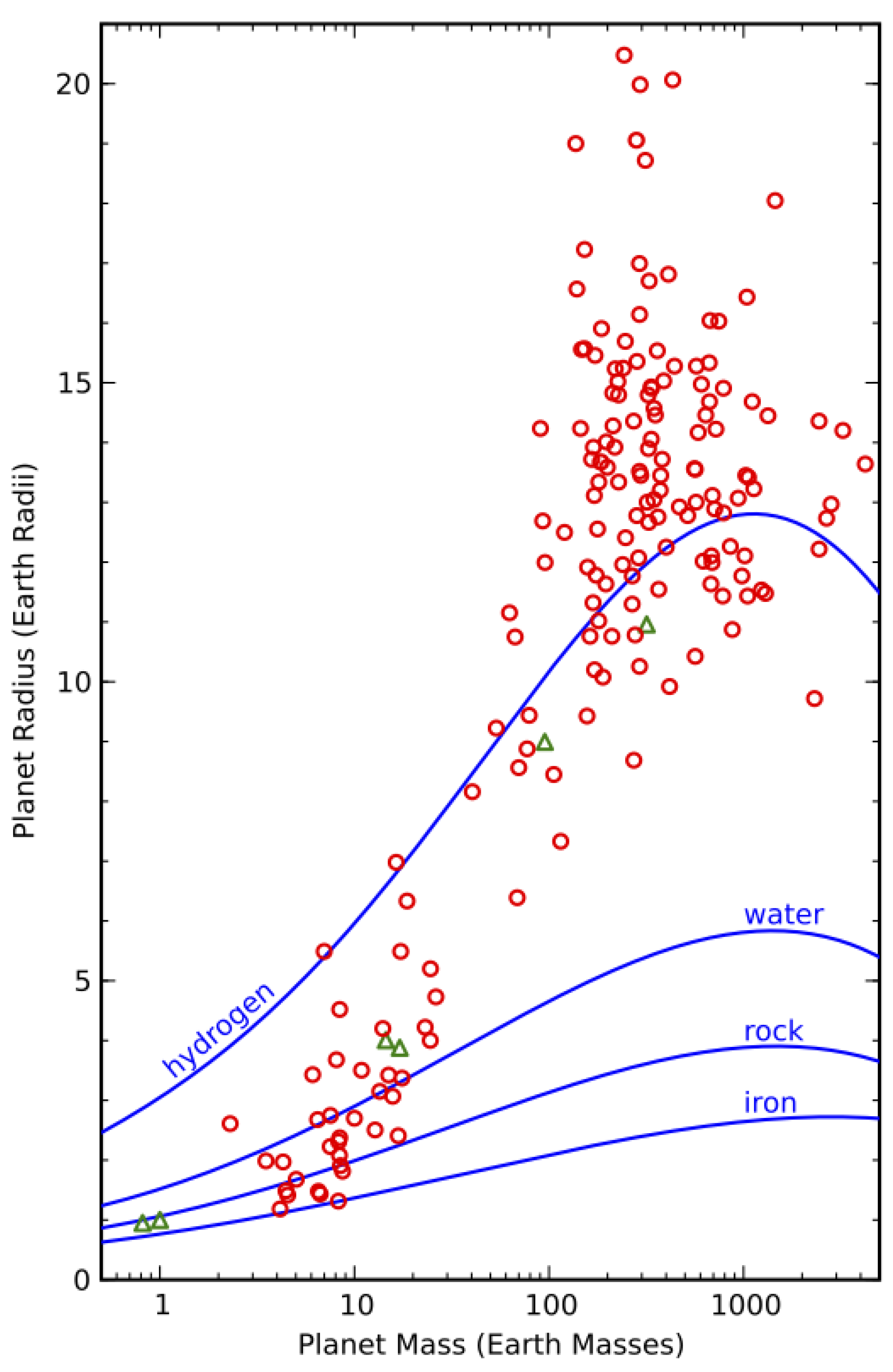
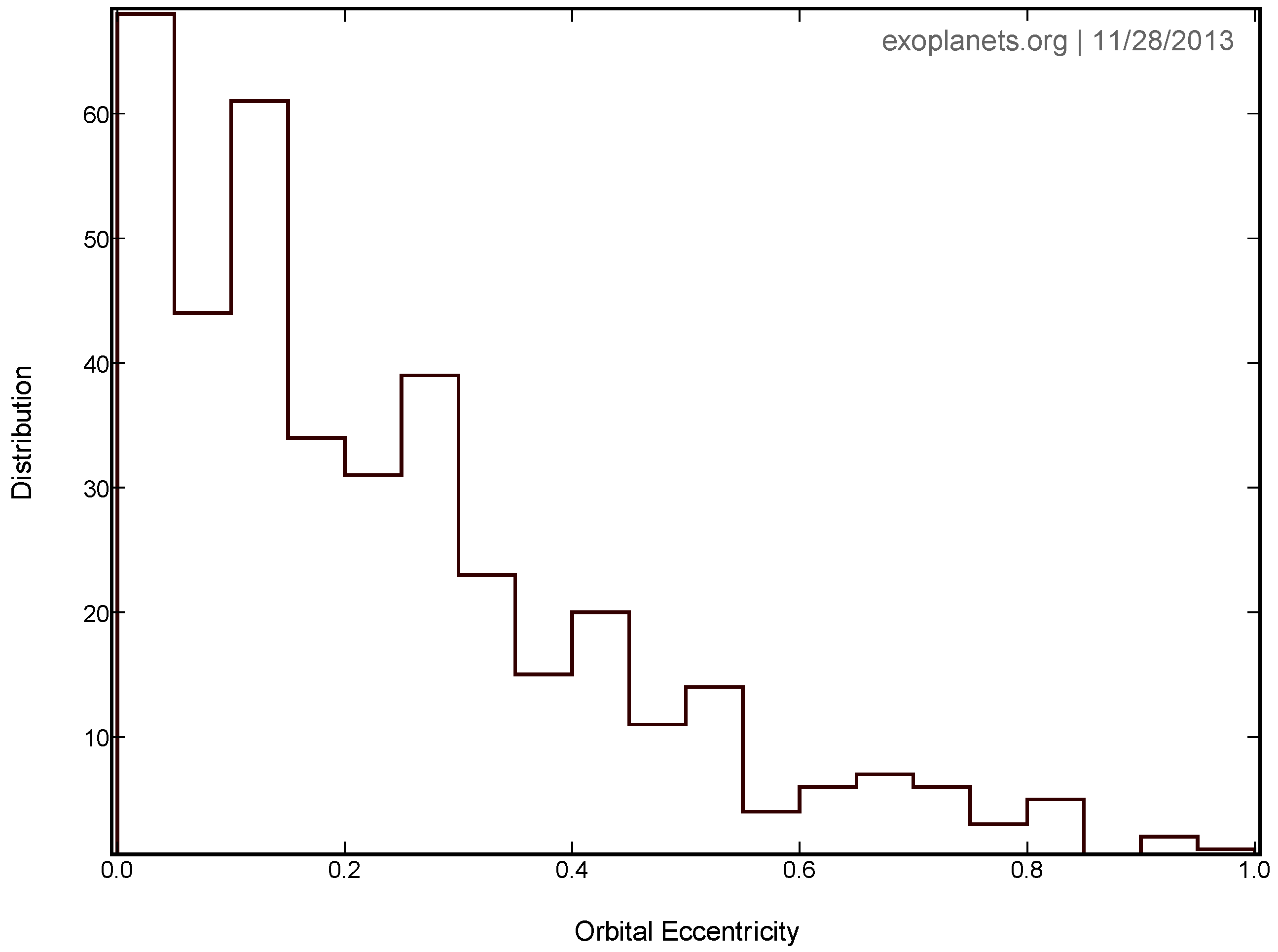
3.2. Exoplanets Theory
3.3. The Solar System
4. A Framework for Estimating the Number of Habitable Planets in the Universe
5. Conclusions
- It is likely that Jovian planet migration occurred in the early Solar System and influenced the formation and evolution of the terrestrial planets.
- The traditional definition of the CHZ, based on the radiant energy from the host star, is outdated and should be replaced with a definition that also includes such considerations as planetary impact rate, orbital dynamical stability and episodic reductions in the size of the astrosphere. Since these processes are partly stochastic, however, they do not lend themselves to analytic treatment.
- A planetary system cannot be isolated from its broader galactic context when considering its formation and evolution in relation to habitability. A broader and more complete understanding of habitability requires merging the CHZ and GHZ concepts.
- Even distant stellar companions can influence the dynamical stability of a planetary system several Gyrs after it formed.
- Habitability factors are often interconnected in a complex web, and some factors can have multiple distinct effects on the habitability of a planetary system. Jupiter and Saturn’s influence on the habitability of the Solar System is a prime example.
Acknowledgments
Conflicts of Interest
References
- Gonzalez, G. Habitable zones in the Universe. Orig. Life Evol. Biosph. 2005, 35, 555–606. [Google Scholar] [CrossRef]
- Bounama, C.; von Bloh, W.; Franck, S. How rare is complex life in the Milky Way? Astrobiology 2007, 7, 745–756. [Google Scholar] [CrossRef]
- Lathe, R. Tidal chain reaction and the origin of replicating biopolymers. Int. J. Astrobiol. 2005, 4, 19–31. [Google Scholar] [CrossRef]
- Lineweaver, C.H.; Chopra, A. The habitability of our Earth and other earths: Astrophysical, geochemical, geophysical, and biological limits on planet habitability. Annu. Rev. Earth Planet. Sci. 2012, 40, 597–623. [Google Scholar] [CrossRef]
- Lammer, H.; Bredehöft, J.H.; Coustenis, A.; Khodachenko, M.L.; Kaltenegger, L.; Grasset, O.; Prieur, D.; Raulin, F.; Ehrenfreund, P.; Yamauchi, M.; et al. What makes a planet habitable? Astron. Astrophys. Rev. 2009, 17, 181–249. [Google Scholar] [CrossRef]
- Forget, F. On the probability of habitable planets. Int. J. Astrobiol. 2013, 12, 177–185. [Google Scholar] [CrossRef]
- Kasting, J.F.; Whitmire, D.P.; Reynolds, R.T. Habitable zones around main sequence stars. Icarus 1993, 101, 108–128. [Google Scholar] [CrossRef]
- Kitzmann, D.; Patzer, A.B.C.; Rauer, H. Clouds in the atmospheres of extrasolar planets. IV. On the scattering greenhouse effect of CO2 ice particles: Numerical radiative transfer studies. Astron. Astrophys. 2013, 557. [Google Scholar] [CrossRef]
- Shields, A.L.; Meadows, V.S.; Bitz, C.M.; Pierrehumbert, R.T.; Joshi, M.M.; Robinson, T.D. The effect of host star spectral energy distribution and ice-albedo feedback on the climate of extrasolar planets. Astrobiology 2013, 13, 715–739. [Google Scholar] [CrossRef]
- Kopparapu, R.K.; Ramirez, R.; Kasting, J.F.; Eymet, V.; Robinson, T.D.; Mahadevan, S.; Terrien, R.C.; Domagal-Goldman, S.; Meadows, V.; Deshpande, R. Habitable zones around main-sequence stars: New estimates. Astrophys. J. 2013, 765. [Google Scholar] [CrossRef]
- Kopparapu, R.K.; Ramirez, R.; Kasting, J.F.; Eymet, V.; Robinson, T.D.; Mahadevan, S.; Terrien, R.C.; Domagal-Goldman, S.; Meadows, V.; Deshpande, R. Erratum: “Habitable zones around main-sequence stars: New estimates”. Astrophys. J. 2013, 770. [Google Scholar] [CrossRef]
- Buccino, A.P.; Lemarchand, G.A.; Mauas, P.J.D. Ultraviolet radiation constraints around the circumstellar habitable zones. Icarus 2006, 183, 491–503. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, F.; Zhang, X.; Han, Z. Habitable zones and UV habitable zones around host stars. Astrophys. Space Sci. 2010, 325, 25–30. [Google Scholar] [CrossRef]
- Melott, A.L.; Thomas, B.C. Astrophysical ionizing radiation and Earth: A brief review and census of intermittent intense sources. Astrobiology 2011, 11, 343–361. [Google Scholar] [CrossRef]
- Potgieter, M. Solar modulation of cosmic rays. Living Rev. Sol. Phys. 2013, 10. [Google Scholar] [CrossRef]
- Kirkby, J. Cosmic rays and climate. Surv. Geophys. 2007, 28, 333–375. [Google Scholar] [CrossRef]
- Thomas, B.C.; Melott, A.L.; Arkenberg, K.R.; Snyder, B.R. Terrestrial effects of possible astrophysical sources of an AD 774-775 increase in 14C production. Geophys. Res. Lett. 2013, 40, 1237–1240. [Google Scholar] [CrossRef]
- Usoskin, I.G.; Kromer, B.; Ludlow, F.; Beer, J.; Friedrich, M.; Kovaltsov, G.A.; Solanki, S.K.; Wacker, L. The AD775 cosmic event revisited: The Sun is to blame. Astron. Astrophys. 2013, 552. [Google Scholar] [CrossRef]
- Kovaltsov, G.A.; Usoskin, I.G. Occurrence probability of large solar energetic particle events: Assessment from data on cosmogenic radionuclides in lunar rocks. Solar Physics 2014, 289, 211–220. [Google Scholar] [CrossRef]
- Shibayama, T.; Maehara, H.; Notsu, S.; Notsu, Y.; Nagao, T.; Honda, S.; Ishii, T.T.; Nogami, D.; Shibata, K. Superflares on solar-type stars observed with Kepler. I. Statistical properties of superflares. Astrophys. J. Suppl. Ser. 2013, 209. [Google Scholar] [CrossRef]
- Shibata, K.; Isobe, H.; Hillier, A.; Choudhuri, A.R.; Maehara, H.; Ishii, T.T.; Shibayama, T.; Notsu, S.; Notsu, Y.; Nagao, T.; et al. Can superflares occur on our Sun? Available online: http://pasj.asj.or.jp/v65/n3/650049/650049-frame.html (accessed on 25 October 2013).
- Notsu, Y.; Shibayama, T.; Maehara, H.; Notsu, S.; Nagao, T.; Honda, S.; Ishii, T.T.; Nogami, D.; Shibata, K. Superflares on solar-type stars observed with Kepler II. Photometric variability of superflare-generating stars: A signature of stellar rotation and starspots. Astrophys. J. 2013, 771. [Google Scholar] [CrossRef]
- Balona, L.A. Kepler observations of flaring in A-F type stars. Mon. Not. R. Astron. Soc. 2012, 423, 3420–3429. [Google Scholar] [CrossRef]
- Smith, D.S.; Scalo, J.; Wheeler, J.C. Importance of biologically active aurora-like ultraviolet emission: Stochastic irradiation of Earth and Mars by flares and explosions. Orig. Life Evol. Biosph. 2004, 34, 513–532. [Google Scholar] [CrossRef]
- Shapiro, A.I.; Schmutz, W.; Cessateur, G.; Rozanov, E. The place of the Sun among the sun-like stars. Astron. Astrophys. 2013, 552. Article 114. [Google Scholar]
- Zendejas, J.; Segura, A.; Raga, A.C. Atmospheric mass loss by stellar wind from planets around main sequence M stars. Icarus 2010, 210, 539–544. [Google Scholar] [CrossRef]
- Zuluaga, J.I.; Cuartas, P.A. The role of rotation in the evolution of dynamo-generated magnetic fields in super earths. Icarus 2012, 217, 88–102. [Google Scholar] [CrossRef]
- Lammer, H.; Selsis, F.; Chassefière, E.; Breuer, D.; Grießmeier, J.-M.; Kulikov, Y.N.; Erkaev, N.V.; Khodachenko, M.L.; Biernat, H.K.; Leblanc, F.; et al. Geophysical and atmospheric evolution of habitable planets. Astrobiology 2010, 10, 45–68. [Google Scholar] [CrossRef]
- Heller, R.; Barnes, R.; Leconte, J. Habitability of extrasolar planets and tidal spin evolution. Orig. Life Evol. Biosph. 2011, 41, 539–543. [Google Scholar] [CrossRef]
- Menou, K. Water-trapped worlds. Astrophys. J. 2013, 774. [Google Scholar] [CrossRef]
- Joshi, M.M.; Haberle, R.M.; Reynolds, R.T. Simulations of the atmospheres of synchronously rotating terrestrial planets orbiting M dwarfs: Conditions for atmospheric collapse and the implications for habitability. Icarus 1997, 129, 450–465. [Google Scholar] [CrossRef]
- Raymond, S.N.; Scalo, J.; Meadows, V.S. A decreased probability of habitable planet formation around low-mass stars. Astrophys. J. 2007, 669, 606–614. [Google Scholar] [CrossRef]
- Barnes, R.; Mullins, K.; Goldblatt, C.; Meadows, V.S.; Kasting, J.F.; Heller, R. Tidal venuses: Triggering a climate catastrophe via tidal heating. Astrobiology 2013, 13, 225–250. [Google Scholar] [CrossRef]
- Kite, E.S.; Gaidos, E.; Manga, M. Climate instability on tidally locked exoplanets. Astrophys. J. 2011, 743. [Google Scholar] [CrossRef]
- Heller, R.; Barnes, R. Exomoon habitability constrained by illumination and tidal heating. Astrobiology 2013, 13, 18–46. [Google Scholar]
- Forgan, D.; Kipping, D. Dynamical effects on the habitable zone for earth-like exomoons. Mon. Not. R. Astron. Soc. 2013, 432, 2994–3004. [Google Scholar] [CrossRef]
- Heller, R.; Zuluaga, J.I. Magnetic shielding of exomoons beyond the circumplanetary habitable edge. Astrophys. J. Lett. 2013, 776. [Google Scholar] [CrossRef]
- Namouni, F. The fate of moons of close-in giant exoplanets. Astrophys. J. Lett. 2010, 719, L145–L147. [Google Scholar] [CrossRef]
- Gong, Y.-X.; Zhou, J.-L.; Xie, J.-W.; Wu, X.-M. The effect of planet-planet scattering on the survival of exomoons. Astrophys. J. Lett. 2013, 769. [Google Scholar] [CrossRef]
- Bruckman, W.; Ruiz, A.; Ramos, E. Earth and Mars crater size frequency distribution and impact rates: Theoretical and observational analysis. Available online: http://arxiv.org/abs/1212.3273 (accessed on 25 October 2013).
- Horner, J.; Mousis, O.; Petit, J.M.; Jones, B.W. Differences between the impact regimes of the terrestrial planets: Implications for primordial D:H ratios. Planet. Space Sci. 2009, 57, 1338–1345. [Google Scholar] [CrossRef]
- Martin, R.G.; Livio, M. On the formation and evolution of asteroid belts and their potential significance for life. Mon. Not. R. Astron. Soc. 2013, 428, L11–L15. [Google Scholar] [CrossRef]
- Raghavan, D.; McAlister, H.A.; Henry, T.J.; Latham, D.W.; Marcy, G.W.; Mason, B.D.; Gies, D.R.; White, R.J.; ten Brummelaar, T.A. A survey of stellar families: Multiplicity of solar-type stars. Astrophys. J. Suppl. Ser. 2010, 190, 1–42. [Google Scholar] [CrossRef]
- Duquennoy, A.; Mayor, M. Multiplicity among solar-type stars in the solar neighbourhood. II—distribution of the orbital elements in an unbiased sample. Astron. Astrophys. 1991, 248, 485–524. [Google Scholar]
- Cuntz, M. S-type and P-type habitability in stellar binary systems: A comprehensive approach. I. Method and applications. Astrophys. J. 2013, 780. [Google Scholar] [CrossRef]
- Forgan, D. Assessing circumbinary habitable zones using latitudinal energy balance modelling. Mon. Not. R. Astron. Soc. 2013, 437, 1352–1361. [Google Scholar] [CrossRef]
- Haghighipour, N.; Kaltenegger, L. Calculating the habitable zone of binary star systems. II. P-type binaries. Astrophys. J. 2013, 777. [Google Scholar] [CrossRef]
- Kaltenegger, L.; Haghighipour, N. Calculating the habitable zone of binary star systems. I. S-type binaries. Astrophys. J. 2013, 777. [Google Scholar] [CrossRef]
- Eggl, S.; Pilat-Lohinger, E.; Funk, B.; Georgakarakos, N.; Haghighipour, N. Circumstellar habitable zones of binary-star systems in the solar neighbourhood. Mon. Not. R. Astron. Soc. 2013, 428, 3104–3113. [Google Scholar] [CrossRef]
- Eggl, S.; Pilat-Lohinger, E.; Georgakarakos, N.; Gyergyovits, M.; Funk, B. An analytic method to determine habitable zones for S-type planetary orbits in binary star systems. Astrophys. J. 2012, 752. [Google Scholar] [CrossRef]
- Gonzalez, G.; Brownlee, D.; Ward, P. The Galactic habitable zone: Galactic chemical evolution. Icarus 2001, 152, 185–200. [Google Scholar] [CrossRef]
- Lineweaver, C.H. An estimate of the age distribution of terrestrial planets in the Universe: Quantifying metallicity as a selection effect. Icarus 2001, 151, 307–313. [Google Scholar] [CrossRef]
- Gonzalez, G. The Galactic Habitable Zone. In Astrophysics of Life; Livio, M., Reid, I.N., Sparks, W.B., Eds.; Cambridge University Press: Cambridge, UK, 2005; pp. 89–97. [Google Scholar]
- Masi, M.; Secco, L.; Gonzalez, G. Effects of the planar galactic tides and stellar mass on comet cloud dynamics. Open Astron. J. 2009, 2, 74–89. [Google Scholar]
- Lineweaver, C.H.; Fenner, Y.; Gibson, B.K. The Galactic habitable zone and the age distribution of complex life in the Milky Way. Science 2004, 303, 59–62. [Google Scholar] [CrossRef]
- Yasui, C.; Kobayashi, N.; Tokunaga, A.T.; Saito, M.; Tokoku, C. The lifetime of protoplanetary disks in a low-metallicity environment. Astrophys. J. 2009, 705, 54–63. [Google Scholar] [CrossRef]
- Fulbright, J.P.; McWilliam, A.; Rich, R.M. Abundances of baade’s window giants from Keck HIRES spectra. I. Stellar parameters and [Fe/H] values. Astrophys. J. 2006, 636, 821–841. [Google Scholar] [CrossRef]
- Stasińska, G.; Tenorio-Tagle, G.; Rodríguez, M.; Henney, W.J. Enrichment of the interstellar medium by metal-rich droplets and the abundance bias in H II regions. Astron. Astrophys. 2007, 471, 193–204. [Google Scholar] [CrossRef]
- Maciel, W.J.; Quireza, C.; Costa, R.D.D. Time variation of radial gradients in the Galactic disk: Electron temperatures and abundances. Astron. Astrophys. 2007, 463, L13–L16. [Google Scholar] [CrossRef]
- Lemasle, B.; François, P.; Genovali, K.; Kovtyukh, V.V.; Bono, G.; Inno, L.; Laney, C.D.; Kaper, L.; Bergemann, M.; Fabrizio, M.; et al. Galactic abundance gradients from cepheids: α and heavy elements in the outer disk. Astron. Astrophys. 2013, 558. [Google Scholar] [CrossRef]
- Luck, R.E.; Lambert, D.L. The distribution of the elements in the Galactic disk. III. A reconsideration of cepheids from l = 30° to 250°. Astron. J. 2011, 142. [Google Scholar] [CrossRef]
- Nieva, M.-F.; Przybilla, N. Present-day cosmic abundances. A comprehensive study of nearby early B-type stars and implications for stellar and Galactic evolution and interstellar dust models. Astron. Astrophys. 2012, 539. [Google Scholar] [CrossRef]
- Nittler, L.R. Constraints on heterogeneous Galactic chemical evolution from meteoritic stardust. Astrophys. J. 2005, 618, 281–296. [Google Scholar] [CrossRef]
- Fuhrmann, K. Nearby stars of the Galactic disc and halo—V. Mon. Not. R. Astron. Soc. 2011, 414, 2893–2922. [Google Scholar] [CrossRef]
- Gowanlock, M.G.; Patton, D.R.; McConnell, S.M. A model of habitability within the Milky Way Galaxy. Astrobiology 2011, 11, 855–873. [Google Scholar] [CrossRef]
- Gardner, E.; Nurmi, P.; Flynn, C.; Mikkola, S. The effect of the solar motion on the flux of long-period comets. Mon. Not. R. Astron. Soc. 2011, 411, 947–954. [Google Scholar] [CrossRef]
- Kataoka, R.; Ebisuzaki, T.; Miyahara, H.; Maruyama, S. Snowball Earth events driven by starbursts of the Milky Way galaxy. New Astron. 2013, 21, 50–62. [Google Scholar] [CrossRef]
- Carigi, L.; García-Rojas, J.; Meneses-Goytia, S. Chemical evolution and the galactic habitable zone of M31. Rev. Mex. Astron. Astrofis. 2013, 49, 253–273. [Google Scholar]
- Suthar, F.; McKay, C.P. The Galactic habitable zone in elliptical galaxies. Int. J. Astrobiol. 2012, 11, 157–161. [Google Scholar] [CrossRef]
- Svensmark, H. Evidence of nearby supernovae affecting life on Earth. Mon. Not. R. Astron. Soc. 2012, 423, 1234–1253. [Google Scholar] [CrossRef]
- Knie, K.; Korschinek, G.; Faestermann, T.; Dorfi, E.A.; Rugel, G.; Wallner, A. 60Fe anomaly in a deep-sea manganese crust and implications for a nearby supernova source. Phys. Rev. Lett. 2004, 93. [Google Scholar] [CrossRef]
- Filipović, M.D.; Horner, J.; Crawford, E.J.; Tothill, N.F.H.; White, G.L. Mass extinction and the structure of the Milky Way. Serbian Astron. J. 2013, 187, 43–52. [Google Scholar]
- Domainko, W.; Bailer-Jones, C.A.L.; Feng, F. A history of the gamma-ray burst flux at the Earth from Galactic globular clusters. Mon. Not. R. Astron. Soc. 2013, 432, 258–263. [Google Scholar] [CrossRef]
- Basu, S.; Stuart, F.M.; Schnabel, C.; Klemm, V. Galactic-cosmic-ray-produced He3 in a ferromanganese crust: Any supernova Fe60 excess on Earth? Phys. Rev. Lett. 2007, 98. [Google Scholar] [CrossRef]
- Feng, F.; Bailer-Jones, C.A.L. Assessing the Influence of Astronomical Phenomena on the Earth’s Biosphere. In Proceedings of the European Planetary Science Congress 2012, Madrid, Spain, 23–28 September 2012; p. 175.
- Sloan, T.; Wolfendale, A.W. Cosmic rays and climate change over the past 1000 million years. New Astron. 2013, 25, 45–49. [Google Scholar] [CrossRef]
- Haas, M.R.; Schaye, J.; Booth, C.M.; Dalla Vecchia, C.; Springel, V.; Theuns, T.; Wiersma, R.P.C. Physical properties of simulated galaxy populations at z = 2—II. Effects of cosmology, reionization and ISM physics. Mon. Not. R. Astron. Soc. 2013, 435, 2955–2967. [Google Scholar] [CrossRef]
- Haas, M.R.; Schaye, J.; Booth, C.M.; Dalla Vecchia, C.; Springel, V.; Theuns, T.; Wiersma, R.P.C. Physical properties of simulated galaxy populations at z = 2—I. Effect of metal-line cooling and feedback from star formation and AGN. Mon. Not. R. Astron. Soc. 2013, 435, 2931–2954. [Google Scholar]
- Yates, R.M.; Henriques, B.; Thomas, P.A.; Kauffmann, G.; Johansson, J.; White, S.D.M. Modelling element abundances in semi-analytic models of galaxy formation. Mon. Not. R. Astron. Soc. 2013, 435, 3500–3520. [Google Scholar] [CrossRef]
- Lara-López, M.A.; Hopkins, A.M.; López-Sánchez, A.R.; Brough, S.; Colless, M.; Bland-Hawthorn, J.; Driver, S.; Foster, C.; Liske, J.; Loveday, J.; et al. Galaxy and mass assembly (GAMA): The connection between metals, specific SFR and H I gas in galaxies: The Z-SSFR relation. Mon. Not. R. Astron. Soc. 2013, 433, L35–L39. [Google Scholar] [CrossRef]
- Lara-López, M.A.; Hopkins, A.M.; López-Sánchez, A.R.; Brough, S.; Gunawardhana, M.L.P.; Colless, M.; Robotham, A.S.G.; Bauer, A.E.; Bland-Hawthorn, J.; Cluver, M.; et al. Galaxy And Mass Assembly (GAMA): A deeper view of the mass, metallicity and SFR relationships. Mon. Not. R. Astron. Soc. 2013, 434, 451–470. [Google Scholar] [CrossRef]
- Foster, C.; Hopkins, A.M.; Gunawardhana, M.; Lara-López, M.A.; Sharp, R.G.; Steele, O.; Taylor, E.N.; Driver, S.P.; Baldry, I.K.; Bamford, S.P.; et al. Galaxy And Mass Assembly (GAMA): The mass-metallicity relationship. Astron. Astrophys. 2012, 547. [Google Scholar] [CrossRef]
- Kepler web site lising planet count. Available online: http://www.nasa.gov/mission_pages/kepler/main/index.html#.UpZM52SG2WZ (accessed on 25 October 2013).
- Moutou, C.; Deleuil, M.; Guillot, T.; Baglin, A.; Bordé, P.; Bouchy, F.; Cabrera, J.; Csizmadia, S.; Deeg, H.J. Corot: Harvest of the exoplanet program. Icarus 2013, 226, 1625–1634. [Google Scholar] [CrossRef]
- Mayor, M.; Marmier, M.; Lovis, C.; Udry, S.; Ségransan, D.; Pepe, F.; Benz, W.; Bertaux, J.-L.; Bouchy, F.; Dumusque, X.; et al. The HARPS search for southern extra-solar planets XXXIV. Occurrence, mass distribution and orbital properties of super-earths and neptune-mass planets. 2011; arXiv:1109.2497. [Google Scholar]
- Petigura, E.A.; Howard, A.W.; Marcy, G.W. Prevalence of earth-size planets orbiting sun-like stars. Proc. Natl. Acad. Sci. USA 2013, 110, 19273–19278. [Google Scholar] [CrossRef]
- Fressin, F.; Torres, G.; Charbonneau, D.; Bryson, S.T.; Christiansen, J.; Dressing, C.D.; Jenkins, J.M.; Walkowicz, L.M.; Batalha, N.M. The false positive rate of Kepler and the occurrence of planets. Astrophys. J. 2013, 766. [Google Scholar] [CrossRef]
- Howard, A.W. Observed properties of extrasolar planets. Science 2013, 340, 572–576. [Google Scholar] [CrossRef]
- Marmier, M.; Ségransan, D.; Udry, S.; Mayor, M.; Pepe, F.; Queloz, D.; Lovis, C.; Naef, D.; Santos, N.C.; Alonso, R.; et al. The CORALIE survey for southern extrasolar planets. XVII. New and updated long period and massive planets. Astron. Astrophys. 2013, 551. [Google Scholar] [CrossRef]
- Lissauer, J.J.; Ragozzine, D.; Fabrycky, D.C.; Steffen, J.H.; Ford, E.B.; Jenkins, J.M.; Shporer, A.; Holman, M.J.; Rowe, J.F.; Quintana, E.V.; et al. Architecture and dynamics of Kepler’s candidate multiple transiting planet systems. Astrophys. J. Suppl. Ser. 2011, 197. [Google Scholar] [CrossRef]
- Quinn, S.N.; White, R.J.; Latham, D.W.; Buchhave, L.A.; Torres, G.; Stefanik, R.P.; Berlind, P.; Bieryla, A.; Calkins, M.C.; Esquerdo, G.A.; et al. HD 285507b: An eccentric hot Jupiter in the Hyades open cluster. Available online: http://arxiv.org/abs/1310.7328 (accessed on 25 October 2013).
- McQuillan, A.; Mazeh, T.; Aigrain, S. Stellar rotation periods of the Kepler objects of interest: A dearth of close-in planets around fast rotators. Astrophys. J. Lett. 2013, 775. [Google Scholar] [CrossRef]
- Gonzalez, G. Parent stars of extrasolar planets—XII. Additional evidence for trends with v sin i, condensation temperature and chromospheric activity. Mon. Not. R. Astron. Soc. 2011, 416, L80–L83. [Google Scholar] [CrossRef]
- Gonzalez, G. The stellar metallicity-giant planet connection. Mon. Not. R. Astron. Soc. 1997, 285, 403–412. [Google Scholar]
- Santos, N.C.; Israelian, G.; Mayor, M. Spectroscopic [Fe/H] for 98 extra-solar planet-host stars: Exploring the probability of planet formation. Astron. Astrophys. 2004, 415, 1153–1166. [Google Scholar] [CrossRef]
- Fischer, D.A.; Valenti, J. The planet-metallicity correlation. Astrophys. J. 2005, 622, 1102–1117. [Google Scholar] [CrossRef]
- Neves, V.; Bonfils, X.; Santos, N.C.; Delfosse, X.; Forveille, T.; Allard, F.; Udry, S. Metallicity of M dwarfs. III. Planet-metallicity and planet-stellar mass correlations of the harps gto m dwarf sample. Astron. Astrophys. 2013, 551. [Google Scholar] [CrossRef]
- Mortier, A.; Santos, N.C.; Sousa, S.; Israelian, G.; Mayor, M.; Udry, S. On the functional form of the metallicity-giant planet correlation. Astron. Astrophys. 2013, 551. [Google Scholar] [CrossRef]
- Sousa, S.G.; Santos, N.C.; Israelian, G.; Mayor, M.; Udry, S. Spectroscopic stellar parameters for 582 FGK stars in the HARPS volume-limited sample. Revising the metallicity-planet correlation. Astron. Astrophys. 2011, 533. [Google Scholar] [CrossRef]
- Dawson, R.I.; Murray-Clay, R.A. Giant planets orbiting metal-rich stars show signatures of planet-planet interactions. Astrophys. J. Lett. 2013, 767. [Google Scholar] [CrossRef]
- Gaidos, E.; Fischer, D.A.; Mann, A.W.; Howard, A.W. An understanding of the shoulder of giants: Jovian planets around late K dwarf stars and the trend with stellar mass. Astrophys. J. 2013, 771. [Google Scholar] [CrossRef]
- Ida, S.; Lin, D.N.C. Toward a deterministic model of planetary formation. IV. Effects of type I migration. Astrophys. J. 2008, 673, 487–501. [Google Scholar] [CrossRef]
- Bromley, B.C.; Kenyon, S.J. Migration of planets embedded in a circumstellar disk. Astrophys. J. 2011, 735. [Google Scholar] [CrossRef]
- Naoz, S.; Farr, W.M.; Rasio, F.A. On the formation of hot Jupiters in stellar binaries. Astrophys. J. Lett. 2012, 754. [Google Scholar] [CrossRef]
- Naoz, S.; Farr, W.M.; Lithwick, Y.; Rasio, F.A.; Teyssandier, J. Hot Jupiters from secular planet-planet interactions. Nature 2011, 473, 187–189. [Google Scholar] [CrossRef]
- Nagasawa, M.; Ida, S. Orbital distributions of close-in planets and distant planets formed by scattering and dynamical tides. Astrophys. J. 2011, 742. [Google Scholar] [CrossRef]
- Wu, Y.; Lithwick, Y. Secular chaos and the production of hot Jupiters. Astrophys. J. 2011, 735. [Google Scholar] [CrossRef]
- Kley, W.; Nelson, R.P. Planet-disk interaction and orbital evolution. Annu. Rev. Astron. Astrophys. 2012, 50, 211–249. [Google Scholar] [CrossRef]
- Alibert, Y.; Carron, F.; Fortier, A.; Pfyffer, S.; Benz, W.; Mordasini, C.; Swoboda, D. Theoretical models of planetary system formation: Mass vs. semi-major axis. Astron. Astrophys. 2013, 558. [Google Scholar] [CrossRef]
- Mordasini, C.; Alibert, Y.; Benz, W.; Naef, D. Extrasolar planet population synthesis. II. Statistical comparison with observations. Astron. Astrophys. 2009, 501, 1161–1184. [Google Scholar] [CrossRef]
- Rasio, F.A.; Ford, E.B. Dynamical instabilities and the formation of extrasolar planetary systems. Science 1996, 274, 954–956. [Google Scholar] [CrossRef]
- Kaib, N.A.; Raymond, S.N.; Duncan, M. Planetary system disruption by Galactic perturbations to wide binary stars. Nature 2013, 493, 381–384. [Google Scholar] [CrossRef]
- Spiegel, D.S.; Raymond, S.N.; Dressing, C.D.; Scharf, C.A.; Mitchell, J.L. Generalized Milankovitch cycles and long-term climatic habitability. Astrophys. J. 2010, 721, 1308–1318. [Google Scholar] [CrossRef]
- Kita, R.; Rasio, F.; Takeda, G. Pervasive orbital eccentricities dictate the habitability of extrasolar earths. Astrobiology 2010, 10, 733–741. [Google Scholar] [CrossRef]
- Dressing, C.D.; Spiegel, D.S.; Scharf, C.A.; Menou, K.; Raymond, S.N. Habitable climates: The influence of eccentricity. Astrophys. J. 2010, 721, 1295–1307. [Google Scholar] [CrossRef]
- Carter-Bond, J.C.; O’Brien, D.P.; Raymond, S.N. The compositional diversity of extrasolar terrestrial planets. II. Migration simulations. Astrophys. J. 2012, 760. [Google Scholar] [CrossRef]
- Raymond, S.N. The search for other Earths: Limits on the giant planet orbits that allow habitable terrestrial planets to form. Astrophys. J. Lett. 2006, 643, L131–L134. [Google Scholar] [CrossRef]
- Cameron, A.G.W. Origin of the solar system. Annu. Rev. Astron. Astrophys. 1988, 26, 441–472. [Google Scholar] [CrossRef]
- Podolak, M.; Hubbard, W.B.; Pollack, J.B.; Lunine, J.I. Gaseous Accretion and the Formation of Giant Planets. In Protostars and Planets III; Levy, E.H., Ed.; University of Arizona Press: Tucson, AZ, USA, 1993; pp. 1109–1147. [Google Scholar]
- Wuchterl, G.; Guillot, T.; Lissauer, J.J. Giant planet formation. In Protostars Planets IV; Mannings, V., Boss, A.P., Russell, S.S., Eds.; University of Arizona Press: Tucson, AZ, USA, 2000; pp. 1081–1109. [Google Scholar]
- Hansen, B.M.S. Formation of the terrestrial planets from a narrow annulus. Astrophys. J. 2009, 703, 1131–1140. [Google Scholar] [CrossRef]
- Tsiganis, K.; Gomes, R.; Morbidelli, A.; Levison, H.F. Origin of the orbital architecture of the giant planets of the Solar System. Nature 2005, 435, 459–461. [Google Scholar] [CrossRef]
- Gomes, R.; Levison, H.F.; Tsiganis, K.; Morbidelli, A. Origin of the cataclysmic late heavy bombardment period of the terrestrial planets. Nature 2005, 435, 466–469. [Google Scholar] [CrossRef] [Green Version]
- Morbidelli, A.; Brasser, R.; Gomes, R.; Levison, H.F.; Tsiganis, K. Evidence from the asteroid belt for a violent past evolution of Jupiter’s orbit. Astron. J. 2010, 140, 1391–1401. [Google Scholar] [CrossRef]
- Agnor, C.B.; Lin, D.N.C. On the migration of Jupiter and Saturn: Constraints from linear models of secular resonant coupling with the terrestrial planets. Astrophys. J. 2012, 745. [Google Scholar] [CrossRef]
- Nesvorný, D.; Vokrouhlický, D.; Morbidelli, A. Capture of irregular satellites during planetary encounters. Astron. J. 2007, 133, 1962–1976. [Google Scholar] [CrossRef]
- Morbidelli, A.; Crida, A. The dynamics of Jupiter and Saturn in the gaseous protoplanetary disk. Icarus 2007, 191, 158–171. [Google Scholar] [CrossRef]
- Nesvorný, D.; Vokrouhlický, D.; Morbidelli, A. Capture of Trojans by jumping Jupiter. Astrophys. J. 2013, 768. [Google Scholar] [CrossRef]
- Walsh, K.J.; Morbidelli, A.; Raymond, S.N.; O’Brien, D.P.; Mandell, A.M. A low mass for Mars from Jupiter’s early gas-driven migration. Nature 2011, 475, 206–209. [Google Scholar] [CrossRef]
- Walsh, K.J.; Morbidelli, A.; Raymond, S.N.; O’Brien, D.P.; Mandell, A.M. Populating the asteroid belt from two parent source regions due to the migration of giant planets—“The Grand Tack”. Meteorit. Planet. Sci. 2012, 47, 1941–1947. [Google Scholar] [CrossRef]
- Pilat-Lohinger, E.; Robutel, P.; Süli, Á.; Freistetter, F. On the stability of earth-like planets in multi-planet systems. Celest. Mech. Dyn. Astron. 2008, 102, 83–95. [Google Scholar] [CrossRef]
- Pilat-Lohinger, E.; Süli, Á.; Robutel, P.; Freistetter, F. The influence of giant planets near a mean motion resonance on Earth-like planets in the habitable zone of sun-like stars. Astrophys. J. 2008, 681, 1639–1645. [Google Scholar] [CrossRef]
- Laskar, J.; Joutel, F.; Robutel, P. Stabilization of the Earth’s obliquity by the Moon. Nature 1993, 361, 615–617. [Google Scholar] [CrossRef]
- Canup, R.M. Forming a moon with an Earth-like composition via a giant impact. Science 2012, 338, 1052–1055. [Google Scholar] [CrossRef]
- Ćuk, M.; Stewart, S.T. Making the moon from a fast-spinning Earth: A giant impact followed by resonant despinning. Science 2012, 338, 1047–1052. [Google Scholar] [CrossRef]
- Brasser, R.; Ida, S.; Kokubo, E. A dynamical study on the habitability of terrestrial exoplanets—I. Tidally evolved planet-satellite pairs. Mon. Not. R. Astron. Soc. 2013, 428, 1673–1685. [Google Scholar] [CrossRef]
- Waltham, D. Anthropic selection for the Moon’s mass. Astrobiology 2004, 4, 460–468. [Google Scholar] [CrossRef]
- Waltham, D. Half a billion years of good weather: Gaia or good luck? Astron. Geophys. 2007, 48, 22–23. [Google Scholar] [CrossRef]
- Waltham, D. Testing anthropic selection: A climate change example. Astrobiology 2011, 11, 105–114. [Google Scholar] [CrossRef]
- Morbidelli, A.; Lunine, J.I.; O’Brien, D.P.; Raymond, S.N.; Walsh, K.J. Building terrestrial planets. Annu. Rev. Earth Planet. Sci. 2012, 40, 251–275. [Google Scholar] [CrossRef]
- Raymond, S.N.; O’Brien, D.P.; Morbidelli, A.; Kaib, N.A. Building the terrestrial planets: Constrained accretion in the inner Solar System. Icarus 2009, 203, 644–662. [Google Scholar] [CrossRef]
- O’Brien, D.P.; Walsh, K.J.; Morbidelli, A.; Raymond, S.N.; Mandell, A.M.; Bond, J.C. Early giant planet migration in the Solar System: Geochemical and cosmochemical implications for terrestrial planet formation. Bull. Am. Astron. Soc. 2010, 42, 948. [Google Scholar]
- Lugaro, M.; Doherty, C.L.; Karakas, A.I.; Maddison, S.T.; Liffman, K.; García-Hernández, D.A.; Siess, L.; Lattanzio, J.C. Short-lived radioactivity in the early Solar System: The super-AGB star hypothesis. Meteorit. Planet. Sci. 2012, 47, 1998–2012. [Google Scholar] [CrossRef]
- Ouellette, N.; Desch, S.J.; Hester, J.J. Injection of supernova dust in nearby protoplanetary disks. Astrophys. J. 2010, 711, 597–612. [Google Scholar] [CrossRef]
- Boss, A.P.; Keiser, S.A. Triggering collapse of the presolar dense cloud core and injecting short-lived radioisotopes with a shock wave. II. Varied shock wave and cloud core parameters. Astrophys. J. 2013, 770. [Google Scholar] [CrossRef]
- Arnould, M.; Goriely, S.; Meynet, G. The production of short-lived radionuclides by new non-rotating and rotating Wolf-Rayet model stars. Astron. Astrophys. 2006, 453, 653–659. [Google Scholar] [CrossRef]
- Gounelle, M.; Meynet, G. Solar System genealogy revealed by extinct short-lived radionuclides in meteorites. Astron. Astrophys. 2012, 545. [Google Scholar] [CrossRef]
- Jura, M.; Xu, S.; Young, E.D. 26Al in the early Solar System: Not so unusual after all. Astrophys. J. Lett. 2013, 775. [Google Scholar] [CrossRef]
- Tang, H.; Dauphas, N. Abundance, distribution, and origin of 60Fe in the solar protoplanetary disk. Earth Planet. Sci. Lett. 2012, 359, 248–263. [Google Scholar] [CrossRef]
- Pfalzner, S. Early evolution of the birth cluster of the Solar System. Astron. Astrophys. 2013, 549. [Google Scholar] [CrossRef]
- Parker, R.J.; Church, R.P.; Davies, M.B.; Meyer, M.R. Supernova enrichment and dynamical histories of solar-type stars in clusters. Mon. Not. R. Astron. Soc. 2013, 437, 946–958. [Google Scholar]
- Laskar, J.; Fienga, A.; Gastineau, M.; Manche, H. La2010: A new orbital solution for the long-term motion of the Earth. Astron. Astrophys. 2011, 532. [Google Scholar] [CrossRef] [Green Version]
- Smith, D.S.; Scalo, J.M. Habitable zones exposed: Astrosphere collapse frequency as a function of stellar mass. Astrobiology 2009, 9, 673–681. [Google Scholar] [CrossRef]
- Cohen, O.; Drake, J.J.; Kóta, J. The cosmic-ray intensity near the archean Earth. Astrophys. J. 2012, 760. [Google Scholar] [CrossRef]
- Svensmark, H. Cosmoclimatology: A new theory emerges. Astron. Geophys. 2007, 48, 18–11. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Gonzalez, G. Setting the Stage for Habitable Planets. Life 2014, 4, 35-65. https://doi.org/10.3390/life4010035
Gonzalez G. Setting the Stage for Habitable Planets. Life. 2014; 4(1):35-65. https://doi.org/10.3390/life4010035
Chicago/Turabian StyleGonzalez, Guillermo. 2014. "Setting the Stage for Habitable Planets" Life 4, no. 1: 35-65. https://doi.org/10.3390/life4010035



