2.2. Simulations
In the simulations, numerous matrices of varying dimension (3 × 3, 4 × 4, 5 × 5, and 6 × 6) filled with random numbers (simulating the universe of theoretically possible information flow/similarities data) were entropy-maximized, then examined for whether any of the resulting configurations corresponded to a Euclidean space. This can be determined through metric multidimensional scaling. “Successful” configurations not only had to correspond to an unambiguous three-dimensional geometric representation—as any zero-stress solution in three dimensions would—but also consist of element scores that as a group were equally weighted on the three cardinal orthogonal axes (that is, each point in the final spatial projection would be both the same distance from the origin, and the same set of distances from one another).
Thus the simulations examined a random sample of the universe of all possible combinations of
n ×
n metric intra-relations, anticipating that some percentage of these—corresponding to real, or possible real, world conditions—would meet the posed conditions. Two sets of random numbers tests were run for each dimensionality: one in which the
n ×
n matrices were filled with randomly-generated six-digit numbers, and one in which they were filled with the random numbers, but in an ij = ji symmetric pattern. In total nearly five hundred thousand sets of data were so treated (see the right margin of
Figure 1 for the totals at each dimensionality). The entropy maximization operation applied was double-standardization (
i.e., bistochastization [
11]), a technique in which all rows, and then columns, and then rows (and so on), are alternately standardized to
z scores until the resulting matrix elements converge to stable values [
12,
13,
14,
15]. About a dozen different forms of
z score arrays result (e.g.,
n ×
n different scores,
n different scores symmetrically arranged,
n different scores asymmetrically arranged,
etc.), but all but one of these classes of patterns—a symmetric matrix of scores with the highest values in the i = j diagonal—will not secondarily project the spatial metric described above.
Figure 1.
Summary of spatial projection simulations for matrix configurations of dimension 3 × 3 through 6 × 6. Circled numbers refer to data at the right margin giving the number of simulations in each test and the standard deviations accompanying the mean values plotted. The plotted numbers are the two mmr and two mamr values obtained at each dimensionality (= “no. of classes in classification”). Colored line coding connecting points is for readability purposes only. Point values 17 through 20 are compiled from subsets of the data leading to point values 2, 6, 10, and 14, respectively. See text for further explanation.
Figure 1.
Summary of spatial projection simulations for matrix configurations of dimension 3 × 3 through 6 × 6. Circled numbers refer to data at the right margin giving the number of simulations in each test and the standard deviations accompanying the mean values plotted. The plotted numbers are the two mmr and two mamr values obtained at each dimensionality (= “no. of classes in classification”). Colored line coding connecting points is for readability purposes only. Point values 17 through 20 are compiled from subsets of the data leading to point values 2, 6, 10, and 14, respectively. See text for further explanation.
Only matrices of dimensionality n = 4 did produce such results. 127 of 25,000 (.51%) of the fully random 4 × 4 matrices double-standardized to the symmetric pattern, while 686 of 40,000 (1.72%) of the symmetric random 4 × 4 matrices did. These are small proportions, but a hopeful outcome: at the very least, they provide a firm starting point against which tests on real world systems might proceed. Two statistics describing the mean degree of structural redundancy within these systems were also compiled from the correlation matrix derived from each initial (random numbers) matrix: (1) the overall mean Pearson correlation coefficients making up each matrix (“mr”); (2) the mean of the absolute values of the column means of the n vectors of r values (i.e., the mean of the deviations from zero of the n vector means of each matrix, “amr”). In either instance the lowest possible mean r value is zero, though invariably by chance there will be some net levels of inter-correlation. The first statistic thus captures net degree of inter-subsystem redundancy, whereas the second accumulates any vector mean differences away from zero, whether negative or positive.
In the simulation analyses to be described, the results across thousands of initial matrices were next averaged to produce the final summary statistics (means) for each set of results (1) and (2) above; these are hereafter referred to as
mmr and
mamr, respectively.
Figure 1 summarizes the results of the simulations.
For each matrix dimensionality of three through six in
Figure 1 there are four points plotting the summary
mmr and
mamr values for each set of simulations (the two redundancy measures combined with the fully random and symmetric random conditions). In addition, values 17 through 20 represent the plotted means for the particular matrices that passed the symmetric
z scores test (at dimension 4 × 4). Two trends are clearly apparent across all the results: the
mmr and
mamr values trend uniformly downward as dimensionality increases, as do the associated standard deviations. Note again that these are “unconstrained” results; that is, the random numbers entered in for analysis have no prior spatial connection.
Given the small but non-negligible portion of the simulations that do pass the spatial projection test (and their varying levels of internal redundancy), it becomes more reasonable to consider whether system patterns in a real world—or first, perhaps, simulated real world—context might do the same (as it is apparent that persistent flows of material/information in real space are often manifest as standing structural patterns). Some years ago, the senior author carried out additional simulations involving two- or three-dimensional spaces populated by randomly-grouped point patterns. These were executed in the same fashion as described above, but in these instances the initial matrix elements consisted of spatial autocorrelation statistics (
i.e., assessing the varying grouped mean nearnesses of all pairings of sets of points in a particular simulation). For several series of simulated two-dimensional systems, about five percent of the patterns produced (that is, when grid-sampled locations were randomly grouped into
n = 4 classes) passed the double standardization-based spatial projection test (the associated
mmr values varied widely, from about 0.05 to 0.20). Other simulations followed on some simple three-dimensional systems, including simulated latitudinal zones around spheres, and concentric zones within spheres. These systems produced higher rates of passage of the spatial projection test, up to fifty percent in the case of the concentric zonations [
16]. These too are encouraging results, as we might expect the rate of evolution to increase as milieus encouraging such change increase over time.
It is fair to ask what the
mr and
amr statistics might “look like” under real world conditions. In simple systems such as molecules this is difficult to say at this point, but in more complicated systems exhibiting complex textures and patterns, some guesses might be made. For example, one might expect higher
mr and
amr values to be associated with systems in early stages of development, as in biological ontogeny, or a newly evolving stream basin system containing lakes, swamps, and waterfalls (and thus a deficiency of gentle, regular, slopes). Lower means might be associated with mature stable systems; higher ones again, for disturbed systems such as newly pirated stream basins, or brains exhibiting the effects of Alzheimer’s disease. Note, however, that there is no one visible “pattern” to look for, since equally high levels of spatial nonrandomness can be expressed through a variety of configurations ranging from regular grid patterns to highly clustered ones [
17]. That said, spatial autocorrelation measures can be used to identify nonrandomness of pattern, whatever the details of the form of the pattern might be.
2.3. Kentucky Stream Basins Analysis
The senior author has performed pilot analyses on the patterns exhibited by several kinds of real world systems in an effort to determine whether they too pass the spatial projection test. The early results seem to suggest so, but most recently a more rigorous study on a set of stream basins in Kentucky was undertaken. Thirty-one basins were selected; to avoid possible complications these were chosen for their relative uniformity of size (ranging in area from 2.8 to 6.6 square miles), outflow into streams of markedly larger size, and absence of complicating surface conditions such as strip mining and karst topography. Basin limits were established manually from USGS topographic maps; elevations across each basin were then grid-sampled using ArcGIS platform data. Three sampling densities were applied for comparative purposes: for the 1× sampling the real-world distance from each sample point on the surface to each of its six nearest neighbors was 860 feet, for the 4× sampling, 430 feet, and for the 16× sampling, 215 feet.
It is a given that every point on the terrestrial surface of the earth constitutes a physical outcome devolving from co-mingling forces of elevation and reduction. These outcomes produce a range of gravitational potential energies that may be expected to interact with one another, especially with respect to their baseline, as conditions evolve. In the context of the present study, it was reasoned that these forces might internally organize, de facto, through a subsystemization manifest in functional zones of elevation—that is, into subzones whose definition is not merely statistical, but actually structurally responsive to one another in an information-sharing, surface reducing/adjusting sense.
How this happens at the microscale is bound to be tied to all sorts of processes invoking both larger- and smaller-scale systems responding to a myriad of influences. Adrian Bejan’s constructal theory [
18] addresses this by suggesting that natural systems evolve in such a manner as to better facilitate the currents of vital materials that flow through, and nourish, them. At different scales, the flows involved may be of entirely different makeups—people in urban commuter systems and blood in the human vascular system, for example—but according to Bejan’s theory, all systems exhibit a tendency to continue to structurally facilitate the flow. A similar understanding is invoked here, but the suggestion is made that the feedbacks that have evolved to operationalize such change flow primarily at the level of subsystem interactions. So, and for example, a stream basin disrupted by a sudden piracy or baseline change event might respond most efficiently through shifts in topographical configuration mediated by an entropy maximization process; that is, through feedbacks passed at the subsystem level (in this case, ranges of potential energies expressed as functional zones of elevation). In Bejan’s theory flows self-organize at different scales and rates dependent only on the ability of hierarchies of such to continue the process; in the model entertained here this is also true, though emergent structure is possible only when entropy is maximized among the subsystems in such a fashion as to correspond to an extended space metric.
The earlier pilot studies suggest that within some natural systems, the “imposed current” (in Bejan’s terminology) is so consistent and/or stable that physically observable boundaries between the subsystems emerge and persist. In more varying and/or multi-causal systems, however, the underlying organization may only be evident through the pattern of secondary indicators of its operation such as temperature or pressure. In the present instance, the topography itself reflects the impact of systemic interactions of gravitational forces. The central matter of interest here is whether evidence can be found that the system is self-organizing as a function of group relations, instead of a myriad of independently operating singularities. For each basin regular (triangular grid) samples of elevations were first classified into three, four, five, and six class structures using a nonhierarchical, information statistic-based, clustering algorithm [
19].
Figure 2 summarizes the results of the clustering operations.
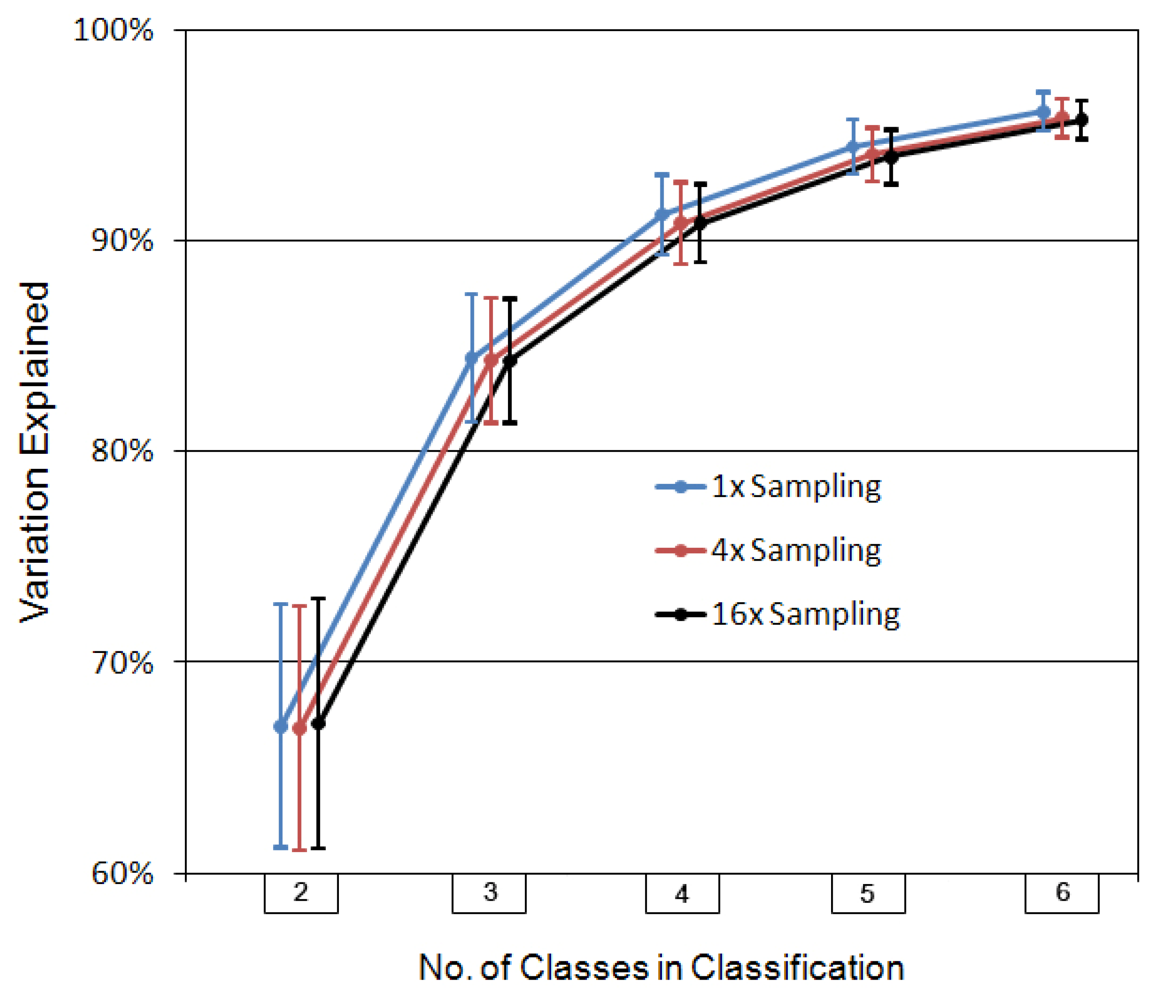
Figure 2.
Summary of variation explained statistics obtained for the clustering of the stream basins data (vectors) into two through six classes. The plotted points are the mean (n = 31) variations-explained for each classification, at three fineness levels of sampling. Colored line coding connecting points is for readability purposes only.
Figure 2.
Summary of variation explained statistics obtained for the clustering of the stream basins data (vectors) into two through six classes. The plotted points are the mean (n = 31) variations-explained for each classification, at three fineness levels of sampling. Colored line coding connecting points is for readability purposes only.
The summary statistics displayed in
Figure 2 are very consistent, even considering they are based on only thirty-one cases. Variation explained increases rather smoothly, at least on the average, with number of classes. This was not unexpected, as only very unusual data will produce models in which a higher number of classes end up explaining less of the variation than a lower number.
A simple sum-of-squares-based (
i.e., not contiguities-based) spatial autocorrelation algorithm [
20] was then applied to the inter-class patterns; the non-proportionalized summary spatial autocorrelation statistics thus generated became the elements of each initial data matrix (as was the case with the two- and three-dimensional simulations mentioned earlier). These statistics were then double-standardized. The results of this analysis are shown in
Figure 3.
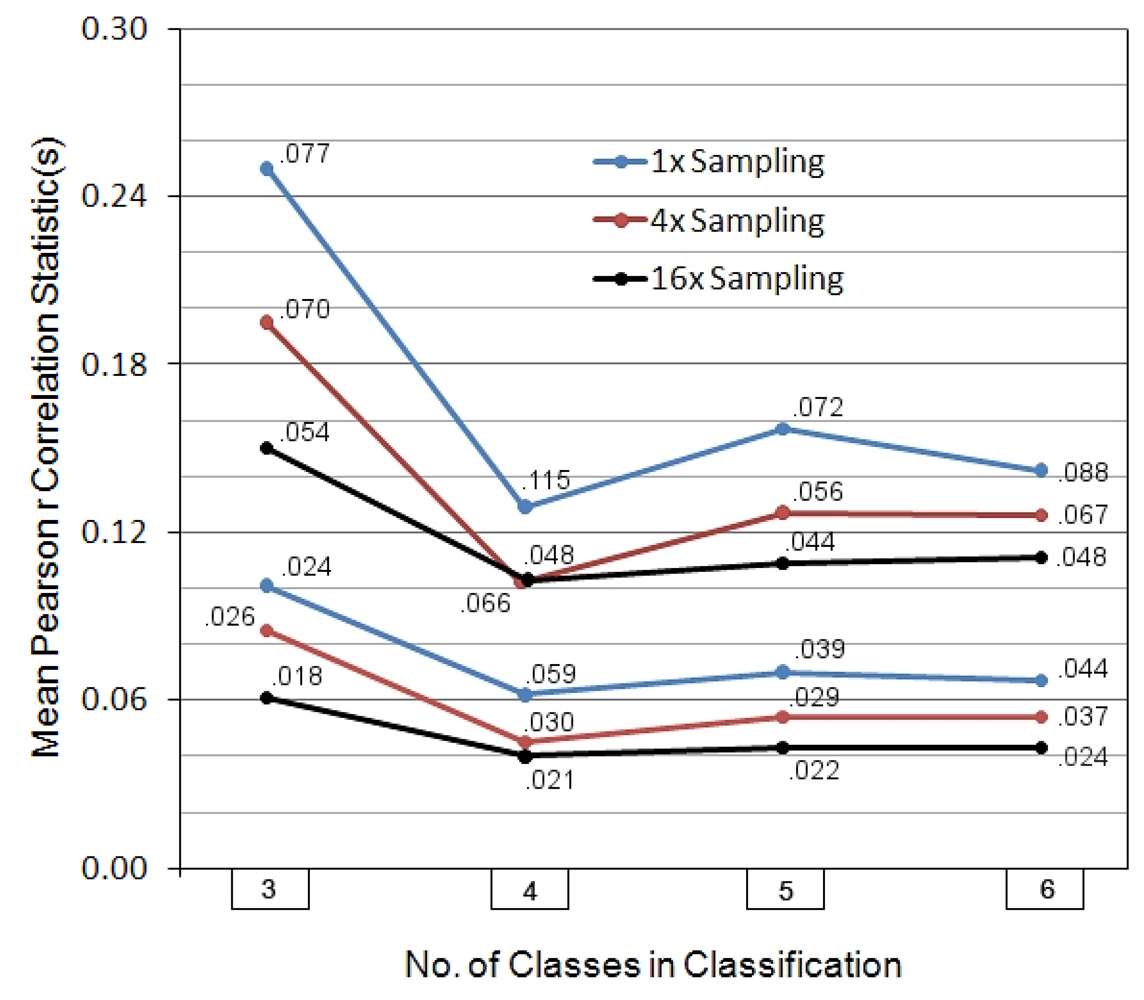
Figure 3.
Summary of spatial subsystemization properties of topography in 31 Kentucky stream basins, based on three fineness levels of sampling. The plotted values in the top three sets of four points are the
mamr values; those in the bottom three are the
mmr values. The associated standard deviations are written out next to each plotted value. Colored line coding connecting points is for readability purposes only. The results as displayed here are in marked contrast to the simulation results shown in
Figure 1, suggesting that the spatial expression of the basins is related to a functional (not just statistically described) subsystemization process.
Figure 3.
Summary of spatial subsystemization properties of topography in 31 Kentucky stream basins, based on three fineness levels of sampling. The plotted values in the top three sets of four points are the
mamr values; those in the bottom three are the
mmr values. The associated standard deviations are written out next to each plotted value. Colored line coding connecting points is for readability purposes only. The results as displayed here are in marked contrast to the simulation results shown in
Figure 1, suggesting that the spatial expression of the basins is related to a functional (not just statistically described) subsystemization process.
Figure 3 displays the full set of
mmr and
mamr statistics across the thirty-one streams, relaying the results at the three sampling densities. All six patterns of results are roughly similar across the four matrix dimensionalities, though as one would expect, with higher fineness of sampling the details of pattern are better exposed, and all of the
mmr and
mamr values and their standard deviations drop. More importantly, these values are considerably lower than those evidenced in the simulations data in
Figure 1, and it is apparent that once actual spatial relations are taken into account there is no longer a smooth pattern of decrease in means as the number of classes increases. In fact, the simulations notwithstanding,
mmr and
mamr actually minimize—absolutely—at the four-class level, not at the five- or six-. This is difficult to explain if there is not an actual, significant, structural causality operating at that level of subsystem definition. One of the earlier-mentioned pilot studies, though more crudely organized, came up with similar (though not quite so conclusive) results on another twenty-five basins of more widely varying size and geographical location, the
mmr values lowering only very little, on the average, from the four- to five- and six-class solutions (four-class, 40% lower than three-; four- and five- very nearly the same; six-, only 13% lower than four-) [
21].
For the four-class solutions, 28 of the 31 16× spatial autocorrelation matrices do double-standardize to a symmetric state passing the spatial projection test described earlier. 28 of 31 also pass at the 4× sampling density, but only 18 of 31 at the 1× (again, likely reflecting the poorer resolution connected to the coarser samples). Parallel analyses employing two other metric spatial autocorrelation measures produced similar results. Remembering that the two-dimensional simulations only yielded about five percent success rates, this is remarkable. In theory, however, all 31 should have passed, so as a check the three nonconforming basins were subjected to a special 64× sampling (capturing even more detail in the topography), whereupon two of the three then produced symmetric z scores, while in the third the mean ij / ji z scores difference (0.1306) had been reduced by about forty-four percent, suggesting that yet higher sampling densities might eventually complete the convergence; that is, to a mean ij / ji difference of 0. (In the earlier pilot study, 24 of 25 passed, with the twenty-fifth, an outlier in terms of basin size and some other characteristics, narrowly missing.)
It possibly will be objected that the main tests merely represent a reconstruction of three-dimensionality that was already built into the setting, but this seems not to be so. First, the
mmr and
mamr statistics (for 16×,
n = 4, 0.0398 and 0.1029, respectively) for the case study are much lower than those connected with any of the parallel simulations (range: 0.1739 to 0.2287): they are thus a subpopulation which is in some sense special. Second, a test of the “reconstruction” hypothesis was fashioned by reclassifying each vector of elevations into two arbitrary sets of four classes markedly differing from the actual classifications in the case study (the highest or lowest 60% of the point elevations were summarily grouped into one class, with the remaining points grouped in elevation order into three smaller, equal-sized, classes), and for both 1× and 16× vectors. After the associated spatial autocorrelation statistics were calculated and subjected to double standardization, only 18 of 62 of the 1× systems passed the test, and 2 of 62 of the 16× systems. The
mmr and
mamr statistics derived from these last analyses (for 1×, 0.1792 and 0.3398; for 16×, 0.1522 and 0.2768, respectively) approached or exceeded those for the original simulations on random systems; that is, they were very much higher than those from the case study analyses [
22].