Identifying Tumor-Associated Genes from Bilayer Networks of DNA Methylation Sites and RNAs
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Collection and Preprocessing
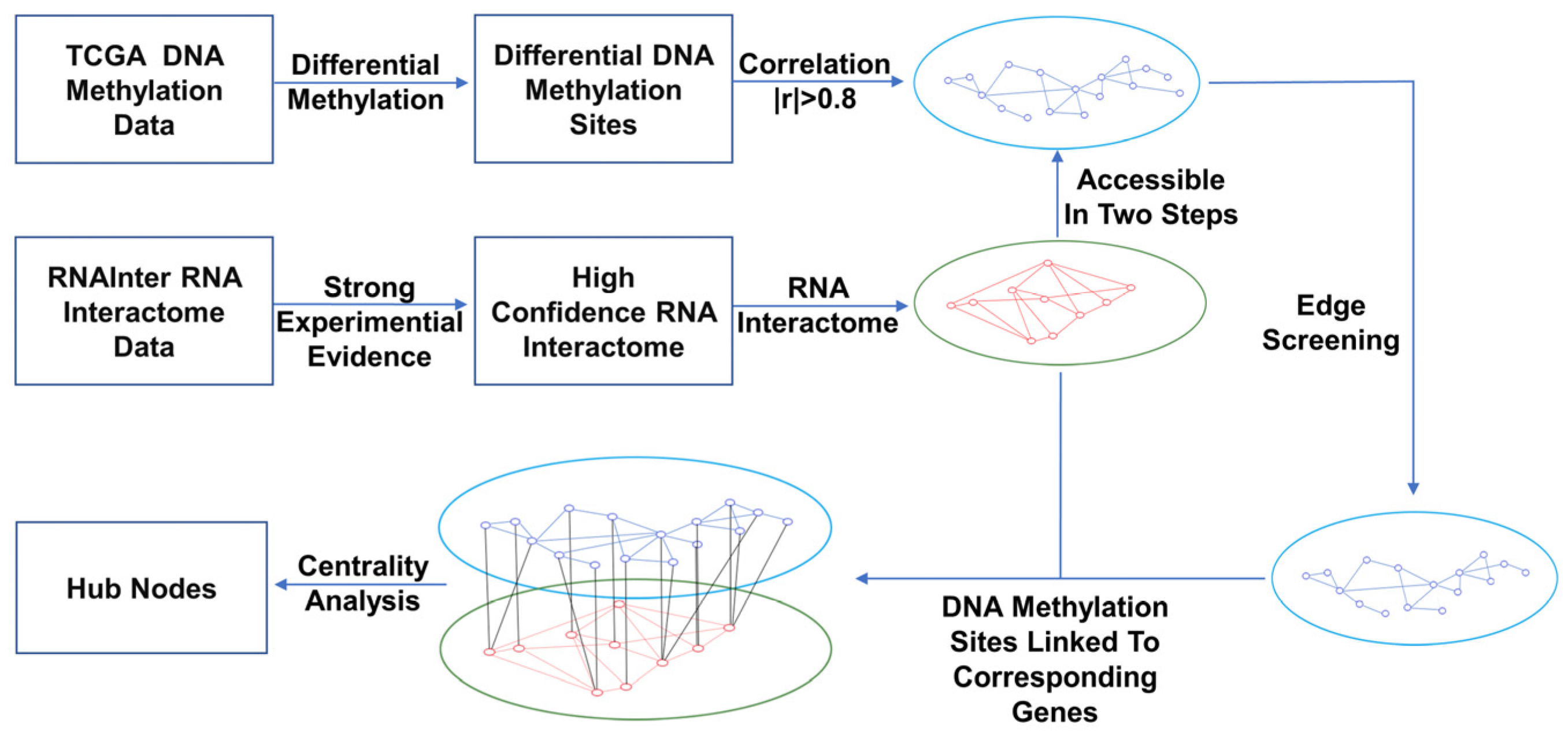
2.2. Network Construction
2.2.1. Construction of the DNA Methylation and RNA Interaction Networks
2.2.2. Construction of Bilayer Network of DNA Methylation Sites–RNAs
2.3. Network Indicators
2.3.1. Degree Centrality (DC)
2.3.2. Betweenness Centrality (BC)
2.3.3. Average Degree
2.3.4. ER Random Network
2.3.5. Clustering Coefficient
2.3.6. Shortest Path Length
2.4. Statistical Analysis
2.4.1. Chi-Squared Test
2.4.2. Log Rank Test
2.5. Identification of Differentially Expressed Genes (DEGs)
2.6. Survival Analysis
2.7. KEGG Pathway Enrichment Analysis
3. Results
3.1. Characteristics of DNA Methylation Sites–RNAs Bilayer Network
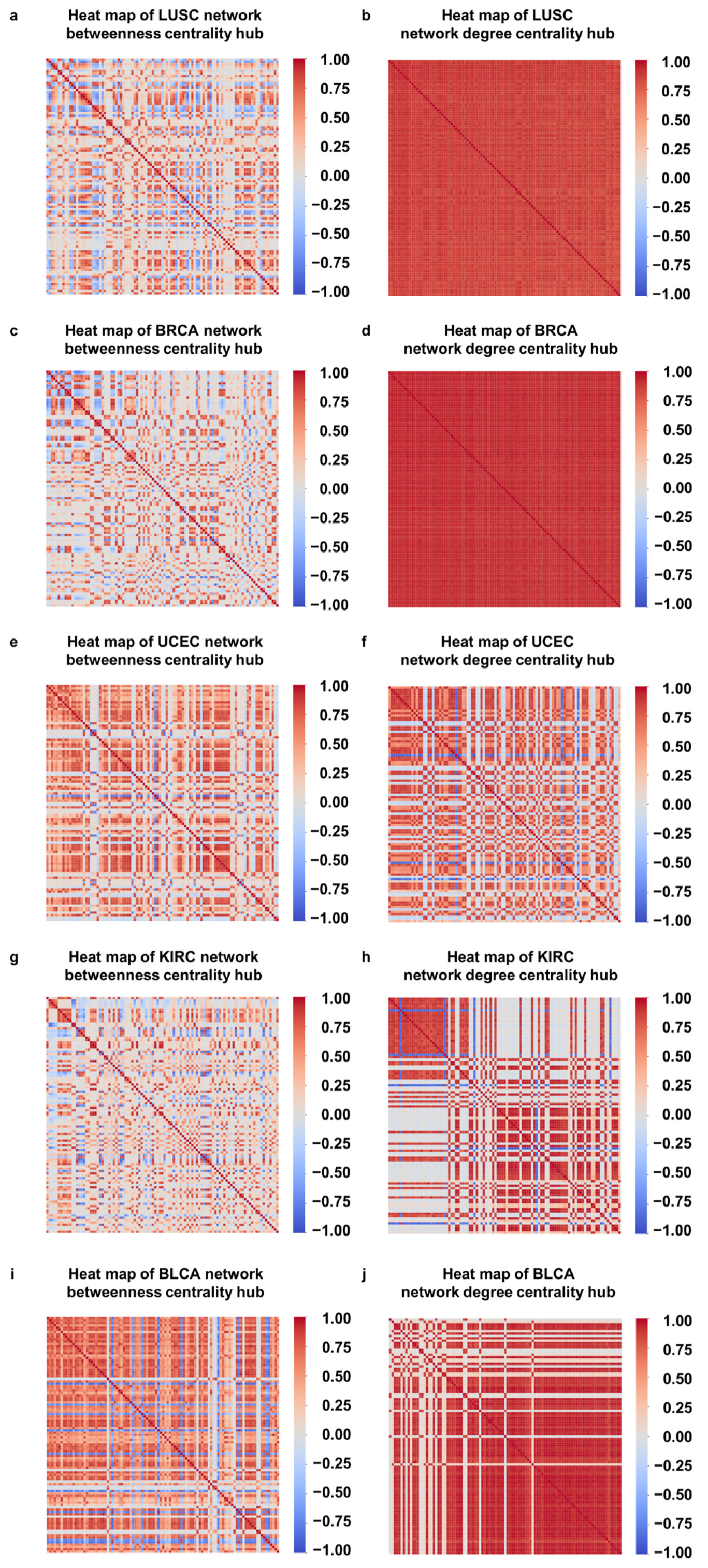
3.2. Correlation of Hubs with Tumor Development Process
3.3. Correlations between DNA Methylation Sites Located on the Same Gene
3.4. Hubs in DNA Methylation Layer Aggregates Differentially Expressed Genes
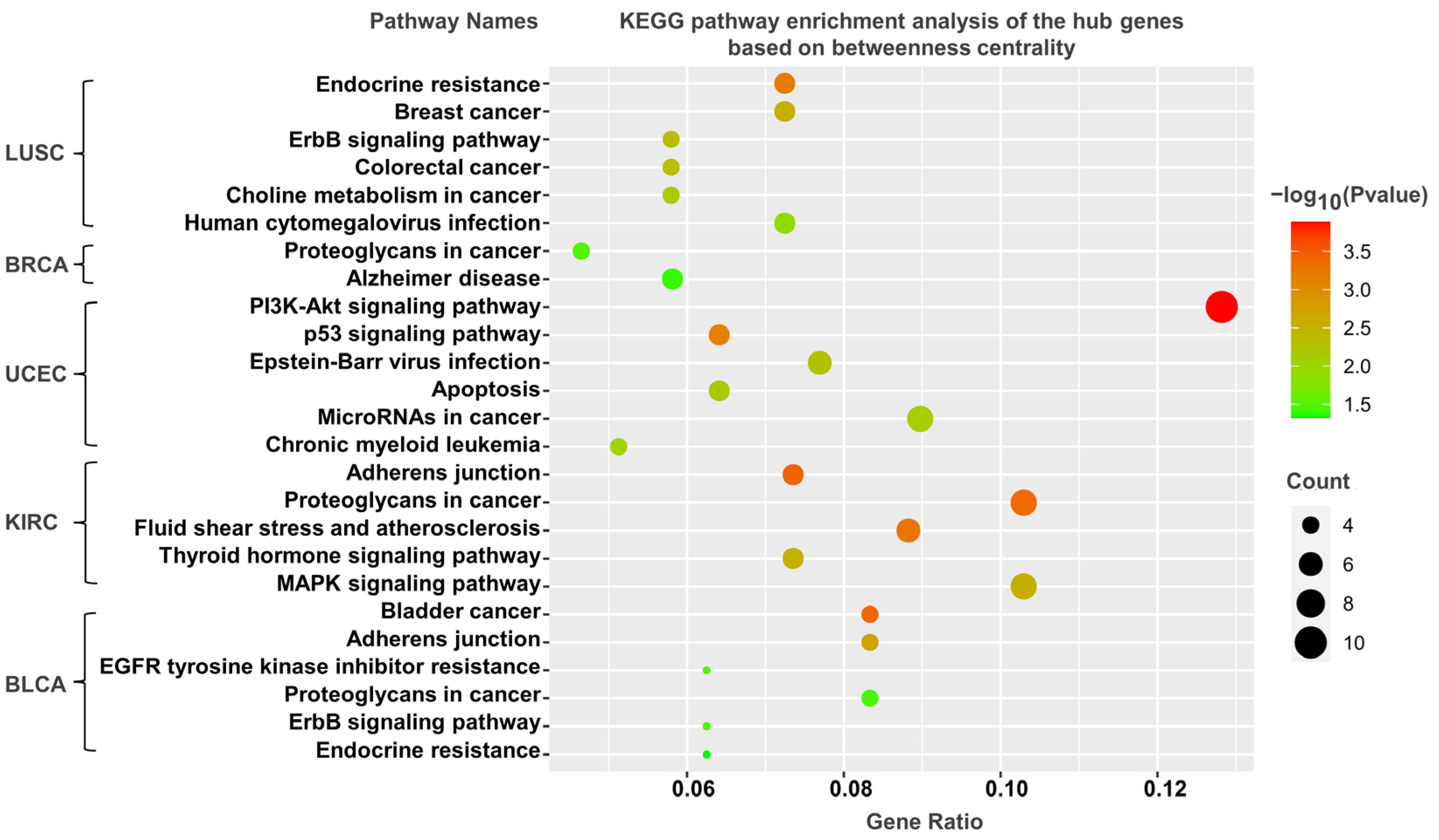
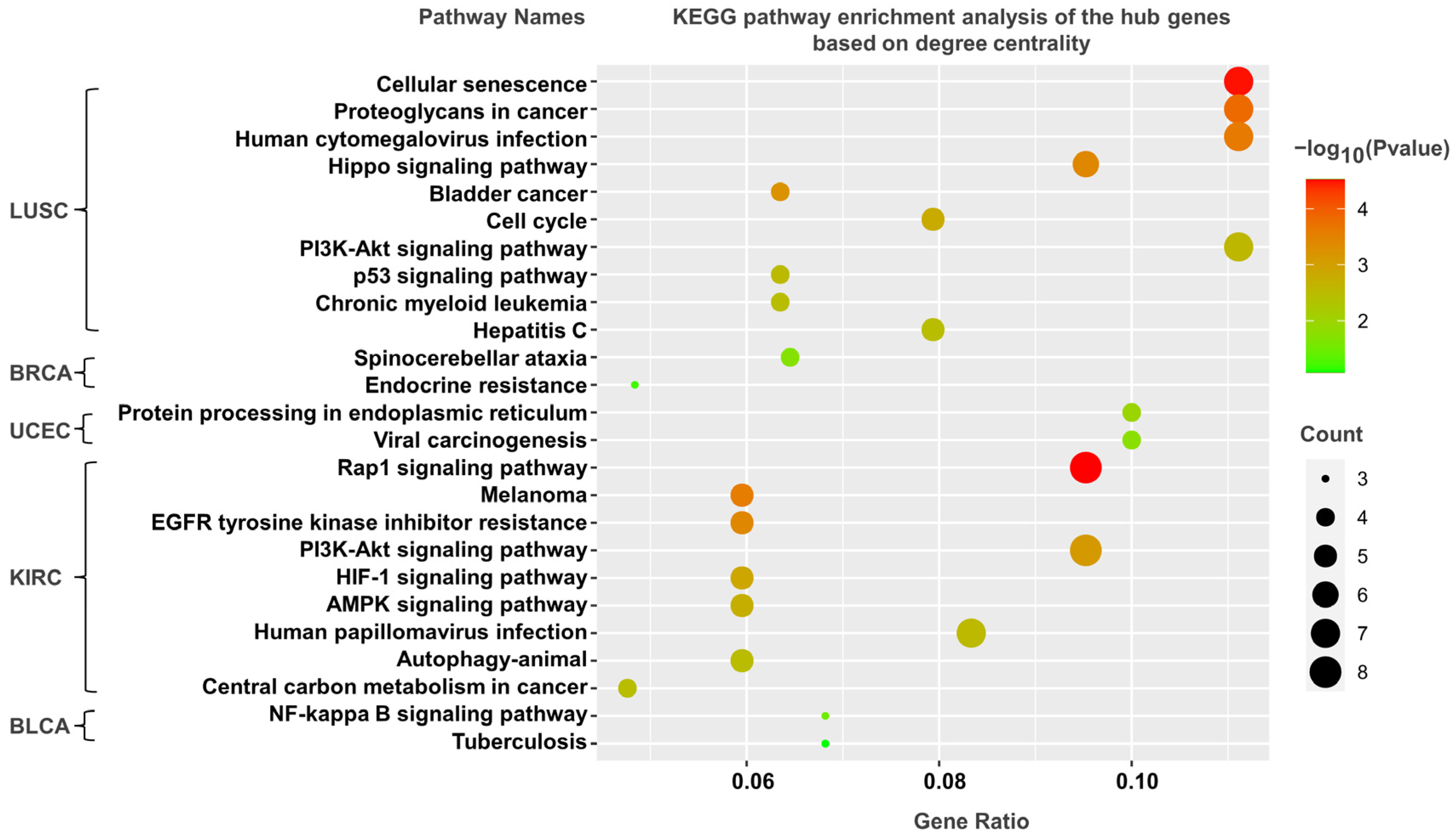
3.5. KEGG Pathway Analysis
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Barabási, A.L.; Gulbahce, N.; Loscalzo, J. Network medicine: A network-based approach to human disease. Nat. Rev. Genet. 2011, 12, 56–68. [Google Scholar] [CrossRef] [Green Version]
- Smith, H.B.; Kim, H.; Walker, S.I. Scarcity of scale-free topology is universal across biochemical networks. Sci. Rep. 2021, 11, 6542. [Google Scholar] [CrossRef]
- Jeong, H.; Mason, S.P.; Barabási, A.L.; Oltvai, Z.N. Lethality and centrality in protein networks. Nature 2001, 411, 41–42. [Google Scholar] [CrossRef] [Green Version]
- Naderi, Y.P.; Richardson, C.; Saule, E.; Loraine, A.; Taghi, M.M. Revisiting the use of graph centrality models in biological pathway analysis. BioData Min. 2020, 13, 5. [Google Scholar] [CrossRef]
- Das, A.B. Small-world networks of prognostic genes associated with lung adenocarcinoma development. Genomics 2020, 112, 4078–4088. [Google Scholar] [CrossRef]
- Van, D.S.; Võsa, U.; Vander, G.A.; Franke, L.; Magalhães, J.P. Gene co-expression analysis for functional classification and gene-disease predictions. Brief. Bioinform. 2018, 19, 575–592. [Google Scholar] [CrossRef]
- Marbach, D.; Lamparter, D.; Quon, G.; Kellis, M.; Kutalik, Z.; Bergmann, S. Tissue-specific regulatory circuits reveal variable modular perturbations across complex diseases. Nat. Methods 2016, 13, 366–370. [Google Scholar] [CrossRef] [Green Version]
- Albert, R.; Jeong, H.; Barabási, A.L. Error and attack tolerance of complex networks. Nature 2000, 406, 378–382. [Google Scholar] [CrossRef] [Green Version]
- Luo, M.; Jiao, J.; Wang, R. Screening drug target combinations in disease-related molecular networks. BMC Bioinform. 2019, 20, 129–138. [Google Scholar] [CrossRef]
- Muhammad, J.; Khan, A.; Ali, A.; Fang, L.; Yanjing, W.; Xu, Q.; Wei, D.Q. Network Pharmacology: Exploring the Resources and Methodologies. Curr. Top. Med. Chem. 2018, 18, 949–964. [Google Scholar] [CrossRef]
- Le, D.H. A network-based method for predicting disease-associated enhancers. PLoS ONE 2021, 16, e0260432. [Google Scholar] [CrossRef] [PubMed]
- Goh, K.I.; Cusick, M.E.; Valle, D.; Childs, B.; Vidal, M.; Barabási, A.L. The human disease network. Proc. Natl. Acad. Sci. USA 2007, 104, 8685–8690. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yan, T.; Ding, F.; Zhao, Y. Integrated identification of key genes and pathways in Alzheimer’s disease via comprehensive bioinformatical analyses. Hereditas 2019, 156, 25. [Google Scholar] [CrossRef]
- Tong, Z.; Zhou, Y.; Wang, J. Identifying potential drug targets in hepatocellular carcinoma based on network analysis and one-class support vector machine. Sci. Rep. 2019, 9, 10442. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez-Esteban, R.; Jiang, X. Differential gene expression in disease: A comparison between high-throughput studies and the literature. BMC Med. Genom. 2017, 10, 59. [Google Scholar] [CrossRef] [Green Version]
- Le, D.H. Machine learning-based approaches for disease gene prediction. Brief. Funct. Genom. 2020, 19, 350–363. [Google Scholar] [CrossRef]
- Li, X.; Li, W.; Zeng, M.; Zheng, R.; Li, M. Network-based methods for predicting essential genes or proteins: A survey. Brief. Bioinform. 2020, 21, 566–583. [Google Scholar] [CrossRef]
- Liu, J.; Hua, P.; Hui, L.; Zhang, L.L.; Hu, Z.; Zhu, Y.W. Identification of hub genes and pathways associated with hepatocellular carcinoma based on network strategy. Exp. Ther. Med. 2016, 12, 2109–2119. [Google Scholar] [CrossRef] [Green Version]
- Bánky, D.; Iván, G.; Grolmusz, V. Equal opportunity for low-degree network nodes: A PageRank-based method for protein target identification in metabolic graphs. PLoS ONE 2013, 8, e54204. [Google Scholar] [CrossRef] [Green Version]
- Lei, X.; Wang, S.; Wu, F. Identification of essential proteins based on improved HITS algorithm. Genes 2019, 10, 177. [Google Scholar] [CrossRef]
- Foutch, D.; Pham, B.; Shen, T. Protein conformational switch discerned via network centrality properties. Comput. Struct. Biotechnol. J. 2021, 19, 3599–3608. [Google Scholar] [CrossRef]
- Gosak, M.; Markovič, R.; Dolenšek, J.; Slak, R.M.; Marhl, M.; Stožer, A.; Perc, M. Network science of biological systems at different scales: A review. Phys. Life Rev. 2018, 24, 118–135. [Google Scholar] [CrossRef]
- Lv, Y.; Huang, S.; Zhang, T.; Gao, B. Application of Multilayer Network Models in Bioinformatics. Front. Genet. 2021, 12, 664860. [Google Scholar] [CrossRef]
- Zhou, G.; Li, S.; Xia, J. Network-based approaches for multi-omics integration. Comput. Methods Data Anal. Metab. 2020, 1, 469–487. [Google Scholar] [CrossRef]
- Cantini, L.; Medico, E.; Fortunato, S.; Caselle, M. Detection of gene communities in multi-networks reveals cancer drivers. Sci. Rep. 2015, 5, 17386. [Google Scholar] [CrossRef] [Green Version]
- Pournoor, E.; Mousavian, Z.; Dalini, A.N.; Masoudi, N.A. Identification of key components in colon adenocarcinoma using transcriptome to interactome multi-layer framework. Sci. Rep. 2020, 10, 4991. [Google Scholar] [CrossRef] [Green Version]
- Mahapatra, S.; Bhuyan, R.; Das, J.; Swarnkar, T. Integrated multiplex network based approach for hub gene identification in oral cancer. Heliyon 2021, 7, e07418. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, J.; Wang, Y.; Wang, D.; Cong, W.; Lai, B.S.; Zhao, Y. Multi-layer network analysis of miRNA and protein expression profiles in breast cancer patients. PloS ONE 2019, 14, e0202311. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Wang, H.; Zou, X. Identifying key nodes in multi-layer networks based on tensor decomposition. Chaos 2017, 27, 063108. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Xu, M.; An, Y. Identifying the essential nodes in network pharmacology based on multilayer network combined with random walk algorithm. J. Biomed. Inform. 2021, 114, 103666. [Google Scholar] [CrossRef]
- Sanchez, V.F.; Mina, M.; Armenia, J.; Chatila, W.K.; Luna, A.; La, K.C.; Dimitriadoy, S.; Liu, D.L.; Kantheti, H.S.; Saghafinia, S.; et al. Oncogenic Signaling Pathways in The Cancer Genome Atlas. Cell 2018, 173, 321–337. [Google Scholar] [CrossRef] [Green Version]
- The Cancer Genome Atlas Research Network. Comprehensive molecular characterization of urothelial bladder carcinoma. Nature 2014, 507, 315–322. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.; Liu, T.; Cui, T.; Wang, Z.; Zhang, Y.; Tan, P.; Huang, Y.; Yu, J.; Wang, D. RNAInter in 2020: RNA interactome repository with increased coverage and annotation. Nucleic Acids Res. 2020, 48, D189–D197. [Google Scholar] [CrossRef]
- Wei, G.; Dong, Y.; He, Z.; Qiu, H.; Wu, Y.; Chen, Y. Identification of hub genes and construction of an mRNA-miRNA-lncRNA network of gastric carcinoma using integrated bioinformatics analysis. PLoS ONE 2021, 16, e0261728. [Google Scholar] [CrossRef]
- Hu, W.L.; Zhou, X.H. Identification of prognostic signature in cancer based on DNA methylation interaction network. BMC Med. Genom. 2017, 10, 81–91. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.; Li, D.; Li, J. Technologies for targeting DNA methylation modifications: Basic mechanism and potential application in cancer. Biochim. Biophys. Acta BBA Rev. Cancer 2021, 1875, 188454. [Google Scholar] [CrossRef]
- Győrffy, B.; Bottai, G.; Fleischer, T.; Munkácsy, G.; Budczies, J.; Paladini, L.; Børresen-Dale, A.L.; Kristensen, V.N.; Santarpia, L. Aberrant DNA methylation impacts gene expression and prognosis in breast cancer subtypes. Int. J. Cancer 2016, 138, 87–97. [Google Scholar] [CrossRef] [Green Version]
- Liang, Y.; Zhang, C.; Dai, D.Q. Identification of differentially expressed genes regulated by methylation in colon cancer based on bioinformatics analysis. World J. Gastroenterol. 2019, 25, 3392–3407. [Google Scholar] [CrossRef]
- Ritchie, M.E.; Phipson, B.; Wu, D.I.; Hu, Y.; Law, C.W.; Shi, W.; Smyth, G.K. limma powers differential expression analyzes for RNA-sequencing and microarray studies. Nucleic Acids Res. 2015, 43, e47. [Google Scholar] [CrossRef]
- Cui, Z.J.; Zhou, X.H.; Zhang, H.Y. DNA methylation module network-based prognosis and molecular typing of cancer. Genes 2019, 10, 571. [Google Scholar] [CrossRef]
- Benedetti, E.; Pučić-Baković, M.; Keser, T.; Gerstner, N.; Büyüközkan, M.; Štambuk, T.; Selman, M.H.; Rudan, I.; Polašek, O.; Hayward, C.; et al. A strategy to incorporate prior knowledge into correlation network cutoff selection. Nat. Commun. 2020, 11, 5153. [Google Scholar] [CrossRef]
- Kim, K.S.; Jekarl, D.W.; Yoo, J.; Lee, S.; Kim, M.; Kim, Y. Immune gene expression networks in sepsis: A network biology approach. PLoS ONE 2021, 16, e0247669. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, D.; Chen, L.; Li, X.; Yang, J.; Fan, D.; Dong, T.; Liu, M.; Tan, P.; Xu, J.; et al. RAID: A comprehensive resource for human RNA-associated (RNA–RNA/RNA–protein) interaction. RNA 2014, 20, 989–993. [Google Scholar] [CrossRef] [Green Version]
- Guttman, M.; Rinn, J.L. Modular regulatory principles of large non-coding RNAs. Nature 2012, 482, 339–346. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Yang, L.; Wang, J.; Hao, Y.; Wang, C.; Lu, Z. The Involvement of Long Non-Coding RNAs in Glioma: From Early Detection to Immunotherapy. Front. Immunol. 2022, 13, 897754. [Google Scholar] [CrossRef]
- Freeman, L.C. Centrality in social networks conceptual clarification. Soc. Netw. 1978, 1, 215–239. [Google Scholar] [CrossRef] [Green Version]
- Freeman, L.C. A set of measures of centrality based on betweenness. Sociometry 1977, 1, 35–41. [Google Scholar] [CrossRef]
- Grobelny, B.T.; London, D.; Hill, T.C.; North, E.; Dugan, P.; Doyle, W.K. Betweenness centrality of intracranial electroencephalography networks and surgical epilepsy outcome. Clin. Neurophysiol. 2018, 129, 1804–1812. [Google Scholar] [CrossRef]
- Newman, M.E. The structure of scientific collaboration networks. Proc. Natl. Acad. Sci. USA 2001, 98, 404–409. [Google Scholar] [CrossRef]
- Hao, D.; Ren, C.; Li, C. Revisiting the variation of clustering coefficient of biological networks suggests new modular structure. BMC Syst. Biol. 2012, 6, 34. [Google Scholar] [CrossRef]
- Ren, Y.; Ay, A.; Kahveci, T. Shortest path counting in probabilistic biological networks. BMC Bioinform. 2018, 19, 465. [Google Scholar] [CrossRef]
- Wallis, K.F. Chi-squared tests of interval and density forecasts, and the Bank of England’s fan charts. Int. J. Forecast. 2003, 19, 165–175. [Google Scholar] [CrossRef] [Green Version]
- Du, S.; Guo, Y.; Huang, J.; Xu, J.; Chen, G. The Expressions and Functions of lncRNA Related to m6A in Hepatocellular Carcinoma from a Bioinformatics Analysis. Comput. Math. Methods Med. 2022, 12, 95557. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D.G. The logrank test. BMJ 2004, 328, 1073. [Google Scholar] [CrossRef] [Green Version]
- Su, P.; Wen, S.; Zhang, Y.; Li, Y.; Xu, Y.; Zhu, Y.; Lv, H.; Zhang, F.; Wang, M.; Tian, Z. Identification of the Key Genes and Pathways in Esophageal Carcinoma. Gastroenterol. Res. Pract. 2016, 2016, 2968106. [Google Scholar] [CrossRef] [Green Version]
- Smith, J.J.; Deane, N.G.; Wu, F.; Merchant, N.B.; Zhang, B.; Jiang, A.; Lu, P.; Johnson, J.C.; Schmidt, C.; Bailey, C.E.; et al. Experimentally derived metastasis gene expression profile predicts recurrence and death in patients with colon cancer. Gastroenterology 2010, 138, 958–968. [Google Scholar] [CrossRef] [Green Version]
- Alvord, W.G.; Roayaei, J.; Stephens, R. The DAVID gene functional classification tool: A novel biological module-centric algorithm to functionally analyze large gene lists. Genome Biol. 2007, 8, R183. [Google Scholar] [CrossRef] [Green Version]
- Chang, H.C.; Chu, C.P.; Lin, S.J.; Hsiao, C.K. Network hub-node prioritization of gene regulation with intra-network association. BMC Bioinform. 2020, 21, 101. [Google Scholar] [CrossRef]
- Ashtiani, M.; Salehzadeh, Y.A.; Razaghi, M.Z.; Hennig, H.; Wolkenhauer, O.; Mirzaie, M.; Jafari, M. A systematic survey of centrality measures for protein-protein interaction networks. BMC Syst. Biol. 2018, 12, 80. [Google Scholar] [CrossRef] [Green Version]
- Duffy, M.J.; O’Grady, S.; Tang, M.; Crown, J. MYC as a target for cancer treatment. Cancer Treat. Rev. 2021, 94, 102154. [Google Scholar] [CrossRef]
- Ijaz, M.; Wang, F.; Shahbaz, M.; Jiang, W.; Fathy, A.H.; Nesa, E.U. The Role of Grb2 in Cancer and Peptides as Grb2 Antagonists. Protein Pept. Lett. 2018, 24, 1084–1095. [Google Scholar] [CrossRef]
- Gao, Y.; Feng, B.; Lu, L.; Han, S.; Chu, X.; Chen, L.; Wang, R. MiRNAs and E2F3: A complex network of reciprocal regulations in human cancers. Oncotarget 2017, 8, 60624. [Google Scholar] [CrossRef] [Green Version]
- Nebenfuehr, S.; Kollmann, K.; Sexl, V. The role of CDK6 in cancer. Int. J. Cancer 2020, 147, 2988–2995. [Google Scholar] [CrossRef]
- Poluri, R.T.; Paquette, V.; Allain, É.P.; Lafront, C.; Joly, B.C.; Weidmann, C.; Droit, A.; Guillemette, C.; Pelletier, M.; Audet, W.É. KLF5 and NFYA factors as novel regulators of prostate cancer cell metabolism. Endocr. Relat. Cancer 2021, 28, 257–271. [Google Scholar] [CrossRef]
- Burgess, J.T.; Bolderson, E.; Adams, M.N.; Duijf, P.H.G.; Zhang, S.D.; Gray, S.G.; Wright, G.; Richard, D.J.; O’Byrne, K.J. SASH1 is a prognostic indicator and potential therapeutic target in non-small cell lung cancer. Sci. Rep. 2020, 10, 18605. [Google Scholar] [CrossRef]
- Xiong, H.; Chen, Z.; Zheng, W.; Sun, J.; Fu, Q.; Teng, R.; Chen, J.; Xie, S.; Wang, L.; Yu, X.F.; et al. FKBP4 is a malignant indicator in luminal A subtype of breast cancer. J. Cancer 2020, 11, 1727. [Google Scholar] [CrossRef] [Green Version]
- Verma, M.; Patel, P.; Verma, M. Biomarkers in prostate cancer epidemiology. Cancers 2011, 3, 3773–3798. [Google Scholar] [CrossRef] [Green Version]
- Chu, Y.; Lai, Y.H.; Lee, M.C.; Yeh, Y.J.; Wu, Y.K.; Tsao, W.; Huang, C.Y.; Wu, S. Calsyntenin-1, clusterin and neutrophil gelatinase-associated lipocalin are candidate serological biomarkers for lung adenocarcinoma. Oncotarget 2017, 8, 107964. [Google Scholar] [CrossRef] [Green Version]
- Humbert, P.O.; Pryjda, T.Z.; Pranjic, B.; Farrell, A.; Fujikura, K.; Dematos, S.R.; Karim, R.; Kozieradzki, I.; Cronin, S.J.F.; Neely, G.G.; et al. TSPAN6 is a suppressor of Ras-driven cancer. Oncogene 2022, 41, 2095–2105. [Google Scholar] [CrossRef]
- Sun, S.; Dammann, J.; Lai, P.; Tian, C. Thorough statistical analyses of breast cancer co-methylation patterns. BMC Genom. Data 2022, 23, 29. [Google Scholar] [CrossRef]
- Kundu, A.; Nam, H.; Shelar, S.; Chandrashekar, D.S.; Brinkley, G.; Karki, S.; Mitchell, T.; Livi, C.B.; Buckhaults, P.; Kirkman, R.; et al. PRDM16 suppresses HIF-targeted gene expression in kidney cancer. J. Exp. Med. 2020, 217, 66–75. [Google Scholar] [CrossRef] [Green Version]
- Sengelaub, C.A.; Navrazhina, K.; Ross, J.B.; Halberg, N.; Tavazoie, S.F. PTPRN 2 and PLC\beta1 promote metastatic breast cancer cell migration through PI (4, 5) P2-dependent actin remodeling. EMBO J. 2016, 35, 62–76. [Google Scholar] [CrossRef]
- Yin, J.; Guo, Y. HOXD13 promotes the malignant progression of colon cancer by upregulating PTPRN2. Cancer Med. 2021, 10, 5524–5533. [Google Scholar] [CrossRef]
- Eckhardt, F.; Lewin, J.; Cortese, R.; Rakyan, V.K.; Attwood, J.; Burger, M.; Burton, J.; Cox, T.V.; Davies, R.; Down, T.A.; et al. DNA methylation profiling of human chromosomes 6, 20 and 22. Nat. Genet. 2006, 38, 1378–1385. [Google Scholar] [CrossRef] [Green Version]
- Huang, J. Current developments of targeting the p53 signaling pathway for cancer treatment. Pharmacol. Ther. 2021, 220, 107720. [Google Scholar] [CrossRef]
- Espinoza, N.A.; Goette, M. Role of cell surface proteoglycans in cancer immunotherapy. Semin. Cancer Biol. 2020, 62, 48–67. [Google Scholar] [CrossRef]
- Ediriweera, M.K.; Tennekoon, K.H.; Samarakoon, S.R. Role of the PI3K/AKT/mTOR signaling pathway in ovarian cancer: Biological and therapeutic significance. Semin. Cancer Biol. 2019, 59, 147–160. [Google Scholar] [CrossRef]

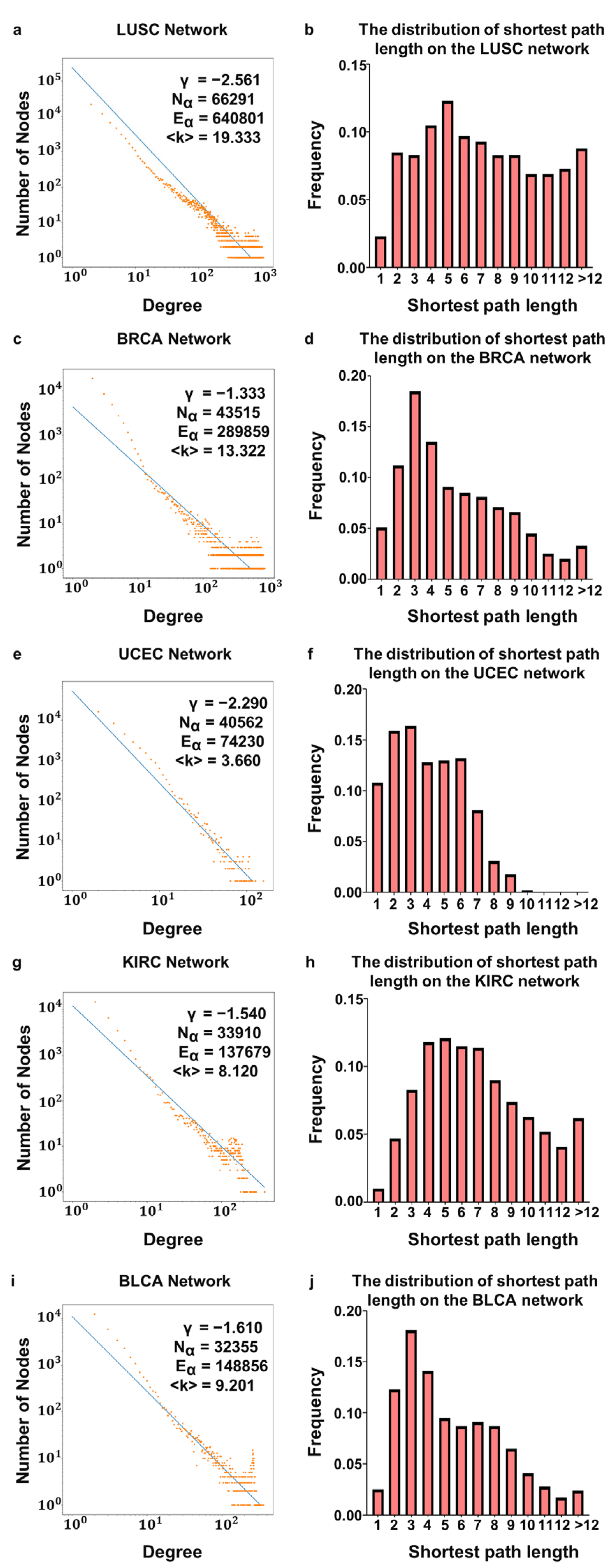

| Tumor Type | Number of Nodes in the DNA Methylation Layer | Number of Edges in the DNA Methylation Layer | Average Degree | Average Clustering | Average Clustering of the ER Network | Average Path Length | Average Path Length of the ER Network |
|---|---|---|---|---|---|---|---|
| LUSC | 66,291 | 640,801 | 19.333 | 0.451 | 0.003 | 8.131 | 11.102 |
| BRCA | 43,515 | 289,859 | 13.322 | 0.436 | 0.003 | 6.227 | 10.681 |
| UCEC | 40,562 | 74,230 | 3.660 | 0.495 | 0.001 | 4.559 | 10.611 |
| KIRC | 33,910 | 137,679 | 8.120 | 0.430 | 0.002 | 6.907 | 10.431 |
| BLCA | 32,355 | 148,856 | 9.201 | 0.466 | 0.002 | 5.596 | 10.385 |
| Degree | Betweenness | |||
|---|---|---|---|---|
| Tumor Type | Hub DNA Methylation Sites | Corresponding Gene | Hub DNA Methylation Sites | Corresponding Gene |
| LUSC | Cg25080152 | MYC | Cg08133058 | SASH1 |
| BRCA | Cg24771570 | GRB2 | Cg26383454 | SMIM13 |
| UCEC | Cg14751398 | E2F3 | Cg18776056 | FKBP4 |
| KIRC | Cg08311343 | CDK6 | Cg19858017 | CLSTN1 |
| BLCA | Cg12931157 | NFYA | Cg01473187 | TSPAN6 |
| Degree | Betweenness | |||
|---|---|---|---|---|
| Tumor Type | Single Network | Bilayer Network | Single Network | Bilayer Network |
| LUSC | 55 | 100 | 60 | 100 |
| BRCA | 51 | 100 | 51 | 100 |
| UCEC | 70 | 100 | 63 | 100 |
| KIRC | 63 | 100 | 59 | 100 |
| BLCA | 54 | 100 | 54 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.-J.; Gao, H.-X.; Zhu, L.-C.; Zhu, R. Identifying Tumor-Associated Genes from Bilayer Networks of DNA Methylation Sites and RNAs. Life 2023, 13, 76. https://doi.org/10.3390/life13010076
Xu X-J, Gao H-X, Zhu L-C, Zhu R. Identifying Tumor-Associated Genes from Bilayer Networks of DNA Methylation Sites and RNAs. Life. 2023; 13(1):76. https://doi.org/10.3390/life13010076
Chicago/Turabian StyleXu, Xin-Jian, Hong-Xiang Gao, Liu-Cun Zhu, and Rui Zhu. 2023. "Identifying Tumor-Associated Genes from Bilayer Networks of DNA Methylation Sites and RNAs" Life 13, no. 1: 76. https://doi.org/10.3390/life13010076








