Conformal-Based Surface Morphing and Multi-Scale Representation
Abstract
:1. Introduction
2. Previous Work
3. Mathematical Background
3.1. Conformal Factor and Curvature of a Riemann Surface

3.2. Representation for Surface
4. Methodology
4.1. Multi-Scale Representation of Surfaces
| Algorithm 1: Multi-scale representation of a surface. |
|
4.2. Surface Morphing
| Algorithm 2: Morphing of surfaces. |
|
5. Numerical Algorithms
5.1. Numerical Implementation of the Representation and Surface Reconstruction
5.2. Numerical Implementation of the Multi-Scale Representation of a Surface
5.3. Numerical Implementation of Surface Morphing
6. Experimental Results
6.1. Surface Reconstruction



| Surface | Max L2 error | Mean L2 error | Max (L2/) error |
|---|---|---|---|
| Human face | 3.0033 | 1.0771 | 0.0167 |
| Human face 2 | 2.5706 | 0.7239 | 0.0150 |
| Cortical surface | 2.2157 | 0.5967 | 0.0114 |
| Teeth surface | 0.1189 | 0.0329 | 0.0098 |
| Buddha surface | 8.7897 | 2.1967 | 0.0183 |
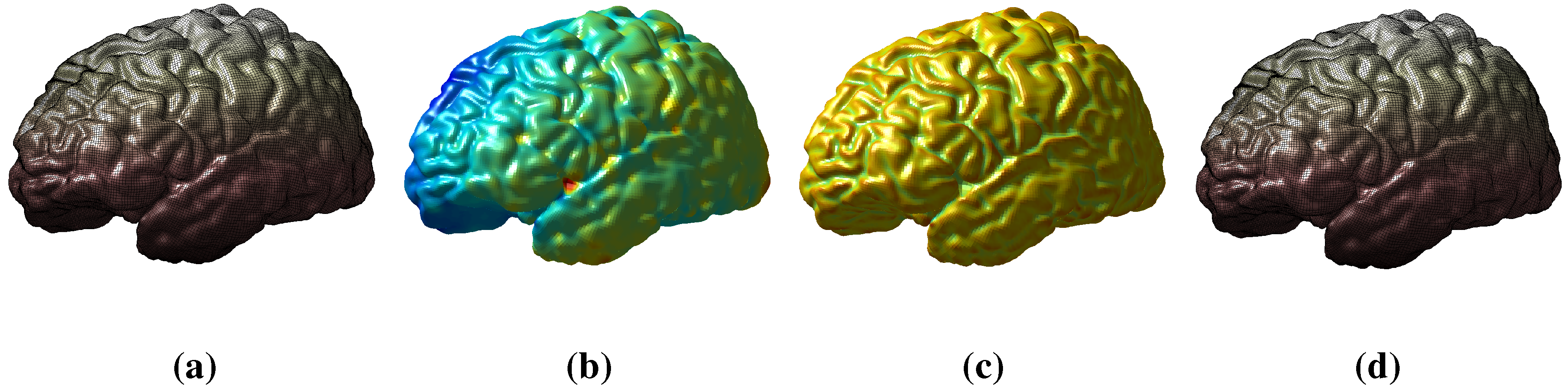
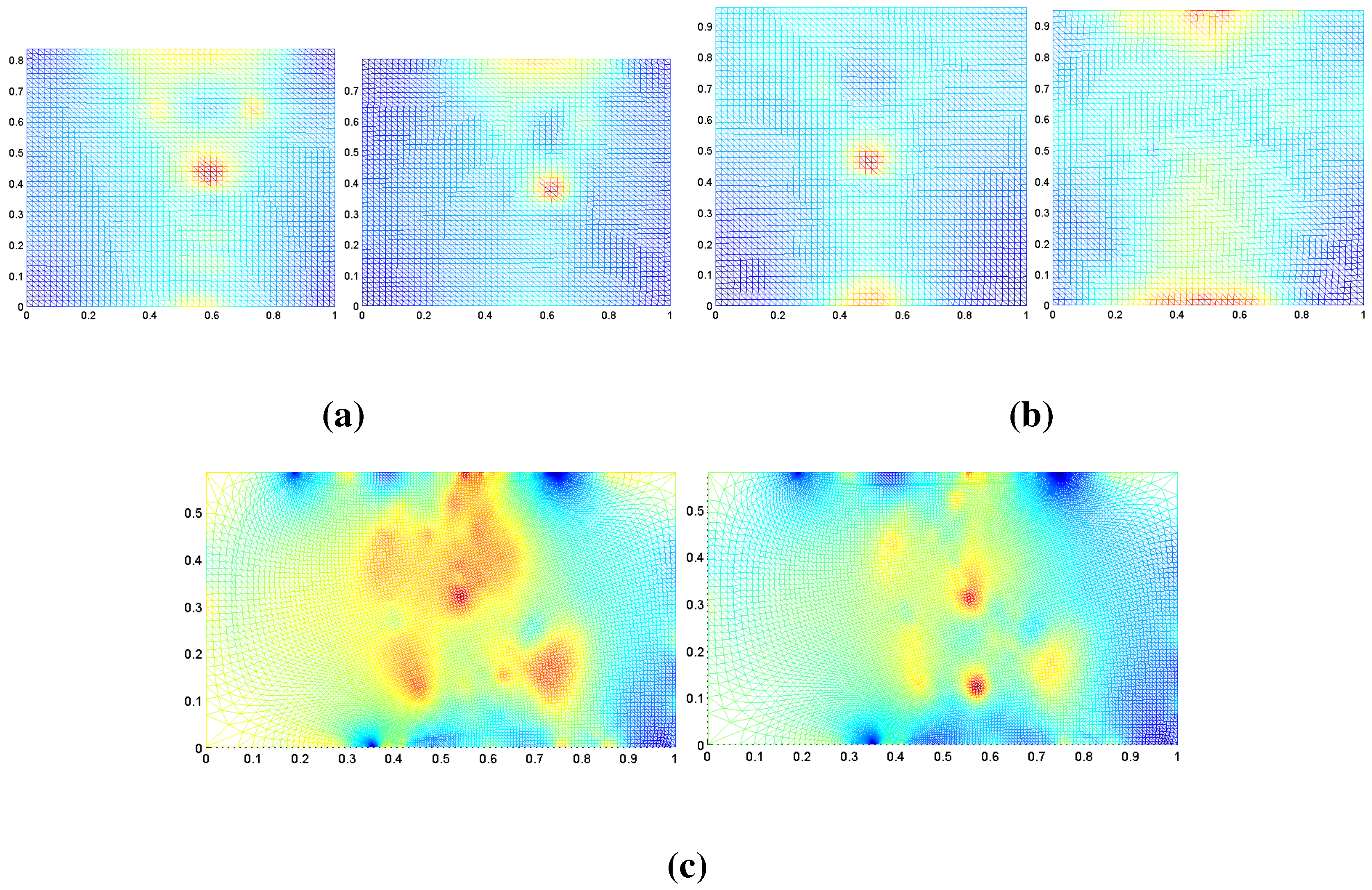
6.2. Multi-Scale Representation of Surfaces
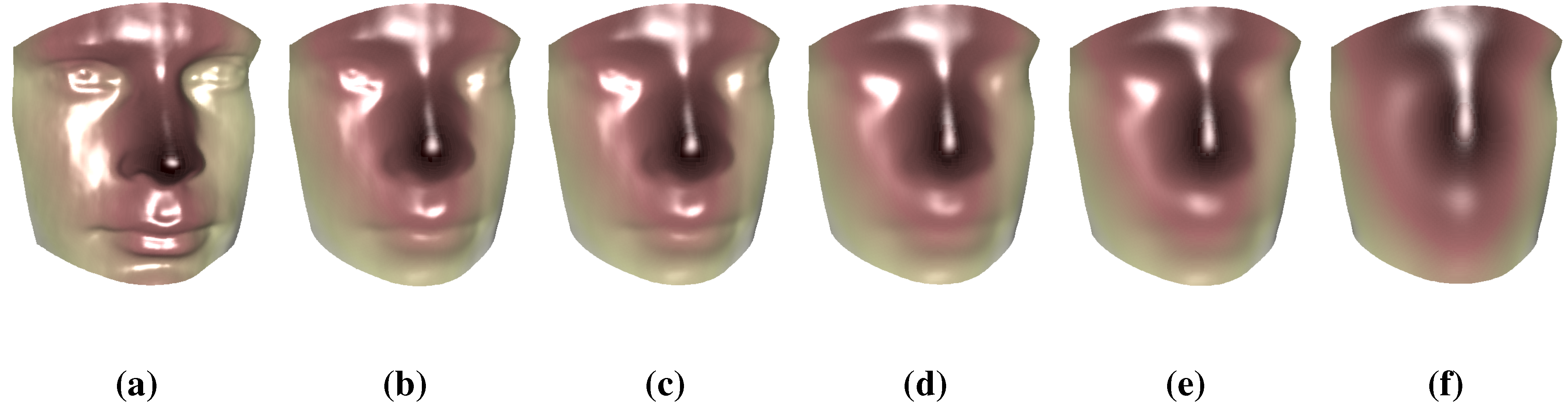

6.3. Surface Morphing
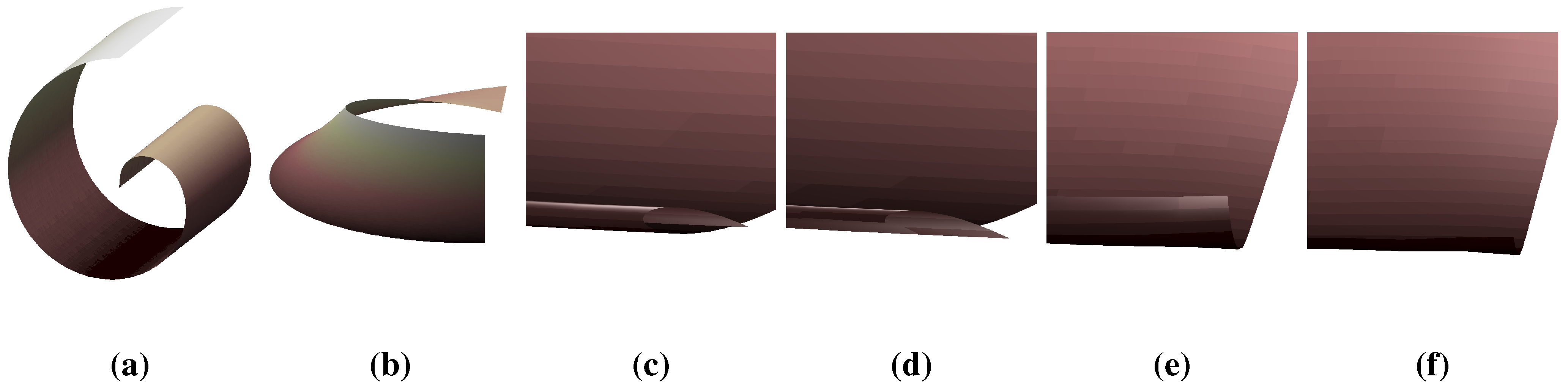

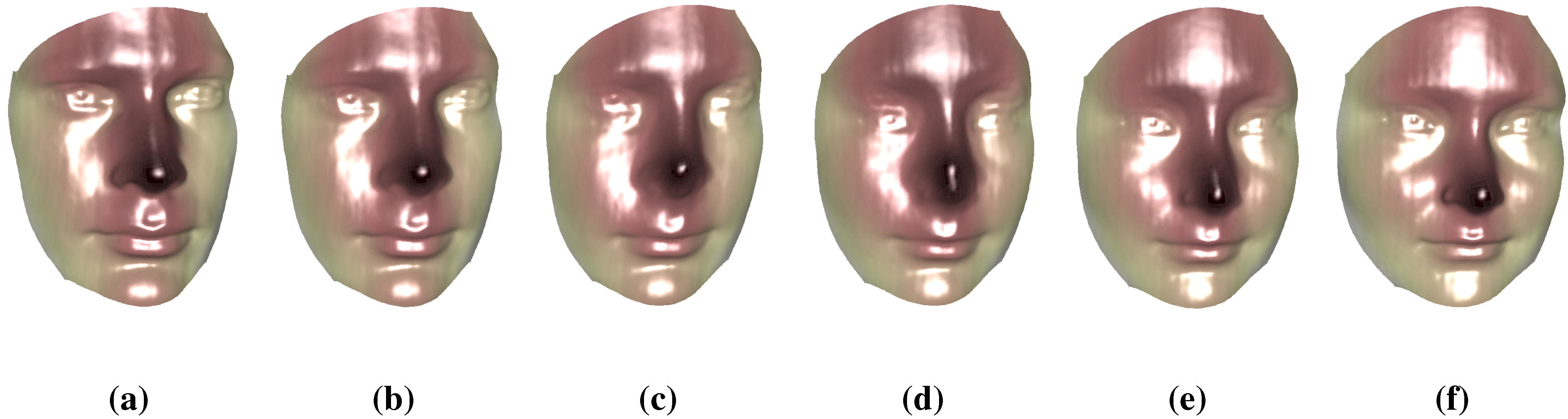
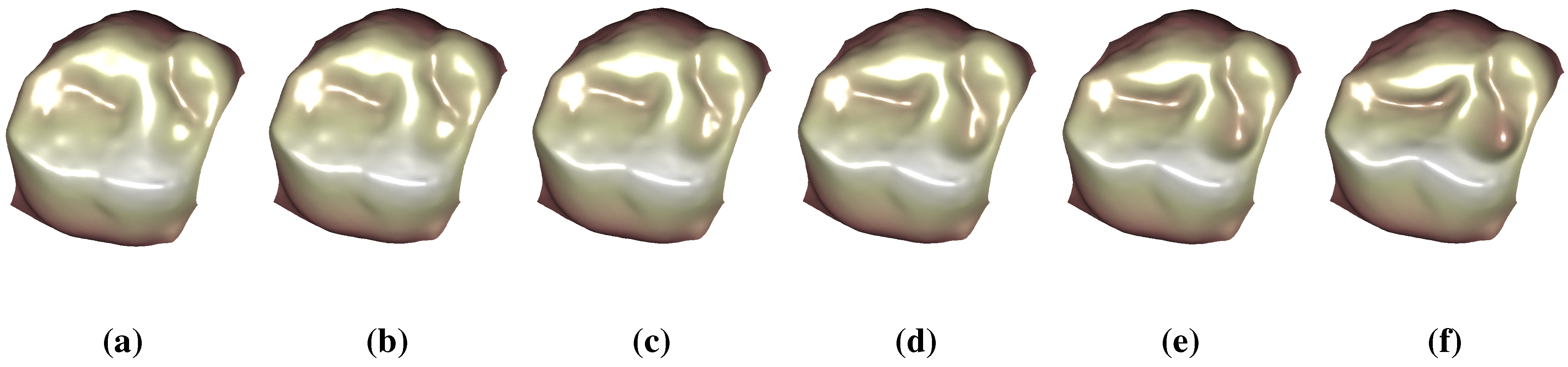

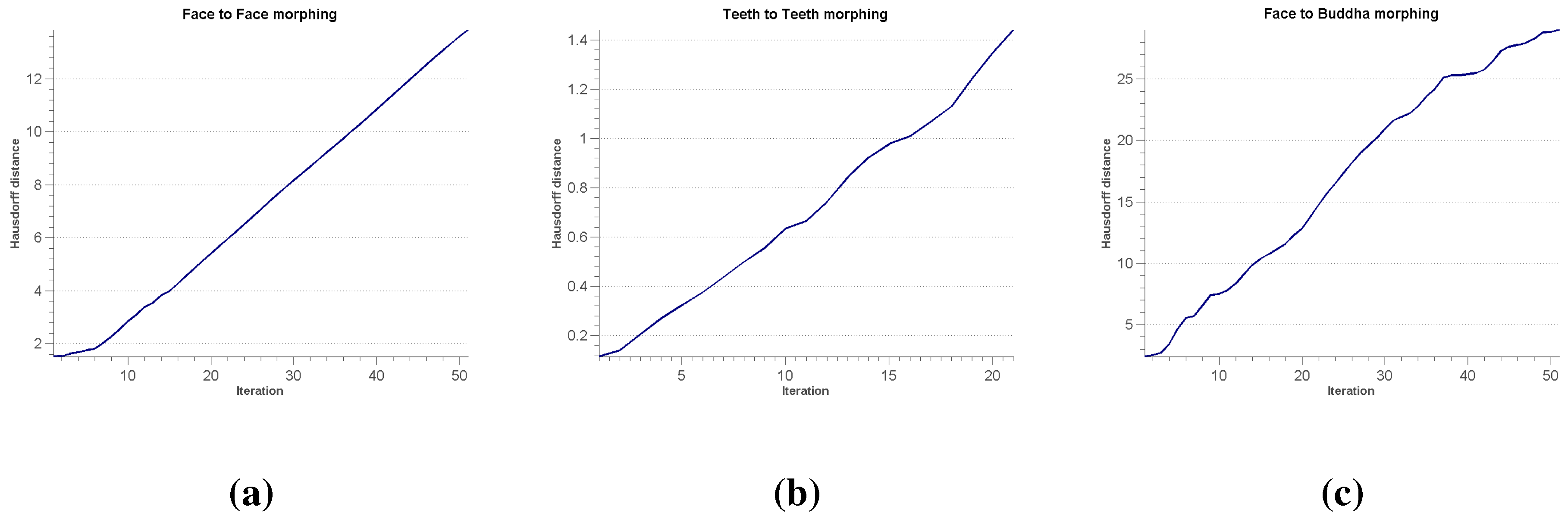
7. Conclusions
Acknowledgments
Conflicts of Interest
References
- Yuen, P.C. Multi-Scale Representation and Recognition of Three Dimensional Surfaces Using Geometric Invariants. Doctoral Dissertation, University of Surrey, Guildford, UK, 2001. [Google Scholar]
- Pauly, M.; Keiser, R.; Gross, M. Multi-scale Feature Extraction on Point Sampled Surfaces. Comput. Graph. Forum 2003, 22, 281–289. [Google Scholar] [CrossRef]
- Fadaifard, H.; Wolberg, G. Multiscale 3D feature extraction and matching. In Proceedings of the 3D Imaging, Modeling, Processing, Visualization and Transmission (3DIMPVT), Hangzhou, China, 16–19 May 2011; pp. 228–235.
- Vaillant, M.; Glaunes, J. Surface matching via currents. In Information Processing in Medical Imaging; Springer: New York, NY, USA, 2005; pp. 381–392. [Google Scholar]
- Yeo, B.T.; Sabuncu, M.R.; Vercauteren, T.; Ayache, N.; Fischl, B.; Golland, P. Spherical demons: Fast diffeomorphic landmark-free surface registration. IEEE Trans. Med. Imaging 2010, 29, 650–668. [Google Scholar] [CrossRef] [PubMed]
- Granger, S.; Pennec, X. Multi-scale EM-ICP: A fast and robust approach for surface registration. Lect. Notes Comput. Sci. 2002, 2353, 418–432. [Google Scholar]
- Risser, L.; Vialard, F.; Wolz, R.; Murgasova, M.; Holm, D.D.; Rueckert, D. Simultaneous multi-scale registration using large deformation diffeomorphic metric mapping. IEEE Trans. Med. Imaging 2011, 30, 1746–1759. [Google Scholar] [CrossRef] [PubMed]
- Kircher, S.; Garland, M. Editing arbitrarily deforming surface animations. ACM Trans. Graph. (TOG) 2006, 25, 1098–1107. [Google Scholar] [CrossRef]
- Gu, X.; Wang, Y.; Chan, T.F.; Thompson, P.M.; Yau, S.T. Genus zero surface conformal mapping and its application to brain surface mapping. In Information Processing in Medical Imaging; Springer: Berlin/Heidelberg, Germany, 2003; pp. 172–184. [Google Scholar]
- Wang, Y.; Lui, L.M.; Gu, X.; Hayashi, K.M.; Chan, T.F.; Toga, A.W.; Yau, S.T. Brain surface conformal parameterization using Riemann surface structure. IEEE Trans. Med. Imaging 2007, 26, 853–865. [Google Scholar] [CrossRef] [PubMed]
- Gu, X.; Yau, S.T. Computing conformal structure of surfaces. Communications in Information and Systems 2002, 2, 121–146. [Google Scholar] [CrossRef]
- Fischl, B.; Sereno, M.I.; Tootell, R.B.; Dale, A.M. High-resolution intersubject averaging and a coordinate system for the cortical surface. Human brain mapping 1999, 8, 272–284. [Google Scholar] [CrossRef]
- Haker, S.; Angenent, S.; Tannenbaum, A.; Kikinis, R.; Sapiro, G.; Halle, M. Conformal surface parameterization for texture mapping. IEEE Trans. Vis. Comput. Graph. 2000, 6, 181–189. [Google Scholar] [CrossRef]
- Hurdal, M.K.; Stephenson, K. Discrete conformal methods for cortical brain flattening. Neuroimage 2009, 45, S86–S98. [Google Scholar] [CrossRef] [PubMed]
- Lévy, B.; Petitjean, S.; Ray, N.; Maillot, J. Least squares conformal maps for automatic texture atlas generation. ACM Trans. Graph. 2002, 21, 362–371. [Google Scholar] [CrossRef]
- Desbrun, M.; Meyer, M.; Alliez, P. Intrinsic parameterizations of surface meshes. In Proceedings of the Eurographics, Saarbruecken, Germany, 2–6 September, 2002; pp. 209–218.
- Lui, L.M.; Wong, T.W.; Zeng, W.; Gu, X.; Thompson, P.M.; Chan, T.F.; Yau, S.T. Optimization of surface registrations using beltrami holomorphic flow. J. Sci. Comput. 2012, 50, 557–585. [Google Scholar] [CrossRef]
- Lui, L.M.; Wong, T.W.; Thompson, P.; Chan, T.; Gu, X.; Yau, S.T. Shape-based diffeomorphic registration on hippocampal surfaces using beltrami holomorphic flow. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention MICCAI, Beijing, China, 20–24 September, 2010; pp. 323–330.
- Khodakovsky, A.; Schroder, P.; Sweldens, W. Progressive geometry compression. In Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques, New Orleans, LA, USA, 23–28 July, 2000; pp. 271–278.
- Peyré, G.; Mallat, S. Surface compression with geometric bandelets. ACM Trans. Graph. (TOG) 2005, 24, 601–608. [Google Scholar] [CrossRef]
- Eck, M.; DeRose, T.; Duchamp, T.; Hoppe, H.; Lounsbery, M.; Stuetzle, W. Multiresolution analysis of arbitrary meshes. In Proceedings of the 22nd Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 6–11 August, 1995; pp. 173–182.
- Gross, M.H.; Hubeli, A. Eigenmeshes. Technical Report. Department of Computer Science, ETH Zurich: Zurich, Switzerland, 2000. [Google Scholar]
- Cipriano, G.; Phillips, G.N.; Gleicher, M. Multi-scale surface descriptors. IEEE Trans. Vis. Comput. Graph. 2009, 15, 1201–1208. [Google Scholar] [CrossRef] [PubMed]
- Ho, H.T.; Gibbins, D. Multi-scale feature extraction for 3D surface registration using local shape variation. In Proceedings of the IEEE 23rd International Conference Image and Vision Computing New Zealand, IVCNZ 2008, Christchurch, New Zealand, 26–28 November, 2008; pp. 1–6.
- Pauly, M.; Kobbelt, L.P.; Gross, M. Point-based multiscale surface representation. ACM Trans. Graph. (TOG) 2006, 25, 177–193. [Google Scholar] [CrossRef]
- Liu, Y.S.; Yan, H.B.; Martin, R.R. As-Rigid-As-Possible Surface Morphing. J. Comput. Sci. Technol. 2011, 26, 548–557. [Google Scholar] [CrossRef]
- Alexa, M.; Cohen-Or, D.; Levin, D. As-rigid-as-possible shape interpolation. In Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques, New Orleans, LA, USA, 23–28 July, 2000; pp. 157–164.
- Kanai, T.; Suzuki, H.; Kimura, F. Three-dimensional geometric metamorphosis based on harmonic maps. Vis. Comput. 1998, 14, 166–176. [Google Scholar] [CrossRef]
- Hojjat, M.; Stavropoulou, E.; Bletzinger, K.U. The vertex morphing method for node-based shape optimization. Comput. Methods Appl. Mech. Eng. 2014, 268, 494–513. [Google Scholar] [CrossRef]
- Rajamani, K.T.; Ballester, M.A.G.; Nolte, L.P.; Styner, M. A novel and stable approach to anatomical structure morphing for enhanced intraoperative 3D visualization. Medical Imaging 2005, 718–725, Proc. SPIE 2005, 5744, 718–725. [Google Scholar]
- Hughes, J.F. Scheduled Fourier volume morphing. In Proceedings of the ACM SIGGRAPH Computer Graphics, Chicago, IL, 27–31 July, 1992; Volume 26, pp. 43–46.
- Turk, G.; O’Brien, J.F. Shape transformation using variational implicit functions. In Proceedings of the ACM SIGGRAPH 2005 Courses, New York, NY, USA, 2–4, August, 2005. [CrossRef]
- Gu, X.; Wang, Y.; Yau, S.T. Geometric compression using Riemann surface structure. Commun. Inf. Syst. 2004, 2, 171–182. [Google Scholar] [CrossRef]
- Lui, L.M.; Wen, C.; Gu, X. A Conformal Approach for Surface Inpainting. AIM Inverse Problems Imaging 2013, 7, 863–884. [Google Scholar]
- Gruen, A.; Akca, D. Least squares 3D surface and curve matching. ISPRS J. Photogramm. Remote Sens. 2005, 59, 151–174. [Google Scholar] [CrossRef]
- Lui, L.M.; Lam, K.C.; Wong, T.W.; Gu, X. Texture map and video compression using Beltrami representation. SIAM J. Imaging Sci. 2013, 6, 1880–1902. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lam, K.C.; Wen, C.; Lui, L.M. Conformal-Based Surface Morphing and Multi-Scale Representation. Axioms 2014, 3, 222-243. https://doi.org/10.3390/axioms3020222
Lam KC, Wen C, Lui LM. Conformal-Based Surface Morphing and Multi-Scale Representation. Axioms. 2014; 3(2):222-243. https://doi.org/10.3390/axioms3020222
Chicago/Turabian StyleLam, Ka Chun, Chengfeng Wen, and Lok Ming Lui. 2014. "Conformal-Based Surface Morphing and Multi-Scale Representation" Axioms 3, no. 2: 222-243. https://doi.org/10.3390/axioms3020222
APA StyleLam, K. C., Wen, C., & Lui, L. M. (2014). Conformal-Based Surface Morphing and Multi-Scale Representation. Axioms, 3(2), 222-243. https://doi.org/10.3390/axioms3020222




