Characteristic Number: Theory and Its Application to Shape Analysis
Abstract
:1. Introduction
2. Characteristic Number
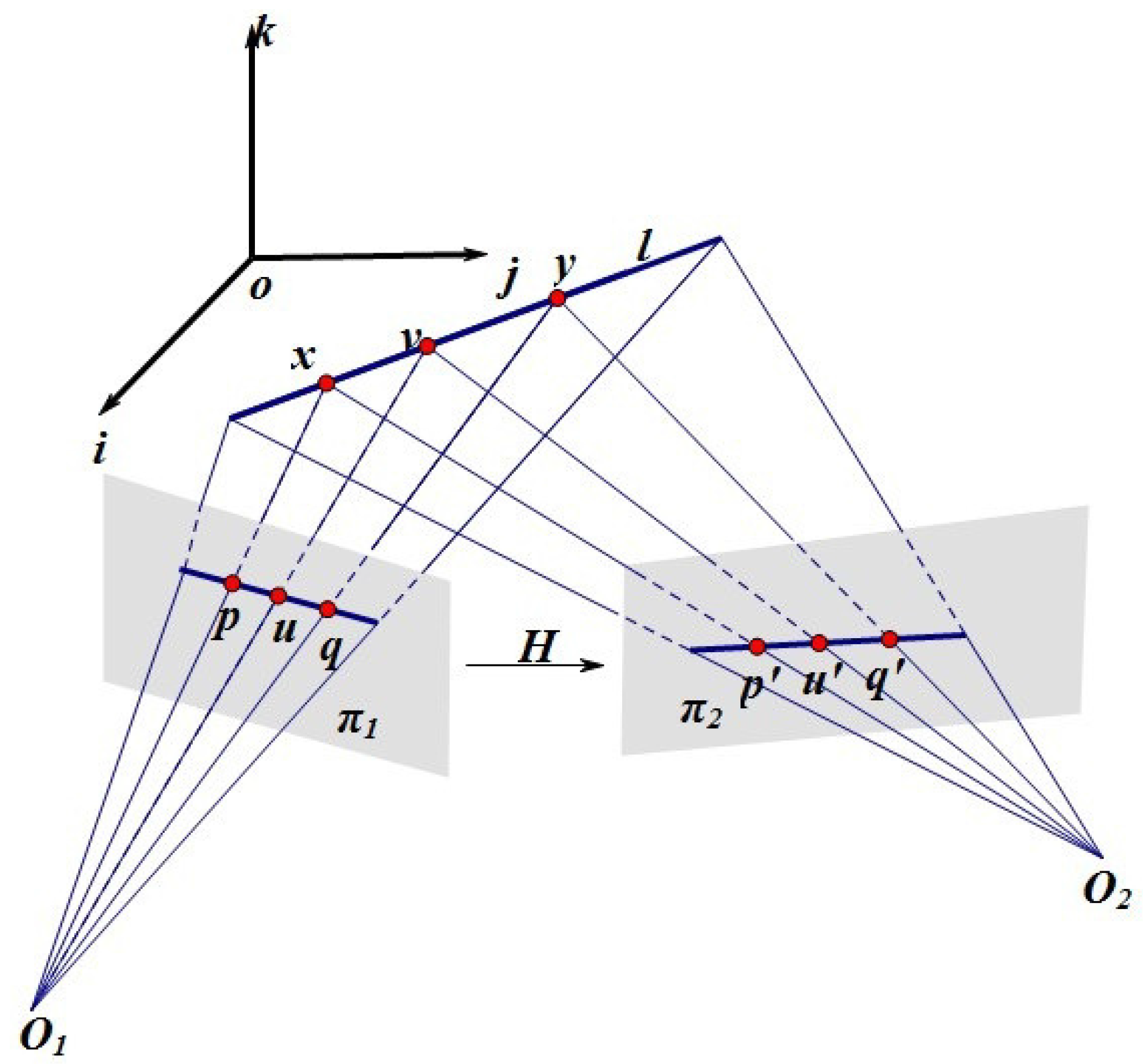
2.1. Characteristic Ratio: An Affine Invariant
2.2. Characteristic Number: A Projective Invariant
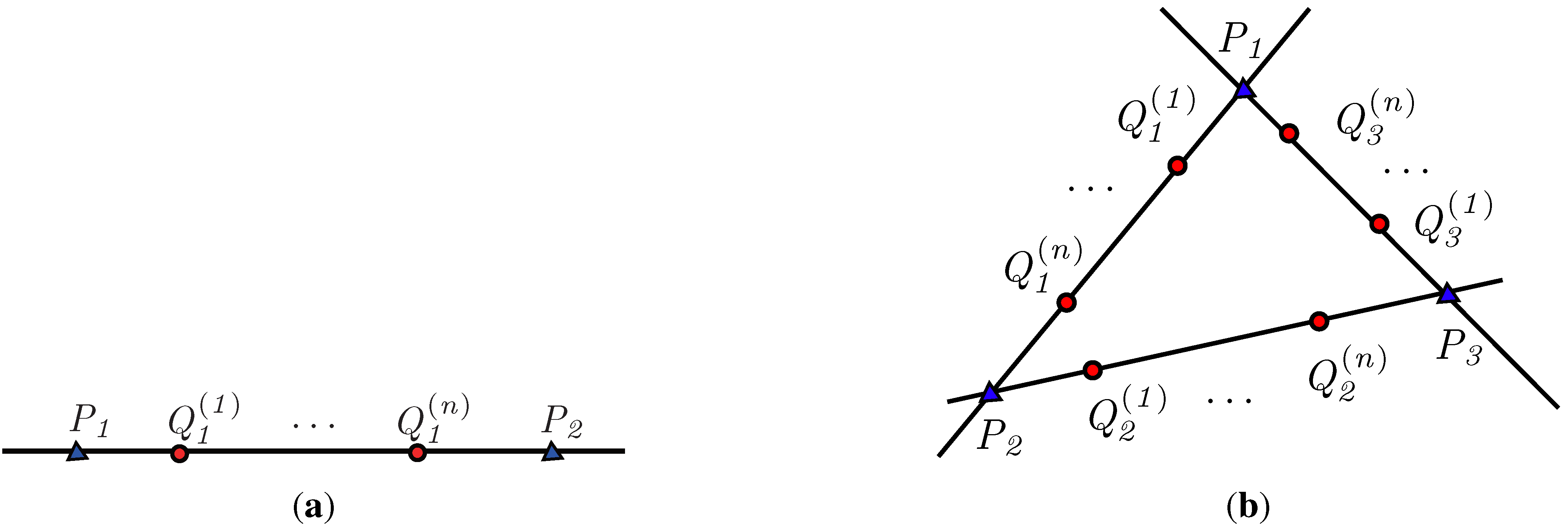
2.3. Intrinsic Properties of a Hypersurface and Curve

2.4. Generalization of Pascal’s Theorem
3. Application I: A Perspective Invariant Shape Descriptor

3.1. Descriptor Construction

- if there are at least two intersections on both sides, and .
- (or ) if there are at least two intersections on the side, (or ), and no more than one intersection on the side, (or ).
- if there is at most one intersection on either or .
- The characteristic number on a triangle is permutable, i.e., . This can be be readily verified by Equation (8).
- The choice of initial point (triangle) does not change individual values in , but determines the order in which CN values appear in . It is also straightforward to derive this property from the above and Equation (10).
- Slight fluctuations of the vertices on the convex hull of bring gradual changes on . It is assumed that three pairs of points, (, ), (, ) and (, ), are neighbors on the smooth part of convex hull. We have , since each side of the triangles to calculate CN values is also close to each other.
- The descriptor presents fluctuations in the case of affine transformations due to jags on the inner intersections. Severe perspective deformations would make it worse. A dynamic programming algorithm, i.e., dynamic time warping (DTW), is employed to align the shape descriptors of query and template shapes, as done in CRS and CHARS. This process can alleviate the deviations brought by the choice of the starting point.
3.2. Performance Evaluation

| CNF | CRS | SIFT | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| az | ||||||||||||
| 43.75 | 50 | 50 | 59.38 | 50 | 62.5 | 46.88 | 46.88 | 6.25 | 9.38 | 6.25 | 15.63 | |
| 93.75 | 100 | 96.88 | 96.88 | 87.5 | 84.38 | 87.5 | 87.5 | 28.13 | 65.63 | 53.13 | 25 | |
| 100 | 100 | 100 | 100 | 93.75 | 90.63 | 90.63 | 87.5 | 12.5 | 71.88 | 71.88 | 21.88 | |
| 71.88 | 75 | 87.5 | 75 | 68.75 | 84.38 | 84.38 | 68.75 | 6.25 | 18.75 | 25 | 3.13 | |
| CNF | CRS | SIFT | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| az | ||||||||||||
| 37.5 | 62.5 | 43.75 | 50 | 53.13 | 53.13 | 34.38 | 34.38 | 6.25 | 6.25 | 0 | 6.25 | |
| 90.63 | 100 | 100 | 78.13 | 84.38 | 84.38 | 81.25 | 75 | 12.5 | 31.25 | 25 | 9.38 | |
| 96.88 | 100 | 93.75 | 87.5 | 87.5 | 90.63 | 87.5 | 71.88 | 18.75 | 46.88 | 40.63 | 9.38 | |
| 56.25 | 75 | 62.5 | 53.13 | 75 | 78.13 | 65.63 | 65.63 | 12.5 | 12.5 | 12.5 | 15.63 | |
| CNF | CRS | SIFT | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| az | ||||||||||||
| 31.25 | 31.25 | 37.5 | 31.25 | 40.63 | 50 | 34.38 | 21.88 | 6.25 | 9.38 | 6.25 | 15.63 | |
| 87.5 | 84.38 | 84.38 | 62.5 | 87.5 | 78.13 | 78.13 | 59.38 | 28.13 | 65.63 | 53.13 | 25 | |
| 87.5 | 93.75 | 90.63 | 75 | 78.13 | 87.5 | 81.25 | 71.88 | 12.5 | 68.75 | 68.75 | 21.88 | |
| 43.75 | 62.5 | 53.13 | 46.88 | 65.13 | 68.75 | 62.5 | 56.25 | 6.25 | 18.75 | 25 | 3.13 | |
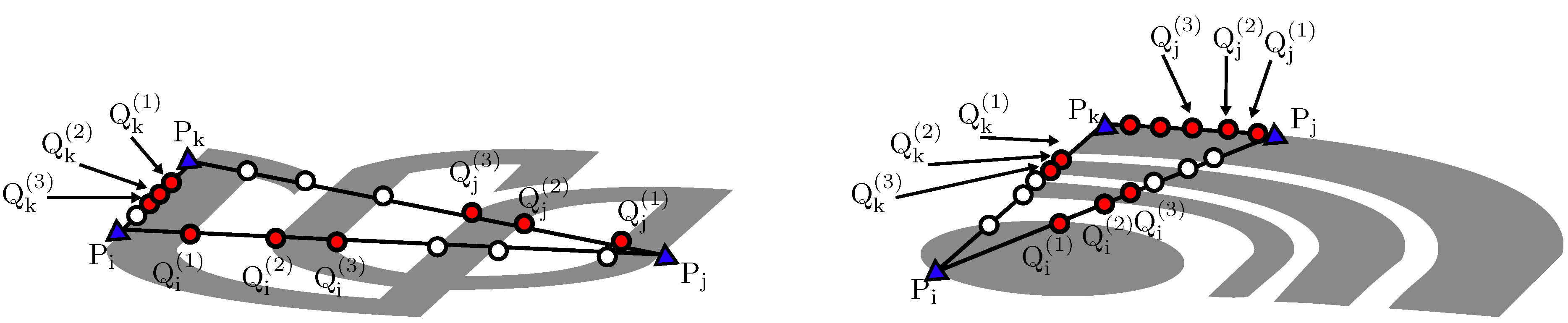
4. Application III: Shape Matching with Characteristic Number
4.1. Shape Priors Using Characteristic Number

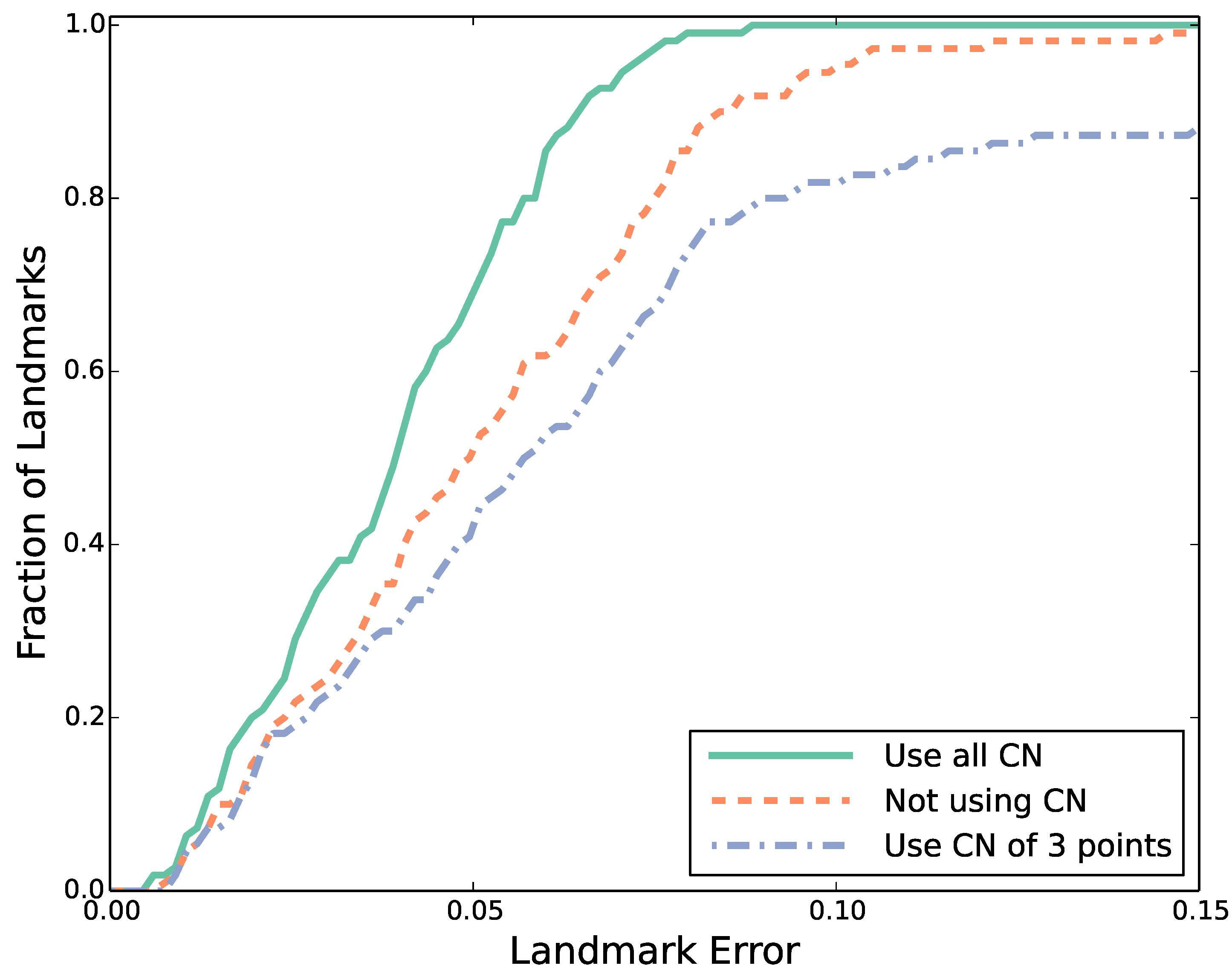
4.2. Performance Evaluation

5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Weiss, I. Geometric invariants and object recognition. Int. J. Comput. Vis. 1993, 10, 207–231. [Google Scholar] [CrossRef]
- Lin, W.Y. Robust Geometrically Invariant Features for 2D Shape Matching and 3D Face Recognition. Ph.D. Thesis, University of Wisconsin-Madson, Madison, WI, USA, 2006. [Google Scholar]
- Goodall, C.R.; Mardia, K.V. Projective shape analysis. J. Comput. Graph. Stat. 1999, 8, 143–168. [Google Scholar]
- Suk, T.; Flusser, J. Point-based projective invariants. Pattern Recognit. 2000, 33, 251–261. [Google Scholar] [CrossRef]
- Quan, L.; Gros, P.; Mohr, R. Invariants of a pair of conics revisited. Image Vis. Comput. 1992, 10, 319–323. [Google Scholar] [CrossRef]
- Li, L.; Tan, C. Recognizing planar symbols with severe perspective deformation. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 755–762. [Google Scholar] [PubMed]
- Luo, Z.; Luo, D.; Fan, X.; Zhou, X.; Jia, Q. A shape descriptor based on new projective invariants. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Melbourne, Australia, 15–18 September 2013.
- Li, W.J.; Lee, T.; Tsui, H.T. Automatic feature matching using coplanar projective invariants for object recognition. In Proceedings of the 5th Asian Conference on Computer Vision (ACCV), Melbourne, Australia, 23–25 January 2002.
- Fan, B.; Wu, F.; Hu, Z. Robust line matching through line–point invariants. Pattern Recognit. 2012, 45, 794–805. [Google Scholar] [CrossRef]
- Yammine, G.; Wige, E.; Simmet, F.; Niederkorn, D.; Kaup, A. A novel similarity-invariant line descriptor for for geometric map registration. In Proceedings of the 20th IEEE International Conference on Image Processing (ICIP), Melbourne, Australia, 15–18 September 2013.
- Fan, X.; Qi, C.; Liang, D.; Huang, H. Probabilistic contour extraction using hierarchical shape representation. In Proceedings of the Tenth IEEE International Conference on Computer Vision (ICCV), Beijing, China, 17–21 October 2005; Volume 1, pp. 302–308.
- Wang, Z.; Liang, M.; Li, Y. Using diagonals of orthogonal projection matrices for affine invariant contour matching. Image Vis. Comput. 2011, 29, 681–692. [Google Scholar] [CrossRef]
- Bryner, D.; Klassen, E.; Le, H.; Srivastava, A. 2D affine and projective shape analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 99. [Google Scholar] [CrossRef] [PubMed]
- Riccio, D.; Dugelay, J.L. Geometric invariants for 2D/3D face recognition. Pattern Recogni. Lett. 2007, 28, 1907–1914. [Google Scholar] [CrossRef]
- Wang, R. Multivariate Spline Functions and their Applications; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Shi, X.; Wang, R. The generalization of Pascal’s theorem and Morgan-Scott’s partition. Comput. Geom.: Lect. Morningside Center Math. 2003, 34, 179–187. [Google Scholar]
- Luo, Z.; Chen, L. The singularity of . J. Inf. Comput. Sci. 2005, 4, 739–746. [Google Scholar]
- Luo, Z.; Liu, F.; Shi, X. On singularity of spline space over Morgan-Scott’s type partition. J. Math. Res. Expo. 2010, 30, 1–16. [Google Scholar]
- Thas, J.; Cameron, P.; Blokhuis, A. On a generalization of a theorem of B. Segre. Geom. Dedicata 1992, 43, 299–305. [Google Scholar] [CrossRef]
- Luo, Z.; Zhou, X.; Gu, D.X. From a projective invariant to some new properties of algebraic hypersurfaces. Sci. China Math. 2014, in press. [Google Scholar] [CrossRef]
- Jia, Q.; Fan, X.; Luo, Z.; Liu, Y.; Guo, H. A new geometric descriptor for symbols with affine deformations. Pattern Recognit. Lett. 2014, 40, 128–135. [Google Scholar] [CrossRef]
- Lowe, D. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Srestasathiern, P.; Yilmaz, A. Planar shape representation and matching under projective transportation. Comput. Vis. Image Underst. 2011, 115, 1525–1535. [Google Scholar] [CrossRef]
- Cootes, T.F.; Taylor, C.J.; Cooper, D.H.; Graham, J. Active shape models—Their training and application. Comput. Vis. Image Underst. 1995, 61, 38–59. [Google Scholar] [CrossRef]
- Cootes, T.F.; Edwards, G.J.; Taylor, C.J. Active appearance models. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 681–685. [Google Scholar] [CrossRef]
- Gee, A.; Cipolla, R. Estimating gaze from a single view of a face. In Proceedings of the 12th IAPR International Conference on Pattern Recognition, Conference A: Computer Vision and AMP, Image Processing, Jerusalem, Palestine, 9–13 October 1994; Volume 1, pp. 758–760.
- Viola, P.; Jones, M.J. Robust real-time face detection. Int. J. Comput. Vis. 2004, 57, 137–154. [Google Scholar] [CrossRef]
- Stegmann, M.; Ersbll, B.; Larsen, R. FAME-a flexible appearance modeling environment. IEEE Trans. Med. Imaging 2003, 22, 1319–1331. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.B.; Ramesh, M.; Berg, T.; Learned-Miller, E. Labeled Faces in the Wild: A Database for Studying Face Recognition in Unconstrained Environments; Technical Report 07-49; University of Massachusetts: Amherst, MA, USA, 2007. [Google Scholar]
- Koestinger, M.; Wohlhart, P.; Roth, P.M.; Bischof, H. Annotated facial landmarks in the wild: A large-scale, real-world database for facial landmark localization. In Proceedings of the First IEEE International Workshop on Benchmarking Facial Image Analysis Technologies, Barcelona, Spain, 6–13 November 2011.
- Gourier, N.; Hall, D.; Crowley, J.L. Estimating face orientation from robust detection of salient facial structures. In Proceedings of the International Workshop on Visual Observation of Deictic Gestures, Cambridge, UK, 23–26 August 2004; pp. 1–9.
- Dibeklioglu, H.; Salah, A.; Gevers, T. A statistical method for 2-D facial landmarking. IEEE Trans. Image Process. 2012, 21, 844–858. [Google Scholar] [CrossRef] [PubMed]
- Cao, X.; Wei, Y.; Wen, F.; Sun, J. Face alignment by explicit shape regression. In Proceedings of the IEEE Conference on Biometrics Compendium Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012; pp. 2887–2894.
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Fan, X.; Luo, Z.; Zhang, J.; Zhou, X.; Jia, Q.; Luo, D. Characteristic Number: Theory and Its Application to Shape Analysis. Axioms 2014, 3, 202-221. https://doi.org/10.3390/axioms3020202
Fan X, Luo Z, Zhang J, Zhou X, Jia Q, Luo D. Characteristic Number: Theory and Its Application to Shape Analysis. Axioms. 2014; 3(2):202-221. https://doi.org/10.3390/axioms3020202
Chicago/Turabian StyleFan, Xin, Zhongxuan Luo, Jielin Zhang, Xinchen Zhou, Qi Jia, and Daiyun Luo. 2014. "Characteristic Number: Theory and Its Application to Shape Analysis" Axioms 3, no. 2: 202-221. https://doi.org/10.3390/axioms3020202
APA StyleFan, X., Luo, Z., Zhang, J., Zhou, X., Jia, Q., & Luo, D. (2014). Characteristic Number: Theory and Its Application to Shape Analysis. Axioms, 3(2), 202-221. https://doi.org/10.3390/axioms3020202




