Hopf Algebra Symmetries of an Integrable Hamiltonian for Anyonic Pairing
Abstract
:1. Introduction
 , deformations of the universal enveloping algebras of a Lie algebra g, which have the structure of a quasi-triangular Hopf algebra. The significance of the quasi-triangular structure is that it affords an algebraic solution of the Yang–Baxter equation. Matrix solutions of the Yang–Baxter equation are then generated through representations of these algebras. The simplest example of the two-dimensional loop representation of the untwisted affine quantum algebra
, deformations of the universal enveloping algebras of a Lie algebra g, which have the structure of a quasi-triangular Hopf algebra. The significance of the quasi-triangular structure is that it affords an algebraic solution of the Yang–Baxter equation. Matrix solutions of the Yang–Baxter equation are then generated through representations of these algebras. The simplest example of the two-dimensional loop representation of the untwisted affine quantum algebra  leads to the six-vertex model solution of the Yang–Baxter equation, which establishes integrability of the anisotropic (XXZ) Heisenberg chain. The precise form of six-vertex solution obtained depends on the choice of gradation for
leads to the six-vertex model solution of the Yang–Baxter equation, which establishes integrability of the anisotropic (XXZ) Heisenberg chain. The precise form of six-vertex solution obtained depends on the choice of gradation for  . The principal gradation leads to the symmetric solution, while the homogeneous gradation leads to an asymmetric solution [11]. Only in the latter case is the solution invariant with respect to the action of the non-affine subalgebra
. The principal gradation leads to the symmetric solution, while the homogeneous gradation leads to an asymmetric solution [11]. Only in the latter case is the solution invariant with respect to the action of the non-affine subalgebra  .
.2. The Integrable Hamiltonian for Anyonic Pairing
 of dimension 4L, given by
of dimension 4L, given by 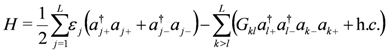
 represent single-particle energy levels (two-fold denegerate labelled by
represent single-particle energy levels (two-fold denegerate labelled by  ) and
) and  are the pairing interaction coupling parameters of the model. For
are the pairing interaction coupling parameters of the model. For  the operators
the operators  satisfy the relations
satisfy the relations 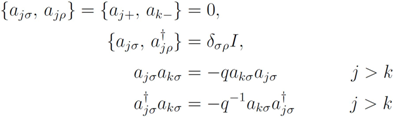
 . The anyonic creation and annihilation operators may be realised in terms of the canonical fermionic operators
. The anyonic creation and annihilation operators may be realised in terms of the canonical fermionic operators  through a generalised Jordan–Wigner transformation
through a generalised Jordan–Wigner transformation 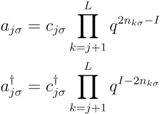
 .
.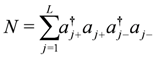
 are introduced with the following constraints imposed:
are introduced with the following constraints imposed: 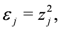
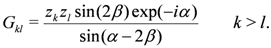
 is constructed as
is constructed as 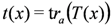
 is the partial trace over an auxiliary space labelled by a. The monodromy matrix is required to satisfy the relation
is the partial trace over an auxiliary space labelled by a. The monodromy matrix is required to satisfy the relation 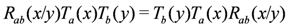
 , with the two auxiliary spaces labelled by a and b. Above,
, with the two auxiliary spaces labelled by a and b. Above, 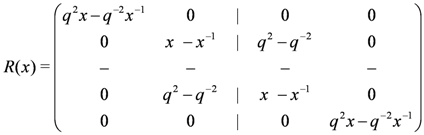
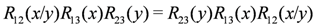
 . The subscripts above refer to the spaces on which the operators act, e.g.,
. The subscripts above refer to the spaces on which the operators act, e.g., 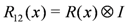
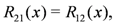
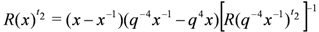
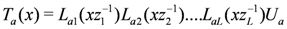

 . Bearing in mind the earlier comments regarding the blocking effect, we may write
. Bearing in mind the earlier comments regarding the blocking effect, we may write 
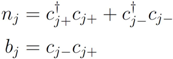

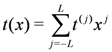

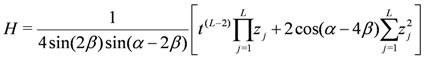
 provides a set of Abelian conserved operators for the system. In this sense the system is said to be integrable.
provides a set of Abelian conserved operators for the system. In this sense the system is said to be integrable. structure, but are realised through the Drinfel’d doubles of dihedral group algebras.
structure, but are realised through the Drinfel’d doubles of dihedral group algebras.3. Drinfel’d Doubles of Dihedral Group Algebras
 satisfying:
satisfying: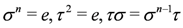

 are their dual elements. This gives an algebra of dimension 4n2. Multiplication of dual elements is defined by
are their dual elements. This gives an algebra of dimension 4n2. Multiplication of dual elements is defined by 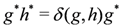
 is the Kronecker delta function. The products
is the Kronecker delta function. The products  are computed using
are computed using 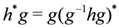
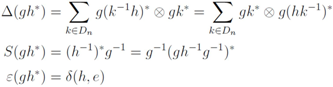
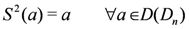
 the universal R-matrix is given by
the universal R-matrix is given by 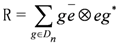
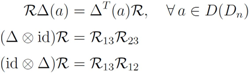
 is the opposite coproduct
is the opposite coproduct 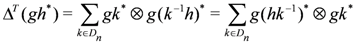
 two-dimensional irreducible representations, and eight
two-dimensional irreducible representations, and eight  -dimensional irreducible representations. When n is odd, D(Dn) admits two one-dimensional irreducible representations,
-dimensional irreducible representations. When n is odd, D(Dn) admits two one-dimensional irreducible representations,  two-dimensional irreducible representations, and two n-dimensional irreducible representations. The explicit irreducible representations are given in [14]. Our interest will be in the two-dimensional irreducible representations. To describe them, let
two-dimensional irreducible representations, and two n-dimensional irreducible representations. The explicit irreducible representations are given in [14]. Our interest will be in the two-dimensional irreducible representations. To describe them, let  . Then these representations have the form
. Then these representations have the form
 if n is even and
if n is even and  if n is odd,
if n is odd,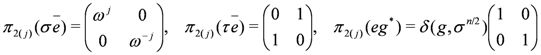
 if n is even, and
if n is even, and
 and where
and where  if n is even, and
if n is even, and  if n is odd.
if n is odd. the tensor product representation applied to the universal R-matrix Equation (18) yields the general form
the tensor product representation applied to the universal R-matrix Equation (18) yields the general form 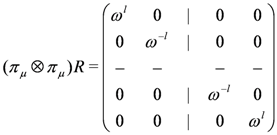
 . Choosing
. Choosing  in Equation (6) we then find
in Equation (6) we then find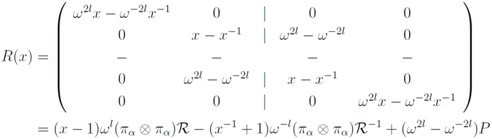
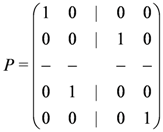
4. Symmetries of the Transfer Matrix and Hamiltonian
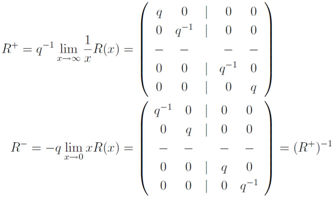
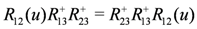
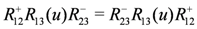
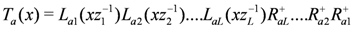
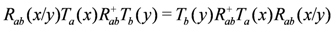
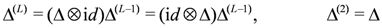
 when dealing with tensor product representations obtained through this action. Whenever we have
when dealing with tensor product representations obtained through this action. Whenever we have 
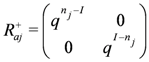
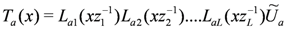
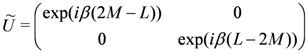
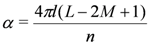
 acts as a particle-hole transformation:
acts as a particle-hole transformation: 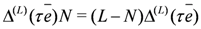
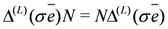

 and
and  are always diagonal in the basis in which the action of N is diagonal. In the same basis, representations of
are always diagonal in the basis in which the action of N is diagonal. In the same basis, representations of  are orthogonal matrices with non-zero off-diagonal entries.
are orthogonal matrices with non-zero off-diagonal entries.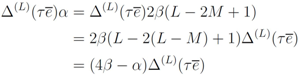
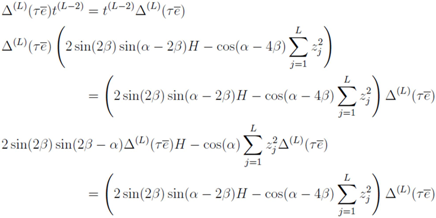
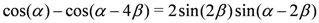
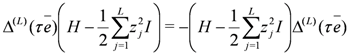
 induced by Equation (28). On the other hand,
induced by Equation (28). On the other hand, 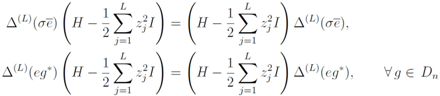
 and
and  leaves the spectrum of the Hamiltonian invariant in each sector with fixed M.
leaves the spectrum of the Hamiltonian invariant in each sector with fixed M.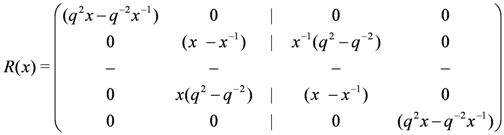
5. Conclusions
Acknowledgments
References
- Bethe, H. Zur Theorie der Metalle: I. Eigenwerte und Eigenfunktionen der linearen Atomkette. Zeitschrift für. Physik 1931, 71, 205–226. [Google Scholar] [CrossRef]
- Lieb, E.H.; Liniger, W. Exact analysis of an interacting Bose gas. I. The general solution and the ground state. Phys. Rev. 1963, 130, 1605–1616. [Google Scholar] [CrossRef]
- Yang, C.N. Some exact results for the many-body problem in one dimension with repulsive delta-function interaction. Phys. Rev. Lett. 1967, 19, 1312–1315. [Google Scholar] [CrossRef]
- Richardson, R.W. A restricted class of exact eigenstates of the pairing-force Hamiltonian. Phys. Lett. 1963, 3, 277–279. [Google Scholar] [CrossRef]
- Lieb, E.H.; Wu, F.Y. Absence of Mott transition in an exact solution of the short-range, one-band model in one dimension. Phys. Rev. Lett. 1968, 20, 1445–1448. [Google Scholar] [CrossRef]
- Takhtadzhan, L.A.; Faddeev, L.D. The quantum method of the inverse problem and the Heisenberg XYZ model. Russ. Math. Surveys 1979, 34, 11–68. [Google Scholar] [CrossRef]
- McGuire, J.B. Study of exactly soluble one-dimensional N-body problems. J. Math. Phys. 1964, 5, 622–636. [Google Scholar] [CrossRef]
- Baxter, R.J. Partition function of the eight-vertex lattice model. Ann. Phys. 1972, 70, 193–228. [Google Scholar] [CrossRef]
- Jimbo, M. A q-difference analog of U(g) and the Yang–Baxter equation. Lett. Math. Phys. 1985, 10, 63–69. [Google Scholar] [CrossRef]
- Drinfel’d, V.G. Quantum Groups. In Proceedings of the International Congress of Mathematicians; Gleason, A.M., Ed.; American Mathematical Society: Providence, Rhode Island, 1986; pp. 798–820. [Google Scholar]
- Bracken, A.J.; Delius, G.W.; Gould, M.D.; Zhang, Y.-Z. Infinite families of gauge equivalent R-matrices and gradations of quantized affine algebras. Int. J. Mod. Phys. B 1994, 8, 3679–3691. [Google Scholar] [CrossRef]
- Gould, M.D. Quantum double finite group algebras and their representations. Bull. Aust. Math. Soc. 1993, 48, 275–301. [Google Scholar] [CrossRef]
- Kitaev, A.Y. Fault-Tolerant quantum computation by anyons. Ann. Phys. 2003, 303, 2–30. [Google Scholar] [CrossRef]
- Dancer, K.A.; Isaac, P.; Links, J. Representations of the quantum doubles of finite group algebras and spectral parameter dependent solutions of the Yang–Baxter equation. J. Math. Phys. 2006, 47, 1–18. [Google Scholar]
- Finch, P.E.; Dancer, K.A.; Isaac, P.; Links, J. Solutions of the Yang–Baxter equation: Descendents of the six-vertex model from the Drinfeld doubles of dihedral group algebras. Nucl. Phys. B 2011, 847, 387–412. [Google Scholar] [CrossRef]
- Finch, P.E. Integrable Hamiltonians with D(Dn) symmetry from the Fateev-Zamolodchikov model. J. Stat. Mech. Theory Exp. 2011. [Google Scholar] [CrossRef]
- Dunning, C.; Ibañez, M.; Links, J.; Sierra, G.; Zhao, S.-Y. Exact solution of the p + ip pairing Hamiltonian and a hierarchy of integrable models. J. Stat. Mech. Theory Exp. 2010. [Google Scholar] [CrossRef]
- Links, J.; Foerster, A. On the construction of integrable closed chains with quantum supersymmetry. J. Phys. A Math. Gen. 1997, 30, 2483–2487. [Google Scholar] [CrossRef]
- Links, J.R.; Gould, M.D. Casimir invariants for Hopf algebras. Rep. Math. Phys. 1992, 31, 91–111. [Google Scholar] [CrossRef]
- Grosse, H.; Pallua, S.; Prester, P.; Raschhofer, E. On a quantum group invariant spin chain with non-local boundary conditions. J. Phys. A Math. Gen. 1994, 27, 4761–4771. [Google Scholar] [CrossRef]
- Karowski, M.; Zapletal, A. Quantum group invariant integrable n-state vertex models with periodic boundary conditions. Nucl. Phys. 1994, 419, 567–588. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Links, J. Hopf Algebra Symmetries of an Integrable Hamiltonian for Anyonic Pairing. Axioms 2012, 1, 226-237. https://doi.org/10.3390/axioms1020226
Links J. Hopf Algebra Symmetries of an Integrable Hamiltonian for Anyonic Pairing. Axioms. 2012; 1(2):226-237. https://doi.org/10.3390/axioms1020226
Chicago/Turabian StyleLinks, Jon. 2012. "Hopf Algebra Symmetries of an Integrable Hamiltonian for Anyonic Pairing" Axioms 1, no. 2: 226-237. https://doi.org/10.3390/axioms1020226




