Molecularly-Limited Fractal Surface Area of Mineral Powders
Abstract
:1. Introduction
1.1. Powders
1.2. Particle Size Distribution
1.3. Surface Fractal Topography
2. Methods
3. Results and Discussion
3.1. Shape Factor and Particle Shape Approximation
3.2. Size Distribution of the Powder Particles
3.3. Determination of the Specific Surface Area (SSA)
3.4. Useful Equations
3.5. Determination of the Surface Fractal Dimension D
3.6. Uncertainty Computation
3.7. Incorrect Use of Fractal Theory for the SSA Evaluation
3.8. Transformation of the SSA Value after the BET Measurement for a New Adsorbate
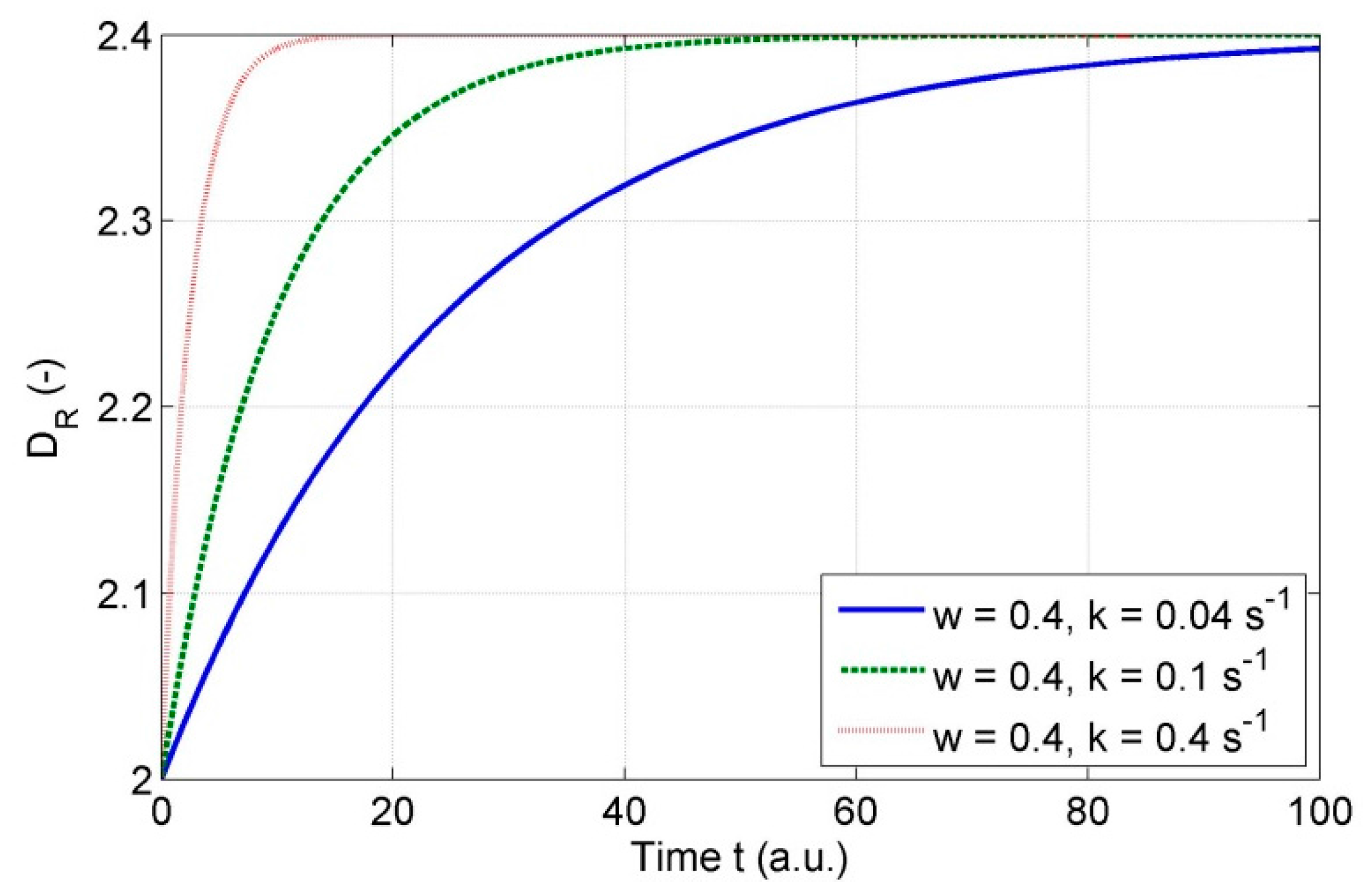
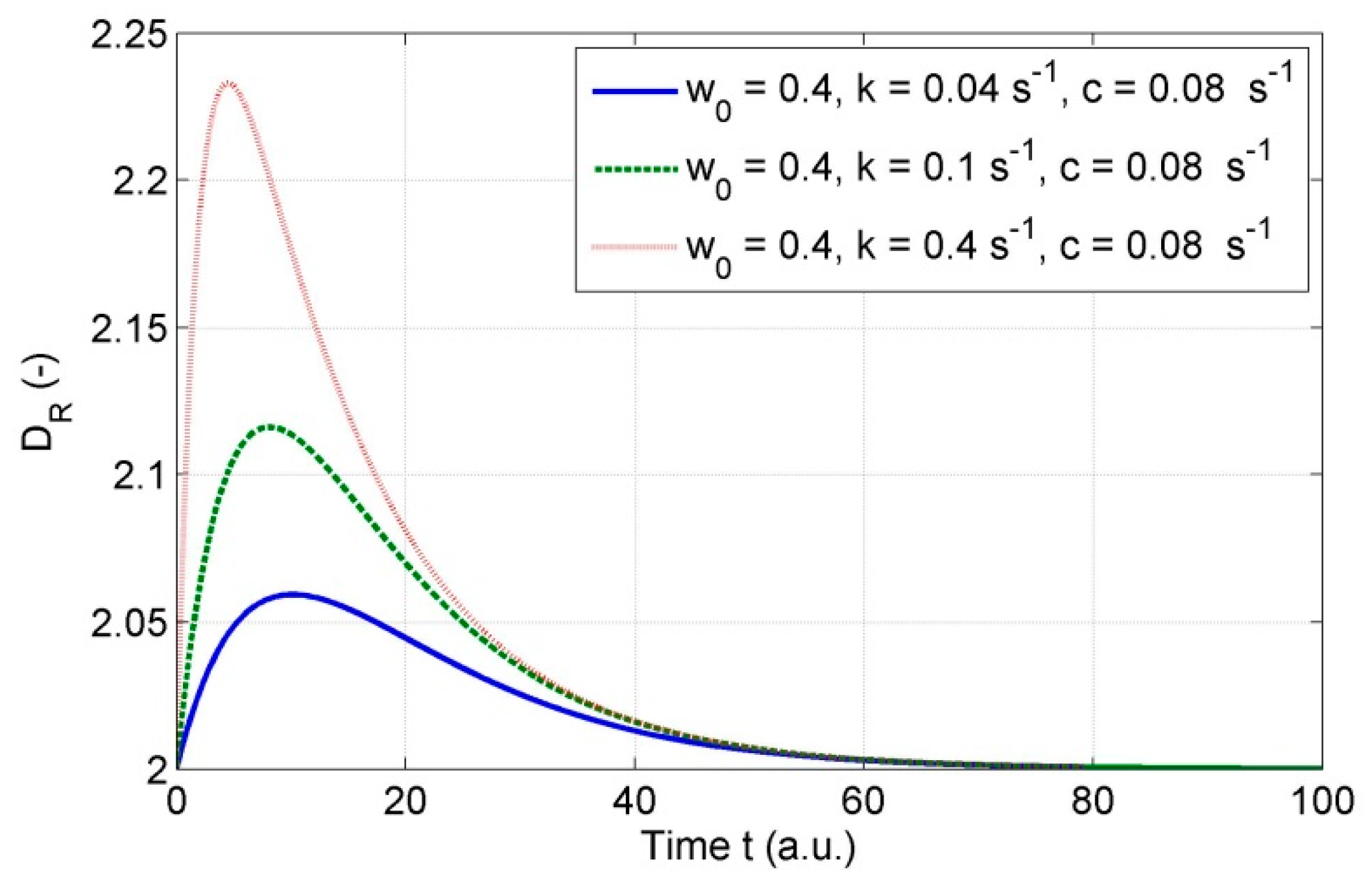
3.9. Discussion on Variability of Fractal Dimension
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Estimation of the xA and xV Effective Particle Dimensions for the Uniform Particle Size Distribution
Appendix B. Estimation of the Effective Particle Dimensions xA and xV for the Linear particle Size Distribution
Appendix C. Estimation of the xA and xV Effective Particle Dimensions for the Experimental Particle Size Distribution
Appendix D. Estimation of the xA and xV Effective Particle Dimensions for the Log-Normal Particle Size Distribution
References
- Greathouse, J.; Johnson, K.; Greenwell, H. Interaction of natural organic matter with layered minerals: Recent developments in computational methods at the nanoscale. Minerals 2014, 4, 519–540. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Hitch, M. Carbon dioxide sorption isotherm study on pristine and acid-treated olivine and its application in the vacuum swing adsorption process. Minerals 2015, 5, 259–275. [Google Scholar] [CrossRef]
- Ozkanlar, A.; Kelley, M.; Clark, A. Water organization and dynamics on mineral surfaces interrogated by graph theoretical analyses of intermolecular chemical networks. Minerals 2014, 4, 118–129. [Google Scholar] [CrossRef]
- Ghanbarian-Alavijeh, B.; Millán, H. The relationship between surface fractal dimension and soil water content at permanent wilting point. Geoderma 2009, 151, 224–232. [Google Scholar] [CrossRef]
- Brunauer, S.; Emmett, P.H.; Teller, E. Adsorption of gases in multimolecular layers. J. Am. Chem. Soc. 1938, 60, 309–319. [Google Scholar] [CrossRef]
- Dokoumetzidis, A.; Macheras, P. A century of dissolution research: From Noyes and Whitney to the biopharmaceutics classification system. Int. J. Pharm. 2006, 321, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Farin, D.; Avnir, D. Reactive fractal surfaces. J. Phys. Chem. 1987, 91, 5517–5521. [Google Scholar] [CrossRef]
- Jandacka, P.; Hlavac, L.M.; Madr, V.; Sancer, J.; Stanek, F. Measurement of specific fracture energy and surface tension of brittle materials in powder form. Int. J. Fract. 2009, 159, 103–110. [Google Scholar] [CrossRef] [Green Version]
- Jandacka, P.; Sancer, J.; Vojtkova, H.; Besta, P.; Brazda, R.; Kolicova, P.; Simkova, L. Fracture energy of selected brittle silicates. Ceram. Silik. 2011, 55, 355–361. [Google Scholar]
- Carman, P.C. Capillary rise and capillary movement of moisture in fine sands. Soil Sci. 1941, 52, 1–14. [Google Scholar] [CrossRef]
- Jandacka, P.; Dvorsky, R.; Lunacek, J. Measurement of powder surface area using capillary elevation method. Inzynieria Miner. 2015, 16, 171–179. [Google Scholar]
- Adamson, W.A. Physical Chemistry of Surfaces; John Wiley & Sons, Inc.: New York, NY, USA, 1990. [Google Scholar]
- Lüttge, A.; Arvidson, S.R. The mineral-water interface. In Kinetics of Water-Rock Interaction; Brantley, L.S., Kubicki, D.J., White, F.A., Eds.; Springer: New York, NY, USA, 2008; pp. 73–107. [Google Scholar]
- Lüttge, A.; Arvidson, R.S.; Fischer, C. Fundamental controls of dissolution rate spectra: Comparisons of model and experimental results. Procedia Earth Planet. Sci. 2013, 7, 537–540. [Google Scholar] [CrossRef]
- Jandacka, P.; Uhlar, R.; Kolenova, I.; Duskova, V.; Mahdalova, V.; Filipkova, K.; Zeman, D. Charakteristika Tvarů Částic Minerálních Partikulárních Látek; Recyklace odpadů XIII, Ostrava, Czech Republic; VSB-TU Ostrava: Ostrava, Czech Republic, 2009. (In Czech) [Google Scholar]
- Zisselmar, R.; Kellerwessel, H. Approximate mathematical description of particle-size distributions—Possibilities and limitations as to the assessment of comminution and classification processes. Part. Part. Syst. Character. 1985, 2, 49–55. [Google Scholar] [CrossRef]
- Eberl, D.D.; Drits, V.A.; Srodon, J. Deducing growth mechanisms for minerals from the shapes of crystal size distributions. Am. J. Sci. 1998, 298, 499–533. [Google Scholar] [CrossRef]
- Mandelbrot, B. The Fractal Geometry of Nature; W. H. Freeman and Company: San Francisco, CA, USA, 1982. [Google Scholar]
- Avnir, D.; Farin, D.; Pfeifer, P. Molecular fractal surfaces. Nature 1984, 308, 261–263. [Google Scholar] [CrossRef]
- Avnir, D.; Farin, D.; Pfeifer, P. Surface geometric irregularity of particulate materials—The fractal approach. J. Colloid Interface Sci. 1985, 103, 112–123. [Google Scholar] [CrossRef]
- Borkovec, M.; Wu, Q.; Degovics, G.; Laggner, P.; Sticher, H. Surface area and size distributions of soil particles. Colloids Surfaces A Physicochem. Eng. Asp. 1993, 73, 65–76. [Google Scholar] [CrossRef]
- Ficker, T. Fractal strength of cement gels and universal dimension of fracture surfaces. Theor. Appl. Fract. Mech. 2008, 50, 167–171. [Google Scholar] [CrossRef]
- Vandamme, H.; Levitz, P.; Bergaya, F.; Alcover, J.F.; Gatineau, L.; Fripiat, J.J. Monolayer adsorption on fractal surfaces—A simple two-dimensional simulation. J. Chem. Phys. 1986, 85, 616–625. [Google Scholar] [CrossRef]
- Stach, S.; Cybo, J.; Chmiela, J. Fracture surface—Fractal or multifractal? Mater. Character. 2001, 46, 163–167. [Google Scholar] [CrossRef]
- Stach, S.; Roskosz, S.; Cybo, J.; Cwajna, J. Multifractal description of fracture morphology: Investigation of the fractures of sintered carbides. Mater. Character. 2003, 51, 87–93. [Google Scholar] [CrossRef]
- Brantley, S.L.; Mellott, N.P. Surface area and porosity of primary silicate minerals. Am. Miner. 2000, 85, 1767–1783. [Google Scholar] [CrossRef]
- Piscitelle, L.; Segars, R. Effect of the particle size distribution in determining a powder´s fractal dimension by single gas BET: A mathematical model. J. Colloid Interface Sci. 1992, 149, 226–232. [Google Scholar] [CrossRef]
- Brož, J.; Roskovec, V.; Valouch, M. Fyzikální a Matematické Tabulky; SNTL: Prague, Czech Republic, 1980. (In Czech) [Google Scholar]
- El-Safty, S.A. Sorption and diffusion of phenols onto well-defined ordered nanoporous monolithic silicas. J. Colloid Interface Sci. 2003, 260, 184–194. [Google Scholar] [CrossRef]
- Fischer, C.; Kurganskaya, I.; Schäfer, T.; Lüttge, A. Variability of crystal surface reactivity: What do we know? Appl. Geochem. 2014, 43, 132–157. [Google Scholar] [CrossRef]
- Ghanbarian, B.; Hunt, A.G. Universal scaling of gas diffusion in porous media. Water Resour. Res. 2014, 50, 2242–2256. [Google Scholar] [CrossRef]
- Fischer, C.; Karius, V.; Weidler, P.G.; Lüttge, A. Relationship between micrometer to submicrometer surface roughness and topography variations of natural iron oxides and trace element concentrations. Langmuir 2008, 24, 3250–3266. [Google Scholar] [CrossRef] [PubMed]
- Arvidson, R.S.; Ertan, I.E.; Amonette, J.E.; Luttge, A. Variation in calcite dissolution rates: A fundamental problem? Geochim. Cosmochim. Acta 2003, 67, 1623–1634. [Google Scholar] [CrossRef]
- Fischer, C.; Arvidson, R.S.; Lüttge, A. How predictable are dissolution rates of crystalline material? Geochim. Cosmochim. Acta 2012, 98, 177–185. [Google Scholar] [CrossRef]
- Tkáčová, K. Mechanical Activation of Minerals; Elsevier: Amsterdam, The Netherlands, 1989. [Google Scholar]



| Powder Material | Process for DR Determination | Particle Size Range (μm) | DR | D a |
|---|---|---|---|---|
| Upper Columbus dolomite (CaCO3-MgCO3) | Acidic dissolution in NH4Cl | 163–2605 | 2.15 ± 0.10 | 2.91 ± 0.02 |
| Upper Columbus dolomite (CaCO3-MgCO3) | Acidic dissolution in oxalate buffer | 163–2605 | 2.34 ± 0.04 | 2.91 ± 0.02 |
| Niagara dolomite (CaCO3-MgCO3) | Acidic dissolution in NH4Cl | 163–2605 | 2.07 ± 0.06 | 2.58 ± 0.01 |
| Niagara dolomite (CaCO3-MgCO3) | Acidic dissolution in oxalate buffer | 163–2605 | 2.19 ± 0.05 | 2.58 ± 0.01 |
| Halimeda skeletal carbonate (green algae) | Acidic dissolution in seawater | 81–513 | 2.05 ± 0.08 | 3.02 ± 0.07 |
| Hybla alkali feldspar (potassium aluminosilicate) | Dissolution in HCl (pH 5) | 56–400 | 2.95 ± 0.16 | 2.36 ± 0.02 |
| Hybla alkali feldspar (potassium aluminosilicate) | Dissolution in boric acid buffer (pH 9) | 56–400 | 3.06 ± 0.06 | 2.36 ± 0.02 |
| Quartz | Dissolution in HF (3.66 M) | 45–1000 | 2.14 ± 0.06 | 2.08 ± 0.08 |
| Ottawa sand (quartz) | Dissolution in HF (3.66 M) | 89–711 | 2.15 ± 0.06 | 2.08 ± 0.08 |
| Madagascar quartz | Dissolution in HF (0.1 M) | 0.4–6 | 1.59 ± 0.05 | 1.99 ± 0.06 |
| Madagascar quartz | Dissolution in dilute NaOH | 0.4–6 | 1.78 ± 0.07 | 1.99 ± 0.06 |
| Vitreous silica | Dissolution in HF (0.1 M) | 0.4–12.6 | 1.95 ± 0.04 | 2.03 ± 0.04 |
| Iceland spar calcite (CaCO3) | Reaction with Fe(ClO4)3 in presence of 2% CO2 | 100–631 | 2.11 ± 0.03 | 2.16 ± 0.04 |
| Iceland spar calcite (CaCO3) | Reaction with Fe(ClO4)3 in presence of 20% CO2 | 64–631 | 2.45 ± 0.04 | 2.16 ± 0.04 |
| Iceland spar calcite (CaCO3) | Dissolution in HCl (pH 3) | 137–631 | 1.80 ± 0.06 | 2.16 ± 0.04 |
| Powder Material | m | D |
|---|---|---|
| Quartz | −1.0 | 2.0 |
| Microcline (Keystone) | −0.8 ± 0.2 | 2.2 ± 0.2 |
| Microcline (Keystone) | −0.8 ± 0.1 | 2.2 ± 0.1 |
| Albite glass | −1.4 ± 0.1 | 1.6 ± 0.1 |
| Albite (Amelia) | −1.0 ± 0.1 | 2.0 ± 0.1 |
| Albite (Evje) | −0.7 ± 0.1 | 2.3 ± 0.1 |
| Oligoclase (Madawaska) | −0.6 ± 0.2 | 2.4 ± 0.2 |
| Labradorite (Labrador) | −0.5 ± 0.1 | 2.5 ± 0.1 |
| Bytownite (Duluth) | −0.5 ± 0.1 | 2.5 ± 0.1 |
| Bytownite (Crystal Bay) | −0.6 ± 0.2 | 2.4 ± 0.2 |
| Anorthite (Miyake Jima) | −1.2 ± 0.2 | 1.8 ± 0.2 |
| Anorthite (Grass Valley) | −0.20 ± 0.05 | 2.80 ± 0.05 |
| Olivine (San Carlos) | −1.1 ± 0.2 | 1.9 ± 0.2 |
| Olivine (Twin Sisters) | −0.3 ± 0.2 | 2.7 ± 0.2 |
| Diopside (Herschel) | −0.6 ± 0.2 | 2.4 ± 0.2 |
| Hornblende (Gore Mtn.) | −0.6 ± 0.1 | 2.4 ± 0.1 |
| Adsorbate | b∙106 (m3∙mol−1) | s∙1010 (m) | Adsorbate | b∙106 (m3∙mol−1) | s∙1010 (m) | Adsorbate | b∙106 (m3∙mol−1) | s∙1010 (m) |
|---|---|---|---|---|---|---|---|---|
| N2 | 38.70 | 4.09 ± 0.03 | HCl | 40.60 | 4.16 ± 0.03 | C3H8 | 90.30 | 5.43 ± 0.02 |
| Ar | 32.00 | 3.84 ± 0.04 | C2H4O2 | 107.00 | 5.74 ± 0.02 | C3H8O | 98.30 | 5.58 ± 0.02 |
| Kr | 39.60 | 4.12 ± 0.03 | SO2 | 56.70 | 4.65 ± 0.03 | Rn | 62.00 | 4.79 ± 0.02 |
| H2 | 26.62 | 3.61 ± 0.04 | CO | 39.54 | 4.12 ± 0.03 | Hg | 16.96 | 3.11 ± 0.06 |
| He | 23.50 | 3.47 ± 0.05 | CO2 | 42.81 | 4.23 ± 0.03 | CS2 | 72.50 | 5.04 ± 0.02 |
| H2O | 30.40 | 3.78 ± 0.04 | O2 | 31.70 | 3.83 ± 0.04 | H2S | 43.00 | 4.24 ± 0.03 |
| C2H6O | 83.95 | 5.30 ± 0.02 | CH4 | 42.75 | 4.23 ± 0.03 | C7H8 | 146.00 | 6.37 ± 0.01 |
| C6H6 | 119.0 | 5.95 ± 0.02 | CH4O | 67.00 | 4.91 ± 0.02 | C8H10 | 176.00 | 6.78 ± 0.01 |
| HF | 73.85 | 5.08 ± 0.02 | O3 | 49.10 | 4.43 ± 0.03 | Br | 44.40 | 4.28 ± 0.03 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jandacka, P.; Pistora, J.; Valicek, J.; Madr, V. Molecularly-Limited Fractal Surface Area of Mineral Powders. Minerals 2016, 6, 44. https://doi.org/10.3390/min6020044
Jandacka P, Pistora J, Valicek J, Madr V. Molecularly-Limited Fractal Surface Area of Mineral Powders. Minerals. 2016; 6(2):44. https://doi.org/10.3390/min6020044
Chicago/Turabian StyleJandacka, Petr, Jaromir Pistora, Jan Valicek, and Vilem Madr. 2016. "Molecularly-Limited Fractal Surface Area of Mineral Powders" Minerals 6, no. 2: 44. https://doi.org/10.3390/min6020044





