Arsenic Adsorption onto Minerals: Connecting Experimental Observations with Density Functional Theory Calculations
Abstract
:1. Introduction
1.1. Arsenic Chemistry, Geochemistry, Prevalence, and Toxicity
1.2. Arsenic Treatment Methods
1.3. Studying As Adsorption with Experimental and Modeling Methods
1.4. Studying As Adsorption with Experiments
1.5. Studying As Adsorption with Mathematical Models
1.6. Studying As Adsorption with Quantum Mechanics Modeling Methods
2. Methods
2.1. Applied Quantum Mechanics Background
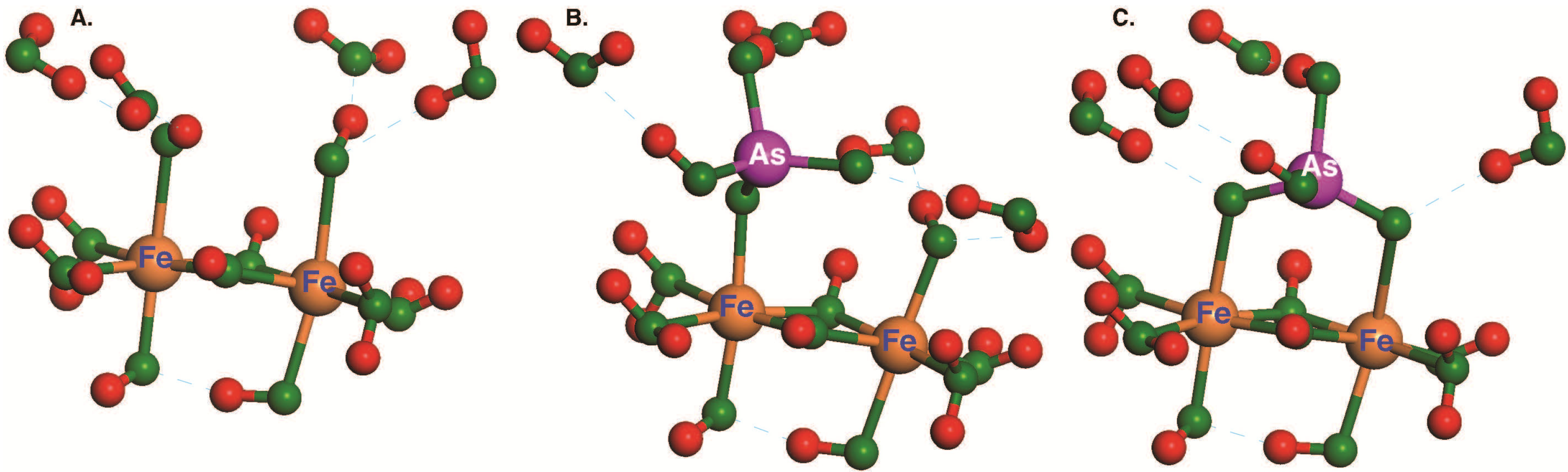
2.2. Molecular Orbital Theory Calculations with Fe Clusters
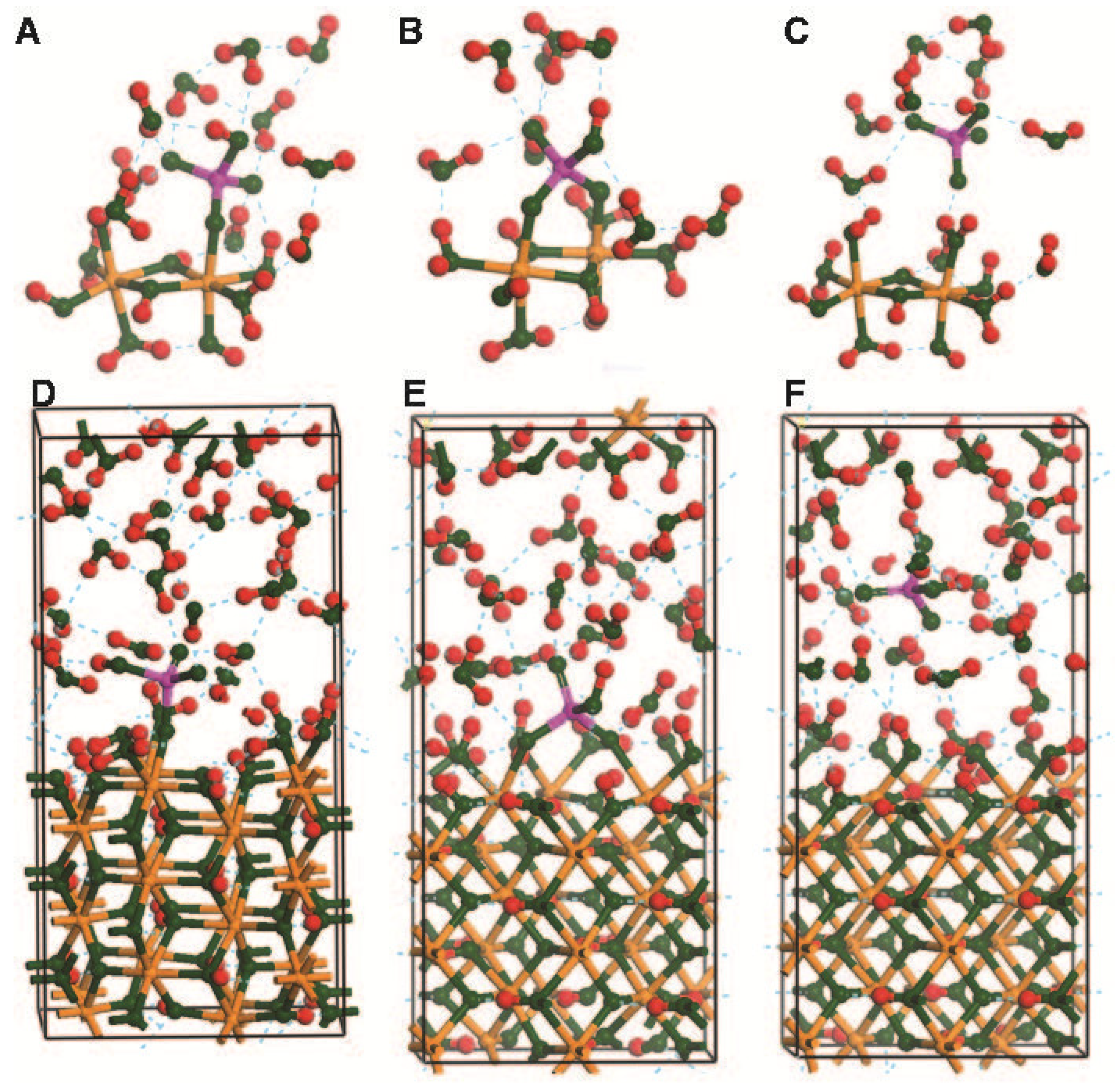
2.3. Planewave Calculations Using α-FeOOH (010)
3. Results and Discussion
3.1. Effect of Cluster Charge on ΔGads
| Reaction # | Reaction | ΔGads (kJ/mol) |
|---|---|---|
| (1) | H3AsO3 + Fe2(OH)6(OH2)40 → Fe2(OH)4(OH2)4HAsO3 + 2H2O | −60 |
| (2) | H3AsO3 + Fe2(OH)2(OH2)84+ + 16H2O → Fe2(OH)2(OH2)6HAsO32+ + 2H3O+·8H2O | −159 |
| (3) | HAsO42− + Fe2(OH)6(OH2)40 + 8H2O → Fe2(OH)4(OH2)4HAsO4 + 2OH−·4H2O | +14 |
| (4) | HAsO42− + Fe2(OH)2(OH2)84+ → Fe2(OH)2(OH2)6HAsO42+ + 2H2O | −263 |
| (5) | H2AsO4− + Fe2(OH)6(OH2)40 + 3H2O → Fe2(OH)4(OH2)4HAsO4 + OH−·4H2O | −309 |
| (6) | H2AsO4− + Fe2(OH)2(OH2)64+ + 7H2O → Fe2(OH)2(OH2)6HAsO42+ + H3O+·8H2O | −336 |
| (7) | H2AsO4− + Fe2(OH)2(OH2)84+ → Fe2(OH)2(OH2)6H2AsO43+ + 2H2O | −338 |
3.2. Effect of Fe Cluster Hydration on ΔGads for Anhydrous and Octahydrated H2AsO4−
| Reaction # | Reaction | ΔGads (kJ/mol) |
|---|---|---|
| (8) | H2AsO4− + Fe2(OH)6(OH2)4 + 3H2O → Fe2(OH)4(OH2)4HAsO4 + OH−·4H2O | −186 |
| (9) | H2AsO4− + Fe2(OH)6(OH2)4·4H2O + 3H2O → Fe2(OH)4(OH2)4HAsO4·4H2O + OH−·4H2O | −195 |
| (10) | H2AsO4− + Fe2(OH)6(OH2)4·8H2O → Fe2(OH)4(OH2)4HAsO4·4H2O + OH−·4H2O + H2O | −217 |
| (11) | H2AsO4− + Fe2(OH)6(OH2)4·8H2O + 3H2O → Fe2(OH)4(OH2)4HAsO4·8H2O + OH−·4H2O | −223 |
| (12) | H2AsO4·8H2O + Fe2(OH)6(OH2)4·4H2O → Fe2(OH)4(OH2)4HAsO4·4H2O + OH−·4H2O + 5H2O | −64 |
| (13) | H2AsO4·8H2O + Fe2(OH)6(OH2)4·8H2O → Fe2(OH)4(OH2)4HAsO4·4H2O + OH−·4H2O + 5H2O | −86 |
3.3. Effect of As Oxidation State and DFT Method on ΔGads
| Reaction # | Reaction | ΔGads (kJ/mol) |
|---|---|---|
| (12) | H3AsO3·8H2O + Fe2(OH)6(OH2)4·4H2O → Fe2(OH)4(OH2)4HAsO3·4H2O + 10H2O | −124 |
| (13) | H3AsO3·8H2O + Fe2(OH)6(OH2)4·8H2O → Fe2(OH)4(OH2)4HAsO3·4H2O + 10H2O | −146 |
| (14) | HAsO42−·8H2O + Fe2(OH)6(OH2)4·4H2O → Fe2(OH)4(OH2)4HAsO4·4H2O + 2OH−·4H2O | +15 |
| (15) | HAsO42−·8H2O + Fe2(OH)6(OH2)4·8H2O → Fe2(OH)4(OH2)4HAsO4·4H2O + 2OH−·4H2O + 4H2O | −6 |
| (16) | H2AsO4−·8H2O + Fe2(OH)6(OH2)4·4H2O → Fe2(OH)4(OH2)4HAsO4·4H2O + OH−·4H2O + 5H2O | −64 a, −35 b, −3 c |
| (17) | H2AsO4−·8H2O + Fe2(OH)6(OH2)4·8H2O → Fe2(OH)4(OH2)4HAsO4·4H2O + OH−·4H2O + 5H2O | −86 |
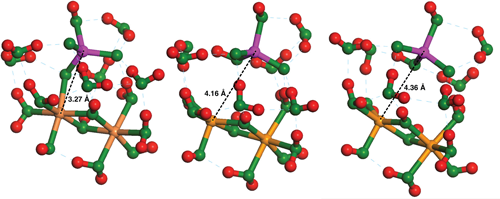
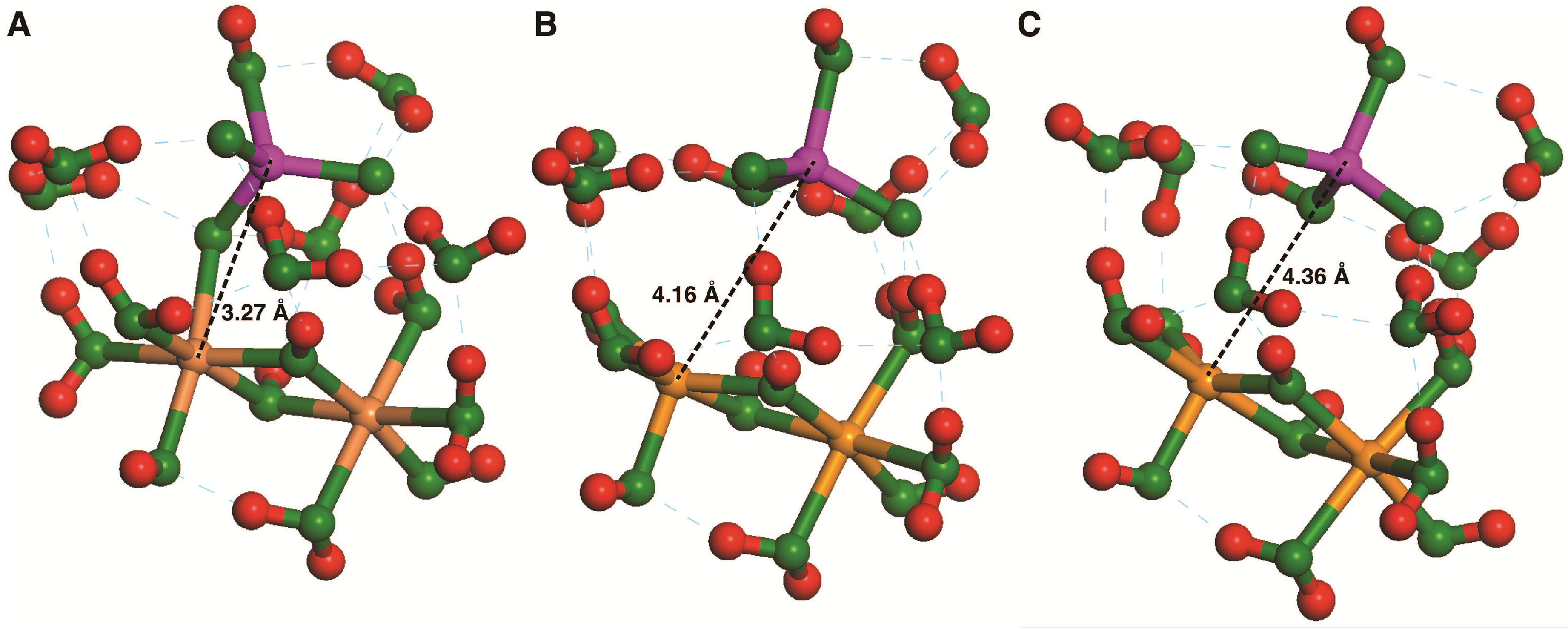
3.4. As—Fe Distance and As-O Bond Length Data from Experiments Compared with Cluster and Periodic Model Results
| AsV Complex | As—Fe (Å) | As—Fe (Å) | As-OFe (Å) | As-OFe (Å) | As-OH (Å) | As-OH (Å) | As=O (Å) |
|---|---|---|---|---|---|---|---|
| Fe2(OH)4(OH2)4HAsVO4 (BB) | 3.13 | 3.25 | 1.71 | 1.73 | 1.83 | 1.63 | |
| Fe2(OH)4(OH2)4HAsVO4·4H2O (BB) | 3.20 x, 3.19 y, 3.08 z | 3.28 x, 3.24 y, 3.29 z | 1.69 x, 1.68 y, 1.69 z | 1.72 x, 1.71 y, 1.72 z | 1.76 x, 1.75 y, 1.79 z | 1.67 x, 1.66 y, 1.65 z | |
| Fe2(OH)4(OH2)4HAsVO4·8H2O (BB) | 3.30 | 3.30 | 1.70 | 1.70 | 1.76 | 1.67 | |
| Goethite (010) periodic model (BB) | 3.56 | 3.68 | 1.72 | 1.72 | 1.78 | 1.73 | |
| Fe2(OH)2(OH2)6H2AsVO43+ (BB) | 3.24 | 3.24 | 1.70 | 1.70 | 1.72 | 1.72 | |
| Fe2(OH)2(OH2)6H2AsVO43+ (BB) a | 3.29 | 3.29 | 1.71 | 1.71 | 1.73 | 1.73 | |
| AsV on Fh (BB) a | 3.27 | 3.38 | 1.70 | 1.70 | 1.67 | 1.64 | |
| AsV on Gt (BB) a | 3.30 | 3.30 | 1.70 | 1.70 | 1.70 | 1.63 | |
| AsV on Lp (BB) a | 3.30 | 3.32 | 1.71 | 1.71 | 1.66 | 1.63 | |
| AsV on Hm (BB) a | 3.24 | 3.35 | 1.70 | 1.70 | 1.70 | 1.62 | |
| AsV on Fh (BB) b | 3.25 (±0.02) | ||||||
| AsV on Gt (BB) b | 3.28 (±0.01) | ||||||
| AsV on Lp (BB) c | 3.31 (±0.014) | 1.69 (±0.004) | |||||
| AsV on Gt (BB) c | 3.30 (±0.008) | 1.69 (±0.004) | |||||
| AsV on Fh (BB) d | 3.27 | ||||||
| Goethite (010) periodic model (MM) | 3.54 | 5.00 † | 1.78 | 1.75 | 1.71 ‡ | 1.68 | |
| AsV on Gt e | 3.25 § | 1.689 | 1.679 | ||||
| AsIII Complex | As—Fe (Å) | As—Fe (Å) | As-O (Å) | As-O (Å) | As-O (Å) | As=O (Å) | |
| Fe2(OH)4(OH2)4HAsIIIO3·4H2O (BB) | 3.26 | 3.41 | 1.77 | 1.74 | 1.90 | na | |
| Fe2(OH)4(OH2)4HAsIIIO3·8H2O (BB) | 3.29 | 3.39 | 1.78 | 1.72 | 1.90 | ||
| AsIII on Lp (BB) c | 3.41 (±0.013) | 1.78 (±0.014) | |||||
| AsIII on Gt (BB) c | 3.31 (±0.013) | 1.78 (±0.012) | |||||
| AsIII on Fh (BB) d | 3.41–3.44 | ||||||
| AsIII on Fh and Hm (BB) f | 3.35 (±0.05) | ||||||
| AsIII on Gt and Lp (BB) f | 3.3–3.4 | ||||||
| AsIII on Gt (BB) g | 3.378 (±0.014) |
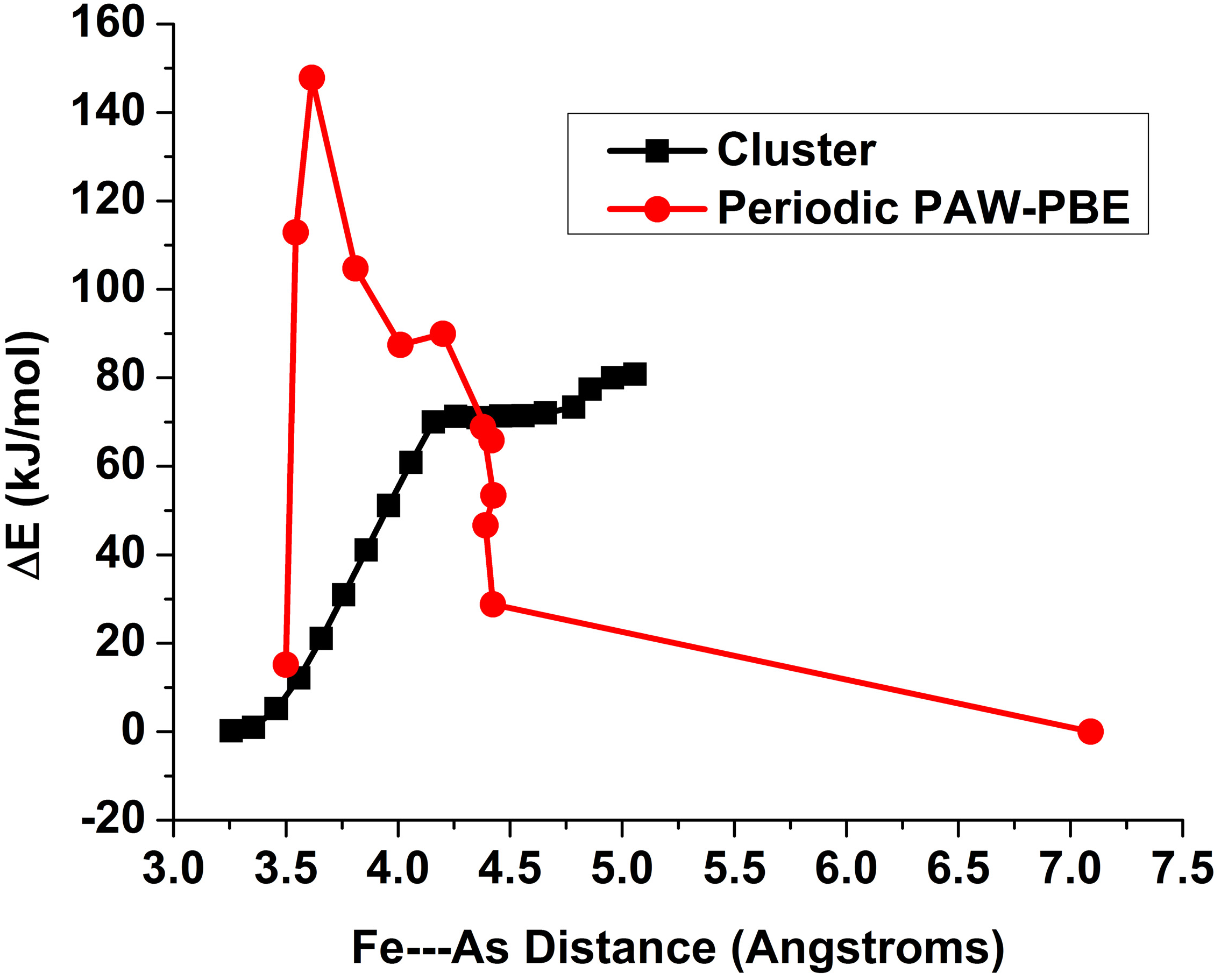
3.5. Sorption Kinetics for iAsV on Cluster and Periodic Models
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References and Notes
- Kim, K.-W.; Chanpiwat, P.; Hanh, H.T.; Phan, K.; Sthiannopkao, S. Arsenic geochemistry of groundwater in Southeast Asia. Front. Med. 2011, 5, 420–433. [Google Scholar]
- Smedley, P.L.; Kinniburgh, D.G. A review of the source, behaviour and distribution of arsenic in natural waters. Appl. Geochem. 2002, 17, 517–568. [Google Scholar] [CrossRef]
- Anawar, H.M.; Akai, J.; Mihaljevič, M.; Sikder, A.M.; Ahmed, G.; Tareq, S.M.; Rahman, M.M. Arsenic contamination in groundwater of bangladesh: Perspectives on geochemical, microbial and anthropogenic issues. Water 2011, 3, 1050–1076. [Google Scholar] [CrossRef]
- Drewniak, L.; Maryan, N.; Lewandowski, W.; Kaczanowski, S.; Sklodowska, A. The contribution of microbial mats to the arsenic geochemistry of an ancient gold mine. Environ. Pollut. 2012, 162, 190–201. [Google Scholar] [CrossRef]
- Signes-Pastor, A.; Burló, F.; Mitra, K.; Carbonell-Barrachina, A.A. Arsenic biogeochemistry as affected by phosphorus fertilizer addition, redox potential and pH in a west Bengal (India) soil. Geoderma 2007, 137, 504–510. [Google Scholar] [CrossRef]
- Oremland, R.S.; Stolz, J.F. The ecology of arsenic. Science 2003, 300, 939–944. [Google Scholar] [CrossRef]
- Dhuldhaj, U.P.; Yadav, I.C.; Singh, S.; Sharma, N.K. Microbial interactions in the arsenic cycle: Adoptive strategies and applications in environmental management. Rev. Environ. Contam. Toxicol. 2013, 224, 1–38. [Google Scholar]
- Moreno-Jiménez, E.; Esteban, E.; Peñalosa, J.M. The fate of arsenic in soil-plant systems. Rev. Environ. Contam. Toxicol. 2012, 215, 1–37. [Google Scholar]
- Wolfe-Simon, F.; Blum, J.S.; Kulp, T.R.; Gordon, G.W.; Hoeft, S.E.; Pett-Ridge, J.; Stolz, J.F.; Webb, S.M.; Weber, P.K.; Davies, P.C.W.; et al. A bacterium that can grow by using arsenic instead of phosphorus. Science 2011, 332, 1163–1166. [Google Scholar] [CrossRef]
- Wolfe-Simon, F.; Blum, J.S.; Kulp, T.R.; Gordon, G.W.; Hoeft, S.E.; Pett-Ridge, J.; Stolz, J.F.; Webb, S.M.; Weber, P.K.; Davies, P.C.W.; et al. Response to comments on “A bacterium that can grow using arsenic instead of phosphorus.”. Science 2011, 332, 1149–1149. [Google Scholar]
- Masscheleyn, P.H.; Delaune, R.D.; Patrick, W.H. Arsenic and selenium chemistry as affected by sediment redox potential and pH. J. Environ. Qual. 1991, 20, 522–527. [Google Scholar] [CrossRef]
- Cullen, W.R.; Reimer, K.J. Arsenic speciation in the environment. Chem. Rev. 1989, 89, 713–764. [Google Scholar] [CrossRef]
- Greenwood, N.N.; Earnshaw, A. Arsenic, Antimony and Bismuth. In Chemistry of the Elements; Pergamon Press: Oxford, UK, 1997; pp. 547–599. [Google Scholar]
- Masscheleyn, P.H.; Delaune, R.D.; Patrick, W.H. Effect of redox potential and pH on arsenic speciation and solubility in a contaminated soil. Environ. Sci. Technol. 1991, 25, 1414–1419. [Google Scholar] [CrossRef]
- Flis, I.E.; Mishchenko, K.P.; Tumanova, T.A.; Russ, J. Dissociation of arsenic acid. J. Inorg. Chem. 1959, 4, 120–124. [Google Scholar]
- Francesconi, K.A. Arsenic species in seafood: Origin and human health implications. Pure Appl. Chem. 2010, 82, 373–381. [Google Scholar] [CrossRef]
- Beauchemin, S.; Fiset, J.-F.; Poirier, G.; Ablett, J. Arsenic in an alkaline AMD treatment sludge: Characterization and stability under prolonged anoxic conditions. Appl. Geochem. 2010, 25, 1487–1499. [Google Scholar] [CrossRef]
- Cheng, H.; Hu, Y.; Luo, J.; Xu, B.; Zhao, J. Geochemical processes controlling fate and transport of arsenic in acid mine drainage (AMD) and natural systems. J. Hazard. Mater. 2009, 165, 13–26. [Google Scholar] [CrossRef]
- Cramer, S.P.; Siskin, M.; Brown, L.D.; George, G.N. Characterization of arsenic in oil shale and oil shale derivatives by X-ray absorption spectroscopy. Energy Fuels 1988, 2, 175–180. [Google Scholar] [CrossRef]
- Pelley, J. Commonarsenical pesticide under scrutiny. Environ. Sci. Technol. 2005, 39, 122–123. [Google Scholar] [CrossRef]
- Arai, Y.; Lanzirotti, A.; Sutton, S.; Davis, J.A.; Sparks, D.L. Arsenic speciation and reactivity in poultry litter. Environ. Sci. Technol. 2003, 37, 4083–4090. [Google Scholar]
- Argos, M.; Kalra, T.; Rathouz, P.J.; Chen, Y.; Pierce, B.; Parvez, F.; Islam, T.; Ahmed, A.; Rakibuz-Zaman, M.; Hasan, R.; et al. Arsenic exposure from drinking water, and all-cause and chronic-disease mortalities in Bangladesh (HEALS): A prospective cohort study. Lancet 2010, 376, 252–258. [Google Scholar]
- Chen, Y.; Graziano, J.H.; Parvez, F.; Liu, M.; Slavkovich, V.; Kalra, T.; Argos, M.; Islam, T.; Ahmed, A.; Rakibuz-Zaman, M.; et al. Arsenic exposure from drinking water and mortality from cardiovascular disease in Bangladesh: Prospective cohort study. Br. Med. J. 2011, 342, d2431. [Google Scholar] [CrossRef]
- Das, N.; Paul, S.; Chatterjee, D.; Banerjee, N.; Majumder, N.S.; Sarma, N.; Sau, T.J.; Basu, S.; Banerjee, S.; Majumder, P.; et al. Arsenic exposure through drinking water increases the risk of liver and cardiovascular diseases in the population of West Bengal, India. BMC Public Health 2012, 12, 639. [Google Scholar] [CrossRef]
- Ferreccio, C.; Smith, A.H.; Durán, V.; Barlaro, T.; Benítez, H.; Valdés, R.; Aguirre, J.J.; Moore, L.E.; Acevedo, J.; Vásquez, M.I.; et al. Case-control study of arsenic in drinking water and kidney cancer in uniquely exposed Northern Chile. Am. J. Epidemiol. 2013, 178, 813–818. [Google Scholar] [CrossRef]
- Meliker, J.R.; Slotnick, M.J.; AvRuskin, G.A.; Schottenfeld, D.; Jacquez, G.M.; Wilson, M.L.; Goovaerts, P.; Franzblau, A.; Nriagu, J.O. Lifetime exposure to arsenic in drinking water and bladder cancer: A population-based case-control study in Michigan, USA. Cancer Causes Control 2010, 21, 745–757. [Google Scholar] [CrossRef]
- Paul, S.; Bhattacharjee, P.; Mishra, P.K.; Chatterjee, D.; Biswas, A.; Deb, D.; Ghosh, A.; Mazumder, D.N.G.; Giri, A.K. Human urothelial micronucleus assay to assess genotoxic recovery by reduction of arsenic in drinking water: A cohort study in West Bengal, India. Biometals 2013, 26, 855–862. [Google Scholar] [CrossRef]
- Smith, A.H.; Marshall, G.; Yuan, Y.; Liaw, J.; Ferreccio, C.; Steinmaus, C. Evidence from Chile that arsenic in drinking water may increase mortality from pulmonary tuberculosis. Am. J. Epidemiol. 2011, 173, 414–420. [Google Scholar] [CrossRef]
- Concha, G.; Broberg, K.; Grandér, M.; Cardozo, A.; Palm, B.; Vahter, M. High-level exposure to lithium, boron, cesium, and arsenic via drinking water in the Andes of northern Argentina. Environ. Sci. Technol. 2010, 44, 6875–6880. [Google Scholar] [CrossRef]
- Kinniburgh, D.G.; Smedley, P.L.; Davies, J.; Milne, C.J.; Gaus, I.; Trafford, J.M.; Ahmed, K.M. The Scale and Causes of the Groundwater Arsenic Problem in Bangladesh. In Arsenic in Ground Water; Springer: Berlin, Germany, 2003; pp. 211–257. [Google Scholar]
- Mondal, D.; Banerjee, M.; Kundu, M.; Banerjee, N.; Bhattacharya, U.; Giri, A.K.; Ganguli, B.; Sen Roy, S.; Polya, D.A. Comparison of drinking water, raw rice and cooking of rice as arsenic exposure routes in three contrasting areas of West Bengal, India. Environ. Geochem. Health 2010, 32, 463–477. [Google Scholar] [CrossRef]
- Sun, G.; Li, X.; Pi, J.; Sun, Y.; Li, B.; Jin, Y.; Xu, Y. Current research problems of chronic arsenicosis in China. J. Health Popul. Nutr. 2011, 24, 176–181. [Google Scholar]
- Nickson, R.; McArthur, J.; Burgess, W.; Ahmed, K.M.; Ravenscroft, P.; Rahman, M. Arsenic poisoning of Bangladesh groundwater. Nature 1998, 395, 338. [Google Scholar] [CrossRef]
- Nicolli, H.B.; Bundschuh, J.; Blanco, M.C.; Tujchneider, O.C.; Panarello, H.O.; Dapeña, C.; Rusansky, J.E. Arsenic and associated trace-elements in groundwater from the Chaco-Pampean plain, Argentina: Results from 100 years of research. Sci. Total Environ. 2012, 429, 36–56. [Google Scholar] [CrossRef]
- Sharma, V.K.; Sohn, M. Aquatic arsenic: Toxicity, speciation, transformations, and remediation. Environ. Int. 2009, 35, 743–759. [Google Scholar] [CrossRef]
- Malik, A.H.; Khan, Z.M.; Mahmood, Q.; Nasreen, S.; Bhatti, Z.A. Perspectives of low cost arsenic remediation of drinking water in Pakistan and other countries. J. Hazard. Mater. 2009, 168, 1–12. [Google Scholar] [CrossRef]
- Welch, A.H.; Stollenwerk, K.G.; Maurer, D.K.; Feinson, L.S. In Situ Arsenic Remediation in a Fractured, Alkaline Aquifer. In Arsenic in Ground Water; Welch, A.H., Stollenwerk, K.G., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2003; pp. 403–419. [Google Scholar]
- Beaulieu, B.; Ramirez, R.E. Arsenic remediation field study using a sulfate reduction and zero-valent iron PRB. Groundw. Monit. Remediat. 2013, 33, 85–94. [Google Scholar]
- Berg, M.; Luzi, S.; Trang, P.T.K.; Viet, P.H.; Giger, W.; Stüben, D. Arsenic removal from groundwater by household sand filters: Comparative field study, model calculations, and health benefits. Environ. Sci. Technol. 2006, 40, 5567–5573. [Google Scholar] [CrossRef]
- Neumann, A.; Kaegi, R.; Voegelin, A.; Hussam, A.; Munir, A.K.M.; Hug, S.J. Arsenic removal with composite iron matrix filters in Bangladesh: A field and laboratory study. Environ. Sci. Technol. 2013, 47, 4544–4554. [Google Scholar] [CrossRef]
- Jeon, C.-S.; Park, S.-W.; Baek, K.; Yang, J.-S.; Park, J.-G. Application of iron-coated zeolites (ICZ) for mine drainage treatment. Korean J. Chem. Eng. 2012, 29, 1171–1177. [Google Scholar] [CrossRef]
- Wu, K.; Liu, R.; Liu, H.; Chang, F.; Lan, H.; Qu, J. Arsenic species transformation and transportation in arsenic removal by Fe-Mn binary oxide–coated diatomite: Pilot-scale field Study. J. Environ. Eng. 2011, 137, 1122–1127. [Google Scholar] [CrossRef]
- Mudhoo, A.; Sharma, S.K.; Garg, V.K.; Tseng, C.-H. Arsenic: An overview of applications, health, and environmental concerns and removal processes. Crit. Rev. Environ. Sci. Technol. 2011, 41, 435–519. [Google Scholar] [CrossRef]
- Ng, K.-S.; Ujang, Z.; Le-Clech, P. Arsenic removal technologies for drinking water treatment. Rev. Environ. Sci. Biotechnol. 2004, 3, 43–53. [Google Scholar] [CrossRef]
- Ali, I.; Khan, T.A.; Asim, M. Removal of arsenic from water by electrocoagulation and electrodialysis techniques. Sep. Purif. Rev. 2011, 40, 25–42. [Google Scholar] [CrossRef]
- Van Genuchten, C.M.; Addy, S.E.A.; Peña, J.; Gadgil, A.J. Removing arsenic from synthetic groundwater with iron electrocoagulation: An Fe and As K-edge EXAFS study. Environ. Sci. Technol. 2012, 46, 986–994. [Google Scholar] [CrossRef]
- Ali, I. Water treatment by adsorption columns: Evaluation at ground level. Sep. Purif. Rev. 2014, 43, 175–205. [Google Scholar] [CrossRef]
- Mohan, D.; Pittman, C.U. Arsenic removal from water/wastewater using adsorbents—A critical review. J. Hazard. Mater. 2007, 142, 1–53. [Google Scholar] [CrossRef]
- Ali, I.; Gupta, V.K. Advances in water treatment by adsorption technology. Nat. Protoc. 2006, 1, 2661–2667. [Google Scholar] [CrossRef]
- Wei, Y.-T.; Zheng, Y.-M.; Chen, J.P. Uptake of methylated arsenic by a polymeric adsorbent: Process performance and adsorption chemistry. Water Res. 2011, 45, 2290–2296. [Google Scholar] [CrossRef]
- Salameh, Y.; Al-Lagtah, N.; Ahmad, M.N.M.; Allen, S.J.; Walker, G.M. Kinetic and thermodynamic investigations on arsenic adsorption onto dolomitic sorbents. Chem. Eng. J. 2010, 160, 440–446. [Google Scholar] [CrossRef]
- Chutia, P.; Kato, S.; Kojima, T.; Satokawa, S. Arsenic adsorption from aqueous solution on synthetic zeolites. J. Hazard. Mater. 2009, 162, 440–447. [Google Scholar] [CrossRef]
- Adra, A.; Morin, G.; Ona-Nguema, G.; Menguy, N.; Maillot, F.; Casiot, C.; Bruneel, O.; Lebrun, S.; Juillot, F.; Brest, J. Arsenic scavenging by aluminum-substituted ferrihydrites in a circumneutral pH river impacted by acid mine drainage. Environ. Sci. Technol. 2013, 47, 12784–12792. [Google Scholar] [CrossRef]
- Giles, D.E.; Mohapatra, M.; Issa, T.B.; Anand, S.; Singh, P. Iron and aluminium based adsorption strategies for removing arsenic from water. J. Environ. Manag. 2011, 92, 3011–3022. [Google Scholar] [CrossRef]
- Manning, B.A.; Goldberg, S. Adsorption and stability of arsenic(III) at the clay mineral–water interface. Environ. Sci. Technol. 1997, 31, 2005–2011. [Google Scholar] [CrossRef]
- Singh, T.S.; Pant, K.K. Equilibrium, kinetics and thermodynamic studies for adsorption of As(III) on activated alumina. Sep. Purif. Technol. 2004, 36, 139–147. [Google Scholar] [CrossRef]
- Gallegos-Garcia, M.; Ramírez-Muñiz, K.; Song, S. Arsenic removal from water by adsorption using iron oxide minerals as adsorbents: A review. Miner. Process. Extr. Metall. Rev. 2012, 33, 301–315. [Google Scholar] [CrossRef]
- Miretzky, P.; Cirelli, A.F. Remediation of arsenic-contaminated soils by iron amendments: A review. Crit. Rev. Environ. Sci. Technol. 2010, 40, 93–115. [Google Scholar] [CrossRef]
- Yang, W.; Kan, A.T.; Chen, W.; Tomson, M.B. pH-dependent effect of zinc on arsenic adsorption to magnetite nanoparticles. Water Res. 2010, 44, 5693–5701. [Google Scholar] [CrossRef]
- Zhang, S.; Niu, H.; Cai, Y.; Zhao, X.; Shi, Y. Arsenite and arsenate adsorption on coprecipitated bimetal oxide magnetic nanomaterials: MnFe2O4 and CoFe2O4. Chem. Eng. J. 2010, 158, 599–607. [Google Scholar] [CrossRef]
- Tian, Y.; Wu, M.; Lin, X.; Huang, P.; Huang, Y. Synthesis of magnetic wheat straw for arsenic adsorption. J. Hazard. Mater. 2011, 193, 10–16. [Google Scholar] [CrossRef]
- Kanel, S.R.; Manning, B.; Charlet, L.; Choi, H. Removal of arsenic(III) from groundwater by nanoscale zero-valent iron. Environ. Sci. Technol. 2005, 39, 1291–1298. [Google Scholar] [CrossRef]
- Yavuz, C.T.; Mayo, J.T.; Suchecki, C.; Wang, J.; Ellsworth, A.Z.; D’Couto, H.; Quevedo, E.; Prakash, A.; Gonzalez, L.; Nguyen, C.; et al. Pollution magnet: Nano-magnetite for arsenic removal from drinking water. Environ. Geochem. Health 2010, 32, 327–334. [Google Scholar] [CrossRef]
- Zhu, J.; Pigna, M.; Cozzolino, V.; Caporale, A.G.; Violante, A. Sorption of arsenite and arsenate on ferrihydrite: Effect of organic and inorganic ligands. J. Hazard. Mater. 2011, 189, 564–571. [Google Scholar] [CrossRef]
- Villalobos, M.; Antelo, J. A unified surface structural model for ferrihydrite: Proton charge, electrolyte binding, and arsenate adsorption. Rev. Int. Contam. Ambie 2011, 27, 139–151. [Google Scholar]
- Huang, J.-H.; Voegelin, A.; Pombo, S.A.; Lazzaro, A.; Zeyer, J.; Kretzschmar, R. Influence of arsenate adsorption to ferrihydrite, goethite, and boehmite on the kinetics of arsenate reduction by Shewanella putrefaciens strain CN-32. Environ. Sci. Technol. 2011, 45, 7701–7709. [Google Scholar] [CrossRef]
- Mamindy-Pajany, Y.; Hurel, C.; Marmier, N.; Roméo, M. Arsenic adsorption onto hematite and goethite. Comptes Rendus Chim. 2009, 12, 876–881. [Google Scholar] [CrossRef]
- Bowell, R.J. Sorption of arsenic by iron oxides and oxyhydroxides in soils. Appl. Geochem. 1994, 9, 279–286. [Google Scholar] [CrossRef]
- Ko, I.; Davis, A.P.; Kim, J.-Y.; Kim, K.-W. Effect of contact order on the adsorption of inorganic arsenic species onto hematite in the presence of humic acid. J. Hazard. Mater. 2007, 141, 53–60. [Google Scholar] [CrossRef]
- Simeoni, M.A.; Batts, B.D.; McRae, C. Effect of groundwater fulvic acid on the adsorption of arsenate by ferrihydrite and gibbsite. Appl. Geochem. 2003, 18, 1507–1515. [Google Scholar] [CrossRef]
- Aryanpour, M.; van Duin, A.C.T.; Kubicki, J.D. Development of a reactive force field for iron-oxyhydroxide systems. J. Phys. Chem. A 2010, 114, 6298–6307. [Google Scholar] [CrossRef]
- Fitts, J.P.; Machesky, M.L.; Wesolowski, D.J.; Shang, X.; Kubicki, J.D.; Flynn, G.W.; Heinz, T.F.; Eisenthal, K.B. Second-harmonic generation and theoretical studies of protonation at the water/α-TiO2 (110) interface. Chem. Phys. Lett. 2005, 411, 399–403. [Google Scholar] [CrossRef]
- Kubicki, J.D.; Paul, K.W.; Sparks, D.L. Periodic density functional theory calculations of bulk and the (010) surface of goethite. Geochem. Trans. 2008, 9. [Google Scholar] [CrossRef]
- Arts, D.; Sabur, M.A.; Al-Abadleh, H.A. Surface interactions of aromatic organoarsenical compounds with hematite nanoparticles using ATR-FTIR: Kinetic studies. J. Phys. Chem. A 2013, 117, 2195–2204. [Google Scholar]
- Bargar, J.R.; Kubicki, J.D.; Reitmeyer, R.; Davis, J.A. ATR-FTIR spectroscopic characterization of coexisting carbonate surface complexes on hematite. Geochim. Cosmochim. Acta 2005, 69, 1527–1542. [Google Scholar] [CrossRef]
- Goldberg, S.; Johnston, C.T. Mechanisms of arsenic adsorption on amorphous oxides evaluated using macroscopic measurements, vibrational spectroscopy, and surface complexation modeling. J. Colloid Interface Sci. 2001, 234, 204–216. [Google Scholar] [CrossRef]
- Sun, X.; Doner, H. An investigation of arsenate and arsenite bonding structures on goethite by FTIR. Soil Sci. 1996, 161, 865–872. [Google Scholar] [CrossRef]
- Zhao, K.; Guo, H. Behavior and mechanism of arsenate adsorption on activated natural siderite: Evidences from FTIR and XANES analysis. Environ. Sci. Pollut. Res. 2014, 21, 1944–1953. [Google Scholar] [CrossRef]
- Müller, K.; Ciminelli, V.S.T.; Dantas, M.S.S.; Willscher, S. A comparative study of As(III) and As(V) in aqueous solutions and adsorbed on iron oxy-hydroxides by Raman spectroscopy. Water Res. 2010, 44, 5660–5672. [Google Scholar] [CrossRef]
- Illera, V.; Rivera, N.A.; O’Day, P.A. Spectroscopic Characterization of Co-Precipitated Arsenic- and Iron-Bearing Sulfide Phases at Circum-Neutral pH. In Proceedings of the 2009 American Geophysical Union Fall Meeting, San Francisco, CA, USA, 14–18 December 2009.
- Manning, B.A.; Fendorf, S.E.; Goldberg, S. Surface structures and stability of arsenic(III) on goethite: Spectroscopic evidence for inner-sphere complexes. Environ. Sci. Technol. 1998, 32, 2383–2388. [Google Scholar] [CrossRef]
- Farquhar, M.L.; Charnock, J.M.; Livens, F.R.; Vaughan, D.J. Mechanisms of arsenic uptake from aqueous solution by interaction with goethite, lepidocrocite, mackinawite, and pyrite: An X-ray absorption spectroscopy study. Environ. Sci. Technol. 2002, 36, 1757–1762. [Google Scholar] [CrossRef]
- Ona-Nguema, G.; Morin, G.; Wang, Y.; Foster, A.L.; Juillot, F.; Calas, G.; Brown, G.E. XANES evidence for rapid arsenic(III) oxidation at magnetite and ferrihydrite surfaces by dissolved O2 via Fe2+-mediated reactions. Environ. Sci. Technol. 2010, 44, 5416–5422. [Google Scholar] [CrossRef]
- Tu, Y.-J.; You, C.-F.; Chang, C.-K.; Wang, S.-L. XANES evidence of arsenate removal from water with magnetic ferrite. J. Environ. Manag. 2013, 120, 114–119. [Google Scholar] [CrossRef]
- Xu, L.; Zhao, Z.; Wang, S.; Pan, R.; Jia, Y. Transformation of arsenic in offshore sediment under the impact of anaerobic microbial activities. Water Res. 2011, 45, 6781–6788. [Google Scholar] [CrossRef]
- Couture, R.-M.; Rose, J.; Kumar, N.; Mitchell, K.; Wallschläger, D.; van Cappellen, P. Sorption of arsenite, arsenate, and thioarsenates to iron oxides and iron sulfides: A kinetic and spectroscopic investigation. Environ. Sci. Technol. 2013, 47, 5652–5659. [Google Scholar] [CrossRef]
- Gao, X.; Root, R.A.; Farrell, J.; Ela, W.; Chorover, J. Effect of silicic acid on arsenate and arsenite retention mechanisms on 6-L ferrihydrite: A spectroscopic and batch adsorption approach. Appl. Geochem. 2013, 38, 110–120. [Google Scholar] [CrossRef]
- Waychunas, G.A.; Davis, J.A.; Fuller, C.C. Geometry of sorbed arsenate on ferrihydrite and crystalline FeOOH: Re-evaluation of EXAFS results and topological factors in predicting sorbate geometry, and evidence for monodentate complexes. Geochim. Cosmochim. Acta 1995, 59, 3655–3661. [Google Scholar] [CrossRef]
- Waychunas, G.A.; Rea, B.A.; Fuller, C.C.; Davis, J.A. Surface chemistry of ferrihydrite: Part 1. EXAFS studies of the geometry of coprecipitated and adsorbed arsenate. Geochim. Cosmochim. Acta 1993, 57, 2251–2269. [Google Scholar] [CrossRef]
- Ladeira, A.C.Q.; Ciminelli, V.S.T.; Duarte, H.A.; Alves, M.C.M.; Ramos, A.Y. Mechanism of anion retention from EXAFS and density functional calculations: Arsenic(V) adsorbed on gibbsite. Geochim. Cosmochim. Acta 2001, 65, 1211–1217. [Google Scholar] [CrossRef]
- Sherman, D.M.; Randall, S.R. Surface complexation of arsenic(V) to iron(III) (hydr)oxides: Structural mechanism from ab initio molecular geometries and EXAFS spectroscopy. Geochim. Cosmochim. Acta 2003, 67, 4223–4230. [Google Scholar] [CrossRef]
- Ona-Nguema, G.; Morin, G.; Juillot, F.; Calas, G.; Brown, G.E. EXAFS analysis of arsenite adsorption onto two-line ferrihydrite, hematite, goethite, and lepidocrocite. Environ. Sci. Technol. 2005, 39, 9147–9155. [Google Scholar] [CrossRef]
- Fuller, C.C.; Davis, J.A.; Waychunas, G.A. Surface chemistry of ferrihydrite: Part 2. Kinetics of arsenate adsorption and coprecipitation. Geochim. Cosmochim. Acta 1993, 57, 2271–2282. [Google Scholar] [CrossRef]
- Goldberg, S. Competitive adsorption of arsenate and arsenite on oxides and clay minerals. Soil Sci. Soc. Am. J. 2002, 66, 413–421. [Google Scholar] [CrossRef]
- Jain, A.; Raven, K.P.; Loeppert, R.H. Arsenite and arsenate adsorption on ferrihydrite: Surface charge reduction and net OH-release stoichiometry. Environ. Sci. Technol. 1999, 33, 1179–1184. [Google Scholar] [CrossRef]
- Maji, S.K.; Kao, Y.-H.; Liao, P.-Y.; Lin, Y.-J.; Liu, C.-W. Implementation of the adsorbent iron-oxide-coated natural rock (IOCNR) on synthetic As(III) and on real arsenic-bearing sample with filter. Appl. Surf. Sci. 2013, 284, 40–48. [Google Scholar] [CrossRef]
- Raven, K.P.; Jain, A.; Loeppert, R.H. Arsenite and arsenate adsorption on ferrihydrite: Kinetics, equilibrium, and adsorption envelopes. Environ. Sci. Technol. 1998, 32, 344–349. [Google Scholar] [CrossRef]
- Antelo, J.; Avena, M.; Fiol, S.; López, R.; Arce, F. Effects of pH and ionic strength on the adsorption of phosphate and arsenate at the goethite–water interface. J. Colloid Interface Sci. 2005, 285, 476–486. [Google Scholar] [CrossRef]
- Hiemstra, T.; van Riemsdijk, W.H. A surface structural approach to ion adsorption: The charge distribution (CD) model. J. Colloid Interface Sci. 1996, 179, 488–508. [Google Scholar] [CrossRef]
- Weng, L.; van Riemsdijk, W.H.; Hiemstra, T. Effects of fulvic and humic acids on arsenate adsorption to goethite: Experiments and modeling. Environ. Sci. Technol. 2009, 43, 7198–7204. [Google Scholar] [CrossRef]
- Dixit, S.; Hering, J.G. Comparison of arsenic(V) and arsenic(III) sorption onto iron oxide minerals: Implications for arsenic mobility. Environ. Sci. Technol. 2003, 37, 4182–4189. [Google Scholar] [CrossRef]
- Ngantcha, T.A.; Vaughan, R.; Reed, B.E. Modeling As(III) and As(V) removal by an iron oxide impregnated activated carbon in a binary adsorbate system. Sep. Sci. Technol. 2011, 46, 1419–1429. [Google Scholar] [CrossRef]
- Que, S.; Papelis, C.; Hanson, A.T. Predicting arsenate adsorption on iron-coated sand based on a surface complexation model. J. Environ. Eng. 2013, 139, 368–374. [Google Scholar] [CrossRef]
- Jeppu, G.P.; Clement, T.P.; Barnett, M.O.; Lee, K.-K. A scalable surface complexation modeling framework for predicting arsenate adsorption on goethite-coated sands. Environ. Eng. Sci. 2010, 27, 147–158. [Google Scholar] [CrossRef]
- Jessen, S.; Postma, D.; Larsen, F.; Nhan, P.Q.; Hoa, L.Q.; Trang, P.T.K.; Long, T.V.; Viet, P.H.; Jakobsen, R. Surface complexation modeling of groundwater arsenic mobility: Results of a forced gradient experiment in a Red River flood plain aquifer, Vietnam. Geochim. Cosmochim. Acta 2012, 98, 186–201. [Google Scholar] [CrossRef]
- Sharifa, S.U.; Davisa, R.K.; Steelea, K.F.; Kima, B.; Haysa, P.D.; Kresseb, T.M.; Fazioc, J.A. Surface complexation modeling for predicting solid phase arsenic concentrations in the sediments of the Mississippi River Valley alluvial aquifer, Arkansas, USA. Appl. Geochem. 2011, 26, 496–504. [Google Scholar] [CrossRef]
- Pakzadeh, B.; Batista, J.R. Surface complexation modeling of the removal of arsenic from ion-exchange waste brines with ferric chloride. J. Hazard. Mater. 2011, 188, 399–407. [Google Scholar] [CrossRef]
- Kanematsu, M.; Young, T.M.; Fukushi, K.; Green, P.G.; Darby, J.L. Arsenic(III,V) adsorption on a goethite-based adsorbent in the presence of major co-existing ions: Modeling competitive adsorption consistent with spectroscopic and molecular evidence. Geochim. Cosmochim. Acta 2013, 106, 404–428. [Google Scholar] [CrossRef]
- Selim, H.; Zhang, H. Modeling approaches of competitive sorption and transport of trace metals and metalloids in soils: A review. J. Environ. Qual. 2013, 42, 640–653. [Google Scholar] [CrossRef]
- Wan, J.; Simon, S.; Deluchat, V.; Dictor, M.-C.; Dagot, C. Adsorption of As(III), As(V) and dimethylarsinic acid onto synthesized lepidocrocite. J. Environ. Sci. Health Part A. Tox Hazard. Subst. Environ. Eng. 2013, 48, 1272–1279. [Google Scholar]
- Cui, Y.; Weng, L. Arsenate and phosphate adsorption in relation to oxides composition in soils: LCD modeling. Environ. Sci. Technol. 2013, 47, 7269–7276. [Google Scholar]
- Weng, L.; van Riemsdijk, W.H.; Koopal, L.K.; Hiemstra, T. Ligand and Charge Distribution (LCD) model for the description of fulvic acid adsorption to goethite. J. Colloid Interface Sci. 2006, 302, 442–457. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, 864–871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, 1133–1138. [Google Scholar] [CrossRef]
- Adamescu, A.; Hamilton, I.P.; Al-Abadleh, H.A. Thermodynamics of dimethylarsinic acid and arsenate interactions with hydrated iron-(oxyhydr)oxide clusters: DFT calculations. Environ. Sci. Technol. 2011, 45, 10438–10444. [Google Scholar] [CrossRef]
- He, G.; Zhang, M.; Pan, G. Influence of pH on initial concentration effect of arsenate adsorption on TiO2 surfaces: Thermodynamic, DFT, and EXAFS interpretations. J. Phys. Chem. C 2009, 113, 21679–21686. [Google Scholar] [CrossRef]
- Zhang, N.; Blowers, P.; Farrell, J. Evaluation of density functional theory methods for studying chemisorption of arsenite on ferric hydroxides. Environ. Sci. Technol. 2005, 39, 4816–4822. [Google Scholar] [CrossRef]
- Adamescu, A.; Mitchell, W.; Hamilton, I.P.; Al-Abadleh, H.A. Insights into the surface complexation of dimethylarsinic acid on iron (oxyhydr)oxides from ATR-FTIR studies and quantum chemical calculations. Environ. Sci. Technol. 2010, 44, 7802–7807. [Google Scholar] [CrossRef]
- Kubicki, J.D.; Kwon, K.D.; Paul, K.W.; Sparks, D.L. Surface complex structures modelled with quantum chemical calculations: Carbonate, phosphate, sulphate, arsenate and arsenite. Eur. J. Soil Sci. 2007, 58, 932–944. [Google Scholar] [CrossRef]
- Tofan-Lazar, J.; Al-Abadleh, H. ATR-FTIR studies on the adsorption/desorption kinetics of dimethylarsinic acid on iron-(oxyhydr)oxides. J. Phys. Chem. A 2012, 116, 1596–1604. [Google Scholar] [CrossRef]
- Tofan-Lazar, J.; Al-Abadleh, H. Kinetic ATR-FTIR studies on phosphate adsorption on iron (oxyhydr)oxides in the absence and presence of surface arsenic: Molecular-level insights into the ligand exchange mechanism. J. Phys. Chem. A 2012, 116, 10143–10149. [Google Scholar] [CrossRef]
- Farrell, J.; Chaudhary, B.K. Understanding arsenate reaction kinetics with ferric hydroxides. Environ. Sci. Technol. 2013, 47, 8342–8347. [Google Scholar]
- Zhu, M.; Paul, K.W.; Kubicki, J.D.; Sparks, D.L. Quantum chemical study of arsenic(III,V) adsorption on Mn-oxides: Implications for arsenic(III) oxidation. Environ. Sci. Technol. 2009, 43, 6655–6661. [Google Scholar] [CrossRef]
- Blanchard, M.; Morin, G.; Lazzeri, M.; Balan, E.; Dabo, I. First-principles simulation of arsenate adsorption on the (1Ī 2) surface of hematite. Geochim. Cosmochim. Acta 2012, 86, 182–195. [Google Scholar] [CrossRef]
- Blanchard, M.; Wright, K.; Gale, J.D.; Catlow, C.R.A. Adsorption of As(OH)3 on the (001) surface of FeS2 pyrite: A quantum-mechanical DFT Study. J. Phys. Chem. C 2007, 111, 11390–11396. [Google Scholar] [CrossRef]
- Duarte, G.; Ciminelli, V.S.T.; Dantas, M.S.S.; Duarte, H.A.; Vasconcelos, I.F.; Oliveira, A.F.; Osseo-Asare, K. As(III) immobilization on gibbsite: Investigation of the complexation mechanism by combining EXAFS analyses and DFT calculations. Geochim. Cosmochim. Acta 2012, 83, 205–216. [Google Scholar] [CrossRef]
- Goffinet, C.J.; Mason, S.E. Comparative DFT study of inner-sphere As(III) complexes on hydrated α-Fe2O3 (0001) surface models. J. Environ. Monit. 2012, 14, 1860–1871. [Google Scholar] [CrossRef]
- Loring, J.; Sandström, M.; Norén, K.; Persson, P. Rethinking arsenate coordination at the surface of goethite. Chem. Eur. J. 2009, 15, 5063–5072. [Google Scholar] [CrossRef]
- Oliveira, A.F.; Ladeira, A.C.Q.; Ciminelli, V.S.T.; Heine, T.; Duarte, H.A. Structural model of arsenic(III) adsorbed on gibbsite based on DFT calculations. J. Mol. Struct. Theochem. 2006, 762, 17–23. [Google Scholar] [CrossRef]
- Otte, K.; Schmahl, W.W.; Pentcheva, R. DFT+ U study of arsenate adsorption on FeOOH surfaces: Evidence for competing binding mechanisms. J. Phys. Chem. C 2013, 117, 15571–15582. [Google Scholar] [CrossRef]
- Stachowicz, M.; Hiemstra, T.; van Riemsdijk, W.H. Surface speciation of As(III) and As(V) in relation to charge distribution. J. Colloid Interface Sci. 2006, 302, 62–75. [Google Scholar] [CrossRef]
- Tanaka, M.; Takahashi, Y.; Yamaguchi, N. A study on adsorption mechanism of organoarsenic compounds on ferrihydrite by XAFS. J. Phys. Conf. Ser. 2013, 430, 012100. [Google Scholar] [CrossRef]
- Klamt, A.; Jonas, V.; Bürger, T.; Lohrenz, J.C.W. Refinement and parametrization of COSMO-RS. J. Phys. Chem. A 1998, 102, 5074–5085. [Google Scholar] [CrossRef]
- Delley, B. The conductor-like screening model for polymers and surfaces. Mol. Simul. 2006, 32, 117–123. [Google Scholar] [CrossRef]
- Kubicki, J.D.; Paul, K.W.; Kabalan, L.; Zhu, Q.; Mrozik, M.K.; Aryanpour, M.; Pierre-Louis, A.-M.; Strongin, D.R. ATR-FTIR and density functional theory study of the structures, energetics, and vibrational spectra of phosphate adsorbed onto goethite. Langmuir 2012, 28, 14573–14587. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; Nakatsuji, H.; Caricato, M.; Li, X.; Hratchian, H.P.; Izmaylov, A.F.; Bloino, J.; Zheng, G.; Sonnenberg, J.L.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Vreven, T.; Montgomery, J.A., Jr.; Peralta, J.E.; Ogliaro, F.; Bearpark, M.; Heyd, J.J.; Brothers, E.; Kudin, K.N.; Staroverov, V.N.; Kobayashi, R.; Normand, J.; Raghavachari, K.; Rendell, A.; Burant, J.C.; Iyengar, S.S.; Tomasi, J.; Cossi, M.; Rega, N.; Millam, N.J.; Klene, M.; Knox, J.E.; Cross, J.B.; Bakken, V.; Adamo, C.; Jaramillo, J.; Gomperts, R.; Stratmann, R.E.; Yazyev, O.; Austin, A.J.; Cammi, R.; Pomelli, C.; Ochterski, J.W.; Martin, R.L.; Morokuma, K.; Zakrzewski, V.G.; Voth, G.A.; Salvador, P.; Dannenberg, J.J.; Dapprich, S.; Daniels, A.D.; Farkas, Ö.; Foresman, J.B.; Ortiz, J.V.; Cioslowski, J.; Fox, D.J. Gaussian 09, Revision B.01; Gaussian, Inc.: Wallingford CT, USA, 2009. Available online: http://www.gaussian.com/g_tech/g_ur/m_citation.htm (accessed on 10 March 2014).
- Curtiss, L.; Redfern, P.; Raghavachari, K. Gaussian-3X (G3X) theory: Use of improved geometries, zero-point energies, and Hartree–Fock basis sets. J. Chem. Phys. 2001, 114, 108–117. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. Density functionals with broad applicability in chemistry. Acc. Chem. Res. 2008, 41, 157–167. [Google Scholar] [CrossRef]
- Leach, A.R. Energy Minimisation and Related Methods for Exploring the Energy Surface. In Molecular Modelling: Principles and Applications; Prentice Hall: Upper Saddle River, NJ, USA, 2001; pp. 253–302. [Google Scholar]
- Szabo, A.; Ostlund, N.S. The Hartree-Fock Approximation. In Modern Quantum Chemistry; Dover Publications: Mineola, NY, USA, 1989; pp. 108–230. [Google Scholar]
- Møller, C.; Plesset, M.S. Note on an approximation treatment for many-electron systems. Phys. Rev. 1934, 46, 618–622. [Google Scholar] [CrossRef]
- Levine, I.N. Electronic Structure of Diatomic Molecules. In Quantum Chemistry; Pearson: Upper Saddle River, NJ, USA, 2009; pp. 369–373. [Google Scholar]
- Levine, I.N. The Variation Method. In Quantum Chemistry; Pearson: Upper Saddle River, NJ, USA, 2009; pp. 211–247. [Google Scholar]
- Matta, C.F.; Boyd, R.J. An Introduction to the Quantum Theory of Atoms in Molecules. In A Chemist’s Guide to Density Functional Theory; Koch, W., Holthausen, M.C., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2001; pp. 1–34. [Google Scholar]
- Korth, M.; Grimme, S. “Mindless” DFT benchmarking. J. Chem. Theory Comput. 2009, 5, 993–1003. [Google Scholar] [CrossRef]
- Becke, A.D. A new mixing of Hartree–Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Bachrach, S.M. Quantum Mechanics for Organic Chemistry. In Computational Organic Chemistry; John Wiley & Sons: Hoboken, NJ, USA, 2007; pp. 8–11. [Google Scholar]
- Clark, T.; Chandrasekhar, J.; Spitznagel, G.W.; Schleyer, P.V.R. Efficient diffuse function-augmented basis sets for anion calculations. III. The 3-21+G basis set for first-row elements, Li-F. J. Comput. Chem. 1983, 4, 294–301. [Google Scholar] [CrossRef]
- Krishnan, R.; Brinkley, J.S.; Seeger, R.; Pople, J.A. Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- Papajak, E.; Zheng, J.; Xu, X.; Leverentz, H.R.; Truhlar, D.G. Perspectives on basis sets beautiful: Seasonal plantings of diffuse basis functions. J. Chem. Theory Comput. 2011, 7, 3027–3034. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B. 1993, 48, 13115–13118. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J.; Hafner, J. Theory of the crystal structures of selenium and tellurium: The effect of generalized-gradient corrections to the local-density approximation. Phys. Rev. B 1994, 50, 13181–13185. [Google Scholar] [CrossRef]
- Myneni, S.C.B.; Traina, S.J.; Waychunas, G.A.; Logan, T.J. Experimental and theoretical vibrational spectroscopic evaluation of arsenate coordination in aqueous solutions, solids, and at mineral-water interfaces. Geochim. Cosmochim. Acta 1998, 62, 3285–3300. [Google Scholar] [CrossRef]
- Cancès, E.; Mennucci, B.; Tomasi, J. A new integral equation formalism for the polarizable continuum model: Theoretical background and applications to isotropic and anisotropic dielectrics. J. Chem. Phys. 1997, 107, 3032–3041. [Google Scholar] [CrossRef]
- Perdew, J.; Burke, K.; Ernzerhof, M. Errata: Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 78, 1396. [Google Scholar] [CrossRef]
- Perdew, J.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. A new local density functional for main-group thermochemistry, transition metal bonding, thermochemical kinetics, and noncovalent interactions. J. Chem. Phys. 2006, 125, 194101. [Google Scholar] [CrossRef]
- Szytuła, A.; Burewicz, A.; Dimitrijević, Ž.; Kraśnicki, S.; Rżany, H.; Todorović, J.; Wanic, A.; Wolski, W. Neutron diffraction studies of α-FeOOH. Phys. Status Solidi 1968, 26, 429–434. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.J.; Sutton, A.P. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+ U study. Phys. Rev. B 1998, 57, 1505–1509. [Google Scholar] [CrossRef]
- Rollmann, G.; Rohrbach, A.; Entel, P.; Hafner, J. First-principles calculation of the structure and magnetic phases of hematite. Phys. Rev. B 2004, 69, 165107. [Google Scholar] [CrossRef]
- Coey, J.M.D.; Barry, A.; Brotto, J.; Rakoto, H.; Brennan, S.; Mussel, W.N.; Collomb, A.; Fruchart, D. Spin flop in goethite. J. Phys. Condens. Matter 1995, 7, 759–768. [Google Scholar] [CrossRef]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511. [Google Scholar] [CrossRef]
- Leung, K.; Nielsen, I.M.B.; Criscenti, L.J. Elucidating the bimodal acid-base behavior of the water-silica interface from first principles. J. Am. Chem. Soc. 2009, 131, 18358–18365. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, C.; Thornton, G.; Michaelides, A. Structure and dynamics of liquid water on rutile TiO2(110). Phys. Rev. B 2010, 82, 161415. [Google Scholar] [CrossRef]
- Kelly, C.P.; Cramer, C.J.; Truhlar, D.G. Adding explicit solvent molecules to continuum solvent calculations for the calculation of aqueous acid dissociation constants. J. Phys. Chem. A 2006, 110, 2493–2499. [Google Scholar] [CrossRef]
- Felipe, M.A.; Xiao, Y.; Kubicki, J.D. Molecular orbital modeling and transition state theory in geochemistry. Rev. Mineral. Geochem. 2001, 42, 485–531. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. Design of density functionals that are broadly accurate for thermochemistry, thermochemical kinetics, and nonbonded interactions. J. Phys. Chem. A 2005, 109, 5656–5667. [Google Scholar] [CrossRef]
- Sarotti, A.M.; Pellegrinet, S.C. Application of the multi-standard methodology for calculating 1H NMR chemical shifts. J. Org. Chem. 2012, 77, 6059–6065. [Google Scholar] [CrossRef]
- Sarotti, A.M.; Pellegrinet, S.C. A multi-standard approach for GIAO 13C NMR calculations. J. Org. Chem. 2009, 74, 7254–7260. [Google Scholar] [CrossRef]
- Villalobos, M.; Pérez-Gallegos, A. Goethite surface reactivity: A macroscopic investigation unifying proton, chromate, carbonate, and lead(II) adsorption. J. Colloid Interface Sci. 2008, 326, 307–323. [Google Scholar] [CrossRef]
- Villalobos, M.; Cheney, M.A.; Alcaraz-Cienfuegos, J. Goethite surface reactivity: II. A microscopic site-density model that describes its surface area-normalized variability. J. Colloid Interface Sci. 2009, 336, 412–422. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Watts, H.D.; Tribe, L.; Kubicki, J.D. Arsenic Adsorption onto Minerals: Connecting Experimental Observations with Density Functional Theory Calculations. Minerals 2014, 4, 208-240. https://doi.org/10.3390/min4020208
Watts HD, Tribe L, Kubicki JD. Arsenic Adsorption onto Minerals: Connecting Experimental Observations with Density Functional Theory Calculations. Minerals. 2014; 4(2):208-240. https://doi.org/10.3390/min4020208
Chicago/Turabian StyleWatts, Heath D., Lorena Tribe, and James D. Kubicki. 2014. "Arsenic Adsorption onto Minerals: Connecting Experimental Observations with Density Functional Theory Calculations" Minerals 4, no. 2: 208-240. https://doi.org/10.3390/min4020208