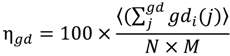3. Results and Discussion
In our previous study of the water|quartz interface, atom number densities (for O- and H-atoms) and orientational sorting (distinguishing between H-atoms that point toward or away from the surface) were used to characterize surface adsorption sites of water and to understand how the dielectric constant of water changes when moving from bulk water to the surface [
5]. Three surface water adsorption sites were identified (
Figure 5) wherein the primary site (labeled S1 in [
5]) consists of a mixture of water that has either (a) both H-atoms pointing away from the surface, or (b) one O-H bonding vector parallel to the surface and one H-atom pointing away from the surface. In this case, waters at the primary adsorption site (S1) would be expected to form at most a single H-bond with a surface –SiOH group. The secondary adsorption site (S2) was found to have both H-atoms of water pointed toward the surface, and was proposed to consist of H
2O wherein each –OH group donates an H-bond to different silanol groups, effectively bridging those groups. The third and final site (S3) was found to derive exclusively from waters that had their –OH vectors parallel to the surface (H-side) and were believed to contribute exclusively to the stable water-water hydrogen bond network. In this case, only a single H-bond from a surface silanol to water would be expected.
Figure 5.
Identification of two of the three surface adsorption sites of H2O on quartz (reproduced with permission from the author). Site S3 is not at a fixed location and is thus not illustrated. Comparisons of the ideal and actual surface coverage values (waters with direct H-bonding interaction with surface –SiOH groups) are presented alongside the percentage of surface bound waters in sites S2 and the combined S1 + S3 sites (which cannot be distinguished using the H-bond distributions).
Figure 5.
Identification of two of the three surface adsorption sites of H2O on quartz (reproduced with permission from the author). Site S3 is not at a fixed location and is thus not illustrated. Comparisons of the ideal and actual surface coverage values (waters with direct H-bonding interaction with surface –SiOH groups) are presented alongside the percentage of surface bound waters in sites S2 and the combined S1 + S3 sites (which cannot be distinguished using the H-bond distributions).
Here, a complementary understanding of the hydrogen bond network of water is obtained; the atom densities are deconstructed into their contributions from both water-water and water-silanol interactions, and the dynamic behavior of the resulting intermolecular networks is elucidated. Beginning with the simplest topological analysis, the distribution of H-bonds over each water and surface silanol group was first examined.
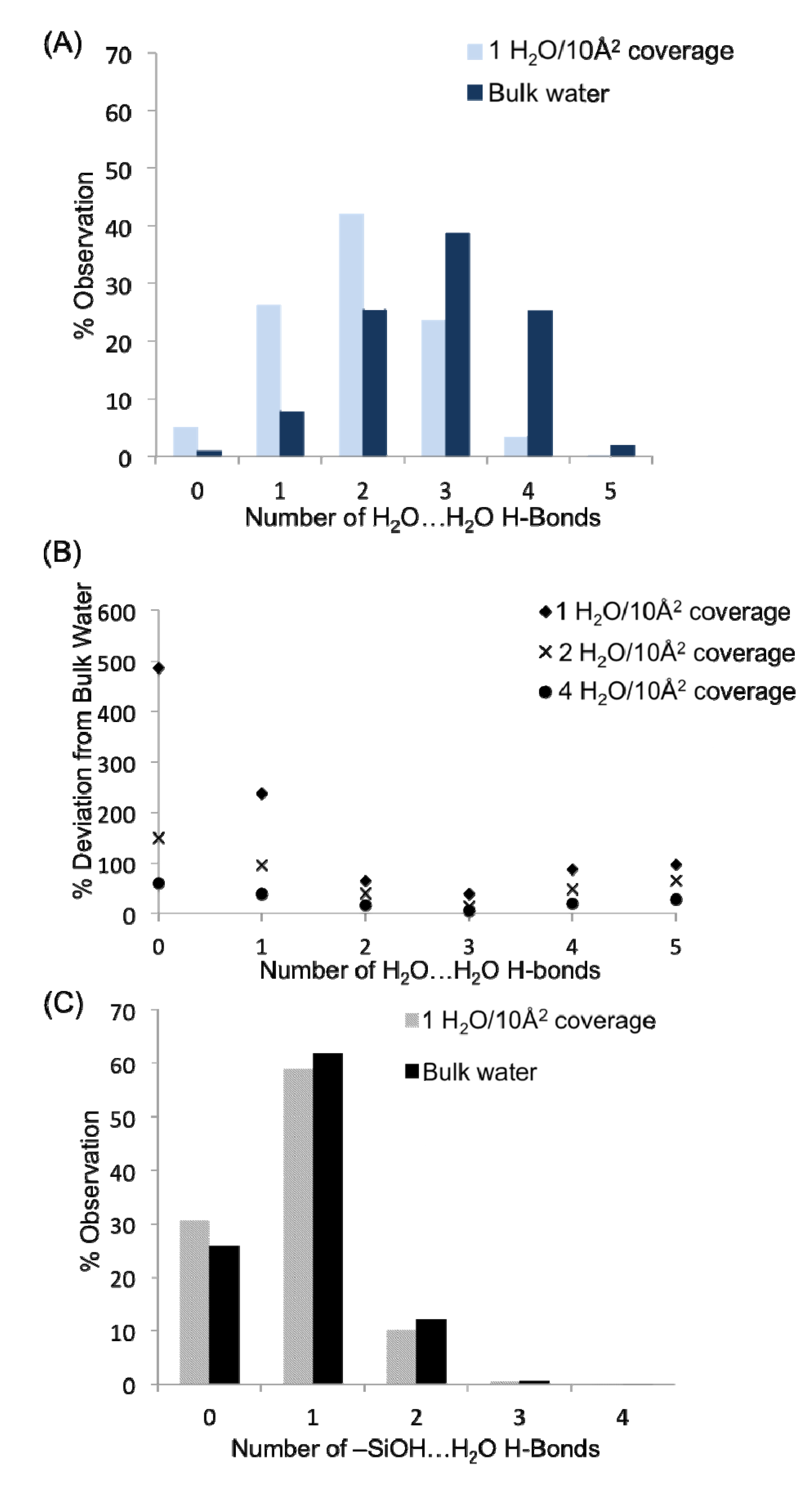
Figure 6A presents a comparison of the hydrogen bond distributions for all water-water H-bonds in the monolayer (1 H
2O/10 Å
2) and bulk systems. Within the two plots, it is apparent that the water-water H-bond distributions (the concentration of waters in the system with a specific number of H-bonds) are quite different in the monolayer system
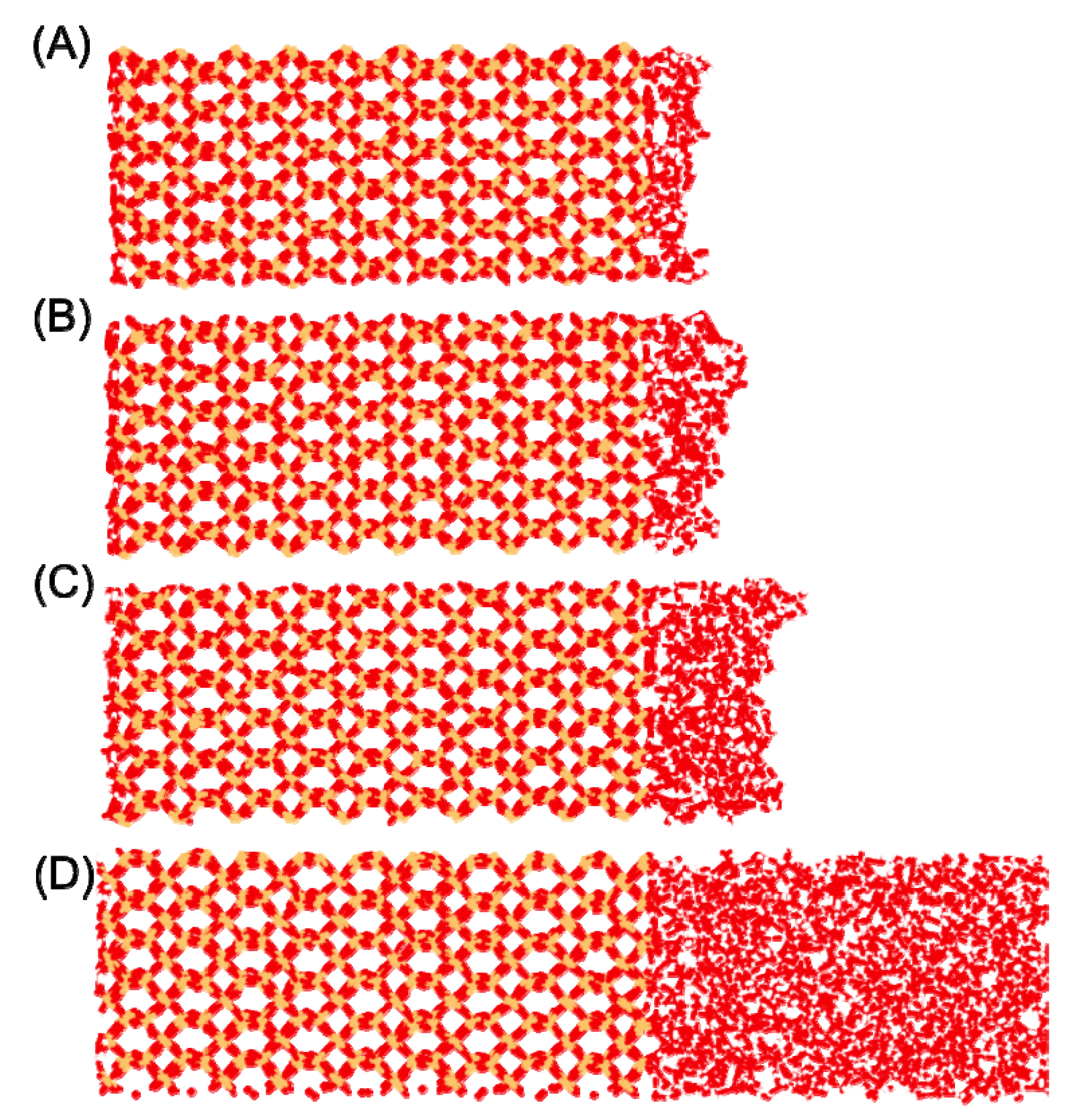
vs. the bulk solution in contact with quartz. This is unsurprising given that waters in the monolayer do not have the benefit of hydrogen bonding with layers of water farther from the surface (though some surface aggregation is observed,
vide infra), in addition to an appreciable fraction of water H-bonds that are tied up with H-bonds to the surface silanol groups. The large concentration of waters with one or two H-bonds agrees very well with the three adsorption sites found previously, in that most waters with the descriptions provided for sites S1–S3 should only have 1–2 H-bonds. Thus, at a monolayer of coverage the average number of water-water H-bonds per molecule is 2.04, significantly less than in bulk water (2.88 H-bonds per molecule). It is possible to determine at what point in the hydration level the system becomes similar to the bulk water over the quartz by considering the % deviation in the concentration of waters with zero, one, two, three, four and five H-bonds from the bulk water values as one progresses from the monolayer to the bilayer and then tetralayer (
Figure 6B). While it is not surprising that the H-bond distribution becomes more “bulk”-like as water is added to the quartz surface, it is interesting how similar even the bilayer is to the bulk system—thus the water-water H-bonds between layers plays a significant role in filling out the water H-bond coordination sphere, helping to progress to the bulk H-bond distribution values. Important deviations in the hydrogen bond distributions relative to bulk still appear at a tetralayer of coverage (4 H
2O/10 Å
2); however, these are mostly attributable to the water|vapor interface (
Figure 1) which causes an appreciable concentration of water molecules with only one or two H-bonds (1% and 11%, respectfully for the 4 H
2O/10 Å
2 system).
The distributions of the H-bonds to the surface silanol groups can be examined from the perspective of the surface –SiOH groups as well as from the perspective of the surface H
2O molecules.
Figure 6C presents the H-bond distribution of the surface –SiOH groups for a monolayer of coverage
vs. the bulk. The H-bond distributions for the two systems are quite similar, indicating that the fundamental H-bonding interaction of water with the surface is relatively unchanged in the presence of the bulk liquid. The majority of silanol groups are found to form a single H-bond with water; however nearly 30% do not have any hydrogen bonds that fit within the designated criterion for the H-bond defined above. Recall that the H-bond criteria for the water-silanol interaction was optimized so as to prevent large populations of waters with unphysical over-coordination (5 or 6 H-bonds), and thus the 30% of silanols with zero H-bonds may reflect a significant population of waters on the surface that have very distorted interactions with the surface –SiOH groups. These may be waters that are “sandwiched” in between silanol groups or unfavorably oriented to form an H-bond with them. Considering the H-bonds to the surface silanols from the perspective of water molecules, 42% of the H
2O in the monolayer (1 H
2O/10 Å
2) do not form a H-bond with –SiOH groups. Thus, ~73 waters have H-bond interactions with the surface that fall within a normal H-bonding range. This places the actual coverage of water on the surface at ~0.6/10 Å
2 (
Figure 5), with the remaining water either aggregating to a second layer on the surface or having a highly distorted interaction with the surface. Of those waters having a direct H-bond with the surface, 71% form a single H-bond with the surface and 27% bridge two separate silanol surface groups (
Figure 5). As such, we can place a minimum value to the population of waters at the previously mentioned site S2 (
Figure 5) at 27%, while at least 71% of the surface waters are either in site S1 or S3. In comparison with the interactions between the bulk liquid and the surface, a similar value of ~80 waters are found to have an H-bond interaction with the surface. Of those waters having a direct interaction with the surface the same distribution of waters with a single H-bond
vs. bridging waters is observed as in the monolayer of coverage discussed above. These data further support the notion that the organizational aspect of the surface interactions between water and the surface is generally unaffected by layers of water farther from the surface.
The hydrogen bond lifetime between water molecules is known to be quite sensitive to the conditions of the system (temperature and pressure) and also the organizational structure about each molecule (the H-bond distribution)
3. As such, it is not surprising that the water-water H-bond persistence does change depending upon the hydration value in a manner consistent with the systematic trends in the H-bond distributions. At the monolayer of coverage, the H-bond persistence between water molecules is found to be 123 fs, which is slightly shorter, though statistically significant, value relative to the bulk (137 fs,
Table 1, and Figure S2 in Supplemental Information). The persistence of the –SiOH…H
2O interaction is ~30% longer than the water H-bond persistence; however, it too is slightly shorter when a monolayer is present
vs. the bulk liquid above the surface (Figure S3 in Supplemental Information). These data are not entirely unsurprising, as thermal effects (librational motion) are expected to be somewhat amplified for the monolayer and the presence of the bulk liquid above the interface may stabilize the dynamics of the H-bonding network at the surface.
Figure 6.
(A) Hydrogen bond distributions as a function of water concentration between water molecules. (B) Convergence of water-water hydrogen bond distributions toward the bulk water values as a function of surface concentration of water. (C) H-bond distributions as a function of water concentration between water and surface –SiOH groups of quartz.
Figure 6.
(A) Hydrogen bond distributions as a function of water concentration between water molecules. (B) Convergence of water-water hydrogen bond distributions toward the bulk water values as a function of surface concentration of water. (C) H-bond distributions as a function of water concentration between water and surface –SiOH groups of quartz.
Table 1.
Persistence (in fs) of H2O…H2O and H2O…SiOH hydrogen bonds as a function of surface concentration of water.
Table 1.
Persistence (in fs) of H2O…H2O and H2O…SiOH hydrogen bonds as a function of surface concentration of water.
| Level of hydration | H2O…H2O H-bond | H2O…SiOH H-bond |
|---|
| 1 H2O/10Å2 (monolayer) | 123 | 162 |
| 2 H2O/10Å2 (bilayer) | 133 | 167 |
| 4 H2O/10Å2 (tetralayer) | 136 | 168 |
| Bulk | 137 | 171 |
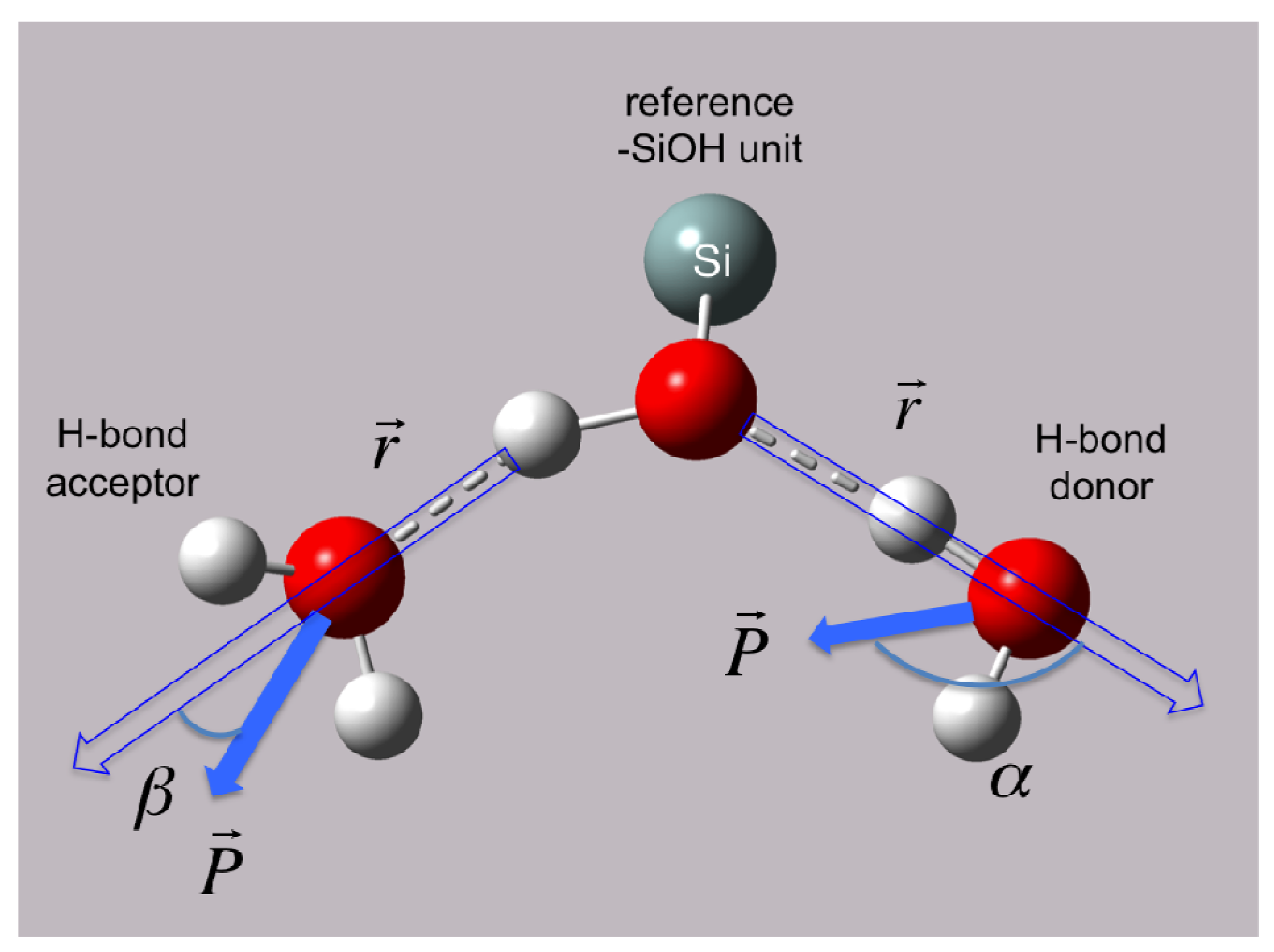
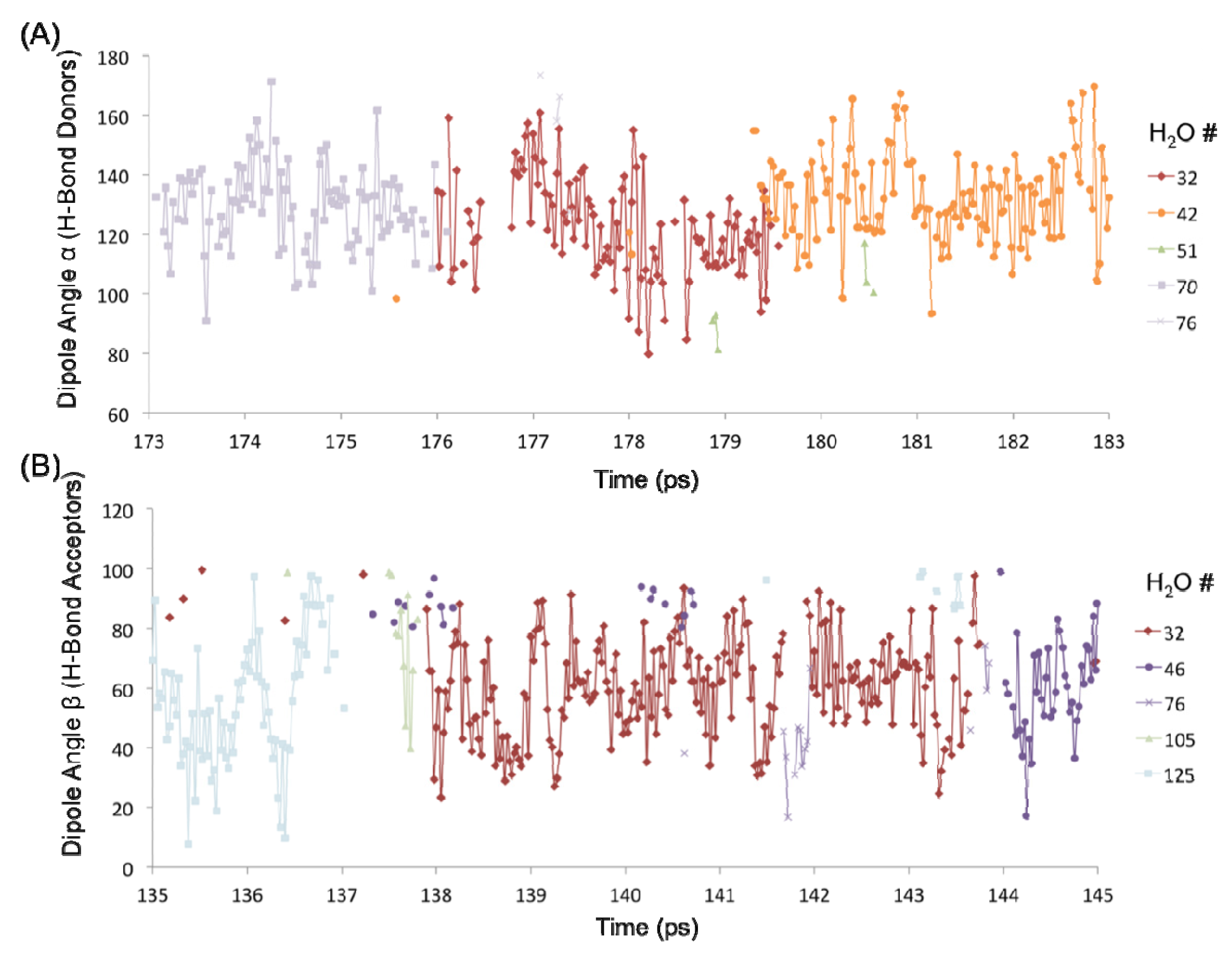
The H-bond persistence values are complemented by the study of the oscillations in the dipole angle that water forms with the surface silanol groups over time. Representative water dipole angle data are shown in
Figure 7 about two silanol groups (designated #1 and #4) in the 1 H
2O/10 Å
2 system. Here, each data point represents a water molecule either donating an H-bond to the surface silanol, or accepting an H-bond from the silanol. There is generally one molecule that is H-bonded to a silanol group at a time, consistent with the H-bond distribution of the –SiOH groups (
Figure 6C). The oscillatory behavior of the dipole angles at short time scales indicates a predominance of librational motion that leads to transient H-bond breaking as indicated by unconnected data points in
Figure 7. It has been generally accepted that librational motions, especially in water, cause an apparent breaking and reforming of a hydrogen bond on a very fast time scale, and that the dynamics on a subpicosecond timescale is primarily due to librations [
13,
14]. The observed transient breaks due to librations are the primary source of the shorter H-bond persistence values. However, the residence time of a water molecule about a surface silanol is on the order of a few picoseconds (~3–7 ps). For example, the donor H
2O molecules numbered 32, 42, and 70 are all H-bonded to silanol #1 (–SiOH group with ID 1) within the time interval 173–183 ps, each with an average residence time of ~3–4 ps (
Figure 7A). It is further observed that H
2O #32 also forms an H-bond (as an acceptor) with silanol #4 that is an immediate neighbor of silanol #1 (separated by an Si–Si distance of ~5 Å) within a time interval of 135–145 ps (
Figure 7B). Thus, the H
2O #32 travels from one silanol group to the neighboring silanol group slowly over a large time interval (~50 ps). This indicates that the dynamics of the first adsorbed layer of waters on the quartz surface tends to be non-translational, but primarily librational in character, which is in agreement with the experimentally observed structural immobility of the adsorption layer [
2,
15,
16,
17,
18].
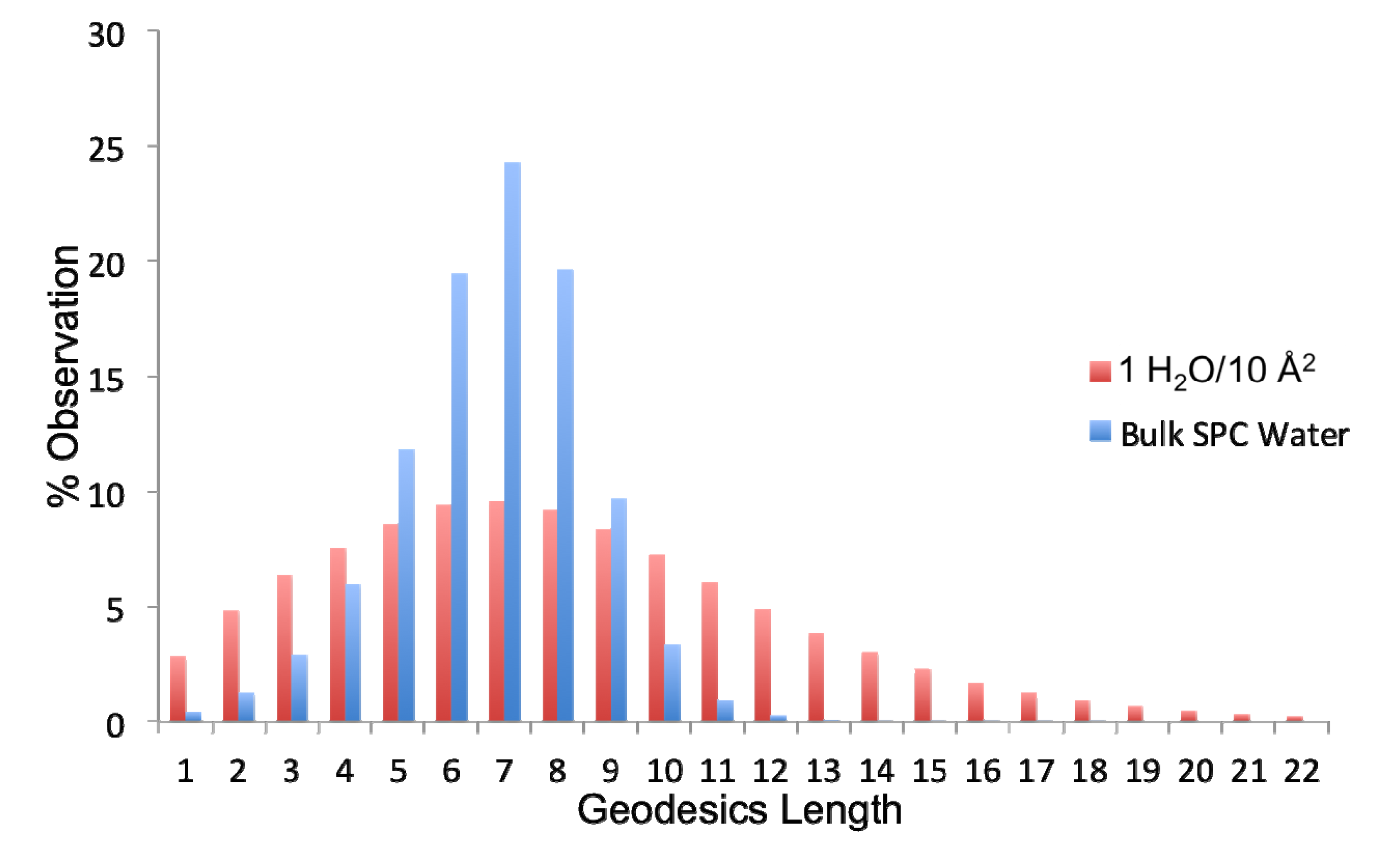
The extent of connectivity within the water-water H-bond network has been assessed using geodesic analysis. A geodesic (gd) is the shortest contiguous hydrogen bond pathway formed between two H
2O vertices. Thus the distribution of geodesics is indicative of the extent of localization of the network about any water therein. As observed in
Figure 8, bulk SPC water has a normal and fairly narrow distribution of geodesics centered around a gd length of seven H-bonds. The distribution of geodesics in the ideal monolayer of surface coverage (1 H
2O/10 Å
2) is also centered about a gd length of seven; however, it is much more broad with significant populations of geodesics of length greater than 10. Thus the average geodesic length in bulk water is 6.7, while it is 8.1 in the monolayer of surface coverage. This indicates that the surface serves to promote contiguous hydrogen bonded paths on the surface. However, when combined with the persistence of individual H-bonds between waters, we can see that this network is more fluxional than bulk water. Another metric that can be used to assess the extent of interconnectivity within the network is the geodesic index, η
gd, which is a measure of the number of geodesics (gd) each vertex
i participates in (labeled gd
i). This value is determined by:
where sum of the geodesics
j that every vertex
i participates is averaged over all atoms and then divided by the number of vertices
N (because the geodesic matrix is
N ×
N) and total number of frames,
M, multiplied by a scaling factor of 100. As a reference, consider that a perfect network of water, wherein each H
2O has exactly four H-bonds (e.g., hexagonal ice) has an η
gd value of 121.3. If there are many broken pathways within the network, then each molecule will participate in a fewer number of contiguous H-bond pathways. In bulk SPC water, η
gd has a value of 28.4, while when a single monolayer of water is present on the surface η
gd has a value of 54.9. The increase in η
gd for the monolayer waters generally derives from the fact that while there are no layers above the monolayer that would extend the geodesic pathways beyond the interfacial region the relative immobility of the surface waters enhance the likelihood of much longer geodesic chains to be formed, as observed in
Figure 8. Thus, there is a larger extension of the H-bond network laterally, which increases the total number of geodesics that each water participates in.
Figure 7.
Dipole angle oscillations on the quartz surface with the monolayer coverage. (A) Dipole angles of H2O molecules donating H-bond to the –SiOH group #1 over the time interval 173–183 ps. (B) Dipole angles of H2O molecules accepting H-bond from the –SiOH group #4 over the time interval 135–145 ps.
Figure 7.
Dipole angle oscillations on the quartz surface with the monolayer coverage. (A) Dipole angles of H2O molecules donating H-bond to the –SiOH group #1 over the time interval 173–183 ps. (B) Dipole angles of H2O molecules accepting H-bond from the –SiOH group #4 over the time interval 135–145 ps.
Figure 8.
Distribution of geodesic (gd) lengths found in bulk simple point charge (SPC) water and the ideal monolayer of water (1H2O/10 Å2).
Figure 8.
Distribution of geodesic (gd) lengths found in bulk simple point charge (SPC) water and the ideal monolayer of water (1H2O/10 Å2).