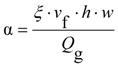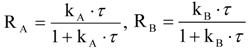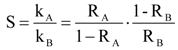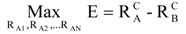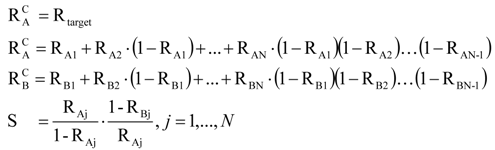1. Introduction
Flotation is used to separate valuable minerals from each other and from gangue. To reach a target metallurgical performance, usually assessed in terms of concentrate grade and recovery, feed is passed through stages such as roughing, cleaning and scavenging. All these stages comprise serial arrangements of flotation cells known as banks, lines or rows.
Although a bank is the simplest interconnection of cells in a circuit,
i.e., the tails of one cell is the feed to the next cell down the bank, how to operate each flotation cell in a way that the whole bank performance is optimized remains a challenge. Significant efforts have been made towards understanding the effect of operating variables on the flotation performance of an isolated cell [
1,
2,
3]. However in the case of banks the variables that can be manipulated increase with the number of cells in the bank and the problem of how to manipulate them to achieve optimum performance is difficult even disregarding variation in ore characteristics [
1]. In general, the more manipulated variables available the better for optimization purposes, however without clear guidance how to effectively use them it becomes an “embarrassment of riches”.
Due to their localized impact, gas rate and/or froth depth are usually used to modify the operating point of a cell in a bank. The problem then becomes to find the optimal profile (e.g., gas rate profile) that achieves the target bank metallurgical objective. This solution is not obvious and a brute force approach based on a trial-and-error search rapidly becomes intractable even for simulation. To exemplify this point, consider a bank of 9 cells and assume that only the froth depth in each cell can be manipulated, then for 10 discrete froth depth values in each cell the number of possible froth depth profiles rises to 109!
Attempts to solve this optimization problem have been proposed [
4,
5,
6] but no industrial applications have been reported.
This paper reviews three operational strategies to improve bank performance that have been successfully implemented in several industrial operations: air rate profiling, mass-pull (froth velocity) profiling, and Peak Air Recovery (PAR) air profiling. Although different in concept they are all ways of manipulating the recovery profile down a bank, which may be the property being exploited. Mathematical analysis has shown that a flat cell-by-cell recovery profile maximizes the separation of two floatable minerals for a given target bank recovery when the relative floatability is constant down the bank [
7]. It is suggested that understanding the role of recovery profiling may help to link these strategies.
3. A Recovery Profiling Approach
Although different in concept and roots the strategies described above are all ways of manipulating the recovery down the bank. In this section a strategy for optimizing banks based on cell-by-cell recovery profiling is argued. For the sake of simplicity two floatable minerals A and B are considered.
Figure 5 depicts a mass-balance on each cell of a bank composed of N cells where R
i is the recovery of cell i.
Figure 5.
Flotation bank composed of N cells.
Figure 5.
Flotation bank composed of N cells.
Making the common assumption of first-order flotation kinetics and fully mixed transport, recovery of mineral A and B in an isolated cell is given by:
where k
A and k
B are the flotation rate constants for mineral A and B and
τ is the average residence time. The relative floatability, S, is defined as the ratio of the flotation rate constants [
20] and can be expressed as a function of the recovery of each mineral.
The relative floatability provides an indication about how difficult the separation is: when S = 1 (R
A = R
B) no separation is possible. Notice that for a given relative floatability the recovery of mineral B is completely determined by the recovery of mineral A. The operational objective of a bank can be expressed as finding the recovery of A in each cell (recovery profile) such that for a target bank recovery of mineral A the bank recovery of mineral B is minimized. Taking as a measure of separation efficiency for two floatable minerals as E = R
A− R
B [
21] the operational objective is equivalent to maximizing the separation efficiency for a given target bank recovery of mineral A. Relative floatability is assumed to be constant down the bank and independent of the operation as observed at Brunswick Mine [
8]. The optimization problem can then be expressed mathematically as follows:
subject to:
where superscript C stands for cumulative.
The optimal strategy that solves this problem was found to be a flat cell-by-cell recovery profile,
i.e., each cell having the same recovery based on the feed to that cell [
7].
Figure 6 gives the general result that includes the solution for the bank recovery. This bank recovery expression is often quoted as ‘the simplified solution’ (all Rs equal) but it appears that there may be good reason to operate that way. To illustrate,
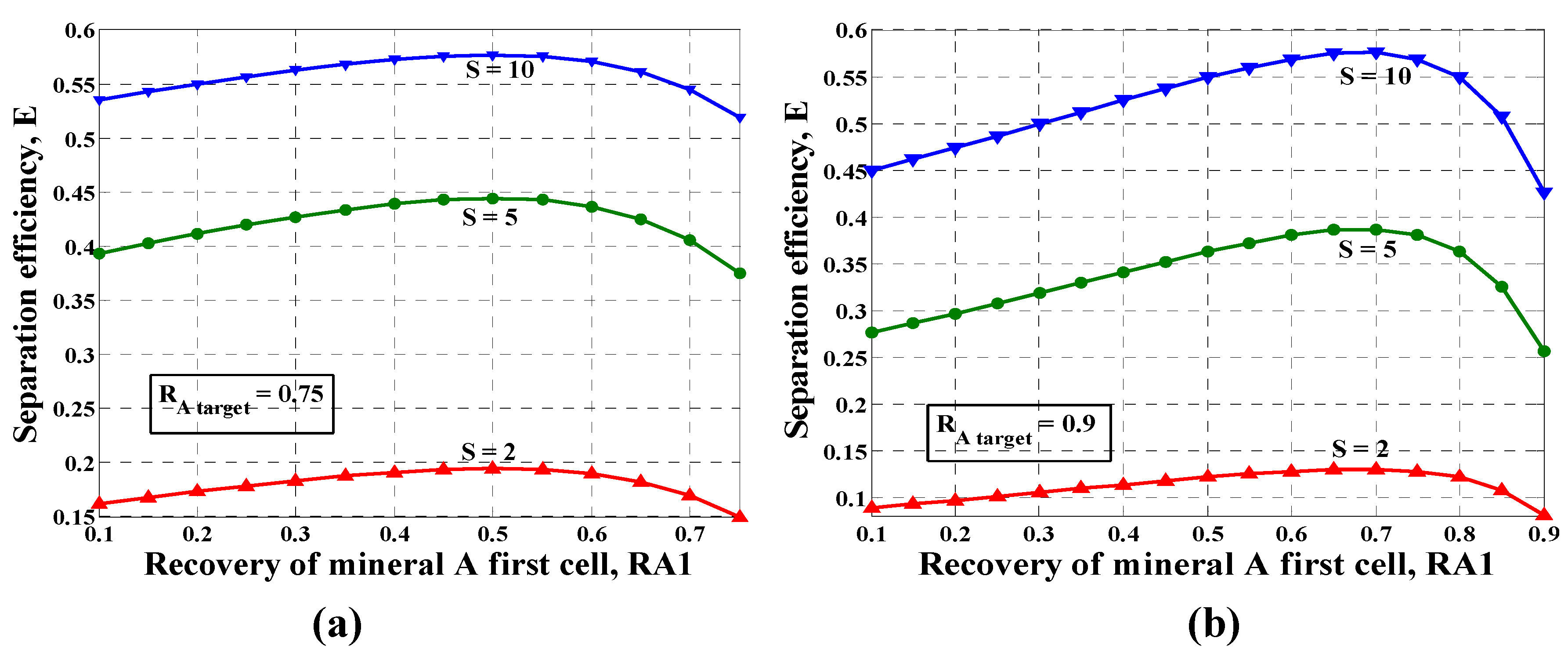
Figure 7 shows the result for a bank comprising two cells: for two target bank recoveries, 75% and 90%, the maximum separation efficiency occurs when the two cell recoveries are equal, respectively 50% and 68.4%, a result independent of S.
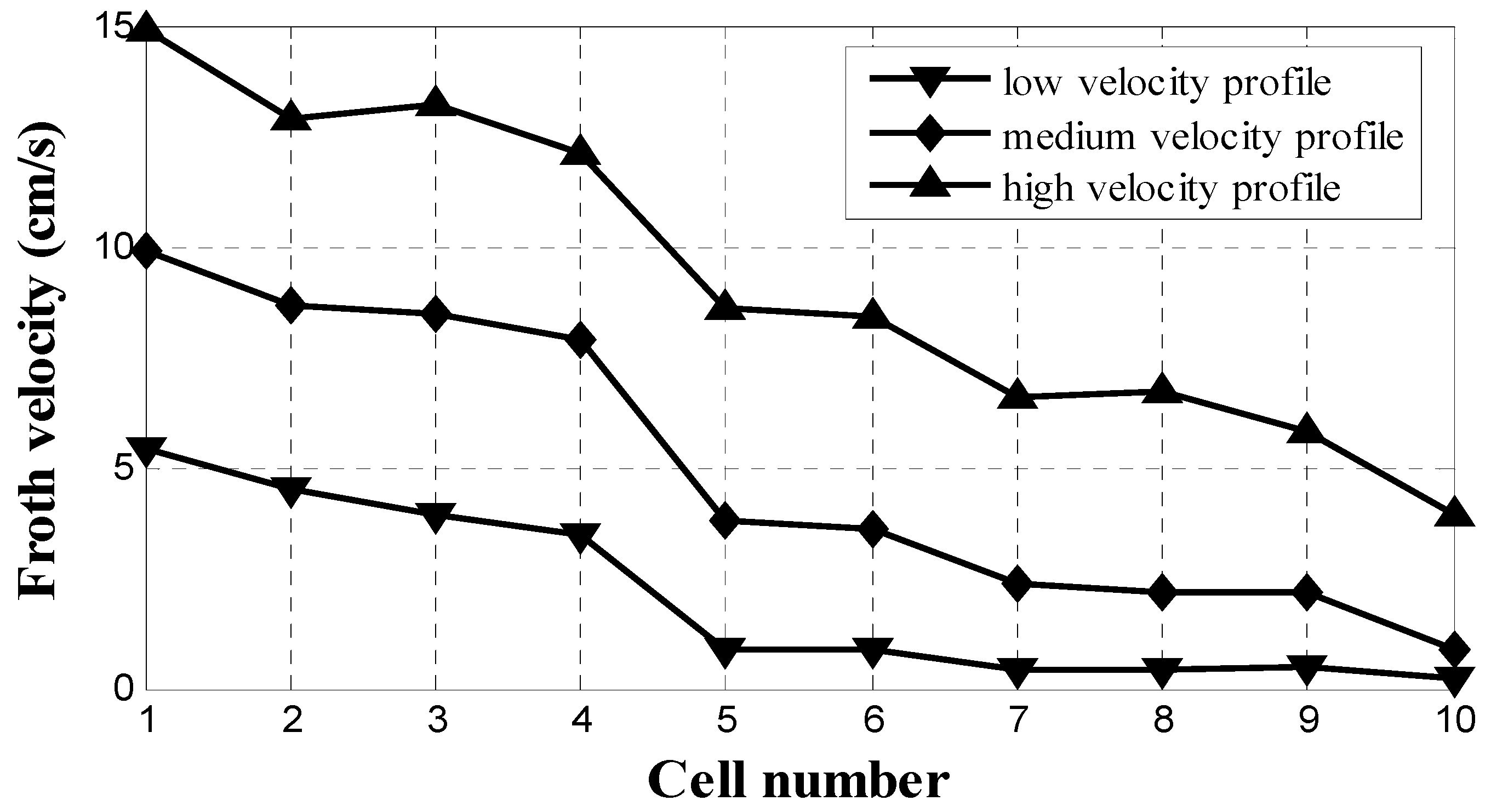
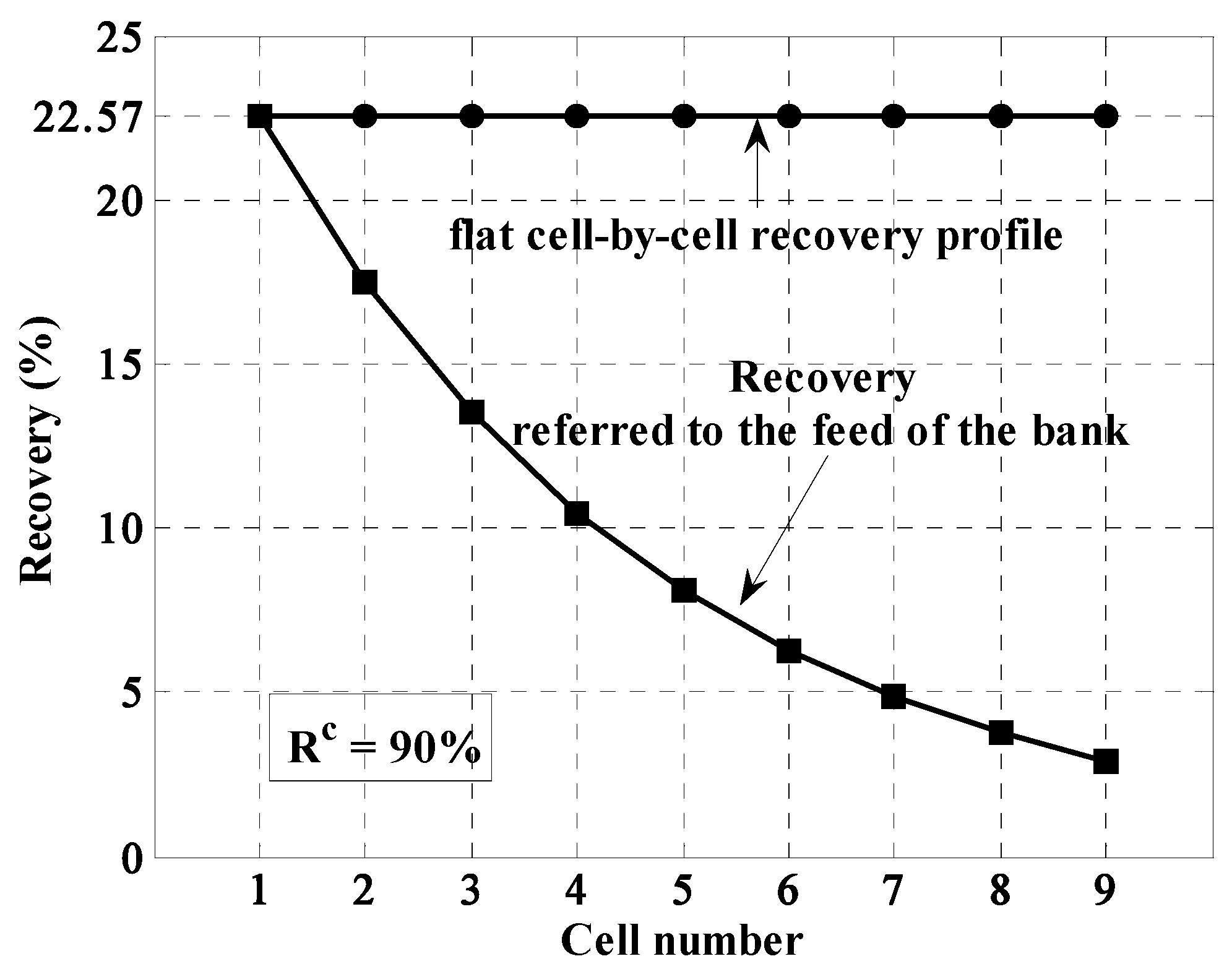
Figure 8 shows the result for a bank of 9 cells, the flat cell-by-cell recovery (recovery based on cell feed) and the corresponding recovery based on feed to the bank which shows a monotonic decrease reminiscent of the froth velocity profiles set to control mass pull (
Figure 3 and
Figure 4).
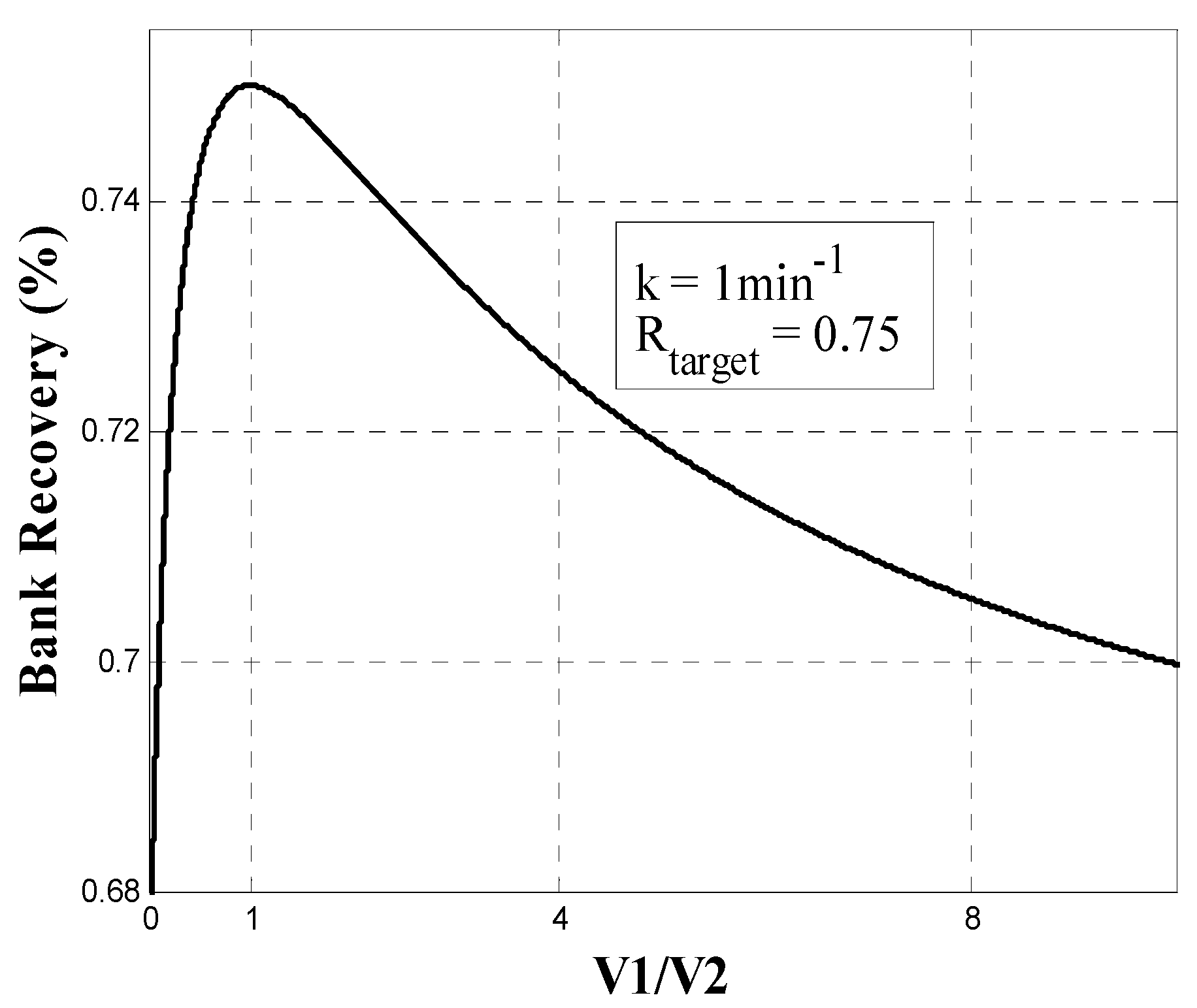
This is the result for separating two floatable minerals, which is our focus. In this case the optimum flat cell-by-cell recovery profile result is independent of changes in rate constant along the bank provided the relative rate constant is unchanged. If we allow for the moment that the rate constant is unchanged then an additional interesting property emerges relevant when recovery of a single floatable mineral is the concern (e.g., bitumen). The flat cell-by-cell recovery profile produces the maximum cumulative bank recovery for a given installed volume. This is illustrated in
Figure 9 for a 2-cell bank where the total cell volume is fixed but the volume of each cell is altered, which is equivalent to changing cell recovery. Setting total bank recovery when cells are equal volume (V
1/V
2 = 1) at 75%, we note that all other volume combinations give less than 75%. Most banks are constructed with cells of the same size and
Figure 9 demonstrates a fundamental case for doing so. Aris [
22] made an equivalent observation for any chemical reactors in series, that they should all have the same residence time, or volume.
Figure 6.
Optimal operation for two floatable minerals (flat recovery profile, i.e., each cell has same recovery R).
Figure 6.
Optimal operation for two floatable minerals (flat recovery profile, i.e., each cell has same recovery R).
Figure 7.
Separation efficiency vs. recovery of mineral A in the first cell for a bank composed of 2 cells and three relative floatabilities. (a) Target cumulative recovery of mineral A 0.75; (b) Target cumulative recovery of mineral A 0.9.
Figure 7.
Separation efficiency vs. recovery of mineral A in the first cell for a bank composed of 2 cells and three relative floatabilities. (a) Target cumulative recovery of mineral A 0.75; (b) Target cumulative recovery of mineral A 0.9.
Figure 8.
Optimal flat cell-by-cell recovery profile for a target bank recovery of 90% giving Ri = 22.57%; and recovery profile based on bank feed.
Figure 8.
Optimal flat cell-by-cell recovery profile for a target bank recovery of 90% giving Ri = 22.57%; and recovery profile based on bank feed.
Figure 9.
Two-cell bank recovery relative to bank recovery when cells are equal volume (V1/V2 = 1).
Figure 9.
Two-cell bank recovery relative to bank recovery when cells are equal volume (V1/V2 = 1).
5. Discussion
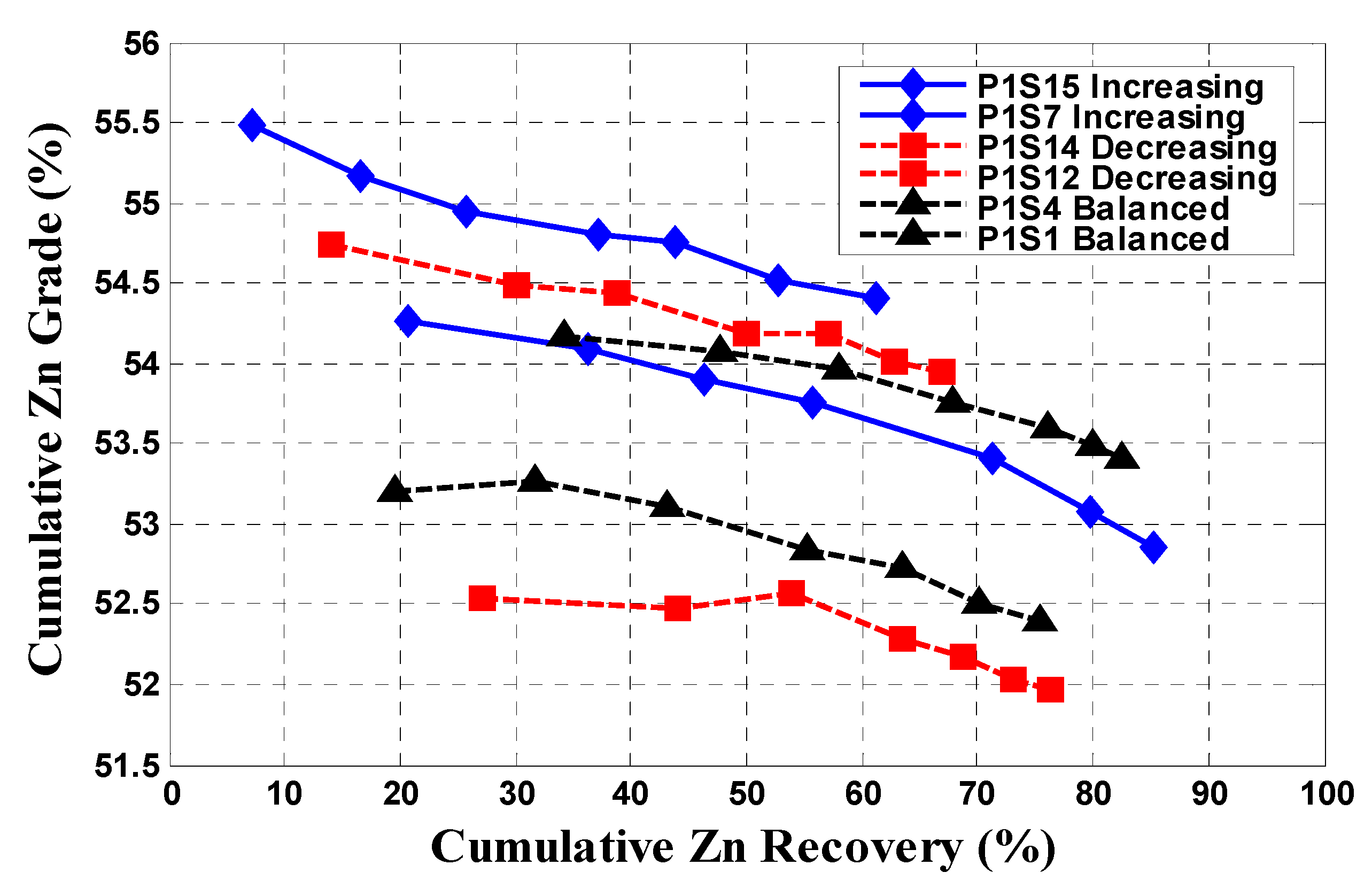
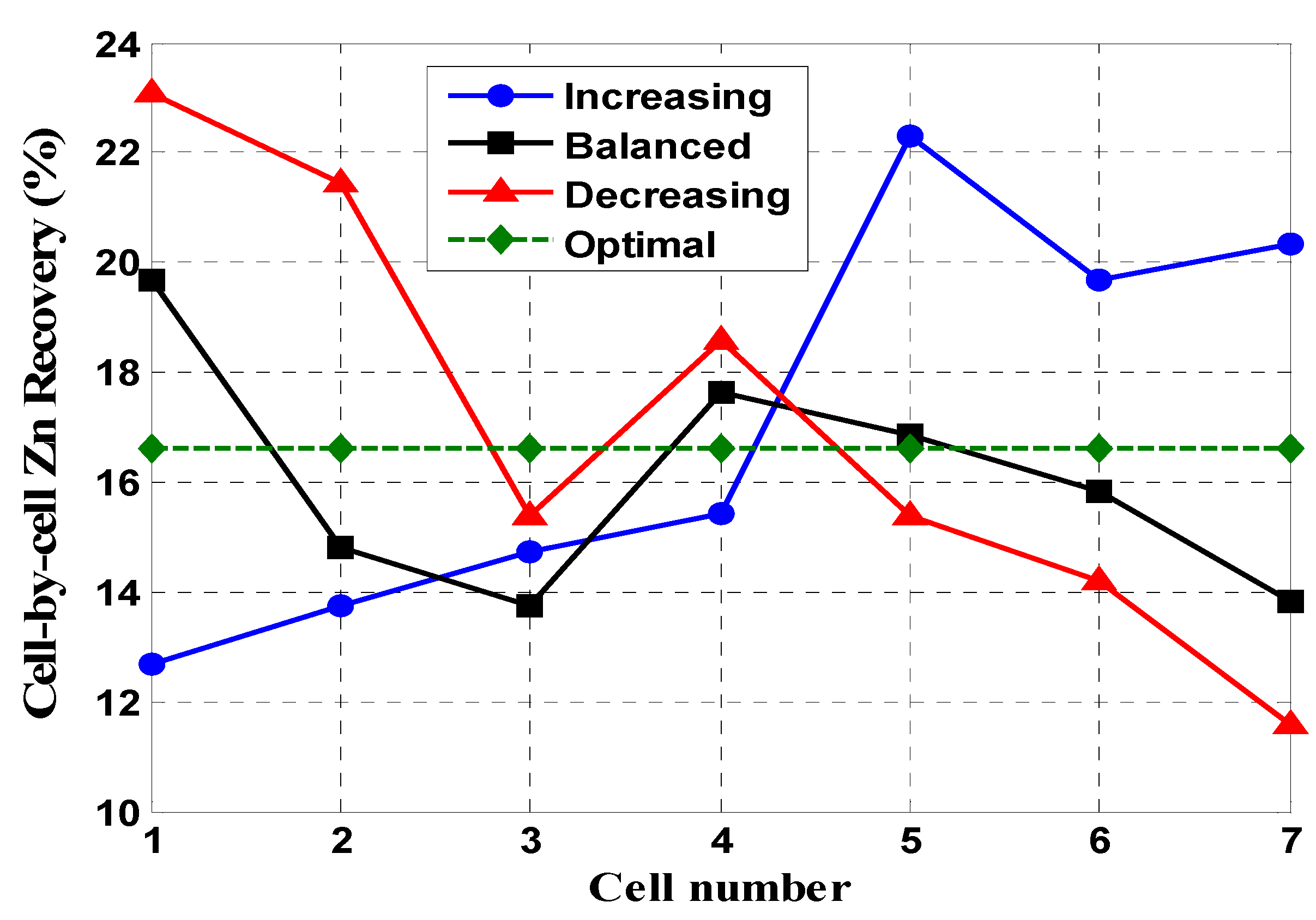
There appears to be no agreed method of operating a bank of cells to achieve optimal performance, however defined. Three strategies to search for the optimum have been described in recent literature: air rate profiling, air recovery profiling, and mass-pull profiling. We introduce the notion that the feature common to these strategies is the way recovery is distributed down the bank, the cell-by-cell recovery profile. Defining optimal as maximizing separation efficiency at a target bank recovery, what has emerged is the potential benefit of a flat cell-by-cell recovery profile. While plant data are limited, the three cases examined lend some support to this conclusion.
The mathematical analysis assumed constant relative floatability, S. The Brunswick Mine data supported this assumption and it is a more defendable than assuming a constant floatability (rate constant) [
1]. What a constant S means is that changes in physical (as opposed to chemical) variables tend to change the rate constant of different floatable minerals proportionally. Lynch
et al. [
1] noted this in the case of air rate:
“Change in the flotation rate of the Mount Isa chalcopyrite by change in aeration will change the flotation rates of all other components proportionally.” Although not stated as directly they made similar remarks regarding froth depth [
1] and we might now add bubble size as controlled by frother addition to the list of physical variables. While the validity of constant S may be debated the lesson of a flat cell-by-cell recovery profile drawn from the commonly applied kinetic model seems worth taking on board in designing strategies for bank operation. It offers to reduce the search effort by using the flat profile as a starting point.
The optimal flat cell-by-cell recovery profile is independent of how the total volume is allocated in the bank; for instance, if one cell in a bank is of different volume (size), the flat cell-by-cell recovery profile is still optimal. This is due to the fact that separation of two minerals is not related to cell volume. As noted, having equal-sized cells gives the highest ratio of bank recovery to bank cell volume. From these points, plants seeking to increase bank volume would be advised to add cells of the same volume, not larger as might be the temptation.
Air profiling is a low cost approach to improve performance of flotation banks which is encouraging its growing application. For cells provided with gas flowrate sensors it can be implemented without capital investment. In their absence, as was the case at Brunswick Mine, use was made of a gas velocity sensor [
24]. For self-aspirated cells air rate can still be controlled this time by manipulating froth depth. Although the evidence is that an increasing air rate profile will be better than other profiles it does not specify the best shape of the increasing profile nor the total bank air to be distributed. Brunswick Mine set an essentially arbitrary increasing profile shape and used total bank air as another degree of freedom to achieve target recovery.
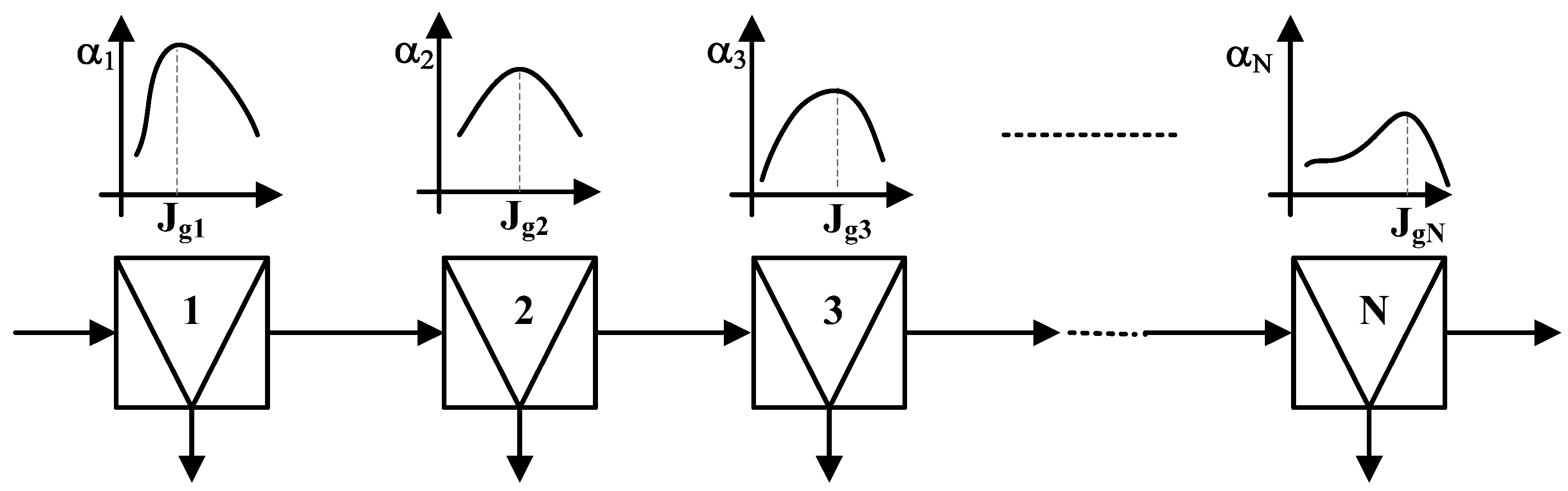
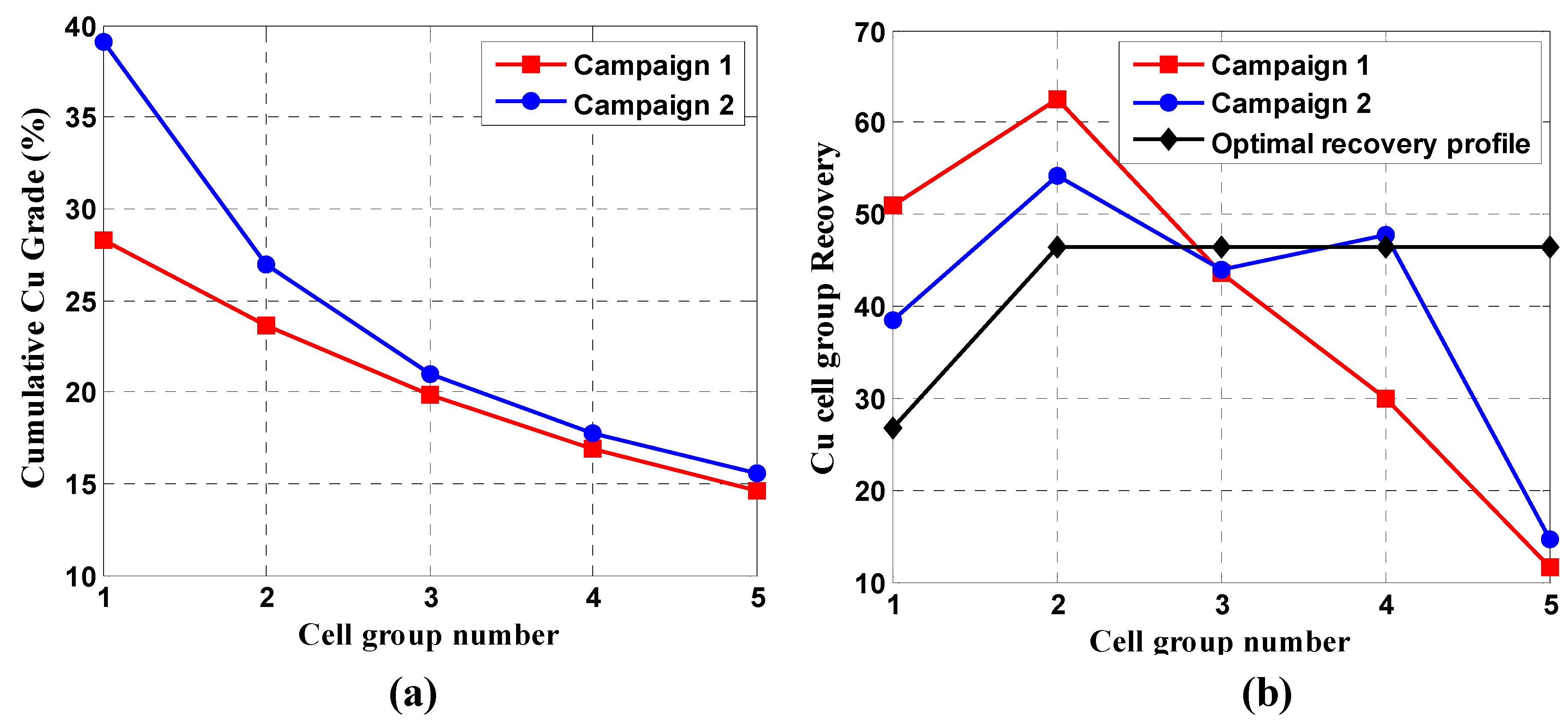
PAR air profiling translates the problem of optimizing a bank of cells to a local problem of optimizing each cell. The total bank air flowrate in this case is completely determined and corresponds to the sum of the gas rate that produces PAR in each cell (J
gT = J
g1 + J
g2 + … + J
gN, see
Figure 2). Although analysis of the data from [
23] suggested the best result also corresponded to a flat cell-by-cell recovery profile the link between PAR air profiling and recovery profiling is not clear.
A limitation in implementing the PAR strategy is the extensive measurement effort and instrumentation required on each cell to calculate air recovery. It may be possible to find a surrogate for air recovery such as equilibrium froth height which is another measure of froth stability.
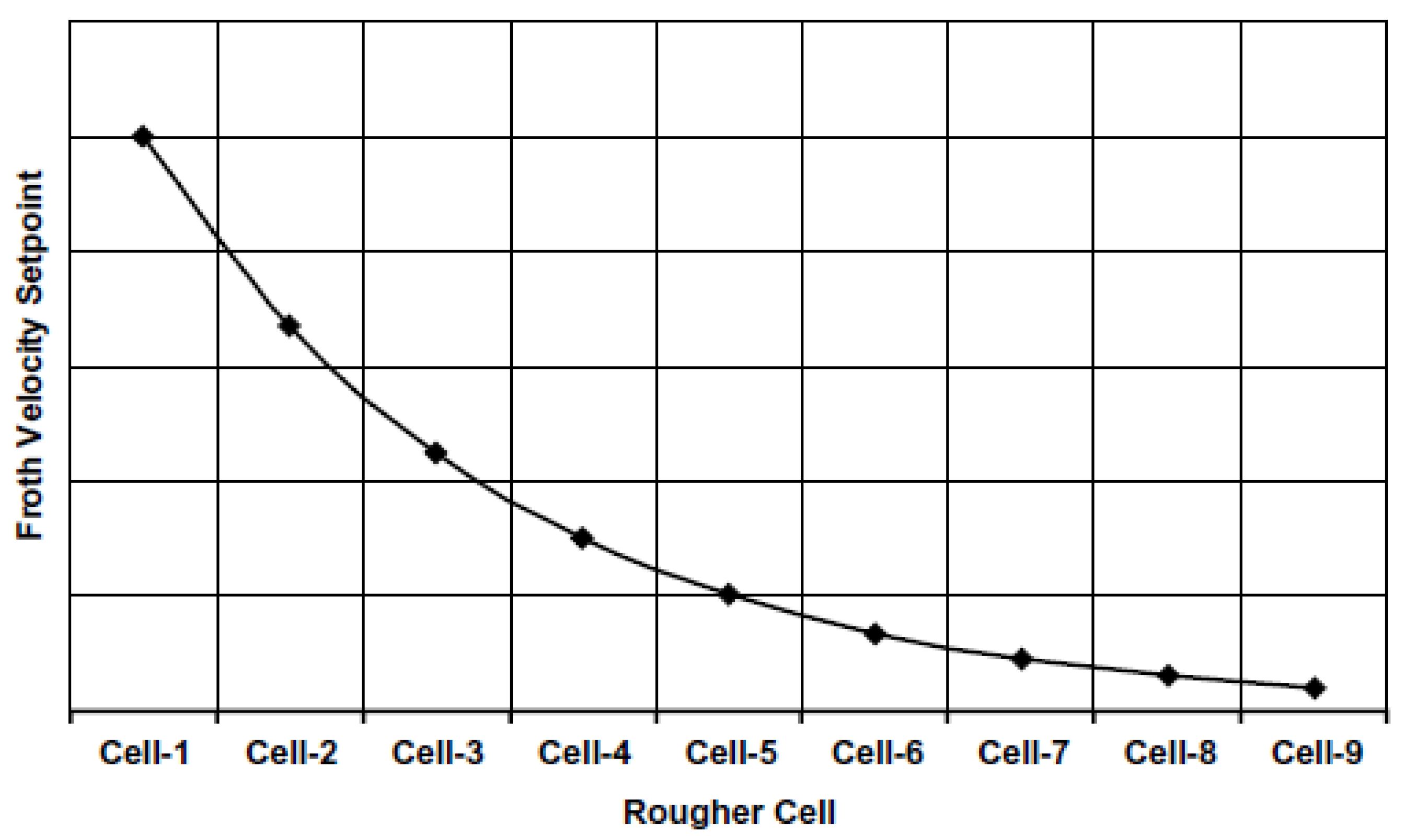
A component in the calculation of air recovery is froth velocity and that may be used independently as in the third strategy, mass-pull control. This now requires a search for the froth velocity profile to achieve the target bank performance. An exponentially decreasing froth velocity profile is usually selected [
18,
19]. The form of the decay function appears to be based on mimicking how the banks are currently operated, which is not necessarily optimal, as the air profiling and PAR studies have shown. Taking the flat cell-by-cell recovery solution, the decay function can be derived (see
Figure 8) and would be, we contend, a practical starting point. A problem that remains is that mass-pull rate and froth velocity may not be uniquely related.
The analysis considers only separation between floatable minerals, not entrainment. The evidence at Brunswick Mine is that probably both are affected by air profiling and by extension recovery profiling. The increasing air rate profile reduces air and mass-pull rate in the first cells both of which benefit entrainment rejection [
25,
26]. The evidence points to either a flat or increasing cell-by-cell recovery profile for both minimizing entrainment and maximizing selectivity between floatable minerals.
6. Conclusions
Three strategies for optimizing flotation bank performance have been reviewed: air profiling, peak air recovery profiling, and mass-pull (froth velocity) profiling. PAR profiling translates the problem of optimizing a bank of cells to a local problem of finding the gas rate (and froth depth) that maximizes air recovery in each cell. Consequently the optimal total air rate is completely determined. A downside of this strategy is the extensive instrumentation required to calculate air recovery which is prone to error propagation. Mass pull profiling strategy uses a vision system to calculate the froth velocity in each cell and then change gas rate and/or froth depth to achieve a target froth velocity. A monotonically decreasing froth velocity profile has been successfully implemented in industrial operations. However it is not clear how to select the froth velocity set point to achieve a target metallurgical performance. Gas rate profiling is the simplest optimizing strategy requiring no capital investment for cells equipped with air flow meters. An increasing air rate profile has been reported to improve metallurgical bank performance. The total air rate is not directly determined as opposed to the PAR profiling but must be manipulated to provide a target bank recovery.
The possibility that the property underlining these strategies is the way recovery is distributed down the bank (recovery profiling) is discussed. It is shown that a flat cell-by-cell recovery profile maximizes separation efficiency for a target bank recovery and for any relative floatability larger than one as long as it is invariant down the bank. A feature of a flat recovery profile is that it is independent of how the total volume is allocated in the bank, i.e., a flat cell-by-cell recovery is still optimal for a bank of cells with different sizes. Moreover, it was proven through a simple example that for a single floatable component with a fixed flotation rate constant the volume allocation that maximizes the bank recovery is when cells are equal volume and consequently give equal recovery.
Although the flat cell-by-cell recovery profile is mathematically proven for true floating minerals and changes to this profile may be necessary to compensate for entrainment, it offers a starting point towards bank optimization. The three case studies lend support to this strategy.