Dynamical Relation between Quantum Squeezing and Entanglement in Coupled Harmonic Oscillator System
Abstract
: In this paper, we investigate into the numerical and analytical relationship between the dynamically generated quadrature squeezing and entanglement within a coupled harmonic oscillator system. The dynamical relation between these two quantum features is observed to vary monotically, such that an enhancement in entanglement is attained at a fixed squeezing for a larger coupling constant. Surprisingly, the maximum attainable values of these two quantum entities are found to consistently equal to the squeezing and entanglement of the system ground state. In addition, we demonstrate that the inclusion of a small anharmonic perturbation has the effect of modifying the squeezing versus entanglement relation into a nonunique form and also extending the maximum squeezing to a value beyond the system ground state.1. Introduction
Entanglement is a fundamental resource for non-classical tasks in the field of quantum information [1]. It has been shown to improve communication and computation capabilities via the notion of quantum dense coding [2], quantum teleportation [3], unconditionally secured quantum cryptographic protocols [4,5], and quantum algorithms for integer factorization [6]. For any quantum algorithm operating on pure states, it has been proven that the presence of multi-partite entanglement is necessary if the quantum algorithm is to offer an exponential speed-up over classical computation [7]. Note, however, that a non-zero value of entanglement might not be the necessary condition for quantum computational speed up of algorithm operating on mixed states [8]. In addition, in order to achieve these goals practically, it is necessary to maintain the entanglement within the quantum states which are fragile against the decohering environment. An approach would be to employ an entangled state with as large an entanglement as possible, and the idea is that the production of such entangled state could be tuned through the operation of quantum squeezing.
Indeed, the relation between quantum squeezing and quantum entanglement has been actively pursued in recent years [9–18]. Notably, the creation of entanglement is shown experimentally to be able to induce spin squeezing [9,10]. Such entanglement-induced squeezing has the important outcome of producing measuring instruments that go beyond the precision of current models. In addition, quantum squeezing is found to be able to induce, enhance and even preserve entanglement in decohering environments [11–13]. Previously, we have investigated the relation between the squeezing and entanglement of the ground state of the coupled harmonic oscillator system [16,17]. The ground state entanglement entropy was found to increase monotonically with an increase in quadrature squeezing within this system. When a small anharmonic perturbing potential is added to the system, a further enhancement in quadrature squeezing is observed. While the entropy-squeezing curve shifts to the right in this case, we realized that the entanglement entropy is still a monotonically increasing function in terms of quadrature squeezing.
In this paper, we have extended our earlier work discussed above by investigating into the dynamical relation between quadrature squeezing and entanglement entropy of the coupled harmonic oscillator system. Coupled harmonic oscillator system has served as useful paradigm for many physical systems, such as the field modes of electromagnetic radiation [19–21], the vibrations in molecular systems [22], and the formulation of the Lee model in quantum field theory [23]. It was shown that the coupled harmonic oscillator system possesses the symmetry of the Lorentz group O(3, 3) or SL(4, r) classically, and that of the symmetry O(3, 2) or Sp(4) quantum mechanically [24]. In addition, the physics of coupled harmonic oscillator system can be conveniently represented by the mathematics of two-by-two matrices, which have played a role in clarifying the physical basis of entanglement [25]. In Section 2 of this paper, we first described the coupled harmonic oscillator model. It is then followed by a discussion on the relation between the dynamically generated squeezing and entanglement of the coupled oscillator systems, which we have determined quantitatively via numerical computation. In Section 3 of the paper, we present analytical results in support of the numerical results obtained in Section 2. Here, we illustrate how the problem can be solved in terms of two-by-two matrices. Then, in Section 4 of the paper, we study how the inclusion of anharmonicity can influence the relation between the dynamically generated squeezing and entanglement. Finally, we give our conclusion in Section 5 of the paper.
2. Dynamical Relation of Quantum Squeezing and Entanglement in Coupled Harmonic Oscillator System
The Hamiltonian of the coupled harmonic oscillator system is described as follow:
Next, let us discuss on the relation between the squeezing and entanglement of the lowest energy eigenstate of this coupled harmonic oscillator system. Note that
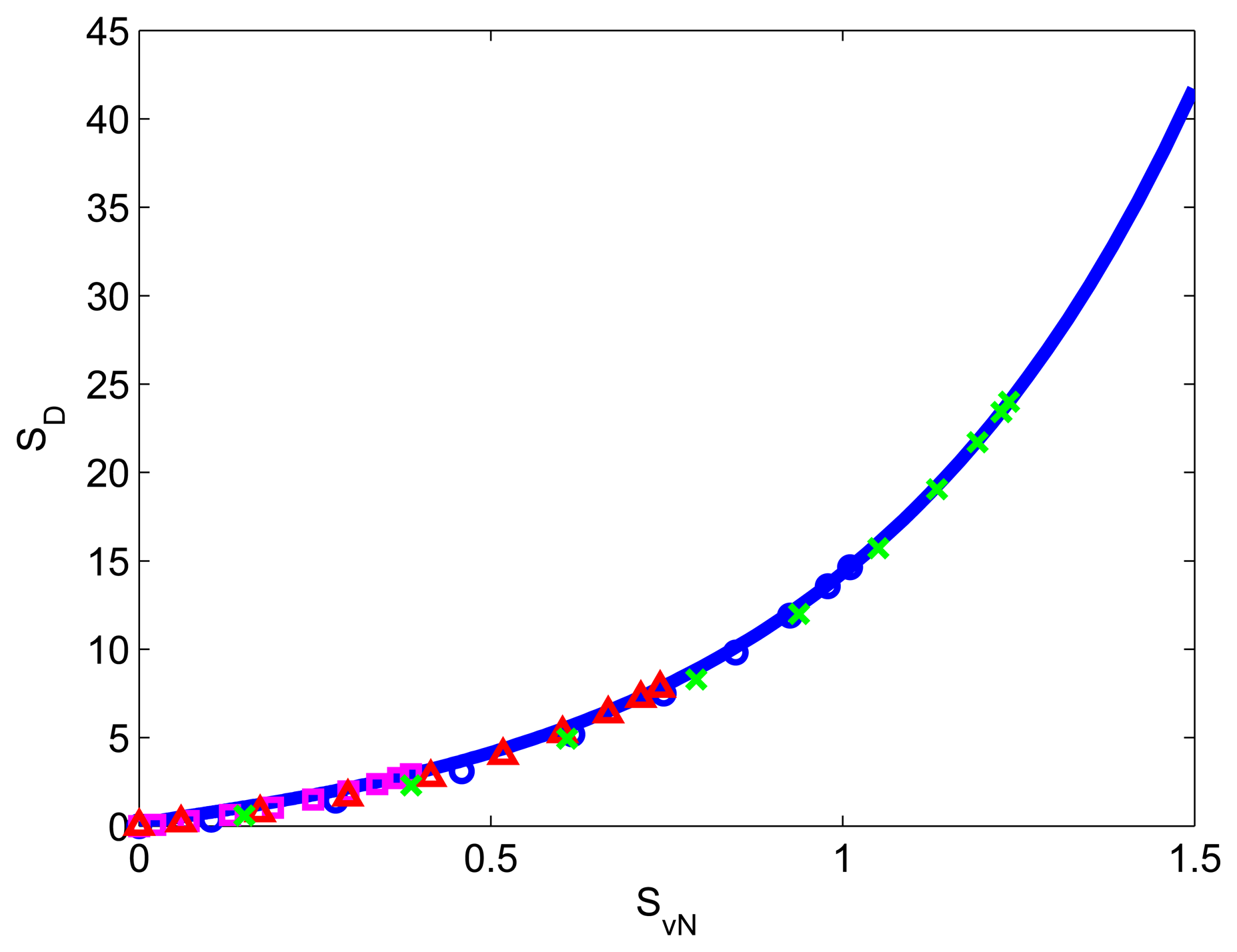
Indeed, the position uncertainty squeezing and the entanglement entropy of the ground state of this oscillator have been solved analytically by previous studies [36,37] as follows:
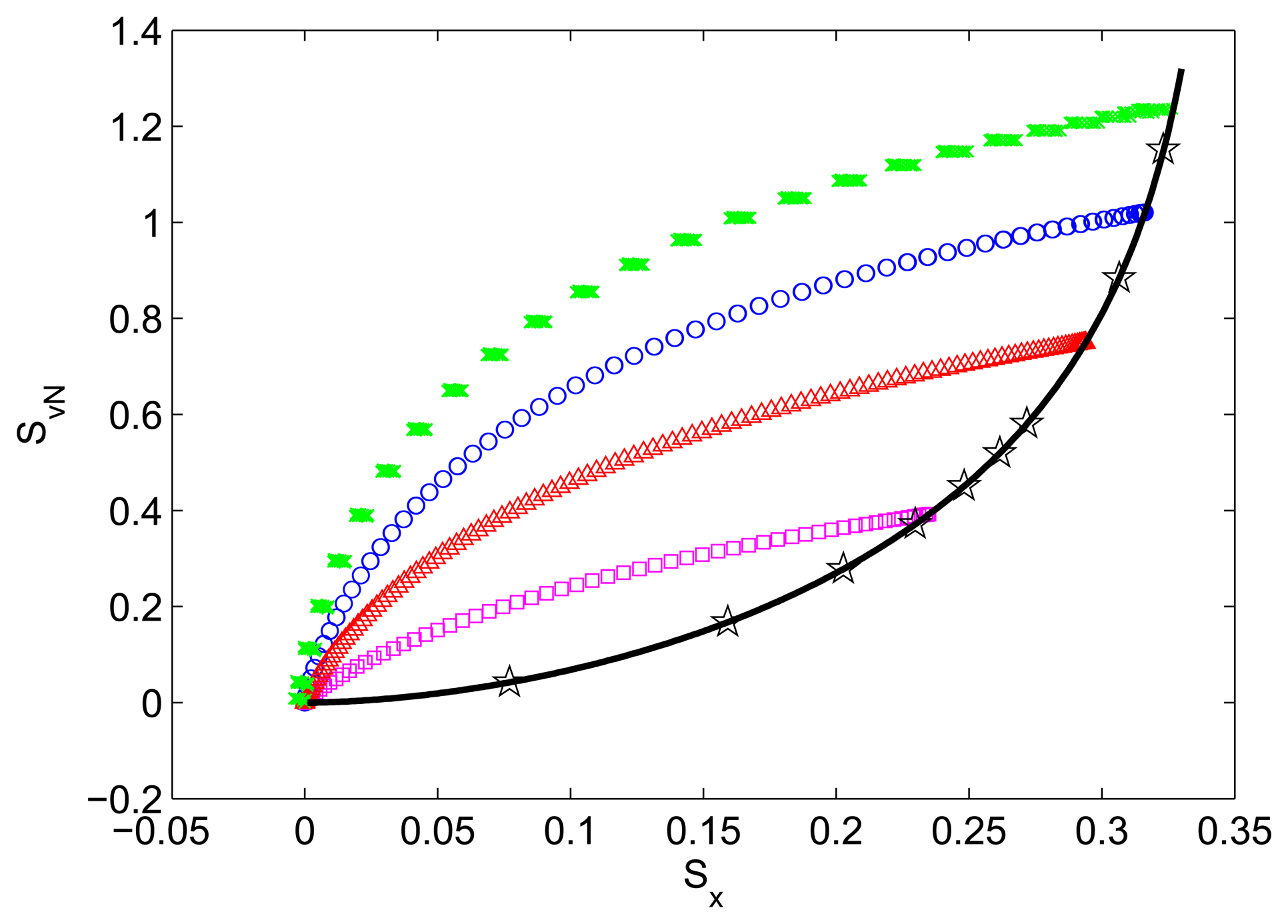
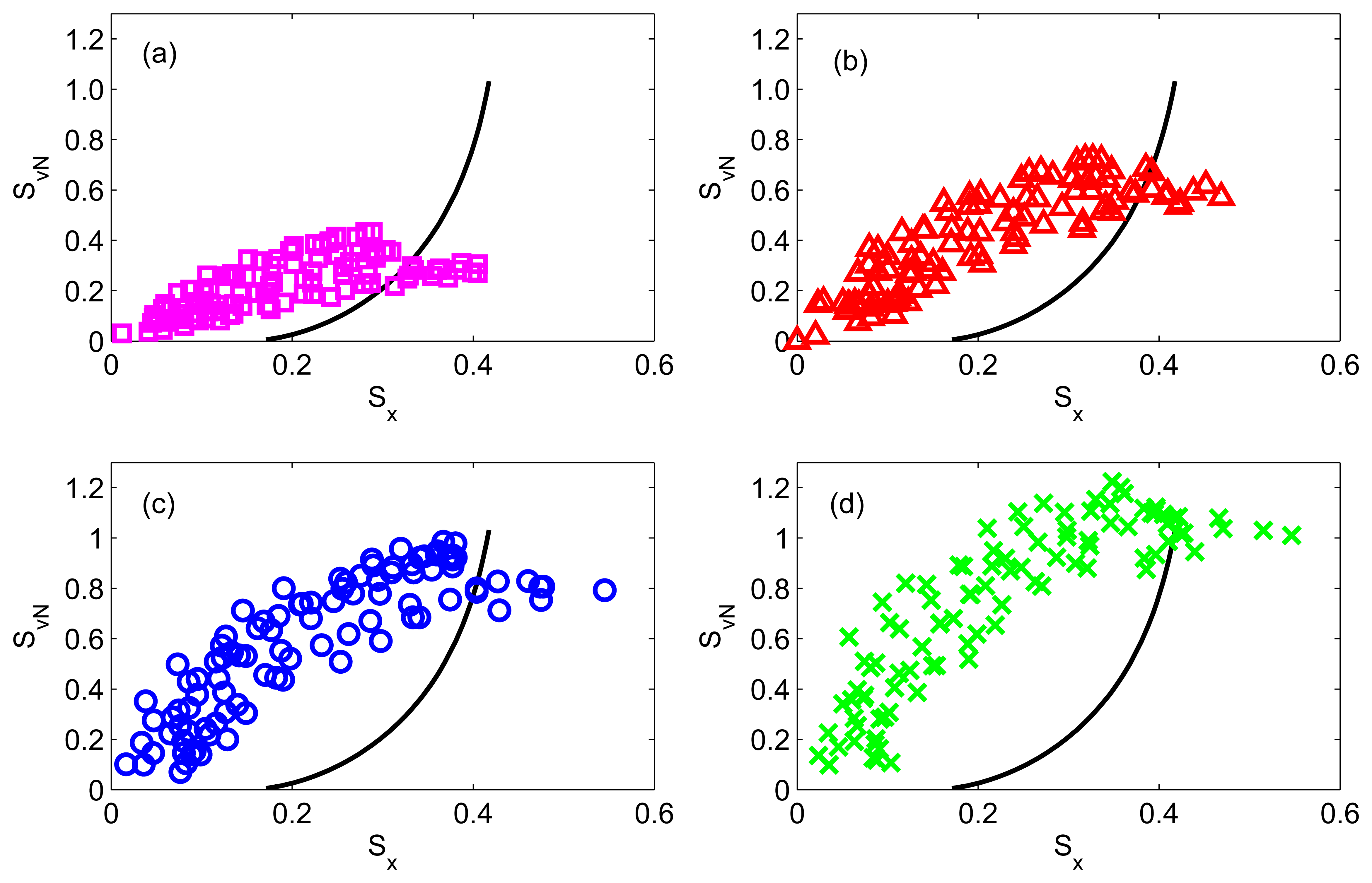
In this paper, we have gone beyond the static relation between squeezing and entanglement based on the stationary ground state. In particular, we have explored numerically into the dynamical generation of squeezing and entanglement via the quantum time evolution, with the initial state being the tensor product of the vacuum states (|0, 0〉) of the oscillators. Note that the obtained results hold true for any initial coherent states (|α1, α2〉) since the entanglement dynamics of the coupled harmonic oscillator system is independent of initial states [38]. In general, the system dynamics is either two-frequency periodic or quasi-periodic depending on whether the ratio of the two frequencies, f1 = 1 and , are rational or irrational. By yielding the values of the squeezing parameter and the entanglement entropy at the same time point within their respective dynamical evolution, we obtained the dynamical relations between the squeezing and entanglement for different coupling constants λ = 0.75, 2, 3.75 and 6, as shown in Figure 1. Interestingly, the results show a smooth monotonic increase of the dynamically generated entanglement entropy as the quadrature squeezing increases for each λ. In addition, the dynamically generated entanglement entropy is observed to be larger for a fixed squeezing as λ increases. It is surprising that the maximum attainable values of these two quantum entities determined dynamically are found to fall consistently on the system ground states' squeezing and entanglement relation as given by Equations (7) and (8) for all values of λ. More importantly, this relation also serve as a bound to the entanglement entropy and squeezing that are generated dynamically.
3. Analytical Derivation on the Dynamical Relation between Quantum Squeezing and Entanglement
In this section, we shall perform an analytical study on the dynamical relationship between quantum squeezing and the associated entanglement production. We first yield the second quantized form of the Hamiltonian of the coupled harmonic oscillator system as follow:
With these results, we are now ready to determine the analytical expressions of both the quantum entanglement and squeezing against time. For entanglement, we shall employ the criterion developed by Duan et al [39] for quantification since it leads to simplification of the analytical expression while remaining valid as a measure of entanglement in coupled harmonic oscillator systems. According to this criterion, as long as
When projected into the x1 − p2 or x2 − p1 plane, the initial coherent state can be represented by a circular distribution with equal uncertainty in both x and p direction. During the time evolution, the circular distribution is being rotated and squeezed. As a result, squeezing and entanglement are generated such that the distribution becomes elliptical in the x1 − p2 or x2 − p1 plane with rotation of the ellipse's major axis away from the x- or p-axis which creates entanglement. The generation of squeezing and entanglement reaches their maximum values at the same time when the major axis of the elliptical distribution has rotated 45° away from the x- or p-axis. Note that at this point, squeezing is merely in the collective modes. On the other hand, as discussed in Reference [37], the ground state wave function of the coupled harmonic oscillator system is separable in their collective modes. In both cases, entanglement and squeezing relates uniquely as given by Equation (7) and (31).
4. Quantum Squeezing and Entanglement in Coupled Anharmonic Oscillator Systems
Next, let us investigate the effect of including an anharmonic potential on the dynamical relation between squeezing and entanglement through the following Hamiltonian systems:
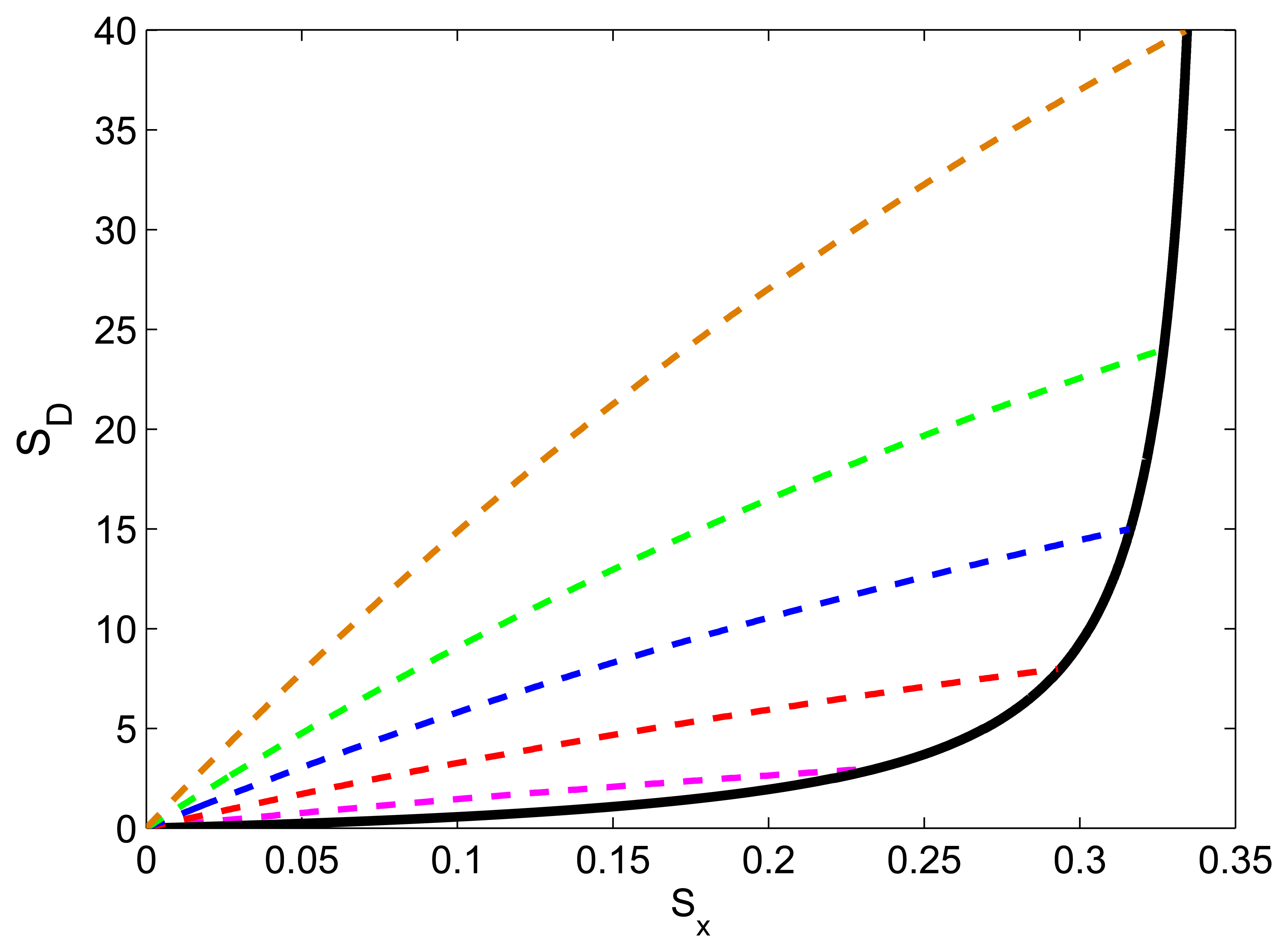
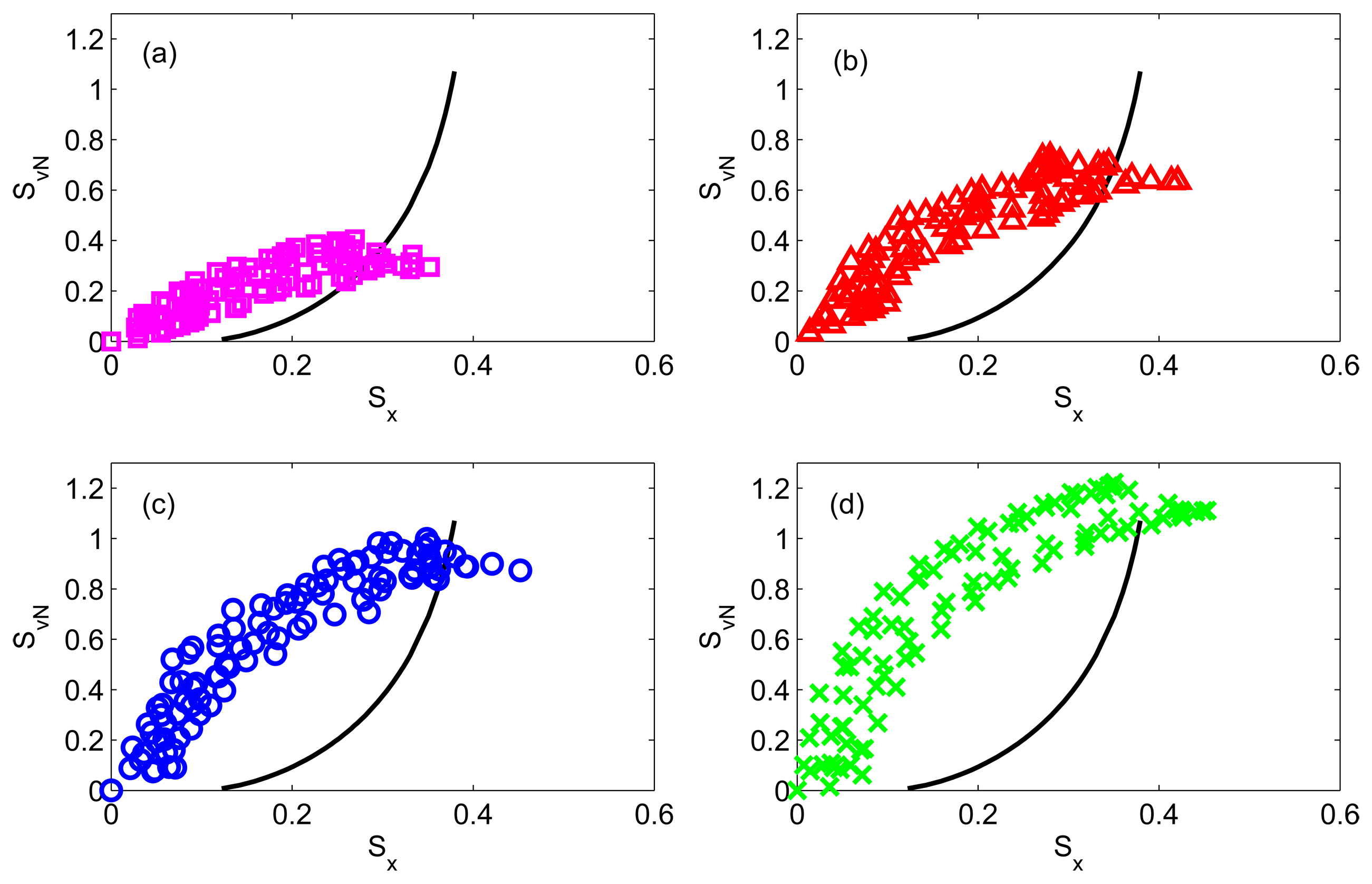
With a small anharmonic perturbation, the dynamically generated entanglement entropy is no longer a smooth monotonically increasing function of the quadrature squeezing as before (see Figure 4). This implies that for coupled anharmonic oscillator systems, the dynamically generated degree of entanglement cannot be characterized through a measurement of the squeezing parameter. In addition, when the anharmonic potential is included, the maximum attainable squeezing is much enhanced. This effect is clearly shown in Figure 4, where we observe that the maximum dynamical squeezing extends far beyond the largest squeezing given by the coupled anharmonic oscillator system's ground state at different λ. In addition, as we increase the anharmonic perturbation from 0.1 to 0.2, we found that the maximum attainable squeezing continues to grow with extension going further beyond the largest squeezing given by the ground state of the coupled anharmonic oscillator system.
5. Conclusions
We have studied into the dynamical generation of quadrature squeezing and entanglement for both coupled harmonic and anharmonic oscillator systems. Our numerical and analytical results show that the quantitative relation that defines the dynamically generated squeezing and entanglement in coupled harmonic oscillator system is a monotonically increasing function. Such a monotonic relation vanishes, however, when a small anharmonic potential is added to the system. This result implies the possibility of characterizing the dynamically generated entanglement by means of squeezing in the case of coupled harmonic oscillator system. In addition, we have uncovered the unexpected result that the maximum attainable entanglement and squeezing obtained dynamically matches exactly the entanglement-squeezing relation of the system's ground state of the coupled harmonic oscillators. When an anharmonic potential is included, we found that the dynamically generated squeezing can be further enhanced. We percieve that this result may provide important insights to the construction of precision instruments that attempt to beat the quantum noise limit.
Acknowledgments
L. Y. Chew would like to thank Y. S. Kim for the helpful discussion on this work during the ICSSUR 2013 conference held in Nuremberg, Germany.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nielson, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Bennett, C.H.; Wiesner, S.J. Communication via one- and two-particle operators on Einstein-Podolsky-Rosen states. Phys. Rev. Lett. 1992, 69, 2881–2884. [Google Scholar]
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wooters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895–1899. [Google Scholar]
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. Proceedings of the IEEE International Conference on Computers, Systems and Signal Processing, New York, NY, USA; 1984; pp. 175–179. [Google Scholar]
- Ekert, A.K. Quantum cryptography based on Bell's theorem. Phys. Rev. Lett. 1991, 67, 661–663. [Google Scholar]
- Shor, P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J. Comput. 1997, 26, 1484–1509. [Google Scholar]
- Jozsa, R.; Linden, N. On the role of entanglement in quantum-computational speed-up. Proc. R. Soc. Lond. A. 2003, 459, 2011–2032. [Google Scholar]
- Lanyon, B.P.; Barbieri, M.; Almeida, M.P.; White, A.G. Experimental quantum computing without entanglement. Phys. Rev. Lett. 2008, 101, 200501:1–200501:4. [Google Scholar]
- Sørensen, A.; Duan, L.M.; Cirac, J.I.; Zoller, P. Many-particle entanglement with Bose-Einstein condensates. Nature 2001, 409, 63–66. [Google Scholar]
- Bigelow, N. Squeezing Entanglement. Nature 2001, 409, 27–28. [Google Scholar]
- Furuichi, S.; Mahmoud, A.A. Entanglement in a squeezed two-level atom. J. Phys. A Math. Gen. 2001, 34, 6851–6857. [Google Scholar]
- Xiang, S.; Shao, B.; Song, K. Quantum entanglement and nonlocality properties of two-mode Gaussian squeezed states. Chin. Phys. B. 2009, 18, 418–425. [Google Scholar]
- Galve, F.; Pachón, L.A.; Zueco, D. Bringing entanglement to the high temperature limit. Phys. Rev. Lett. 2010, 105. [Google Scholar] [CrossRef]
- Ulam-Orgikh, D.; Kitagawa, M. Spin squeezed and decoherence limit in Ramsey spectroscopy. Phys. Rev. A. 2001, 64. [Google Scholar] [CrossRef]
- Wolf, M.M.; Eisert, J.; Plenio, M.B. Entangling power of passive optical elements. Phys. Rev. Lett. 2003, 90, 047904:1–047904:4. [Google Scholar]
- Chung, N.N.; Er, C.H.; Teo, Y.S.; Chew, L.Y. Relation of the entanglement entropy and uncertainty product in ground states of coupled anharmonic oscillators. Phys. Rev. A 2010, 82. [Google Scholar] [CrossRef]
- Chew, L.Y.; Chung, N.N. Quantum entanglement and squeezing in coupled harmonic and anharmonic oscillators systems. J. Russ. Laser Res. 2011, 32, 331–337. [Google Scholar]
- Er, C.H.; Chung, N.N.; Chew, L.Y. Threshold effect and entanglement enhancement through local squeezing of initial separable states in continuous-variable systems. Phys. Scripta 2013, 87. [Google Scholar] [CrossRef]
- Han, D.; Kim, Y.S.; Noz, M.E. Linear canonical transformations of coherent and squeezed states in the Wigner phase space. Phys. Rev. A 1988, 37, 807–814. [Google Scholar]
- Han, D.; Kim, Y.S.; Noz, M.E. Linear canonical transformations of coherent and squeezed states in the Wigner phase space. II. Quantitative analysis. Phys. Rev. A 1989, 40, 902–912. [Google Scholar]
- Han, D.; Kim, Y.S.; Noz, M.E. Linear canonical transformations of coherent and squeezed states in the Wigner phase space. III. Two-mode states. Phys. Rev. A 1990, 41, 6233–6244. [Google Scholar]
- Wilson, E.B.; Decius, J.C.; Cross, P.C. Molecular Vibration; McGraw-Hill: New York, NY, USA, 1955. [Google Scholar]
- Schweber, S.S. An Introduction to Relativistic Quantum Field Theory; Row-Peterson: New York, NY, USA, 1961. [Google Scholar]
- Han, D.; Kim, Y.S.; Noz, M.E. O(3,3)-like symmetries of coupled harmonic-oscillators. J. Math. Phys. 1995, 36, 3940–3954. [Google Scholar]
- Kim, Y.S.; Noz, M.E. Coupled oscillators, entangled oscillators, and Lorentz-covariant harmonic oscillators. J. Opt. B Quantum Semiclass. Opt. 2005, 7, S458–S467. [Google Scholar]
- Eisert, J.; Plenio, M.B.; Bose, S.; Hartley, J. Towards quantum entanglement in nanoelectromechanical devices. Phys. Rev. Lett. 2004, 93, 190402:1–190402:4. [Google Scholar]
- Joshi, C.; Jonson, M.; Öhberg, P.; Andersson, E. Constructive role of dissipation for driven coupled bosonic modes. Phys. Rev. A 2013, 87, 062304:1–062304:4. [Google Scholar]
- Joshi, C.; Hutter, A.; Zimmer, F.E.; Jonson, M.; Andersson, E. Öhberg, P. Quantum entanglement of nanocantilevers. Phys. Rev. A 2010, 82. [Google Scholar] [CrossRef]
- Ikeda, S.; Fillaux, F. Incoherent elastic-neutron-scattering study of the vibrational dynamics and spin-related symmetry of protons in the KHCO3 crystal. Phys. Rev. B 1999, 59, 4134–4145. [Google Scholar]
- Fillaux, F. Quantum entanglement and nonlocal proton transfer dynamics in dimers of formic acid and analogues. Chem. Phys. Lett. 2005, 408, 302–306. [Google Scholar]
- Audenaert, K.; Eisert, J.; Plenio, M.B.; Werner, R.F. Symmetric qubits from cavity states. Phys. Rev. A 2002, 66, 042327:1–042327:6. [Google Scholar]
- Martina, L.; Soliani, G. Hartree-Fock approximation and entanglement. Available online: http://arxiv.org/abs/0704.3130 (accessed on 18 April 2014).
- Chung, N.N.; Chew, L.Y. Energy eigenvalues and squeezing properties of general systems of coupled quantum anharmonic oscillators. Phys. Rev. A. 2007, 76. [Google Scholar] [CrossRef]
- Chung, N.N.; Chew, L.Y. Two-step approach to the dynamics of coupled anharmonic oscillators. Phys. Rev. A. 2009, 80. [Google Scholar] [CrossRef]
- Jellal, A.; Madouri, F.; Merdaci, A. Entanglement in coupled harmonic oscillators studied using a unitary transformation. J. Stat. Mech. 2011. [Google Scholar] [CrossRef]
- McDermott, R.M.; Redmount, I.H. Coupled classical and quantum oscillators. Available online: http://arxiv.org/abs/quant-ph/0403184 (accessed on 18 April 2014).
- Han, D.; Kim, Y.S.; Noz, M.E. Illustrative example of Feymann's rest of the universe. Am. J. Phys. 1999, 67, 61–66. [Google Scholar]
- Chung, N.N.; Chew, L.Y. Dependence of entanglement dynamics on the global classical dynamical regime. Phys. Rev. E. 2009, 80, 016204:1–016204:7. [Google Scholar]
- Duan, L.M.; Giedke, G.; Cirac, J.I.; Zoller, P. Inseparable criterion for continuous variable systems. Phys. Rev. Lett. 2000, 84, 2722–2725. [Google Scholar]
- Joshi, C.; Jonson, M.; Andersson, E.; Öhberg, P. Quantum entanglement of anharmonic oscillators. J. Phys. B At. Mol. Opt. Phys. 2011, 44. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chew, L.Y.; Chung, N.N. Dynamical Relation between Quantum Squeezing and Entanglement in Coupled Harmonic Oscillator System. Symmetry 2014, 6, 295-307. https://doi.org/10.3390/sym6020295
Chew LY, Chung NN. Dynamical Relation between Quantum Squeezing and Entanglement in Coupled Harmonic Oscillator System. Symmetry. 2014; 6(2):295-307. https://doi.org/10.3390/sym6020295
Chicago/Turabian StyleChew, Lock Yue, and Ning Ning Chung. 2014. "Dynamical Relation between Quantum Squeezing and Entanglement in Coupled Harmonic Oscillator System" Symmetry 6, no. 2: 295-307. https://doi.org/10.3390/sym6020295




