Development of Symmetry Concepts for Aperiodic Crystals
Abstract
: An overview is given of the use of symmetry considerations for aperiodic crystals. Superspace groups were introduced in the seventies for the description of incommensurate modulated phases with one modulation vector. Later, these groups were also used for quasi-periodic crystals of arbitrary rank. Further extensions use time reversal and time translation operations on magnetic and electrodynamic systems. An alternative description of magnetic structures to that with symmetry groups, the Shubnikov groups, is using representations of space groups. The same can be done for aperiodic crystals. A discussion of the relation between the two approaches is given. Representations of space groups and superspace groups play a role in the study of physical properties. These, and generalizations of them, are discussed for aperiodic crystals. They are used, in particular, for the characterization of phase transitions between aperiodic crystal phases.1. Introduction
Symmetry plays an important role in the study of physical systems. A symmetry group is a group of transformations leaving both the structure of the physical system and the physical equations invariant. If new systems show new degrees of freedom, the symmetry groups usually have to be adapted. For example, macroscopic properties of crystals are described using point groups. When the internal microscopic structure is taken into account, space groups take over the role of point groups. Mathematically speaking, these space groups are extensions of the point group by the translations: the translation subgroup is an invariant subgroup, and the quotient of the space group by the translation subgroup is isomorphic to the point group. (Sometimes, one says that the translation group is extended by the point group.) Considering magnetic structures, the symmetry groups become magnetic space groups, which, in turn, become generalized magnetic space-time groups when time-dependent electromagnetic fields are considered. These groups are discrete subgroups of the four-dimensional Galilean group, have a four-dimensional subgroup of translations and a four-dimensional point group, the elements of which are combinations of 3D orthogonal transformations with time reversal. They are the prototype of the superspace groups used for the description of incommensurate modulated phases. The full list of four-dimensional magnetic space-time groups was published in [1]. It differs from the list of superspace groups, because of another definition of equivalence.
Section 2 gives a short review of the theory of superspace. In Section 3, it is shown that the superspace approach may also be used for the study of physical properties of a periodic or aperiodic crystal in an external electromagnetic field. Section 4 discusses the additional symmetry operators for systems with magnetic moments. Here, magnetic groups and magnetic space-time groups are discussed. In Section 5, two alternative ways of describing aperiodic crystals, by superspace groups or using representations, are compared. A general procedure to go from one formulation to the other is discussed. In Section 6, a more general type of representation, the so-called projective unitary-antiunitary (PUA) representations, is discussed. Earlier results are completed to cover all aperiodic crystals up to rank six. In Section 7, it is shown that in aperiodic crystals, there is a larger variety of phase transitions than for 3D lattice periodic systems. Several transitions are discussed where the superspace group changes. Finally, in Section 8, yet another type of symmetry operations is discussed: scale operations. These are important for quasi-periodic tilings, quasicrystals and in the context of relativistic space-time symmetries. The present paper is not meant as a review. For a historic overview, see [2]; for a deeper introduction, see [3].
2. Symmetry of Aperiodic Crystals
When incommensurate modulated phases were discovered, the role of space groups was taken over by superspace groups. The diffraction pattern of incommensurate (IC) modulated phases has sharp diffraction spots at positions:
One then defines a density function in n dimensions by considering each H as the projection of an n-dimensional reciprocal vector (H,HI) and defining:
The action of an element, g, of the superspace group on a function, ρs(r, rI), is given by:
This description in Fourier space is an alternative to crystallography in direct space. This has already been discussed in [5]. Mermin and collaborators have used this approach also for quasi-periodic crystals [6]. Because the two approaches are related by a Fourier transform, they are equivalent. There is, however, a difference in practice. In reciprocal space, long-range order is more easily seen, whereas the local structure is described more clearly in direct space. This is the reason why the structure determination of aperiodic crystals usually is done using the direct space [7], although based on the structure factor, which is a function on reciprocal space [3,8]. In the superspace approach, both spaces are considered. The phase shifts in Fourier components accompanying translations may be considered as “compensating gauge transformations” (see Section 5), and these correspond to the phase shifts appearing in the symmetry elements in the treatment by Mermin and collaborators. The latter use the interesting concept of “physical indistinguishability” and then show that the extra phase shifts are linear in the wave vector, as also follows from Equation (7).
Equation (6) describes the action of an element, g, on the scalar function, ρ. Analogously, one obtains the action of g on other types of embedded functions, like vector fields (e.g., displacements), pseudo-vector fields (e.g., magnetic moments) or tensor fields (e.g., elastic tensors).
3. Generalized Magnetic Space-Time Groups
A further extension of the symmetry groups are the generalized magnetic space-time groups mentioned before (Section 2). These are discrete subgroups of the 4D Poincaré group and group extensions of a magnetic point group with a 4D lattice group. They occur as symmetry groups of time-dependent electromagnetic fields. If the 4D space were Euclidean, the space groups would simply be the 4D space groups. However, in the 4D Minkowski space-time, one has to make a distinction between space-like, time-like and isotropic vectors (with positive, negative and zero norm, resp., for the metric −1,1,1,1 in the space, ct, x, y, z). The groups that are subgroups of both the Poincaré and the Euclidean group are called generalized magnetic space-time groups.
The space-time symmetry of an electromagnetic field is a subgroup of the Poincaré group. For example, the symmetry of a transverse monochromatic plane wave is a (continuous) Lie group with a component of the identity generated by [9]:
For a constant homogeneous magnetic field along the z-direction, the symmetry group is generated by three 3D translations, rotations in the xy-plane and a z-mirror combined with time reversal, θ [10]. Because the field is time-independent, the time-translations are continuous. Then, the magnetic space-time group is not a crystallographic group. If it is superposed to a time-independent crystal potential, the symmetry group is not a generalized magnetic space-time group, either, because there is one continuous translation direction.
The situation, however, is different when one considers the problem of a quantum mechanical charged particle in such a combination of fields, because in the Hamilton operator, the potential, A(r), appears, which is not invariant under arbitrary translations. For the symmetric gauge , a symmetry is a translation, t, combined with a gauge transformation χt(r) = Hytx. In this case, the symmetry of the potential comes in. The superposition of the crystal potential, V(r), and the potential of the magnetic field then may be embedded in a 4D space as (V(r),A(r)). The space-time symmetry group of this potential is also a symmetry group for the field, but the converse is not true. A symmetry operation of the potential is a combination of a symmetry group element, g, of the field and a compensating gauge transformation with gauge function χ(r). Consider a time-independent crystal potential with cubic symmetry and basis vectors of length a. Then, apply a homogeneous constant magnetic field, H(r), in the c-direction. The field (0,0,H) may be obtained from a potential . A symmetry translation, t, of the fields needs a compensating gauge function equal to χ(r) = Hya. For quantum mechanical states in this field, the gauge function gives a phase factor exp(ieχ/ℏc) = exp(iβy) with β = eHa/ℏc. This gives a periodicity for the phase factors with periodicity 2π/β = a/α, with α = a2He/2πℏc, which is a dimensionless quantity The periodicity in the phase of the gauge function gives an additional reciprocal lattice vector equal to . Then, the Fourier module is of rank four, and the combined field of crystal and magnetic field may be embedded in four-dimensional superspace with basis vectors:
The formulation of the problem of an electron in an aperiodic crystal in a homogeneous magnetic field is now straight-forward, if one uses the superspace formulation. However, one should be aware of the difficulty that the existence of a superspace group does not reduce the problem of electrons or phonons as it does for 3D lattice periodic crystals. For the latter, the phonon problem is reduced from an infinite to a finite problem, with the number of degrees of freedom three times the number of particles in the unit cell. Because the number of points on the atomic surfaces (the infinite collection of points in the nD unit cell) in an aperiodic crystal is still infinite, this simplification does not occur.
4. Additional Symmetry Operations for Aperiodic Structures
If a crystal structure has magnetic moments, an additional symmetry operation is the time reversal, θ. The symmetry groups in this case are the magnetic space groups or Shubnikov groups. Their elements are either isochronous (not containing θ) or antichronous (products of a Euclidean transformation and θ). The groups without antichronous elements are called non-magnetic; the groups containing θ itself are trivial magnetic space groups, and those with antichronous elements, but without θ itself, are non-trivial magnetic space groups.
In the same way as for 3D space groups, one may proceed for superspace groups. Combing superspace group elements with θ leads to magnetic superspace groups [13]. The magnetic superspace group of a crystal with a modulated nuclear structure and an incommensurate magnetic structure is the group of all g = {(R,RI) ∣(t,tI)} and g′θ = {(R′,R′I)∣(t′,t′I)}θ, such that both the aperiodic magnetic moment structure, M(r,rI), and the aperiodic nuclear structure, u(r,rI), are invariant:
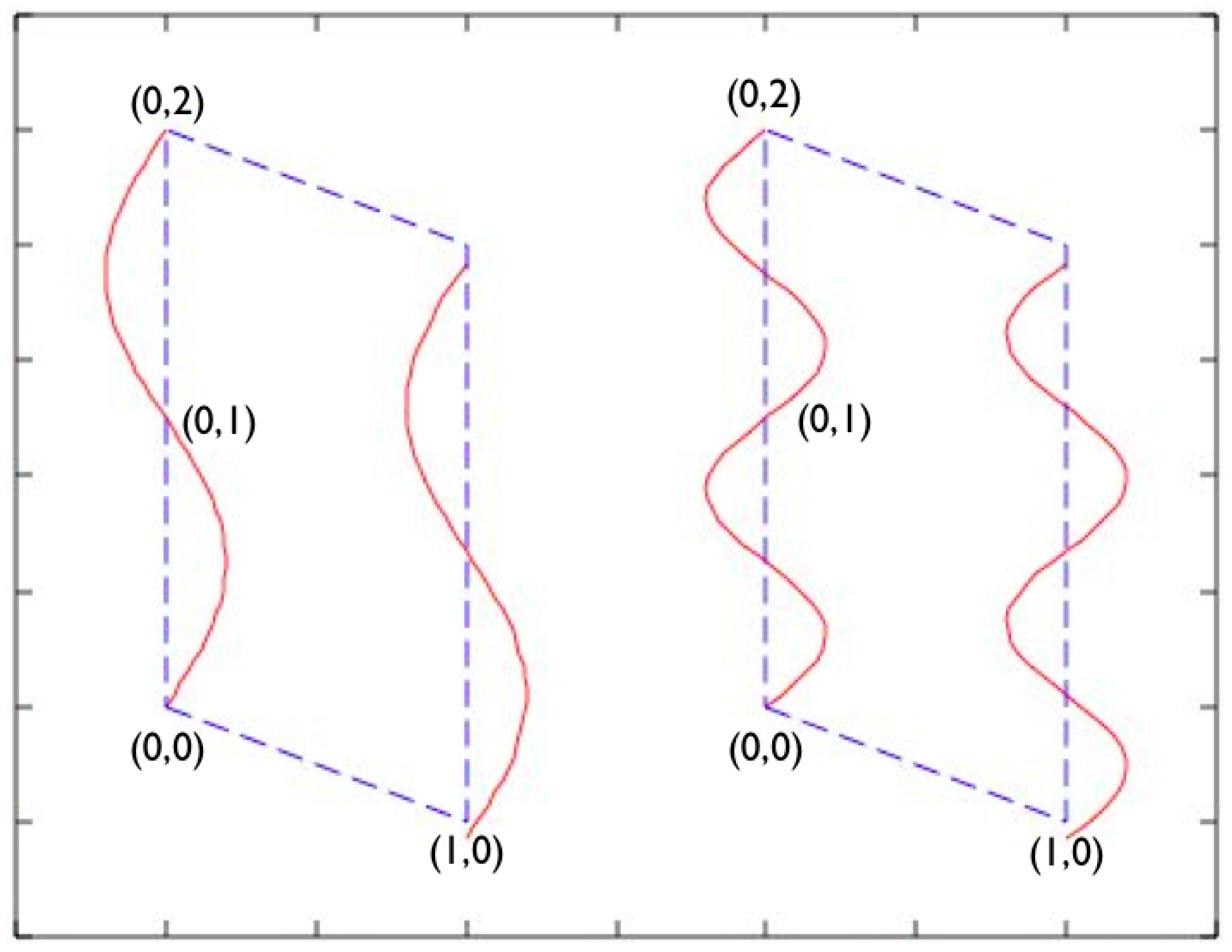
If an incommensurate magnetic structure has magnetic moments given by Mcos(q.n), its embedding is (Mcos(q.n + 2πr I), r I). Under a shift of in internal space, it gets a minus sign, and the same holds for the time reversal, θ. In that case, the operation is is a symmetry operator [16]. In general, there will also be higher harmonics with wave vector mq, and the corresponding component of the magnetic wave is only invariant under if m is odd. Moreover, because of the spin-lattice interaction, there will be a displacement wave, which is invariant under θ and {1|0001}, but generally not under . If it is a symmetry operator, this puts restrictions on the displacement wave. An invariant displacement wave would be ucos(q.n + 4πrI). Because, often, the higher satellites are weak, it will be difficult to determine experimentally whether this operator is a symmetry operator. The operator on itself is not so interesting, but it should be considered with care, because of the higher harmonics and the spin-lattice interaction. If there is a coupling term between the elasticity tensor and the magnetic moment of the type eijSiSj, this occurrence of q in one system and 2q in the other may appear in low order [17]. However, this is not necessarily the case and should be checked. In Figure 1, the 2D superspace group of the non-magnetic basic structure is p1̄(α), and the magnetic superspace group of the whole structure is pd1̄(α), because in this case, the non-magnetic structure has a basis vector (0,1); but this is a magnetic translation. As is the convention in three dimensions, the symbol for the magnetic group is given by the symbol for the non-magnetic group with a prime for those elements in the symbol which are combined with θ, and for groups where lattice translations occur, which are combined with θ (magnetic translations), by a subindex indicating a representative of the magnetic translations. In this case, this is the basis vector (0,1), indicated by d. Notice that the point group element, 1̄(1̄), only occurs if the phases of the two incommensurate waves have the proper relation. If this condition is not satisfied, the magnetic superspace group is pd1(α).
If the magnetic structure is given by spinors S in spin space, the action of the (magnetic) space group elements is via SU(2) operators, i.e. the group of 2 × 2 unitary matrices with determinant equal to 1. Then, the relevant representations are co-representations. These representations of a pair (G,H) of groups, where G is a group of transformations and H is a subgroup of Index 1 or 2 in G, satisfy the rule D(h1)D(h2) = D(h1h2) for elements h1 and h2 from H, but D(gh) = D(g)*D(h) for h in H and g in G, but not in H. In this case, the nuclear structure is embedded in (real) superspace, but the values of the spinor field are in a 2D complex space. The superspace transformations then are pairs of a Euclidean superspace transformation and an associated SU(2) element (see e.g., reference [18]).
An example of a rather complicated incommensurate magnetic structure is ErFe4Ge2 [19]. Above the Curie temperature, the nuclear structure has space group P42/mnm [20]. Below this temperature, there is a mixture of a commensurate and an incommensurate magnetic phase. The latter has modulation wave vector (0β0). The incommensurate spin wave may be characterized by irreps of the basic structure, which has space group Pnnm. Although, according to Landau theory, one expects an order parameter belonging to one irrep; here, the Fe subsystem belongs to the irrep, Γ2, of the little group of q and the Er subsystem to the reducible representation, Γ2 + Γ3. According to what will be discussed in Section 5, this leads to two different superspace groups, Pn21m(0β0)s0s and Pn21m(0β0)ss0. The total symmetry then is the intersection, Pn11(0β0)s00, which is equivalent with Pb(αβ0) in the standard setting of the International Tables for Crystallography Vol. C [21]. Here, one sees that in the first approximation, two subsystems belong to different representations. However, because of the interaction, the superspace group is in fact one group, Pb(αβ0). In addition, one has the symmetry operations involving time reversal. If the magnetic structure only has components with mq, the operator is a symmetry operator and the magnetic superspace group is Pd ( αβ0), but only when the nuclear structure is modulated with 2q. Otherwise, the elements with internal shift should be replaced by time reversal and no shift. Then, the superspace groups become Pn′2m′(0β0) and and the intersection is Pb′(αβ0).
5. Representations of Space Groups and Superspace Groups
The first symmetry considerations of magnetic structures used magnetic space groups (Shubnikov groups) [22,23]. An alternative was proposed by Bertaut [24]. A magnetic structure with moments M(r) in a crystal with a (basic) structure with space Group G, may be described, as well, by means of representations of G, like any vector field in the crystal [25]. In principle, one needs co-representations [26] for magnetic structures, but not when the spins are real quantities. In the nineteen seventies, there was a fierce discussion between defendants of the Shubnikov group approach (Opechowski) and the representation method (Bertaut) [27].
A similar difference of the description method existed in the early years of aperiodic crystals. Incommensurate modulated phases often have their origin in the instability of a phonon mode. The latter are usually described using representations of the basic structure.
Incommensurate modulated phases originate from lattice periodic structures by an incommensurate displacive or occupational modulation. These are vector valued (for displacive modulation) or scalar (for occupational modulation) functions on the set of atomic positions in a basic structure. This leads to an alternative way of describing these aperiodic structures, in terms of representations of the symmetry group of the basic structure. This is a 3D space group [28]. A function on a set with symmetry Group G may be decomposed into components belonging to the irreducible representations of G. The irreducible representations of space groups are characterized by a star, *q, of a vector, q, i.e., all transforms of q under the point group and an irreducible representation (irrep) of the “little group of q” Kq, the subgroup of the point group that leaves q invariant, up to reciprocal lattice vectors. These irreps may also be projective, i.e., representations up to a phase factor (also called ray representations).
The symmetry group of the lower symmetry structure is the subgroup for which the restriction of the representation to this group is the identity representation. If the high-symmetry group is a space group or superspace group, and the modulation is incommensurate, then there is no space group symmetry for the lower symmetry phase. Then, one still can characterize the structure using the representation (which is irreducible in simple Landau theory). This is an alternative to the use of superspace groups.
The relation between the representation of the space group and the superspace group is easily demonstrated if the star of the modulation vector, q, only contains two points (±q) and the representation of Kq is one-dimensional.
The relation between representations of the space group and the resulting superspace group is more complicated when the star of q (i.e., *q) has more than two branches or when the representation of Kq is not one-dimensional [28]. If *q has two branches (±q), but the dimension of the irrep of Kq is more-dimensional, then the vectors in the representation space may determine different symmetries for the low symmetry phase. As an example, consider the case of high-symmetry group P4mm and q = γc*. Then, Kq = 4 mm. When the displacement is in the ab-plane, the irrep is two-dimensional. For a vector (x,y) in this plane, one gets a phase factor exp(iφ) = exp(−πi/2) for the generator 4 (of 4 mm) acting on (−i, 1) and space factors −1, resp. +1, for mx and my acting on (1,0). Although both vectors belong to the same irrep of Kq, the two corresponding superspace groups are different. They are P4(00γ)q or P2mm(00γ)0ss, respectively. The same situation occurs for the star of αa* for the same P4mm, which has four branches. The representations of the little group are one-dimensional. The corresponding superspace group, either Pm(αβ0) or Pm(αβ0)s, depends on the contributions of the different branches of the star. This does not mean that the superspace description is less precise. It just means that knowing the irrep does not give the full information. One has to specify the components in the representation space.
What is said here for the transition from a lattice periodic 3D structure to an incommensurate modulated structure holds also for transitions from an aperiodic structure with one superspace group to one with another superspace group. Furthermore, in that case, the transition may be described either with representations of the first group or with a transition from one superspace group to another.
6. Generalized Representations
Not only the usual (vector) representations play a role. Besides them, one has to consider projective representations, i.e., representations up to a factor, and co-representations, with anti-linear elements. This happens, e.g., in considering conventional representations of non-symmorphic space groups, systems with spin where the actual symmetry group is a double group and magnetic systems. In general, PUA (projective unitary-antiunitary) representations play a role. These representations were considered in the literature already a long time ago, but the groups relevant for quasicrystals have not yet been fully discussed. In the following, we consider these PUA representations for general aperiodic crystals up to rank six.
A PUA-representation of Group G with Subgroup H of Index 1 or 2 is a mapping of the Group G into a group of unitary operators or a group of unitary and antiunitary operators, D(g), such that H is presented by unitary operators and the following relation holds:
The PUA-representations of Group G are conventional (co)-representations of a group, which is an extension of G with the so-called (co-)multiplicator, M(G,H), but (in this case, at least) also a group extension of G by a group, C2, because all multiplicators are products of Groups C2. These groups are found by enlarging the number of generators and the number of defining relations. For example, the icosahedral group has generators α and β and relations α5 = β3 = (αβ)2 = E. The projective representations can be obtained from the conventional representations of a group with generators α, β and γ with relations α5 = γ,β3 = γ2 = E, (αβ)2 = E, αγα−1γ−1 = βγβ−1γ−1 = E. This is a group of order 120. It is sometimes called the covering group. There are five irreducible representations with a trivial factor system and four with a non-trivial one (Table 2). One (Γ6) corresponds to the so-called double group, which plays a role for systems with spin. The matrices of this representation are SU(2)-matrices.
The projective representations of the point groups are needed for some of the irreducible representations of non-symmorphic superspace groups, those with a wave vector on the border of the Brillouin Zone. This is well known for three-dimensional space groups and holds also in arbitrary dimensions. An irreducible representation of the little group of the vector, k, in the n-dimensional Brillouin Zone is given by:
7. Phase Transitions
Incommensurate modulated phases usually originate from a lattice periodic structure. According to the Landau theory of phase transitions, the transitions can be described in terms of irreducible representations of the “high symmetry” phase. In this case, the transitions are treated using irreducible representations of the 3D space group of the lattice periodic structure. However, phase transitions happen to occur also from one aperiodic structure to another. Here, one has to distinguish two types. For the first, the rank of the Fourier module (the dimension of the superspace) does not change. In the second, this rank is different for the two phases. Moreover, Landau theory can only be used for the situation in which the two phases have a group-subgroup relation between their symmetry groups. Therefore, one has to distinguish four types: yes or no for the group-subgroup relation and yes or no for the change in the dimension. The phase transitions occur in all three classes of aperiodic crystals and also in systems with magnetic moments.
When the two phases have a group-subgroup relation and the rank of the crystal does not change, the transition may be described using irreps of the high symmetry space group, resp. the superspace group. The theory of these irreps is well known. These representations are also sufficient for systems with magnetic moments, if the magnetic moments are real. If the spins are complex, one has to consider the co-representations.
When the rank of the crystal changes at the phase transition, a priori there is no group-subgroup relation between the symmetry groups. However, if the dimension of the higher-rank structure is the n2-dimensional group, G2, and that of the lower-dimensional structure is the n1-dimensional group, G1, then G2 may be a subgroup of the direct product of G1 with the Euclidean group in n2-n1 dimensions, and one can again use irreps of the latter to describe the structure of the former. The irreps of E(n) are also well known. Then, the superspace symmetry of the higher-rank structure follows from the properties of the irrep involved, as explained above.
Some examples of different types of phase transitions in aperiodic crystals are the following.
- (a)
K2SeO4 [31] has a 3D orthorhombic structure above 130 K with space group Pnam [20].In this phase, a mode becomes soft near 130 K, which has an incommensurate wave vector q = γa*. The wave vector is temperature dependent and becomes a*/3 at 93 K. The first transition is from n = 3 with space group Pnam to an IC phase with n = 4 and superspace group Pnam(α00)0ss. This corresponds to an irrep for the little group of q with characters χ(my, mz) = (− 1, − 1). The second transition goes back from n = 4 to n = 3.
- (b)
A compound with an incommensurate modulation, that goes down in temperature as low as one has measured, is biphenyl [32]. Above 38 K, it has rank three and space group P21/a. In this phase, a soft mode develops with wave vectors q = (±α, ±β, 0). Below the phase transition, the symmetry group is the rank five superspace group, P21/a(αβ0)0v. Here, v is the symbol 0 or s, for which the value here does not matter. Finally, at 21 K, there is a second phase transition to a rank four superspace group, P21/a(0β0)uv (u, v = 0 or s). Here, v is the symbol 0 or s, for which the value here does not matter. This is a partial lock-in transition. One has not found a full lock-in at still lower temperatures.
- (c)
A complicated magnetic structure has been found in ErFe4Ge2 [19], as mentioned in Section 4 Below the Curie temperature, there is a mixture of two magnetic phases, one commensurate and the other incommensurate. This has been discussed in Section 4. Depending on temperature, the volume ratio between the two phases changes. This means that there are domains with a three-dimensional magnetic structure and others with a four-dimensional magnetic structure, and their ratio changes if the temperature changes.
- (d)
A phase transition with a change of rank has also been found in composites. An example is nonadecane-urea [33]. In the pressure-temperature phase diagram, several phases are found. At high enough a temperature, the alkane is fluid inside channels in the urea host structure. At low pressure, a ferroelastic deformation occurs, where the alkane orders with a lattice constant incommensurate with that of the urea (Phase II). This gives an ordered structure with a rank-four superspace group. At still lower temperatures, new satellites occur, and the structure becomes five-dimensional (Phase III). For higher pressures, there is a direct transition from Phase I to the five-dimensional Phase IV, with superspace group C2221(00γ,10δ). (Caveat: The precise symmetry group in this case is not yet known, because a detailed structure analysis is missing. It is possible that the real symmetry is a subgroup of the one mentioned here.)
The phase transition from the four-dimensional structure with superspace group P6122(00γ) to the five-dimensional structure with superspace group C2221(00γ,10δ) corresponds to an order parameter with wave vector (10δ). Its Kq is six. Its irreps are one-dimensional, and for each, there exists a compensating phase shift (compensating gauge transformation). The resulting superspace group depends on these phases, which are unknown until a precise structure determination will have been made.
- (e)
An example of a phase transition in quasicrystals is the transition from an icosahedral quasicrystal to a tetrahedral (a subgroup of m3̄) or a rhombohedral (subgroup of 3̄m) approximant. Such a transition is usually first-order. This is a transition from a lattice periodic structure in six dimensions to a three-dimensional lattice periodic structure [34]. The point group changes from the icosahedral group, 5̄3m (or better 5̄3m(5̄23m)), to the tetrahedral group, m3̄, or a rhombohedral group. For some P-type icosahedral quasicrystals (with primitive icosahedral superspace group;, approximants are known [35]. For F-type quasicrystals (with icosahedral face centered superspace group), recently, an approximant was studied [36]. Experimental investigations of such phase transitions are difficult because of the slow kinetics. A comparable phase transition is that in the decagonal quasicrystal, AlCoNi [37]. Another example of a phase transition related to quasicrystals is one in an approximant of the quasicrystal, CdYb [38]. For phase transitions from a quasicrystal to a modulated quasicrystal, one may use the same technique as for the transition from a lattice periodic structure to an incommensurate modulated phase [39,40].
- (f)
Interesting cases of phase transitions are those where two phase transitions are coupled; e.g., this is the case of multiferroics. Examples are TbMnO3 and DyMnO3 [41–43]. There is coupling between electric and magnetic polarizations, and the magnetic structure is incommensurate. For TbMnO3, there is a Neel temperature TN = 41 K, below which there is an incommensurate magnetic wave with wave vector (0,0,γ) and polarization along c. The superspace group is either Pmcn(00γ) or Pmcn(00γ)s00 for the nuclear structure. For the total structure, including the magnetic wave, it is Pdmcn(00γ) or Pdmcn(00γ)s00 (in the setting of Vol. C of the International Tables of Crystallography [21]) if the modulations of the nuclear and the magnetic structure have wave vectors q and 2q, respectively. Notice that the subscript, d, means the presence of a magnetic translation . At Tc = 28 K, the linearly polarized wave changes to helicoidal and a spontaneous electric polarization along c is observed. Then, the superspace group symmetry loses its center of inversion (otherwise, no ferroelectric field could be produced). In [15], a magnetic superspace group is proposed, which in our setting, corresponds to Pd21cn(00γ)ss0. Moreover, under an external magnetic field, there is an additional transition with a lock-in, where the irrational value of γ changes to a rational value. For DyMnO3, similar behavior is found, but for the lock-in transition under an external magnetic field. The basic structure has space group Pmcn [20]; below the Neel temperature, there is a magnetic wave with wave vector (00γ).
Only for a number of phase transitions (semi-)microscopic models exist [44,45]. The number of ab initio calculations for these phase transitions is even smaller (see e.g., [46]).
8. Scale Symmetries
Symmetries that are non-crystallographic in three dimensions, like octagonal or decagonal groups, have matrix representations, which are irreducible if one considers integers, but reducible for real numbers. For real representations, this means that there may be invariant subspaces of the superspace and lattice transformations, leaving these subspaces also invariant. An example is an aperiodic crystal, or tiling, with octagonal symmetry of 8 mm. The superspace has dimension four in that case. The symmetry group has generators A and B; the superspace has invariant subspaces VE and VI, which are, in turn, invariant under an operation, C, which leaves both subspaces invariant, with:
Other examples of scale transformations that leave the points of the Fourier module invariant combine scale factors with a rotation. An example of such a roto-scale is the following. The Fourier module of the Penrose tiling has a symmetry group with two generators. One is a rotation over 2π/5 in VE combined with one over 4π/5 in VI. An element of the normalizer of the point group in direct space is generated by:
In superspace, the scale transformations are non-physical, because the laws of nature are, generally, not invariant under scale transformations. This is different for crystallographic systems with relativistic symmetry [51]. The relativistic point group generated by:
9. Summary
We have argued that new phenomena in solid state materials may lead to a generalization of symmetry considerations. This applies to the generalizations from point groups, to space groups, space-time groups and superspace groups, but also to magnetic space groups and magnetic superspace groups. Moreover, this procedure can be extended to lattice periodic and aperiodic crystals in external electromagnetic fields, both static and time-dependent. For the study of states in aperiodic crystals, we have seen a completion of the list of ordinary and projective unitary-antiunitary representations (multiplier co-representations). Finally, a short overview is given of the various types of phase transitions that may occur in aperiodic crystals.
Acknowledgments
The author thanks Tohoku University, Japan, and especially An Pang Tsai for the hospitality during a stay when part of this paper was written.
Conflicts of Interest
The author declares no conflict of interest.
References
- Fast, G.; Janssen, T. Generalized Magnetic Space-Time Groups; Technical Report 6-68; University of Nijmegen: Nijmegen, The Netherlands, 1968; pp. 1–73. [Google Scholar]
- Janssen, T. Fifty years of aperiodic crystals. Acta Cryst. A 2012, 68, 667–674. [Google Scholar]
- Ted, J.; Chapuis, G.; de Boissieu, M. Aperiodic Crystals: From Incommensurate Phases to Quasicrystals; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Janssen, T.; Janner, A.; Ascher, E. Crystallographic groups in space and time: I. General definitions and basic properties. Physica 1969, 41, 541–565. [Google Scholar]
- Bienenstock, A.; Ewald, P. Symmetry of Fourier space. Acta Cryst. 1962, 15, 1253–1261. [Google Scholar]
- Rokhsar, D.S.; Wright, D.C.; Mermin, N.D. The two-dimensional quasi-crystallographic space groups with rotational symmetries of less than 23-fold. Acta Cryst. A 1988, 44, 197–211. [Google Scholar]
- Yamamoto, A. Crystallography of quasiperiodic crystals. Acta Cryst. A 1996, 52, 509–560. [Google Scholar]
- Van Smaalen, S. Incommensurate Crystallography; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Janner, A.; Janssen, T. A charged particle in the field of a transverse electromagnetic plane wave. Physica 1972, 60, 292–321. [Google Scholar]
- Chen, L.C.; Janssen, T. A charged particle in a uniform electromagnetic field. Physica 1974, 77, 290–310. [Google Scholar]
- Hofstadter, D. Energy levels and wave functions of Bloch electrons in rational and irrational magnetic fields. Phys. Rev. B 1976, 14, 2239–2249. [Google Scholar]
- De Lange, C.; Janssen, T. Incommensurability and recursivity: Lattice dynamics of modulated crystals. J. Phys. C Solid State Phys. 1981, 14, 5269–5292. [Google Scholar]
- Janner, A.; Janssen, T. Symmetry of Incommensurate Crystal Phases. I. Commensurate Basic Structures. Acta Cryst. A 1980, 36, 399–408. [Google Scholar]
- Souvignier, B. The four-dimensional magnetic point and space groups. Z. Krist. 2006, 221, 77–82. [Google Scholar]
- Perez-Mato, J.M.; Ribeiro, J.L.; Petricek, V.; Aroyo, M.I. Magnetic superspace groups and symmetry constraints in incommensurate magnetic phases. J. Phys. Condens. Matter 2012, 24. [Google Scholar] [CrossRef]
- Schobinger-Papamantellos, P.; Janssen, T. The symmetry of the incommensurate magnetic phase ErFe4Ge2. Z. Krist. 2006, 221, 732–734. [Google Scholar]
- Walker, M.B. Phenomenological theory of the spin-density wave in chromium. Phys. Rev. B 1980, 22, 1338–1347. [Google Scholar]
- Authier, A. International Tables for Crystallography; IUCr and Kluwer: Dordrecht, The Netherlands, 2003; Volume D. [Google Scholar]
- Schobinger-Papamantellos, P.; Rodriguez-Carvajal, J.; Buschow, K.H.J. Double symmetry breaking and magnetic transitions in ErFe4Ge2. J. Magn. Magn. Mater. 2007, 310, 63–75. [Google Scholar]
- Hahn, Th. International Tables for Crystallography; IUCr and Kluwer: Dordrecht, The Netherlands, 1992; Volume A. [Google Scholar]
- Wilson, A.J.C.; Prince, E. International Tables for Crystallography; IUCr and Kluwer: Dordrecht, The Netherlands, 1999; Volume C. [Google Scholar]
- Opechowski, W.; Dreyfus, T. Classification of magnetic structures. Acta Cryst. A 1971, 27, 470–484. [Google Scholar]
- Opechowski, W.; Guccione, R. Magnetic Symmetry. In Magnetism; Rado, G.T., Suhl, H., Eds.; Academic Press: New York, NY, USA, 1965; pp. 105–165. [Google Scholar]
- Bertaut, E.F. Representation analysis of magnetic structures. Acta Cryst. A 1968, 24, 217–231. [Google Scholar]
- Rodriguez-Carvajal, J. Recent advances in magnetic structure determination by neutron powder diffraction. Phys. B 1993, 192, 55–69. [Google Scholar]
- Dimmock, J.O.; Wheeler, R.G. Irreducible representations of magnetic groups. J. Phys. Chem. Solids 1962, 6, 729–741. [Google Scholar]
- Opechowski, W.; Litvin, D. Remarks on Bertaut's article: Simple derivation of magnetic space groups. Ann. Phys. 1977, 2, 121–125. [Google Scholar]
- Janssen, T.; Janner, A. Superspace groups and representations of ordinary space groups: Alternative approaches to the symmetry of incommensurate crystal phases. Physica A 1984, 126, 163–176. [Google Scholar]
- Janner, A.; Janssen, T. Electromagnetic compensating gauge transformations. Physica 1971, 53, 1–27. [Google Scholar]
- Janssen, T. On Projective Unitary-Antiunitary Representations of Finite Groups. J. Math. Phys. 1972, 13, 342–351. [Google Scholar]
- Iizumi, M.; Axe, J.D.; Shirane, G. Structural phase transformation in K2SeO4. Phys. Rev. B 1977, 15, 4392–4411. [Google Scholar]
- Cailleau, H.; Moussa, F.; Mons, J. Incommensurate phases in biphenyl. Solid State Commun. 1979, 31, 521–524. [Google Scholar]
- Toudic, B.; Rabiller, P.; Bourgeois, L.; Huard, M.; Ecolivet, C.; McIntyre, G.J.; Bourges, P.; Breczewski, T.; Janssen, T. Temperature-pressure phase diagram of an aperiodic host guest compound. Eur. Phys. Lett. 2011, 93, 16003:1–16003:5. [Google Scholar]
- Wang, J.; Zhaot, J.; Yang, L.; Shen, B. The structural transition and magnetism of the Al65Cu20Fe15 quasicrystal. J. Phys. Condens. Matter 1993, 5, L285–L288. [Google Scholar]
- Takakura, H.; Pay Gomez, C.; Yamamoto, A.; de Boissieu, M.; Tsai, A.P. Atomic structure of the binary icosahedral CdYb quasicrystal. Nat. Mater. 2007, 6, 58–63. [Google Scholar]
- Fujita, N.; Takano, H.; Yamamoto, A.; Tsai, A.P. Cluster-packing geometry for Al-based F-type icosahedral alloys. Acta Cryst. A 2013, 69, 322–340. [Google Scholar]
- Haibach, T.; Estermann, M.A.; Cervellino, A.; Steuer, W. Phase transitions in quasicrystals—The example of decagonal AlCoNi. Mater. Sci. Eng. 2000, 294–296, 117–122. [Google Scholar]
- Watanuki, T.; Machida, A.; Ikeda, T.; Aoki, K.; Kaneko, H.; Shobu, T.; Sato, T.J.; Tsai, A.P. Pressure-Induced Phase Transitions in the Cd-Yb Periodic Approximant to a Quasicrystal. Phys. Rev. Lett. 2006, 96. [Google Scholar] [CrossRef]
- Audier, M.; Bréchet, Y.; de Boissieu, M.; Guyot, P.; Janot, C.; Dubois, J.M. Perfect and modulated quasicrystals in the system AlCuFe. Phil. Mag. B 1991, 63, 1375–1393. [Google Scholar]
- Janssen, T. Commensurate approximants of icosahedral quasicrystals. Europhys. Lett. 1991, 14, 131–136. [Google Scholar]
- Aliouane, N.; Argyriou, D.N.; Strempfer, J.; Zegkinoglou, I.; Landsgesell, S.; Zimmermann, M.V. Field-induced linear magnetoelastic coupling in multiferroic TbMnO3. Phys. Rev. B 2006, 73, 020102:1–020102:4. [Google Scholar]
- Ribeiro, J.L. Symmetry and magnetically driven ferroelectricity in rare-earth manganites RMnO3(R = Gd,Dy,Tb). Phys. Rev. B 2007, 76. [Google Scholar] [CrossRef]
- Strempfer, J.; Bohnenbuck, B.; Mostovoy, M.; Aliouane, N.; Argyriou, D.N.; Schrettle, F.; Hemberger, J.; Krimmel, A.; Zimmermann, M.V. Absence of commensurate ordering at the polarization flop transition in multiferroic DyMnO3. Phys. Rev. B 2007, 75, 212402:1–212402:4. [Google Scholar]
- Janssen, T. Models for incommensurate phases in crystals with Pcmn symmetry. Z. Phys. B 1992, 86, 277–283. [Google Scholar]
- Parlinski, K. Phase diagram of the square-lattice model with 1q and 2q incommensurate modulations. Phys. Rev. B 1993, 48, 3016–3021. [Google Scholar]
- Cao, K.; Guo, G.-C.; Vanderbilt, D.; He, L. First-principles modeling of multiferroic RMn2O5. Phys. Rev. Lett. 2009, 103. [Google Scholar] [CrossRef]
- Guyot, P.; Audier, M. A quasicrystal model for AlMn. Phil. Mag. B 1985, 52, L15–L19. [Google Scholar]
- Janner, A. Which symmetry will an ideal quasicrystal admit? Acta Cryst. A 1991, 47, 577–590. [Google Scholar]
- Janner, A. From an affine extended icosahedral group towards a toolkit for viral architecture. Acta Cryst. A 2013, 69, 151–163. [Google Scholar]
- Janssen, T. The symmetry of quasiperiodic crystals. Acta Cryst. A 1991, 47, 633–647. [Google Scholar]
- Janner, A.; Ascher, E. Relativistic crystallographic point groups in two dimensions. Physica 1969, 45, 67–85. [Google Scholar]
| G | H | a | M(G,H) | g1 | g2 | g3 | g4 | g5 | g6 |
|---|---|---|---|---|---|---|---|---|---|
| αl | βm | (αβ)n | γ2 | αγα−1γ−1 | βγβ−1γ−1 | ||||
| C2n+1 | C2n+1 | e | C1 | u2n+1 | |||||
| C2n | C2n | e | C1 | u2n | |||||
| C2n | Cn | α2 | C2 | ±1 | |||||
| D2n+1 | D2n+1 | e | C1 | u2n+1 | v2 | u2v2 | |||
| D2n+1 | C2n+1 | β | C2 | u2n+1 | σ | σ | |||
| D2n | D2n | e | C2 | ±u2n | v2 | u2v2 | |||
| D2n | C2n | β | C2 × C2 | u2n | ±1 | ±1 | |||
| D2n | Dn | α | C2 × C2 | ±1 | v2 | ±1 | |||
| I | I | e | C2 | u5 | v3 | ±u2v2 | |||
| I × C2 | I × C2 | e | C2 × C2 | u5 | v3 | ±u2v2 | w2 | ±w2 | w2 |
| I × C2 | I | β | C2 × C2 × C2 | u5 | ±v3 | ±u2v2 | σw2 | w2 | σw2 |
| l = n (for Cn); l,m,n = N, 2, 2 (for DN,N = 5,8,10,12); l,m,n = 5,3,2 (for I); σ = ±1 | |||||||||
| Γ | ϵ | −ϵ | α | −α | α2 | −α2 | β | −β | αβ |
|---|---|---|---|---|---|---|---|---|---|
| order: | 1 | 1 | 12 | 12 | 12 | 12 | 20 | 20 | 30 |
| Γ1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Γ2 | 3 | 3 | 1 + τ | 1 + τ | −τ | −τ | 0 | 0 | −1 |
| Γ3 | 3 | 3 | −τ | −τ | 1 + τ | 1 + τ | 0 | 0 | −1 |
| Γ4 | 4 | 4 | −1 | −1 | −1 | −1 | 1 | 1 | 0 |
| Γ5 | 5 | 5 | 0 | 0 | 0 | 0 | −1 | −1 | 1 |
| Γ6 | 2 | −2 | 1 + τ | −1 − τ | τ | −τ | 1 | −1 | 0 |
| Γ7 | 2 | −2 | −τ | τ | −1−τ | 1 + τ | 1 | −1 | 0 |
| Γ8 | 4 | −4 | 1 | −1 | −1 | 1 | −1 | 1 | 0 |
| Γ9 | 6 | −6 | −1 | 1 | 1 | −1 | 0 | 0 | 0 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Janssen, T. Development of Symmetry Concepts for Aperiodic Crystals. Symmetry 2014, 6, 171-188. https://doi.org/10.3390/sym6020171
Janssen T. Development of Symmetry Concepts for Aperiodic Crystals. Symmetry. 2014; 6(2):171-188. https://doi.org/10.3390/sym6020171
Chicago/Turabian StyleJanssen, Ted. 2014. "Development of Symmetry Concepts for Aperiodic Crystals" Symmetry 6, no. 2: 171-188. https://doi.org/10.3390/sym6020171
APA StyleJanssen, T. (2014). Development of Symmetry Concepts for Aperiodic Crystals. Symmetry, 6(2), 171-188. https://doi.org/10.3390/sym6020171




