Using Symmetries (Beyond Geometric Symmetries) in Chemical Computations: Computing Parameters of Multiple Binding Sites

Abstract

We show how transformation group ideas can be naturally used to generate efficient algorithms for scientific computations. The general approach is illustrated on the example of determining, from the experimental data, the dissociation constants related to multiple binding sites. We also explain how the general transformation group approach is related to the standard (backpropagation) neural networks; this relation justifies the potential universal applicability of the group-related approach.

1. Why Use Symmetries (and Groups) in General Scientific Computations?

1.1. What We Plan to Do in This Paper

In this paper, on an important example of determining the dissociation constants related to multiple binding sites, we show that symmetries and groups can be useful in chemical computations.

1.2. Use of Symmetries in Chemistry: A Brief Reminder

In many practical situations, physical systems have symmetries, i.e., transformations that preserve certain properties of the corresponding physical system. For example, a benzene molecule C₆H₆ does not change if we rotate it 60°: this rotation simply replaces one carbon atom by another one. The knowledge of such geometric symmetries helps in chemical computations; see, e.g., [1–3].

1.3. Group Theory: A Mathematical Tool for Studying Symmetries

Since symmetries are useful, once we know one symmetry, it is desirable to know all the symmetries of a given physical system. In other words, once we list the properties which are preserved under the original symmetry transformation, it is desirable to find all the transformations that preserve these properties.

If a transformation f preserves the given properties, and the transformation g preserves these properties, then their composition h(x) = f(g(x)) also preserves these properties. For example, if the lowest energy level of the molecule does not change when we rotate it 60°, and does not change when we rotate it 120° around the same axis, then it also will not change if we first rotate it 60° and then 120°, to the total of 180°.

Similarly, if a transformation f does not change the given properties, then the inverse transformation f⁻¹ also does not change these properties. So, the set of all transformations that preserve given properties is closed under composition and inverse; such a set is called a transformation group or symmetry group. Mathematical analysis of such transformation is an important part of group theory.

1.4. Problems of Scientific Computations: A Brief Reminder

In this paper, we argue that symmetries can be used in scientific computations beyond geometric symmetries. To explain our idea, let us briefly recall the need for scientific computations.

One of the main objectives of science is to be able to predict future behavior of physical systems. To be able to make these predictions, we must find all possible dependencies y = F(x₁,…, x_n) between different physical quantities. Often, we only know the general form of the dependence, i.e., we know that y = G(x₁, …, x_n, c₁, … , c_m) for a known expression G(x₁, …, c_m), but we do not know the exact values of the corresponding parameters c₁, … , c_m. These values must be determined from the empirical data. For example, Newton's equations provide a general description of how the acceleration of each celestial body depends on its spatial location, but this description contains masses c_i of celestial bodies; these masses must be determined based on the astronomical observations.

In general, to be able to predict the value of a desired quantity y for which we know the form of the dependence y = G(x₁, … , x_n, c₁, … , c_m), we must do the following:

• first, we use the known observations $x_i^{(k)}$ and y^(k) of x_i and y to find the parameters c_i of the corresponding dependence from the condition that $y^{(k)}\approx G(x_1^{(k)},\dots ,x_n^{(k)},c_1,\dots ,c_m)$;

• after that, we measure the current values x_i of the corresponding quantities, and use these measured values and the reconstructed values of the parameters c_i to estimate y as y = G(x₁, …, x_n, c₁, …,c_m).

In scientific computation, the first problem is known as the inverse problem and the second problem as the forward problem. Usually:

• the forward problem is reasonably straightforward: it consists of applying a previously known algorithm, while

• an inverse problem is much more complex since it requires that we solve a system of equations, and for this solution, no specific algorithm is given.

1.5. Inverse Problem As the Problem of Finding the Inverse Transformation: Ideal Case When Measurement Errors Can be Ignored

We assume that we know the form of the dependence y = G(x₁, … , x_n, c₁, …, c_m) between the quantities x_i and y; the only unknowns are the parameters c₁, … , c_m. We want to find the values of these parameters c_i based on the measurement results.

In the idealized case when we can ignore the measurement uncertainty, the measured values $x_i^{(k)}$ and y^(k) coincide with the actual values of the corresponding quantities. Thus, based on each measurement k, we can conclude that $y^{(k)}=G(x_1^{(k)},\dots ,x_n^{(k)},c_1,\dots ,c_m)$. So, each measurement leads to an equation that with m unknowns c₁, … , c_m.

In general, we need m equations to find m unknowns. Thus, in this idealized case, it is sufficient to perform m measurements, and then determine the desired values c₁, … , c_m from the corresponding systems of m equations with n unknowns c₁, … , c_m:

$$\begin{array}{cc}{y}^{(1)}& =G(x_1^{(1)},\dots ,x_n^{(1)},c_1,\dots ,c_m);\\ & \dots \\ y^{(m)}& =G(x_1^{(m)},\dots ,x_n^{(m)},c_1,\dots ,c_m).\end{array}$$

The dependence y = G(x₁, … , x_n, c₁, … , c_m) is often highly non-linear; so, to find the desired values c_i, we need to solve a system of nonlinear equations. Such systems are often difficult to solve (in precise terms, the problem of solving a system of non-linear equations is known to be NP-hard; see, e.g., [4,5]).

Once the measurements of the quantities $x_i^{(k)}$ have been performed, the problem of solving the above system of equations can be equivalently reformulated as follows:

• we have a transformation f : ℝ^m → ℝ^m which maps an m-dimensional tuple c = (c₁,…, c_m) into an m-dimensional tuple y = f(c) with components y = (y₁,…, y_m) which are determined by the formula $y_k=G(x_1^{(k)},\dots ,x_n^{(k)},c_1,\dots ,c_m)$

• we know the measured values y_meas = (y⁽¹⁾, … , y^(m));

• we want to find the tuple c for which f(c) = y_meas.

One way to solve this system is to find the inverse transformation f⁻¹, and then to apply this inverse transformation to the tuple y_meas consisting of the measured values of the quantity y, resulting in the desired tuple c = f⁻¹(y_meas).

1.6. Inverse Problem: General Case

So far, we have considered the ideal case, when the measurement errors are so small that they can be safely ignored. In most practical situations, measurement errors must be taken into account. Because of the measurement errors, the measurements results ỹ^(k) and ${\stackrel{\sim }{x}}_i^{(k)}$ are, in general, different from the actual (unknown) values y^(k) and $x_i^{(k)}$ of the corresponding quantities: ỹ^(k) = y^(k) + Δy_k and ${\stackrel{\sim }{x}}_i^{(k)}=x_i^{(k)}+\mathrm{\Delta }{x}_{ki}$, where $\mathrm{\Delta }{y}_k\stackrel{\text{def}}{=}{\stackrel{\sim }{y}}^{(k)}-y^{(k)}$ and $\mathrm{\Delta }{x}_{ki}\stackrel{\text{def}}{=}{\stackrel{\sim }{x}}_i^{(k)}-x_i^{(k)}$ are the corresponding measurement errors.

The formula $y^{(k)}=G(x_1^{(k)},\dots ,x_n^{(k)},c_1,\dots ,c_m)$ relates the actual (unknown) values of the corresponding quantities. To determine the coefficients c_i from the observed values ỹ^(k) and ${\stackrel{\sim }{x}}_i^{(k)}$, we need to describe this formula in terms of the measurement results ỹ^(k) and ${\stackrel{\sim }{x}}_i^{(k)}$. Substituting y^(k) = y^(k) − Δy_k and $x_i^{(k)}={\stackrel{\sim }{x}}_i^{(k)}-\mathrm{\Delta }{x}_{ki}$ into this formula, we conclude that ${\stackrel{\sim }{y}}^{(k)}-\mathrm{\Delta }{y}_k=G({\stackrel{\sim }{x}}_1^{(k)}-\mathrm{\Delta }{x}_{k1},\dots ,{\stackrel{\sim }{x}}_n^{(k)},c_1,\dots ,c_m)$.

Usually, the measurement errors Δy_k and Δx_ki are relatively small, so we can expand the above expression in Taylor series and ignore terms which are quadratic (or of higher order) in terms of these measurement errors. Thus, we conclude that ${\stackrel{\sim }{y}}^{(k)}=G({\stackrel{\sim }{x}}_1^{(k)},\dots ,{\stackrel{\sim }{x}}_n^{(k)},c_1,\dots ,c_m)+{\mathrm{\Delta }}_k$, where ${\mathrm{\Delta }}_k\stackrel{\text{def}}{=}\mathrm{\Delta }{y}_k-\sum _{i=1}^n{h}_{ki}\cdot \mathrm{\Delta }{x}_{ki}$ and $h_{ki}\stackrel{\text{def}}{=}\frac{\partial G}{\partial x_i}$.

In many practical situations, measurement errors Δy_k and Δx_ki are independent and normally distributed, with zero mean and known variances ${\sigma }_k^2$ and ${\sigma }_{ki}^2$; see, e.g., [6]. In this case, the values Δ_k are also normally distributed with zero mean and variances $V_k={\sigma }_k^2+\sum _{i=1}^n{h}_{ki}^2\cdot {\sigma }_{ki}^2$. Thus, according to the Maximum Likelihood Method, the best estimate for the parameters c_i is the one that comes from the Least Squares method and minimizes the sum $S({\stackrel{\sim }{y}}^{(1)},\dots ,{\stackrel{\sim }{x}}_1^{(1)},\dots c_1,\dots ,c_m)\stackrel{\text{def}}{=}\sum _{k=1}^K\frac{{\left({\stackrel{\sim }{y}}^{(k)}-G({\stackrel{\sim }{x}}_1^{(k)},\dots ,{\stackrel{\sim }{x}}_n^{(k)},c_1,\dots c_m)\right)}^2}{V_k}$; see, e.g., [7].

In the general case, when the probability distributions of measurement errors may be different from normal, the Maximum Likelihood method may lead to the minimization of a different functional S. The corresponding values c_i can be found from the fact that when S attains its minimum, we have $D_i({\stackrel{\sim }{y}}^{(1)},\dots ,{\stackrel{\sim }{x}}_1^{(1)},\dots ,c_1,\dots ,c_m)=0$, where $D_i\stackrel{\text{def}}{=}\frac{\partial S}{\partial c_i}$.

In the absence of measurement errors, the measurement results coincide with the actual values, and thus, the solution c_i to the system of equations D_i = 0 coincides with the no-noise solution $c_i^{(0)}$ to the system of m equations ${\stackrel{\sim }{y}}^{(k)}=G({\stackrel{\sim }{x}}_1^{(k)},\dots ,{\stackrel{\sim }{x}}_n^{(k)},c_1,\dots ,c_n)$, 1 ≤ k ≤ m. Since the measurement errors are small, the measurement results ỹ^(k) and ${\stackrel{\sim }{x}}_i^{(k)}$ are close to the actual values y^(k) and $x_i^{(k)}$, and thus, the solution c_i to the system is close to the non-noise solution $c_i^{(0)}$, i.e., $c_i=c_i^{(0)}+\mathrm{\Delta }{c}_i$, where the differences Δc_i are small. Substituting the expressions $c_i=c_i^{(0)}+\mathrm{\Delta }{c}_i$ into the formula for D_i, we get $D_i(c_i^{(0)}+\mathrm{\Delta }{c}_1,\dots ,c_m^{(0)}+\mathrm{\Delta }{c}_m)=0$. Expanding D_i in Taylor series and ignoring terms which are quadratic or higher order in Δc_i, we get a system of linear equations $D_i(c_i^{(0)},\dots ,c_m^{(0)})+\sum _{i=1}^m{d}_{ij}\cdot \mathrm{\Delta }{c}_j=0$, where $d_{ij}\stackrel{\text{def}}{=}\frac{\partial D_i}{\partial c_j}$. Solving systems of linear equations is computationally feasible and efficient.

Thus, once we know how to efficiently solve the inverse problem in the idealized no-noise case, we can also efficiently extend the corresponding algorithm to the general noisy case:

• first, we solve the non-noise system ${\stackrel{\sim }{y}}^{(k)}=G({\stackrel{\sim }{x}}_1^{(k)},\dots ,{\stackrel{\sim }{x}}_n^{(k)},c_1,\dots ,c_n)$, 1 ≤ k ≤ m, and get the approximate values $c_i^{(0)}$;

• then, we find the differences Δc_i by solving the above system of linear equations $D_i(c_i^{(0)},\dots ,c_m^{(0)})+\sum _{i=1}^m{d}_{ij}\cdot \mathrm{\Delta }{c}_j=0$; and

• finally, we compute $c_i=c_i^{(0)}+\mathrm{\Delta }{c}_i$.

In other words, the main computational complexity of solving the inverse problem occurs already in the non-noise case: once this case is solved, the general solution is straightforward. Because of this fact, in this paper, we concentrate on solving the no-noise problem—keeping in mind that the above linearization procedure enables us to readily extend the no-noise solution to the general case.

1.7. Often, Computations Can be Simplified if We Represent the to-be-Inverted Transformation f As a Composition

In many practical situations, we can make computations easier if, instead of directly solving a complex inverse problem, we represent it as a sequence of easier-to-solve problems.

For example, everyone knows how to solve a quadratic equation a · x² + b · x + c = 0. This knowledge can be effectively used if we need to solve a more complex equation a · x⁴ + b · x² + c = 0. For that, we represent a · x⁴ + b · x² + c as a · y² + b · y + c, where y = x². Then:

• first, we solve the equation a · y² + b · y + c and find y;

• next, we solve an equation x² = y with this y and find the desired value x.

In general, if we represent a transformation f as a composition f = f₁ ∘ … ∘ f_n of transformations f_i, then the inverse transformation f⁻¹ can be represented as $f_n^{-1}\circ \dots \circ f_1^{-1}$. Thus, if we can represent the original difficult-to-invert transformation f as a composition of several easier-to-invert transformations f_i, this will simplify the inversion of f.

1.8. Conclusion: Transformations (and Transformation Groups) Can Help in Scientific Computations

In transformation terms, solving an inverse problem means finding the inverse transformation, and simplification of this process means using compositions—and a possibility to invert each of the composed transformations. For this idea to work, the corresponding class of transformations should be closed under composition and inverse, i.e., it should form a transformation group.

In a transformation group, the multiplication of two transformations f and g is their composition f ∘ g, and the inverse element to a transformation f is the inverse transformation f⁻¹.

1.9. How Symmetries and Groups Can Help in Scientific Computations: General Idea Summarized

The inverse problem of scientific computations—the problem of estimating the parameters of the model which are the best fit for the data—is often computationally difficult to solve. From the mathematical viewpoint, this problem can be reduced to finding the inverse f⁻¹ to a given transformation. The computation of this inverse can be simplified if we represent f as a composition of easier-to-invert transformations f = f₁ ∘ … ∘ f_N; then, we can compute f⁻¹ as $f^{-1}=f_N^{-1}\circ \dots \circ f_1^{-1}$.

2. How To Use Symmetries (and Groups) in General Scientific Computations: General Idea

2.1. Main Idea: Reminder

An inverse problem of interval computations consists of finding an inverse f⁻¹ to a given transformation f. This inverse is sometimes difficult to compute. To simplify computation of f⁻¹, we try to represent f as a composition of easier-to-invert transformations f_i.

2.2. Which Transformations Are the Easiest-to-Invert

Which transformations are easier to invert? Inverting a transformation f : ℝ^m → ℝ^m means solving a system of m equations f_k(c₁, … , c_m) = y^(k) with m unknowns c₁, … , c_m.

The simplest case is when we have a system of linear equations. In this case, there are well-known feasible algorithms for solving this system (i.e., for inverting the corresponding linear transformation). It would be nice if we could always only use linear transformations, but alas, a composition of linear transformations is always linear. So, to represent general non-linear transformations, we need to also consider some systems of non-linear equations.

For nonlinear systems, in general, the fewer unknowns we have, the easier it is to solve the system. Thus, the easiest-to-solve system of non-linear equations is the system consisting of a single nonlinear equation with one unknown.

2.3. Resulting Approach to Scientific Computing

We would like to represent an arbitrary transformation f as a composition of linear transformations and functions of one variable.

2.4. The Corresponding Representation is Always Possible

We are interested in transformations

$$f:{\text{ℝ}}^m\to {\text{ℝ}}^m$$

which can be obtained as multiple compositions of:

• (reversible) linear transformation and

• transformations of the type (x₁, … ,x_n) → (f₁(x₁), …, f_m(x_m)) which consist of applying (reversible) smooth (differentiable) functions of one variable to the components of the input tuple.

One can easily check that such transformations form a group : namely, it is a transformation group generated by the union of two smaller transformation groups—the group of linear transformations and the group of component-wise transformations.

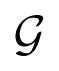
To analyze which transformations can be approximated by compositions from this group, let us consider its closure (in some reasonable sense as described, e.g., in [8–10]). This closure also forms a group. It is known (see, e.g., [8–10]) that if a group of smooth (differentiable) transformations is closed (in some reasonable sense) and contains all invertible linear transformations, then it coincides either with the group of all linear transformations, or with the group of all projective transformations, or with the group of all smooth transformations. Since some transformations (x₁,…, x_n) → (f₁(x₁), …, f_m(x_m)) from the group are not linear and not projective (in 1-D case, this means not fractionally linear), we thus conclude that the closure coincides with the group of all invertible smooth transformations.

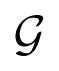
By definition of the closure, this means that any differentiable transformation f : ℝ^m → ℝ^m can be approximated, with any given accuracy, by a transformation from the group , i.e., by a composition of linear and component-wise transformation. Since in practice, we only know the values and dependencies with certain accuracy anyway, this means that, from the practical viewpoint, any transformation can be represented as a composition of linear and component-wise transformations.

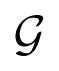
2.5. Comments

• The same arguments show that we can still approximate a general transformation if, instead of generic non-linear functions f_i(x_i), we allow only one specific not-fractionally-linear function, e.g., the sigmoid function $s_0(x)=\frac{1}{1+exp(-x)}$; see, e.g., [9,11,12].

• Linear and component-wise transformations are not only computationally convenient: from the physical viewpoint, they can be viewed as symmetries in the sense that they preserve some structure of the original system. For example, for polynomial systems, linear transformations preserve the order of the polynomial: after such a transformation, quadratic systems remain quadratic, and cubic systems remain cubic. In their turn, component-wise transformations preserve independence: e.g., dynamical systems $\frac{d{x}_i}{dt}=h_i(x_i)$ which describe n independent subsystems retain the same independence structure after component-wise transformations $x_i\to x_i^{\prime }=f_i(x_i)$.

2.6. Once We Know the Corresponding Representation, We Can Solve the Inverse Problem

Our objective is to find the tuple of the parameters c = (c₁, …, c_m) by solving a system of non-linear equations f(c) = y_meas. Our idea is to find the inverse transformation f⁻¹ and then to compute c as c = f−¹(y_meas).

Once we know how to represent the transformation f as a composition f = f₁ ∘ … ∘ f_N of easy-to-invert linear and component-wise transformations f₁, … , f_N, then we have $f^{-1}=f_N^{-1}\circ \dots \circ f_1^{-1}$. Thus, we can efficiently compute c = f⁻¹(y_meas) as

$$c=f_N^{-1}(f_{N-1}^{-1}(\dots f_1^{-1}(y_{\text{meas}})\dots )),$$

i.e., by starting with the tuple y_meas and by sequentially applying easy-to-compute transformations $f_1^{-1}$, $f_2^{-1},\dots ,f_N^{-1}$.

2.7. To Make This Idea Practically Useful, We Need to be Able to Represent a Generic Transformation As a Desired Composition

For this method to be useful, we need to be able to represent a general non-linear transformation f : ℝ^m → ℝ^m as a composition of linear and component-wise transformations.

In some cases, the desired representation can be obtained analytically, by analyzing a specific expression for the transformation f. One of such cases is described in the next section.

To obtain such a representation in the general case, we can use the fact that the desired compositions

$$f(x)=f_1\circ f_2\cdot \dots \circ f_{N-1}(x)\circ f_N(x)=f_1(f_2(\dots (f_{N-1}(f_N(x)))\dots ))$$

correspond to computations by multi-layer neural networks. Namely:

• we start with the input layer, in which we input m values x₁, … , x_m;

• in the first processing layer, we apply the transformation f_N to the inputs x and get m intermediate results – components of the tuple f_N(x);

• in the second processing layer, we apply the transformation f_n−1 to the results f_n(x) of the first layer and thus, get the tuple f_N−1(f_N(x));

• …

• finally, at the last (N-th) processing layer, we apply the transformation f₁ to the results f₂(… (f_n (x)) …) of the previous processing layer, and thus, get the desired tuple

  $$f(x)=f_1(f_2(\dots (f_N(x))\dots )).$$

A general linear transformation has the form $y_k=\sum _{i=1}^m{w}_{ik}\cdot x_i-w_{k0}$; the corresponding layer consists of m linear neurons each of which takes, as inputs, all the signals from the previous layer and compute the corresponding value $\sum _{i=1}^m{w}_{ik}\cdot x_i-w_{k0}$. Similarly, a non-linear transformation y_i = f_i(x_i) consists of m non-linear neurons each of which take only one input x_i and transforms it into the value f_i(x_i).

This is a usual arrangement of neural networks. For example, in one of the most widely used 3-layer neural network with K hidden neurons:

• we first compute K linear combinations of the inputs $y_k=\sum _{i=1}^m{w}_{ki}\cdot c_i-w_{k0}$;

• then, we apply, to each value y_k, a function s₀(y) of one variable s₀(y), resulting in z_k = s₀(y_k); usually, a sigmoid function $s_0(y)=\frac{1}{1+exp(-y)}$ is used;

• finally, we compute a linear combination $y=\sum _{k=1}^K{W}_k\cdot z_k-w_0$.

(It is worth mentioning that a similar universal approximation result is known for neural networks: we can approximate an arbitrary continuous transformation (with any given accuracy) by an appropriate 3-layer neural network, i.e., as a composition of linear transformations and functions of one variable; see, e.g., [9,11,12].)

Neural networks are widely used in practice; one of the main reasons for their practical usefulness is that an efficient backpropagation algorithm is known for their training, i.e., for computing the weights w_ki and W_i for which the neural network represent the given dependence y = F(x), i.e., for which, for given inputs x, we get the desired output y = F(x); see, e.g., [11]. Since a general representation of a transformation f(c) as a composition of linear and component-wise functions is equivalent to its representation by the corresponding multi-linear neural network, we can use the general backpropagation algorithm to find the coefficients of the corresponding neurons and thus, to find a representation of the original non-linear transformation f(c) as the composition of linear and component-wise functions; see, e.g., [9,11,12].

As we have mentioned, once such a representation is found, we can invert each of the components and thus, easily compute c = f⁻¹(y_meas), i.e., solve the inverse problem in the non-noise case. As described earlier, we can then use linearization to transform this idealized no-noise solution into a solution which takes into account noise (=measurement errors).

3. Case Study: Finding Reaction Parameters of Multiple Binding Sites

3.1. Case Study: Description

The general description of the above methodology is rather complicated. However, in some specific computational problems, it is possible to directly find the desired decomposition into linear and component-wise functions—which makes the application of the above ideas much simpler.

Let us show that such a simpler application is possible for a specific important problem of chemical computations: the problem of finding reaction parameters of multiple binding sites.

When there is a single binding site at which a ligand L can bind to a receptor R, the corresponding chemical kinetic equations L + R → LR and LR → L + R with intensities k⁺ and k⁻ lead to the following equilibrium equation for the corresponding concentrations [L], [R], and [LR]:

$$k^{+}\cdot [\text{L}]\cdot [\text{R}]=k^{-}\cdot [\text{LR}].$$

From this, we get $\frac{[\text{R}]}{[\text{LR}]}=\frac{k_d}{[\text{L}]}$, where we denoted $k_d\stackrel{\text{def}}{=}\frac{k^{-}}{k^{+}}$. Thus,

$$\frac{[\text{R}]+[\text{LR}]}{[\text{LR}]}=1+\frac{k_d}{[\text{L}]}=\frac{k_d+[\text{L}]}{[\text{L}]}.$$

Hence, the bound proportion of the receptor $B\stackrel{\text{def}}{=}\frac{[\text{LR}]}{[\text{R}]+[\text{LR}]}$ depends on the concentration [L] of the ligand as

$$B=\frac{[\text{L}]}{k_d+[\text{L}]}.$$

The presence of the bound ligands can be experimentally detected by the dimming of the fluorescence. The original intensity of the fluorescence is proportional to the original concentration [R]⁽⁰⁾ of the receptor; since some of the receptor molecules got bound, this original concentration is equal to [R]⁽⁰⁾ = [R] + [LR]. The dimming is proportional to the concentration [LR] of the bound receptor. Thus, the relative decrease in the fluorescence intensity is proportional to the ratio B.

Let us now consider the case of several (S) binding sites. Each binding site can be bound by one ligand molecule. Let us denote the ligand molecule bound to the s-th site by L_(s). In these terms, for example, the molecule in which two ligands are bound to the first and the third sites will be denoted by L₍₁₎L₍₃₎R. For each binding site s, we have reactions L + R → L_(s)R and L_(s)R → L + R with intensities $k_s^{+}$ and $k_s^{-}$. We assume that the reactions at different binding sites are independent, so that the the intensities with which the ligand attached to the s-th site does not depend on whether other binding sites are bound or not. For example, for s′ ≠ s, the reactions L + L_(s′)R → L_(s)L_(s′)R and L_(s)L_(s′)R → L + L_(s′)R have the same intensities $k_s^{+}$ and $k_s^{-}$ which do not depend on s′. Because of this independence, we can summarize all the reactions in which a ligand is added to or deleted from the s-th binding site into two reactions: R_−s + L → R_+s with intensity $k_s^{+}$ and a reaction R_+s → L + R_−s with intensity $k_s^{-}$, where R_−s is the total concentration of all the receptor molecules for which the s-th binding site is free, and R_+s is the total concentration of all the receptor molecules for which there is a ligand bound to the s-th binding site.

These summarized reactions lead to the following equilibrium equation for the corresponding concentrations [L], [R_−s], and [R_−s]:

$$k^{+}\cdot [\text{L}]\cdot [{\text{R}}_{-s}]=k^{-}\cdot [{\text{R}}_{+s}].$$

From this, we get $\frac{[{\text{R}}_{-s}]}{[{\text{R}}_{+s}]}=\frac{k_{ds}}{[\text{L}]}$, where we denoted $k_{ds}\stackrel{\text{def}}{=}\frac{k_s^{-}}{k_s^{+}}$. Thus,

$$\frac{[{\text{R}}_{-s}]+[{\text{R}}_{+s}]}{[{\text{R}}_{+s}]}=1+\frac{k_d}{[\text{L}]}=\frac{k_d+[\text{L}]}{[\text{L}]},$$

and hence,

$$\frac{[{\text{R}}_{+s}]}{[{\text{R}}_{-s}]+[{\text{R}}_{+s}]}=\frac{[\text{L}]}{k_{ds}+[\text{L}]}.$$

Similarly to the case of the single binding site, the presence of bound ligands dims the fluorescence. Let w_s be the dimming (per unit concentration) caused by the presence of the ligand at the s-th site. The total dimming D_s caused by all the molecules at which the ligand is bound of the s-th site is thus equal to D_s = w_s · [R_+s]. Since the different binding sites are independent, it is reasonable to assume that the dimmings corresponding to different binding sites simply add up. Thus, the overall dimming D is equal to the sum of the dimmings D_s corresponding to different binding sites s, i.e., to

$$D=\sum _{s=1}^S{D}_s=\sum _{s=1}^S{w}_s\cdot [{\text{R}}_{+s}].$$

The original intensity of the fluorescence I is proportional to the original concentration [R]⁽⁰⁾ of the receptor: I = k · [R]⁽⁰⁾, where for every s, we have [R]⁽⁰⁾ = [R_−s] + [R_+s]. Thus, the relative dimming $B=\stackrel{\text{def}}{=}\frac{D}{I}$ takes the form

$$B=\frac{D}{I}=\frac{\sum _{s=1}^S{w}_s\cdot [{\text{R}}_{+s}]}{k\cdot {[\text{R}]}^{(0)}}=\sum _{s=1}^S\frac{w_s\cdot [{\text{R}}_{+s}]}{k\cdot {[\text{R}]}^{(0)}}=\sum _{s=1}^S\frac{w_s}{k}\cdot \frac{[{\text{R}}_{+s}]}{[{\text{R}}_{-s}]+[{\text{R}}_{+s}]}.$$

Substituting the above expression for the ratio $\frac{[{\text{R}}_{+s}]}{[{\text{R}}_{-s}]+[{\text{R}}_{+s}]}$ into this formula, we conclude that

$$B=\sum _{s=1}^S\frac{w_s}{k}\cdot \frac{[\text{L}]}{k_{ds}+[\text{L}]},$$

i.e.,

$$B=\sum _{s=1}^S\frac{r_s\cdot [\text{L}]}{k_{ds}+[\text{L}]}$$

(1)

where we denoted $r_s\stackrel{\text{def}}{=}\frac{w_s}{k}$.

3.2. Inverse Problem Corresponding to the Case Study

The problem is to find the values r_s and k_ds from the observations. In other words, we observe the bound proportions y^(k) for different ligand concentrations [L] = x^(k), and we want to find the values r_s and k_ds for which

$$y^{(k)}=\sum _{s=1}^S\frac{r_s\cdot x^{(k)}}{k_{ds}+x^{(k)}}$$

(2)

3.3. How to Use Group-Theoretic Ideas to Simplify the Corresponding Computations: Analysis of the Problem

The system (2) is a difficult-to-solve system of nonlinear equations with 2S unknowns. To simplify the solution of this system, let us represent its solution as a composition of linear transformations and functions of one variable.

By adding all S fractions $\frac{r_s\cdot x}{k_{ds}+x}$, we get a ratio of two polynomials $\frac{P(x)}{Q(x)}$. Here, Q(x) is the product of all S denominators x + k_ds, and is, thus, a S-th order polynomial with the leading term x^S:

$$Q(x)=x^S+q_{S-1}\cdot x^{S-1}+\dots +q_1\cdot x+q_0$$

(3)

Similarly, since P(x) is divisible by x, we get P(x) = p_S · x^S + p_S−1 · x^S−1 + … + p₁ · x.

The equations $y^{(k)}=\frac{P(x^{(k)})}{Q(x^{(k)})}$ can be equivalently represented as y^(k) · Q(x^(k)) = P(x^(k)), i.e., as

$$y^{(k)}\cdot {\left(x^{(k)}\right)}^S+q_{S-1}\cdot y^{(k)}\cdot {\left(x^{(k)}\right)}^{S-1}+\dots +q_1\cdot y^{(k)}\cdot x^{(k)}+q_0\cdot y^{(k)}=p_S\cdot {\left(x^{(k)}\right)}^S+p_{S-1}\cdot {\left(x^{(k)}\right)}^{S-1}+\dots +p_1\cdot x^{(k)}$$

(4)

This is a system of linear equations with 2S unknowns p_i and q_i. Solving this system of linear equations is relatively easy.

Once we solve this linear system and find the values q_i, we can find the parameters k_ds from the condition that for x = −k_ds, we have x + k_ds = 0 and thus, the product Q(x) of all such terms is equal to 0. The equation Q(−k_ds) = 0 is a nonlinear equation with one unknown, i.e., exactly the type of nonlinear equation that we want to solve.

Finally, once we find all the values k_ds, the Equation (2) becomes a linear system of equations for the remaining unknowns r_s.

Thus, the decomposition of the original difficult-to-invert transformation into a composition of easier-to-invert transformations (linear transformations and functions of one variable) leads to the following algorithm for computing the parameters of multiple binding sites.

3.4. Inverse Problem Corresponding to the Case Study: Resulting Algorithm

We start with the values y^(k) of the bound proportion corresponding to different ligand concentrations x^(k). Our objective is to find the parameters r_s and k_ds of different binding sites s = 1, …, S. To compute these parameters, we do the following:

• first, we solve the linear system (4) with 2S unknowns p_i and q_i;

• we then use the computed values q_i to form the polynomial (3) and to solve the equation Q(−x) = 0 with one unknown x; as a result, we get 2S solutions k_ds;

• we then substitute the resulting values k_ds into the formula (1) and solve the resulting system of S linear equations with S unknowns r_s.

3.5. Comment

Our numerical experiments confirmed the computational efficiency of the new algorithm.

4. Conclusions

Geometric symmetries has been effectively used to simply scientific computations, in particular, computations related to chemical problems. In this paper, we show that non-geometric “symmetries” (transformations) can also be very helpful in scientific computations. Specifically, we show that the inverse problem—the problem of finding the parameters of the model based on the measurement results—can be solved by computing the inverse to a transformation describing the forward problem—the problem of predicting the measurement results based on the known values of the model's parameters. In general, the computation of such an inverse (i.e., solving the corresponding system of non-linear equations) is a complex computational problem. This computation can be simplified if we can represent the to-be-inverted forward transformation as a composition of several easier-to-invert transformations, e.g., linear and component-wise transformations. In some cases, such a representation can be obtained by analyzing the original transformation; such a case related to computing parameters of multiple binding sites is described in the paper. In general, to find such a composition, we can use the fact that the desired representation means that the to-be-inverted transformation is computed by an appropriate multi-layer neural network; then, the backpropagation algorithm (typical for training neural networks) can be used to compute the corresponding representation.