Using Symmetries (Beyond Geometric Symmetries) in Chemical Computations: Computing Parameters of Multiple Binding Sites
Abstract
: We show how transformation group ideas can be naturally used to generate efficient algorithms for scientific computations. The general approach is illustrated on the example of determining, from the experimental data, the dissociation constants related to multiple binding sites. We also explain how the general transformation group approach is related to the standard (backpropagation) neural networks; this relation justifies the potential universal applicability of the group-related approach.1. Why Use Symmetries (and Groups) in General Scientific Computations?
1.1. What We Plan to Do in This Paper
In this paper, on an important example of determining the dissociation constants related to multiple binding sites, we show that symmetries and groups can be useful in chemical computations.
1.2. Use of Symmetries in Chemistry: A Brief Reminder
In many practical situations, physical systems have symmetries, i.e., transformations that preserve certain properties of the corresponding physical system. For example, a benzene molecule C6H6 does not change if we rotate it 60°: this rotation simply replaces one carbon atom by another one. The knowledge of such geometric symmetries helps in chemical computations; see, e.g., [1–3].
1.3. Group Theory: A Mathematical Tool for Studying Symmetries
Since symmetries are useful, once we know one symmetry, it is desirable to know all the symmetries of a given physical system. In other words, once we list the properties which are preserved under the original symmetry transformation, it is desirable to find all the transformations that preserve these properties.
If a transformation f preserves the given properties, and the transformation g preserves these properties, then their composition h(x) = f(g(x)) also preserves these properties. For example, if the lowest energy level of the molecule does not change when we rotate it 60°, and does not change when we rotate it 120° around the same axis, then it also will not change if we first rotate it 60° and then 120°, to the total of 180°.
Similarly, if a transformation f does not change the given properties, then the inverse transformation f−1 also does not change these properties. So, the set of all transformations that preserve given properties is closed under composition and inverse; such a set is called a transformation group or symmetry group. Mathematical analysis of such transformation is an important part of group theory.
1.4. Problems of Scientific Computations: A Brief Reminder
In this paper, we argue that symmetries can be used in scientific computations beyond geometric symmetries. To explain our idea, let us briefly recall the need for scientific computations.
One of the main objectives of science is to be able to predict future behavior of physical systems. To be able to make these predictions, we must find all possible dependencies y = F(x1,…, xn) between different physical quantities. Often, we only know the general form of the dependence, i.e., we know that y = G(x1, …, xn, c1, … , cm) for a known expression G(x1, …, cm), but we do not know the exact values of the corresponding parameters c1, … , cm. These values must be determined from the empirical data. For example, Newton's equations provide a general description of how the acceleration of each celestial body depends on its spatial location, but this description contains masses ci of celestial bodies; these masses must be determined based on the astronomical observations.
In general, to be able to predict the value of a desired quantity y for which we know the form of the dependence y = G(x1, … , xn, c1, … , cm), we must do the following:
first, we use the known observations and y(k) of xi and y to find the parameters ci of the corresponding dependence from the condition that ;
after that, we measure the current values xi of the corresponding quantities, and use these measured values and the reconstructed values of the parameters ci to estimate y as y = G(x1, …, xn, c1, …,cm).
In scientific computation, the first problem is known as the inverse problem and the second problem as the forward problem. Usually:
the forward problem is reasonably straightforward: it consists of applying a previously known algorithm, while
an inverse problem is much more complex since it requires that we solve a system of equations, and for this solution, no specific algorithm is given.
1.5. Inverse Problem As the Problem of Finding the Inverse Transformation: Ideal Case When Measurement Errors Can be Ignored
We assume that we know the form of the dependence y = G(x1, … , xn, c1, …, cm) between the quantities xi and y; the only unknowns are the parameters c1, … , cm. We want to find the values of these parameters ci based on the measurement results.
In the idealized case when we can ignore the measurement uncertainty, the measured values and y(k) coincide with the actual values of the corresponding quantities. Thus, based on each measurement k, we can conclude that . So, each measurement leads to an equation that with m unknowns c1, … , cm.
In general, we need m equations to find m unknowns. Thus, in this idealized case, it is sufficient to perform m measurements, and then determine the desired values c1, … , cm from the corresponding systems of m equations with n unknowns c1, … , cm:
The dependence y = G(x1, … , xn, c1, … , cm) is often highly non-linear; so, to find the desired values ci, we need to solve a system of nonlinear equations. Such systems are often difficult to solve (in precise terms, the problem of solving a system of non-linear equations is known to be NP-hard; see, e.g., [4,5]).
Once the measurements of the quantities have been performed, the problem of solving the above system of equations can be equivalently reformulated as follows:
we have a transformation f : ℝm → ℝm which maps an m-dimensional tuple c = (c1,…, cm) into an m-dimensional tuple y = f(c) with components y = (y1,…, ym) which are determined by the formula
we know the measured values ymeas = (y(1), … , y(m));
we want to find the tuple c for which f(c) = ymeas.
One way to solve this system is to find the inverse transformation f−1, and then to apply this inverse transformation to the tuple ymeas consisting of the measured values of the quantity y, resulting in the desired tuple c = f−1(ymeas).
1.6. Inverse Problem: General Case
So far, we have considered the ideal case, when the measurement errors are so small that they can be safely ignored. In most practical situations, measurement errors must be taken into account. Because of the measurement errors, the measurements results ỹ(k) and are, in general, different from the actual (unknown) values y(k) and of the corresponding quantities: ỹ(k) = y(k) + Δyk and , where and are the corresponding measurement errors.
The formula relates the actual (unknown) values of the corresponding quantities. To determine the coefficients ci from the observed values ỹ(k) and , we need to describe this formula in terms of the measurement results ỹ(k) and . Substituting y(k) = y(k) − Δyk and into this formula, we conclude that .
Usually, the measurement errors Δyk and Δxki are relatively small, so we can expand the above expression in Taylor series and ignore terms which are quadratic (or of higher order) in terms of these measurement errors. Thus, we conclude that , where and .
In many practical situations, measurement errors Δyk and Δxki are independent and normally distributed, with zero mean and known variances and ; see, e.g., [6]. In this case, the values Δk are also normally distributed with zero mean and variances . Thus, according to the Maximum Likelihood Method, the best estimate for the parameters ci is the one that comes from the Least Squares method and minimizes the sum ; see, e.g., [7].
In the general case, when the probability distributions of measurement errors may be different from normal, the Maximum Likelihood method may lead to the minimization of a different functional S. The corresponding values ci can be found from the fact that when S attains its minimum, we have , where .
In the absence of measurement errors, the measurement results coincide with the actual values, and thus, the solution ci to the system of equations Di = 0 coincides with the no-noise solution to the system of m equations , 1 ≤ k ≤ m. Since the measurement errors are small, the measurement results ỹ(k) and are close to the actual values y(k) and , and thus, the solution ci to the system is close to the non-noise solution , i.e., , where the differences Δci are small. Substituting the expressions into the formula for Di, we get . Expanding Di in Taylor series and ignoring terms which are quadratic or higher order in Δci, we get a system of linear equations , where . Solving systems of linear equations is computationally feasible and efficient.
Thus, once we know how to efficiently solve the inverse problem in the idealized no-noise case, we can also efficiently extend the corresponding algorithm to the general noisy case:
first, we solve the non-noise system , 1 ≤ k ≤ m, and get the approximate values ;
then, we find the differences Δci by solving the above system of linear equations ; and
finally, we compute .
In other words, the main computational complexity of solving the inverse problem occurs already in the non-noise case: once this case is solved, the general solution is straightforward. Because of this fact, in this paper, we concentrate on solving the no-noise problem—keeping in mind that the above linearization procedure enables us to readily extend the no-noise solution to the general case.
1.7. Often, Computations Can be Simplified if We Represent the to-be-Inverted Transformation f As a Composition
In many practical situations, we can make computations easier if, instead of directly solving a complex inverse problem, we represent it as a sequence of easier-to-solve problems.
For example, everyone knows how to solve a quadratic equation a · x2 + b · x + c = 0. This knowledge can be effectively used if we need to solve a more complex equation a · x4 + b · x2 + c = 0. For that, we represent a · x4 + b · x2 + c as a · y2 + b · y + c, where y = x2. Then:
first, we solve the equation a · y2 + b · y + c and find y;
next, we solve an equation x2 = y with this y and find the desired value x.
In general, if we represent a transformation f as a composition f = f1 ∘ … ∘ fn of transformations fi, then the inverse transformation f−1 can be represented as . Thus, if we can represent the original difficult-to-invert transformation f as a composition of several easier-to-invert transformations fi, this will simplify the inversion of f.
1.8. Conclusion: Transformations (and Transformation Groups) Can Help in Scientific Computations
In transformation terms, solving an inverse problem means finding the inverse transformation, and simplification of this process means using compositions—and a possibility to invert each of the composed transformations. For this idea to work, the corresponding class of transformations should be closed under composition and inverse, i.e., it should form a transformation group.
In a transformation group, the multiplication of two transformations f and g is their composition f ∘ g, and the inverse element to a transformation f is the inverse transformation f−1.
1.9. How Symmetries and Groups Can Help in Scientific Computations: General Idea Summarized
The inverse problem of scientific computations—the problem of estimating the parameters of the model which are the best fit for the data—is often computationally difficult to solve. From the mathematical viewpoint, this problem can be reduced to finding the inverse f−1 to a given transformation. The computation of this inverse can be simplified if we represent f as a composition of easier-to-invert transformations f = f1 ∘ … ∘ fN; then, we can compute f−1 as .
2. How To Use Symmetries (and Groups) in General Scientific Computations: General Idea
2.1. Main Idea: Reminder
An inverse problem of interval computations consists of finding an inverse f−1 to a given transformation f. This inverse is sometimes difficult to compute. To simplify computation of f−1, we try to represent f as a composition of easier-to-invert transformations fi.
2.2. Which Transformations Are the Easiest-to-Invert
Which transformations are easier to invert? Inverting a transformation f : ℝm → ℝm means solving a system of m equations fk(c1, … , cm) = y(k) with m unknowns c1, … , cm.
The simplest case is when we have a system of linear equations. In this case, there are well-known feasible algorithms for solving this system (i.e., for inverting the corresponding linear transformation). It would be nice if we could always only use linear transformations, but alas, a composition of linear transformations is always linear. So, to represent general non-linear transformations, we need to also consider some systems of non-linear equations.
For nonlinear systems, in general, the fewer unknowns we have, the easier it is to solve the system. Thus, the easiest-to-solve system of non-linear equations is the system consisting of a single nonlinear equation with one unknown.
2.3. Resulting Approach to Scientific Computing
We would like to represent an arbitrary transformation f as a composition of linear transformations and functions of one variable.
2.4. The Corresponding Representation is Always Possible
We are interested in transformations
(reversible) linear transformation and
transformations of the type (x1, … ,xn) → (f1(x1), …, fm(xm)) which consist of applying (reversible) smooth (differentiable) functions of one variable to the components of the input tuple.
One can easily check that such transformations form a group
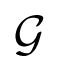
To analyze which transformations can be approximated by compositions from this group, let us consider its closure

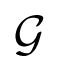

By definition of the closure, this means that any differentiable transformation f : ℝm → ℝm can be approximated, with any given accuracy, by a transformation from the group
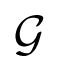
2.5. Comments
The same arguments show that we can still approximate a general transformation if, instead of generic non-linear functions fi(xi), we allow only one specific not-fractionally-linear function, e.g., the sigmoid function ; see, e.g., [9,11,12].
Linear and component-wise transformations are not only computationally convenient: from the physical viewpoint, they can be viewed as symmetries in the sense that they preserve some structure of the original system. For example, for polynomial systems, linear transformations preserve the order of the polynomial: after such a transformation, quadratic systems remain quadratic, and cubic systems remain cubic. In their turn, component-wise transformations preserve independence: e.g., dynamical systems which describe n independent subsystems retain the same independence structure after component-wise transformations .
2.6. Once We Know the Corresponding Representation, We Can Solve the Inverse Problem
Our objective is to find the tuple of the parameters c = (c1, …, cm) by solving a system of non-linear equations f(c) = ymeas. Our idea is to find the inverse transformation f−1 and then to compute c as c = f−1(ymeas).
Once we know how to represent the transformation f as a composition f = f1 ∘ … ∘ fN of easy-to-invert linear and component-wise transformations f1, … , fN, then we have . Thus, we can efficiently compute c = f−1(ymeas) as
2.7. To Make This Idea Practically Useful, We Need to be Able to Represent a Generic Transformation As a Desired Composition
For this method to be useful, we need to be able to represent a general non-linear transformation f : ℝm → ℝm as a composition of linear and component-wise transformations.
In some cases, the desired representation can be obtained analytically, by analyzing a specific expression for the transformation f. One of such cases is described in the next section.
To obtain such a representation in the general case, we can use the fact that the desired compositions
we start with the input layer, in which we input m values x1, … , xm;
in the first processing layer, we apply the transformation fN to the inputs x and get m intermediate results – components of the tuple fN(x);
in the second processing layer, we apply the transformation fn−1 to the results fn(x) of the first layer and thus, get the tuple fN−1(fN(x));
…
finally, at the last (N-th) processing layer, we apply the transformation f1 to the results f2(… (fn (x)) …) of the previous processing layer, and thus, get the desired tuple
A general linear transformation has the form ; the corresponding layer consists of m linear neurons each of which takes, as inputs, all the signals from the previous layer and compute the corresponding value . Similarly, a non-linear transformation yi = fi(xi) consists of m non-linear neurons each of which take only one input xi and transforms it into the value fi(xi).
This is a usual arrangement of neural networks. For example, in one of the most widely used 3-layer neural network with K hidden neurons:
we first compute K linear combinations of the inputs ;
then, we apply, to each value yk, a function s0(y) of one variable s0(y), resulting in zk = s0(yk); usually, a sigmoid function is used;
finally, we compute a linear combination .
(It is worth mentioning that a similar universal approximation result is known for neural networks: we can approximate an arbitrary continuous transformation (with any given accuracy) by an appropriate 3-layer neural network, i.e., as a composition of linear transformations and functions of one variable; see, e.g., [9,11,12].)
Neural networks are widely used in practice; one of the main reasons for their practical usefulness is that an efficient backpropagation algorithm is known for their training, i.e., for computing the weights wki and Wi for which the neural network represent the given dependence y = F(x), i.e., for which, for given inputs x, we get the desired output y = F(x); see, e.g., [11]. Since a general representation of a transformation f(c) as a composition of linear and component-wise functions is equivalent to its representation by the corresponding multi-linear neural network, we can use the general backpropagation algorithm to find the coefficients of the corresponding neurons and thus, to find a representation of the original non-linear transformation f(c) as the composition of linear and component-wise functions; see, e.g., [9,11,12].
As we have mentioned, once such a representation is found, we can invert each of the components and thus, easily compute c = f−1(ymeas), i.e., solve the inverse problem in the non-noise case. As described earlier, we can then use linearization to transform this idealized no-noise solution into a solution which takes into account noise (=measurement errors).
3. Case Study: Finding Reaction Parameters of Multiple Binding Sites
3.1. Case Study: Description
The general description of the above methodology is rather complicated. However, in some specific computational problems, it is possible to directly find the desired decomposition into linear and component-wise functions—which makes the application of the above ideas much simpler.
Let us show that such a simpler application is possible for a specific important problem of chemical computations: the problem of finding reaction parameters of multiple binding sites.
When there is a single binding site at which a ligand L can bind to a receptor R, the corresponding chemical kinetic equations L + R → LR and LR → L + R with intensities k+ and k− lead to the following equilibrium equation for the corresponding concentrations [L], [R], and [LR]:
The presence of the bound ligands can be experimentally detected by the dimming of the fluorescence. The original intensity of the fluorescence is proportional to the original concentration [R](0) of the receptor; since some of the receptor molecules got bound, this original concentration is equal to [R](0) = [R] + [LR]. The dimming is proportional to the concentration [LR] of the bound receptor. Thus, the relative decrease in the fluorescence intensity is proportional to the ratio B.
Let us now consider the case of several (S) binding sites. Each binding site can be bound by one ligand molecule. Let us denote the ligand molecule bound to the s-th site by L(s). In these terms, for example, the molecule in which two ligands are bound to the first and the third sites will be denoted by L(1)L(3)R. For each binding site s, we have reactions L + R → L(s)R and L(s)R → L + R with intensities and . We assume that the reactions at different binding sites are independent, so that the the intensities with which the ligand attached to the s-th site does not depend on whether other binding sites are bound or not. For example, for s′ ≠ s, the reactions L + L(s′)R → L(s)L(s′)R and L(s)L(s′)R → L + L(s′)R have the same intensities and which do not depend on s′. Because of this independence, we can summarize all the reactions in which a ligand is added to or deleted from the s-th binding site into two reactions: R−s + L → R+s with intensity and a reaction R+s → L + R−s with intensity , where R−s is the total concentration of all the receptor molecules for which the s-th binding site is free, and R+s is the total concentration of all the receptor molecules for which there is a ligand bound to the s-th binding site.
These summarized reactions lead to the following equilibrium equation for the corresponding concentrations [L], [R−s], and [R−s]:
Similarly to the case of the single binding site, the presence of bound ligands dims the fluorescence. Let ws be the dimming (per unit concentration) caused by the presence of the ligand at the s-th site. The total dimming Ds caused by all the molecules at which the ligand is bound of the s-th site is thus equal to Ds = ws · [R+s]. Since the different binding sites are independent, it is reasonable to assume that the dimmings corresponding to different binding sites simply add up. Thus, the overall dimming D is equal to the sum of the dimmings Ds corresponding to different binding sites s, i.e., to
The original intensity of the fluorescence I is proportional to the original concentration [R](0) of the receptor: I = k · [R](0), where for every s, we have [R](0) = [R−s] + [R+s]. Thus, the relative dimming takes the form
3.2. Inverse Problem Corresponding to the Case Study
The problem is to find the values rs and kds from the observations. In other words, we observe the bound proportions y(k) for different ligand concentrations [L] = x(k), and we want to find the values rs and kds for which
3.3. How to Use Group-Theoretic Ideas to Simplify the Corresponding Computations: Analysis of the Problem
The system (2) is a difficult-to-solve system of nonlinear equations with 2S unknowns. To simplify the solution of this system, let us represent its solution as a composition of linear transformations and functions of one variable.
By adding all S fractions , we get a ratio of two polynomials . Here, Q(x) is the product of all S denominators x + kds, and is, thus, a S-th order polynomial with the leading term xS:
The equations can be equivalently represented as y(k) · Q(x(k)) = P(x(k)), i.e., as
This is a system of linear equations with 2S unknowns pi and qi. Solving this system of linear equations is relatively easy.
Once we solve this linear system and find the values qi, we can find the parameters kds from the condition that for x = −kds, we have x + kds = 0 and thus, the product Q(x) of all such terms is equal to 0. The equation Q(−kds) = 0 is a nonlinear equation with one unknown, i.e., exactly the type of nonlinear equation that we want to solve.
Finally, once we find all the values kds, the Equation (2) becomes a linear system of equations for the remaining unknowns rs.
Thus, the decomposition of the original difficult-to-invert transformation into a composition of easier-to-invert transformations (linear transformations and functions of one variable) leads to the following algorithm for computing the parameters of multiple binding sites.
3.4. Inverse Problem Corresponding to the Case Study: Resulting Algorithm
We start with the values y(k) of the bound proportion corresponding to different ligand concentrations x(k). Our objective is to find the parameters rs and kds of different binding sites s = 1, …, S. To compute these parameters, we do the following:
first, we solve the linear system (4) with 2S unknowns pi and qi;
we then use the computed values qi to form the polynomial (3) and to solve the equation Q(−x) = 0 with one unknown x; as a result, we get 2S solutions kds;
we then substitute the resulting values kds into the formula (1) and solve the resulting system of S linear equations with S unknowns rs.
3.5. Comment
Our numerical experiments confirmed the computational efficiency of the new algorithm.
4. Conclusions
Geometric symmetries has been effectively used to simply scientific computations, in particular, computations related to chemical problems. In this paper, we show that non-geometric “symmetries” (transformations) can also be very helpful in scientific computations. Specifically, we show that the inverse problem—the problem of finding the parameters of the model based on the measurement results—can be solved by computing the inverse to a transformation describing the forward problem—the problem of predicting the measurement results based on the known values of the model's parameters. In general, the computation of such an inverse (i.e., solving the corresponding system of non-linear equations) is a complex computational problem. This computation can be simplified if we can represent the to-be-inverted forward transformation as a composition of several easier-to-invert transformations, e.g., linear and component-wise transformations. In some cases, such a representation can be obtained by analyzing the original transformation; such a case related to computing parameters of multiple binding sites is described in the paper. In general, to find such a composition, we can use the fact that the desired representation means that the to-be-inverted transformation is computed by an appropriate multi-layer neural network; then, the backpropagation algorithm (typical for training neural networks) can be used to compute the corresponding representation.
Acknowledgments
This work was supported in part by the National Science Foundation grants HRD-0734825 and HRD-1242122 (Cyber-ShARE Center of Excellence) and DUE-0926721, by Grants 1 T36 GM078000-01 and 1R43TR000173-01 from the National Institutes of Health, and by a grant N62909-12-1-7039 from the Office of Naval Research. The authors are thankful to Mahesh Narayan for his help, to Larry Ellzey and Ming-Ying Leung for their encouragement, and to the anonymous referees for valuable suggestions.
References
- Jaffé, H.H.; MacKenzie, R.E. Symmetry in Chemistry; Dover: New York, NY, USA, 2012. [Google Scholar]
- Kettle, S.F.A. Symmetry and Structure: Readable Group Theory for Chemists; Wiley: New York, NY, USA, 2007. [Google Scholar]
- Wigner, E.P. Group Theory and Its Application to the Quantum Mechanics of Atomic Spectra; Academic Press: Waltham, MA, USA, 1959. [Google Scholar]
- Garey, M.G.; Johnson, D.S. Computers and Intractability: A Guide to the Theory of NP-Completeness; Freeman: San Francisco, CA, USA, 1979. [Google Scholar]
- Kreinovich, V.; Lakeyev, A.; Rohn, J.; Kahl, P. Computational Complexity and Feasibility of Data Processing and Interval Computations; Kluwer: Dordrecht, the Netherlands, 1997. [Google Scholar]
- Rabinovich, S. Measurement Errors and Uncertainties: Theory and Practice; American Institute of Physics: New York, NY, USA, 2005. [Google Scholar]
- Sheskin, D.J. Handbook of Parametric and Nonparametric Statistical Procedures; Chapman and Hall/CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Guillemin, V.M.; Sternberg, S. An algebraic model of transitive differential geometry. Bull. Am. Math. Soc. 1964, 70, 16–47. [Google Scholar]
- Nguyen, H.T.; Kreinovich, V. Applications of Continuous Mathematics to Computer Science; Kluwer: Dordrecht, the Netherlands, 1997. [Google Scholar]
- Singer, I.M.; Sternberg, S. Infinite groups of Lie and Cartan, Part 1. J. d'Anal. Math. 1965, XV, 1–113. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Kreinovich, V. Arbitrary nonlinearity is sufficient to represent all functions by neural networks: A theorem. Neural Netw. 1991, 4, 381–383. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ortiz, A.; Kreinovich, V. Using Symmetries (Beyond Geometric Symmetries) in Chemical Computations: Computing Parameters of Multiple Binding Sites. Symmetry 2014, 6, 90-102. https://doi.org/10.3390/sym6010090
Ortiz A, Kreinovich V. Using Symmetries (Beyond Geometric Symmetries) in Chemical Computations: Computing Parameters of Multiple Binding Sites. Symmetry. 2014; 6(1):90-102. https://doi.org/10.3390/sym6010090
Chicago/Turabian StyleOrtiz, Andres, and Vladik Kreinovich. 2014. "Using Symmetries (Beyond Geometric Symmetries) in Chemical Computations: Computing Parameters of Multiple Binding Sites" Symmetry 6, no. 1: 90-102. https://doi.org/10.3390/sym6010090



