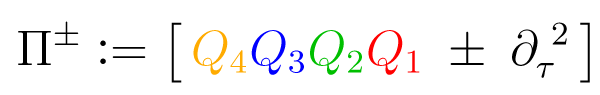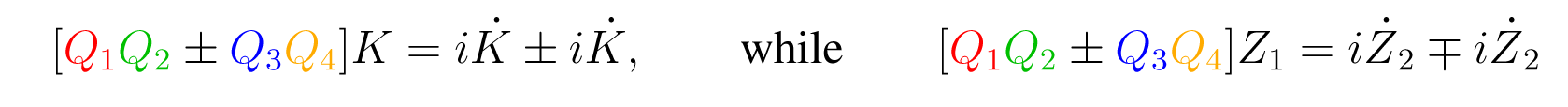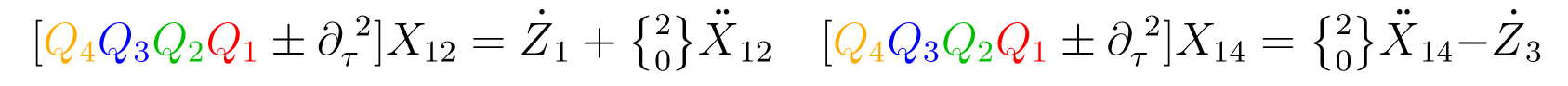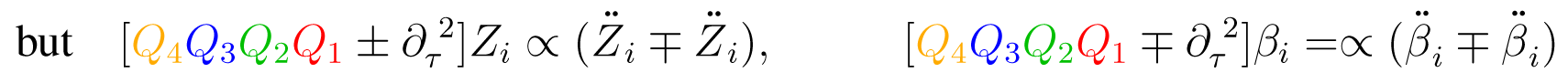On General Off-Shell Representations of World Line (1D) Supersymmetry
Abstract
: Every finite-dimensional unitary representation of the N-extended world line supersymmetry without central charges may be obtained by a sequence of differential transformations from a direct sum of minimal Adinkras, simple supermultiplets that are identifiable with representations of the Clifford algebra. The data specifying this procedure is a sequence of subspaces of the direct sum of Adinkras, which then opens an avenue for the classification of the continuum of the so-constructed off-shell supermultiplets.1. Introduction
The study of off-shell supermultiplets in one dimension, i.e., finite-dimensional unitary off-shell representations of N-extended world line supersymmetry, as originally started in [1–6], has been reinvigorated in the past decade or so [7–31]. In particular, an unprecedented abundance of new supermultiplets has been discovered [22,25], largely due to a graphical description of such supermultiplets using so-called Adinkras [9,12]. Yet, in addition to all of these new recently supermultiplets, several off-shell supermultiplets have been analyzed [27–29], which cannot be depicted by Adinkras, but represent various generalizations thereof; in fact, there are infinitely many such, more general supermultiplets [27].
Herein, we prove that all off-shell world line supermultiplets subject to physics-standard conditions can be analyzed in terms of Adinkras, as well as synthesized from them in a finite number of operations called lowering; see Theorem 3.1 in Section 3.
We then illustrate this procedure on two examples from the recent literature: (1) the N = 3 gauged world line off-shell supermultiplet of [27,31], and (2) the world line (1D) shadow [28] of the 4D
2. Supermultiplets
We consider linear off-shell representations of the N-extended supersymmetry algebra in one dimension without central charge:
Any particular choice of component fields (ϕa|ψα) used to represent a supermultiplet should be considered a basis of the supermultiplet and is subject to redefinitions. Local linear changes of variables Φa = Φa(ϕ, ∂τϕ,⋯) and Ψα = Ψα(ψ, ∂τψ,⋯) produce equivalent representations of the same supermultiplet. Since the operators, QI, are themselves fermionic, their application on any one component field must produce a linear combination of the fields of the opposite statistics and their τ-derivatives. It follows that a supermultiplet, , is a closed Q-orbit, in that the result of the application of any sequence of QI-operators on any component field of must result in a linear combination of the component fields in and their τ-derivatives.
We next define a few additional useful properties of off-shell supermultiplets, assuming only supersymmetry algebra Equation (1). In particular, we make no assumption about any Lagrangian or intended dynamics for the supermultiplets.
2.1. Engineerable Supermultiplets
As done in Equation (1), we adopt the “natural” system of units, fixing c and ħ as two basic units, which we then never write explicitly [33,34]. The physical units of each quantity then reduce to a power of a single unit, which we choose to be mass. For a quantity, X, with units (mass)[x], the exponent, [X], is called the engineering dimension of the quantity, X. For an operator,




In particular, since time has engineering dimension [τ] = − 1, [∂τ] = 1. If the QI in Equation (1) are to have unambiguous engineering dimensions [35], the supersymmetry algebra Equation (1) implies that for all I = 1, ⋯, N. In the Q-transformation rules, the action of each QI is specified on each component field. If [F] = f for a component field F, , and QI(F) is a linear combination of component fields of engineering dimension , as well as τ-derivatives of component fields of engineering dimension . Formalizing this, we have:
Definition 2.1
A supermultiplet is engineerable if it is possible to consistently assign engineering dimensions to all the component fields, such that for every component field, F, with [F] = f.
All supermultiplets commonly used in the literature are engineerable. Nevertheless, this is a logical assumption that deserves to be spelled out, since it will be used in the mathematical proof of our main theorem. In turn, non-engineerable supermultiplets are logically possible if there is a fixed mass parameter. For instance, in Planck units (including Newton's gravitational constant, GN, as an unwritten unit), non-engineerable supermultiplets are possible, since the action of QI on certain component fields may involve (unwritten) powers of the Planck mass. As an aside, a non-engineerable “Escheric” supermultiplet was discussed in [9].
Proposition 2.1
If an engineerable supermultiplet, contains a boson, ϕ, and a fermion, ψ, for which, must decompose as a direct sum of at least two supermultiplets, ⊇ 1 ⊕ 2, such that ϕ ∈ 1 and ψ ∈ 2.
Proof: Let [ϕ] =m be the engineering dimension of ϕ ∈ . Then, QI(ϕ) has engineering dimension and is a linear combination of some of the fermions and their τ-derivatives. Since [∂τ] = 1, each fermion occurring in QI(ϕ) has the engineering dimension . In turn, applying QJ on each of these fermions must produce a linear combination of bosons and their τ-derivatives, where each of these resulting bosons has the engineering dimension, m (mod ℤ). Iterating this argument eventually maps out a sub-supermultiplet, 1 ⊂ , wherein all bosons and fermions have the engineering dimensions, m (mod ℤ) and , respectively. By construction, throughout 1.
Since , ψ ∉ 1 and ψ must belong to a separate sub-supermultiplet of . Repeating the above construction starting with ψ maps out this other 2 ⊂ .
In most physics applications, the relation [36] is enforced by dynamical considerations even for (component) fields that are completely unrelated, by supersymmetry or otherwise. However, no bosonic-fermionic pair of fields satisfying can belong to an indecomposable supermultiplet.
Nomenclature: A representation (and so, also, a supermultiplet) is said to be indecomposable if it cannot be decomposed into a direct sum of two or more sub-representations. A representation is called irreducible if it contains no proper sub-representation. The latter condition is stronger, in that indecomposable representations need not be irreducible, whereas all irreducible representations are necessarily indecomposable.
For example, the well-known real vector superfield
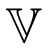
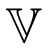
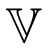
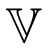
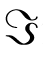
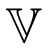
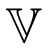
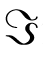
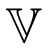
2.2. Adinkraic Supermultiplets
All off-shell world line supermultiplets discussed in [9] and then formalized rigorously in [12,13] admit a basis of component fields, such that the application of any one supercharge, QI, on any one component field always produces precisely one other of the component fields or its τ-derivative. Such supermultiplets were called adinkraic and can be depicted by Adinkras, specific graphs that faithfully encode the precise supersymmetry transformations within each such supermultiplet. By extension, a supermultiplet for which an adinkraic basis of component fields can be obtained by means of local component field redefinitions is called adinkrizable.
As [12] proves, in adinkraic supermultiplets, it is always possible to rescale the (real) component fields, so that (with no summations):
There of course exist non-adinkraic off-shell supermultiplets, which do not admit a basis of component fields, wherein simple pattern Equation (2) holds. Nevertheless, recent study shows that all off-shell supermultiplets from the familiar literature on simple supersymmetry in four-dimensional spacetime [23,26,28,30] are either themselves adinkraic or can be described in terms of Adinkras. This is also true of at least several off-shell supermultiplets of
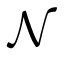
In all these examples of non-Adinkraic off-shell supermultiplets, the application of the supercharges, QI, on individual component fields does not always result in monomials Equation (2), but requires a binomial or larger linear combination of component fields and their τ-derivatives. Furthermore, all these non-adinkraic supermultiplets may be related to adinkraic ones by means of non-local field redefinitions. Our subsequent results will not only prove that this is in fact true of all off-shell world line supermultiplets, but will also provide a constructive algorithm to this end.
2.3. Valise Supermultiplets
If the component fields in an engineerable supermultiplet have only two distinct engineering dimensions , one for bosons and another for fermions, we call this a valise supermultiplet. In [20], Adinkras with this property were called isoscalar and isospinor, for when bosons or fermions have a lower engineering dimension, respectively; the boson/fermion-indiscriminate moniker “valise” was adopted in [21], so this is a generalization of that terminology This was also called the “Clifford algebraic supermultiplet” in [6] and plays a prominent role in the “root superfield” formalism [6,9,10], which is then also generalized by the subsequent results.
We are now in position to state and prove the following important result.
Theorem 2.1 (valises)
Every valise supermultiplet is adinkraic and decomposes as a direct sum of minimal valise supermultiplets, each identifiable with a minimal valise Adinkra.
Proof: Without loss of generality, suppose the bosonic component fields in the valise supermultiplet have the lower engineering dimension. Then, if ϕ is any boson, QI(ϕ) is a linear combination of the fermions, while if ψ is any fermion, QI(ψ) = ∂t(ℓ), where ℓ is a linear combination of the bosons.
If we choose a basis φ1,…, φd for the bosons and χ1,…, χd for the fermions, these Q-transformation rules can be written as:
It is a standard result [40] that all real representations of Cl(0, N+1) decompose into a direct sum of irreducible representations: for N = 0 (mod 4), there exist two equal-sized, but distinct isomorphism classes of irreducible representations [41]; otherwise, there exists only one.
It was shown in [21,25] that the irreducible representation(s) of Cl(0, N+1) are adinkrizable. That is, each of them corresponds 1−1 to a valise supermultiplet akin to Equation (3), but where the linear combinations in the result of applying the QI-operators to reduce to monomials [42]. This valise supermultiplet then may be depicted by an Adinkra, by assigning a node to each component field and an I-colored edge for every instance of a relation QI(φa) = ±iχα, drawing the edge solid for the positive sign and dashed for the negative sign. Furthermore, these irreducible representations of Cl(0, N+1) are clearly minimal and so must correspond to minimal valise Adinkras and supermultiplets for any given N.
Now, we return to our real representation, M. It is a standard result [25] that, as a representation of Cl(0, N+1), M decomposes into a direct sum of irreducible representations. For each direct summand, choose the basis given so that its corresponding valise supermultiplet is described using an Adinkra, as per [20,25]. The result is a basis for M in which valise supermultiplet Equation (3) is adinkraic and, in fact, decomposes as the corresponding direct sum of minimal Adinkras (for the given N).
Without loss of generality, we identify an Adinkra with the supermultiplet it depicts.
It also follows that there exist two distinct isomorphism classes of minimal valise supermultiplets for N = 0 (mod 4), one being referred to as the twisted version of the other [43,44]. In turn, there is only one isomorphism class for N ≠ 0 (mod 4). References [20,25] prove that:
where:
2.4. Raising and Lowering
References [2,3] and then [6,9,10] started exploring the systematic use of an operation variously called “automorphic duality”, “1D duality” and “auxiliary/physical duality”, of which a refinement (to individual component fields) was named “node raising and lowering”, owing to its manifest depiction in terms of Adinkras [12]. These operations easily generalize to all engineerable supermultiplets:
Definition 2.2 (raising/lowering)
Let be an engineerable off-shell supermultiplet and ℓ = ∑A cAFA a real linear combination of component fields of , all with the same engineering dimension.
If QI (ℓ) involves no derivative of any component field of for any I, replacing any one of FA ∈ with L = ℓ̇ and assigning QI(L) = ∂t(QI(ℓ)) produces a new engineerable off-shell supermultiplet, . This is called “raising ℓ”, and [L] = [ℓ ]+1.
If QI(ℓ) = ∂τ(fI) is a total τ-derivative for each I, replacing any one of FA ∈ with L = ∫dτ ℓ and assigning QI(ℓ) = fI produces a new engineerable off-shell supermultiplet, . This is called “lowering ℓ”, and [L] = [ ℓ ] − 1.
Note: For the subsequent theorem, we will only need the special case of the raising operation when ℓ is in fact a single component field. There is no reason, however, not to provide the general definition.
If can be depicted by an Adinkra and ℓ is a single component field (represented by a node), the operations of raising/lowering ℓ then reduce to “node raising/lowering” [12], i.e., “auxiliary/physical duality” of [6]. When performed simultaneously on each one of the component fields equal to QI1 ⋯QIk(ϕ) for a fixed ϕ and k, and replacing each of these component fields separately with another one of one unit higher or lower engineering dimension, these operations reproduce the “automorphic duality” of [2,3,6,9]. A matrix realization of the node-raising operation was also introduced in [4] and was subsequently called the “dressing transformation” [11].
In the general cases covered by the above definitions, the linear combinations of fields being raised or lowered can extend over any subset of component fields of the same engineering dimension in the original off-shell supermultiplet, . The coefficients in the linear combination are here assumed to be real [45], but are otherwise arbitrary and can be varied continuously.
3. The Main Theorem
The foregoing discussion was framed to state:
Theorem 3.1 (adinkraic analysis/synthesis)
Every engineerable off-shell world line supermultiplet, , with finitely many component fields is equivalent by local field redefinitions to a supermultiplet obtained from a direct sum of minimal valise Adinkras, by iteratively lowering linear combinations of nodes.
Proof: Proposition 2.1 decomposes into parts in each of which ; we work with each of these parts, in turn. For simplicity, each such part on which we focus iteratively will continue to be denoted by .
Consider the 2D component fields, , and their engineering dimensions. Let m be the minimum and M the maximum of these engineering dimensions in . If , is already a valise supermultiplet ( = υ), skip to Part 2; if , proceed.
Part 1: Choose any one component field, f1, with engineering dimension m, and raise it. This results in a new engineerable supermultiplet, . The new raised field now has engineering dimension m + 1, and if M − m ≥ 1, then will still have maximum engineering dimension M. Repeating this process reduces the number of component fields with engineering dimension m, until there are none. Then, we have a new supermultiplet with the minimum engineering dimension . Keep repeating this process, until the minimum engineering dimension increases to .
This transforms the original supermultiplet, , into an associated valise supermultiplet, υ, with a finite sequence of component fields (ϕ1, ⋯ ϕd|ψ1, ⋯ ψd), where and [ψα] = M, or the other way around.
Part 2: By Theorem 2.1, the valise supermultiplet, υ, admits a basis (φ1, ⋯ φd|χ1,⋯, χd), where each of the component fields (φa|χα) is a linear combination of the component fields (ϕa|ψα), which decomposes as a direct sum of minimal valise supermultiplets. Each minimal valise supermultiplet, , may be identified with a minimal valise Adinkra and each of the basis elements (φa|χα) with a node.
Part 3: Inverting the linear combinations from Part 2, the fields, ϕa, ψα ∈ υ, can now be written as linear combinations of the nodes, . Reversing the procedure of Part 1, we iteratively lower ϕ1 (as a linear combination of the nodes φa), then ϕ2, and so on, until each of these the nodes is lowered to its original engineering dimension.
The result is the original supermultiplet, , reconstructed as a systematically iterated lowering of the direct sum of minimal valise Adinkras, .
Note: It may well happen that the supermultiplet can decompose into a direct sum of minimal supermultiplets before Part 1 of the procedure in the proof is completed; see Section 4.1.
This general result, true for all N-extended supersymmetry algebras without central extension (1), covers the N = 4 partial results obtained to date for a handful of supermultiplets obtained by dimensional reduction from simple supersymmetry in four-dimensional spacetime; see Table 1 of [26] and Tables 10–12 of [30].
4. Non-Adinkraic Supermultiplets
While the most familiar and oft-used supermultiplets of simple supersymmetry in four-dimensional spacetime turn out to be adinkraic and are easily depicted using Adinkras [23,26], there do exist examples where this is not true. We now turn to such non-adinkraic examples, to demonstrate the effectiveness of Theorem 3.1. The Adinkras or Adinkra-like graphs depicting the supersymmetry transformations will illustrate the procedure.
4.1. A Gauge-Quotient Example
Reference [27] constructs an off-shell gauge-quotient supermultiplet of N = 3 world line supersymmetry,



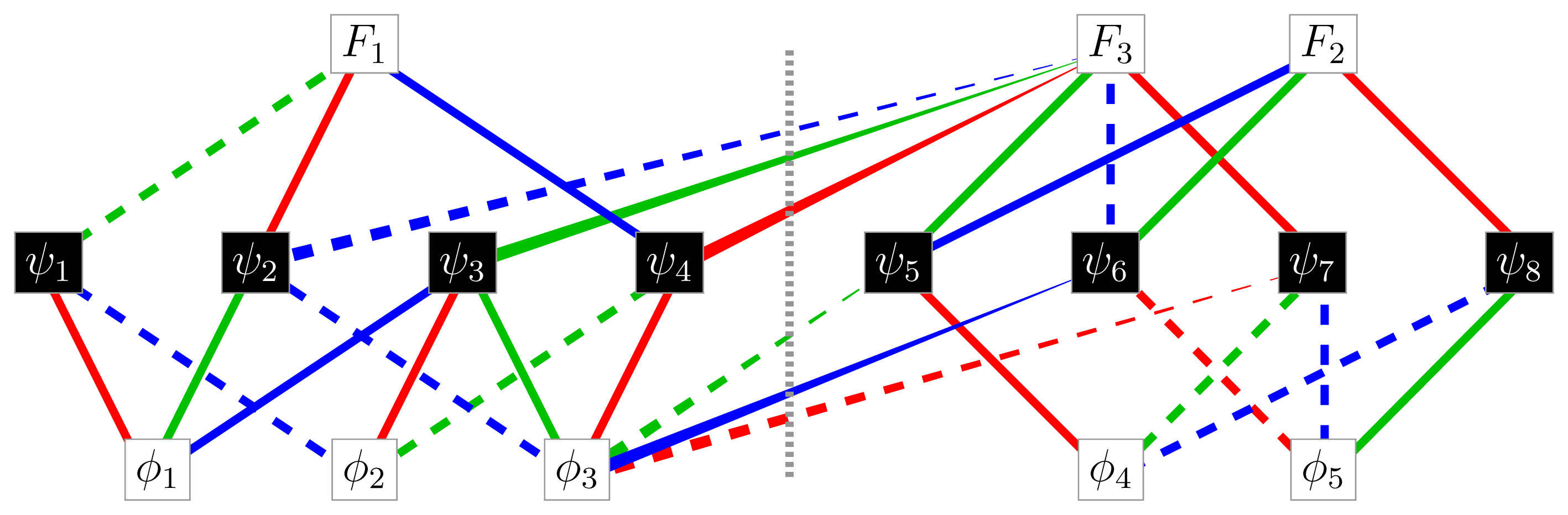
Nevertheless, the transformation rules (8) can be represented graphically, but doing so requires that several edges (depicted by tapering lines) to indicate a “one way” QI-transformation; see Figure 1.
These correspond to the entries in the table (8) that are set in a lighter ink. For example, Q1(ϕ3) includes both ψ4 and ψ7, but only the transformation of Q1 (ψ4) contains ϕ̇3; the transformation, Q1 (ψ7), does not. The two-way Q1-transformation ϕ3 ⇔ ψ4 is then depicted by a standard edge [46], while the one-way Q1-transformation ϕ3 → −ψ7 is depicted by a tapering edge, which is also dashed, indicating the negative sign.
Following the constructive proof of Theorem 3.1, in this supermultiplet, we: (1) raise the node corresponding to ϕ3 ↦ ϕ̇3 (this loses the constant term in ϕ3), and (2) perform the linear combination change of variables ϕ̇3 ↦ Z := ϕ̇3+F3, the net effect of which is the field substitution.

Note that the single component field redefinition (9) procedure transformed:
the (5|8|3)-component supermultiplet (8) into a (4|8|4)-component one (10),
which decomposes even before completing the procedure in the proof of Theorem 3.1.
By Equation (6), the minimal representation of the N = 3-extended world line supersymmetry has four bosons and four fermions, and the two Adinkras in Figure 2 are indeed minimal.
Reversing this transformation, we can start with the adinkraic supermultiplet (10) and lower the linear combination:
The reader might wonder whether perhaps the non-local transformation (11) in fact somehow establishes an effective equivalence of Equations (8) and (10). To show that this is not so, [31] constructs a 13-parameter family of Lagrangians (even while restricting to just bilinear terms!), where for generic choices [47] of the 13 parameters, the following holds:
The generic (even if just bilinear) Lagrangians [31] for the supermultiplet (8) depend on the component field, ϕ3, in ways that the transformation (11) cannot be used to eliminate ϕ3 → Z without rendering the generic Lagrangian non-local.
These ultimately dynamical considerations prove that the supermultiplet (8) must be considered physically inequivalent from Equation (10). In turn, Theorem 3.1 provides a direct, but non-local relationship suitable for classification purposes; see below.
4.2. The Complex Linear Supermultiplet
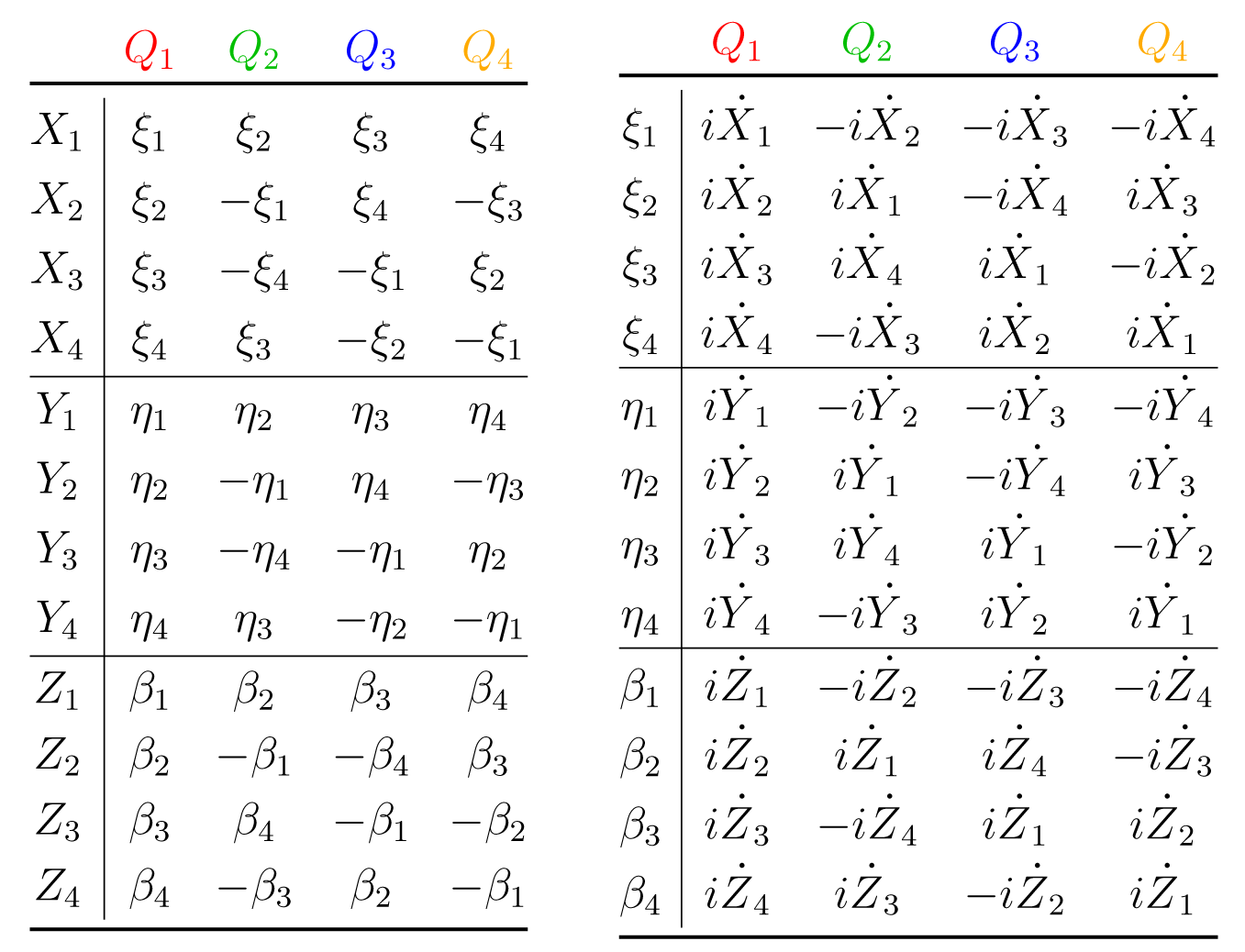
Reference [28] analyzes a well-documented representation of simple supersymmetry in four-dimensional spacetime, the complex linear supermultiplet [32], dimensionally reduced to the n = 4-extended supersymmetry of the one-dimensional world line. This supermultiplet is defined by way of the complex superfield satisfying the quadratic superdifferential constraint, D̄α̇ D̄α̇Σ = 0, and [28] then traces through the ensuing conditions and identifications imposed on the real and imaginary parts of the complex component fields, settling finally on a basis that maximally simplifies the result. Table 1 presents the supersymmetry transformations in a slightly adapted version of this optimal basis, which is also faithfully depicted by the graph in Figure 3.
Notably, a quarter of the QI-transformations of individual component fields are binomials rather than monomials, and each of these binomials is depicted by two edges, one standard, the other (depicting a “one-way” action) tapered. Already, the number (twenty-four) of binomials in Table 1 should indicate that the procedure of the proof of Theorem 3.1 will be considerably more involved than in the previous example. However, the statement of Theorem 3.1 also indicates a powerful tool in deciphering the optimal strategy and, even, the eventual outcome.
Namely, Theorem 3.1 provides that, upon an adequate number of component field raising operations, the supermultiplet decomposes into a direct sum of minimal valise Adinkras. In turn, [20,25] proved that in these minimal Adinkras, certain precisely specified higher order QI-operators act as quasi-projection operators. For the case at hand, in N = 4 supersymmetry, these quasi-projection operators are:

Now, the basis used for Table 1 is definitely not the one in which the decomposition is made manifest, even after we raise the component fields: K, L into K̇, L̇, and then, ζi, ρi into ζ̇i, ρ̇i. However, Operators (12) and (13) simplify the task of finding this basis as follows.
Apply the quadratic Operator (13) on any component field. For example:
For these to vanish, we must chose the lower sign for K, but the upper sign for Z1, indicating that these two component fields will (upon some field redefinitions, perhaps) belong to distinct minimal Adinkras.Apply the quartic operators (12) to any component field. For instance [48],
The fact that the quasi-projections (15d) on (Zi|βi) act as ∂τ-multiples of the identity for the lower choice of the sign indicate that these fields already form a separate (4|4)-component minimal valise Adinkra. This is visible from the graph in Figure 3, upon noticing that no edges emanate from this (top-most) portion, as was already noted in [28].
Next, given now that (Zi|βi) form a separate sub-supermultiplet, the relations, such as Equation (15a)–(15c), indicate that: (1) the right-hand side field combinations should be used in component field redefinitions, and (2) we must use the upper sign-choices, not to duplicate the fields (Zi|βi).
Following the procedure in the proof of Theorem 3.1, we first notice that the bosonic component fields, K, L, satisfy the conditions for the “raising” part of Definition 2.2, and we raise them. In the resulting supermultiplet, now, the fermionic components, ζ1, ⋯, ζ4, ρ1,⋯ρ4, all satisfy the conditions of the “raising” part of Definition 2.2, and we raise them, too. This results in a valise supermultiplet with 12 bosons, all with the same engineering dimension, and 12 fermions, all with the engineering dimension higher than the bosons. According to Theorem 2.1, this decomposes into a direct sum of minimal valise Adinkras. We exhibit this decomposition by employing the component field redefinitions given by the computations of the type of (15):
where we have underlined the component fields that are being eliminated by each definition. The QI-transformations in this (16)-transform of the complex linear supermultiplet decouple and may be depicted by the three minimal N = 4 Adinkras given in Figure 4. The middle one is “twisted” as compared to the flanking ones: in it, all edges of the fourth color have their solidness/dashed-ness flipped, which corresponds to swapping Q4 → −Q4. Correspondingly, the middle Adinkra in Figure 4 is annihilated by Operators (12) and (13), with one choice of the relative sign, while the flanking Adinkras are annihilated by these operators with the opposite choice of the relative sign. This agrees with the computations of [26].Finally, the original, world line “shadow” of the complex linear supermultiplet (Table 1 and Figure 3) is then reconstructed by applying the (non-local) inverse of the component field redefinitions (16) on the direct sum Adinkra (17), depicted in Figure 4. Note that the component field redefinitions (16) lose the constant terms in the original component fields K,L,ζi,ρi and that the inverse of (16) then re-supplies these constant terms by way of integration constants. For example,
and so on.5. A Continuum of Supermultiplets and Their Classification
The fact that the procedure of the proof of Theorem 2.1 employs linear combinations of component fields where the coefficients are not restricted to be integers is rather suggestive. Indeed, we now demonstrate how a continuum of N = 5 supermultiplets may be obtained from a certain N = 5 Adinkra, by lowering a non-trivial linear combination of nodes.
We begin with the N = 5 Adinkraic supermultiplet with the following field content:
where the indices are SO(5) indices from the supersymmetry, BIJ = −BJI and χIJ = −χJI. The supersymmetry transformations within this supermultiplet are given as follows:where bracketed indices are antisymmetrized with weight . As written here, it may not be immediately obvious that the result of the application of any one supercharge on any one component field in fact is a monomial. We thus include a sampling of these supersymmetry transformation rules below to illustrate this fact, i.e., that this supermultiplet is Adinkraic:The interested reader may complete the table using the above formulae for the transformation rules. Instead of drawing the Adinkra in full detail [12], it is more illustrative this time to see a somewhat more collapsed diagram:
where we have partially collapsed nodes as in [9] for convenience, but not all the way, to exhibit the different types of component fields more clearly. Note that this can be obtained from the unconstrained real N = 5 superfield by lowering the top fermion, ω, and then lowering all components of the five-vector, VI.We can now lower a linear combination of the xIJ and ω by defining for example:
and replace ω with λ. That is, we consider the (1|6|15|9)-dimensional supermultiplet with the component field content:wherein the supersymmetry transformation rules are as in Equation (20), except that:All appearances of ω; in Equation (20), which occur only in QI(VJ) for I = J, are now replaced by:
The row for QI(ω) in Equation (20) is now replaced by a row for QI(λ), which results in:
Thus, some of the supersymmetry transformation rules now involve linear combinations of fields. We may think of the sin θ-terms in Equations (23) and (26) as generating a deformation of the adinkraic supermultiplet (21), being “tuned” by the continuous angle, θ.To prove that there exists no local change of basis that can remove the occurrence of linear combinations from the results of applying the QI on the component fields, we proceed, by contradiction, assuming that there exists a basis in which the supermultiplet, θ, is adinkraic and systematically search for such a basis.
Start with A, and note that there is no other component field or τ-derivative thereof with the engineering dimension [A], simply because A has the lowest engineering dimension within the supermultiplet θ. The only possible field redefinition of A is then a real re-scaling, A ↦ cAA, with some non-zero cA ∈ ℝ Within an Adinkraic basis for θ, it would have to be that QI(A) are all basis elements, as well, so that the ψI are all (up to a multiplicative constant) also basis elements. Proceeding in this way, the BIJ, χIJ and VI are likewise all basis elements, each one up to a multiplicative constant. However, now, the QI(VJ) involve a linear combination of λ̇ and χ12:
failing the defining property of adinkraic supermultiplets unless θ is an integral multiple of . To solve this, we would have to implement the inverse of the component field redefinition (25),which is non-local and, so, not allowed in general.We thus conclude that the supermultiplet, θ, is truly non-adinkrizable when θ is not an integeral multiple of π.
Furthermore, this argument also shows that these supermultiplets are also inequivalent for different values of θ. This provides an example of a continuum of distinct supermultiplets.
In principle, there may well exist usable Lagrangians for the supermultiplet, θ, wherein the component field, λ, only occurs with a τ-derivative acting on it, so that the non-locality of the transformation (28) does not show up in the dynamics of these models. However, recent explicit computations for similar supermultiplets show that this is not the case in most general (still unitary) Lagrangians [49] and that observable couplings to external (probing) fields exist that would detect such non-locality [31]; the variety of employed value(s) of θ is thus observable.
Reconsider now the examples of (20)–(22). Instead of (23), we could lower any other, more general linear combination:
Each particular of these continuously many choices would result in a distinct supermultiplet, thus defining an 11-parameter continuous family of (1|6|15|9)-dimensional supermultiplets generalizing (24). Modulo the overall scaling, these parameters form the projective space, ℝℙ10.Certain of these resulting supermultiplets may be shown to be equivalent to each other by local component field redefinitions alone. Further equivalence relations may be provided by allowing the supersymmetry charges, QI, to rotate using their SO(5) R-symmetry. Tempting as this latter option may be, note that one can easily construct models employing two or more distinct so-constructed supermultiplets, each with a different linear combination of χIJ and ω. Using R-symmetries, then, cannot, in general, reduce the number of effective linear combination coefficients in all of the so-constructed supermultiplets to the same smaller number of effective coefficients in each supermultiplet simultaneously. Nor can one hope to be able to transform two distinct so-constructed supermultiplets simultaneously into any one particular version, even by using R-symmetries together with local component field redefinitions.
Ultimately, the determination of whether or not R-symmetries provide admissible equivalence relations is then a fundamentally dynamical question, depending on the choice of a Lagrangian to govern the dynamics. Similarly, as discussed in Section 4.1, whether or not even some non-local field redefinitions provide admissible equivalence relations depends on limitations (such as gauge symmetries) that one may impose on the choice of the Lagrangian.
In principle, the parameters in Equation (29) provide a “rough parameter space”, wherein one is yet to identify the various points that correspond to equivalent supermultiplets. The transformations relating such points are expected to form a group usually called the “mapping class group”. The above considerations, however, indicate that a proper definition of such a mapping class group, which would reduce a rough parameter space of such linear combinations into a proper moduli space, is rather a delicate problem and well beyond the scope of this article. Suffice it to say that finding this “moduli space” of supermultiplets would be to consider the projective space of lines in the space spanned by χIJ and ω, and then, quotienting by the action of SO(5) should R-symmetries be physically/dynamically permissible.
Of course, it is also possible to lower several linearly independent combinations of the form of (29), rather than just one. Furthermore and depending on the result at this stage as pertaining to Definition 2.2b, one may next entertain the lowering of one or more nontrivial linear combinations:
and so on.Quite generally, then, to classify off-shell world line supermultiplets, one could start with direct sums of Adinkras, then progressively lower linear combinations of nodes in all possible ways and any number of times, subject to the conditions of Definition 2.2b. This leads to considering projective spaces if we lower a single linear combination, or Grassmannian manifolds if we lower many. If we continue to lower linear combinations of component fields in this manner, there may emerge complicated interrelations between these lowered subspaces, resulting in certain specific types of flag-varieties.
While the general classification of these constructions remains difficult, it is a straightforward project to generate all possible lowering from any one particular direct sum of Adinkras.
6. Conclusions
This paper illustrates a method for writing any off-shell engineerable supermultiplet in one dimension as a finite number of lowering from an Adinkra. We have illustrated this method with two examples from recent literature, as well as an example specially constructed for this purpose.
Off-shell supermultiplets of N = 1 and N = 2 supersymmetry are, in fact, adinkrizable without the need for lowering. This can be proven using the following method: since we know that such supermultiplets can be obtained by lowering an Adinkra, examine Adinkras where a lowering of a linear combination of nodes is possible, then show that there exists a change of basis that results in the linear combination being a single node.
The situation with N = 3 supermultiplets is somewhat special in a different way: most of the N = 3 supermultiplets, in fact, admit a fourth supersymmetry and, sometimes, even in several distinct ways [31]. In fact, this is always possible, except for the situation where an irreducible N = 3 supermultiplet takes up four different engineering dimensions, in which case, this is the real unconstrained superfield with N = 3, and such a supermultiplet is not only adinkrizable, but, in fact, is equal to the “top Adinkra” in the language of [9].
With N = 4 and higher, however, lowering linear combinations may be necessary. This leads to an approach to classifying off-shell engineerable supermultiplets: start with a direct sum of minimal Adinkras; then, map out all the ways of lowering linear combinations of nodes. Equivalently, we can say that we are iteratively lowering linear subspaces spanned by these linear combinations. A classification of off-shell supermultiplets then must include a classification of possible choices of subspaces that can be iteratively lowered; we defer the exploration of this avenue to a subsequent effort.
Acknowledgments
We should like to thank M. Faux and S.J. Gates, Jr. for extended discussions on issues of supersymmetry, during which, many of the concepts used in this paper were developed. C.D. acknowledges the support from the Natural Sciences and Engineering Resource Council of Canada, the Pacific Institute for the Mathematical Sciences and the McCalla Professorship at the University of Alberta. T.H. thanks the Department of Physics, University of Central Florida, Orlando, FL, and the Physics Department of the Faculty of Natural Sciences of the University of Novi Sad, Serbia, for the recurring hospitality and resources. G.L. acknowledges the support by a grant from the Simons Foundation (Award Number 245784).
Conflicts of Interest
The authors declare no conflict of interest.
References and Notes
- Gates, S.J., Jr.; Rana, L. Ultramultiplets: A new representation of rigid 2-d, N = 8 supersymmetry. Phys. Lett. B 1995, 342, 132–137. [Google Scholar]
- Gates, S.J., Jr.; Rana, L. A theory of spinning particles for large N-extended supersymmetry. Phys Lett. B 1995, 352, 50–58. [Google Scholar]
- Gates, S.J., Jr.; Rana, L. A theory of spinning particles for large N-extended supersymmetry. II. Phys. Lett. B 1996, 369, 262–268. [Google Scholar]
- Pashnev, A.; Toppan, F. On the classification of N-extended supersymmetric quantum mechanical systems. J. Math. Phys. 2001, 42, 5257–5271. [Google Scholar]
- Gates, S.J., Jr.; Linch, W.D., III; Phillips, J.; Rana, L. The fundamental supersymmetry challenge remains. Gravit. Cosmol 2002, 8, 96–100. [Google Scholar]
- Gates, S.J., Jr.; Linch, W.D., III; Phillips, J. When superspace is not enough. Available online: http://arxiv.org/abs/hep-th/0211034 (accessed on 24 January 2014).
- Bellucci, S.; Ivanov, E.; Krivonos, S.; Lechtenfeld, O. N = 8 superconformal mechanics. Nucl. Phys. B 2004, 684, 321–350. [Google Scholar]
- Bellucci, S.; Ivanov, E.; Krivonos, S.; Lechtenfeld, O. ABC of N = 8, d = 1 supermultiplets. Nucl. Phys. B 2004, 699, 226–252. [Google Scholar]
- Faux, M.; Gates, S.J., Jr. Adinkras: A graphical technology for supersymmetric representation theory. Phys. Rev. D 2005, 71, 065002:1–065002:21. [Google Scholar]
- Bellucci, S.; Krivonos, S.; Marrani, A.; Orazi, E. “Root” action for N = 4 supersymmetric mechanics theories. Phys. Rev. D 2006, 73, 025011:1–025011:9. [Google Scholar]
- Kuznetsova, Z.; Rojas, M.; Toppan, F. Classification of irreps and invariants of the N-extended supersymmetric quantum mechanics. JHEP 2006. [CrossRef]
- Doran, C.F.; Faux, M.G.; Gates, S.J., Jr.; Hübsch, T.; Iga, K.M.; Landweber, G.D. On graph-theoretic identifications of Adinkras, supersymmetry representations and superfields. Int. J. Mod. Phys. A 2007, 22, 869–930. [Google Scholar]
- Doran, C.F.; Faux, M.G.; Gates, S.J., Jr.; Hübsch, T.; Iga, K.M.; Landweber, G.D. Off-shell supersymmetry and filtered Clifford supermodules. Available online: http://arxiv.org/abs/math-ph/0603012 (accessed on 24 January 2014).
- Delduc, F.; Ivanov, E. Gauging N = 4 Supersymmetric Mechanics. Nucl. Phys. B 2006, 753, 211–241. [Google Scholar]
- Delduc, F.; Ivanov, E. Gauging N = 4 supersymmetric mechanics II: (1,4,3) models from the (4,4,0) ones. Nucl. Phys. B 2007, 770, 179–205. [Google Scholar]
- Kuznetsova, Z.; Toppan, F. Refining the classification of the irreps of the 1D N-extended supersymmetry. Mod. Phys. Lett. A 2008, 23, 37–51. [Google Scholar]
- Ivanov, E.; Lechtenfeld, O.; Sutulin, A. Hierarchy of N = 8 mechanics models. Nucl. Phys. B 2008, 790, 493–523. [Google Scholar]
- Delduc, F.; Ivanov, E. The Common origin of linear and nonlinear chiral multiplets in N = 4 mechanics. Nucl. Phys. B 2007, 787, 176–197. [Google Scholar]
- Delduc, F.; Ivanov, E. New Model of N = 8 Superconformal Mechanics. Phys. Lett. B 2007, 654, 200–205. [Google Scholar]
- Doran, C.F.; Faux, M.G.; Gates, S.J., Jr.; Hübsch, T.; Iga, K.M.; Landweber, G.D.; Miller, R.L. Topology types of Adinkras and the corresponding representations of N-extended supersymmetry. Available online: http://arxiv.org/abs/0806.0050 (accessed on 24 January 2014).
- Doran, C.F.; Faux, M.G.; Gates, S.J., Jr.; Hübsch, T.; Iga, K.M.; Landweber, G.D.; Miller, R.L. Adinkras for clifford algebras, and world line supermultiplets. Avaiable online: http://arxiv.org/abs/0811.3410 (accessed on 24 January 2014).
- Doran, C.F.; Faux, M.G.; Gates, S.J., Jr.; Hübsch, T.; Iga, K.M.; Landweber, G.D. A superfield for every dash-chromotopology. Int. J. Mod. Phys. A 2009, 24, 5681–5695. [Google Scholar]
- Gates, S.J., Jr.; Gonzales, J.; MacGregor, B.; Parker, J.; Polo-Sherk, R.; Rodgers, V.G.J.; Wassink, L. 4D,
= 1 supersymmetry genomics (I). JHEP 2009. [Google Scholar] [CrossRef]
- Delduc, F.; Ivanov, E. N = 4 mechanics of general (4, 4, 0) multiplets. Nucl. Phys. B 2012, 855, 815–853. [Google Scholar]
- Doran, C.F.; Faux, M.G.; Gates, S.J., Jr.; Hübsch, T.; Iga, K.M.; Landweber, G.D.; Miller, R.L. Codes and supersymmetry in one dimension. Adv. Theor. Math. Phys 2011, 15, 1909–1970. [Google Scholar]
- Gates, S.J., Jr.; Hallett, J.; Parker, J.; Rodgers, V.G.J.; Stiffler, K. 4D,
= 1 supersymmetry genomics (II). JHEP 2012. doi:10.1007/JHEP06(2012)071. [Google Scholar]
- Hübsch, T.; Katona, G.A. On the construction and the structure of off-shell supermultiplet quotients. Int. J. Mod. Phys. A 2012, 29. doi:10.1142/S0217751X12501734. [Google Scholar]
- Gates, S.J., Jr.; Hallett, J.; Hübsch, T.; Stiffler, K. The real anatomy of complex linear superfields. Int. J. Mod. Phys. A 2012, 27. [Google Scholar] [CrossRef]
- Gonzales, M.; Iga, K.; Khodaee, S.; Toppan, F. Pure and entangled N= 4 linear supermultiplets and their one-dimensional sigma-models. J. Math. Phys. 2012, 53. [Google Scholar] [CrossRef]
- Chappell, I.; Gates, S.J., Jr.; Linch, W.D., III; Parker, J.; Randall, S.; Ridgeway, A.; Stiffler, K. 4D, N= 1 supergravity genomics. JHEP 2013. [Google Scholar] [CrossRef]
- Hübsch, T.; Katona, G.A. Golden ratio controlled chaos in supersymmetric dynamics. Int. J. Mod. Phys. A 2013, 28. [Google Scholar] [CrossRef]
- Gates, S.J., Jr.; Grisaru, M.T.; Roček, M.; Siegel, W. Superspace; Benjamin/Cummings Pub. Co.: Reading, MA, USA, 1983. [Google Scholar]
- Bjorken, J.D.; Drell, S.D. Relativistic Quantum Fields; McGraw-Hill Inc.: New York, NY, USA, 1964. [Google Scholar]
- Peskin, M.E.; Schroeder, D.V. An Introduction to Quantum Field Theory; Addison-Wesley Pub. Co.: Reading, MA, USA, 1995. [Google Scholar]
- Abstract Hermitian operators may be assigned the physical units of the physical observable to which they correspond. This rule does not apply to fermionic operators, as they cannot correspond to any physical observable.
- When not using the “ħ = 1 = c” units, this relationship is [fermion] − [boson] = [Q] + n[ħ∂τ], with n ∈ ℤ.
- Buchbinder, I.L.; Kuzenko, S.M. In Ideas and Methods of Supersymmetry and Supergravity; Studies in High Energy Physics Cosmology and Gravitation. IOP Publishing Ltd: Bristol, UK, 1998. [Google Scholar]
- Siegel, W. Fields, 3rd ed. Available online: http://arxiv.org/abs/hep-th/9912205 (accessed on 3 February 2014).
- Doran, C.F.; Faux, M.G.; Gates, S.J., Jr.; Hübsch, T.; Iga, K.M.; Landweber, G.D. On the matter of N = 2 matter. Phys. Lett. B 2008, 659, 441–446. [Google Scholar]
- Lawson, H.B., Jr.; Michelsohn, M.-L. Chapter I: Clifford Algebras, Spin Groups and their Representations, Section 5: Representations. In Spin Geometry; Princeton Mathematical Series; Princeton University Press: Princeton, NJ, USA, 1989; Volume 38, pp. 30–33. [Google Scholar]
- It is the existence of these two distinct isomorphism classes that makes supermultiplet twisting [43,44] nontrivial. As representations of Cl(0, N+1) also correspond to the somewhat more familiar spinor representations of Spin(N), the Reader may recognize this fact by recalling that for k,n ∈ (x02124;, Spin(n, 8k+n) have Majorana-Weyl minimal spinors, while Spin(n, 4k+n) for odd k have complex conjugate pairs of minimal spinors.
- The [LI]- and [RI]-matrices then have a single nonzero entry in every row and column, and are called monomial.
- Gates, S.J., Jr. Superspace formulation of new nonlinear sigma models. Nucl. Phys. B 1984, 238, 349–366. [Google Scholar]
- Gates, S.J., Jr.; Hull, C.M.; Roček, M. Twisted multiplets and new supersymmetric nonlinear sigma models. Nucl. Phys. B 1984, 248, 157–186. [Google Scholar]
- The definitions are straightforward to adapt to working over complex or hypercomplex supermultiplets.
- Edges drawn in the I th color signify QI-transformation: Solid for a positive sign and dashed for a negative sign.
- These choices do span a 13-dimensional open region where the Lagrangians define unitary models [31].
- The Operators (12) and (13) are defined to have the relative signs flipped if applied on fermions.
- Hübsch, T.; Katona, G.A. A Q-continuum of off-shell supermultiplets. Available online: http://arxiv.org/abs/1310.3256 (accessed on 24 January 2014).
Figure 1. A graphical depiction of the gauge-quotient supermultiplet of [27].Figure 1. A graphical depiction of the gauge-quotient supermultiplet of [27].Figure 2. A graphical depiction of the adinkrized supermultiplet of [27]. The two numbered arrows indicate the (1) raising ϕ3 and (2) combining ϕ̇3+F3 into Z; it is the latter, now local field redefinition that disconnects the two Adinkras.Figure 2. A graphical depiction of the adinkrized supermultiplet of [27]. The two numbered arrows indicate the (1) raising ϕ3 and (2) combining ϕ̇3+F3 into Z; it is the latter, now local field redefinition that disconnects the two Adinkras.Figure 3. A graph depicting the world line “shadow” of the complex linear supermultiplet, adapted from [28].Figure 3. A graph depicting the world line “shadow” of the complex linear supermultiplet, adapted from [28].Figure 4. The three separate minimal Adinkras into which the world line “shadow” of the complex linear supermultiplet may be transformed by means of iterative raising and linear combinations.Figure 4. The three separate minimal Adinkras into which the world line “shadow” of the complex linear supermultiplet may be transformed by means of iterative raising and linear combinations.Table 1. The supersymmetry transformation rules in the complex linear supermultiplet dimensionally reduced to the one-dimensional world line, adapted from [28].Table 1. The supersymmetry transformation rules in the complex linear supermultiplet dimensionally reduced to the one-dimensional world line, adapted from [28]. Q1 Q2 Q3 Q4 K ζ1 ζ2 ζ3 ζ4 L −ρ4 −ρ3 −ρ2 ρ1 X12 ζ̇2 −ζ̇1 ζ̇4−β3 −ζ̇3−β4 X14 ζ̇4 ζ̇3+β3 ζ̇2−β1 −ζ̇1 X24 −ζ̇3−β4 ζ̇4 ζ̇1−β2 −ζ̇2 Y12 ρ̇3 ρ̇4 ρ̇1−β2 ρ̇2+β1 Y14 ρ̇1 −ρ̇2−β1 −ρ̇3−β4 ρ̇4 Y24 ρ̇2+β1 ρ̇1 −ρ̇4+β3 ρ̇3 Z1 β1 β2 β3 β4 Z2 β2 −β1 −β4 β3 Z3 β3 β4 −β1 −β2 Z4 β4 −β3 β2 −β1 ζ1 iK̇ −iX12 i(X24+Z4) −iX14 ζ2 iX12 iK̇ −i(X14−Z3) −iX24 ζ3 −i(X24+Z4) i(X14−Z3) iK̇ −i(X12+Z1) ζ4 iX14 iX24 i(X12 +Z1) iK̇ ρ1 iY14 iY24 i(Y12+Z4) iL̇ ρ2 i(Y24−Z1) −i(Y14−Z2) −iL̇ i(Y12+Z4) ρ3 iY12 iL̇ −i(Y14−Z2) −iY24 ρ4 −iL̇ iY12 −i(Y24−Z1) iY14 β1 iŻ1 −iŻ2 −iŻ3 −iŻ4 β2 iŻ2 iŻ1 iŻ4 −iŻ3 β3 iŻ3 −iŻ4 iŻ1 iŻ2 β4 iŻ4 iŻ3 −iŻ2 iŻ1 © 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
MDPI and ACS StyleDoran, C.F.; Hübsch, T.; Iga, K.M.; Landweber, G.D. On General Off-Shell Representations of World Line (1D) Supersymmetry. Symmetry 2014, 6, 67-88. https://doi.org/10.3390/sym6010067
AMA Style
Doran CF, Hübsch T, Iga KM, Landweber GD. On General Off-Shell Representations of World Line (1D) Supersymmetry. Symmetry. 2014; 6(1):67-88. https://doi.org/10.3390/sym6010067
Chicago/Turabian Style
Doran, Charles F., Tristan Hübsch, Kevin M. Iga, and Gregory D. Landweber. 2014. "On General Off-Shell Representations of World Line (1D) Supersymmetry" Symmetry 6, no. 1: 67-88. https://doi.org/10.3390/sym6010067
APA Style
Doran, C. F., Hübsch, T., Iga, K. M., & Landweber, G. D. (2014). On General Off-Shell Representations of World Line (1D) Supersymmetry. Symmetry, 6(1), 67-88. https://doi.org/10.3390/sym6010067
Article Metrics